スポンサードリンク
こんにちは、ももやまです。
解析系の記事のまとめをしたいと思います。
今回から1変数ではなく、2変数を同時に扱う単元となります。
目次
スポンサードリンク
1.2変数関数とは
(1) 1変数の場合の復習
今までは、ある数 \( x \) に対して、実数 \( y \) の数がただ1つ定まるとき、\( y \) は \( x \) の関数であるといい、\[ y = 2x^3 + 5x + 6 \]\[ f(x) = 2x^3 + 5x + 6 \]のような形で表していましたね。
(2) 2変数の場合だと……?
2変数ということは、ある2つの数 \( x,y \) に対して実数の \( z \) がただ1つ定まるということですね。この \( z \) が1つに定まるとき、\( z \) は \( x,y \) の関数であるといいます。式にすると、\[ z = x^2 + y^2 \]\[ f(x,y) = x^2 + y^2 \] の形で表します。
スポンサードリンク
2.2変数関数の定義域
(1) 1変数の場合の復習
今までの定義域と値域は、\( y = f(x) \) のある数 \( x \) が取りうる値の範囲を定義域(つまり入力)、結果 \( y \) (つまり出力)が取りうる値の範囲を値域と呼んでいましたね。
1問復習してみましょうか。
例題1(復習)
\[ y = \sqrt{1-x^2} \]の定義域と値域を求めなさい。
解説1
ルートの中身は必ず0以上なので、定義域は \[ 1 - x^2 \geqq 0 \]\[ x^2 \leqq 1\]となる。
また、そのときの結果(出力) \( y \) はルートのは必ず0以上なので \( 0 \leqq y \) である。また、\( x^2 \) は負とならないのでルート内の最大値になるときは \( x^2 = 0 \) のときである。よって、\[ 0 \leqq y \leqq 1\] となる。
(2) 2変数の場合だと……?
2変数ということは、ある2つの数 \( x,y \) に対して実数の \( z \) がただ1つ定まるということですね。この \( z \) が1つに定まるとき、\( z \) は \( x,y \) の関数であるといいます。式にすると、\[ z = x^2 + y^2 \]\[ f(x,y) = x^2 + y^2 \] の形で表します。
ある2つの数(入力) \( x,y \) が取りうる値の範囲を定義域、出力 \( z \) が取りうる値の範囲を値域と呼びます。
こちらも練習してみましょう。
例題2
\[ z = \sqrt{9-x^2-y^2} \]の定義域と値域を求めなさい。
解説2
ルートの中身は必ず0以上なので、定義域は \[ 9 - x^2 - y^2 \geqq 0 \]\[ x^2 + y^2 \leqq 9\]となる。(定義域は2変数 \( x,y \) で表されるので注意)
また、そのときの結果(出力) \( z \) はルートのは必ず0以上なので \( 0 \leqq z \) である。また、\( x^2 + y^2 \) は負とならないのでルート内の最大値になるときは \( x^2 = 0, y^2 = 0 \) のときである。よって、\[ 0 \leqq z \leqq 3\] となる*1。
スポンサードリンク
3.2変数関数の曲面の概形
2変数関数を図示しようとすると立体になるため、1変数関数に比べてグラフの想像がしにくくなります。
例題や練習問題を解きながらどのような曲面があるかを見ていきましょう。
例題3
\[ z = \sqrt{9-x^2-y^2} \]の概形を(書くのはめんどいと思うので)想像しなさい。
解説3
\( z \geqq 0 \) なのはわかりますね。
このような問題の場合は、一旦 \( x,y \) のどちらかを0と仮定すると1変数になるため、想像がしやすくなります。
(1) \( y = 0 \) のとき
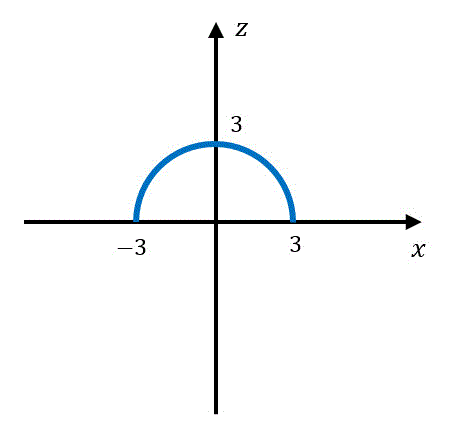
このときは、\( z = \sqrt{9 - x^2} \) となるため、半径3の半円となりますね。
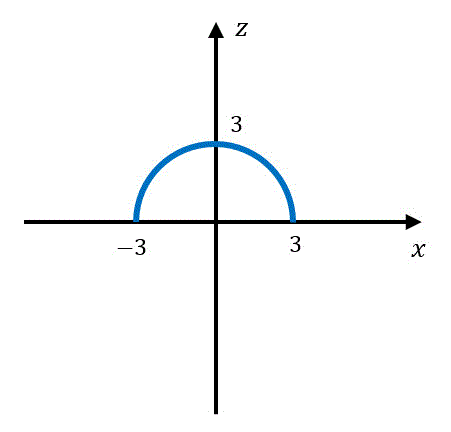
この \( x^2 \) の部分が \( x^2 + y^2 \) となったのが例題3の式ですね。
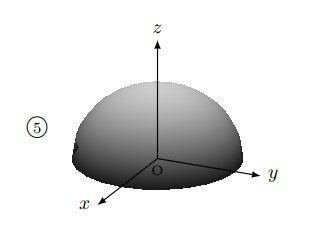
つまり、半径3の半円を \( z \) 軸周りに回転させた図形が \( z = \sqrt{9 - x^2 - y^2} \) に相当しますね。
つまり、以下のような図形となります(練習問題2の選択⑤に相当)。
4.練習問題
では、少しだけですが練習をしましょう。
練習1
つぎの(1)〜(3)の定義域と値域を求めなさい。
(1) \[ f(x,y) = \frac{1}{x^2 - y^2} \]
(2) \[ f(x,y) = \sqrt{x^2 - x- y} \]
(3) \[ f(x,y) = \frac{1}{\sqrt{1-x^2-y^2}} \]
練習2
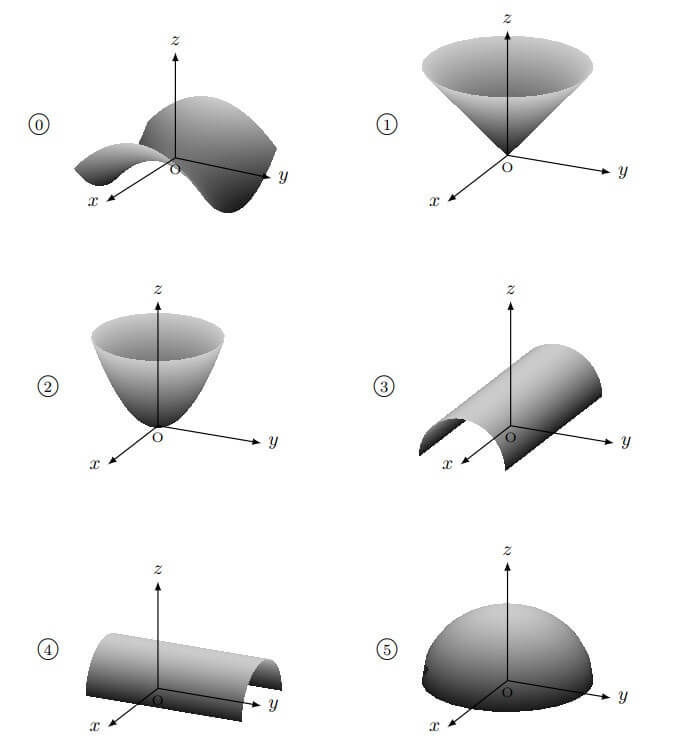
つぎの (1), (2) の概形として正しいものを⓪~⑤から選び、番号で答えなさい。
[工学系数学統一試験 EMaT 2018年度より]
(1) \( z = \sqrt{1-x^2} \)
(2) \( z = \sqrt{x^2 + y^2} \)
5.練習問題の解答
解答1
(1)
定義域は分母 \( x^2 - y^2 \) が0にならないときである。よって、\( x^2 - y^2 \not = 0 \) より、\( x^2 \not = y^2 \) となる。
(言い換えて \( y \not = \pm x \) でもOK)
また、\( x^2 - y^2 \) は、正にも負にもなりえるため、実数全体が値域になりそうだが、\( x^2 - y^2 \) をどれだけ大きくしても、\( f(x,y) \) が完全に0になることはない。
よって値域は \( f(x,y) \not = 0 \) となる。
(2)
ルートの中は0未満とはならない(実数範囲なので)。
なので定義域は \( x^2 - x- y \geqq 0 \) である。
また、ルートは負の値を取らない。よって値域は \( f(x,y) \geqq 0 \) である。
(3)
(2)と同じく、ルートの中は0とはならない。
ただし、(2)に加えて分母が0にならないことにも注意。
よって定義域は \( 1-x^2-y^2 \gt 0 \) である。
(書き換えると \( x^2 + y^2 \lt 1 \) となる。)
また、\( 0 \lt \sqrt{1-x^2-y^2} \leqq 1 \) である。
よって、値域は \( f(x,y) \geqq 1 \) となる。
解答2
(1)
解答:④
\( z = \sqrt{1-x^2} \) は、\( xz \) 平面上では原点中心の半径1の半円を表しますね。
また、\( z = \sqrt{1-x^2} \) には \( y \) が含まれていませんね。
なので、\( y \) の値が変わってもずっと \( xz \) 平面上で同じ半円を描き続けているものが答えとなります。
(2)
解答:①
(②と間違えないように! ②は \( z = x^2 + y^2 \) です。)
\( y = 0 \) を仮定します。
このときは、\( z = \sqrt{x^2} = \pm x \) なので、\( xz \) 平面上では直線を描いていますね。
この \( x^2 \) の部分が \( x^2 + y^2 \) となったのが(2)の式となります。。
つまり、\( z = \pm x \) を \( z \) 軸を中心に回転してできる立体となります(円錐になります)。
6.さいごに
今回は2変数関数についての基礎的な知識として2変数関数の定義域・値域、2変数関数の図示(というか想像)の仕方についてまとめました。
2変数関数の図示の方法は様々な方法があるので参考までにしてください。
*1:書いていませんが \( \sqrt{9} = 3 \) です。
関連広告・スポンサードリンク