スポンサードリンク
こんにちは、ももやまです。
今回は「P vs NP問題」について少しわかりやすめにまとめました。
この問題は、数学上の未解決問題となっており、2019年6月現在でも6つが解決していません。その問題の1つが「P vs NP問題」となっています。
これらの未解決問題は、アメリカのクレイ数学研究所によって、100万ドル(約1億円)の懸賞金がかけられています。*1トリビアの泉でも紹介されました。
No.681
「数学の世界には解くと賞金1億円がもらえる問題がある」
(番組評価 85/100へえ)
もちろん「P vs NP問題」も懸賞金がかけられている問題の1つです。
そんな「P vs NP問題」とはどんな問題なのかをわかりやすく説明していきたいと思います。
※注意
今回は問題はYesかNoかを判定する問題だけを考えます。このような問題を決定問題と言います。決定問題の例としては、
- 300円以内で500g以上食べるアイスの組み合わせはあるか?(Yes/No)
- \( 3x^2 + 2x + 4 = 0 \) を満たす \( x \) は存在するか? (Yes/No)
- 仕事のシフトで24時間どのタイミングでも最低2人以上入れられる組み合わせが存在するか? (Yes/No)
などがあります。いずれもYes/Noとして答えることができますね。
目次
スポンサードリンク
1.P、NPって何?
まずはP問題、NP問題の違いについて説明していきましょう。
ですが、説明の際に、多項式時間という単語が出てくるので、まずは、多項式時間についての説明をしておきましょう。
多項式時間とは
多項式時間*2とは、\( a \) を定数として、\( O(n^a) \) 以下の時間のことを表します。
多項式時間の例としては、 \( O(n^3) \) 、\( O(n \log{n}) \) 、\( O(n^{100}) \) などがあります。
多項式時間ではない例としては、指数関数以上のオーダーのもの、たとえば \( O(2^n) \), \( O(1.2^n) \), \( O(n!) \) などがあります。
今回は、わかりやすく説明するために、多項式時間以内で解けるアルゴリズムのことを効率の良いアルゴリズム、多項式時間以内で解けないアルゴリズムのことを効率の悪いアルゴリズムと呼びます。
オーダーなどがちょっとイマイチ… という人はこちらの記事に書いてあるのでこちらを読んで下さい。
(1) クラスP
クラスPとは、多項式時間以内で解くことができるアルゴリズムが存在するような問題のことを表します。
(一応参考までに:チューリングマシンを使った厳密な定義は、決定性チューリング機械において、多項式時間以内で判定可能な問題のことを表します。)
クラスPのPは、polynomial(多項式)を表します。
(2) クラスNP
クラスNPは、多項式時間以内で、問題の解が本当に合っているかの検証を判定することができる問題のことを表します。Not Pな問題*3のことではないので注意してください。
(一応参考までに:チューリングマシンを使った厳密な定義は、非決定性チューリングマシンによって多項式時間以内で解くことができる問題のことを表します。上の文章のNPの説明と同値なことが証明されています。)
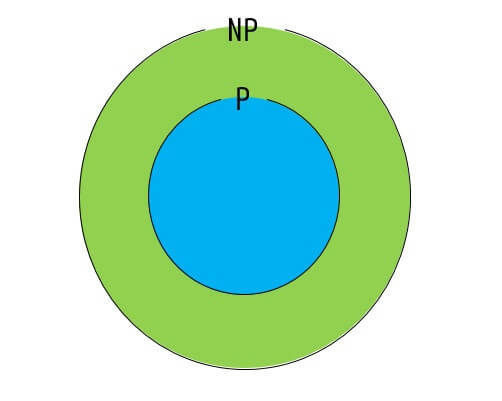
効率よくアルゴリズムを解けるP問題は、当然効率よく解が本当にあっているかの検証も効率よくできるため、P問題はNP問題に含まれます。
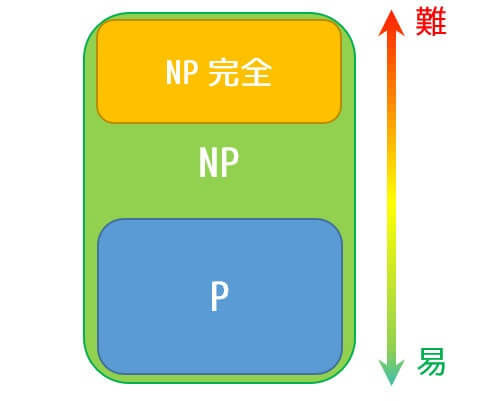
図示すると、下のようになります。
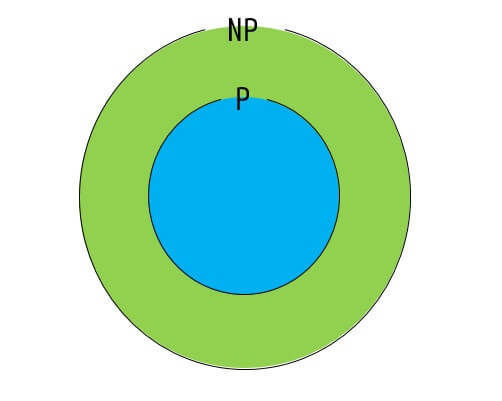
クラスNP:効率よく解が正しいか検証できる問題
クラスPに属する問題はクラスNPにも属する ( \( \mathrm{P} \subseteq \mathrm{NP} \) )
スポンサードリンク
3.多項式時間還元(多項式時間帰着)
問題が効率よく解けることを示すのは実際に効率よく解けるアルゴリズムを作ってしまえばいいのでまだ簡単にできます。しかし、効率よく解けないことを示すのはアルゴリズムを作ればいいわけではない*4ので難しいです。
このような効率よく解けないことを示したいときに多項式時間還元を使います。
ある問題 A,B が、問題Aから問題Bへ多項式時間還元が可能というのは、定義としては「多項式時間で計算可能な問題Aの問題例から問題Bの問題例への関数を \( f \) をし、問題Bの問題例が受理できるとき、問題Aの問題例が受理されるような関数 \( f \) が存在すること。」となります。
定義だけでは、何を言っているのかがちょっとよくわからないのでもう少しわかりやすく説明したいと思います。
問題Aを問題Bに出力が変わらないように(効率よく)変換するような関数があるとします。問題A、問題Bも出力(答え)は変わらないので問題Bを解いてあげると自動的に問題Aも答えが出せますね。このとき、AからBへの多項式時間還元可能*5と言います。
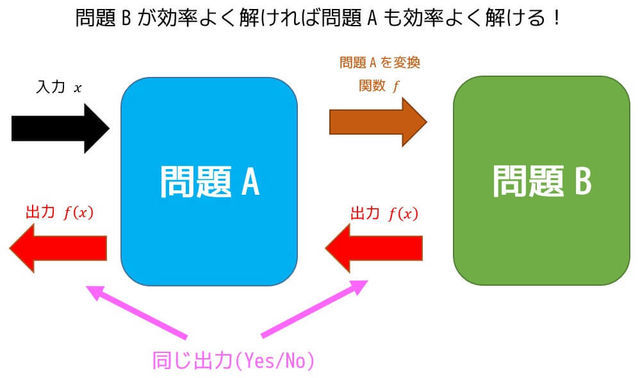
多項式時間還元は、効率がよいアルゴリズムが見つからないような問題(問題Aとします)とセットで使います。問題Aから問題Bへの多項式時間還元が存在することを示せば、「問題Bが効率よく解ければ問題Aも効率よく解けるが、問題Bは効率よく解くアルゴリズムが見つからないので、問題Aも同様に効率よく解くアルゴリズムは見つからない」と言うことができます(詳しくは次の章のNP完全で説明します。)。
また、多項式時間可能性には推移性が成り立ちます。
つまり、AからBへの多項式時間還元ができ、さらにBからCへの多項式時間還元が可能であれば、AからCへの多項式時間還元もできるということです。
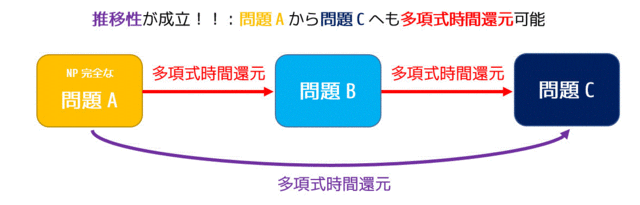
言い換えると、「問題Bが多項式時間で解ければ問題Aも多項式時間を解く」ことが示せ、さらに「問題Cが多項式時間で解ければ問題Bを多項式時間で解く」ことが示せれば、「問題Cが多項式時間で解ければ問題Aも多項式時間で解くことができる」ことを示すことができます。
スポンサードリンク
4.NP困難・NP完全
(1) NP困難
すべてのクラスNPが問題Aへ多項式還元可能なとき、AはNP困難と言うことができます。
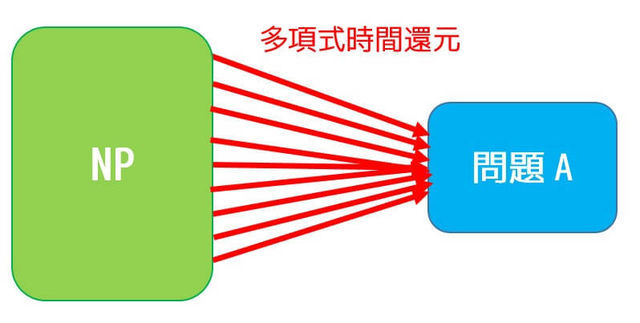
問題AはクラスNPに属している必要はないところがポイントです。
なので、決定問題(Yes/Noで答えられる問題)である必要もありません。
ちょっと難しいので言い換えてみましょう。言い換えると、「問題Aが多項式時間で解けるならば、クラスNPに属するすべての問題も多項式時間で解ける」と言えますね。
難しそうに聞こえますね。その勘は正しく、NP困難な問題は、どんなNP問題と同等もしくは難しい問題となります。難しさを図で表すとこのようになります(NP完全は下で説明してあります)。
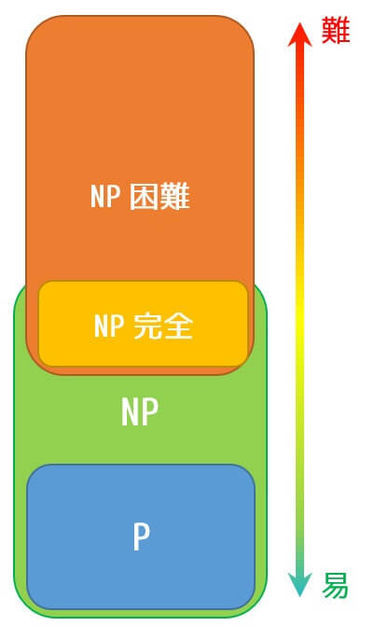
(2) NP完全
(1)の条件に加えて問題AがクラスNPに属する場合、AはNP完全と言うことができます。
つまり、AがNP完全と言うためには、
- 問題AがクラスNPに属している
- すべてのNP問題が問題Aへ多項式還元可能
この2つの条件を満たしている必要があると思います。
NP完全なプログラムは、「すべてのクラスNP問題がある問題へ多項式還元可能」を示す必要があるため、クラスNPの中でも難しい問題となります。
最初にNP完全であることが証明された問題には、「SAT」、日本語で言うと「充足可能性問題」があります。
SATとは、「n 個の論理変数を使ってランダムに主乗法標準系(和積標準系、CNF)の論理式*6が与えられたとき、そのときの値は充足可能(1,True)になるか?」のような問題を指します。つまり、
入力:主乗法標準系の論理式 \( f = (x_1,x_2,\cdots, x_n) \)
出力:\( f = 1 \) になる組み合わせはあるか?(Yes/No)
となります。「n変数の論理式で、f = 1 となる組み合わせがあるかどうかは」は、真理値表を書いてあげないと確認することができません。つまり、\( 2^n \) 通りすべて確認しないといけません。これは \( O(2^n) \) となってしまい、多項式時間では解くことができないため、クラスPの問題ではありません。
しかし、論理式 \( x_1,x_2,\cdots,x_n \) に論理値(0 or 1)を代入して、実際に \( f \) が1か0かを確認することはすぐにできますね。なので、クラスNPには属します。
「すべてのNP問題が問題Aへ多項式還元可能」というのを示すためには、チューリング機械(計算理論系)の知識が前提となってきてしまい、かなり難しいので今回はこの証明は省きます。
他にNP完全問題の例としては
- 彩色問題(n色を使って塗り分けできる?(Yes/No)
- ぷよぷよ(ぷよの組を与えたときにn連鎖以上組める?(Yes/No)
- 部分和問題 (整数の組からいくつか抜き取ってnを作れる?(Yes/No)
- テトリス(テトリスの組を与えたときにn列以上消せる?(Yes/No)
「すべてのNP問題が問題Aへ多項式還元可能」と言えないと問題AがNP完全と言うことができないうえに、証明するためにはチューリング機械を使う必要があって難しいですよね。
しかし、上で説明した、多項式時間還元の推移性を使うことで、チューリング機械の知識を使わずに「すべてのクラスNP問題がある問題へ多項式還元可能」であることを示すことができます。
NP完全だと判明している問題Aがあるとします。このとき、問題AからクラスNPの問題Bを多項式還元可能であることを示してあげれば、推移性により、すべてのクラスNP問題から問題Bが多項式還元可能となり、NP完全であることを示してあげることができます。
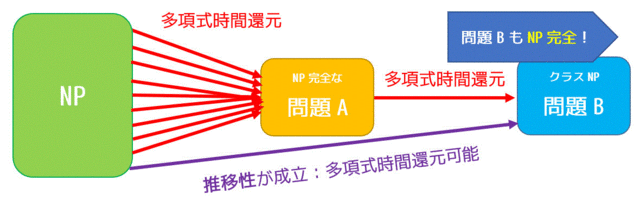
この手法をわかりやすくすると、
「この問題Bのアルゴリズムを効率よく解く方法が見つからないなぁ……。 そうだ、この問題を使えば効率よく方法が見つからない問題Aも解決できることを示せば、今考えている問題Bのアルゴリズムは問題A以上に難しい問題と言うことができるぞ…!」
となります。
5.P vs NP問題とは?
(1) 概要
P問題とNP問題が分かったところで、P vs NP問題について説明していきましょう。
上の説明で、PはNPに含まれると説明しました。
しかし、いまだに、P = NP (PとNPが等しい)か、 P ≠ NP(PとNPは等しくないか)かどうかは判明していません。これを「P vs NP問題」と呼んでいます。
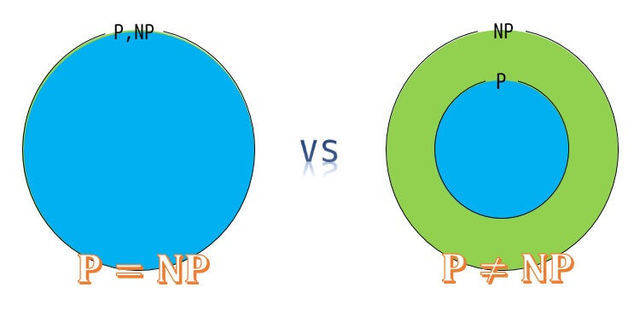
「P = NP」であることが証明されてしまった場合、NPに属するあらゆるアルゴリズムが多項式時間、つまり効率よく解けてしまうため、多くの研究者は「P ≠ NP」であると予想しています。
しかし、一部では「P = NP」だと予想している研究者もいることから、いまだにどちらが正しいのかは示されていません。
(2) 証明の手口
「P vs NP問題」で大きく鍵になってくるのが先程説明したNP完全な問題です。
実は、どれか1つのNP完全な問題1つだけを使うことで「P = NP」・「P ≠ NP」かを示すことができます。
ここからは、NP完全な問題(問題Aとします)がどうなれば「P = NP」もしくは「P ≠ NP」が示せるかを説明していきたいと思います。
(i) P = NP を示すためには
問題AはNP完全な問題なため、「すべてのクラスNP問題が問題Aへ多項式還元可能」、言い換えれば「問題Aが多項式時間で計算できるのであれば、すべてのクラスNP問題も多項式時間で計算可能」となりますね。
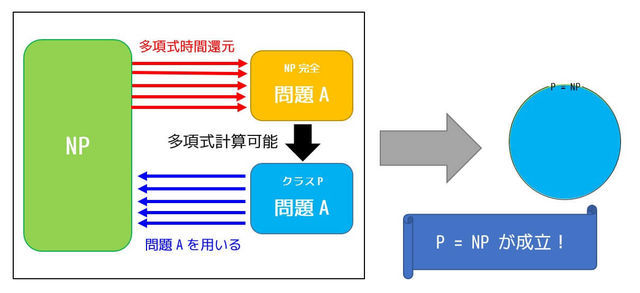
つまり、たくさんあるNP完全な問題のどれか1つでも多項式時間で解けることを示してしまえば、「P = NP」と言うことができます。
(ii) P ≠ NP を示すためには
P ≠ NPを示すためには、NP完全な問題AがクラスPに属さない、つまり多項式時間ではどうやっても解くことができないことを示せればよいことになります。
クラスNPに属するのにPには属さないということは、「P ≠ NP」ですね。
このように、どのNP完全問題でもいいので、それらの1つを使えば「P = NP」・「P ≠ NP」を示すことができますね。と簡単に言っていますがそれがすごく難しいので1億円もの懸賞金がかけられているのです……。
6.さいごに
今回はP vs NP問題とはどんな問題なのかをP、NP、NP完全、NP困難などの用語をわかりやすく説明しながらまとめました。
わかりやすく説明したつもりですが、万が一「ここおかしいよ」などがあればコメントなどで指摘お願いします。
余裕がある人は、ぜひ「P = NP」・「P ≠ NP」のどちらかになるかを証明してみてみましょう。1億円もらえますよ。
7.参考文献など
アルゴリズム入門(7) 宮崎修一 京都大学 学術情報メディアセンター
2019年6月9日アクセス
Qiita P、NP、NP完全、NP困難… 似て非なる階層構造
2019年6月9日アクセス
一般化ぷよぷよのNP完全性 松金輝久・竹永康彦 電気通信大学
2019年6月9日アクセス
計算の複雑さとNP完全問題 東京大学
2019年6月9日アクセス
解けたら賞金1億円!数学の7つの未解決問題のひとつ「P≠NP」問題へのアプローチがもたらすもの
2019年6月9日アクセス
トリビアの泉で沐浴
2019年6月9日アクセス
関連広告・スポンサードリンク