うさぎでもわかるコンパイラ　第4羽　左再帰の除去

2022年9月20日 2022年9月20日 39分18秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

前回は1文字だけの先読みで構文解析ができる文法であるLL(1)文法について説明していきました。

しかし、文法の中に左再帰な規則が入ってしまうと、文法内の他の規則に関わらず、絶対にLL(1)文法となることはありません。言い換えると、左再帰な規則は先読みしながらの構文解析の壁の1つといえます。

そこで今回は、

そもそも左再帰とは？
左再帰な規則が入るとLL(1)文法でなくなる理由
左再帰の除去（例題・練習問題あり）

について、お勉強していきましょう。

文字表記に関する注意

本記事では特に指示がない限り、文章中に出てくる小文字・大文字・ギリシャ文字は

小文字 $a$ , $b$ , $c$ , $d$ , … → 終端記号
大文字 $S$ , $A$ , $B$ , $C$ , … → 非終端記号
$ε$ を除くギリシャ文字 $α$ , $β$ , … → 終端記号と非終端記号から出来る文字列
（例: $a b A b$ , $A b C$ , $A B C$ , $a b c$ など…）
$ε$ → 空文字

を表します。

※

目次 [hide]

1. 左再帰・左再帰文法とは？
- [余談1] 右再帰とは？
- [余談2] 間接的な左(右)再帰
2. 左再帰文法の問題点
- 厳密に証明してみる
- 右再帰文法は大丈夫なの？
3. 左再帰の除去
5. 練習問題
- 練習1. 左再帰が1つの場合
- 練習2. 左再帰が複数ある場合
6. 練習問題の答え
- 解答1. 左再帰が1つの場合
- 解答2. 左再帰が複数の場合
7. さいごに

スポンサードリンク

1. 左再帰・左再帰文法とは？

左再帰(規則)とは、生成規則の中に生成元の非終端記号と生成先の文字列の1文字目(先頭)が同じになっている規則、つまり規則中に $A \to A α$ となる規則のことをさします。

また、左再帰 $A \to A α$ が含まれている文法のことを左再帰文法と呼びます。（ただし $α \neq ε$ ）

例えば、生成規則が $\begin{aligned} P = {S & \to a A \\ A & \to A b a | c d \\ B & \to S c | a} \end{aligned}$ で表される文法は、左再帰 $A \to A b a$ が含まれていますね。そのため、この文法は左再帰文法です。

左再帰文法には、左再帰の核部分 $A \to A α$ に加えて再帰をストップする規則の形 $A \to β$ が含まれているのが特徴です。

[余談1] 右再帰とは？

「左再帰があるなら、右再帰な文法もあるんじゃね？」と思った人もいると思います。

想像の通り、右再帰もあります。具体的には、 $A \to α A$ の形の規則を右再帰と呼び^[1]日本語で説明すると、生成元の非終端記号と生成先の文字列の終端が同じになっている規則が右再帰です。、右再帰な規則が含まれている文法のことを右再帰文法と呼びます。（左再帰の時と同じく $α \neq ε$ ）

右再帰文法も、左再帰文法と同じように規則の核部分に加えて再帰をストップする規則の形 $A \to β$ が含まれているのが特徴です。

[余談2] 間接的な左(右)再帰

下の文法 $A \to B b, B \to A a, A \to α$ のように、見た目的には左再帰になっていないものの、規則を適用していくと、 $A \overset{A \to B b}{\to} B b \overset{B \to A a}{\to} A a b$ のように左再帰な形が出てくる規則のことを、間接左再帰と呼びます^[2]一方、見た目的に明らかな左再帰の形 $A \to A α$ をしている左再帰のことを、直接左再帰と呼ぶこともあります。。

同じように下の文法 $A \to b B, B \to a A, A \to α$ のように、見た目的には右再帰になっていないものの、規則を適用していくと、 $A \overset{A \to b B}{\to} b B \overset{B \to a A}{\to} b a A$ のように右再帰な形が出てくる規則のことを、間接右再帰と呼びます^[3]一方、見た目的に明らかな右再帰の形 $A \to α A$ が含まれている場合、直接右再帰と呼ぶこともあります。。

※ 今回の記事では、 $A \to A α$ の形が出てくる直接的な左再帰の除去だけについて説明します。（間接的な左再帰の除去は本記事では割愛します。）

スポンサードリンク

2. 左再帰文法の問題点

左再帰が含まれている文法（左再帰文法）の最大の問題点は、絶対にLL(1)文法とはならないからです。言い換えると、左再帰が含まれている文法は、1文字先読みすることで後戻りなしに構文解析することができません。

LL(1)文法にならない理由を具体例を踏まえてみていきましょう。

例えば、次の左再帰規則 $A \to A a, A \to b$ を持つ文法があったとします。（出発記号 $A$ ）

ここで、もしLL(1)文法であれば、1文字先読みするだけで $A \to A a$ , $A \to b$ のどちかを判別することができますよね。

しかしこの2つの規則は、

$A \to A a$ ：生成先の先頭 $A$ は最終的に $A \to b$ により $b$ になる
$A \to b$ ：生成先の先頭 $b$ である

ため、1文字先読みしたとしても、どちらの規則を適用すればよいかわかりません。

厳密に証明してみる

[お知らせ] 証明で使うDirector集合・First集合・Follow集合の解説はこちらで行っています。

もっと厳密に、Director集合を使って左再帰規則 $A \to A α, A \to β$ がLL(1)文法でないことを示してみましょう。

まず、生成規則 $A \to A a$ に関するDirector集合 $Director (A, A α)$ は、 $\begin{aligned} Director (A, A α) & = First (A α) \\ = First (A) \\ = First (β) \end{aligned}$ と計算できます。

※ $ε \notin First (A α) = First (β)$ の条件を仮定

また、 $A \to β$ に関するDirector集合は、 $ε \notin First (β)$ のとき $\begin{aligned} = First (A α) \\ = First (A) \\ = First (β) \end{aligned}$ と計算できます。

※ $ε \notin First (β)$ の条件を仮定

よって、 $ε \notin First (β)$ のときに $Director (A, A α) \cap Director (A, β) = First (β)$ が成立するため、LL(1)文法ではない。

※ ほんの一部の条件に対してでもDirector集合の積集合が $ϕ$ 以外になったらLL(1)文法ではない。

右再帰文法は大丈夫なの？

右再帰文法（生成規則に右再帰が含まれている）だからといって絶対にLL(1)文法ではなくなるとは限りません。

例えば、 $A \to a A, A \to b$ のような文法は $A \to a A$ が含まれているため右再帰文法ですが、

$A \to a A$ ：生成先の先頭 $A$ は $a$ である
$A \to b$ ：生成先の先頭 $A$ は $b$ である

のため、生成先の先頭文字を見るだけで $A \to a A$ , $A \to b$ のどちらを適用すべきかが一意に定まりますね。そのため、LL(1)文法と言えます^[4]厳密に示したい場合は\[\begin{align*}\mathrm{Director} ( A, aA) \cap \mathrm{Director} (A, b) & = \mathrm{First} (a) \cap \mathrm{First} (b)\ & = \{ a \} \cap \{ b \}\ & = … Continue reading。

スポンサードリンク

3. 左再帰の除去

(1) 左再帰除去の手順

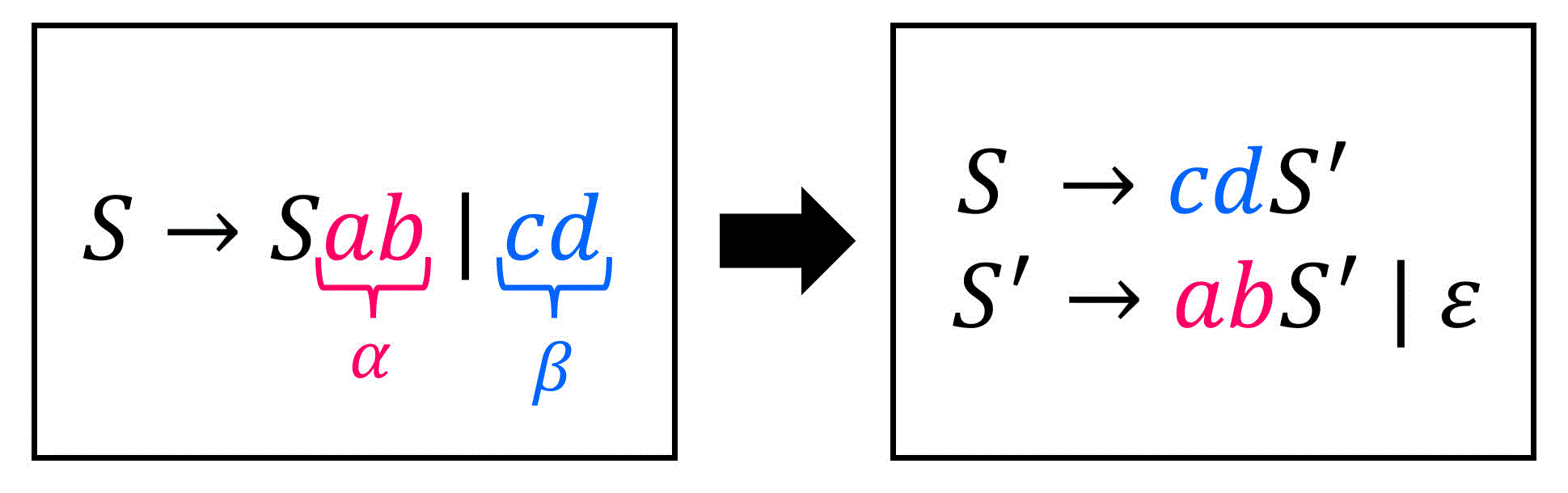
左再帰文法は、次の公式を使うことによって簡単に左再帰ではない文法に書き換えることができます。

左再帰の除去 (左再帰が1つの場合)

左再帰が含まれる規則 $A \to A α | β$ は、以下のように変形をすることで左再帰ではない等価な規則に変形できる。 $\begin{aligned} A & \to β A^{'} \\ A^{'} & \to α A^{'} | ε \end{aligned}$ ※ 新たな非終端記号 $A^{'}$ を追加している。

ここで、 $α$ , $β$ は下の3つの条件を満たす非終端記号と終端記号が並んだ文字列である。

$α \neq ε$
$β$ の先頭文字は $B$ 以外である。
（先頭以外であれば $β$ の中に $B$ が含まれていてもOK）
$α$ , $β$ は非終端記号だけ、終端記号だけで構成されていてもOK

[注意]

※1. 左再帰に関係がない非終端記号（上の例の場合は $A$ 以外）から始まる生成規則からはそのままでOK。
※2. 変形後は非終端記号 $A^{'}$ が増える点に注意！
※3. $β = ε$ の場合は $A \to α A | ε$ と置き換えるだけで左再帰の除去が可能。（非終端記号が増えない）

[公式導出] (やみくもに丸暗記するのではなく、導出過程を理解してから覚えましょう！)

まず最初に左再帰が含まれる規則 $A \to A α | β$ にはどのような文字列が含まれるかを書きだしてみましょう。

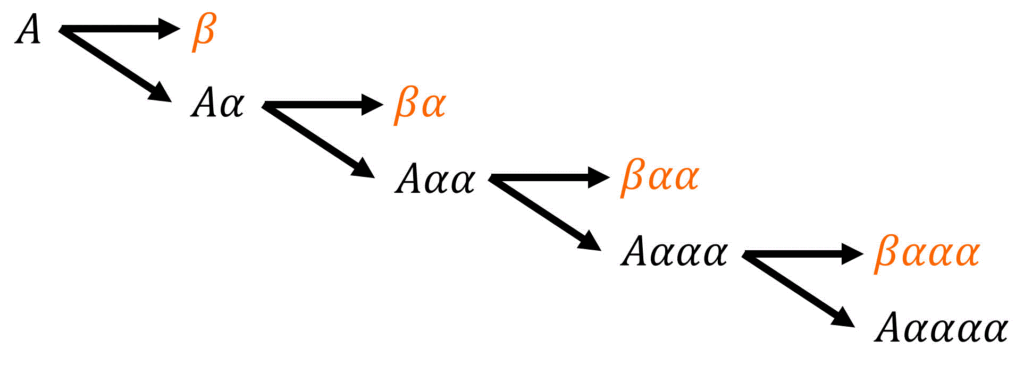
すると、

$β$
$β α$
$β α α$
$β α α α$

のように、 $β$ が1文字来たあとに $α$ が連続するような文字列 $β \underset{0 回以上繰り返し}{\underset{⏟}{α α α \dots}}$ が当てはまることがわかりますね。

つまり、左再帰の規則を書き換える際には、左再帰ではない規則で $β \underset{0 回以上繰り返し}{\underset{⏟}{α α α \dots}}$ となる文字列を表せればOKです。

ここからは、左再帰規則 $A \to A α | β$ を左再帰でない規則に書き換えるために文字列 $β \underset{0 回以上繰り返し}{\underset{⏟}{α α α \dots}}$ を [ア] $β$ の部分と [イ] $α$ の繰り返し部分に分けます。

[ア] $β$ の部分

$β$ の部分は1回だけ $β$ を出力するために新しい非終端記号 $A^{'}$ を使って $A \to β A^{'}$ とします。

[イ] 0回以上の $α$ 繰り返しの部分

つぎに、 $A^{'}$ の部分で0回以上の $α$ の繰り返しを左再帰を使わずに表します。ここで左再帰は使ったらダメだけど、右再帰を使ったらダメとは一言も言っていない点が重要です。

そのため、0回以上の $α$ の繰り返しは右再帰 $A^{'} \to α A^{'} | ε$ を使って表現します。

※ $α$ は0回以上の繰り返し（＝空文字も含める）なので、右再帰をストップする条件は $A^{'} \to ε$ となります。

(a), (b)をまとめる

あとは [ア] と [イ] の規則を合わせるだけで、左再帰の除去をした（元の文法と等価な）文法の完成です！ $\begin{aligned} A & \to β A^{'} \\ A^{'} & \to α A^{'} | ε \end{aligned}$

(2) 例題で確認 [左再帰の除去]

例題1

次の文法 $G$ がある。 $G = ({S, A, B}, {a, b, c, d}, P, S)$ $\begin{aligned} P = {S & \to A a B \\ A & \to A c b | b \\ B & \to S c | d} \end{aligned}$ つぎの(1), (2)の問いに答えなさい。

(1) $G$ は左再帰文法である。その理由を答えなさい。
(2) $G$ に対して左再帰の除去を適用し、左再帰ではない文法 $G^{'}$ に書き換えなさい。

[解説1]

(1)

生成規則 $A \to A c b$ において、生成元の非終端記号と生成先の1文字目(先頭文字)が一致しているため。

(2)

左再帰が発生している部分について、下のように $α$ , $β$ をおきます。 $A \to A \underset{α}{\underset{⏟}{c b}} | \underset{β}{\underset{⏟}{b}}$

あとは、左再帰の除去規則を使って規則を書き換えればOKです。 $\begin{aligned} A & \to \underset{β}{\underset{⏟}{b}} A^{'} \\ A^{'} & \to \underset{α}{\underset{⏟}{c b}} A^{'} | ε \end{aligned}$

左再帰の発生に関係のない非終端記号（今回の場合は $A$ 以外）の生成規則 $S \to A a B, B \to S c | d$ はそのままでOKなので、文法 $G$ と等価な左再帰ではない文法 $G^{'}$ は、 $G^{'} = ({S, A, A^{'}, B}, {a, b, c, d}, P^{'}, S)$ $\begin{aligned} P^{'} = {S & \to A a B \\ A & \to b A^{'} \\ A^{'} & \to c b A^{'} | ε \\ B & \to S c | d} \end{aligned}$ となります。

※ ピンク色を付けて書いた部分は忘れがちなので要注意！

(3) 左再帰が複数含まれる場合

下のように左再帰が複数含まれる規則 $\begin{aligned} A & \to A α_{1} | A α_{2} | \dots \\ A & \to β_{1} | β_{2} | \dots \end{aligned}$ であっても、左再帰の適用が可能です。

[色の意味]

桃色の規則 … 左再帰の核となる $A \to A α_{k}$ が含まれた規則
水色の規則 … 左再帰をストップする規則 $A \to β_{k}$ が含まれた規則^[5] $A$ が生成元で、生成先の先頭が $A$ で始まらない（つまり桃色の規則に当てはまらない）規則は全て水色の規則に含まれる。（ $A \to b A$ … Continue reading

左再帰が含まれていない $A \to A α_{k}$ が含まれた規則

左再帰の除去 (左再帰が複数出てくる場合)

左再帰が複数含まれる規則 $\begin{aligned} A & \to A α_{1} | A α_{2} | \dots | A α_{m} \\ A & \to β_{1} | β_{2} | \dots | β_{n} \end{aligned}$ でも、以下のように変形をすることで左再帰ではない等価な規則に変形できる。 $\begin{aligned} A & \to β_{1} A^{'} | β_{2} A^{'} | \dots | β_{n} A^{'} \\ A^{'} & \to α_{1} A^{'} | α_{2} A^{'} | \dots | α_{m} A^{'} | ε \end{aligned}$

ここで、 $α_{1}$ , $α_{2}$ , …, $β_{1}$ , $β_{2}$ , … は下の3つの条件を満たす非終端記号と終端記号が並んだ文字列である。

$α_{1}$ , $α_{2}$ , … は空文字以外であれば何でもOK
$β_{1}$ , $β_{2}$ , … の先頭文字は $B$ 以外である。
（先頭以外であれば $β$ の中に $B$ が含まれていてもOK）
$α_{1}$ , $α_{2}$ , …, $β_{1}$ , $β_{2}$ , … は非終端記号だけ、終端記号だけで構成されていてもOK

[注意]

※1. 左再帰に関係がない非終端記号（上の例の場合は $A$ 以外）から始まる生成規則からはそのままでOK。
※2. 変形後は非終端記号 $A^{'}$ が増える点に注意！

(4) 例題で確認 [左再帰が複数含まれる場合]

例題2

次の文法 $G$ がある。 $G = ({S, A, B, C}, {a, b, c, d}, P, S)$ $\begin{aligned} P = {S & \to a B c \\ A & \to b B | a A \\ B & \to B a A | B S | a a | d B a | C d \\ C & \to c c | c c c} \end{aligned}$ この文法 $G$ に対して、左再帰の除去を適用することで、 $G$ と等価な左再帰ではない文法 $G^{'}$ に書き換えなさい。

左再帰の直接的な原因は $B \to B a A$ , $B \to B S$ の2つ（共に $B$ が生成元の規則）ですね。

ここで、 $B$ が生成元の規則は先ほどの2つのほかに $B \to a a$ , $B \to d B a$ , $B \to C d$ の3つがあります。

なので、文字列を $\begin{aligned} B & \to B \underset{α_{1}}{\underset{⏟}{a A}} | B \underset{α_{2}}{\underset{⏟}{S}} \\ B & \to \underset{β_{1}}{\underset{⏟}{a a}} | \underset{β_{2}}{\underset{⏟}{d B a}} | \underset{β_{3}}{\underset{⏟}{C d}} \end{aligned}$ とおきましょう。

あとは、左再帰の除去公式で置き換えてあげればOKです！ $\begin{aligned} B & \to \underset{β_{1}}{\underset{⏟}{a a}} B^{'} | \underset{β_{2}}{\underset{⏟}{d B a}} B^{'} | \underset{β_{3}}{\underset{⏟}{C d}} B^{'} \\ B^{'} & \to \underset{α_{1}}{\underset{⏟}{a A}} B^{'} | \underset{α_{2}}{\underset{⏟}{S}} B^{'} | ε \end{aligned}$

左再帰の発生に関係のない非終端記号（今回の場合は $A$ 以外）の生成規則はそのままでOKなので、文法 $G$ と等価かつ左再帰ではない文法 $G^{'}$ は、 $G^{'} = ({S, A, B, B^{'}}, {a, b, c, d}, P^{'}, S)$ $\begin{aligned} P^{'} = {S & \to a B c \\ A & \to b B | a A \\ B & \to a a B^{'} | d B a B^{'} | C d B^{'} \\ B^{'} & \to a A B^{'} | S B^{'} | ε \\ C & \to c c | c c c} \end{aligned}$ となります。（ピンク色を付けて書いた部分が変更箇所）

5. 練習問題

それでは、今回習った左再帰の除去について2問の練習問題を用意しました。

練習1. 左再帰が1つの場合

練習1

次の文法 $G$ がある。 $G = ({S, A, B}, {a, b, c}, P, S)$ $\begin{aligned} P = {S & \to S a b | c \\ A & \to B a A | a \\ B & \to c A | b b} \end{aligned}$ つぎの(1), (2)の問いに答えなさい。

(1) $G$ は左再帰文法である。その理由を答えなさい。
(2) $G$ に対して左再帰の除去を適用し、左再帰ではない文法 $G^{'}$ に書き換えなさい。

練習2. 左再帰が複数ある場合

練習2

次の文法 $G$ がある。 $G = ({S, A, B, C}, {a, b, c, d}, P, S)$ $\begin{aligned} P = {S & \to d S | b b a b \\ A & \to a A | b B | c C | d \\ B & \to b | S b \\ C & \to C a b | C b | C B S | c c | A d} \end{aligned}$ この文法 $G$ に対して、左再帰の除去を適用することで、 $G$ と等価な左再帰ではない文法 $G^{'}$ に書き換えなさい。

6. 練習問題の答え

解答1. 左再帰が1つの場合

(1)

生成規則 $S \to S a b$ において、生成元の非終端記号と生成先の1文字目(先頭文字)が一致しているため。

(2)

まず、左再帰が発生している $S$ が生成元の規則に対して、 $α$ , $β$ を以下のようにおく。 $S \to S \underset{α}{\underset{⏟}{a b}} | \underset{β}{\underset{⏟}{c}}$

あとは、左再帰の除去規則を使って規則を書き換えればOK。 $\begin{aligned} S & \to \underset{β}{\underset{⏟}{c}} S^{'} \\ S^{'} & \to \underset{α}{\underset{⏟}{a b}} S^{'} | ε \end{aligned}$

左再帰の発生に関係のない非終端記号（今回の場合は $S$ 以外）の生成規則はそのままでOKなので、文法 $G$ と等価な左再帰ではない文法 $G^{'}$ は、 $G^{'} = ({S, A, A^{'}, B}, {a, b, c, d}, P^{'}, S)$ $\begin{aligned} P^{'} = {S & \to c S^{'} \\ S^{'} & \to a b S^{'} | ε \\ A & \to B a A | a \\ B & \to c A | b b} \end{aligned}$ となる。

解答2. 左再帰が複数の場合

左再帰の直接的な原因は $C \to C a b$ , $C \to C b$ , $C \to C B S$ の3つ（共に $C$ が生成元の規則）。

また、 $C$ が生成元の規則は先ほどの3つのほかに $C \to c c$ , $C \to A d$ の2つがある。

なので、 $α_{1}$ , $α_{2}$ , $α_{3}$ , $β_{1}$ , $β_{2}$ を用いて文字列を $\begin{aligned} C & \to C \underset{α_{1}}{\underset{⏟}{a b}} | C \underset{α_{2}}{\underset{⏟}{b}} | C \underset{α_{3}}{\underset{⏟}{B S}} \\ C & \to \underset{β_{1}}{\underset{⏟}{c c}} | \underset{β_{2}}{\underset{⏟}{A d}} \end{aligned}$ とおく。

あとは、左再帰の除去公式で置き換えるだけ。 $\begin{aligned} C & \to \underset{β_{1}}{\underset{⏟}{c c}} C^{'} | \underset{β_{2}}{\underset{⏟}{A d}} C^{'} \\ C^{'} & \to \underset{α_{1}}{\underset{⏟}{a b}} C^{'} | \underset{α_{2}}{\underset{⏟}{b}} C^{'} | \underset{α_{3}}{\underset{⏟}{B S}} C^{'} | ε \end{aligned}$

左再帰の発生に関係のない非終端記号（今回の場合は $S$ 以外）の生成規則はそのままでOKなので、文法 $G$ と等価かつ左再帰ではない文法 $G^{'}$ は、 $G^{'} = ({S, A, B, C, C^{'}}, {a, b, c, d}, P^{'}, S)$ $\begin{aligned} P^{'} = {S & \to d S | b b a b \\ A & \to a A | b B | c C | d \\ B & \to b | S b \\ C & \to c c C^{'} | A d C^{'} \\ C^{'} & \to a b C^{'} | b C^{'} | B S C^{'} | ε} \end{aligned}$ となります。

7. さいごに

今回は、左再帰が含まれる文法（左再帰文法）と、左再帰の除去について説明していきました。

最後に左再帰の除去公式をおさらいしておきましょう！

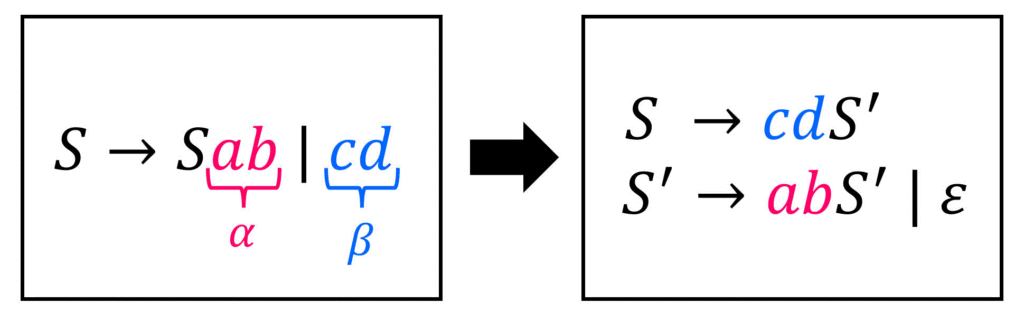
左再帰文法の問題点や、左再帰の除去について少しでも理解していただけたのであれば本当にうれしいです！

注釈[+]

注釈
↑1	日本語で説明すると、生成元の非終端記号と生成先の文字列の終端が同じになっている規則が右再帰です。
↑2	一方、見た目的に明らかな左再帰の形 $A \to A α$ をしている左再帰のことを、直接左再帰と呼ぶこともあります。
↑3	一方、見た目的に明らかな右再帰の形 $A \to α A$ が含まれている場合、直接右再帰と呼ぶこともあります。
↑4	厳密に示したい場合は $\begin{aligned} Director (A, a A) \cap Director (A, b) & = First (a) \cap First (b) \\ = {a} \cap {b} \\ = ϕ \end{aligned}$ とすればOK。
↑5	$A$ が生成元で、生成先の先頭が $A$ で始まらない（つまり桃色の規則に当てはまらない）規則は全て水色の規則に含まれる。（ $A \to b A$ のように、自身を生成する規則であっても生成先の先頭が $A$ でない文法であれば当てはまるので注意。）