うさぎでもわかる微分方程式　Part01　変数分離形（1階微分方程式）

2020年3月30日 2021年12月13日 34分41秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

今回からいよいよ本格的に微分方程式の解き方について説明していきたいと思います。

まずは、1階微分方程式の中でも直接積分形の次に簡単な変数分離形について説明していきたいと思います。

※ なお、今回以降の記事では、特異解（一般解だけでは表せない解）を考慮していません。あらかじめご了承ください。

前回の微分方程式の記事はこちらです↓↓

www.momoyama-usagi.com

スポンサードリンク

１．変数分離形とは

まず、今回説明する変数分離形とはどんな微分方程式で、どうやって解けるのかを説明しましょう。

変数分離系

1階常微分方程式 $\frac{d y}{d x} = f (x, y)$ の右辺 $f (x, y)$ が $g (x) \cdot h (y)$ のように、 $x$ のみの関数 $g (x)$ と $y$ のみの関数 $h (y)$ に変形でき、 $\frac{1}{h (y)} \cdot \frac{d y}{d x} = g (x)$ の形に変形できる微分方程式のことを変数分離形と呼ぶ。

（ただし $h (y) \neq 0$ に注意！）

変数分離形の微分方程式は上の式を両辺を $x$ で積分すると、 $\int \frac{1}{h (y)} \cdot \frac{d y}{d x} d x = \int g (x) d x$ の形になるので、一般解は $\int \frac{1}{h (y)} d y = \int g (x) d x$ を計算することで求められる*1。

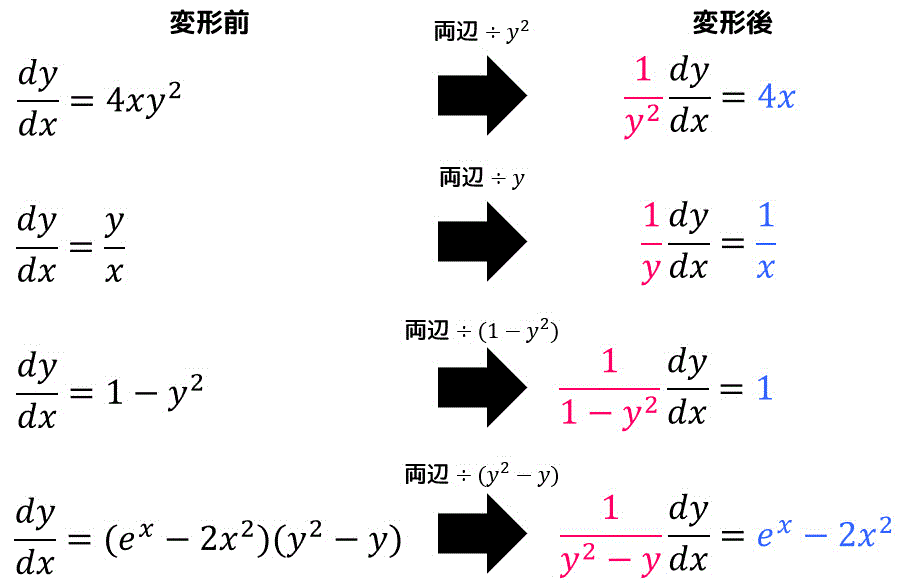
下のように、両辺に何かを掛けたり割ったりすることで左辺側を $y$ の式 × $\frac{d y}{d x}$ 、右辺側を $x$ の式に変形することができれば、変数分離形を用いて微分方程式を解くことができます。

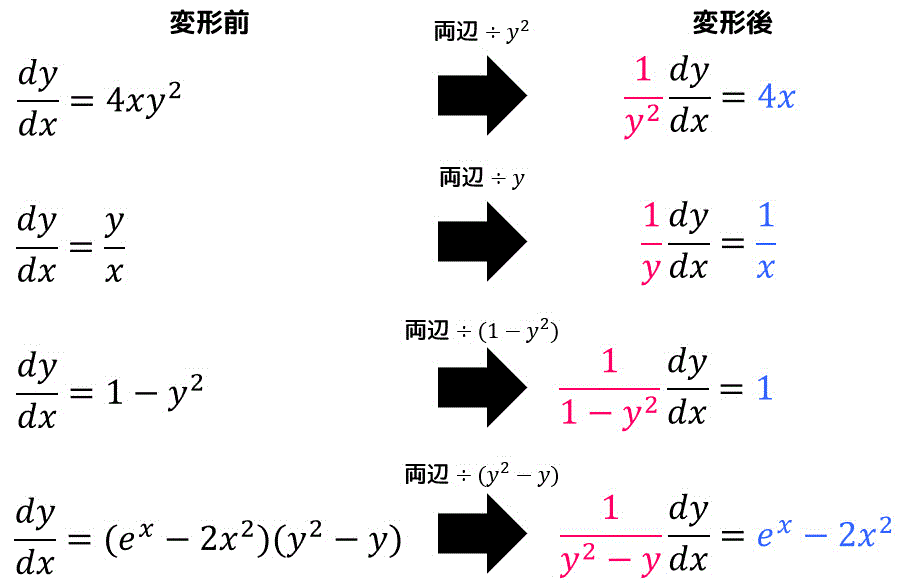
意外と忘れがちですが、 $\frac{d y}{d x} = 1 - y^{2}$ のような $x$ が含まれないような式でも、 $x$ 側（右辺）を1にすることで変数分離系に持ち込むことができます。

（ただし $y \neq \pm 1$ に注意。厳密に微分方程式を解く場合は分母が0などで定義されない値は別に計算する必要がある*2が、「うさぎでもわかる微分方程式」では、定義されない値については無視することにします。）

また、 $\frac{d y}{d x} = y - x^{2}$ のような微分方程式を見て、変数分離形使えそうじゃんと思う人もいるのですが、 $\frac{d y}{d x} - y = - x^{2}$ のように左辺側を $y$ の式 × $\frac{d y}{d x}$ の形にできないので変数分離形は使えません。

なお、前回説明した直接積分形は、 $\frac{d y}{d x} = 2 x + 3$ のように、 $h (y) = 1$ の場合の特殊な変数分離形として考えることもできます。

（変数分離形の特殊なパターンが直接積分形）

スポンサードリンク

２．変数分離形の計算例

では、実際に変数分離形であらわされた微分方程式を解いてみましょう。

例題1

1階微分微分方程式 $\frac{d y}{d x} = 4 x y^{2}$ について、(1), (2)の問いに答えなさい。

(1) 一般解を求めなさい。
(2) 初期条件 $y (1) = 1$ を満たす特解を求めなさい。

解説1

(1)

まず、変数分離形にするために左辺を $y$ の式 × $\frac{d y}{d x}$ 、右辺を $x$ の式に変形しましょう。すると、 $\frac{1}{y^{2}} \cdot \frac{d y}{d x} = 4 x$ と変形できます。

（両辺を $y$ で割っているので、 $y \neq 0$ に要注意。これ以降はいちいち書かないことにする。）

さらに、両辺を $x$ で積分すると、 $\int \frac{1}{y^{2}} \cdot \frac{d y}{d x} d x = \int 4 x d x$ となるので、 $\int \frac{1}{y^{2}} d y = \int 4 x d x$ を計算することで一般解を求められます。

よって、一般解は任意定数 $C$ を用いて $- \frac{1}{y} = 2 x^{2} + C$ となり、変形して $y = - \frac{1}{2 x^{2} + C}$ と求めることができます。

（基本的に指示がない場合は y = の形に変形しなくてもOKです。y = の形に変形するときに間違えるのは非常にもったいないので……）

(2)

前回（Part00）の復習です。

初期条件 $y (1) = 1$ なので、 $x = 1$ のとき $y = 1$ を満たす。

ここで、 $x = 1$ を代入すると、 $\begin{aligned} y & = - \frac{1}{2 x^{2} + C} \\ = - \frac{1}{2 + C} \\ = 1 \end{aligned}$ となるので、 $C = - 3$ となる。

よって、特解は $y = - \frac{1}{2 x^{2} - 3}$ となる。

※もちろん $- \frac{1}{y} = 2 x^{2} - 3$ の形でもOKです。

（今回は y = にした形の式から計算しましたが、基本的に y = にする前の式を使って任意定数 $C$ の値を決定することをおすすめします。）

スポンサードリンク

３．応用例1　ニュートンの冷却の法則

皆さんは喫茶店やカフェなどで熱いコーヒーを頼んだことはありますか？

せっかく頼んだ熱いコーヒーも、しばらくすると冷めちゃいますね。

実はコーヒーなどの熱い飲み物が冷めるまでの速度（温度の下降速度）は、コーヒーの温度と室温の温度差に比例するのです！　これをニュートンの冷却の法則と呼びます。

早速ニュートンの冷却の法則を使った例題を1問解いてみましょう。

例題2

たまにスターバッ〇スに通う私ももやまは、甘いものが大好きなので「ホワイトモカ」を注文した。

注文後に店員に用意していただいた「ホワイトモカ」は90℃と大変あったかいが、私がいた場所はなんと札幌！　外の気温はなんと-10℃だった！　このままではすぐに冷めてしまう！

そこで、ふと私は「このホワイトモカっていつ冷めるんだろう？」と考えてみることにした。次の(1)～(3)の問いに答えなさい。

ただし、90℃のときから $t$ 分経過したコーヒーの温度を $y (t)$ ℃とし、ホワイトモカの温度の下降速度 $\frac{d y}{d x}$ はホワイトモカの温度と気温の差に比例するものとし、この比例定数を $k$ （ただし $k < 0$ ）とする。

(1) $y (t)$ が満たす微分方程式と初期条件を書きなさい。
(2) (1)の微分方程式の一般解と特解を求めなさい。
(3) 4分後に再びホワイトモカの温度を測定したところ70℃に低下していたことがわかった。8分後のホワイトモカの温度は何度に低下しているかを、比例定数 $k$ を求めることで計算しなさい。（有効数字は2桁とすること）

解説2

(1)

初期条件は、 $t = 0$ 分のときの 90℃ なので、 $y (0) = 90$ となる。

また、ホワイトモカの下降速度 $\frac{d y}{d t}$ はホワイトモカの温度(90℃)と、気温 (-10℃)の差に比例するので、 $\begin{aligned} \frac{d y}{d t} & = k (y (t) - (- 10)) \\ = k (y (t) + 10) \end{aligned}$ となる。

(2)

以下、 $y (t)$ を $y$ と表す。

微分方程式 $\begin{array}{r} \frac{d y}{d t} = k (y + 10) \end{array}$ を変数分離形にするために左辺を $y$ の式 × $\frac{d y}{d t}$ 、右辺を $t$ の式に変形します。すると、 $\frac{1}{y + 10} \cdot \frac{d y}{d t} = k$ と変形できます。。

さらに、両辺を $t$ で積分すると、 $\int \frac{1}{y + 10} \cdot \frac{d y}{d t} d t = \int k d t$ となるので、 $\int \frac{1}{y + 10} d y = \int k d t$ を計算することで一般解を求められます。

よって、一般解は任意定数 $C_{1}$ を用いて $\log | y + 10 | = k t + C_{1}$ となります。さらに変形すると、 $y + 10 = e^{k t} e^{C_{1}}$ となるので、 $C = e^{C_{1}}$ とすることで、 $y = C e^{k t} - 10$ となります。

ここで、初期値 $y (0) = 90$ より、 $t = 0$ , $y = 90$ を代入すると、 $90 = C - 10$ となるので、 $C = 100$ と求められます。よって特解は $y = 100 e^{k t} - 10$ と求められます。

（基本的に指示がない場合は y = の形に変形しなくてもOKです。y = の形に変形するときに間違えるのは非常にもったいないので……）

(3)

4分後に温度が70℃になっていたので、 $y (4) = 70$ が成立する。

$t = 4$ , $y = 70$ を代入すると、 $70 = 100 e^{4 k} - 10$ となるので、 $e^{4 k} = \frac{4}{5}$ と求められます。

よって、8分後の温度 $y$ は、 $\begin{aligned} y & = 100 e^{8 k} - 10 \\ = 100 {(e^{4 k})}^{2} - 10 \\ = 100 {(\frac{4}{5})}^{2} - 10 \\ = 54 \end{aligned}$ となり、54℃と求められます。

なお、経過時間 $t$ と、コーヒーの温度 $y$ のグラフは下のようになります。

ちなみに比例定数 $k$ は、 $4 k = \log \frac{4}{5}$ $k = - \frac{1}{4} \log \frac{5}{4}$ と計算することができます。

４．応用例2　ロジスティック方程式

人間などの生物の個体数 $y$ の増加速度 $\frac{d y}{d t}$ は、十分よい環境であれば、個体数 $y$ と比例し、比例定数 $k$ （ただし $k > 0$ ）を用いて $\frac{d y}{d t} = k y$ と表すことができます。この法則をマルサスの法則と呼びます。

しかし、食料不足などの問題が発生するため、人間や他の生物の人口の増加は無限に続かず、いつか増加の限界がやってきます。

そこで、生物の個体数（人口） $y$ の上限を $L$ とし、 $y$ が $L$ に近づくほど増加速度が遅くなるな式が考えられました。

具体的には $\frac{d y}{d t} = k (1 - \frac{y}{L}) y$ のように、比例定数 $k$ が、個体数 $y$ が増えれば増えるほど減り*3、 $y = L$ と上限に達したら増加が止まるような式が考えられました。

この微分方程式 $\frac{d y}{d t} = k (1 - \frac{y}{L}) y$ のことをロジスティック方程式と呼びます。

例題で具体的に解いてみましょう。

例題3

現在、最大10,000匹がすめるうさぎ島には100匹のうさぎが住んでいる。

この島のうさぎが増える速さ $\frac{d y}{d t}$ は、うさぎの数 $y$ 、上限数 $L$ 、比例定数 $k$ を用いて $\frac{d y}{d t} = k (1 - \frac{y}{L}) y$ と表すことができる。（ロジスティック方程式）

このとき、つぎの(1)～(3)の問いに答えなさい。ただし、必要であれば $11^{x} = 99$ の解が $x = 1.91$ であることを用いてよい。

(1) ロジスティック方程式の一般解を求めなさい。
(2) 初期条件 $y (0) = 100$ , $L = 10000$ を代入し、特解を求めなさい。
(3) 10日後にうさぎ島のうさぎは1,000匹に増えていた。うさぎが5,000匹を超えるのは何日目かを、比例定数 $k$ を求めることで計算しなさい。（有効数字3桁で）

（ (3)は電卓を使ってもOK）

解説3

微分方程式 $\begin{aligned} \frac{d y}{d t} & = k (1 - \frac{y}{L}) y \\ \frac{d y}{d t} & = k y \cdot \frac{L - y}{L} \end{aligned}$ を変数分離形にするために左辺を $y$ の式 × $\frac{d y}{d t}$ 、右辺を $t$ の式に変形します。すると、 $\frac{1}{y (L - y)} \cdot \frac{d y}{d t} = \frac{k}{L}$ と変形できます。

さらに、両辺を $t$ で積分すると、 $\int \frac{1}{y (L - y)} \cdot \frac{d y}{d t} d t = \int \frac{k}{L} d t$ となるので、 $\int \frac{1}{y (L - y)} d y = \int \frac{k}{L} d t$ を計算することで一般解を求められます。

ここで左辺の積分は、 $\begin{aligned} \int \frac{1}{y (L - y)} d y & = \int \frac{1}{L} (\frac{1}{y} + \frac{1}{L - y}) d y \\ = \frac{1}{L} \int \frac{1}{y} d y + \frac{1}{L} \int \frac{1}{L - y} d y \\ = \frac{1}{L} \log y - \frac{1}{L} \log (L - y) \end{aligned}$ と求められる。（積分定数は省略）

（部分分数分解の積分が怪しいひとはこちらで復習すること！）

よって、一般解は、任意定数 $C_{1}$ を用いて $\frac{1}{L} \log y - \frac{1}{L} \log (L - y) = \frac{k}{L} t + C_{1}$ と求められる。

式を変形していくと、 $\log \frac{y}{L - y} = k t + L C_{1}$ $- \log \frac{L - y}{y} = \log e^{k t} + \log e^{L C_{1}}$ $\frac{L - y}{y} = e^{- k t} e^{- L C_{1}}$ $\frac{L}{y} - 1 = e^{- k t} e^{- L C_{1}}$ $\frac{L}{y} = 1 + e^{- k t} e^{- L C_{1}}$ $\frac{L}{y} = 1 + e^{- k t} e^{- L C_{1}}$ $y = \frac{L}{1 + e^{- k t} e^{- L C_{1}}}$ と変形できるので、 $C = e^{- L C_{1}}$ とあらためて任意定数をおくことで、 $y = \frac{L}{1 + C e^{- k t}}$ と一般解を解くことができます。

(2)

初期値 $y (0) = 100$ より、 $t = 0$ , $y = 100$ を代入すると、 $100 = \frac{L}{1 + C}$ となり、さらに $L = 10000$ なので、 $100 = \frac{10000}{1 + C}$ となります。よって、 $C = 99$ と求められ、特解は $y = \frac{10000}{1 + 99 e^{- k t}}$ と求められます。

(3)

10日後に1,000匹になっていたので、 $y (10) = 1000$ が成立する。

$t = 10$ , $y = 1000$ を代入すると、 $1000 = \frac{10000}{1 + 99 e^{- 10 k}}$ となるので、 $e^{- 10 k} = \frac{1}{11}$ と求められます。

よって、 $10 n$ 日後のうさぎの数は、 $\frac{10000}{1 + 99 e^{- 10 k}} = \frac{10000}{1 + {(\frac{1}{11})}^{n}}$ を計算することで求めることができます。

求めたいのは、5,000匹になる日にちなので、 $\begin{aligned} 5000 & = \frac{10000}{1 + 99 \cdot {(\frac{1}{11})}^{n}} \\ = \frac{10000 \cdot 11^{n}}{11^{n} + 99} \end{aligned}$ と変形できるので、 $11^{n} = 99$ が成立します。

問題文より $n = 1.91$ なので、19.1日後にうさぎの数が5,000匹になることがわかります。

なお、ある日付 $t$ によるウサギの数 $y$ のグラフは、下のようになります。

日数が経過すればするほど、限界値である $L$ （今回は10,000）に近づいていることがよくわかりますね！

このグラフはロジスティクス曲線と呼ばれ、生物（今回はうさぎ）の増加具合を表しています。この曲線の特徴として、

グラフがs字型の曲線を描く
最初は個体数が少ないので緩やかに増加
個体数が増えると増加速度が上がる
限界 $L$ に近くなると増加速度は下がる
限界を迎えると増加速度は0になる

があります。

５．練習問題

では、3問ほど練習してみましょう。

2問が変数分離形の計算問題、残り1問が「放射線物質の崩壊」に関する文章問題となっております。

練習1

1階微分微分方程式 $\frac{d y}{d x} = \frac{x y}{x^{2} + 1}$ について、(1), (2)の問いに答えなさい。

(1) 一般解を求めなさい。
(2) 初期条件 $y (1) = 2$ を満たす特解を求めなさい。

練習2

1階微分微分方程式 $x \frac{d y}{d x} + 2 y = x y$ について、(1), (2)の問いに答えなさい。

(1) 一般解を求めなさい。
(2) 初期条件 $y (1) = e$ を満たす特解を求めなさい。

練習3　放射性物質の崩壊

放射性物質は、現在の物質量に比例した速さで崩壊（減衰）していく。この比例速度を $k$ （ただし $k < 0$ ）とする。

このとき、(1)～(5)の問いに答えなさい。必要であれば $\sqrt{2} = 1.4$ を用いること。

(1) ある時刻 $t$ （日目）における物質量が $y (t)$ [g] だったとき、 $y (t)$ が満たす微分方程式を書きなさい。
(2) (1) で求めた微分方程式の一般解を求めなさい。
(3) ある放射線物質の初期の量が10 [g]、つまり $y (0) = 10$ とする。このときの特解を比例定数 $k$ を用いて求めなさい。
(4) ある放射線物質の半減期は4日だった。(3)の特解から比例定数 $k$ を求めなさい。
(5) (4)の放射線物質が10[g]あるとする。10日後の放射線物質の量を有効数字2桁で求めなさい。

６．練習問題の答え

解答1

(1)

まず、変数分離形にするために左辺を $y$ の式 × $\frac{d y}{d x}$ 、右辺を $x$ の式に変形してみよう。すると、 $\frac{1}{y} \cdot \frac{d y}{d x} = \frac{x}{x^{2} + 1}$ と変形できる。

よって、両辺を $x$ で積分すると、 $\int \frac{1}{y} \cdot \frac{d y}{d x} d x = \int \frac{x}{x^{2} + 1} d x$ となるので、 $\int \frac{1}{y} d y = \int \frac{x}{x^{2} + 1} d x$ を計算することで一般解を求められる。

それぞれの積分計算は $\int \frac{1}{y} d y = \log | y |$ $\begin{aligned} \int \frac{x}{x^{2} + 1} & = \frac{1}{2} \int \frac{2 x}{x^{2} + 1} \\ = \frac{1}{2} \log (x^{2} + 1) \end{aligned}$ となる。（ただし、任意定数は省略した。）

よって、一般解は任意定数 $C$ を用いて、 $\log | y | = \frac{1}{2} \log (x^{2} + 1) + C$ と求められる。

[y = の形に変えていく]

ここで、 $C = \frac{1}{2} \log D_{1}$ とおくと、 $\log | y | = \frac{1}{2} \log (x^{2} + 1) + \frac{1}{2} \log D_{1}$ となるので、 $\log$ の計算法則により、 $\log | y | = \frac{1}{2} \log D_{1} (x^{2} + 1)$ となるので、 $| y | = \sqrt{D_{1}} \sqrt{x^{2} + 1}$ $y = \pm \sqrt{D_{1}} \sqrt{x^{2} + 1}$ となる。さらに $D_{2} = \pm \sqrt{D_{1}}$ とおくことで、 $y = D_{2} \sqrt{x^{2} + 1}$ と y = の式に変形することができる。

(2)

初期条件 $y (1) = 2$ なので、 $x = 1$ のとき $y = 2$ を満たす。

ここで、(1)の解に $x = 1$ , $y = 2$ を代入すると、 $\begin{array}{r} \log 2 = \frac{1}{2} \log 2 + C \end{array}$ となるので、 $C = \frac{1}{2} \log 2$ となる。

よって、特解は $\log | y | = \frac{1}{2} \log (x^{2} + 1) + \frac{1}{2} \log 2$ となる。

y = の形の場合だと、 $D_{2} = \sqrt{2}$ となるので、 $y = \sqrt{2 (x^{2} + 1)}$ が答え。

解答2

(1)

変数分離形にするために左辺を $y$ の式 × $\frac{d y}{d x}$ 、右辺を $x$ の式に変形しよう。

両辺を $x y$ で割ると、 $\frac{1}{y} \frac{d y}{d x} + \frac{2}{x} = 1$ となる（ただし $x \neq 0$ , $y \neq 0$ に注意）ので、さらに移項させると $\frac{1}{y} \frac{d y}{d x} + \frac{2}{x} = 1$ と変形できる。

すると、 $\frac{1}{y} \frac{d y}{d x} = 1 - \frac{2}{x}$ と変形できる。

さらに、両辺を $x$ で積分すると、 $\int \frac{1}{y} \frac{d y}{d x} d x = 1 - \frac{2}{x} d x$ となるので、 $\int \frac{1}{y} d y = \int 1 - \frac{2}{x} d x$ を計算することで一般解を求められる。

よって、一般解は任意定数 $C$ を用いて $\log y = x - 2 \log x + C$ となる。

なお、y = の形に変形すると $\begin{aligned} \log y & = \log e^{x} - \log x^{2} + \log e^{C} \\ = \log \frac{e^{C} e^{x}}{x^{2}} \end{aligned}$ となるので、任意定数を $D = e^{C}$ とおきなおし、 $y = \frac{D e^{x}}{x^{2}}$ としてもよい。

でも変形ミス多発するから自信のある人か指示されたとき以外はやめようね！

(2)

初期条件 $y (1) = e$ なので、 $x = 1$ のとき $y = e$ を満たす。

ここで、(1)の解に $x = 1$ , $y = e$ を代入すると、 $\begin{aligned} \log e & = 1 - \log 1 + C \\ = 1 + C \\ = 1 \end{aligned}$ となるので、 $C = 0$ となる。

よって、特解は $\log y = x - 2 \log x$ となる。

y = の形の場合だと、 $D = 1$ となるので、 $y = \frac{e^{x}}{x^{2}}$ が答え。

解答3

(1)

放射線物質の物質量 $y (t)$ は、比例速度 $k$ に比例して崩壊するので、 $\frac{d y}{d t} = k y (t)$ となる。 $k$ は負の値なので、マイナスをつけないように注意！

(2)

以下、 $y (t)$ を $y$ と記す。

変数分離形にするために左辺を $y$ の式 × $\frac{d y}{d t}$ 、右辺を $t$ の式に変形しよう。すると、 $\frac{1}{y} \cdot \frac{d y}{d t} = k$ と変形できる。

よって、両辺を $t$ で積分すると、 $\int \frac{1}{y} \cdot \frac{d y}{d x} d x = \int k d t$ となるので、 $\int \frac{1}{y} d y = \int k d t$ を計算することで一般解を求められる。

よって、一般解は任意定数 $C$ を用いて $\log y = k t + C$ となる。

なお、y = の形に変形すると $\begin{array}{r} \log y = \log e^{k t} + \log e^{C} \end{array}$ となるので、任意定数を $D = e^{C}$ とおきなおし、 $y = C e^{k t}$ としてもよい。

(3)

初期条件 $y (0) = 10$ なので、 $t = 0$ のとき $y = 10$ を満たす。

ここで、(1)の解に $t = 0$ , $y = 10$ を代入すると、 $\begin{array}{r} \log 10 = C \end{array}$ となるので、 $C = \log 10$ となる。

よって、特解は $\log y = k t + \log 10$ となる。

y = の形の場合だと、 $D = 10$ となるので、 $y = 10 e^{k t}$ が答え。

(4)

半減期が4日なので、 $t = 4$ のとき、 $y = 5$ （初日は $y = 10$ だったので半減期経過すると物質は半分）となる。つまり、 $\log 5 = 4 k + \log 10$ となる。変形すると、 $- 4 k = \log 2$ となるので、比例定数 $k$ は、 $k = - \frac{1}{4} \log 2$ となる。（確かに $k$ が負になってるね！）

(5)

10日後なので、 $t = 10$ を代入すればよい。 $\log y = - \frac{5}{2} \log 2 + \log 10$ $\log y = \log \frac{10}{4 \sqrt{2}} = \log \frac{5}{2 \sqrt{2}}$ となるので、 $\begin{aligned} y & = \frac{5}{2 \sqrt{2}} \\ = \frac{5 \sqrt{2}}{4} \\ = \frac{7}{4} \\ = 1.75 \end{aligned}$ となるので、10日後に放射線物質は 1.8 [g] となることがわかる*4。

なお、時間経過 $t$ と、物質量 $y$ のグラフを下に示しているので参考までにどうぞ。

７．さいごに

今回は、1階微分方程式の中でも簡単にとける変数分離形の微分方程式の解き方について説明し、応用例として

ニュートンの冷却の法則
ロジスティック方程式
放射線崩壊の崩壊速度

について紹介しました。

次回は、置き換えることで簡単に解くことができる同次形の微分方程式について説明していきたいと思います。

では、さらば！

*1:厳密には合成関数の微分を使い、 $\begin{aligned} \frac{1}{h (y)} \frac{d y}{d x} & = \frac{d}{d y} (\int \frac{1}{h (y)} d y) \frac{d y}{d x} \\ = \frac{d}{d x} \int \frac{1}{h (y)} d y \end{aligned}$ と変形できるので、 $\frac{d}{d x} \int \frac{1}{h (y)} d y = g (x)$ の両辺を $x$ で積分し、 $\int \frac{1}{h (y)} d y = \int g (x) d x$ とすることで一般解を算出できる。