うさぎでもわかる複素解析　Part3　複素べき級数の収束半径・複素べき級数の総和

こんにちは、ももやまです。

今回は、複素べき級数の収束半径を求めるダランベールの法則・アダマールの法則、および複素べき級数の総和を求める方法についてまとめていきたいと思います。

 

 

前回の複素解析（応用数学）の記事はこちら！

www.momoyama-usagi.com

 

スポンサードリンク

１．複素べき級数とは

収束半径を説明する前にまず、複素べき級数について説明したいと思います。

複素べき級数とは、\[\begin{align*}
f(z) & = \sum^n_{i = 0} a_n z^n
\\ & = c_0 + c_1 z + c_2 z^2 + \cdots + c_n z^n + \cdots
\end{align*} \]のように複素数 \( z \) の整数乗 \( z^n \) からつくられる級数のことを表します。（係数 \( c_n \) は複素数でもOKです！）

 

さらに上の式の \( z \) を \( z-a \) と置き換え、\[\begin{align*}
f(z) & = \sum^n_{i = 0} c_n (z-a)^n
\\ & = c_0 + c_1 (z-a) + c_2 (z-a)^2 + \cdots + c_n (z-a)^n + \cdots
\end{align*} \]の \( a \) を展開の中心と言います。

 

例えば、\[\begin{align*}
f(z) & = \sum^n_{i = 0} c_n (z-2)^n
\\ & = c_0 + c_1 (z-2) + c_2 (z-2)^2 + \cdots + c_n (z-2)^n + \cdots
\end{align*} \]であれば、\( z = 2 \) が中心のべき級数展開と呼びます。

（\( z = 0 \) のべき級数展開場合を単にべき級数展開と呼ぶこともあります。単にべき級数展開すると書いている場合は、\( z = 0 \) 中心のべき級数展開だと思ってください。）

 

スポンサードリンク

２．収束半径とは

1で説明したべき級数 \( f(z) \) がどこまでなら収束し、どこから発散するのかを展開の中心 \( a \) からの半径で示したものが収束半径となります。 

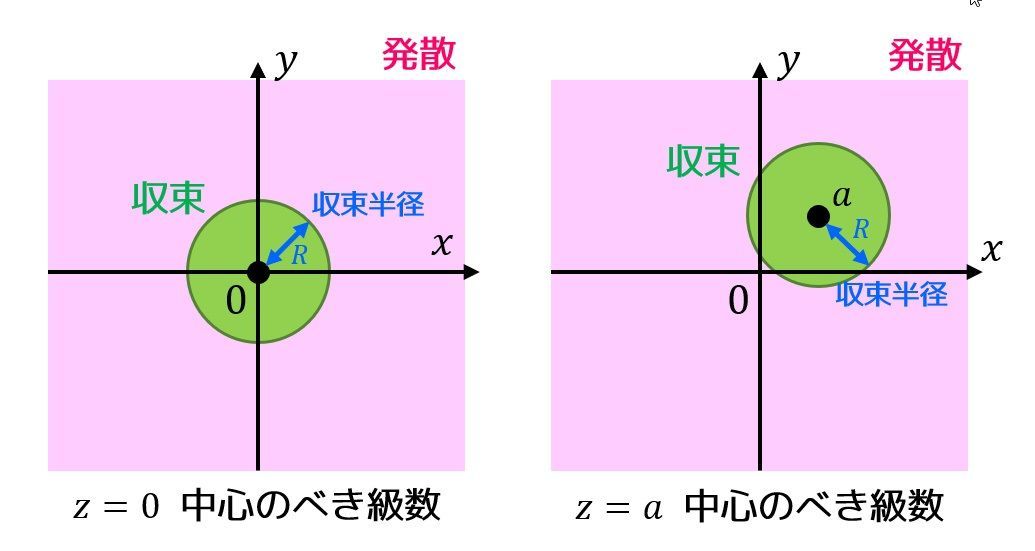
例えばある複素べき級数の収束半径が3であれば、原点からの距離が3未満である \( |z-a| \lt 3 \) で収束し、距離が3を超えた \( |z-a| \gt 3 \) で発散することをしてしています*1。

また、収束半径が0であればその級数は常に発散することを示し、収束半径が無限大であればその級数が常に収束することを示します。

 

では、収束半径を求める方法を説明していきましょう。

2つの方法があるので順番に説明していきたいと思います。

その1：ダランベールの公式

べき級数が収束するためには、\( n \) が大きくなるにつれて、項の大きさ \( c_n \) が小さくなる必要がありますね。

言い換えると、\( n \) 項にくらべて次の項 \( n+1 \) 項が小さくなればいいですね。数式にすると、\[
| c_n (z-a)^n | > | c_{n+1} (z-a)^{n+1}  |
\]を満たす必要があります。この式を変形すると、\[
| c_n | > | c_{n+1} (z-a) | \\
R =  \left| \frac{ c_n }{  c_{n+1}  } \right| > |z|
\]となります。

よって収束半径 \( R \) を調べるには、\[
\lim_{n \to \infty} \left| \frac{ c_n }{ c_{n+1} } \right|
\]を調べればいいことがわかりますね！

これをダランベールの公式と呼びます。

 

とある項 \( z^n \) の係数をその次の項 \( z^{n+1} \) の係数で割って \( n \to \infty \) に飛ばすだけで収束半径は求められると頭には入れておきましょう*2。 

 

では、1問例題を解いてみましょう！

例題1

つぎの複素級数\[
\sum^{\infty}_{n = 1} ( 3^n - 2 ) z^{n-1} = 1 + 7z + 25z^2 + 79z^3 
 \]の収束半径を求めなさい。

解説1

ダランベールの公式より収束半径は、\[\begin{align*}
R = & \lim_{n \to \infty} \left| \frac{ 3^n - 2}{3^{n+1} - 2} \right| 
\\ = & \ \lim_{n \to \infty} \left| \frac{ 3 \cdot 3^n - 2}{3^{n+1} - 1} \right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ 1 - 2 \left( \frac{1}{3} \right)^n }{3 - 2 \left( \frac{1}{3} \right)^n} \right|
\\ = & \ \frac{1}{3}
\end{align*} \]で求められる。

 

その2：アダマールの公式

しかし、ダランベールの公式だけでは収束半径が求められないことがあります。そういうときに便利なのがアダマールの法則です。

今回は先に公式のほうを紹介してしまいます！

 

この公式は、特に \( n \) 乗が含まれている複素べき級数に対して効果を発揮します。

 

例題2

つぎの複素級数\[
\sum^{\infty}_{n = 1} \frac{(-1)^n}{3^n} z^n 
 \]の収束半径を求めなさい。 

解答2

アダマールの公式より収束半径は、\[\begin{align*}
R = & \lim_{n \to \infty} \frac{1}{  \sqrt[n]{ \left| \frac{ (-1)^n }{ 3^n } \right| } }
\\ = & \frac{1}{ \frac{1}{3} } 
\\ = & \ 3
\end{align*} \]となる。

 

[別解]

ダランベールの公式を使っても解くことができる。

収束半径は、\[\begin{align*}
R = & \lim_{n \to \infty} \left| \frac{ \frac{(-1)^n}{3^n} }{ \frac{(-1)^{n+1} }{3^{n+1} } } \right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ \frac{(-1)^n}{3^n} }{ \frac{-1 (-1)^{n} }{3 \cdot 3^n} } \right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ \frac{( -\frac{1}{3} )^n }{1} }{ \frac{-1 (- \frac{1}{3} )^n }{3} } \right|
\\ = & \ 3
\end{align*} \]で求められる。

 

スポンサードリンク

３．無限級数の計算順序

(1) 計算順序の入れ替えには要注意！

皆さんは計算をする際にの計算しやすくするために計算順序を変えてから計算することがありますよね。例えば、\[
 666 + 25252 - 1666 - 5252
\]の計算をする際に、計算の順番を変えて\[
25252 - 5252 + 666 - 1666
\]と計算しても同じ結果（19000）が得られますね。

しかし、項が無限個になると必ずしも計算順序を変更しても同じ答えになるとは限りません。

ということで1つ例をみてみましょう。

 

今回はアンサイクロペディアにすごくいい例があったので紹介します。

足し算を利用した証明方法\[\begin{align*}
0 & = 0 + 0 + 0 + \cdots
\\ & = (1-1) + (1-1) + (1-1) + \cdots
\\ & = 1 + (-1+1) + (-1+1) +(-1+1)
\\ & = 1 + 0 + 0 + 0 + \cdots
\\ & = 1
\end{align*} \]このことから、\[
0 = 1
\]よって、\[
1 = 2
\]（引用元：アンサイクロペディア「1=2」）

あれ、1=2 が示せちゃった！！

と思うじゃないですか。これ、反例なんですよ。

てなわけで、なんで 1=2 が示せちゃったのかを下のほうで説明していきましょう。

(2) 絶対収束

次のような無限級数があったとします。\[
a_1 + a_2 + \cdots + a_n + \cdots
\]。この級数のそれぞれの項に絶対値を付けて、\[
| a_1 | + | a_2 | + \cdots + | a_n | + \cdots
\]とします。この状態（各項に絶対値がついた状態）でも無限級数が収束する場合、その無限級数は絶対収束すると言います。

 

さらに、無限級数が絶対収束することを示せば無限個の項の和を計算する際でも計算順序を入れ替えてもよいことを示せます。

言い換えると、無限級数が絶対収束しないということは、無限級数の計算順序を変えてしまうと和が別の値に収束してしまう or 発散する可能性があります。

先ほどの例でいくと、\[\begin{align*} &
\sum^{\infty}_{n = 1} (-1)^{n-1} 
\\ = & \ 1 - 1 + 1 - 1 + \cdots  
 \end{align*} \]の絶対値を取ると、\[\begin{align*} &
\sum^{\infty}_{n = 1} \left| (-1)^{n-1} \right|
\\ = & \ 1 + 1 + 1 + 1 + \cdots  
\\ = & \ \lim_{n \to \infty} n
 \end{align*} \]となるので正の無限大に発散してしまい、絶対収束しません*3。

なので、計算順序を変えてしまうと和が変化してしまうかもしれないことがわかりますね*4。

 

(3) 無限級数同士の和の入れ替え条件

先ほどは無限級数内での和の入れ替え可能条件について説明しました。

では、無限級数同士の和の場合はどうなるでしょうか。

 

この定理は、2つの無限級数が両方収束することを示せば、計算順序が\[
a_1 + b_1 + a_2 + b_2 + a_3 + b_3 + \cdots
\]であっても、\[
a_1 + a_2 + \cdots + b_1 + b_2 + \cdots
\]のように入れ替えてあげることができます。

 

試しに計算順序を入れ替られることを確認するために1問例題を思っていたのですが、一応念のため無限級数の和の計算方法について確認しておきましょう。

 

(4) 無限等比数列の総和（復習）

念のため、べき級数（無限等比数列）の和の公式を確認しておきましょう。

初項 \( a \) 公比 \( r \) の等比数列の和の公式は\[
\frac{a (1 - r^n) }{1 - r}
\]ですね。

この和を \( n \to \infty \) に飛ばせばいいので、\(   |r| \lt 1 \) のとき、\[
\lim_{n \to \infty} \frac{a (1 - r^n) }{1 - r} = \frac{a}{1 - r}
\]に収束することがわかりますね。

（ \( |r| \geqq 1 \) の場合は発散します）

 

 

ではここで例題をもう1問解いてみましょう。

例題3

つぎの複素べき級数\[
\sum^{\infty}_{n = 1} ( 3^n - 2 ) z^{n-1} = 1 + 7z + 25z^2 + 79z^3 
 \]の収束円内における和 \( S \) を計算しなさい。

解答3

収束円内における和なので、計算順序を入れ替えても総和は変わりませんね*5。

なので、計算順序を入れ替えて、\[\begin{align*}
S & = \sum^{\infty}_{n = 1} ( 3^n - 2 ) z^{n-1} 
\\ & = \sum^{\infty}_{n = 1} ( 3 \cdot 3^{n-1} - 2 ) z^{n-1} 
\\ & = 3 \sum^{\infty}_{n = 1} 3^{n-1} z^{n-1} - 2 z^{n-1}
\\ & = 3 \sum^{\infty}_{n = 1} (3z)^{n-1} - 2 \sum^{\infty}_{n = 1} z^{n-1}
\end{align*}\]も総和 \( S \) は変わらない。

 

あとは個別に総和を計算するだけ。\[
\sum^{\infty}_{n = 1} (3z)^{n-1}
\]は初項1、公比 \( 3z \) の無限等比級数なので、\[
\sum^{\infty}_{n = 1} (3z)^{n-1} = \frac{1}{1-3z}
\]となり、\[
\sum^{\infty}_{n = 1} z^{n-1}
\]は初項1、公比 \( z \) の無限等比級数なので、\[
\sum^{\infty}_{n = 1} z^{n-1} = \frac{1}{1-z}
\]となる。

よって、\[\begin{align*}
S & = \sum^{\infty}_{n = 1} ( 3^n - 2 ) z^{n-1} 
\\ & = \ 3 \sum^{\infty}_{n = 1} (3z)^{n-1} - 2 \sum^{\infty}_{n = 1} z^{n-1}
\\ & = \ 3 \cdot \frac{1}{1-3z} - 2 \cdot \frac{1}{1-z}
\\ & = \frac{3(1-z) - 2(1-3z)}{ (1-3z)(1-z) }
\\ & = \frac{3z+1}{ (1-3z)(1-z) }
\end{align*}\]と求めることができます。

 

(4) 無限級数同士の和の入れ替え条件

例えば、下のような級数の第5項までの和\[
\sum^{5}_{n =  1} z^{n-1} = 1 + z + z^2 + z^3 + z^4 + z^5
\]の両辺を微分して、\[\begin{align*}
\frac{d}{dz} \sum^{5}_{n =  1} z^{n-1} & = \frac{d}{dz} (1 + z + z^2 + z^3 + z^4 + z^5 )
\\ & = 1 + 2z + 3z^2 + 4z^3 + 5z^4
\\ & = \sum^{5}_{n=1} n z^{n-1}
\end{align*} \]と変形できるので、\[
\frac{d}{dz} \sum^{5}_{n =  1} z^{n-1} =  \sum^{5}_{n =  1} \frac{d}{dz} z^{n-1} 
\]が成立しますね！　これを項別微分と呼びます。

 

しかし、無限級数となるとどうでしょうか。

無限という概念が入ってしまうため「無限」を微分とかいうわけわからんことが起こりますね。

なので、無限級数が収束するかどうかを確認してから項別微分を行いましょう。

 

さらに例題を1問みてみましょう。

例題4

つぎの複素べき級数\[
1 + z + 2z^2 + 3z^3 + \cdots + n z^n + \cdots
 \]について、次の問いに答えなさい。

(1) 収束半径 \( R \) を求めなさい。
(2) (1)で求めた収束円内における総和 \( S \) を求めなさい。

解説4

(1)

複素べき級数は、\[
1 + \sum^{\infty}_{n = 1} n z^n
\]となる。つまり、\[
\sum^{\infty}_{n = 1} n z^n
\]の収束半径を求めればいい。（最初の1はあってもなくても収束半径は変わらない）

ここで、ダランベールの公式より、\[\begin{align*}
R = & \lim_{n \to \infty} \left| \frac{ n }{ n+ 1} \right| 
\\ = & \ 1
\end{align*} \]となるので収束半径 \( R \) は1である。

(2)

今回は、\[
\sum^{\infty}_{n = 1} n z^n = z + 2z^2 + 3z^3 + \cdots + n z^n + \cdots
\]の形なので、計算順序の入れ替えでは総和を求められない。

ここで、初項1、公比 \( z \) の無限等比数列\[
\frac{1}{1-z} = 1 + z + z^2 + z^3 + \cdots + z^n +
\]を考える。

収束円内における和なので、項別微分を行うことができる。つまり、\[\begin{align*}
\frac{d}{dz} \frac{1}{1-z} = & 1 + 2z + 3z^2 + \cdots + n z^{n-1} + (n+1) z^n
\\ = & \frac{1}{(1-z)^2}
\end{align*} \]が成立する。

ここで、項別微分したものから元のやつを引くことを考える。すると、\[\begin{align*}
\frac{1}{(1-z)^2} - \frac{1}{1-z} = z + 2z^2 + 3z^3 + \cdots + n z^n + \cdots
\end{align*}\]となる。（計算過程は下の画像参照）

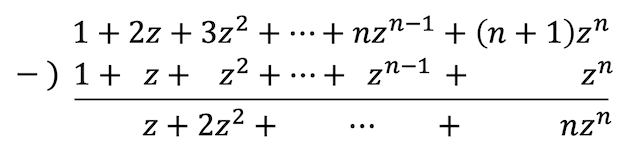
この計算結果に1を加えると題意の複素べき級数となる。よって、\[\begin{align*} &
1 + z + 2z^2 + 3z^3 + \cdots + n z^n + \cdots 
\\ = & \ \frac{1}{(1-z)^2} - \frac{1}{1-z} + 1
\\ = & \ S
\end{align*} \]となる。

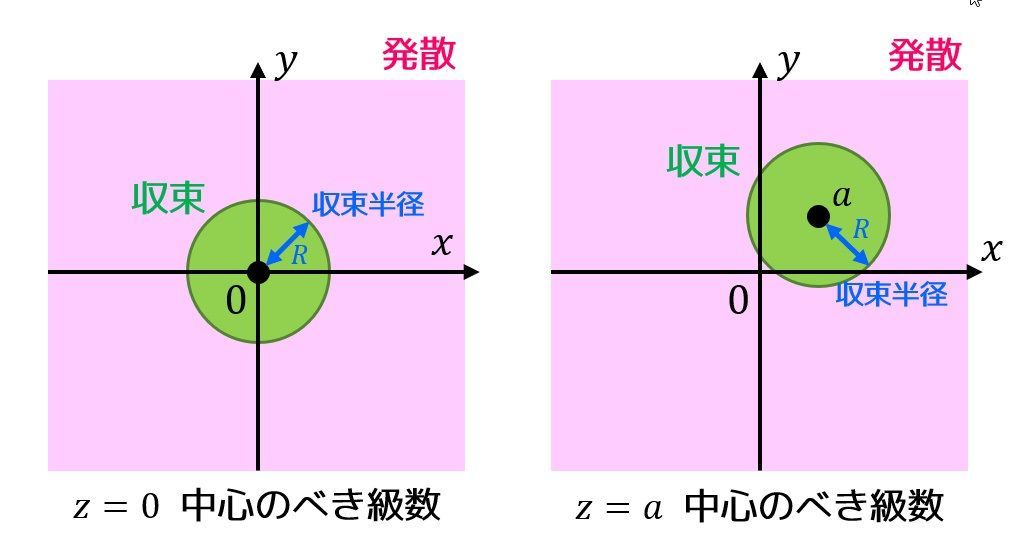
４．特異点と収束半径

例えば、\[
f(z) = \frac{1}{1+z}
\]は、\( z = -1 \) のとき、関数 \( f(z) \) の分母が0になってしまって定義されませんよね。

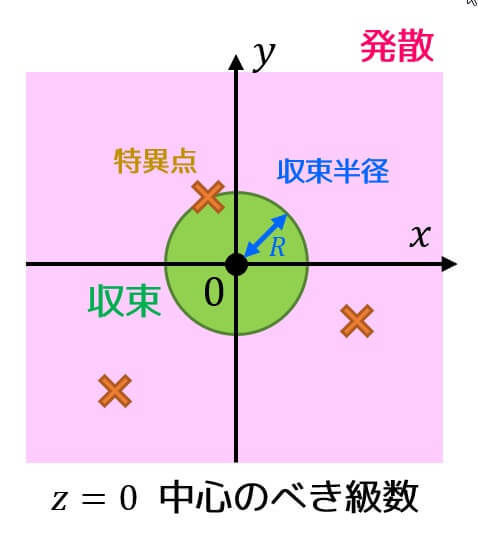
このように、ある点 \( z \) において定義されない（正則ではない）ような点を特異点と呼びます*6。

さきほどべき級数の総和を求める方法を説明しました。
実はべき級数の収束半径は、展開の中心から最も近い特異点までの距離となるのです！

図で書くとわかりやすいとおもうので図を下に書いてみました。

例えば、例題1のべき級数の和\[
\frac{3z+1}{ (1-3z)(1-z) }
\]の特異点は \( z = 1, 1/3 \) の2つでしたね。なので最も近い特異点 \( z = 1/3 \) と中心の距離は \( 1/3 \) なので、確かに収束半径が \( 1/3 \) となっていることがわかりますね。

 

５．練習問題

では、2問だけですが練習してみましょう。

練習1

つぎの複素級数\[
\sum^{\infty}_{n = 1} \frac{(3!)^2}{(2n+1)!} z^n 
 \]の収束半径を求めなさい。 

解答1

ダランベールの公式より収束半径は、\[\begin{align*}
R = & \lim_{n \to \infty} \left| \frac{ \frac{(3n!)^2}{(2n+1)!} }{ \frac{ \left( 3(n+1)! \right)^2 }{ 2( (n+1) + 1) } } \right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ \frac{(3n!)^2}{(2n+1)!} }{ \frac{ \left( 3(n+1)! \right)^2 }{ 2( (n+1) + 1) } } \right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ \frac{ 9 \cdot (n!)^2 }{ (2n+1)!} }{ \frac{9 \left( (n+1)! \right)^2 }{(2n+3)!} } \right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ ( n! )^2 \cdot (2n+3)! }{ ( (n+1)! )^2 \cdot (2n+1)! } \right|
\\ = & \ \lim_{n \to \infty} \left| \left( \frac{n!}{(n+1)!} \right)^2 \cdot \frac{(2n+3)!}{(2n+1)!} \right|
\\ = & \ \lim_{n \to \infty} \left| \left( \frac{1}{n+1} \right)^2 \cdot (2n+3)(2n+2) \right|
\\ = & \ \lim_{n \to \infty} \left| \frac{4n^2 + 10n + 6}{n^2+2n+1} \right|
\\ = & \ 4
\end{align*} \]で求められる。

 

練習2

つぎの複素べき級数\[
\sum^{\infty}_{n = 1} (3^n - 2^n) z^{n-1} 
 \]について、つぎの問いに答えなさい。

(1) 収束半径 \( R \) を求めなさい。
(2) (1)で求めた収束円内における総和 \( S \) を求めなさい。

 

解説2

(1)

ダランベールの公式より収束半径は、\[\begin{align*}
R = & \ \lim_{n \to \infty} \left| \frac{ 3^n - 2^n }{ 3^{n+1} - 2^{n+1} }\right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ 3^n - 2^n }{3 \cdot 3^{n} - 2 \cdot 2^{n} }\right|
\\ = & \ \lim_{n \to \infty} \left| \frac{ 1 - \left( \frac{2}{3} \right)^n }{3 - 2 \cdot \left( \frac{2}{3} \right)^n }\right|
\\ = & \ \frac{1}{3}
\end{align*} \]で求められる。

 

(2)

収束円内における和なので、計算順序を入れ替えても総和は変化しない。

なので、計算順序を入れ替えて、\[\begin{align*}
S & = \sum^{\infty}_{n = 1} (3^n - 2^n) z^{n-1} 
\\ & = \sum^{\infty}_{n = 1} ( 3 \cdot 3^{n-1} - 2 \cdot 2^{n-1} ) z^{n-1} 
\\ & = 3 \sum^{\infty}_{n = 1} 3^{n-1} z^{n-1} - 2 \sum^{\infty}_{n = 1} 2^{n-1} z^{n-1}
\\ & = 3 \sum^{\infty}_{n = 1} (3z)^{n-1} - 2 \sum^{\infty}_{n = 1} (2z)^{n-1} 
\end{align*}\]としても総和 \( S \) は変わらない。

 

個別に総和を計算する。\[
\sum^{\infty}_{n = 1} (3z)^{n-1}
\]は初項1、公比 \( 3z \) の無限等比級数なので、\[
\sum^{\infty}_{n = 1} (3z)^{n-1} = \frac{1}{1-3z}
\]となり、\[
\sum^{\infty}_{n = 1} z^{n-1}
\]は初項1、公比 \( 2z \) の無限等比級数なので、\[
\sum^{\infty}_{n = 1} (2z)^{n-1} = \frac{1}{1-2z}
\]となる。

よって、\[\begin{align*}
S & = \sum^{\infty}_{n = 1} (3^n - 2^n) z^{n-1} 
\\ & = 3 \sum^{\infty}_{n = 1} (3z)^{n-1} - 2 \sum^{\infty}_{n = 1} (2z)^{n-1} 
\\ & = \ 3 \cdot \frac{1}{1-3z} - 2 \cdot \frac{1}{1-2z}
\\ & = \frac{3(1-2z) - 2(1-3z)}{ (1-3z)(1-2z) }
\\ & = \frac{1}{ (1-3z)(1-2z) }
\end{align*}\]と求めることができます。

（特異点は \( z = 1/3 \), \( z = 1/2 \) の2つで、中心 \( z = 0 \) から最も近い特異点 \( z = 1/3 \) までの距離は確かに収束半径と同じ \( R = 1/3 \) と一致しますね。）  

 

６．さいごに

今回は複素べき級数の収束半径を求める際に使うダランベールの公式、アダマールの公式、および複素べき級数の絶対収束、項別微分が可能な条件、計算順序の入れ替えができる条件についてまとめました。

 

複素べき級数の総和を求める際には必ず計算順序が入れ替えできるということを確認してから（答案に確認したことを書いてから）計算順序の入れ替えや項別微分を行いましょう。