スポンサードリンク
こんにちは、ももやまです。
三角関数表記のフーリエ級数変換、\( a_k \), \( b_k \), \( a_0 \) のように3つ係数が出てきて非常にめんどくさいですよね。
そこで、今回はこの3つある表記を複素数の力を借りて1つにする方法について説明していきましょう!
(この内容は、次のフーリエ変換につながるので、仕組みを理解しましょう!!)
目次
スポンサードリンク
1. (復習) 三角関数表記のフーリエ級数・実フーリエ級数
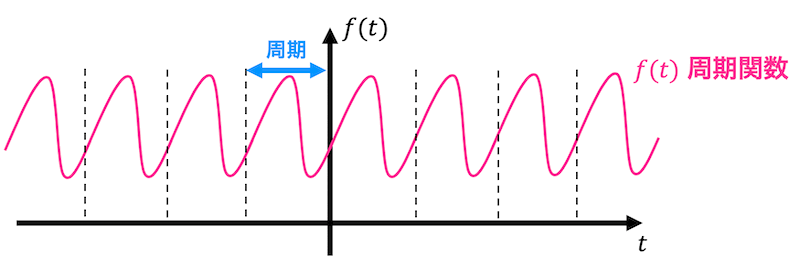
まずは、三角関数表記のフーリエ級数展開について復習しましょう!
周期 \( T \) の区分的な連続関数 \( f(t) \) のフーリエ級数展開は、\[
f(t) = \frac{ a_0 }{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\]と表せる。ただし、\[
a_k = \frac{2}{T} \int^{T}_{0} f(t) \cos k \omega t \ dt \ \ (k = 0, 1, 2, \cdots)
\]\[
b_k = \frac{2}{T} \int^{T}_{0} f(t) \sin k \omega t \ dt \ \ (k = 1, 2, 3, \cdots)
\]\[
\omega = \frac{ 2 \pi }{T}
\]である。
このような三角関数表記のフーリエ級数展開は、実フーリエ級数展開と呼ばれることが多いです。
[注意点]※1. \( a_k \), \( b_k \) の積分範囲は1周期分であればどこでもよい。例えば\[
a_k = \frac{2}{T} \int^{ \frac{T}{2} }_{ - \frac{T}{2} } f(t) \cos k \omega t \ dt\]\[
b_k = \frac{2}{T} \int^{ \frac{T}{2} }_{ - \frac{T}{2} } f(t) \sin k \omega t \ dt
\]
※2. \( f(t) = \) の部分の \( = \) を \( \approx \) と書いてある参考書もあり。\( \approx \) の意味は \( \fallingdotseq \) と同じ
もし忘れてしまってるなぁって思った人は、下の「うさぎでもわかるフーリエ級数展開」にて復習をしましょう…!
aa
スポンサードリンク
2. 三角関数と複素数(オイラーの公式)
ここでは、フーリエ級数展開を複素数で表すために、三角関数を複素数で表す方法について復習しましょう。
(1) オイラーの公式
複素数を用いて、\( \cos \theta \) と \( \sin \theta \) をひとまとめにして書くことができます。
\[
e^{i \theta} = \cos \theta + i \sin \theta
\]
(2) sinθ, cosθを複素数で表す
オイラーの公式から、\( \sin \theta \), \( \cos \theta \) を複素数で表す方法を考えましょう。
まず、\( \cos (- \theta ) = \cos \theta \), \( \sin (- \theta ) = - \sin \theta \) より、\[\begin{align*}
e^{- i \theta} & = \cos ( - \theta ) + i \sin ( - \theta )
\\ & = \cos \theta - i \sin \theta
\end{align*}\]となりますね。
よって、\[\begin{align*}
e^{i \theta} & = \ \ \cos \theta + i \sin \theta \\
+) \ \ \ \ \ \ \ \ \ \ e^{- i \theta} & = \ \ \cos \theta - i \sin \theta \\
\hline e^{i \theta} + e^{- i \theta} & = 2 \cos \theta
\end{align*}\]より、\[
\cos \theta = \frac{1}{2} \left( e^{i \theta} + e^{- i \theta} \right)
\]と表せますね。
同様に \( sin \theta \) も\[\begin{align*}
e^{i \theta} & = \ \ \cos \theta + i \sin \theta \\
-) \ \ \ \ \ \ \ \ \ \ e^{- i \theta} & = \ \ \cos \theta - i \sin \theta \\
\hline e^{i \theta} - e^{- i \theta} & = 2i \sin \theta
\end{align*}\]より、\[
\sin \theta = \frac{1}{2i} \left( e^{i \theta} - e^{- i \theta} \right)
\]と表せます。
\[\begin{align*}
\cos \theta & = \frac{1}{2} \left( e^{i \theta} + e^{- i \theta} \right) \\
\sin \theta & = \frac{1}{2i} \left( e^{i \theta} - e^{- i \theta} \right)
\end{align*} \]
オイラーの公式についてのより詳しい記事はこちらにあるので、もし興味がある方はぜひご覧ください!
スポンサードリンク
3. フーリエ級数展開から複素フーリエ級数展開の導出
ここからが本題です。
および、\[
a_k = \frac{2}{T} \int^{T}_{0} f(t) \cos k \omega t \ dt \ \ (k = 0, 1, 2, \cdots)
\]\[
b_k = \frac{2}{T} \int^{T}_{0} f(t) \sin k \omega t \ dt \ \ (k = 1, 2, 3, \cdots)
\]を複素数の形に変形しましょう。
(1) 展開公式を複素数の形にしよう
まずは三角関数のフーリエ級数展開\[
f(t) = \frac{ a_0 }{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right) \tag{1}
\]を複素数表記にしましょう。
(1-i) シグマ式部分の変形
まず、第2章(2)の式を使って、\( \cos k \omega t \), \( \sin \omega t \) を複素数の表記にしましょう。すると、
\[\begin{align*}
\cos k \omega t & = \frac{1}{2} \left( e^{i k \omega t} + e^{- i k \omega t} \right) \\
\sin k \omega t & = \frac{1}{2i} \left( e^{i k \omega t} - e^{- i k \omega t} \right)
\end{align*} \]となりますね。
この2つの式を式(1)のシグマ式の中身\[
a_k \cos k \omega t + b_k \sin k \omega t
\]に代入すると、\[\begin{align*}
& a_k \cos k \omega t + b_k \sin k \omega t
\\ = \ & a_k \cdot \frac{1}{2} \left( e^{i k \omega t} + e^{- i k \omega t} \right) + b_k \cdot \frac{1}{2i} \left( e^{i k \omega t} - e^{- i k \omega t} \right)
\\ = \ & \left( \frac{a_k}{2} + \frac{b_k}{2i} \right) e^{i k \omega t} + \left( \frac{a_k}{2} - \frac{b_k}{2i} \right) e^{- i k \omega t}
\\ = \ & \frac{a_k - i b_k}{2} \cdot e^{i k \omega t} + \frac{a_k + i b_k}{2} \cdot e^{- i k \omega t} \tag{2}
\end{align*}\]と変形ができます。[1] \( \frac{1}{i} = \frac{i}{i^2} = - i \) です。
ここで、\[
c_k = \frac{ a_k - i b_k }{2}
\]とおきましょう。さらに、\( c_k \) の共役複素数 \( \overline{c_k} \) を \( c_{-k} \) とします。すると、\[\begin{align*}
c_{-k} & = \overline{c_k}
\\ & = \frac{ a_k + i b_k }{2}
\end{align*}\]となります。よって、式(2)を\[
c_k \cdot e^{i k \omega t} + c_{-k} \cdot e^{- i k \omega t}
\]と変形できます。
よって、シグマ式部分を\[\begin{align*}
& \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\\ = \ & \sum^{\infty}_{k = 1} \left( \frac{a_k - i b_k}{2} \cdot e^{i k \omega t} + \frac{a_k + i b_k}{2} \cdot e^{- i k \omega t} \right)
\\ = \ & \sum^{\infty}_{k = 1} \left( c_k \ e^{i k \omega t} + c_{-k} \ e^{- i k \omega t} \right)
\\ = \ & \sum^{\infty}_{k = 1} c_k \ e^{i k \omega t} + \sum^{\infty}_{k = 1} c_{-k} \ e^{- i k \omega t}
\end{align*} \]と変形することができますね。
(1-ii) 初項 a_0/2 の変形
シグマ式の部分はうまく複素数の形で表せましたが、初項 \( \frac{a_0}{2} \) がまだ残っていますね。
ここで、\( \frac{a_0}{2} \) を \( c_0 \) を含んだ式で表す事を考えましょう。
(1-ii)より、\( c_0 \) は\[
c_0 = \frac{ a_0 - i b_0 }{2}
\]と表せますね。ここで、\( b_0 \) は、\[\begin{align*}
b_0 & = \frac{2}{T} \int^{T}_{0} f(t) \sin 0 \ \omega t \ dt
\\ & = \frac{2}{T} \int^{T}_{0} 0 \ dt
\\ & = 0
\end{align*}\]となるため、 \( b_0 = 0 \) ですね。
よって、\[\begin{align*}
c_0 & = \frac{ a_0 - i b_0 }{2}
\\ & = \frac{a_0}{2}
\end{align*}\]となるため、\[
\frac{a_0}{2} = c_0
\]と \( c_0 \) を使って表すことができますね!
(1-iii) (i), (ii)から式を簡単にしてみよう。
(i), (ii)の式を使うことで、\[\begin{align*}
f(t) & = \frac{ a_0 }{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\\ & = c_0 + \sum^{\infty}_{k = 1} c_k \ e^{i k \omega t} + \sum^{\infty}_{k = 1} c_{-k} \ e^{- i k \omega t}
\end{align*}\]と変形ができますね。
さらにこの式を短くしてみましょう。まず、\( c_k \ e^{i k \omega t} \) に、\( k = 0 \) を代入すると、\[
c_0 \ e^{0} = c_0
\]となりますね。そのため、\[\begin{align*}
c_0 + \sum^{\infty}_{k = 1} c_k \ e^{i k \omega t} = \sum^{\infty}_{k = 0} c_k \ e^{i k \omega t}
\end{align*}\]と1つにまとめることができます。
また、\( c_k \ e^{i k \omega t} \) の \( k \) を \( -k \) にすると、\[
c_{-k} \ e^{- i k \omega t}
\]となりますね。よって、\[
\sum^{\infty}_{k = 1} c_{-k} \ e^{- i k \omega t} = \sum^{-1}_{k = - \infty} c_{k} \ e^{i k \omega t}
\]と書き換えることができますね。
よって、\[\begin{align*}
f(t) & = c_0 + \sum^{\infty}_{k = 1} c_k \ e^{i k \omega t} + \sum^{\infty}_{k = 1} c_{-k} \ e^{- i k \omega t}
\\ & = \sum^{\infty}_{k = 0} c_k \ e^{i k \omega t} + \sum^{-1}_{k = - \infty} c_{k} \ e^{i k \omega t}
\\ & = \sum^{\infty}_{k = - \infty} c_k \ e^{i k \omega t}
\end{align*}\]となり、\( f(t) \) の複素フーリエ級数の公式が導出できましたね!
三角関数のフーリエ級数公式\[
f(t) = \frac{ a_0 }{2} + \sum^{\infty}_{k = 1} \left( a_k \cos k \omega t + b_k \sin k \omega t \right)
\]は、複素数 \( i \) を使うことで、\[
f(t) = \sum^{\infty}_{k = - \infty} c_k \ e^{i k \omega t}
\]と書き換えることができる。ただし、\[
c_k = \frac{a_k - i b_k}{2}, \ \ \ c_{-k} = \overline{c_k}
\]である。
(\( \overline{c_k} \) は \( c_k \) の共役複素数)
※ 積分の中身に複素数 \( i \) が入っており、「そのまま計算しても大丈夫なのか?」と思うかもしれませんが、何事もなかったのように普通に計算してOKです!(厳密にはよくないんですけどね…)
(2) c_kを求める公式を導出しよう
いざ複素フーリエ級数の公式が求められたとしても、いちいち \( c_k \) を求めるために三角関数のフーリエ級数展開公式で出てくる \( a_k \), \( b_k \) を求めていては本末転倒ですよね。
そこで、\( c_k \) を直接求める方法を導出してみましょう。
まず、\( a_k \), \( b_k \)を導出する公式は\[
a_k = \frac{2}{T} \int^{ T }_{ 0 } f(t) \cos k \omega t \ dt
\]\[
b_k = \frac{2}{T} \int^{ T }_{0 } f(t) \sin k \omega t \ dt
\]でしたね。
この2つの公式を1つにまとめて、\( c_k \) の積分公式を導出しましょう。すると、\[\begin{align*}
c_k & = \frac{a_k - i b_k}{2}
\\ & = \frac{1}{2} \left( \frac{2}{T} \int^{ T }_{ 0 } f(t) \cos k \omega t - i \cdot \frac{2}{T} \int^{ T }_{ 0 } f(t) \sin k \omega t \ dt \right)
\\ & = \frac{1}{T} \int^{ T }_{ 0 } f(t) \cos k \omega t \ dt - i \cdot \frac{1}{T} \int^{ T }_{ 0 } f(t) \sin k \omega t \ dt
\\ & = \frac{1}{T} \int^{ T }_{ 0 } f(t) \cos k \omega t \ dt - \frac{1}{T} \int^{ T }_{ 0 } i \cdot f(t) \sin k \omega t \ dt
\\ & = \frac{1}{T} \int^{ T }_{ 0 } f(t) \cos k \omega t - i \cdot f(t) \sin k \omega t \ dt
\\ & = \frac{1}{T} \int^{ T }_{ 0 } f(t) ( \cos k \omega t - i \sin k \omega t ) \ dt
\\ & = \frac{1}{T} \int^{ T }_{ 0 } f(t) e^{- i k \omega t} \ dt
\end{align*}\]と公式を導出することができますね。
(最後の1行の変形は、オイラーの公式を適用しています。)
\[
c_k = \frac{1}{T} \int^{ T }_{ 0 } f(t) e^{- i k \omega t} \ dt
\]
※ 積分範囲は1周期分であればどこでもOK。例えば\[
c_k = \frac{1}{T} \int^{ \frac{T}{2} }_{ - \frac{T}{2} } f(t) e^{- i k \omega t} \ dt
\]でも可。
(3) c_kの分母が0になるときは…?
複素フーリエ級数を計算すると、時々 \( c_k \) の分母が0になることがあります。(次の例題なのがまさにそうです)
この場合は、以下の式に \( k = 0 \) を代入することで \( c_0 \) を独立して計算します。\[
c_k = \frac{1}{T} \int^{ T }_{ 0 } f(t) e^{- i k \omega t} \ dt
\]\( k = 0 \) を代入すると、\[\begin{align*}
c_0 & = \frac{1}{T} \int^{ T }_{ 0 } f(t) e^{- i k \omega t} \ dt
\\ & = \frac{1}{T} \int^{ T }_{ 0 } f(t) e^{0} \ dt
\\ & = \frac{1}{T} \int^{ T }_{ 0 } f(t) \ dt
\end{align*}\]と求めることができます。
求めた \( c_k \) の分母が0になる場合は、\( k = 0 \) のとき、つまり \( c_0 \) を別に考える。
つまり、\[
c_0 = \frac{1}{T} \int^{ T }_{ 0 } f(t) \ dt
\]を計算し、\[
f(t) = c_0 + \sum^{-1}_{k = - \infty} c_k \ e^{i k \omega t} + \sum^{\infty}_{k = 1} c_k \ e^{i k \omega t}
\]と複素フーリエ級数を計算する。
4. 例題で理解を深めよう!
では、早速複素フーリエ級数に関する問題を1問解いてみましょう。
以下の図で表される周期 2 の関数\[
f(t) = |t|
\]について、次の問いに答えなさい。
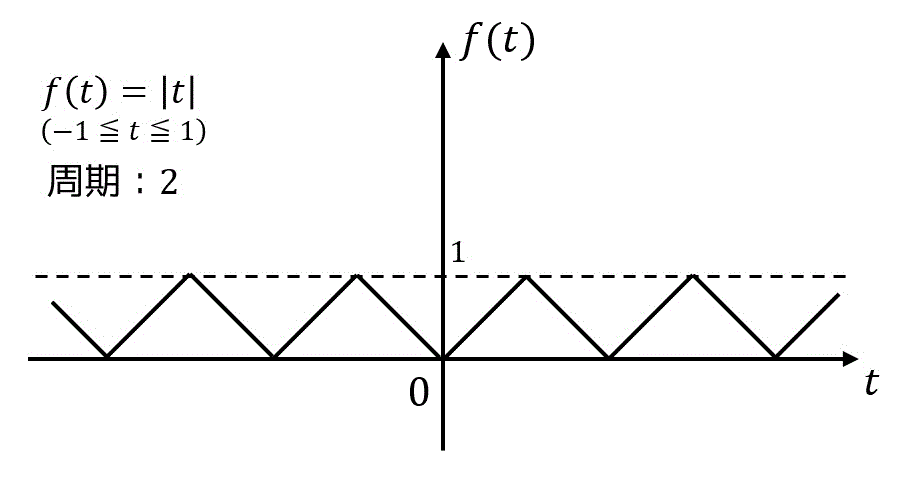
(1) \( f(t) \) の複素フーリエ級数を計算しなさい。
(2) (1)で求めた複素フーリエ級数が、実フーリエ級数\[
f(t) = \frac{1}{2} + \sum^{\infty}_{k = 1} \frac{2}{k^2 \pi^2} \left( (-1)^k - 1 \right) \cos 2k \pi t
\]と一致することを確認しなさい。(実フーリエ級数の \( a_k \), \( b_k \) と複素フーリエ級数の \( c_k \) の関係式が成り立つことの確認用の問題です)
解説
(1)
まずは、角速度 \( \omega \) を求めましょう。
周期が \( T = 2 \) なので、角速度 \( \omega \) は、\[
\omega = \frac{ 2 \pi }{2} = \pi
\]となります。
つぎに、\( c_k \) を求めましょう。\( c_k \) を求めるためには、\[\begin{align*}
c_k & = \frac{1}{2} \int^{1}_{-1} |t| e^{-ik \pi t} \ dt
\\ & = \frac{1}{2} \int^{1}_{0} t e^{- ik \pi t} \ dt + \frac{1}{2} \int^{0}_{-1} -t e^{- ik \pi t} \ dt
\\ & = \frac{1}{2} \int^{1}_{0} t e^{- ik \pi t} \ dt - \frac{1}{2} \int^{0}_{-1} t e^{- ik \pi t} \ dt
\end{align*}\]を計算すればよい。
※ 今回は積分範囲を 0 → 2 とするよりも -1 → 1 としたほうが式が簡単になるため、-1 → 1 で積分を行っております。
ここで、\[\begin{align*}
\int t e^{- ik \pi t} \ dt & = \frac{1}{- i k \pi} t e^{- ik \pi t} - \frac{1}{(-ik \pi)^2} e^{- ik \pi t}
\\ & = \frac{i}{k \pi} t e^{- ik \pi t} - \frac{1}{i^2 k^2 \pi^2 } e^{- ik \pi t}
\\ & = \frac{i}{k \pi} t e^{- ik \pi t} + \frac{1}{k^2 \pi^2 } e^{- ik \pi t}
\\ & = \frac{i k \pi t + 1}{k^2 \pi^2 } e^{- ik \pi t}
\end{align*} \]と計算できる。(積分定数は省略した。)
また、\[\begin{align*}
\int^{1}_{0} t e^{- ik \pi t} \ dt & = \left[ \frac{i k \pi t + 1}{k^2 \pi^2 } e^{- ik \pi t} \right]^{1}_{0}
\\ & = \frac{i k \pi + 1}{k^2 \pi^2} e^{- ik \pi} - \frac{1}{k^2 \pi^2}
\\ & = \frac{i k \pi + 1}{k^2 \pi^2} (-1)^k - \frac{1}{k^2 \pi^2}
\end{align*}\]\[\begin{align*}
\int^{0}_{-1} t e^{- ik \pi t} \ dt & = \left[ \frac{i k \pi t + 1}{k^2 \pi^2 } e^{- ik \pi t} \right]^{0}_{-1}
\\ & = \frac{1}{k^2 \pi^2} - \frac{- i k \pi + 1}{ k^2 \pi^2 } e^{ik \pi}
\\ & = \frac{1}{k^2 \pi^2} - \frac{- i k \pi + 1}{ k^2 \pi^2 } (-1)^k
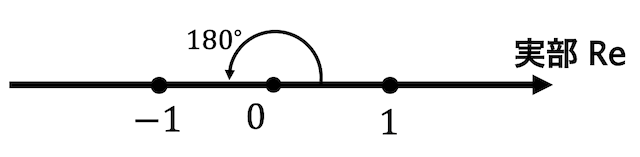
\end{align*}\]となる[2]\( k \) は整数なので \( e^{- ik \pi} \) と \( e^{ik \pi} \) を\[e^{- ik \pi} = \cos (-k \pi) + i \sin ( - k \pi) = (-1)^k\]\[e^{ik \pi} = \cos k \pi+ i \sin k \pi = … Continue reading。
よって、\( c_k \) は\[\begin{align*}
c_k & = \frac{1}{2} \int^{1}_{-1} |t| e^{-ik \pi t} \ dt
\\ & = \frac{1}{2} \int^{1}_{0} t e^{- ik \pi t} \ dt - \frac{1}{2} \int^{0}_{-1} t e^{- ik \pi t} \ dt
\\ & = \frac{1}{2} \left( \frac{i k \pi + 1}{k^2 \pi^2} (-1)^k - \frac{1}{k^2 \pi^2} \right) - \frac{1}{2} \left( \frac{1}{k^2 \pi^2} - \frac{- i k \pi + 1}{ k^2 \pi^2 } (-1)^k \right)
\\ & = \frac{i k \pi + 1 + (-i k \pi + 1)}{2 k^2 \pi^2} (-1)^k - \frac{2}{2 k^2 \pi^2}
\\ & = \frac{2}{2 k^2 \pi^2} (-1)^k - \frac{1}{ k^2 \pi^2}
\\ & = \frac{(-1)^k - 1}{k^2 \pi^2}
\end{align*}\]と求められます。
ただし \( c_0 \) のとき、分母 \( k^2 \pi^2 \) が0になってしまうため、\( c_0 \) のときを独立して計算します。\[\begin{align*}
c_0 & = \frac{1}{2} \int^{1}_{-1} |t| \ dt
\\ & = \int^{1}_{0} t \ dt
\\ & = \left[ \frac{1}{2} t^2 \right]^{1}_{0}
\\ & = \frac{1}{2}
\end{align*}\]
よって、複素フーリエ級数は\[\begin{align*}
f(t) & = \frac{1}{2} + \sum^{-1}_{k = - \infty} \frac{ (-1)^k - 1}{k^2 \pi^2} e^{ik\pi t } + \sum^{\infty}_{k = 1} \frac{ (-1)^k - 1}{k^2 \pi^2} e^{ik\pi t }
\end{align*}\]と求められます。
(2)
実フーリエ級数が\[
\frac{1}{2} + \sum^{\infty}_{k = 1} \frac{2}{k^2 \pi^2} \left( (-1)^k - 1 \right) \cos 2k \pi t
\]ということは、\[
a_k = \frac{2}{k^2 \pi^2} \left( (-1)^k - 1 \right), \ \ \ b_k = 0
\]である。(本来は \( a_k \), \( b_k \) を求めてから実フーリエ級数を計算します。)
ここで、実フーリエ級数の係数 \( a_k \), \( b_k \) と複素フーリエ級数の係数 \( c_k \) には\[
c_k = \frac{a_k - i b_k}{2}
\]の関係が成り立ちますね。\( a_k \), \( b_k \) の値を代入すると、\[\begin{align*}
c_k & = \frac{a_k - i b_k}{2}
\\ & = \frac{2}{2 k^2 \pi^2} \left( (-1)^k - 1 \right)
\\ & = \frac{(-1)^k - 1}{ k^2 \pi^2 }
\end{align*}\]と計算でき、確かに関係式が成り立っていることがわかりますね。
5. 練習問題
では、1問練習問題を解いてみましょう。
問題
周期 \( \pi \) の関数\[
f(t) = \frac{e^t + e^{-t}}{2} \ \left( = \cosh t \right)
\]を複素フーリエ級数展開しなさい。
解答
周期 \( T = \pi \) なため、角速度 \( \omega \) は、\[
\omega = \frac{ 2 \pi }{T} = 2
\]となる。
つぎに、\( c_k \) を求める。\[\begin{align*}
c_k & = \frac{1}{T} \int^{ T }_{ 0 } f(t) e^{- i k \omega t} \ dt
\\ & = \frac{1}{ \pi } \int^{ \pi }_{0} \left( \frac{e^t + e^{-t}}{2} \right) e^{- 2 i k t} \ dt
\\ & = \frac{1}{ 2 \pi } \int^{ \pi }_{0} e^{(1- 2ik)t} + e^{(-1-2ik)t} \ dt
\\ & = \frac{1}{ 2 \pi } \left[ \frac{1}{1 - 2ik} e^{(1- 2ik)t} + \frac{1}{-1-2ik} e^{(-1-2ik)t} \right]^{ \pi }_{0}
\\ & = \frac{1}{ 2 \pi } \left[ \frac{1}{1 - 2ik} e^t e^{-2ikt} - \frac{1}{1+2ik} e^{-t} e^{-2ikt} \right]^{ \pi }_{0}
\\ & = \frac{1}{ 2 \pi } \left[ \left( \frac{1}{1 - 2ik} e^t - \frac{1}{1+2ik} e^{-t} \right) e^{-2ikt} \right]^{ \pi }_{0}
\\ & = \frac{1}{ 2 \pi } \left\{ \left( \frac{1}{1-2ik} e^{\pi} - \frac{1}{1+2ik} e^{- \pi} \right) e^{-2ik \pi} - \left( \frac{1}{ 1 - 2ik } - \frac{1}{1 + 2ik} \right) \right\}
\\ & = \frac{1}{ 2 \pi } \left( \frac{1}{1-2ik} e^{\pi} - \frac{1}{1+2ik} e^{- \pi} - \frac{ (1+2ik)-(1-2ik) }{(1-2ik)(1+2ik)} \right)
\\ & = \frac{1}{ 2 \pi } \left( \frac{1}{1-2ik} e^{\pi} - \frac{1}{1+2ik} e^{- \pi} - \frac{4ik}{1 + 4k^2} \right)
\end{align*}\]と計算できる[3]ここで \( k \) は整数なので、\[ e^{-2ik \pi} = \cos (-2k \pi ) + i \sin ( - 2k \pi ) = 1 \]となります。。
ここで、\( c_k \) に \( k = 0 \) を代入しても分母は0にならないため、\( c_0 \) を別途計算する必要はない。
よって、複素フーリエ級数は\[\begin{align*}
f(t) & = \sum^{\infty}_{k = - \infty} c_k \ e^{i k \omega t}
\\ & = \sum^{\infty}_{k = - \infty} \frac{1}{ 2 \pi } \left( \frac{1}{1-2ik} e^{\pi} - \frac{1}{1+2ik} e^{- \pi} - \frac{4ik}{1 + 4k^2} \right) \ e^{2 i k t}
\\ & = \frac{1}{ 2 \pi } \sum^{\infty}_{k = - \infty} \left( \frac{1}{1-2ik} e^{\pi} - \frac{1}{1+2ik} e^{- \pi} - \frac{4ik}{1 + 4k^2} \right) \ e^{2 i k t}
\end{align*}\]となる。
[双曲線関数を使うと……]
\( c_n \) は双曲線関数\[
\sinh t = \frac{e^t - e^{-t}}{2} , \ \ \ \cosh t = \frac{e^t + e^{-t}}{2}
\]を使うともう少しきれいになる。
\[\begin{align*}
c_k & = \frac{1}{ 2 \pi } \left( \frac{1}{1-2ik} e^{\pi} - \frac{1}{1+2ik} e^{- \pi} - \frac{4ik}{1 + 4k^2} \right)
\\ & = \frac{1}{ 2 \pi } \left( \frac{(1+2ik) e^{\pi} + (1-2ik) e^{- \pi}}{(1-2ik)(1+2ik)} - \frac{4ik}{1 + 4k^2} \right)
\\ & = \frac{1}{ 2 \pi } \left( \frac{e^{\pi} - e^{- \pi} + 2ik (e^{\pi} + e^{- \pi} ) }{1+4k^2} - \frac{4ik}{1 + 4k^2} \right)
\\ & = \frac{1}{ 2 \pi } \left( \frac{ 2 \sinh \pi + 4ik \cosh \pi }{1+4k^2} - \frac{4ik}{1 + 4k^2} \right)
\\ & = \frac{1}{ 2 \pi} \cdot \frac{ 2 \sinh \pi + 4ik \cosh \pi + 4ik }{1 + 4k^2}
\\ & = \frac{ \sinh \pi + 2ik \cosh \pi + 2ik }{\pi (1 + 4k^2)}
\end{align*}\]
となるので、双曲線関数を用いることで複素フーリエ級数を\[
f(t) = \sum^{\infty}_{k = - \infty} \frac{ \sinh \pi + 2ik \cosh \pi + 2ik }{\pi (1 + 4k^2)} \cdot e^{2 i k t}
\]とより簡単な形にすることができる。
6. さいごに
今回は、三角形式のフーリエ級数展開(実フーリエ展開)を複素数を用いてより簡潔に用いて表す方法について説明していきました。
最後に公式を確認しておきましょう。

いよいよ次回は、今回導出した複素フーリエ級数展開を使って、理系大学生おなじみのフーリエ変換を導出する方法について説明していきましょう…!
注釈
| ↑1 | \( \frac{1}{i} = \frac{i}{i^2} = - i \) です。 |
|---|---|
| ↑2 | \( k \) は整数なので \( e^{- ik \pi} \) と \( e^{ik \pi} \) を\[ e^{- ik \pi} = \cos (-k \pi) + i \sin ( - k \pi) = (-1)^k \]\[ e^{ik \pi} = \cos k \pi+ i \sin k \pi = (-1)^k \]と計算することができます。 |
| ↑3 | ここで \( k \) は整数なので、\[ e^{-2ik \pi} = \cos (-2k \pi ) + i \sin ( - 2k \pi ) = 1 \]となります。 |
関連広告・スポンサードリンク