スポンサードリンク
こんにちは、ももやまです!
線形代数の計算、とくに逆行列と行列式の計算で欠かせない余因子計算についてまとめてみました。
\( a \)aa
前回の記事はこちら
スポンサードリンク
1.余因子って何? 求め方は?
余因子とは、正方行列*1の各要素ごとのもとの行列の要素の行と列を消し、残りの行列からなる要素で行列式を計算し、さらに正負の記号を要素の場所によって決めたものとなります。
正負の記号は、行と列の場所で決まります。行番号と列番号が偶数の場合は計算結果がそのまま、奇数の場合には計算結果の正負が入れ替わります。例えば、3×3行列、4×4行列の場合は、
\[\left( \begin{array}{ccc} + & - & + \\ - & + & - \\ + & - & + \end{array} \right)\]
\[\left( \begin{array}{ccc} + & - & + & -\\ - & + & - & + \\ + & - & + & -\\ - & + & - & + \end{array} \right)\] の -(マイナス)で表されている場所で正負が入れ替わります。
例えばつぎの行列を考えてみましょう。
\[\left( \begin{array}{ccc} 1 & -2 & -3 \\ -1 & -3 & 0 \\ 1 & -1 & -4 \end{array} \right)\]
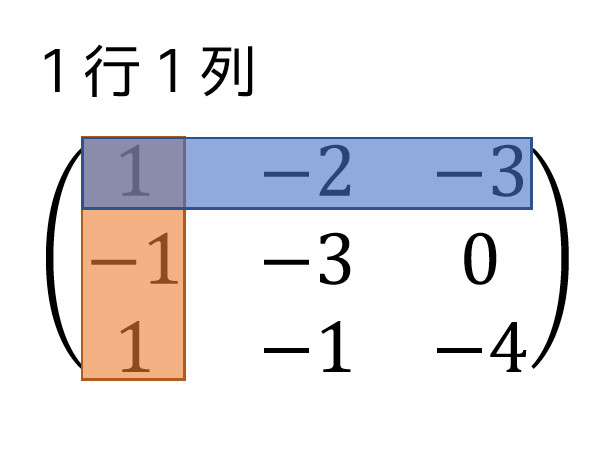
例えば、この行列の1行1列の余因子を求めてみましょう。
まず、1行にある行列の要素と1列にある行列の要素を抜きます。
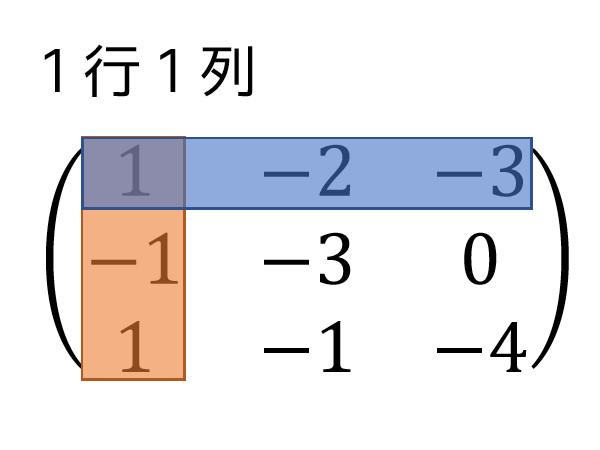
つぎに、抜いた要素以外の行列式を求めます。この場合は、
\[\left| \begin{array}{ccc} -3 & 0 \\ -1 & -4 \end{array} \right|
= 12
\]
となります。今回は1行1列なので行番号と列番号の合計は2で偶数なので、計算結果の正負は入れ替わりません。よって1行1列の余因子 \( \Delta_{11} \) は12となります。
同様に1行2列の余因子も求めてみましょう。
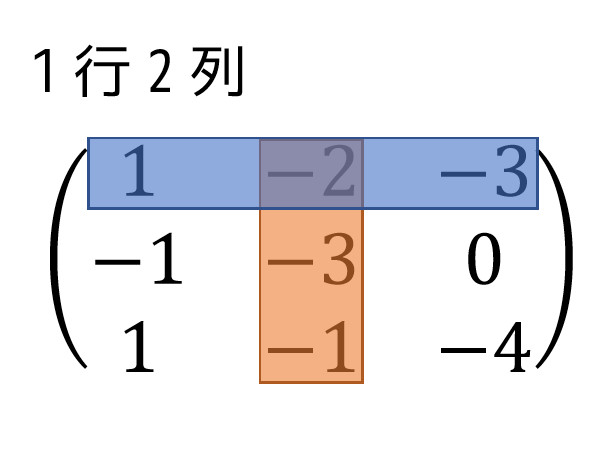
抜いた要素以外の行列式は、
\[\left| \begin{array}{ccc} -1 & 0 \\ 1 & -4 \end{array} \right|
= 4
\]
となります。今回は1行2列なので行番号と列番号の合計は3で奇数なので、計算結果の正負が入れ替わります。よって1行2列の余因子 \( \Delta_{12} \) は-4となります。
同様に下の計算式ですべての要素の余因子を求めていくと、
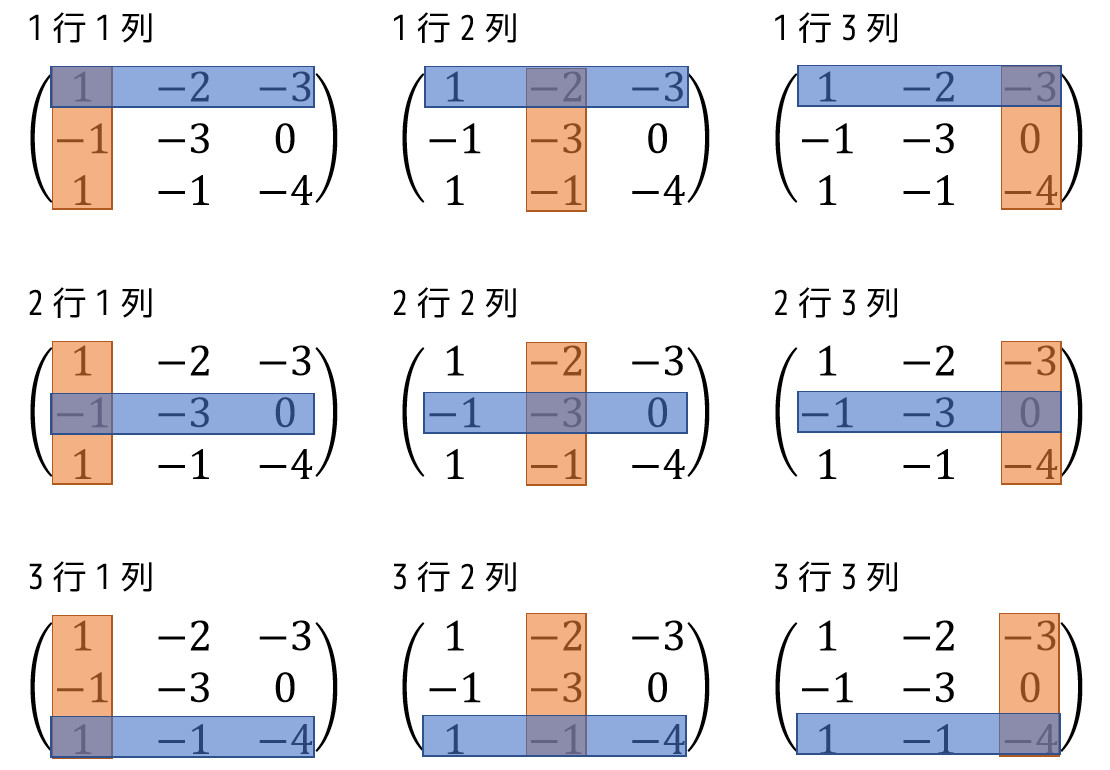
\[ \Delta_{13} = \left| \begin{array}{ccc} -1 & -3 \\ 1 & -1 \end{array} \right| = 4 \] \[ \Delta_{21} = \left| \begin{array}{ccc} -2 & -3 \\ -1 & -4 \end{array} \right| \times (-1) = -5 \] \[ \Delta_{22} = \left| \begin{array}{ccc} 1 & -3 \\ 1 & -4 \end{array} \right| = -1 \] \[ \Delta_{23} = \left| \begin{array}{ccc} 1 & -2 \\ 1 & -1 \end{array} \right| \times (-1) = -1 \] \[ \Delta_{31} = \left| \begin{array}{ccc} -2 & -3 \\ -3 & 0 \end{array} \right| = -9 \] \[ \Delta_{32} = \left| \begin{array}{ccc} 1 & -3 \\ -1 & 0 \end{array} \right| \times (-1) = 3 \] \[ \Delta_{33} = \left| \begin{array}{ccc} 1 & -2 \\ -1 & -3 \end{array} \right| = -5 \]
と求めることができます。
スポンサードリンク
2.使い方その1 逆行列算出
余因子を使って逆行列を算出することができます。
上の例と同じ行列、
\[A = \left( \begin{array}{ccc} 1 & -2 & -3 \\ -1 & -3 & 0 \\ 1 & -1 & -4 \end{array} \right)\]
の逆行列を余因子を使って求めてみましょう。
まず、逆行列を求める前に、余因子行列 \( \tilde{A} \) を求めます。
余因子行列は、先程計算した余因子を順番に並べればいいのですが、この際に行と列が入れ替わるので注意してください。
余因子行列 \( \tilde{A} \) は、
\[
\tilde{A} =
\left( \begin{array}{cc} \Delta_{11} & \Delta_{21} & \Delta_{31} \\ \Delta_{12} & \Delta_{22} & \Delta_{32} \\ \Delta_{13} & \Delta_{23} & \Delta_{33} \end{array} \right)
=
\left( \begin{array}{cc} 12 & -5 & -9 \\ -4 & -1 & 3 \\ 4 & -1 & -5 \end{array} \right)
\]
となる。逆行列は、余因子行列の要素すべてを行列式で割ったものとなる。
ということで行列式を求めよう。3×3の行列式なのでサラスの公式で行列式を求める。
\[
\begin{align*}
|A| & =\left| \begin{array}{ccc} 1 & -2 & -3 \\ -1 & -3 & 0 \\ 1 & -1 & -4 \end{array} \right| \\
& = 12 + 0 - 3 - (9 - 8 + 0) \\ & = 9 - 1 = 8
\end{align*}
\]
と求められ、行列式が8とわかる。なので余因子行列すべての要素を8で割れば逆行列 \( A^{-1} \) が求められることがわかる。よって逆行列は、
\[
\begin{align*}
A^{-1} & = \frac{1}{8} \left( \begin{array}{ccc} 12 & -5 & -9 \\ -4 & -1 & 3 \\ 4 & -1 & -5 \end{array} \right) \\
& = \left( \begin{array}{ccc} 12 & -5 & -9 \\ -4 & -1 & 3 \\ 4 & -1 & -5 \end{array} \right)
\end{align*}
\]
と求められる。
スポンサードリンク
3.使い方その2 行列式算出
もとの行列式を「行列の中の1行or1列の中のそれぞれの要素と要素ごとの余因子の積をすべて足したもの」に分解してしまうことを余因子展開といいます。余因子展開の前後では行列式は変化しません。
なので、4×4以上のサイズの大きな行列式を計算するときには余因子展開で3×3や2×2まで小さくしてから計算をします。この方法は大学の期末試験、大学院試験、数検では確実に使うので覚えておきましょう。*2
では、1つ余因子展開の例をわかりやすくお見せしましょう。
先程と同じ行列を使います。
\[|A| = \left| \begin{array}{ccc} 1 & -2 & -3 \\ -1 & -3 & 0 \\ 1 & -1 & -4 \end{array} \right|\]
例えば、2行目で余因子展開してみましょう。
紫色の部分がそれぞれの要素、緑色の部分の行列式(と符号)が余因子となり、これらを掛け合わせます。
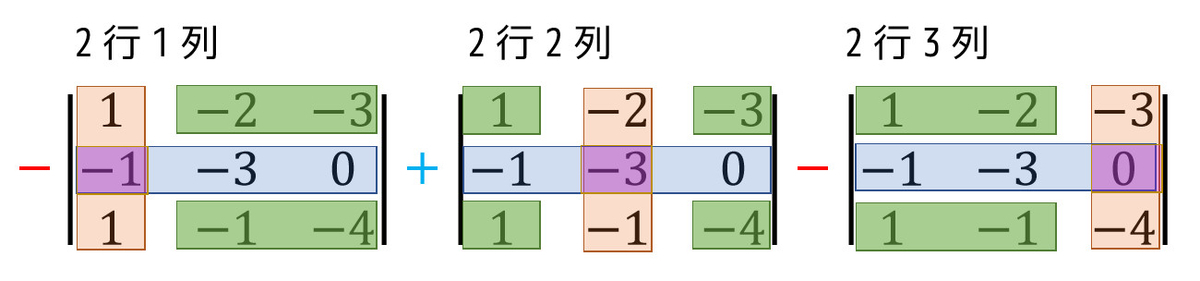
\( \Delta_{21} = -5, \ \Delta_{22} = -1, \ \Delta_{23} = -1 \) なので、
\[|A| = \Delta_{21} \times (-1) + \Delta_{22} \times (-3) + \Delta_{23} \times 0 = 5 + 3 = 8 \]
と求められます。
もちろん列を使った余因子展開も出来ます。
1列目で余因子展開してみます。
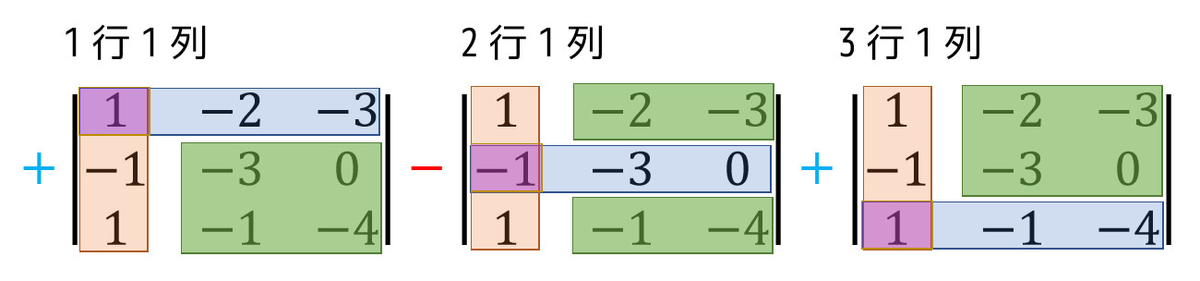
\( \Delta_{11} = 12, \ \Delta_{21} = -5, \ \Delta_{31} = -9 \) なので、
\[|A| = \Delta_{11} \times 1 + \Delta_{21} \times (-1) + \Delta_{31} \times 1 = 12 + 5 - 9 = 8 \]
と同じ結果が出ますね。
しかし、それでもなるべくなら単純計算する回数を減らしたいですよね。なので、行列式を行基本変形や列基本変形して0を作ってから余因子展開をすると計算量が減らせます。具体的に言うと、
\[
\begin{align*}
|A|
& = \left| \begin{array}{ccc} 1 & -2 & -3 \\ -1_{+1} & -3_{-2} & 0_{-3} \\ 1_{-1} & -1_{+2} & -4_{+3} \end{array} \right| \\
& = \left| \begin{array}{ccc} 1 & -2 & -3 \\ 0 & -5 & -3 \\ 0 & 1 & -1 \end{array} \right|
\end{align*}
\]
としてから1列目で余因子展開します。1行2列と1行3列には0の要素があるので、1行2列と1行3列に関する余因子は計算しなくてもOKですね。*3
なので、1行1列の余因子だけ求めればよいことになります。計算式は、
\[
\begin{align*}
\left| \begin{array}{ccc} 1 & -2 & -3 \\ 0 & -5 & -3 \\ 0 & 1 & -1 \end{array} \right| = 1 \times \left| \begin{array}{ccc} -5 & -3 \\ 1 & -1 \end{array} \right|
= 5 - (-3) = 8
\end{align*}
\]
となり、すごく簡単に求めることができますね。
4×4の行列式でもやってみましょう。
\[
\begin{align*} &
\left| \begin{array}{ccc} -1 & 2 & 3 & 2 \\ 2_{-2} & -2_{+4} & -3_{+6} & 1_{+4} \\ 1_{-1} & -3_{+2} & -4_{+3} & 0_{+2} \\ 0 & 1 & 2 & -1 \end{array} \right| \\ \ = \ &
\left| \begin{array}{ccc} -1 & 2 & 3 & 2 \\ 0 & 2 & 3 & 5 \\ 0 & -1 & -1 & 2 \\ 0 & 1 & 2 & -1 \end{array} \right| \\ \ = \ &
-1 \times \left| \begin{array}{ccc} 2_{-2} & 3_{-4} & 5_{+2} \\ -1_{+1} & -1_{+2} & 2_{-1} \\ 1 & 2 & -1 \end{array} \right| \\ \ = \ &
-1 \times \left| \begin{array}{ccc} 0 & -1 & 7 \\ 0 & 1 & 1 \\ 1 & 2 & -1 \end{array} \right| \\ \ = \ &
-1 \times 1 \times \left| \begin{array}{ccc} -1 & 7 \\ 1 & 1 \end{array} \right| \\ \ = \ &
-1(-1-7) = 8
\end{align*}
\]
より、変形をうまく使えば計算する回数を減らして行列式をうまく出すことができますね。
↓ もっと問題演習をしたい人はこちらの記事をご覧ください!
4.さいごに
今回は余因子の求め方、そして余因子を使って逆行列や行列式を求める方法をまとめました。
逆行列の出し方、行列式の出し方は別にまとめてあるのでそちらもぜひご覧ください!
練習問題は逆行列編、行列式編にまとめる予定なので、こちらには載せていません。
関連広告・スポンサードリンク