スポンサードリンク
こんにちは、ももやまです。
今回は部分分数分解のやり方・部分分数分解を用いた積分の方法についてまとめたいと思います。
※注意
こちらの記事は、大学数学となっていますが、こちらの記事は高校数学の復習なので高校数学を履修している方もぜひ読んでください!
目次
スポンサードリンク
1.部分分数分解とは
部分分数分解は、分母が多項式の積(例えば \( x \) と \( x+1 \))で表されたような数を2つ以上の単純な分数(しかも分子の次数が分母の次数より小さい)に分解することを表します。
簡単に言うと、通分の逆です。
部分分数分解が使えるのは、
- 分母が多項式の積で表されたような数の場合
- 分子の次数が分母の次数より小さいこと
の2つを満たすときです。2の条件を満たしていないもの、例えば\[ \frac{x^2}{x+1} \]のような分数のときには、\[ \frac{x^2}{x+1} = x - 1 + \frac{1}{x+1} \] のように次数を下げてから \[ \frac{1}{x+1} \] に(次数が下がった分数)に部分分数分解を適用します。
実際に例を見てもらったほうが早いと思うので、いくつか例を紹介します。
例題1
\[ \frac{1}{x(1-x)}\] という分数を部分分数分解しなさい。
解説1
例題1の分数は\[
\frac{1}{x(1-x)} = \frac{a}{x} + \frac{b}{1-x} \] という2つの分数に分解することができます(分解後の分数のそれぞれの分子は必ず分母よりも次数は小さくなります)。
分解する際の係数 \( a \) と \( b \) の値が不明なので、実際に計算をすることで係数の値を決めます。
まずは、分数の形のままだと面倒なので、分数が消えるように両辺に \( x(1-x) \) を掛けます。
すると、\[ 1 = a (1-x) + bx \] となります。
解き方Part1 厳密に恒等式を解く 係数比較法
厳密に記述過程を書く必要がある場合(部分分数分解がメインの問題)は、この方法で解きましょう。\[ 1 = (-a+b)x + a \]が成り立てば良いので、\[\left\{ \begin{array}{l} -a + b = 0 \\ a = 1 \end{array}\right.\]の連立方程式を解けばよいです。
計算の結果、\( a = 1 \), \( b = 1 \) となります。なので、\[
\frac{1}{x(1-x)} = \frac{1}{x} + \frac{1}{1-x} \]となります。
解き方Part2 簡単になるxの値を代入 数値代入法
私が一番おすすめするのはこの数値代入法です。
厳密に記述の過程を書く必要がない場合(積分計算のために部分分数分解をする問題のように部分分数分解が過程の一部の場合など)は、こちらの数値代入法を行ったほうが早く計算が可能です。
早速計算していきましょう。\[ 1 = a (1-x) + bx \]に、\( x = 0 \) を代入すると、\( bx \) の部分が0となり、\( 1 = a \) がすぐに求められます。同様に \( x = 1 \) を代入すると、\( 1 = b \) が同様に求まります。
よって、\( a = 1 \), \( b = 1 \) となり、\[ \frac{1}{x(1-x)} = \frac{1}{x} + \frac{1}{1-x} \]が求められます。
この方法は、\( x \) の値を限定して \( a,b \) の値を出しているため、十分性の確認が不十分となります。なので、厳密に十分性を確認したい場合はPart1のやり方をおすすめします。
なお、積分計算の一部として部分分数分解をする場合は、途中過程は省略できることが多いのでこちらのPart2のやり方をすることをおすすめします。
今回の練習問題もこのPart2のやり方で説明をしています。
解き方Part3 ヘビサイドの方法を利用
ヘビサイドの方法を用いた部分分数分解は、ヘビサイドの展開定理を少し利用したものです。(ヘビサイドのカバーアップ法・ヘビサイドの目隠し法などと呼ばれています)
高校生にもわかるように変形をしてわかりやすく紹介しています。
この方法は展開した分母に2次式がない場合のときに早く計算をすることができます。
(左辺の分子が定数項ではない場合は、少し微分の計算が大変になります。)
\[
\frac{1}{x(1-x)} = \frac{a}{x} + \frac{b}{1-x} \]に、\( x \)を掛けます。すると、\[
\frac{1}{1-x} = a + \frac{bx}{1-x} \]となります。
ここに、\( x = 0 \) を代入すると、右辺の分数は0になり、\( a \) を素早く求めることができます。
同様に \( 1-x \) を掛けると、\[
\frac{1}{x} = \frac{a(1-x)}{x} + b \]となります。ここに \( x = 1 \) を代入すると、右辺の分数部分が0となり、\( b \) の値を素早く求めることができます。
よって、\( a = 1 \), \( b = 1 \) を求めることができます。
ヘビサイドのカバーアップ法についてはフェルミウム湾さんのこちらの記事を参考にしました。詳しくはこちらの記事をご覧ください。
スポンサードリンク
2.( )^2 の形がある場合
つぎのようなカッコの2乗の形の場合には注意が必要です。
例題2
\[\frac{3x+4}{(x+2)^2}\]を部分分数分解しなさい。
解説2
このような形
\[\frac{3x+4}{(x+2)^2} = \frac{a}{x+2} + \frac{b}{(x+2)^2}\]にします。
カッコの1乗の分母とカッコの2乗の分母に分けてあげるところがポイントです。
(あまりないですが、( )^3 の形であればカッコの1乗の分母+カッコの2乗の分母+カッコの3乗の分母となります。)
パターン1:数値代入法(推奨)
まずは、数値代入法で計算します。両辺に \( (x+2)^2 \) を掛けます。すると、\[3x + 4 = a(x+2) + b\]となります。
まずは、\( a \) を消すために \( x = -2 \) を代入します。すると、\( -2 = b \) が求められます。
しかし、\( b \) を消すためには \( x \) に何を代入しても消すことができませんね。
そんなときに使うのが微分です。恒等式は、微分しても恒等式なので。\[3x + 4 = a(x+2) + b\]の両辺を微分すると、\( 3 = a \) が求められます。
よって、\( a = 3 \), \( b = 2 \) となり、\[\frac{3x+4}{(x+2)^2} = \frac{3}{x+2} - \frac{2}{(x+2)^2}\]が計算できます。
パターン2:ヘビサイドのカバーアップ法
ヘビサイドのカバーアップ法を使ったやり方も紹介します。\[\frac{3x+4}{(x+2)^2} = \frac{a}{x+2} + \frac{b}{(x+2)^2}\]の両辺に \( (x + 2)^2 \) を掛けると、\[3x+4 = a(x+2) + b \]となります。ここで、\( x = -2 \) を代入すると、\( b = -2 \) を求めることができます。
同様に \( x+2 \) を掛けた式だと、\[\frac{3x+4}{(x+2)} = a + \frac{b}{(x+2)}\] となってしまいます。このまま \( x = -2 \) を代入すると、分母が0になってしまいます。
ここで \( b \) を求めるためにつかったこちらの式を思い出しましょう。\[3x+4 = a(x+2) + b \]
ここで使うのが(パターン1と同じく)微分です。恒等式は微分しても恒等式なので。
すると、\( 3 = a \) を計算することができます。
スポンサードリンク
3.展開した分母が2次式の場合
分母に2乗が含まれているものにも注意が必要です。
分母に2次式がある場合、分子に1次式が残ることがあります。
(分子の次数は、必ず分母の次数より小さくなるため。 分母に3次式が来れば分子は2次式。)
例題3
\[\frac{1}{x^3 - 1}\]を部分分数分解しなさい。
解説3
\[x^3 - 1 = (x-1)(x^2 + x + 1)\] と変形できます。なので、
\[\frac{1}{(x-1)(x^2 + x + 1)} = \frac{a}{x-1} + \frac{bx + c}{x^2 + x + 1}
\]とします。
ここで注意するのは、\( bx + c \) とおいたところは、分母が2次のため、分子が定数項だけでなく、\( x \) の項も残る可能性があります。
両辺に \( (x-1)(x^2 + x + 1) \) を掛けます。すると、\[1 = a(x^2 + x + 1) + (bx + c)(x-1) \]となります。
(i) \( x = 1 \) のとき、\( 1 = 3a \) より \( a = 1/3 \)
(ii) \( x = 0 \) のとき、\[ 1 = a - c = \frac{1}{3} - c\] より、\( c = -2/3 \)
(iii) \( x = -1 \) のとき、\[1 = a +2b - 2c = \frac{1}{3} + 2b + \frac{4}{3} = \frac{5}{3} + 2b \]より、\( b = -1/3 \)となります。よって、\[ a = \frac{1}{3} , \ \ b = - \frac{1}{3} , \ \ c = - \frac{2}{3} \]と求められ、
\[ \frac{1}{x^3 -1} = \frac{1}{3} \cdot \frac{1}{x-1} - \frac{1}{3} \cdot \frac{x+2}{x^2-x+1} \]と計算できます*1。
4.部分分数分解を用いた積分
いよいよ本題です。
部分分数分解を用いて積分を行いましょう。
例題4
不定積分 \[ \int \frac{1}{x(1-x)} dx \] を求めなさい。
解説4
例題1の結果、\[
\frac{1}{x(1-x)} = \frac{1}{x} + \frac{1}{1-x} \]を使います。
例題1より、\[ \int \frac{1}{x(1-x)} dx = \int \frac{1}{x} dx + \int \frac{1}{1-x} dx \]となります。
あとは、それぞれの積分を計算するだけです。
\( C_1 \), \( C_2 \) は積分定数とすると、
\[\int \frac{1}{x} dx = \log |x| + C_1 \\ \int \frac{1}{1-x} dx = \log |1-x| + C_2 \\
\]より、\( C \) を積分定数として、\[ \int \frac{1}{x(1-x)} dx = \log |x| + \log |1-x| + C\]となります。
このように、一見難しそうに見える積分でも、このように部分分数分解を使うことでそれぞれの積分が簡単なものとなり、それらを加算(減算)することで積分結果を求めることができます。
分数系で、分母が因数分解できる場合(もしくはもともと因数分解されていた場合)には部分分数分解が使える可能性が高いので部分分数分解を試してみましょう。
5.練習問題
では、何問か練習しましょう。
すべて不定積分の問題となっております。
練習
つぎの不定積分を求めなさい。
ただし、積分定数は \( C \) とする。
(1) \[\int \frac{x}{x^2 + x - 6} dx \](2) \[\int \frac{x^3 + 3x - x - 3}{x^2 + 2x - 3} dx \](3) \[\int \frac{3x + 1}{(x+3)^2} dx \](4) \[\int \frac{1}{x^3 - x} dx \](5) \[\int \frac{1}{(x-2)(x^2 +1)} dx \](6) \[\int \frac{x^2 - 6x + 11}{(x+1)(x-2)^2} dx \](7) \[\int \frac{1}{x^4 - 1} dx \](8) \[\int \frac{2x^2+2x}{(x-1)^2 (x^2+1)} dx \](9) \[\int \frac{1}{\sin x} dx \]
6.練習問題の解答
(1)

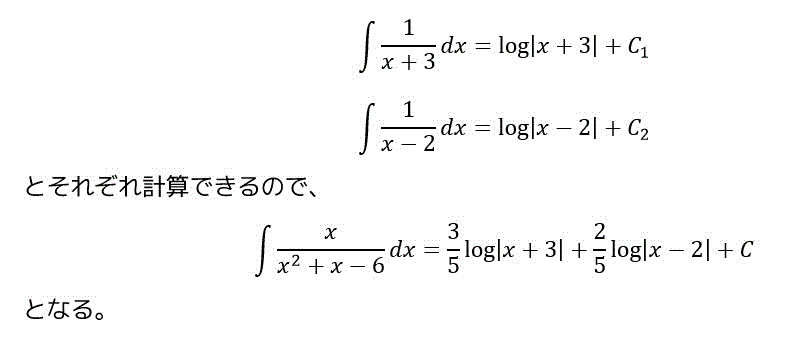
(2)

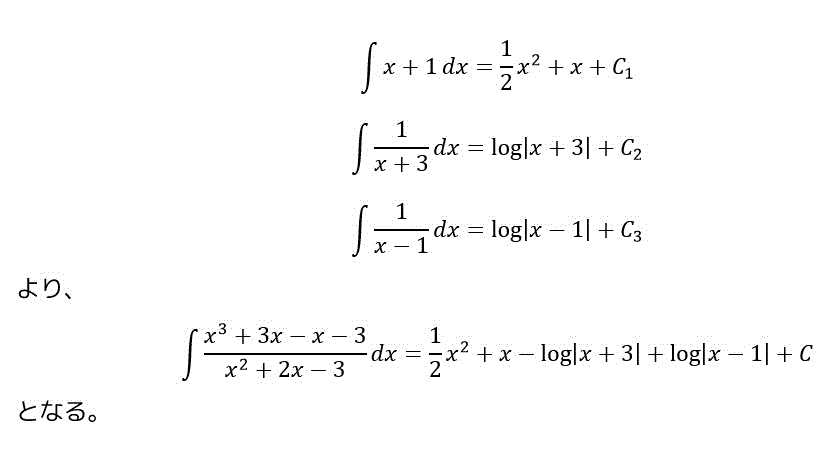
(3)
カッコの2乗のパターンです。

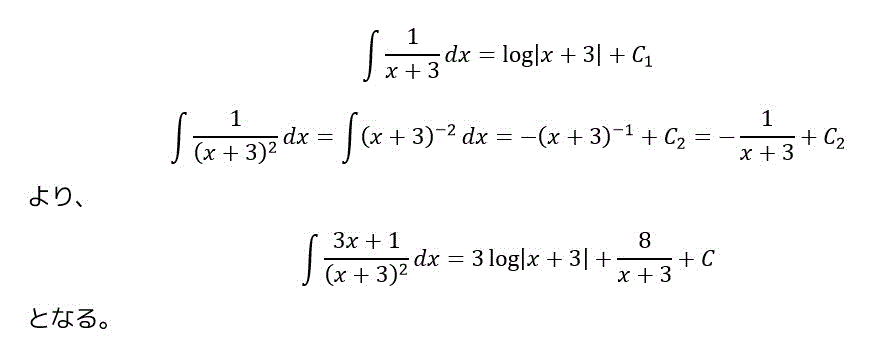
(4)

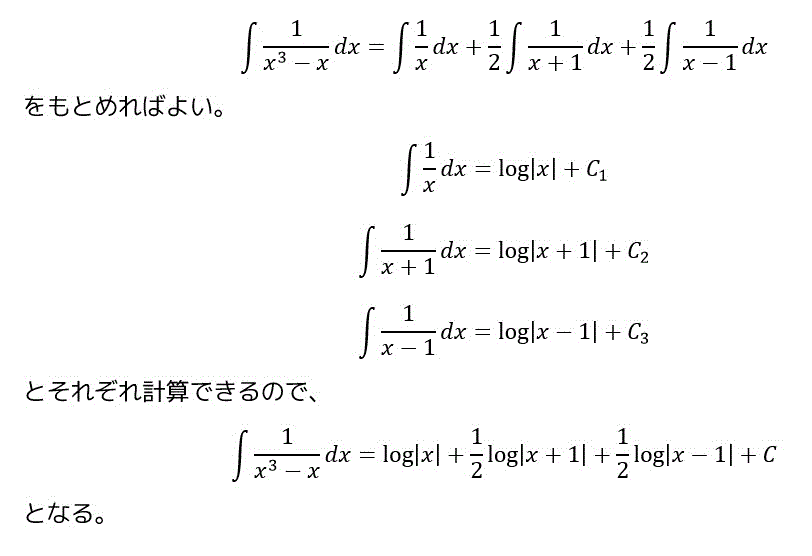
(5)
分母が2次式となるので、分子を \( bx + c \) と1次式も想定されるような置き方をする必要があります。

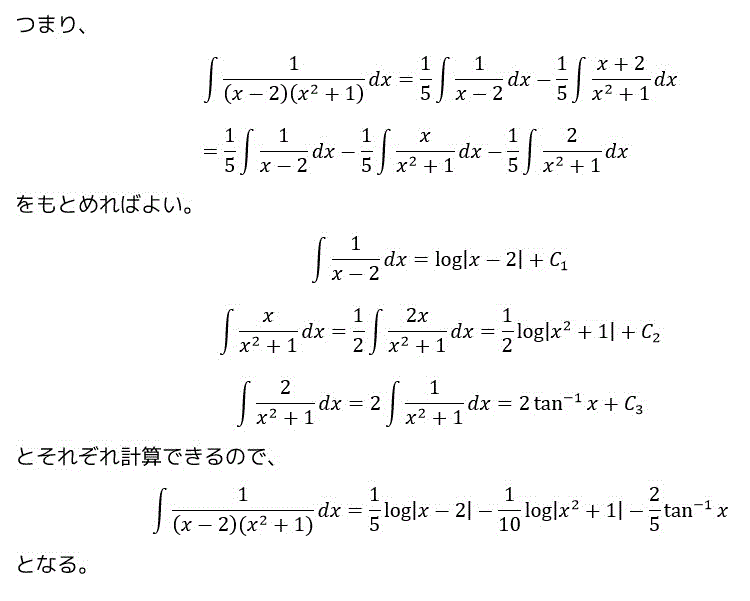
(6)
(3)に分数の数が増えたバージョンです。

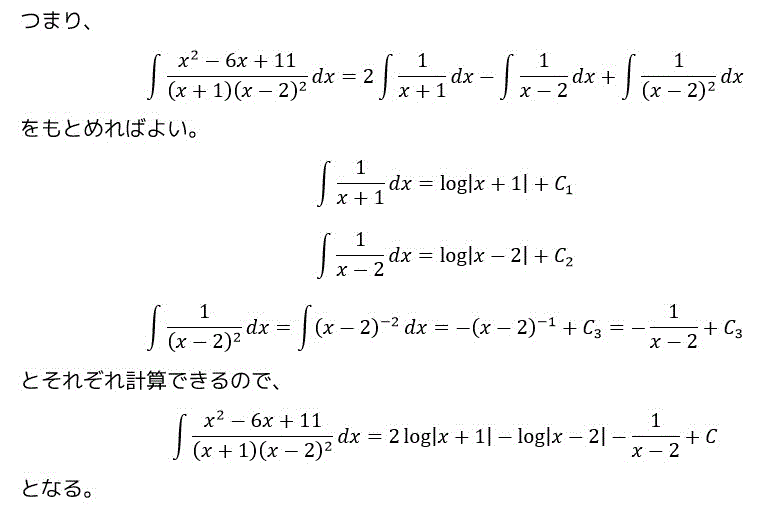
ヘビサイドのカバーアップ法を用いた部分分数分解の別解

このように \( a = 2 \), \( b = -1 \), \( c = 1 \) を求めてもOK。
(7)
だいぶ複雑になってきました。

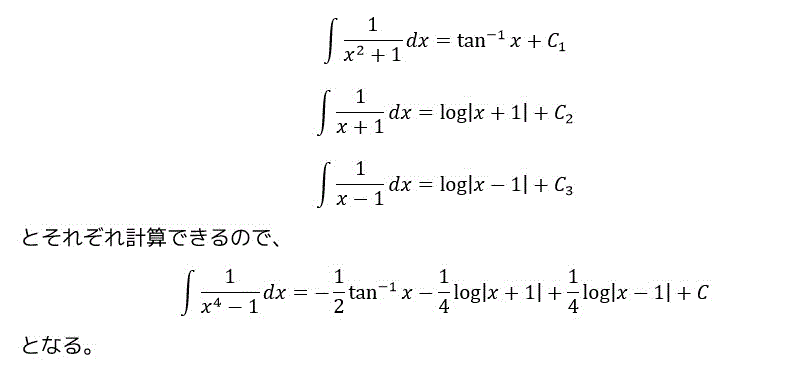
(8)
今回の中で一番問題です。
カッコの2乗と分母の2乗がセットで含まれている問題です。

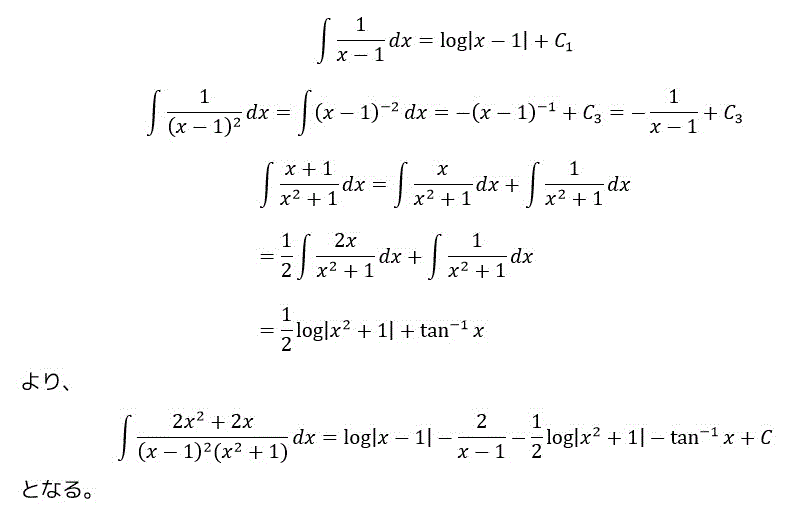
(9) (8)より計算は簡単ですが、思い浮かぶかがポイントになってきます。

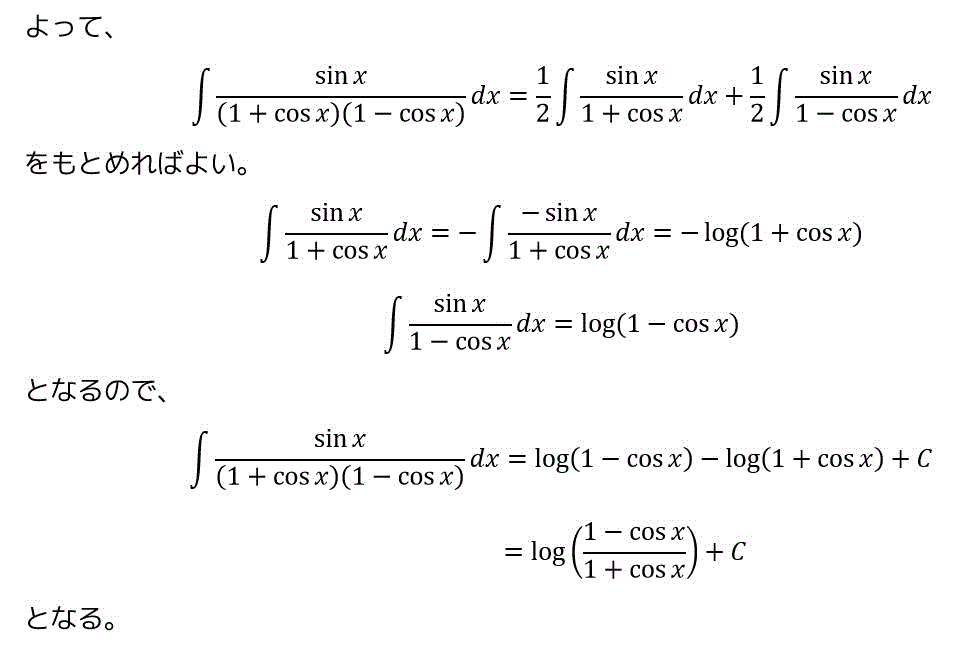
次回以降こちらの問題を別パターンで解いてみましょう。
7.さいごに
今回は、部分分数分解を用いた積分について説明しました。
数3ではもちろん重要な分野ですが、大学の解析学以外にも様々な場面で部分分数分解は使うことになるので必ずマスターしましょう。
*1:\[ \frac{- \frac{1}{3} x - \frac{2}{3}}{x^2 -x + 1} = -\frac{1}{3} \cdot \frac{x+2}{x^2-x+1}\]と計算している。
関連広告・スポンサードリンク