スポンサードリンク
制御工学の期末試験対策用に作成しております。
期末試験前の確認などにご利用ください。
(基礎的な部分しか載せられていません。ご両所ください。)
目次
スポンサードリンク
1. 制御工学で使う基本的な計算
主に周波数特性(ゲイン特性・位相特性)の計算で使います。
(1) 基本的な対数計算

(2) 複素数の大きさ(絶対値)・偏角
オイラーの公式は、そこまで(信号処理に比べて)使いませんが一応載せています。
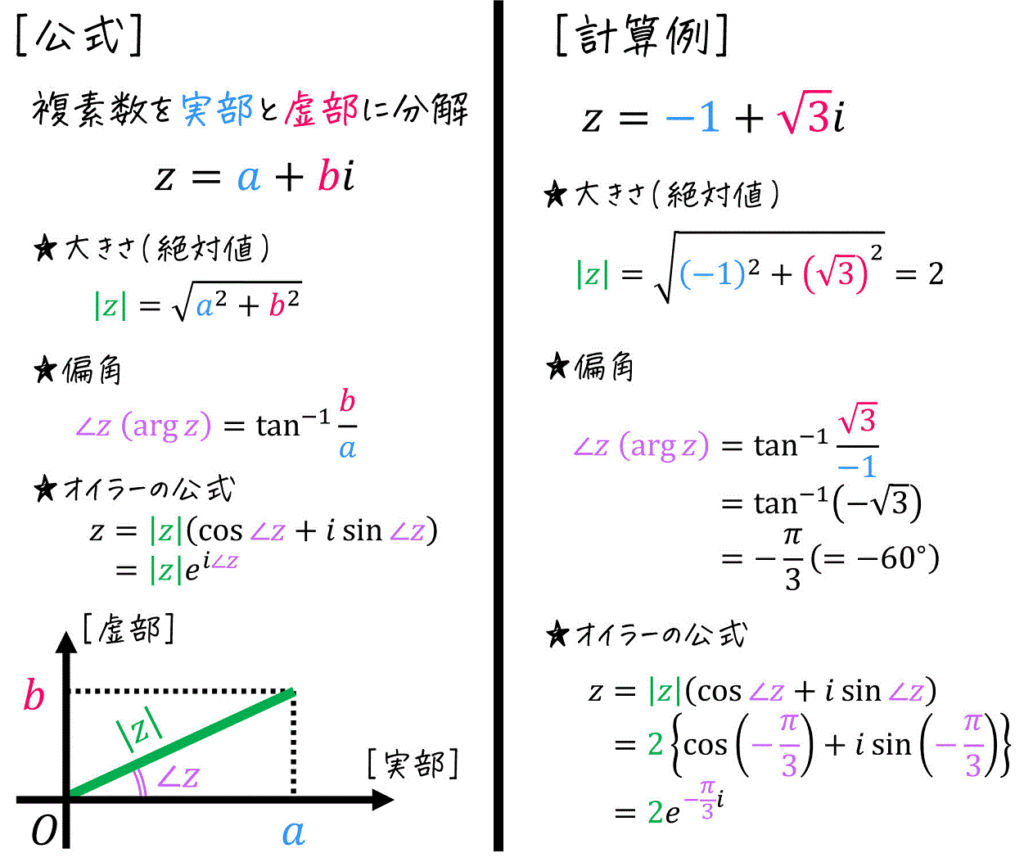
(3) 複素数の積と大きさ・偏角

計算例にも挙げている(実数)÷(複素数)の計算は、周波数応答の部分で出てくるので使いこなせるようになりましょう!
(信号処理を習う人は、信号処理でも使うので覚えておくと一石二鳥です)
スポンサードリンク
2. ラプラス変換・ラプラス逆変換
(1) 定義式
(i) ラプラス変換
\[
F (s) = \mathcal{L} [ f(t) ] = \int^{\infty}_{0} e^{-st} \ dt
\]
[変数の意味]
\( f(t) \) … 時間関数
\( F(s) \) … \( f(t) \) のラプラス変換
制御工学の世界では、定義式からラプラス変換を計算することはありませんが、一応頭に入れておきましょう。
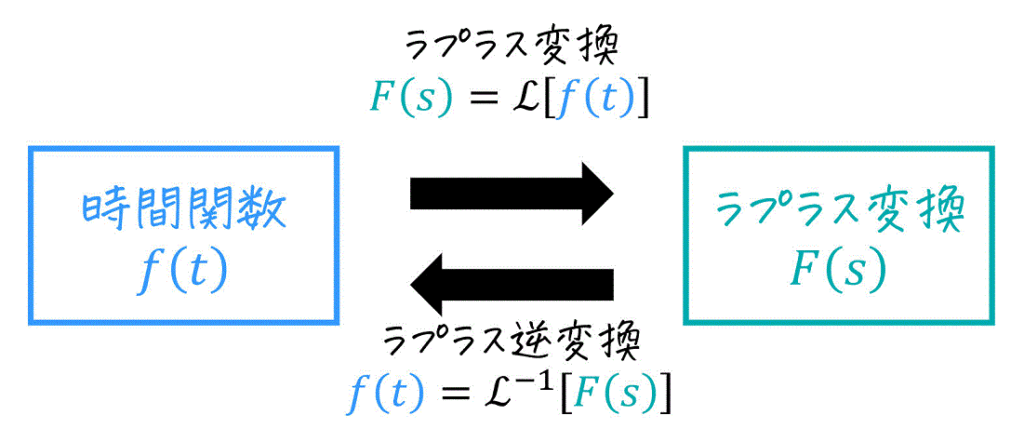
(ii) ラプラス逆変換(逆ラプラス変換)
ラプラス変換前の関数 \( f(t) \)(時間関数)とそのラプラス変換 \( F(s) \) は1対1対応しているため、ラプラス逆変換はラプラス変換を逆にたどることで求めることができます。
(2) ラプラス変換表を用いたラプラス変換の計算 [重要]
制御工学の世界では、ラプラス変換表を使ってラプラス変換を行います。
(ラプラス変換表はこちらからダウンロードできます)

超重要公式なので必ずできるようになっておきましょう!
(3) ラプラス変換表を用いたラプラス逆変換の計算 [重要]
ラプラス逆変換も、ラプラス変換と同じくラプラス変換表から計算を行います。
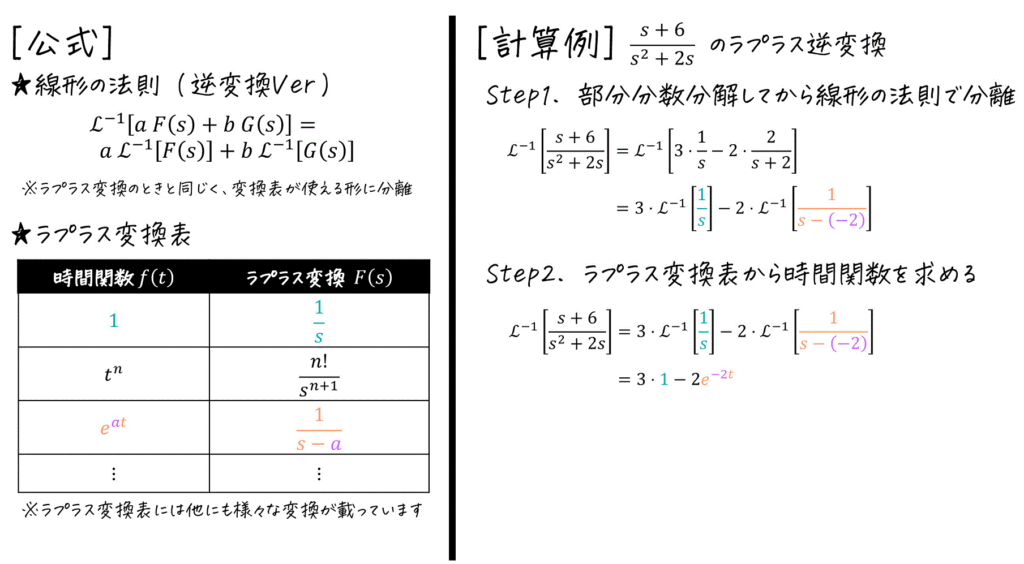
こちらも、ラプラス変換と並ぶ超重要公式です。
(4) 部分分数分解とラプラス逆変換
ラプラス逆変換で計算する部分分数分解は、制御工学ではほぼ必須のスキルです。
★Step1. 分母を因数分解する\[
\frac{1}{s^2-3s+2} = \frac{1}{(s-3)(s+2)}
\]
★Step2. 分数の形を作る\[
\frac{1}{(s-3)(s+2)} = \frac{a}{s-3} + \frac{b}{s+2}
\]

★Step5. あとは代入すればOK
\[\begin{align*}
\frac{1}{(s-3)(s+2)} & = \frac{ \frac{1}{5} }{s-3} + \frac{- \frac{1}{5}}{s+2}
\\ & = \frac{1}{5} \cdot \frac{1}{s-3} - \frac{1}{5} \cdot \frac{1}{s+2}
\end{align*}\]
部分分数分解について復習したい人向けの記事を下に用意しているので、もしよろしければご覧ください。
(5) 制御工学で使うラプラス変換の微分公式
ラプラス変換表が与えられない場合は、次の公式を頭に入れておきましょう。
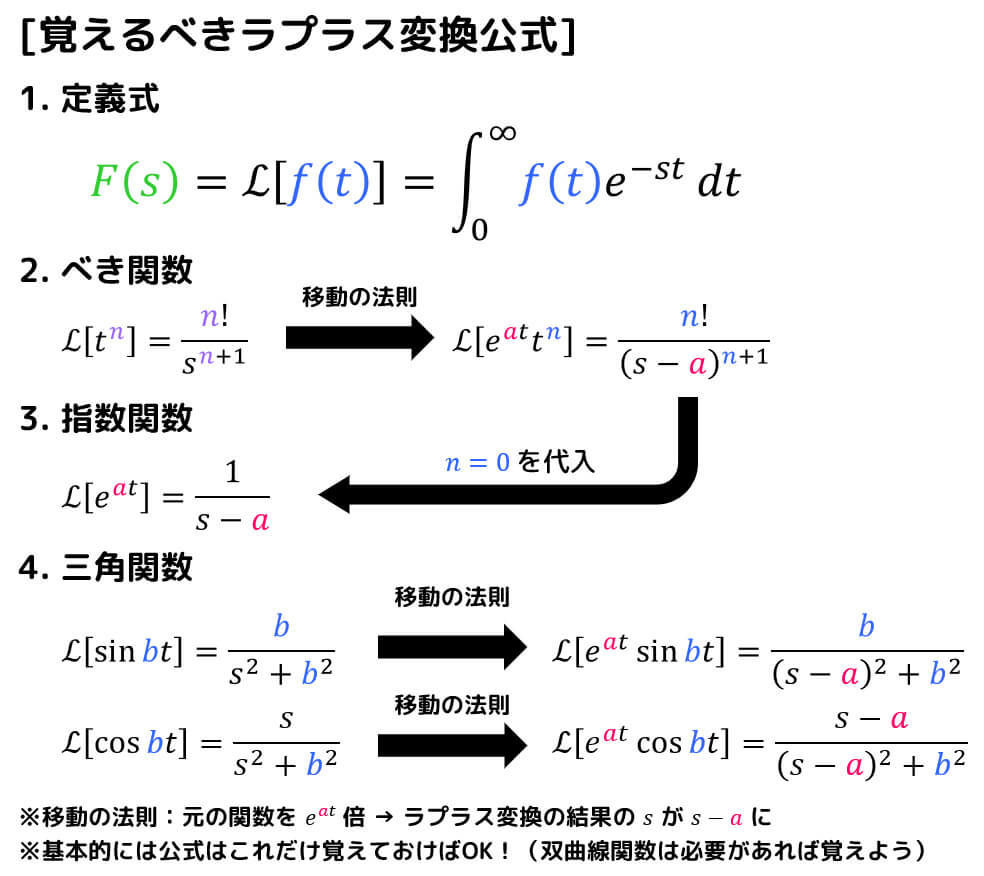
(6) 制御工学で使うラプラス変換の微分公式
インパルス応答、ステップ応答、ランプ応答など、与えられたシステムに対する出力を求める際に使用します。
\[
\begin{align*}
\mathcal{L} \left[\frac{dy}{dt} \right] & = s Y(s) \\
\mathcal{L} \left[\frac{d^2 y}{dt^2} \right] & = s^2 Y(s) \\
\mathcal{L} \left[\frac{d^3 y}{dt^3} \right] & = s^3 s Y(s) \\
\mathcal{L} \left[ \frac{d^n y}{dt^n} \right] & = s^n Y(s)
\end{align*}
\]
※ 制御工学の世界では、微分方程式の初期値は何にしようが伝達関数は変わらないので、一番計算が簡単になるように初期値 \( y(0) = 0 \), \( y'(0) = 0 \), … にしている。もし初期値を考える必要がある場合は、この微分方程式の公式が変わってくる。
(7) 初期値定理・最終値定理

ラプラス変換された値 \( F(s) \) をもとに戻すことなく初期値 \( f(0) \)、および 最終値 \( f(t) , \ (t \to \infty) \) の値を求められるので非常に便利な公式です。
[余談] ちなみに、今回の計算例のラプラス変換を逆変換でもとに戻すと、\( f(t) = 3 - 2e^{-2t} \) となります。初期値定理、最終値定理の計算結果と \( f(0) \) と \( f(t ) , \ (t \to \infty) \) の値が一致することがわかりますね。ラプラス変換についてさらに復習したい方は下の記事をご覧ください!
(初期値を考える場合のラプラス変換の微分公式も下の記事に載せています)
スポンサードリンク
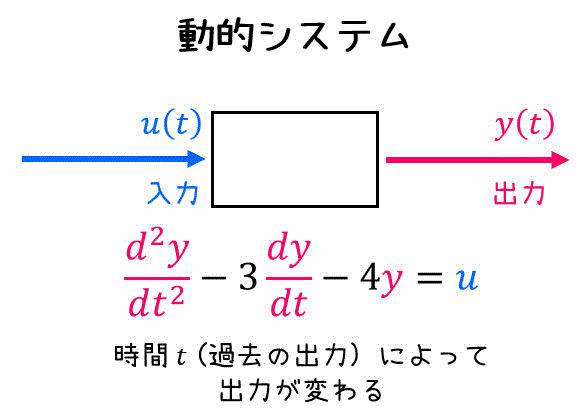
3. 動的システムの伝達関数と様々な応答
(1) 制御工学で使う特別な関数
(1) 制御工学の世界で出てくる様々な関数
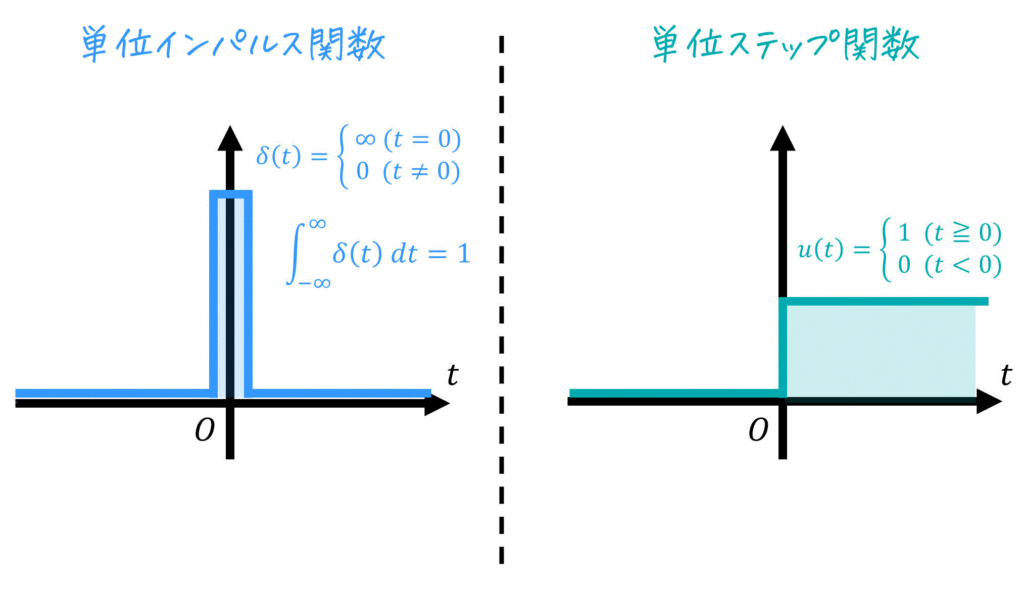
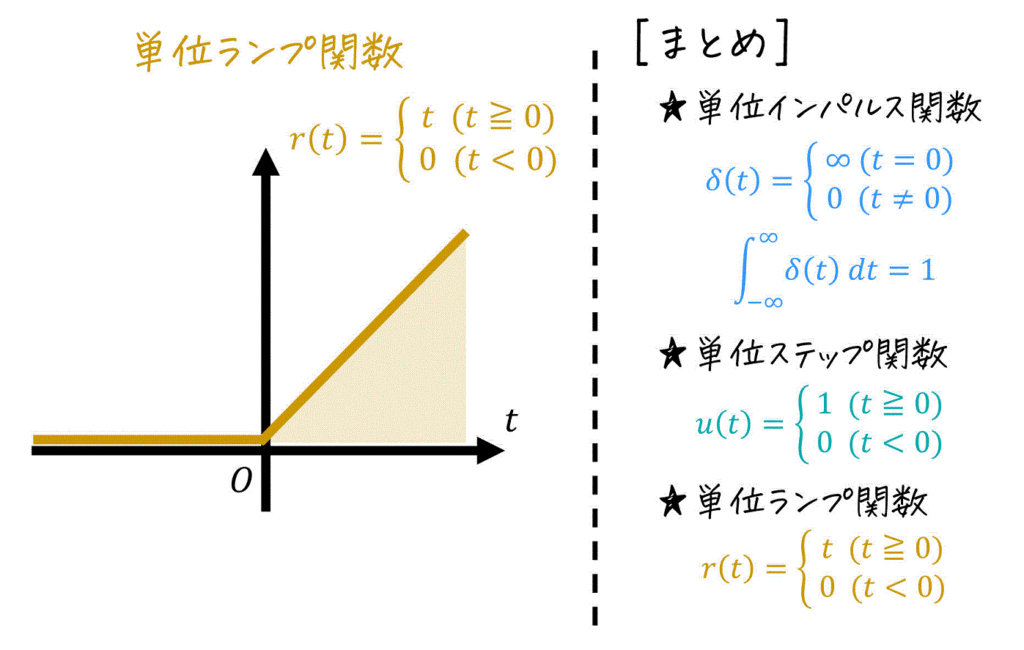
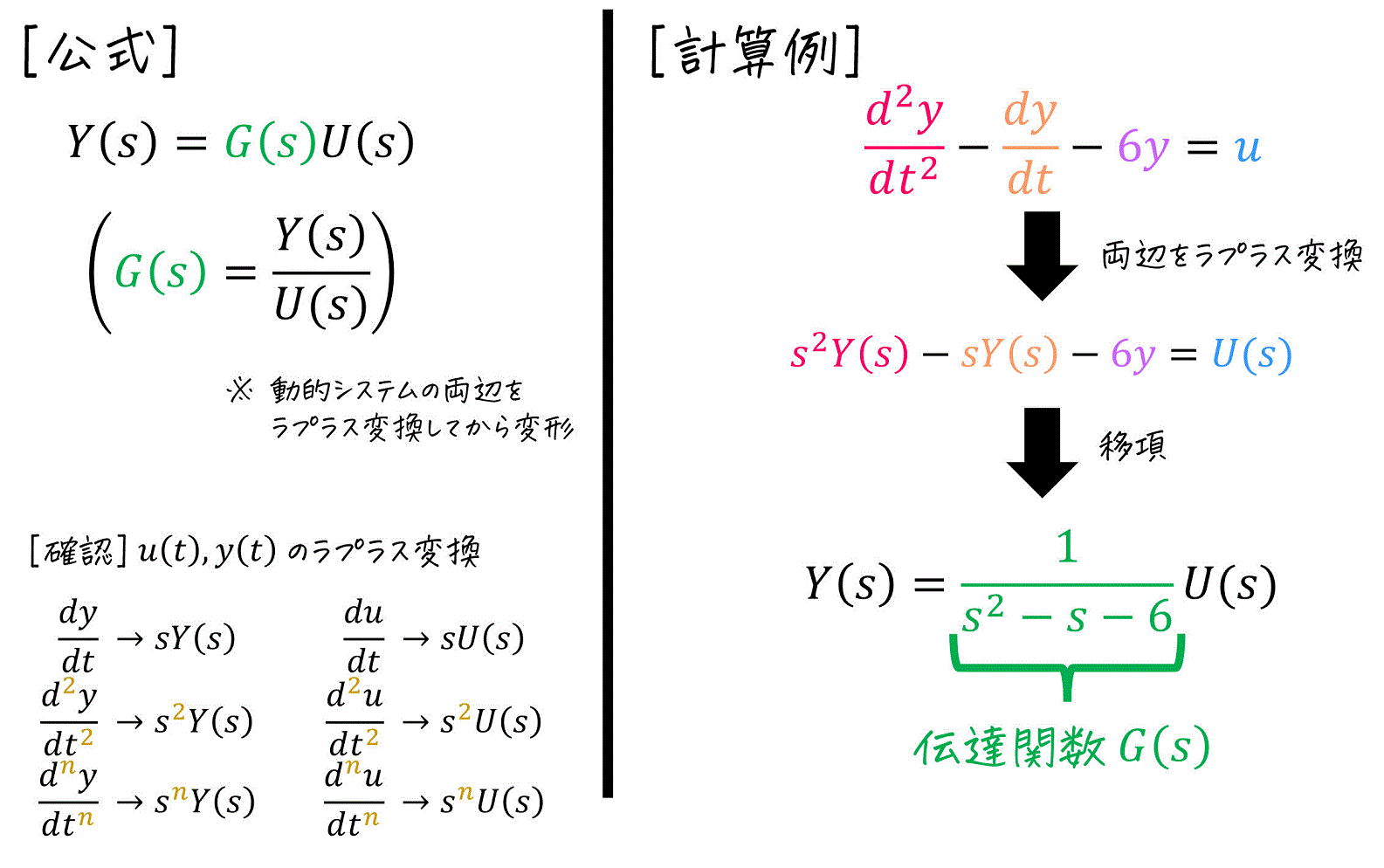
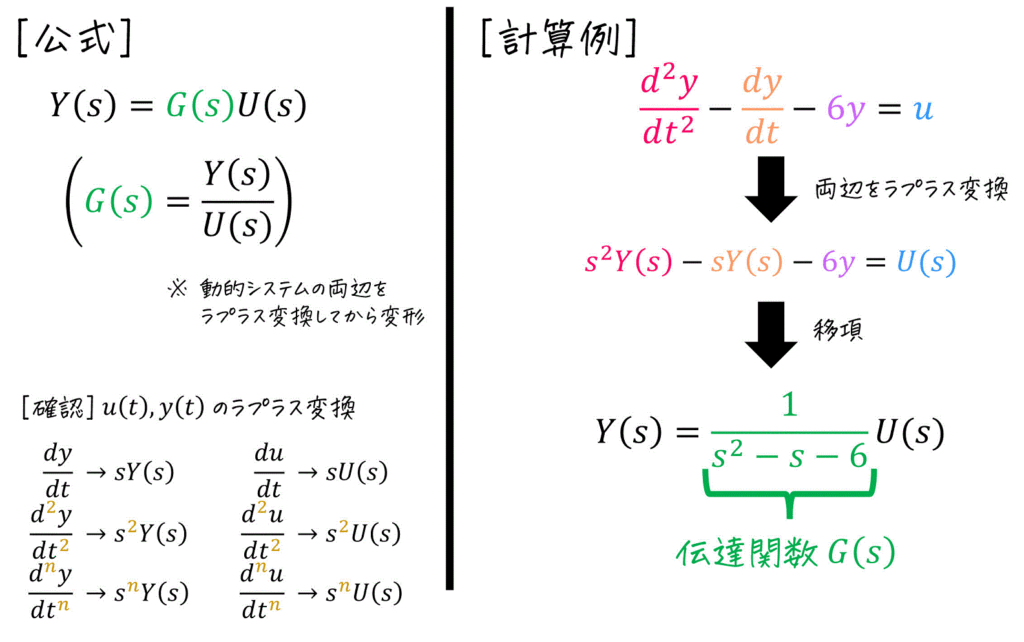
(2) 伝達関数
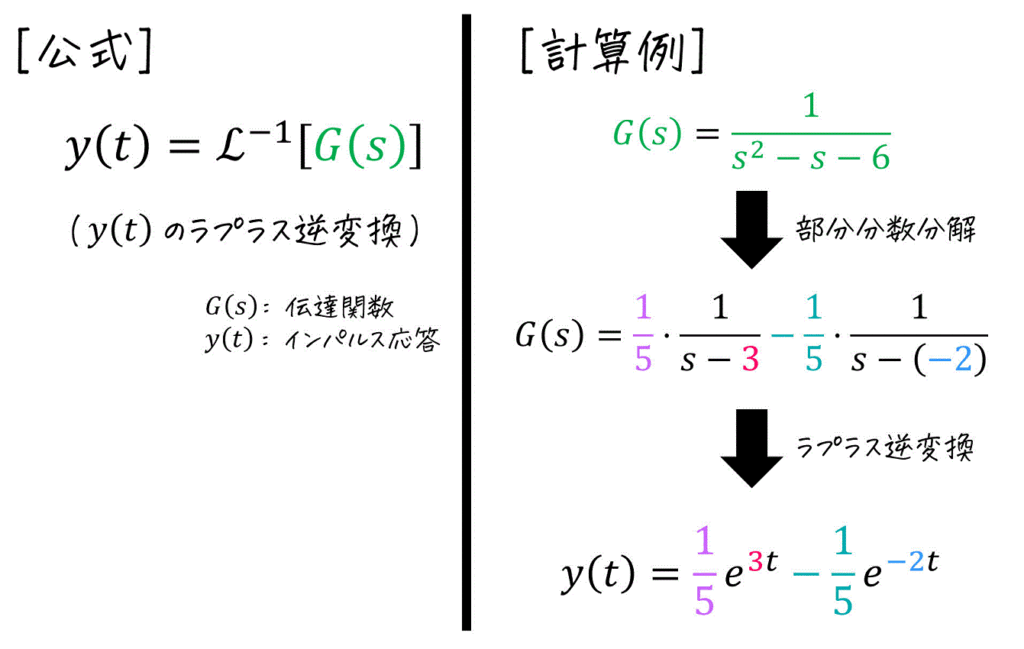
(3) インパルス応答
伝達関数を逆ラプラス変換すればOK。
(4) ステップ応答
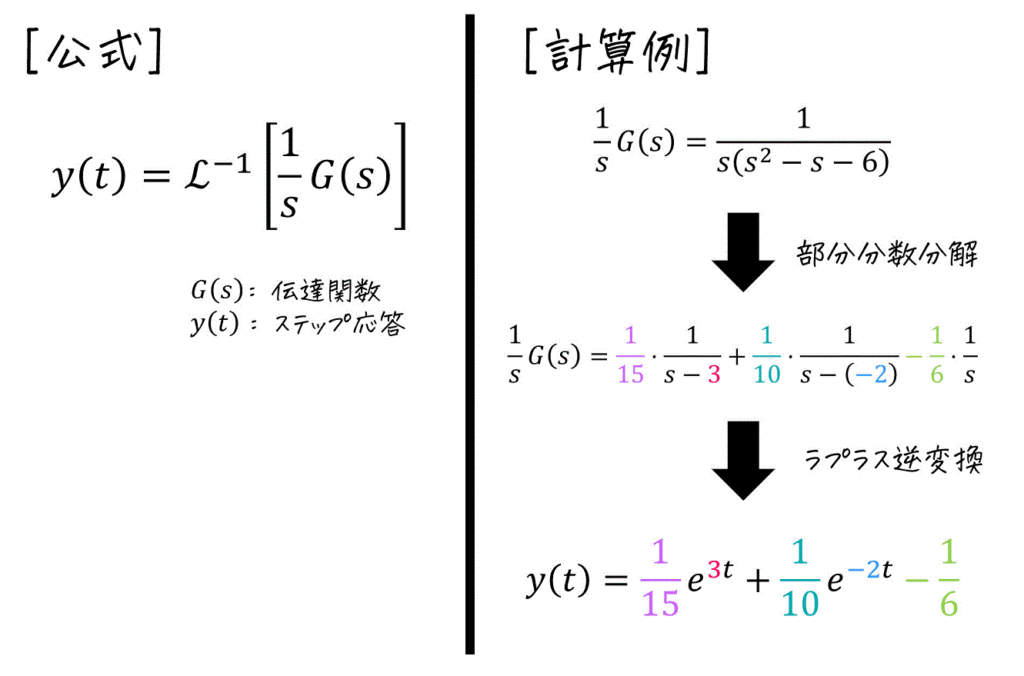
※ インパルス応答をすでに計算している場合は、(6)の公式でステップ応答を求める方法がおすすめ
(5) ランプ応答
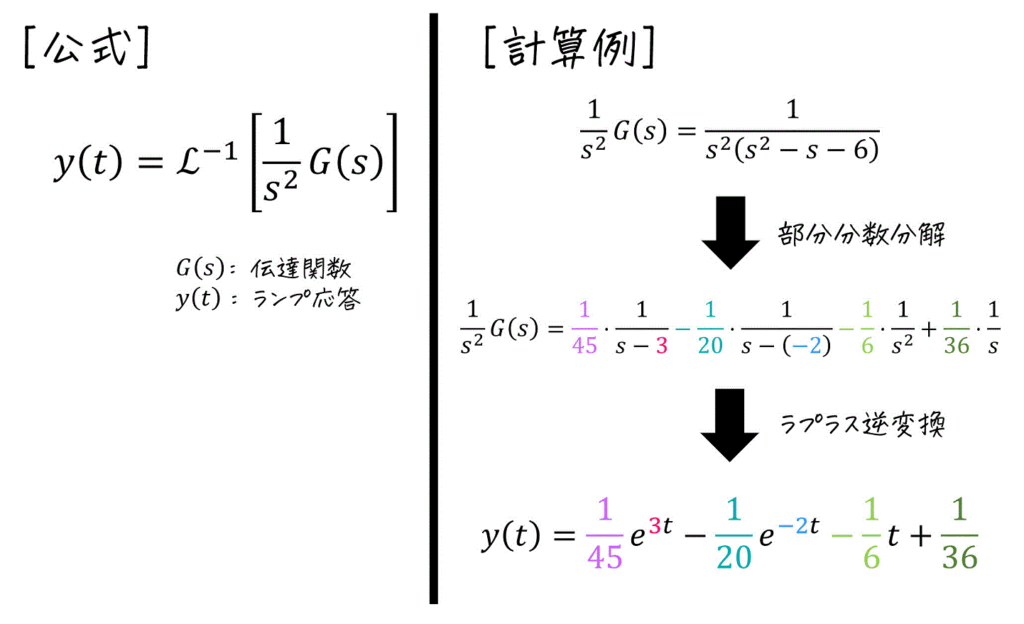
※ この公式からランプ応答を計算する場合、部分分数分解の計算の覚悟が必要。ステップ応答をすでに計算している場合は、(6)の公式でランプ応答を求める方法がおすすめ
(6) インパルス応答からステップ応答、ランプ応答を求める魔法の公式
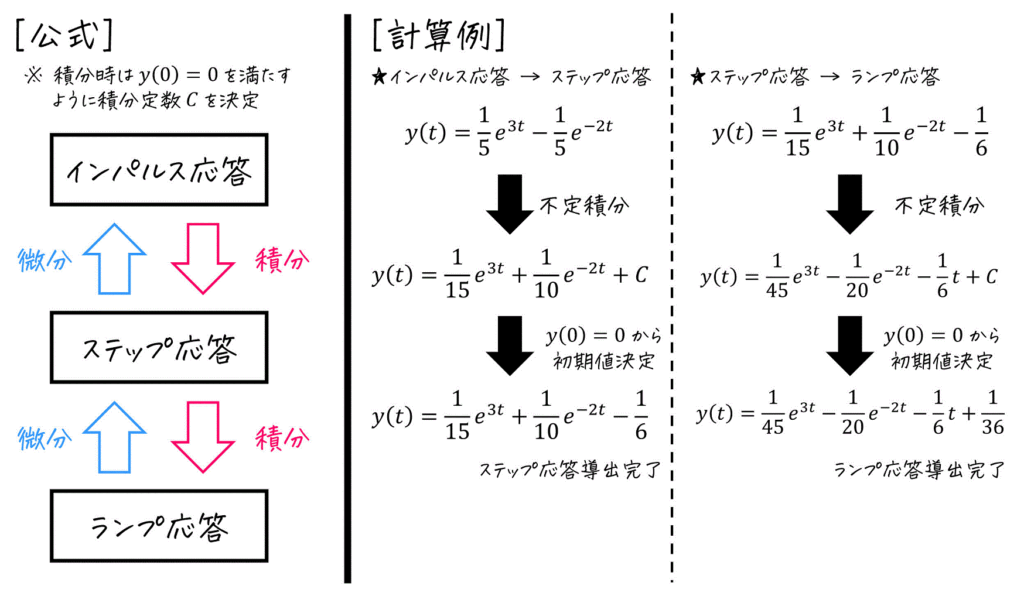
かなり使える公式なので、
- インパルス応答を積分して \( y(0) = 0 \) を満たすような \( C \) を決定 → ステップ応答
- ステップ応答を積分して \( y(0) = 0 \) を満たすような \( C \) を決定 → ランプ応答
と覚えておきましょう!
動的システムの基礎(伝達関数、様々な応答)の復習をさらに行いたい方は、下の記事をご覧ください。
4. 極・零点と動的システムの安定性
(1) 極・零点

(2) 安定性
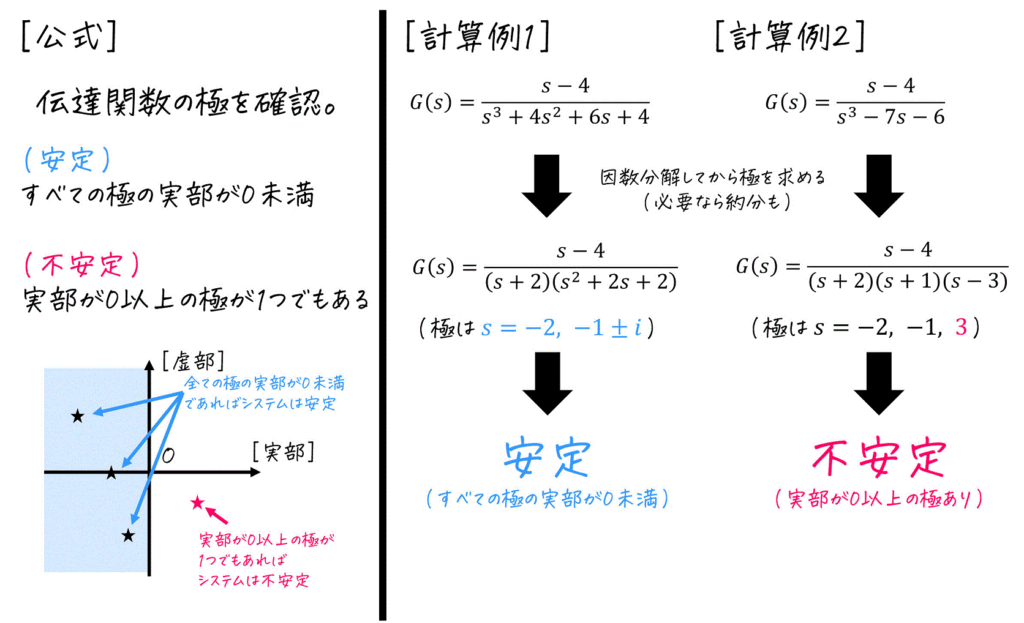
※ 信号処理(ディジタルシステム)を履修している人は、安定性の条件をごちゃまぜに覚えないようにしましょう。
[動的システムの世界] すべての極 \( s \) の実部が0未満であればOK[ディジタルシステムの世界] すべての極 \( z \) が \( |z| < 1 \) であればOK
極・零点や動的システムの安定性について、さらに復習を行いたい方は、下の記事をご覧ください。
5. 周波数特性・ゲイン特性・位相特性
この単元(およびボード線図)をさらに復習したい方は下の記事をご覧ください。
(1) 周波数特性

※ 信号処理(ディジタルシステム)を履修している人は、周波数特性の求め方をごちゃまぜに覚えないようにしましょう。
[動的システムの世界] \( s = i \omega \) で計算[ディジタルシステムの世界] \( z = e^{i \omega} \) で計算
(2) ゲイン(振幅)特性・位相特性
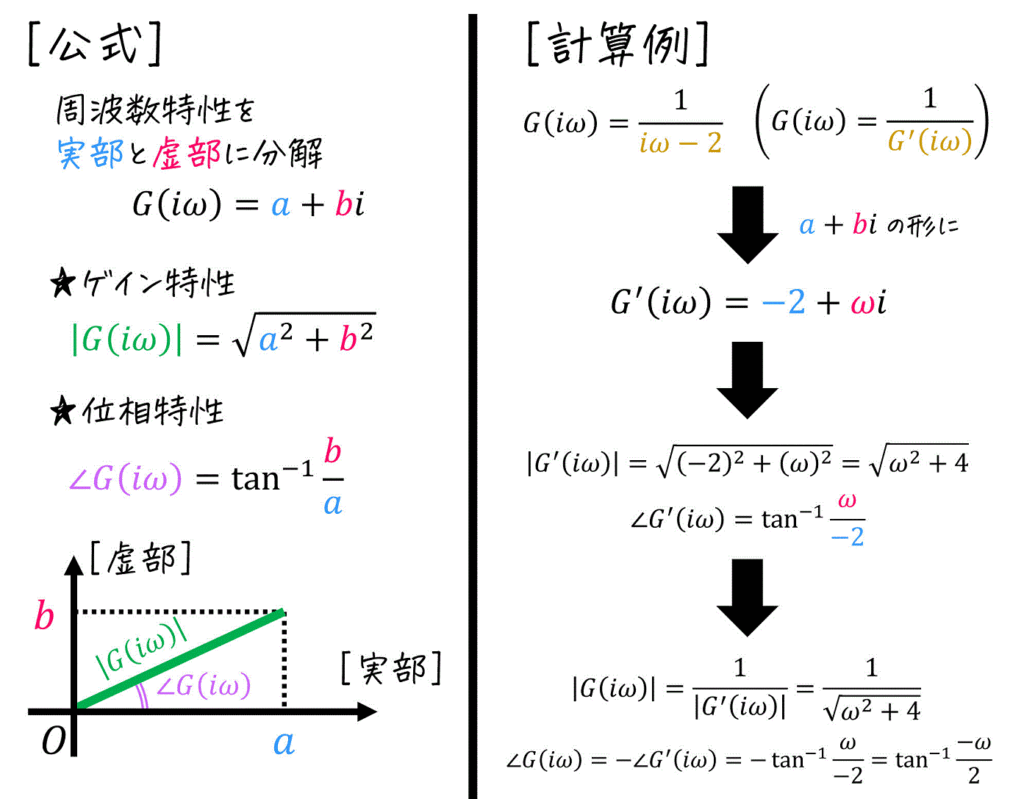
6. ボード線図
(1) 周波数特性のゲインとデシベル[dB]

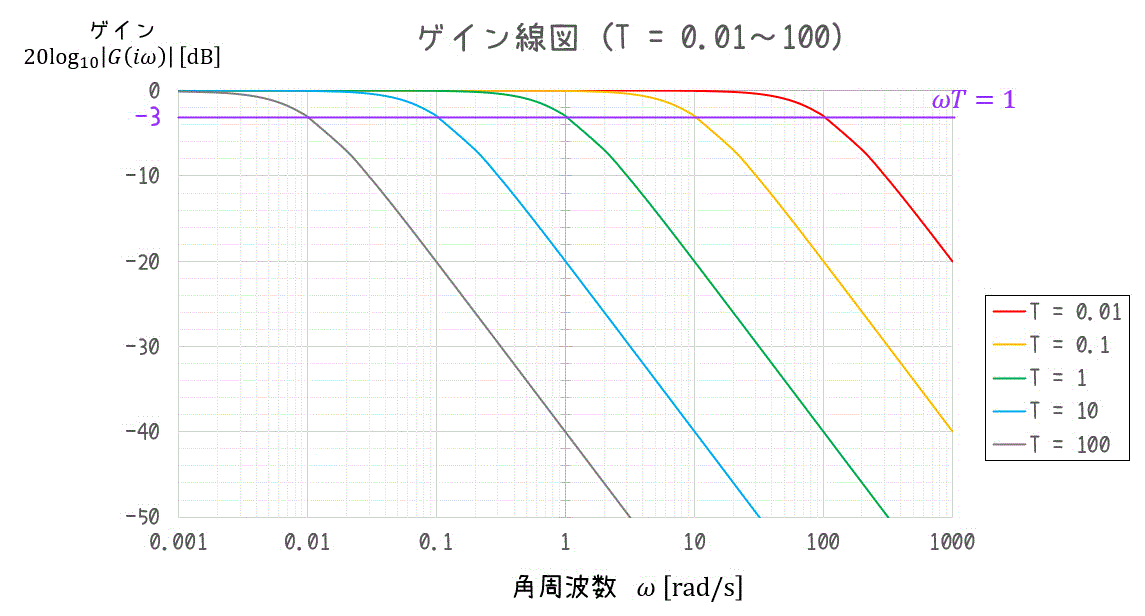
(2) ゲイン線図
[公式]
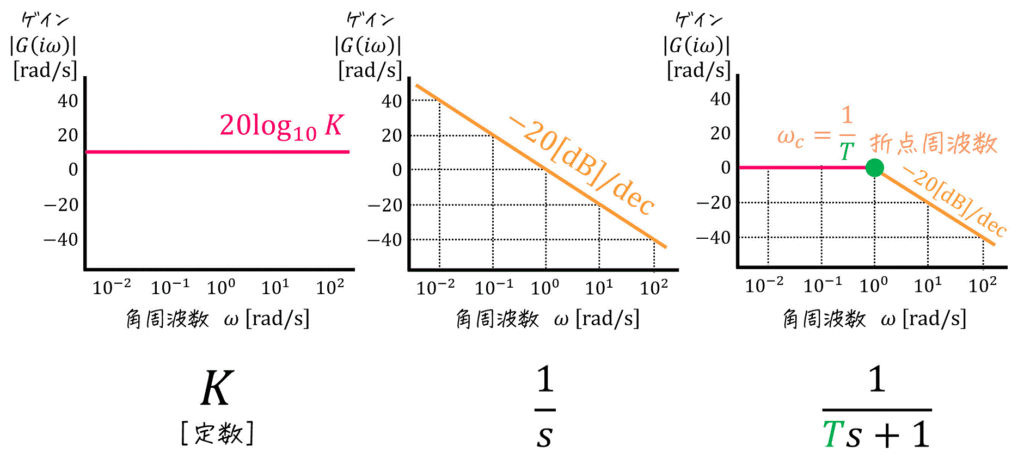
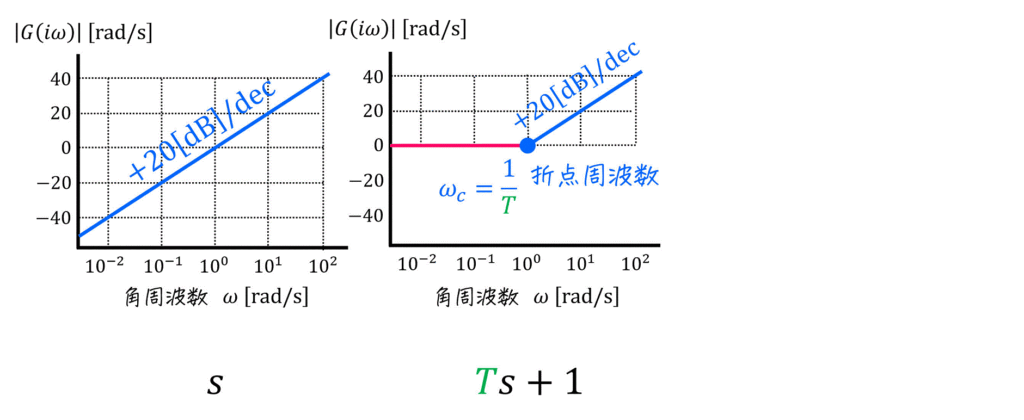
[計算例]
「伝達関数の積=ゲイン線図の和」であることを利用するために、伝達関数を分解してから計算します。
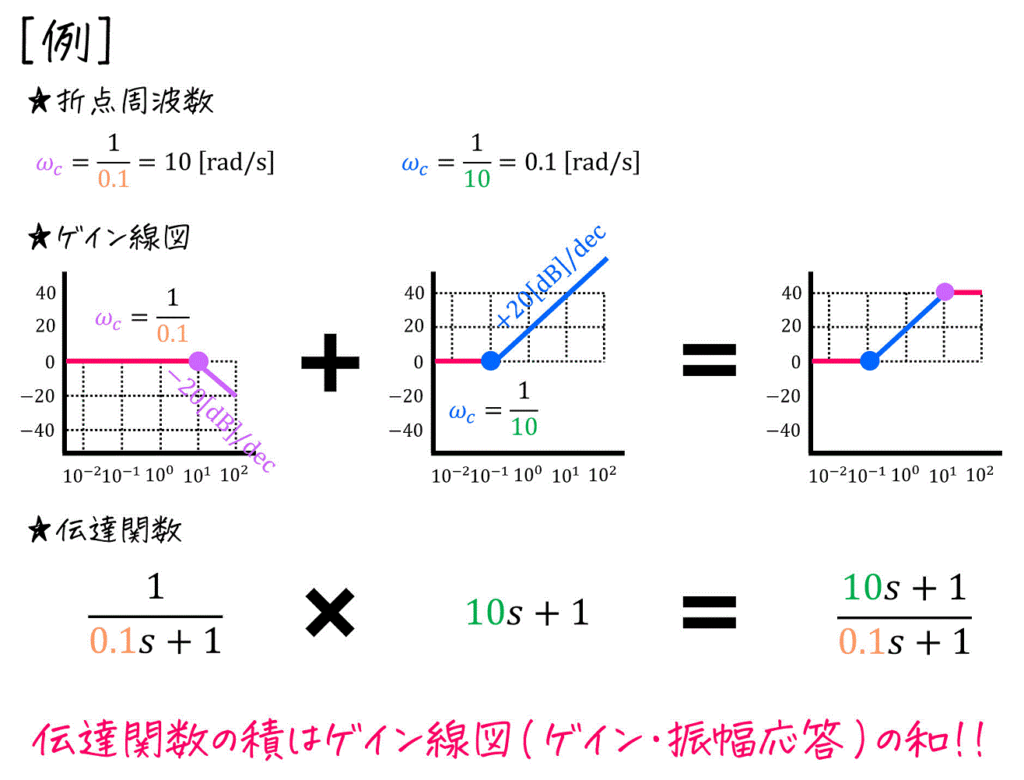
\[
G(s) = \frac{10s + 1}{s + 10}
\]のように、分子分母に \( Ts + \textcolor{magenta}{1} \) でない形が出てきた場合は、\[
G(s) = \frac{10s + 1}{10(0.1s + \textcolor{magenta}{1})}
\]のように \( Ts = 1 \) の形にしてから\[
G(s) = (10s+1) \cdot \frac{1}{10} \cdot \frac{1}{0.1s + 1}
\]と分解し、ゲイン線図を求めていきましょう。
(3) 位相線図
[公式]
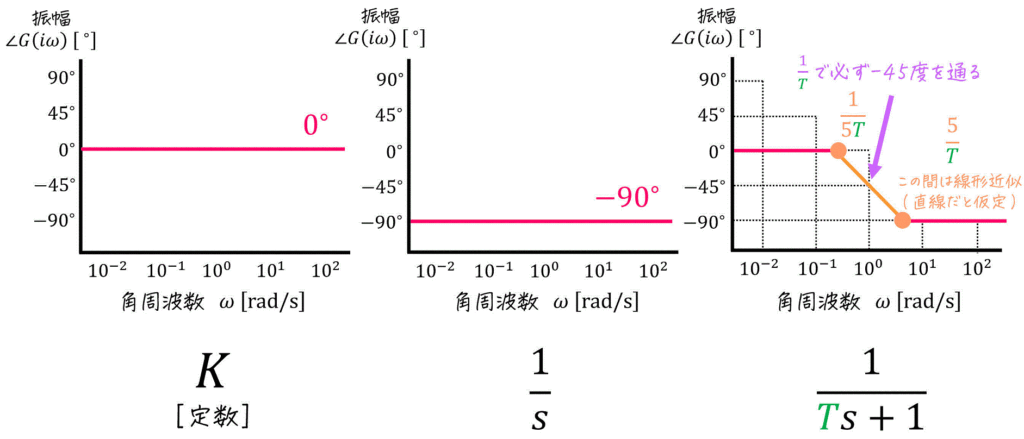
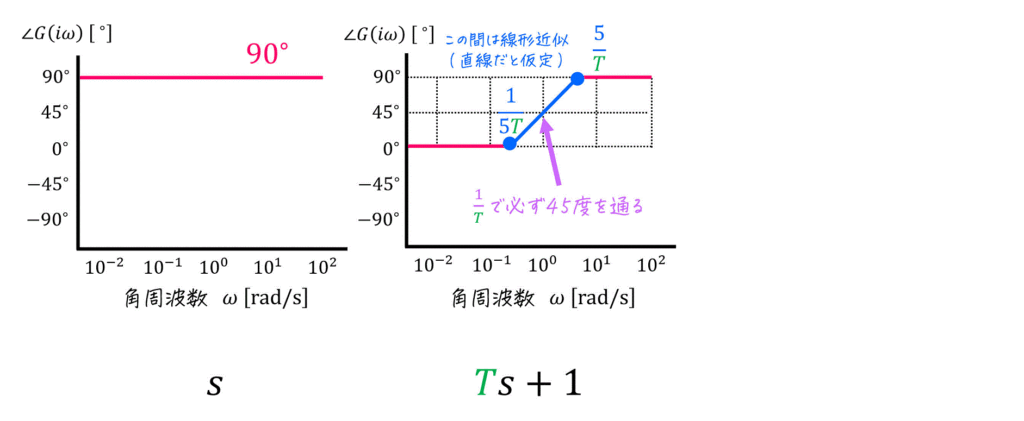
[計算例]
こちらも「伝達関数の積=位相線図の和」あることを利用するために、伝達関数を分解してから計算します。
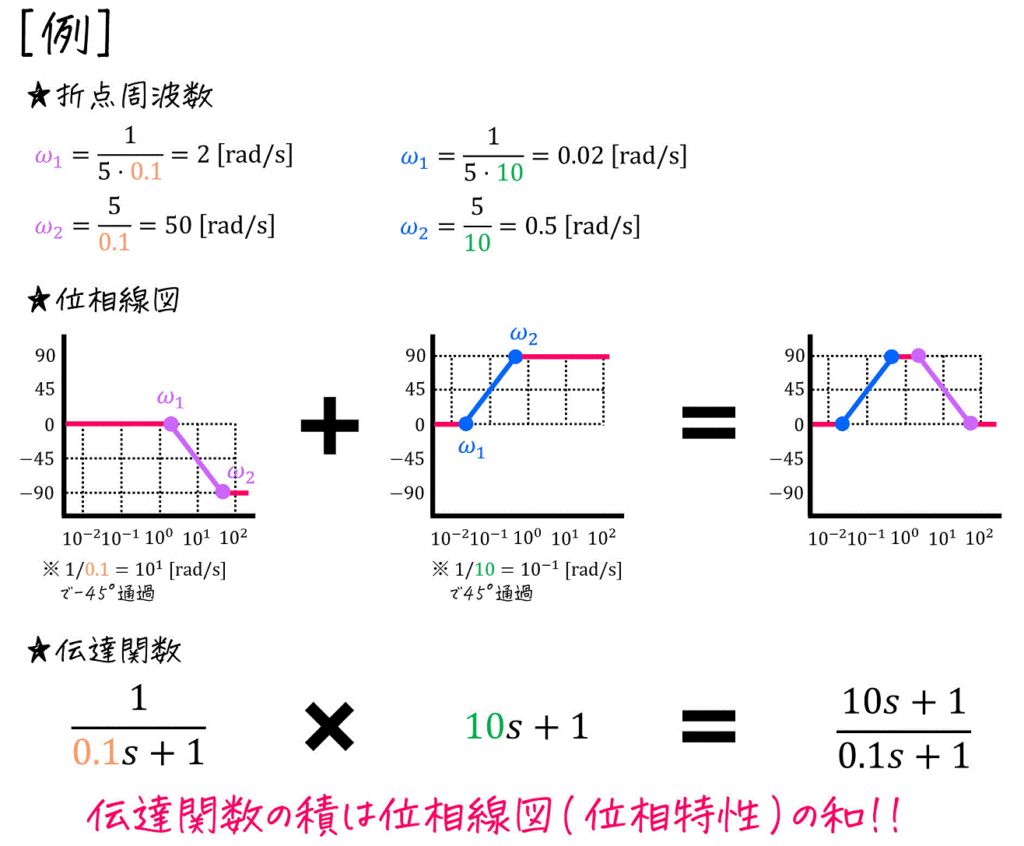
\[
G(s) = \frac{10s + 1}{s + 10}
\]のように、分子分母に \( Ts + \textcolor{magenta}{1} \) でない形が出てきた場合は、ゲイン線図を求めるときと同じように、\[
G(s) = \frac{10s + 1}{10(0.1s + \textcolor{magenta}{1})}
\]のように \( Ts = 1 \) の形にしてから\[
G(s) = (10s+1) \cdot \frac{1}{10} \cdot \frac{1}{0.1s + 1}
\]と分解し、位相線図を求めていきましょう。
周波数応答(ゲイン特性・位相特性)およびボード線図についてさらに復習をしたい方はこちらをご覧ください。
関連広告・スポンサードリンク