スポンサードリンク
こんにちは、ももやまです。
今回はオートマトンと言語理論の中でも重要な文脈自由文法についてまとめていきたいと思います。
前回の記事の内容(Myhill-Nerodeの定理・正則ではない言語の証明法)はこちら↓
目次
スポンサードリンク
1.文脈自由文法とは
文脈自由文法は、以下の4つの要素で構成されるような文法を表します。
(出発記号 \( S \) 以外はすべて集合です。)

非終端記号(変数) \( N \)
後ほど説明する生成規則 \( P \) によって書き換えることができるような文字(記号)の集まりを表します。基本的に \( S \), \( A \), \( B \) などの大文字が使われます。
終端記号 \( \Sigma \)
それ以上書き換えることができない文字の集まりです。
生成規則 \( P \)
1文字の終端記号を終端記号と非終端記号が組み合わされた複数の記号に変換するためのルール(置き換えルール)の一覧が書かれています。
生成規則は「○は□△である」のルールが集まっているものだと考えてください。
出発記号 \( S \)
文法解析の出発記号(非終端記号の1つ)を表します。
最初に置き換える記号です。
文脈自由文法を用いることで、正則言語よりも多くの文法、言語を表現することができます。また、多くのプログラミング言語の文法は文脈自由文法で構成されています。
スポンサードリンク
2.文脈自由文法の読み方
では、実際に文脈自由文法を読み取る練習をしてみましょう。先ほどの文法\[
G = \left( \{S,A,B\}, \{a,b\}, P,S \right)
\\ P = \{ S \to AB, \ A \to a, \ A \to aAa, \ B \to b, \ B \to bBb \}
\]はどんな文法なのかを調べてみましょう。
(1) 文字列の導出の方法
まずは、文字列がどのように導出されるかについて説明してみましょう。
文脈自由文法を導出する際には出発記号 \( S \) から生成規則(変換ルール)を連鎖的に適用していきます。
例えば、\( abbb \) を導出する場合、下のように4回生成規則を適用することで文字列を導出することができます。

(2) 最左導出・最右導出
導出の際に「テキトーに非終端記号選んで置き換えちゃえ!☆ヾ( ̄ ̄*)えいっ」とやるのは受理する文字列の列挙忘れの原因になったりします。
なので、実際に受理する文字列を列挙する際には左から優先的に非終端記号を変形していく最左導出、もしくは右から優先的に非終端記号を変形していく最右導出のどちらかで行うことが多いです(本記事では最左導出を採用しています)。
先ほどの文法で \( abbb \) を最左導出、最右導出した場合、以下のような変形で求めることができます。
最左導出の場合

最右導出の場合

(3) 列挙していく
文字列がどのように導出されるかを説明したので、実際に上の文法 \( G \) に含まれるような言語 \( L(G) \) を列挙していきましょう。
今回は練習なので6文字以下の \( L(G) \) に含まれる言語を探していきます。
列挙していく際には下のような木構造(ほぼ樹形図)を書いていくとわかりやすいかと思われます。
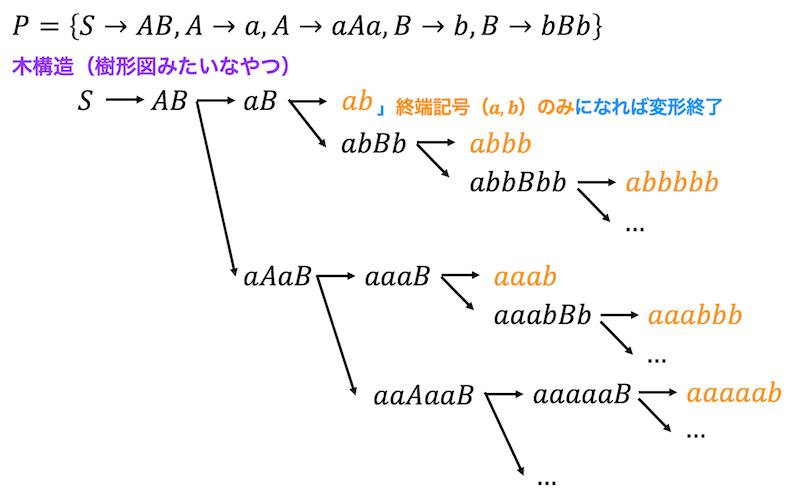
よって、\( L(G) \) に含まれる6文字以下の文字列は\[
ab, \ abbb, \ abbbbb, \ aaab, \ aaabbb, \ aaaaab
\]の6個となります。
(4) 列挙の結果からどのような言語かを推測する
ある程度列挙すると、文法の法則がつかめてきますよね。
今回の場合は、少し考えると、\( a \) が奇数回続いたあとに \( b \) がさらに奇数回続くような文字列が受理されていることがわかりますね。
数式で表すと、下のように表せます。
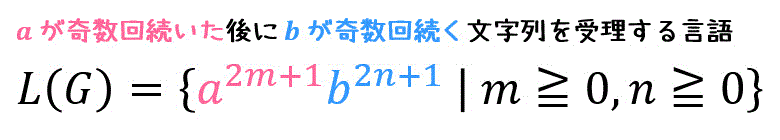
おまけ:決定性オートマトンを書いてみよう
実は、言語 \( L(G) \) は決定性オートマトンを用いて表すこともできます。決定性オートマトンを用いると、
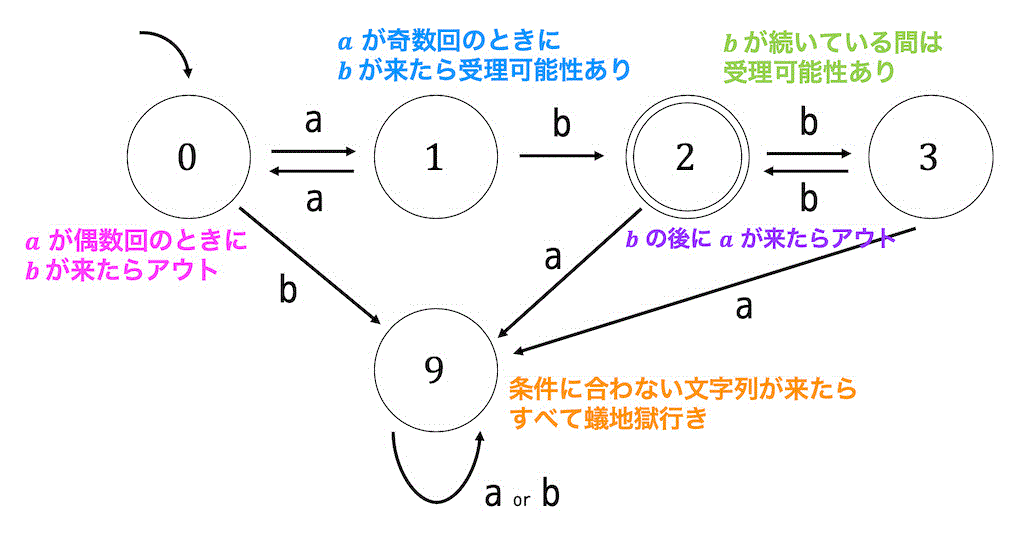
と表せます。
(難しいと思った人は \( a^{2m+1} \) と \( b^{2n+1} \) を受理するようなオートマトンを書いてから連接してあげるといいと思います。でも状態数増えてこっちもめんどくさい……)
スポンサードリンク
3.特別な文法・標準形
文脈自由文法の中でも特別な条件を満たすような言語は名前がつけられています。
今回は名前がつけられている文脈自由文法の中でも有名なものを3つほど紹介していきましょう。
(1) 正則文法(正規文法)
正則文法は、右正則文法(右正規文法)と左正則文法(左正規文法)の2つに分けられています。
(区別せずに正則文法と呼ぶ人も多い)
正則文法の特徴として、正則文法で記述される言語は必ず正則である、つまり(決定性)有限オートマトンを記述することができるという特徴があります*1。
もちろん正規文法に含まれるものは文脈自由文法にも含まれます。
右正則文法 (右正規文法)
右正則文法とは、下のように \( A \to a \) のような非終端記号を終端記号1文字に置き換える規則、もしくは \( A \to aB \) のような非終端記号を終端記号1文字のあとに非終端記号1文字をつけたものに置き換えるような規則の2つのみで構成されているような文法を表します。
左正則文法 (左正規文法)
左正則文法とは、下のように \( A \to a \) のような非終端記号を終端記号1文字に置き換える規則、もしくは \( A \to Bb \) のような非終端記号を非終端記号1文字のあとに終端記号1文字をつけたものに置き換えるような規則の2つのみで構成されているような文法を表します。
(右正則文法と左正則文法の違いは、左側の文字から終端記号になるか、右側の文字から終端記号になるかの違いだけです!)

注意!
右正則文法の規則 \( A \to aB \) と左正則文法 \( A \to Ba \) の両方を1つの文法で使うことはできません。どちらか片方のみの規則を使うこと(もしくは両方使わないこと)が正則文法の条件です。
(2) チョムスキー(Chomsky)標準形
チョムスキー標準形とは、下のように \( A \to a \) のような非終端記号を終端記号1文字に置き換える規則、もしくは \( A \to BC \) のような非終端記号を非終端記号2文字に置き換える規則(もしくは開始記号 \( S \) が空文字にしかならない規則のみ)で構成されるような文法のことを表します。
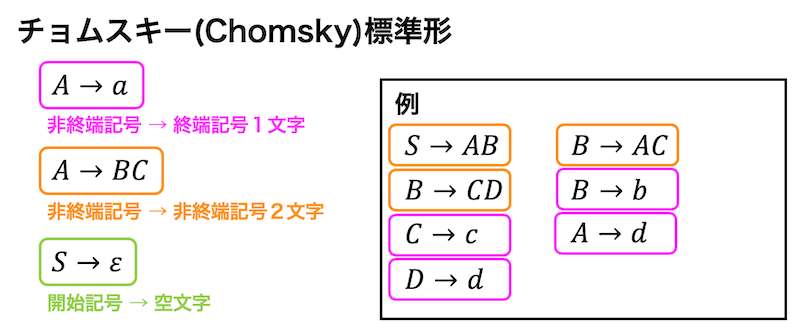
チョムスキー標準形の文法の特徴として、CYK法(CKY法)などによる構文解析が可能なことがあげられます。
また、すべての文脈自由文法は等価なチョムスキー標準形に変換してあげることができます(今回はチョムスキー標準形への変換については割愛します)。
(3) グライバッハ(Greibach)標準形
グライバッハ標準形とは、下のように \( A \to aX \) のような非終端記号を終端記号1文字のあとに非終端記号が1文字以上並んだものに変換する規則(もしくは開始記号を空文字にするような規則)のみで構成された文脈自由文法を表します。
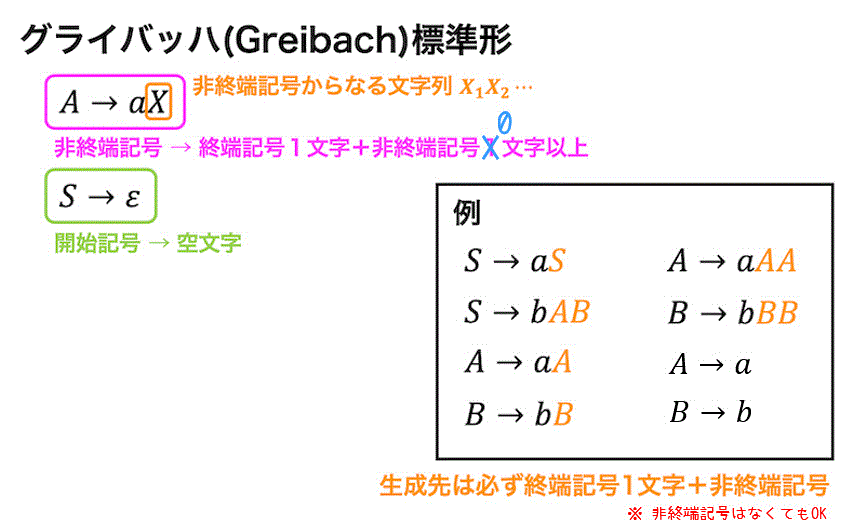
※ \( X \) には複数文字の非終端記号を入れても、非終端記号を入れなくてもOKです。
グライバッハ標準形の特徴として、生成規則を適用した回数がそのまま文字列の長さになるという特徴があります。(例えば4回適用すると文字列は必ず4文字となります。)
4.練習問題
では、1問だけですが練習をしてみましょう。
練習
つぎの文法 \( G_1 \), \( G_2 \) が定義されているとする。\[
G_1 = \left( \{S,A\}, \{a,b\},\{ S \to aSb, \ S \to A, \ A \to a, A \to aA \},S \right) \\
G_2 = \left( \{S,B\}, \{a,b\},\{ S \to aSb, \ S \to B, \ B \to b, B \to Bb \},S \right)
\]
(1) \( G_1 \) が生成する言語 \( L(G_1) \) で、文字列の長さが5文字以下のものを木構造を図示することによりすべて列挙しなさい。
(2) \( G_2 \) が生成する言語 \( L(G_2) \) で、文字列の長さが5文字以下のものを木構造を図示することによりすべて列挙しなさい。
文法 \( L_u \) を \( L_u = L(G_1) \cup L(G_2) \) とする。
(3) 言語 \( L_u \) はどのような文字列を受理するか。日本語で簡潔に説明するか、数式で書きなさい。
(4) 言語 \( L_u \) は正則か、正則でないか判定しなさい。
(5) 言語 \( L_u \) が正則であれば \( L_u \) を受理するような最小状態決定性オートマトンを求め、正則でなければ正則でないことを証明しなさい。
5.練習問題の答え
(1)
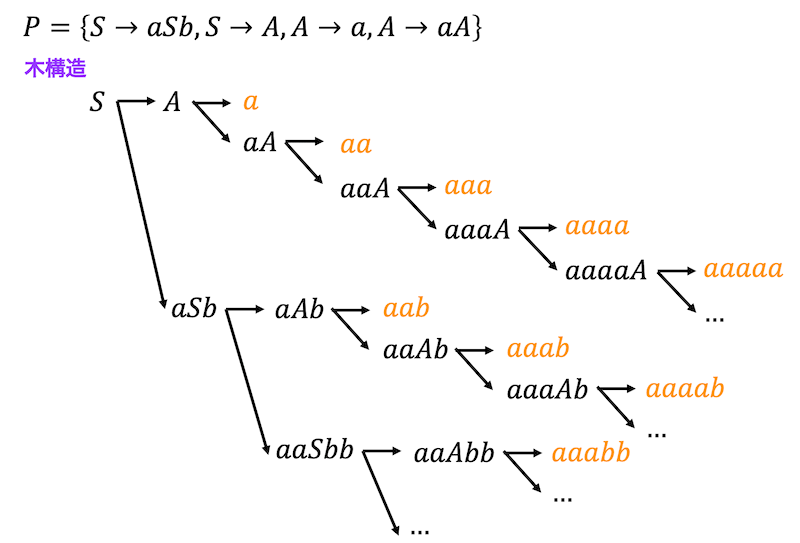
より、\[
a,\ aa, \ aaa, \ aaaa, \ aaaaa, \ aab, \ aaab, \ aaaab, \ aaabb
\]の9個。
(2)
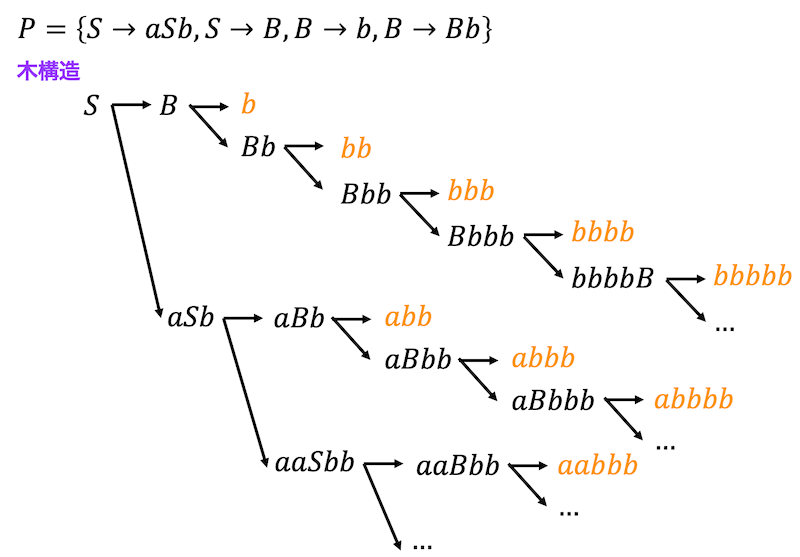
より、\[
b, \ bb, \ bbb, \ bbbb, \ bbbbb, \ abb, \ abbb, \ abbb, \ abbbb, \ aabbb
\]の合計9個。
(3)
(1), (2) で生成した18個の文字列に注目する。

※画像の \( L(G) \) は \( L_u \) のミスです……
すると、\( a \) のあとに \( b \) がくるような文字列が受理されていることはわかるだろう。あとは \( a \), \( b \) が同じ数のときに受理されていないことに注目すればOK。答えは
\( a \) だけの文字列の後に \( b \) だけの文字列を連接したもので、さらに \( a \) の数が \( b \) の数が異なる文字列。
数式で表すと、\( m,n \) を自然数(0が含むか含まないかは考えなくてOK)として、\[
L_u = \left\{ a^m b^n \ \middle| \ \ m \not = n \right\}
\]と表せる。
(4)
正則ではない
(5)
正則ではないので証明を書く。

6.さいごに
今回は文脈自由文法についてまとめていきました。
文脈自由文法は構文解析に応用されるのでオートマトンと言語理論以外の分野でも出くわすかもしれないのでもし出くわしたときはこの記事のことを思い出していただければ幸いです。
次回はオートマトンと言語理論の総復習としてある言語が正則であるかの判定、正則だった場合に決定性オートマトンを書く練習、および正則ではない場合に正則ではないことを示す練習をできる問題を持ってこようと思います。
*1:正則文法でないからといって有限オートマトンを記述できないというわけではないので注意。ただし、有限オートマトンを記述できないような言語は正則言語ではない。
関連広告・スポンサードリンク