スポンサードリンク
こんにちは、ももやまです。
今回はとある言語が正則かどうかを判定する練習、および正則だった場合に決定性オートマトンを書く練習、および正則でない場合に証明を書く練習をする総復習問題を作成しました。
ぜひ練習にお使いください。
前回の記事(第07羽)はこちら!
(文脈自由文法は総復習の内容には入れてないので各自で復習してください。)
演習前の注意
(1) 特に指示のない場合、\( m,n \) などの数に関する変数が出た場合、それは0以上の整数だと思ってください。
(2) 特に指示のない場合、\( \Sigma = \{ a,b \} \) としてください。
(つまり \( a,b \) からなる文字列が入力対象となる)
(3) Myhill-Nerodeで証明する際に最初の定義部分は省略して書いているのでご了承ください。
↓詳しいMyhill-Nerodeの定理の書き方などはこちらでご覧ください
目次
スポンサードリンク
パターン1 a^mとb^nの連接パターン
では、まずは基本的な \( a^m \) のあとに \( a^n \) が来るような言語で練習をしてみましょう。\( m \), \( n \) に様々な制限がついてきます。
練習1
つぎの(1), (2)の言語 \( L \) が正則か正則でないかを判定し、正則であれば最小状態決定性オートマトンを書き、正則でない場合は証明をしなさい。
(1)
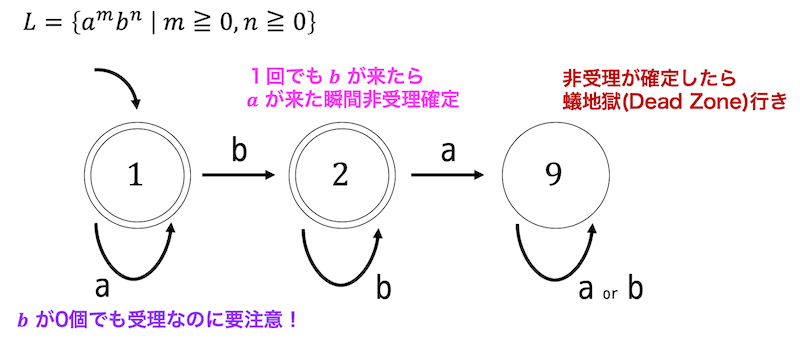
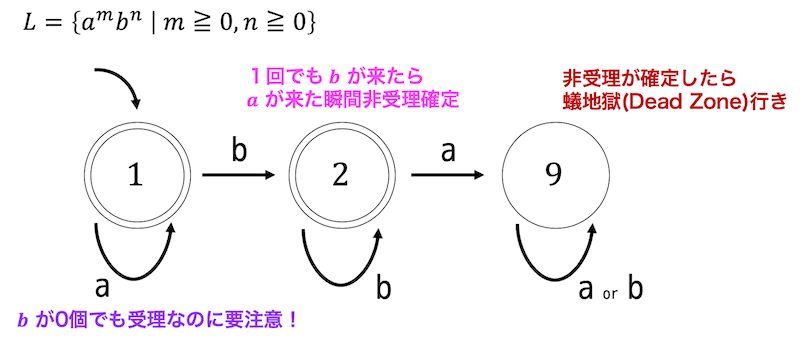
\[ L = \left\{ a^m b^n \ \middle| \ \ m \geqq 0, n \geqq 0 \ \right\} \]
(2)
\[ L = \left\{ a^n b^n \ \middle| \ \ n \geqq 0 \ \right\} \]
(3)
\[ L = \left\{ a^{2m} b^{2n} \ \middle| \ \ m,n \geqq 0 \ \right\} \]
解説1
正則かどうかを判定する際に大切なのが、無限に続く文字列に対し、有限個の状態でオートマトンを記述できるかどうかです。有限個の状態のオートマトン(有限オートマトン)を書くことができれば正則であるといえます。
逆に無限の文字列が来ることを考えたとき、無限の状態を記憶しないと受理するどうかを判定できない場合は正則とはいえません。
(1)
正則判定:正則である
(2)
正則判定:正則ではない
(\( a \) のあとに \( a \) と同じ数だけ \( b \) が続くような文字列かどうかを判定するためには、(無限に続く)\( a \) の数を記憶させる必要があるため、正則とはいえません。)
[証明]有限指数より \( a^i \underset{L}{\equiv} a^j \) となる自然数 \( i,j \)(ただし \( i \not = j \))が存在。
また、右不変より \( a^i b^i \underset{L}{\equiv} a^j b^i \) が成立。
\( a^i b^i \in L \) なので \( \underset{L}{\equiv} \) の定義より \( a^j b^i \in L \) だが、\( i \not = j \) なので \( a^j b^i \notin L \) なので矛盾。
よって正則ではない。
(3)
正則判定:正則である。
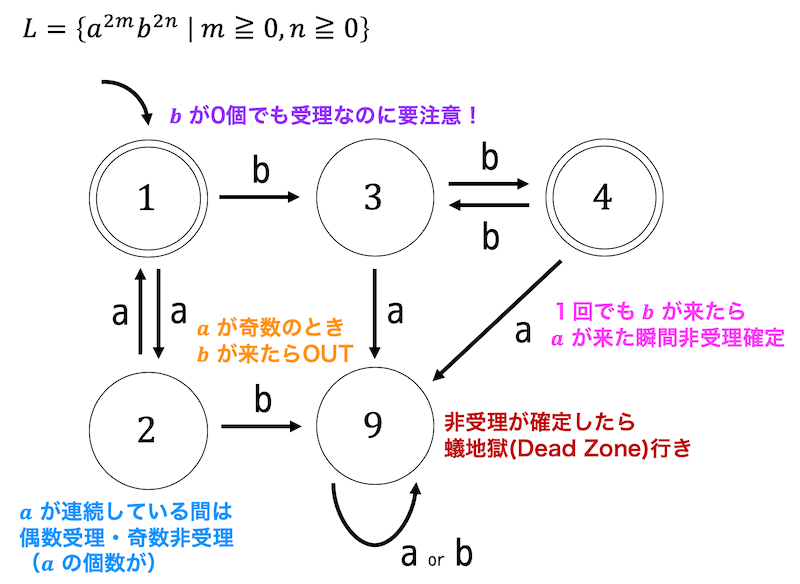
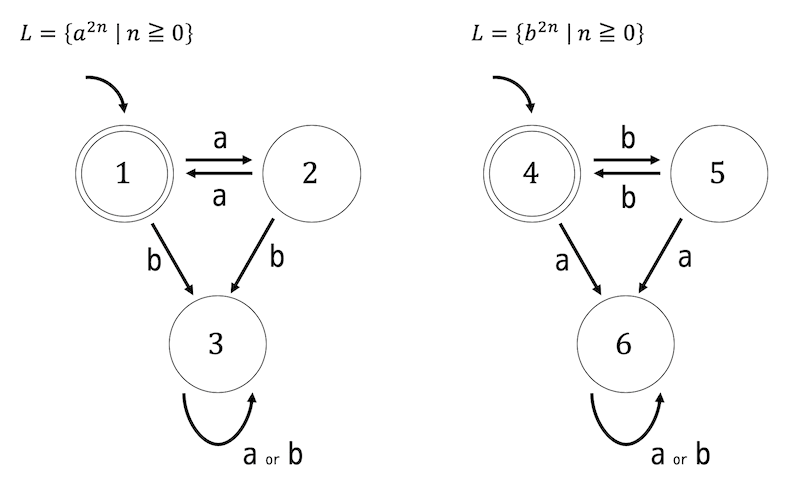
文字列 \( a^{2n} \) を受理するような言語のあとに文字列 \( b^{2n} \) を受理するようなオートマトンを連接させる方法でも作れますが、状態数がかなりの数になってめんどくさいのでできれば直接作れるようにしましょう。
↓ \( a^{2n} \) を受理するオートマトンと \( b^{2n} \) を受理するようなオートマトン
スポンサードリンク
パターン2 文字数系
つぎに文字数を基準とした言語が正則となるかどうかの判定をしてもらいましょう。
※注意
\( |w| \) は語 \( w \) の長さ(文字数)、\( |w|_a \) は語の中の文字数 \( a \) の数、\( |w|_b \) は語中の \( b \) の数を表します。
練習2
つぎの(1), (2), (3)の言語 \( L \) が正則か正則でないかを判定し、正則であれば最小状態決定性オートマトンを書き、正則でない場合は証明をしなさい。
(1)
\[ L = \left\{ w \ \middle| \ \ w \in \Sigma^* , \ \ |w|_a \not = |w|_b \right\} \]
(2)
\[ L = \left\{ w \ \middle| \ \ w \in \Sigma^* , \ \ |w|_a \times |w|_b = 2k + 1\ を満たす \ k \geqq 0 \ が存在 \right\} \]
(3)
\[ L = \left\{ w \ \middle| \ \ w \in \Sigma^* , \ \ |w|_a - |w|_b = 2k \ を満たす \ k \geqq 0 \ が存在 \right\} \]
(4)
\[ L = \left\{ w \ \middle| \ \ w \in \Sigma^* , \ \ |w| = 3 |w|_a \right\} \]
解説2
(1)
正則判定:正則ではない
((無限に続く)文字列の \( a \) の数と \( b \) の数を記憶させるためには無限の状態を記憶させる必要がある。よって正則ではない。)
[証明]有限指数より \( a^i \underset{L}{\equiv} a^j \) となる自然数 \( i,j \)(ただし \( i \not = j \))が存在。
また、右不変より \( a^i b^j \underset{L}{\equiv} a^j b^j \) が成立。
\( i \not = j \) より \( a^i b^j \in L \) なので \( \underset{L}{\equiv} \) の定義より \( a^j b^j \in L \) だが、\( a^j b^j \notin L \) なので矛盾。
よって正則ではない。
(2)
正則判定:正則である
\( |w|_a \times |w|_b = 2n + 1 \) ということは、\( a \) の文字数と \( b \) の文字数がともに奇数となるときに受理させるようにすればOK。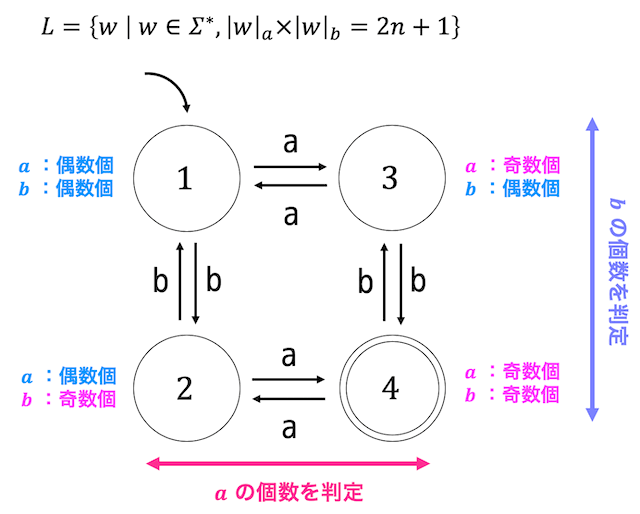
参考までに条件 \( |w|_a \times |w|_b = 2n + 1 \) が少し変化したときの受理状態の変化の様子を下に示しておきます。
\( |w|_a \times |w|_b = 2n \):\( a \) の文字数、\( b \) の文字数がどちらが偶数
→状態1,2,3が受理状態となる。
\( |w|_a + |w|_b = 2n \):\( a \) の文字数、\( b \) の文字数ともに偶数かともに奇数
→状態1,4が受理状態となる。
と変化します。
(3)
正則判定:正則ではない
(ポイント \( k \leqq 0 \) の条件があるため、\( |w|_a - |w|_b \leqq 0 \) の判定も必要となる。つまり、無限に続く文字列の中から \( a \) の文字数と \( b \) の文字数を判定しなければならず、これは有限の状態数では記憶させることができない。よって正則ではない。)
[証明]有限指数より \( a^i \underset{L}{\equiv} a^j \) となる自然数 \( i,j \)(ただし \( i \gt j \))が存在。(文字数の大小を判定に使うので > を使う)
また、右不変より \( a^i b^i \underset{L}{\equiv} a^j b^i \) が成立。
\( a^i b^i \in L \) なので \( \underset{L}{\equiv} \) の定義より \( a^j b^i \in L \) だが、\( i \gt j \) なので \( a^j b^i \notin L \) なので矛盾。
よって正則ではない。
(4)
正則判定:正則ではない
( \( |w| = 3 |w|_a \) なので、全体の文字数の1/3が \( a \) であることがわかる。ということは文字列の \( a \), \( b \) の割合はそれぞれ 1:2 となればよい。\( a \) と \( b \) の割合が 1:2 かどうかを確認するためには(上限数がない) \( a \), \( b \) の数を記憶させる必要がある。なので正則ではない。)
[証明]
有限指数より \( a^i \underset{L}{\equiv} a^j \) となる自然数 \( i,j \)(ただし \( i \not = j \))が存在。
また、右不変より \( a^i b^{2i} \underset{L}{\equiv} a^j b^{2i} \) が成立。
(左辺を a:b = 1:2 にするように右不変を適用する。)
\( a^i b^{2i} \in L \) なので \( \underset{L}{\equiv} \) の定義より \( a^j b^{2i} \in L \) だが、\( i \not = j \) なので \( a^j b^{2i}\notin L \) なので矛盾。
よって正則ではない。
スポンサードリンク
パターン3 複数の文字列の組み合わせ・文字列の逆転
つぎは複数文字を組み合わせたり、文字列の反転などが含まれた言語が正則かどうかを判定してもらいます。
今回の練習で一番むずかしいのがこのパターン3にあたります。
練習3
つぎの(1)〜(6)の言語 \( L \) が正則か正則でないかを判定し、正則であれば最小状態決定性オートマトンを書き、正則でない場合は正則でないことの証明をしなさい。
※ \( w^R \) は語 \( w \) の反転を表します。
(1)
\[
L = \left\{x ww^R y \ \middle| \ \ x, y \in \Sigma^* , \ w \in \Sigma^+ \right\}
\]
(2)
\[
L = \left\{w w^R \ \middle| \ \ w \in \Sigma^* \ \right\}
\]
(3)
\[
L = \left\{x w x^R \ \middle| \ \ x \in \Sigma^+ , \ w \in \Sigma^* \right\}
\]
(4)
\[
L = \left\{x x^R w \ \middle| \ \ x,w \in \Sigma^* \right\}
\]
(5)
\[
L = \left\{x x^R w \ \middle| \ \ w \in \Sigma^* \ \ x \in \Sigma^+ \right\}
\]
(6)
\[
L = \left\{xwx \ \middle| \ \ x \in \Sigma^+ , \ w \in \Sigma^* \right\}
\]
解答3
(1)
このようなパターンは、下のように \( \Sigma^* \) にほとんどの文字を押し込み、\( \Sigma^+ \) 側の文字を1文字とすることで条件を簡単にすることができます。

今回の場合は、連続する2文字が含まれていれば受理する、と言い換えられます。これは下のような有限オートマトンで記述できます。
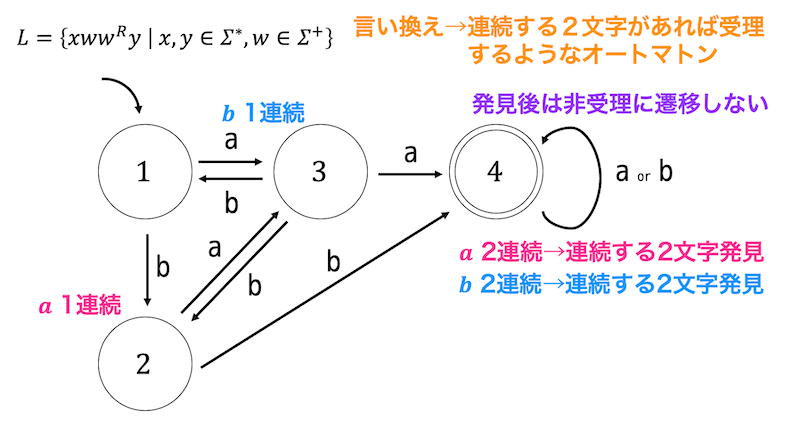
(2)
正則判定:正則ではない
(うまく文字を押し込めない場合は正則とはなりません……)
ポイントは有限指数の決め方、ただ単に \( a^i \underset{L}{\equiv} a^j \) とするだけではうまく背理法に持ち込めません。なので \( (ab)^i \underset{L}{\equiv} (ab)^j \) とし、\( ab \) の有限指数(異なる状態数の2項関係がある)としましょう。
[証明]有限指数より \( (ab)^i \underset{L}{\equiv} (ab)^j \) となる自然数 \( i,j \)(ただし \( i \not = j \))が存在。
また、右不変より \( (ab)^i (ba)^i \underset{L}{\equiv} (ab)^i (ba)^j \) が成立。
(左辺を a:b = 1:2 にするように右不変を適用する。)
\( (ab)^i (ba)^i \in L \) なので \( \underset{L}{\equiv} \) の定義より \( (ab)^i (ba)^j \in L \) だが、\( i \not = j \) なので \( (ab)^i (ba)^j \notin L \) なので矛盾。
よって正則ではない。
(3)
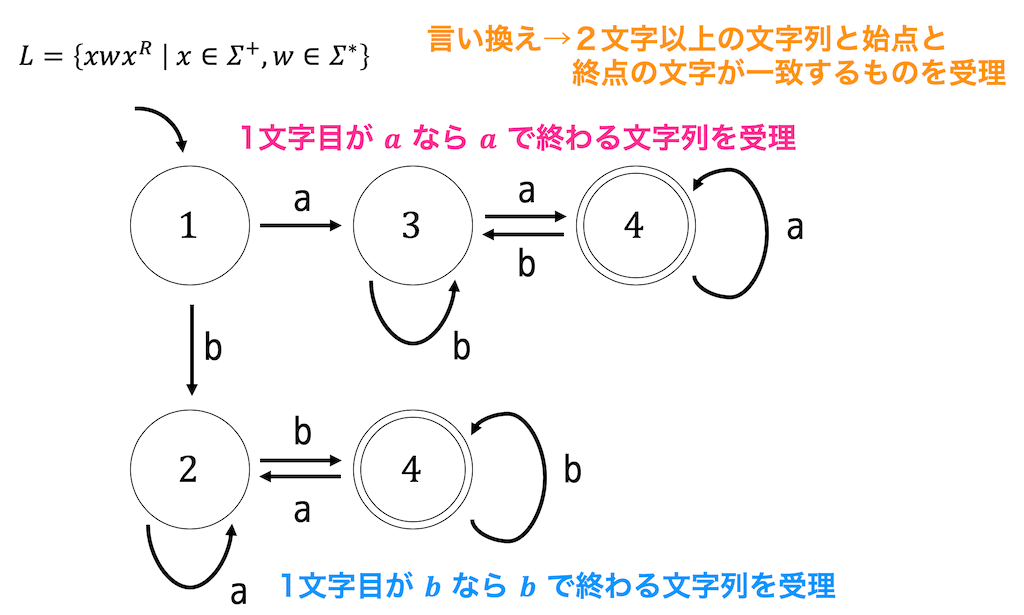
この問題も \( \Sigma^* \) にほとんどの文字を押し込み、\( \Sigma^+ \) 側の文字を1文字とすることで条件を簡単にすることができます。

文字列の始点と終点の文字が一致しているような文字列*1を受理するような言語が正則かどうか、と言い換えることができます。これは下のような有限オートマトンを書くことができます。
(4)
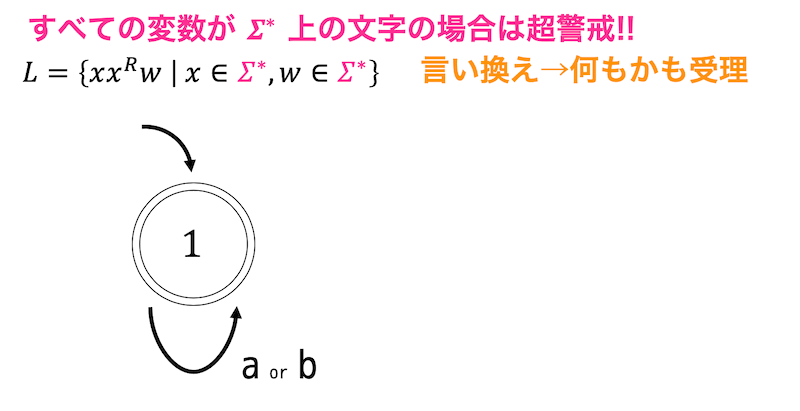
このようにすべての変数が \( \Sigma^* \) 上の文字列の場合は特に気をつけてください。
今回の場合、\( x = \varepsilon \) (空文字)とすると、\[
L = \left\{w \ \middle| \ \ w \in \Sigma^* \right\}
\]と言いかえられます。つまり、すべての文字を受理するような言語が正則かどうかを判定すればいいことになります。
もちろん、\( \Sigma^* \) を受理するような文字列は正則です。
下のような有限オートマトンが \( \Sigma^* \) を受理するようなオートマトンとなります。
(5)
(お詫び:証明部分を間違えていたため、11月7日に修正を行いました。申し訳有りません。修正箇所を赤色で示しています。)
正則判定:正則ではない
(実は(2)のパターン( \( x x^R \) )に \( \Sigma^* \) 上の文字 \( w \) が付け加わっただけ。ただし、\( w \) があることにより \( i \not = j \) ではうまく背理法が適用できないことに要注意)
このように実際に何個か試してみましょう。

有限指数より \( (ab)^i \underset{L}{\equiv} (ab)^j \) となる自然数 \( i,j \)(ただし \( i \lt j \))が存在。
また、右不変より \( (ab)^i (ba)^i \underset{L}{\equiv} (ab)^{ \color{red}{j} } (ba)^{ \color{red}{i} } \) が成立。
\( (ab)^i (ba)^i \in L \) なので \( \underset{L}{\equiv} \) の定義より \( (ab)^i (ba)^i \in L \) だが、\( i \lt j \) なので \( (ab)^{ \color{red}{j} } (ba)^{ \color{red}{i} } \notin L \) なので矛盾。
よって正則ではない。
(6)
正則判定:正則ではない
(おそらく今回の演習の中で一番むずかしい問題。)
(5)のように実際に何個か試してみましょう。\( i \not = j \) ではダメな理由がわかると思います……。

有限指数より \( a^i \underset{L}{\equiv} a^j \) となる自然数 \( i,j \)(ただし \( i \lt j \))が存在。
また、右不変より \( a^i b a^i b \underset{L}{\equiv} a^j b a^i b \) が成立。
\( a^i b a^i b \in L \) なので \( \underset{L}{\equiv} \) の定義より \( a^j b a^i b \in L \) だが、\( i \lt j \) なので \( a^j b a^i b \notin L \) なので矛盾。
よって正則ではない。
パターン4 2進数に絡んだ問題
つぎに、0,1で与えられる文字列を2進数と考えるタイプの問題も練習していきましょう。
ここからは \( \Sigma = \{ 0,1 \} \) としてください。
練習4
\( \Sigma = \{ 0,1 \} \) のとき、つぎの(1)〜(3)の言語 \( L \) が正則か正則でないかを判定し、正則であれば最小状態決定性オートマトンを書きなさい。正則でない場合の証明は不要。
(1)
\[
L = \left\{1x \ \middle| \ \ 1x \ を2進数と見たとき、4 \ の倍数となるもの \right\}
\]
(2)
\[
L = \left\{1x \ \middle| \ \ 1x \ を2進数と見たとき、3 \ の倍数となるもの \right\}
\]
(3)
\[
L = \left\{x \ \middle| \ \ x \ を2進数と見たとき、2^n \ の倍数となるもの \right\}
\]
解説4
(1)
10進数に直したときに4の倍数となるようなものを順番に書いていけば法則がわかるかもしれないので書いていこう。
4→100b, 8→1000b, 12→1100b, 16→ 10000b ……
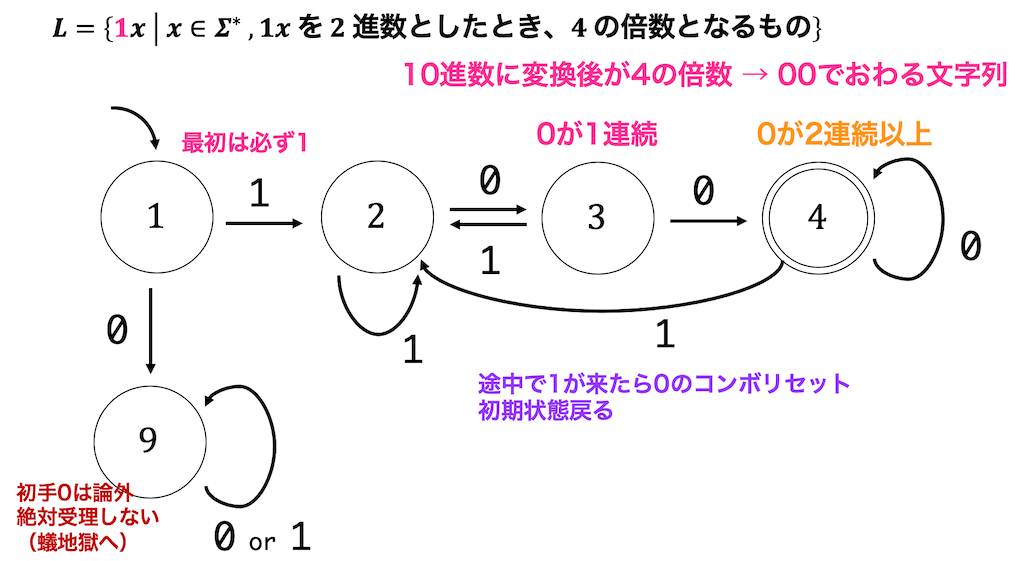
と書いてくと、00で終わるような文字列は必ず4の倍数となることがわかるだろう。
00で終わるような文字列は下のような有限オートマトンで記述することができるので正則である。
(2)
3の倍数は4の倍数ような単純な規則とはならない。なので正則ではないと思ったそこのあなた…
どんな数(範囲は無限大)でも3で割ったあまりは0か1か2の3通りしかありませんよね。0,1,2の3通りは当然有限個なので有限オートマトンを書くことができ、正則なのです。
ということで、とある2進数を3で割ったあまりが0のとき、1のとき、2のときの3つに場合分けをする。
また、それぞれの状態(あまりが0,1,2それぞれの2進数の状態)に0を加えたとき、1を加えたときに3で割ったあまりがどうなるかを考える。
ある2進数の右端に0を加えると、その2進数の値は2倍に、1を加えると2倍+1されることに注意すると以下のように表せる*2。
(i) ある2進数を3で割ったときのあまりが0のとき
2進数は \( 3k \) と書ける(\( k \) は1以上の自然数)。
0を加える:値は2倍\[ 2 \times 3k = 6k \equiv 0 \ ( \bmod 3 )\]
1を加える:値は2倍+1\[ 2 \times 3k + 1 = 6k + 1 \equiv 0 \ ( \bmod 3 )\]
(ii) ある2進数を3で割ったときのあまりが1のとき
2進数は \( 3k+1 \) と書ける(\( k \) は1以上の自然数)。
0を加える:値は2倍\[ 2(3k+1) = 6k + 2 \equiv 0 \ ( \bmod 3 )\]
1を加える:値は2倍+1\[ 2(3k+1) + 1 = 6k + 3 \equiv 0 \ ( \bmod 3 )\]
(iii) ある2進数を3で割ったときのあまりが2のとき
2進数は \( 3k+2 \) と書ける(\( k \) は1以上の自然数)。
0を加える:値は2倍\[ 2(3k+2) = 6k + 4 \equiv 1 \ ( \bmod 3 )\]
1を加える:値は2倍+1\[ 2(3k+2) + 1 = 6k + 5 \equiv 2 \ ( \bmod 3 )\]
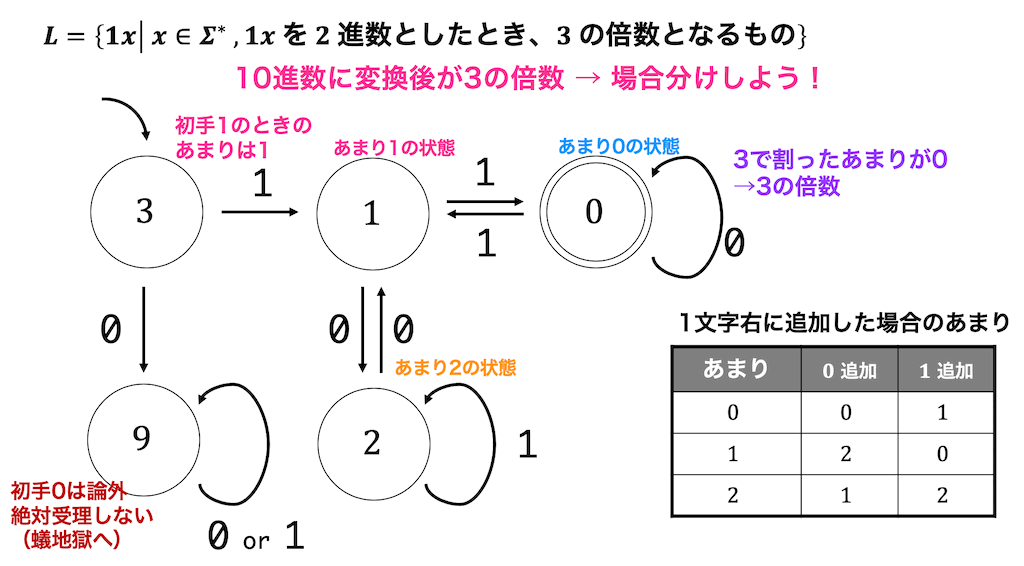
それぞれの2進数のあまりが0,1,2のときに0を加えたとき、1を加えたときのあまりを表にし、最初に1が来た場合と0が来た場合を場合分けすると下のような状態遷移図で表せる。
(3)
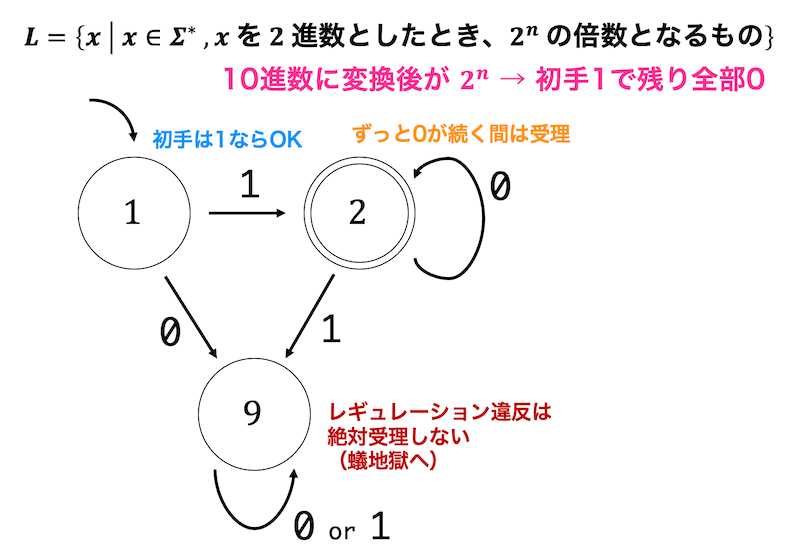
10進数に直したときに \( 2^n \) となるようなものを \( n = 0 \) から順番に書いていけば法則がわかるかもしれないので書いていこう。
\( 2^0 \to 1 \), \( 2^1 \to 10 \), \( 2^2 \to 100 \), \( 2^3 \to 1000 \) ……
とすると、最初に1が来てその後ずっと0の文字列を10進数になおすと \( 2^n \) となることがわかるだろう。
パターン5 文字数が有限以下/以上の場合
最後に文字列に制限がかかったバージョンも練習してみましょう。
文字数制限をかけることによって言語が受理するかどうかが変化することがよくあります。では、5問ほど練習してみましょう。
練習5
つぎの(1)〜(3)の言語 \( L \) が正則か正則でないかを判定しなさい。
(1)
\[ L = \left\{ a^n b^n \ \middle| \ \ n \leqq 100 \ \right\} \]
(2)
\[ L = \left\{ a^n b^n \ \middle| \ \ n \geqq 100 \ \right\} \]
(3)
\[ L = \left\{ a^m b^n \ \middle| \ \ m,n \geqq 100 \ \right\} \]
(4)
\[ L = \left\{ w w^R \ \middle| \ \ w \in \Sigma^*, \ \ |w| \leqq 100 \ \right\} \]
(5)
\[ L = \left\{ w \ \middle| \ \ w \in \Sigma^* , \ \ |w| \geqq 1000 \ \right\} \]
解答5
(1)
解答:正則である
理由:この言語の受理非受理を確認するためには、\( a \) が来た後に \( a \) と同じ回数の \( b \) が来るかどうかを \( a \) の数を記憶させることで判定をしなければならない。なので本来は(無限に続くかもしれない) \( a \) の数を記憶させなければならないため正則ではない。
しかし今回は \( n \leqq 100 \) なので、\( n \) が101文字以上きたその瞬間に非受理が確定するため、\( n \) の状態数を101個以上記憶させる必要はない(有限の記憶で判定ができる)。よって正則。
(2)
解答:正則ではない
(1)に似てるが、この言語の受理非受理を確認するためには、\( n \) が100文字以上でかつ、\( a \) のあとに \( a \) の数だけ \( b \) が来てるかどうかを \( a \) の数を記憶させることで判定をする必要がある。
なので100文字以上(無限)の \( a \) の数の記憶が必要なため、正則ではない。
(3)
解答:正則である
(2)に似ているが、この言語の受理非受理を確認するためには \( a \) が100文字以上来た後に \( b \) が100文字以上来るかどうかを確かめればよい。
なので \( a \) の数100個分と \( b \) の数100個分の合計200個(有限個)の記憶状態があれば有限オートマトンを作成することができる。
よって正則である。
(4)
解答:正則である
\( w \) に100文字以下という制限がついてるため、\( w \) の文字列がどうなっているかを100文字分だけ記憶させることで \( ww^R \) が受理するかどうかを判定することができる。(101文字以上来た瞬間に非受理確定なので記憶させる必要がない)
よって正則。
(5)
解答:正則である
一見100文字以上(つまり無限大まで含まれる)の制限がついてるため正則ではないように見えるが実際は100文字未満か以上かを判定するだけでよいので100文字分あるかどうかを記憶させればよい。(100文字以上は必ず受理なので記憶させる必要なし)
よって正則。
さいごに
今回はオートマトンと言語理論における正則判定の練習、正則だった場合の決定性オートマトン(最小状態の)、および正則でなかった場合の証明練習についてまとめました。
基本的にオートマトンは理論さえ知ってしまえばあとはパズルゲーに近いので、ひたすら練習して頭を柔らかくしていきましょう!
今回でしばらくオートマトンと言語理論の記事はお休みします。
関連広告・スポンサードリンク