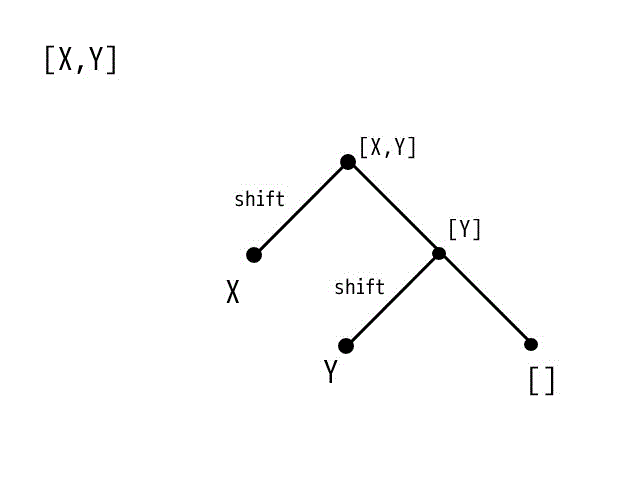
スポンサードリンク
こんにちは、ももやまです!
今回は論理プログラム(Prolog)におけるリスト構造について簡単に説明していきたいと思います。
★注意★
この記事では、数式で論理プログラムを表す場合、
\( x,y,z,w,u,v \) は変数(Prologでいう大文字の変数)
\( a,b,c,d \) は定数記号(Prologでいう小文字の変数)
とします。
また、代入記号はPrologの場合 = ですが、数式で表す場合は \( := \) となります。
たとえば、Prologで
[[[X|Y]|Z]|W] = [[[a,b]]|]
のように書かれる式は、数式だと
\( [ [ [x|y ]|z ]|w ] := [ [ [a,b ] ]| \)
となります。
スポンサードリンク
1. 2つのリスト構造
論理プログラム、Prologで使われるリストの書き方は2つあります。
どちらの書き方であった場合でも、Prologのリスト構造は木構造で図示してあげるとわかりやすくなります。
(1) [X,Y]
まずは、[X,Y] の形です。これは、他の多くのプログラミング言語でも使われている表記です。
例えば、[a,b,c] だと、順番にa,b,cが格納されているリストを表します。
数学で出てくる集合と異なり順番があるので注意してください。例えば、[a,b,c] と [b,c,a] は異なったものとして扱います。
(1)を木構造で表現すると下の図のようになります。
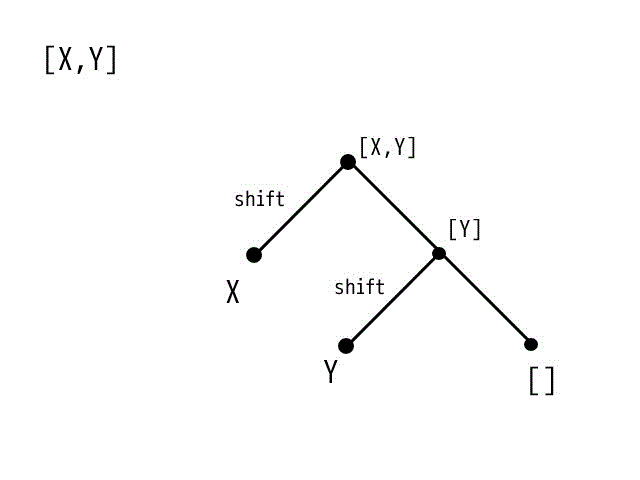
[] になるまで繰り返していきます。
では、3つほど具体例を出して木構造で表現してみたいと思います。
例1:[a]
まずは、要素数が1つの場合です。[a]をshiftすると、aと[]に分解できます。なのでこのような木構造となります。
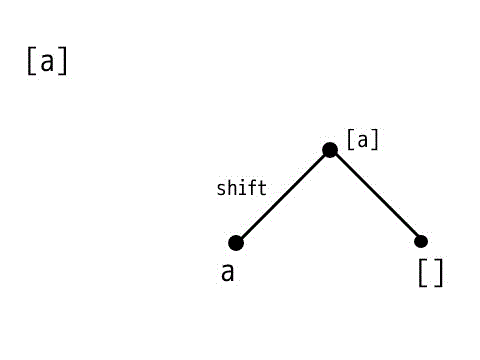
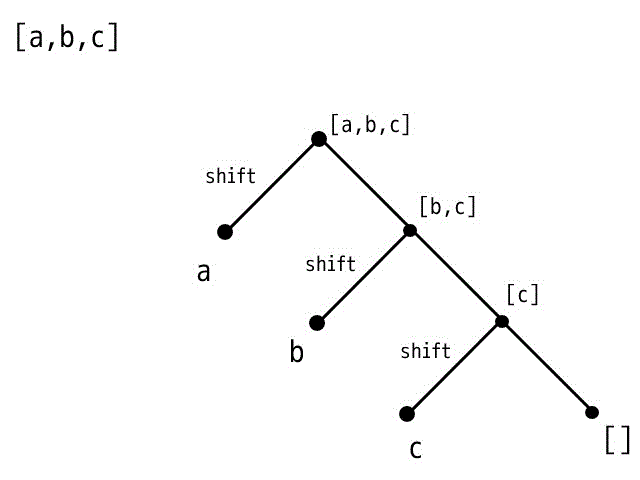
例2:[a,b,c]
要素数を3つに増やしてみましょう。
[a,b,c]をshiftします。aと[b,c]に分解できます。[b,c]をshiftします。bとに分解できます。をshiftします。cと[]に分解できます。
すべてを要素と空リストに分解できましたね。なので木構造の完成です。
左側に要素以外(木構造)が来たので左側を順番に分解します。
例3:[a,b,],f]
そろそろ複雑なリストの木構造表現にチャレンジしてみましょう。
今までの例とは違い、shiftする時に左側にもリストが現れてきます。
このような場合は、左側のリストも要素と空リストに分解できるまで分解していきます。
[a,b,],f]をshiftします。aと[b,],f]に分解できます。[b,],f]をshiftします。bと[c,[d,e],f]に分解できます。[c,[d,e],f]をshiftします。]と[f]に分解できます。]をshiftします。cと[[d,e]]に分解できます。[[d,e]]をshiftします。[d,e]と[]に分解できます。[d,e]をshiftします。dと[e]に分解できます。[e]をshiftします。eと[]に分解できます。
[f]をshiftします。fと[]に分解できます。
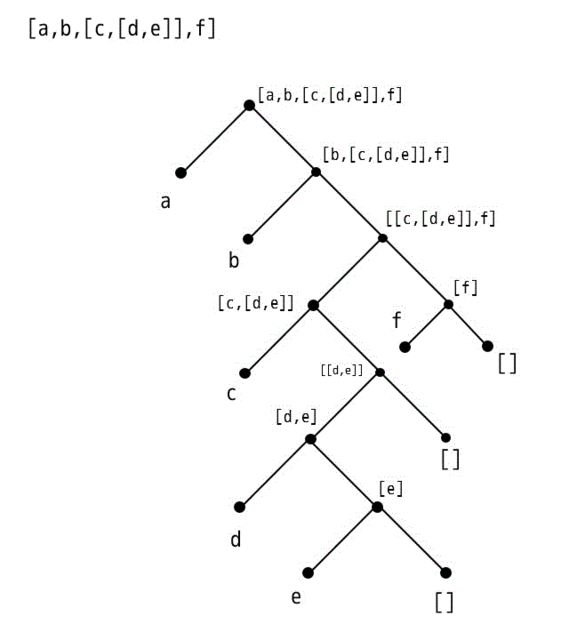
木構造をリスト化する
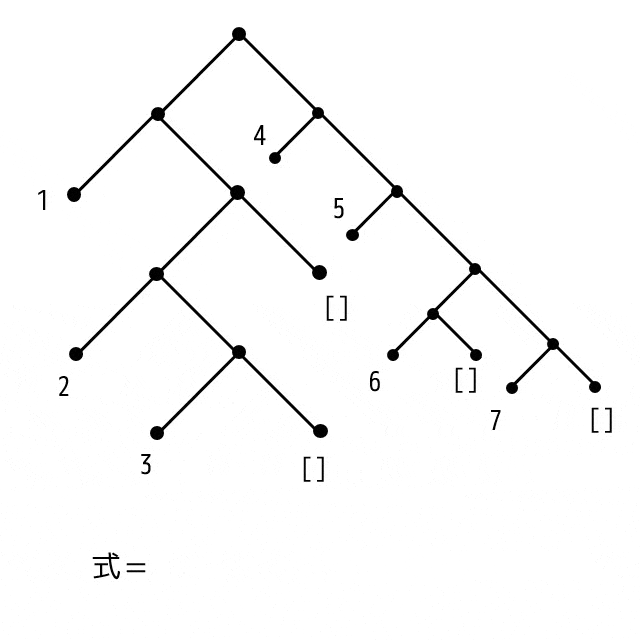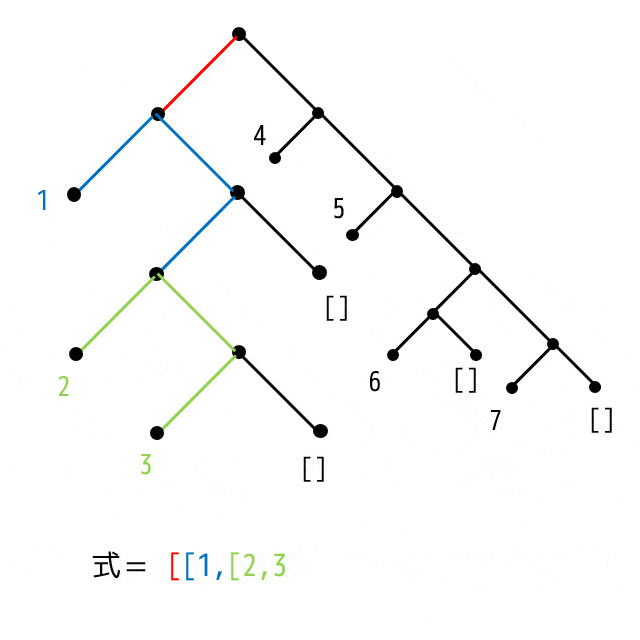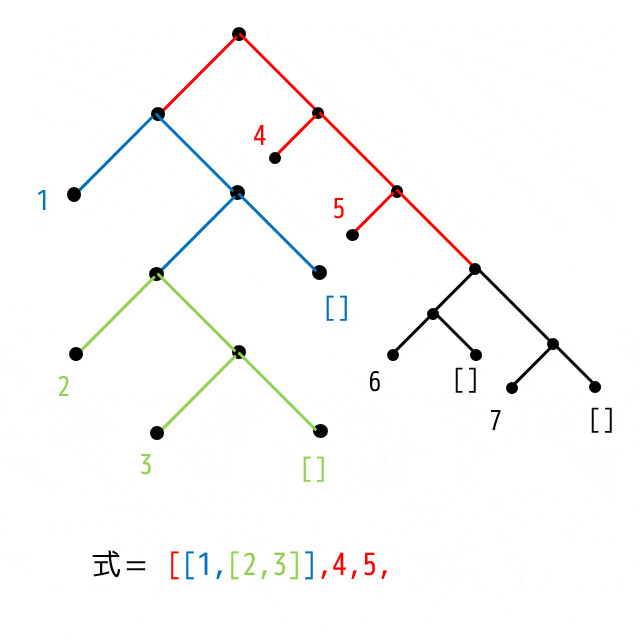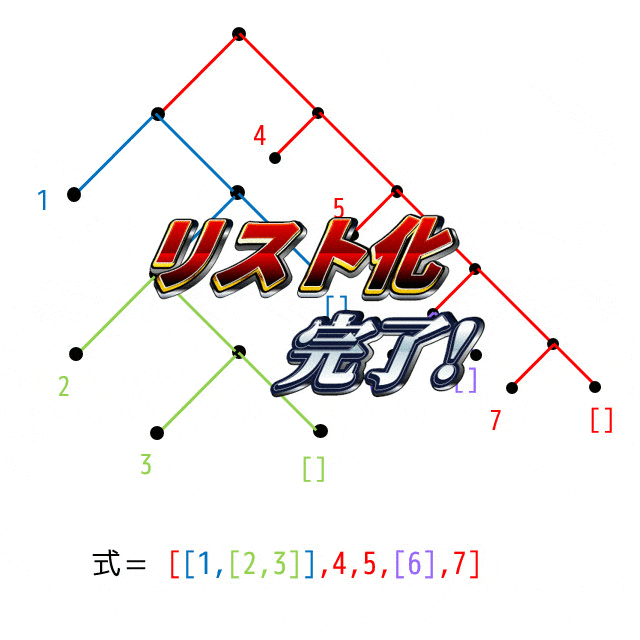
また、木構造を、次のようなステップでリストに戻すことができます。
ルール(文字よりアニメーションのほうがわかりやすいのでそちらをご覧ください)
- 行きがけ順(先行順、pre-order)で木構造を読みます
- 左側にかかれているノードをリストに追加します
- 2回連続左ノードに移動した場合はリストを作ります
- []に到達したらリストを閉じます
- 左側に辿れなくなったら右側も見ます
- 全部木構造を辿ったら終了です。
(2) [X|Y]
Prolog独特の表現として、この [X|Y] があります。
これは、「リストYの先頭に要素Xを追加したもの*2」を表します。言い換えると「リスト[X|Y]から要素Xをshiftしたもの」と言うこともできます。これを木構造で表すと、つぎのような形になります。
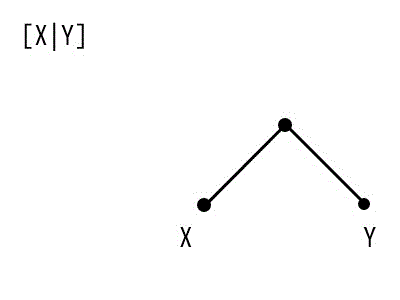
のようになります。
(1)と同じように3つほど例をみてみましょう。
例1: [a,b|] = [a,b,c]
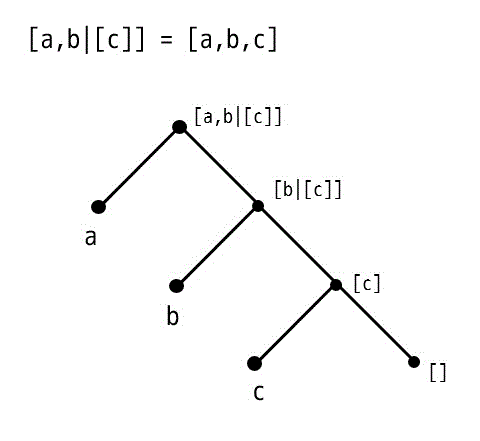
リスト化すると、[a,b,c]と同じことがわかりますね。
このレベルの例なら木構造書かなくてもわかるようになるのが理想です。
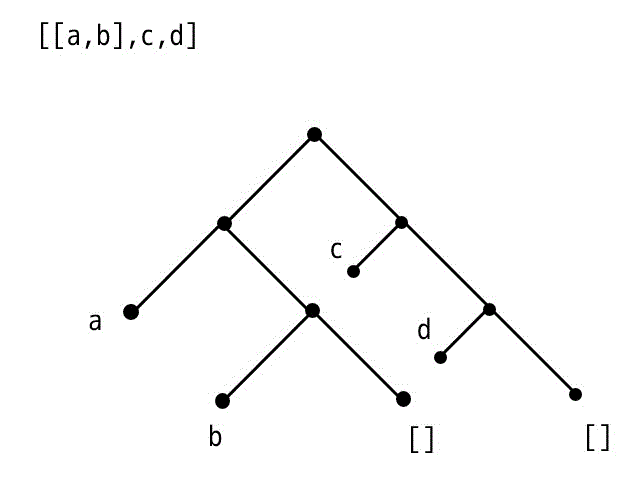
例2: [[a,b]|] = [[a,b],c,d]
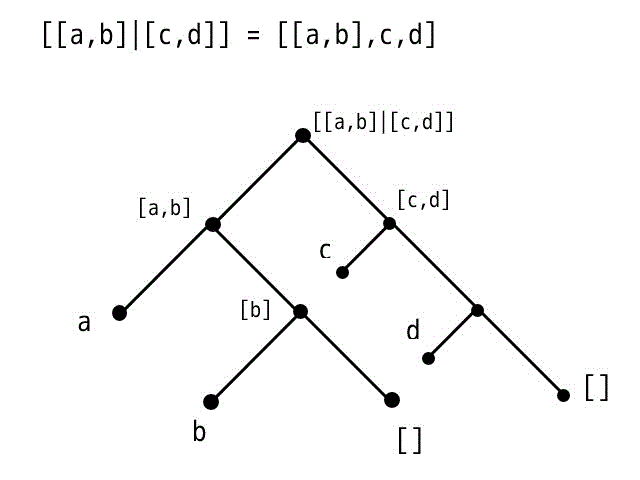
複雑なリストになった場合でも木構造を書けばすぐリストの中身がわかります。
例3: [ [a|[b,c] ]|[d]] = [[a,b,c],d]
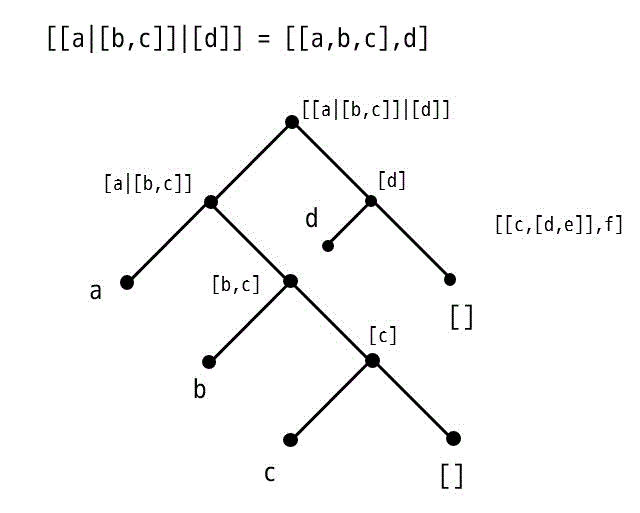
リストの追加記号が2つになって見た目は複雑そうに見えるのですが、木構造を書けばリストの中にリストが入っている程度なのであまり複雑ではないことがわかります。
ちなみに次のような表記法はないので注意してください。
[X|Y|Z] % 文法エラー、リスト内での結合 | は1回のみ [X|Y,Z] % 文法エラー、リスト内での結合 | 後に要素をコンマで足すことはできない
スポンサードリンク
2. リストの単一化
2つの項(式やリスト)同士を等しくすることを単一化といいます。
例えば、[a,b]と[a|[b]]は見た目こそ違いますが、木構造を書けば全く同じリストとなるので単一化されていることがわかりますね。
期末試験でよく出題されるものとして、「XやYなどの未知変数が用意されており、X,Yになにか変数を入れて単一化できる場合はその変数を答えなさい」というものがあります。
また、単一化は、最汎単一化代入(most general unification)と呼ばれ、「MGUを求めよ。」と呼ばれる場合があります。
例題1
[X|Y] = [[a,b],c,d].
\( [x,y] = [ [a,b ],c,d ] \)
を単一化させるような変数X,Yをもとめなさい。
(変数 X,Y の最汎単一化代入[MGU]を求めなさい。)
解答1
単一化させる問題の場合は、2つの項それぞれの木構造を書き、比較すると変数X,Yが見つけやすくなります。
[X|Y]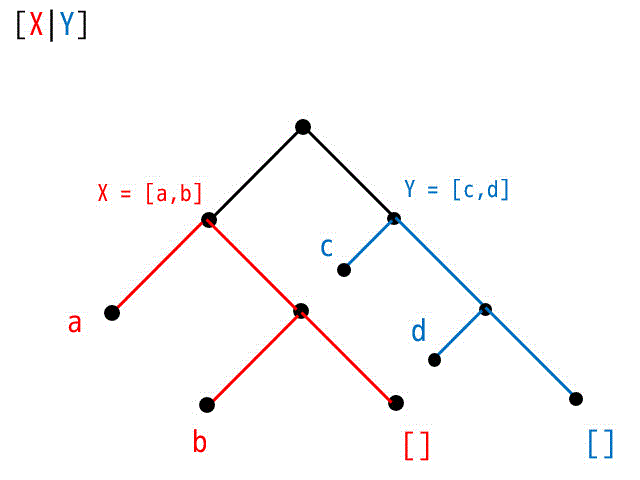
この場合、木構造を書くと
X = [a,b], Y =
とすれば2つの木構造が一致、つまり左の項と右の項を全く一緒(単一化)することができますね。
つぎに関数の単一化の例を見てみましょう。
例題2
p([X|Y],Y) = p([a,b,c],[Z|W]).
を単一化させるような変数X,Y,Z,Wをもとめなさい。
解答2
関数が出てきた場合は、まず引数の数を確認してください。
今回は両方とも2つです。
もしこの引数の数が一致していない場合は単一化をすることができないため、木構造を書く必要はありません。
一致している場合は、木構造を書いて単一化を調べます。それぞれの引数ごとに単一化をさせる必要があるため、今回は4つ木構造を書く必要があります。
まずは1つ目の引数の単一化
[X|Y]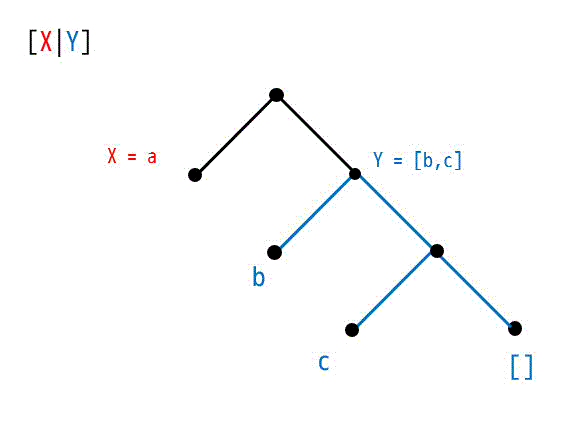 [a,b,c]
[a,b,c]
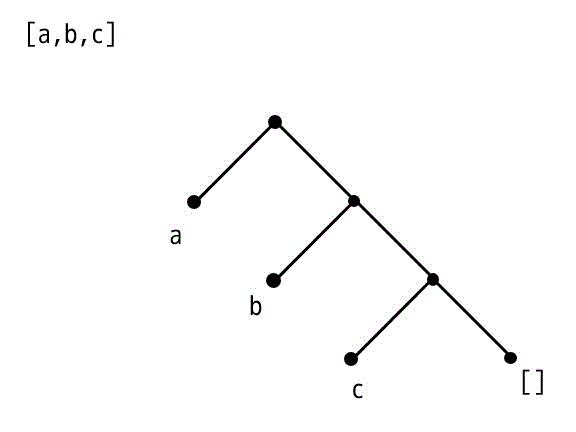
よって、X = a, Y = [b,c]となりますね。ではもう1つもやっちゃいましょう!
Y = [b,c]
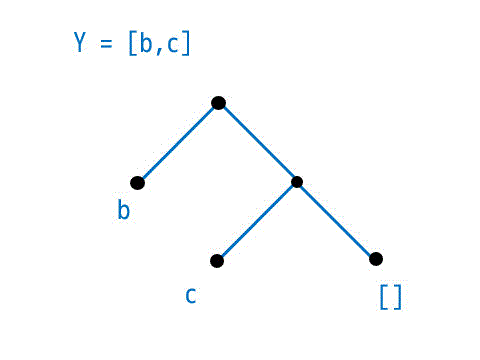
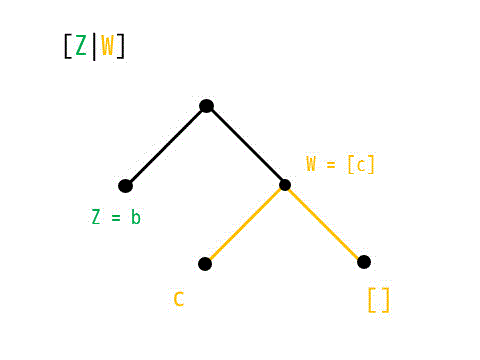
よって、Z = b, W = となりますね。
この2つより、最小化は
X = a, Y = [b,c], Z = b, W =
となる。
では、次のページからは練習問題を解いてみましょう!
スポンサードリンク
3. 練習問題
では、単一化の練習をしてみましょう!
問題
つぎの(1)〜(8)の左辺の項と右辺の項が単一化できる場合は、各変数に代入される文字を、単一化できない場合は✕を答えなさい。
[X|[Y|Z]] = [a,b,c,d]. % (1) [X,Y|Z] = [a,X,Y]. % (2) [a,b,Y] = [X,b]. % (3) [[X|Y],Y] = [[a,b,c],[U,V]]. % (4) p([a,b]) = p([X,Y|Z]). % (5) p([[a,b]]) = p([X|Y]). % (6) p([a,b],[Y]) = p([a|X],X). % (7) p([a],b|X) = p([U|V]). % (8)
解説
簡単な問題は脳内処理してもいいですが、わからなければ木構造を書きましょう。
(1) [X|[Y|Z]] = [a,b,c,d]
[X|[Y|Z]] の木構造
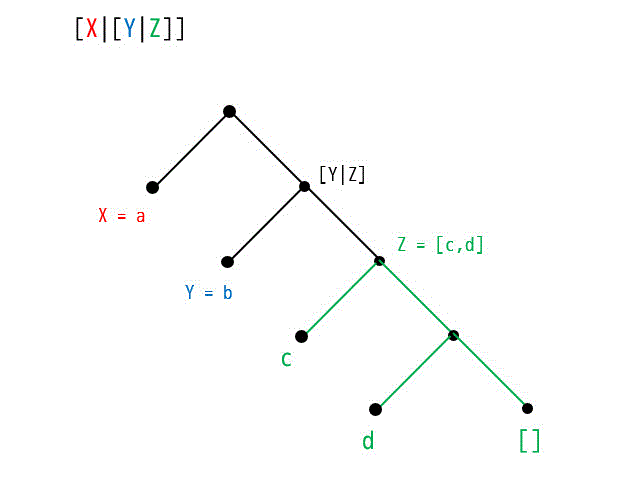
[a,b,c,d] の木構造
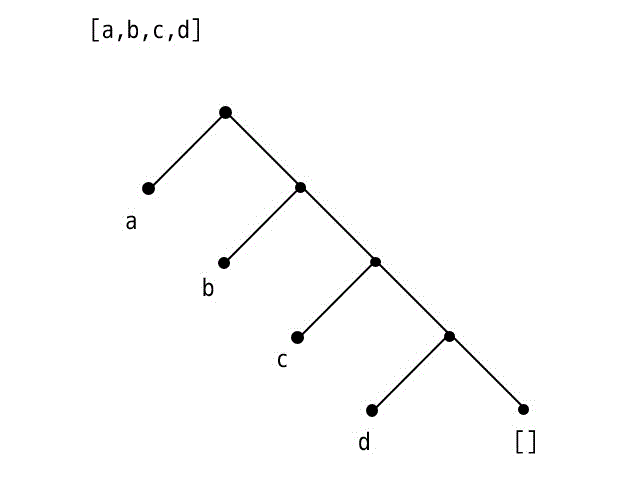
よって最小化は
X = a, Y = b, Z =
となる。
(2) [X,Y|Z] =[a,X,Y]
[X,Y|Z] の木構造
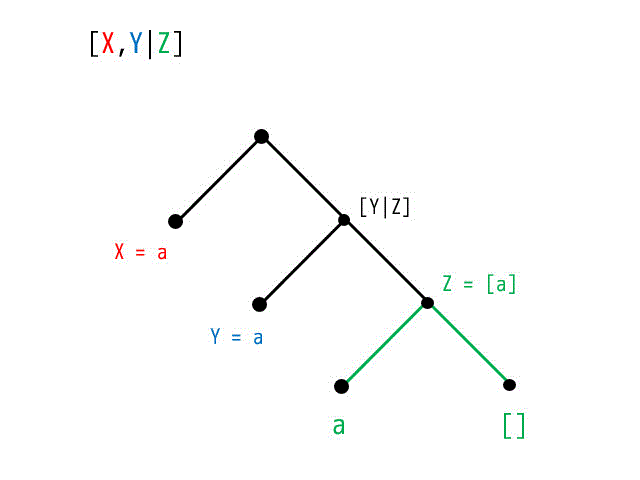
[a,X,Y] の木構造
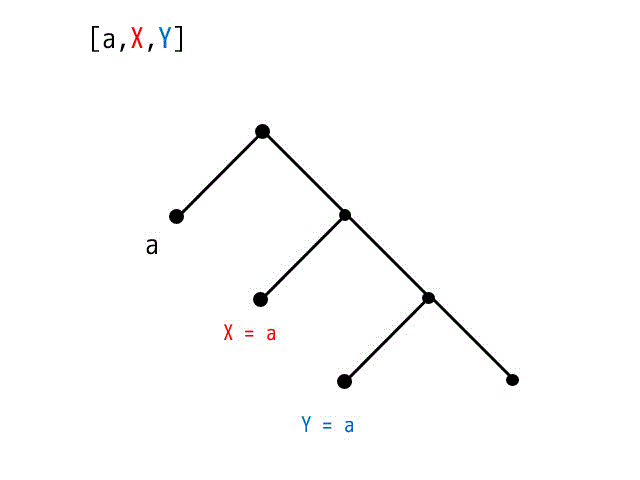
よって最小化は
X = a, Y = a, Z = [a]
となる。
(3) [a,b,Y] = [X,b]
[a,b,Y] の木構造
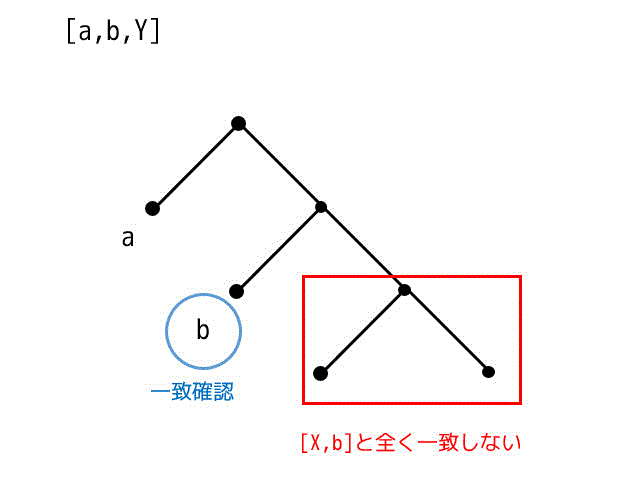
[X,b] の木構造
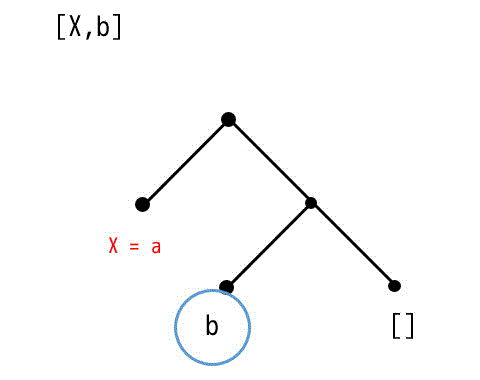
2つの木構造をどうやっても一致させることができない。なので最小化できない。×。
(4) [[X|Y],Y] = [[a,b,c],[U,V]]
[[X|Y],Y] の木構造
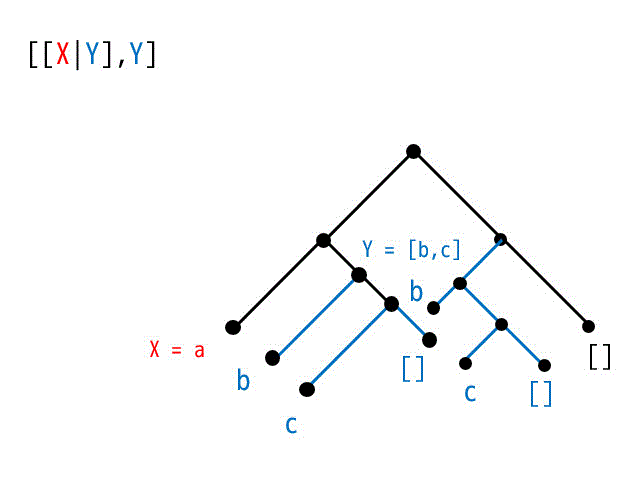
[[a,b,c],[U,V]] の木構造
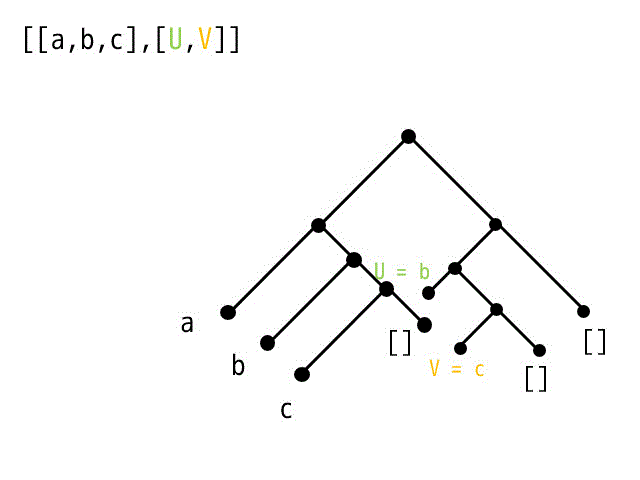
よって最小化は
X = a, Y = [b,c], U = b, V = c
となる。
(5) p([a,b]) = p([X,Y|Z])
ここからが関数。落ち着いて木構造を書こう。
[a,b] の木構造
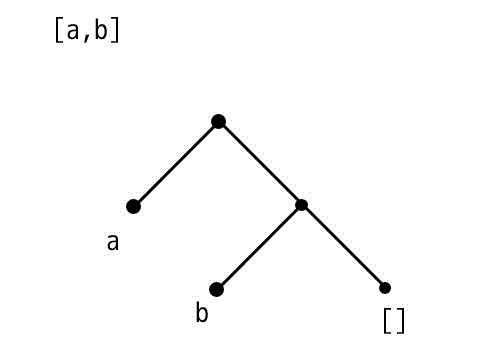
[X,Y|Z] の木構造
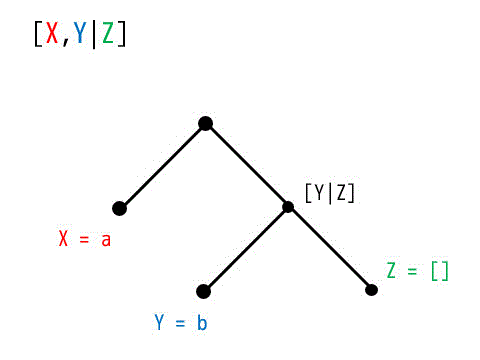
よって最小化は
X = a, Y = b, Z = []
となる。
(6) p([ [a,b] ]) = p([X|Y])
[[a,b]] の木構造
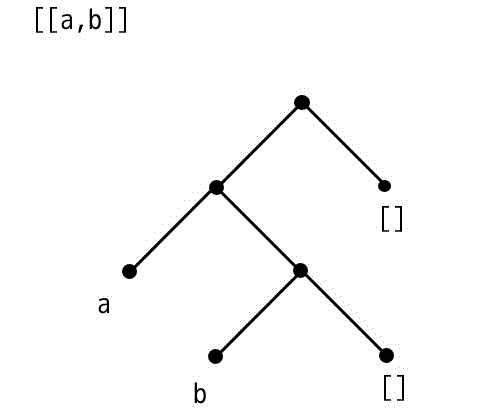
[X,Y|Z] の木構造
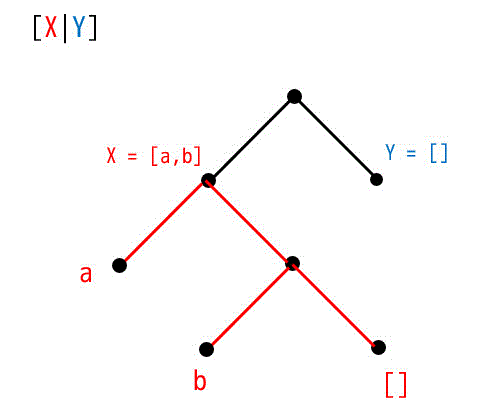
よって最小化は
X = [a,b], Y = []
となる。
(7) p([a,b],[Y]) = p([a|X],X)
項が2つあるので必要な木構造は2ペアとなる。
[a,b] の木構造
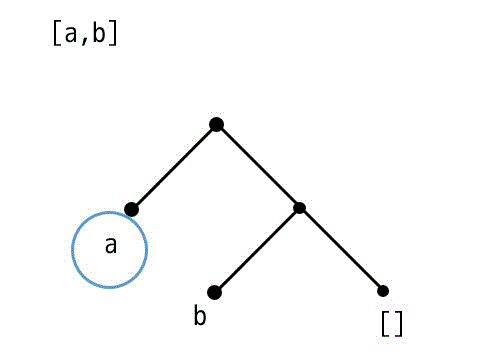
[a|X] の木構造
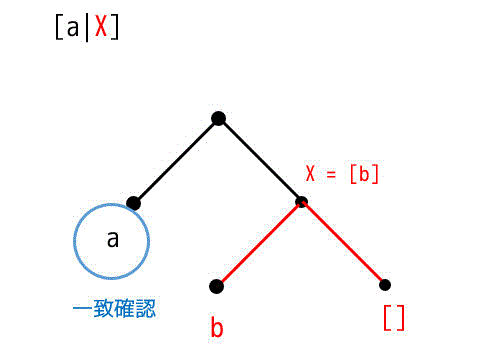
よって、X = [b]。
aの木構造が同じ位置にあるかを確認すること。位置が違っていた場合にも単一化は失敗するので注意!
2つめの引数の木構造も書いていく。今回は単純なので1つの木構造を書くだけで単一化を行った。
[Y] = X = [b] の木構造
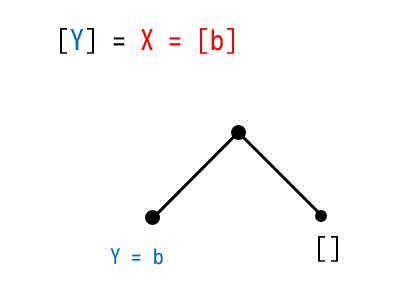
よって、Y = b。 このくらいなら木構造書かずに脳内処理しても全然OK。
X = [b], Y = b
となる。
(8) p([a],b|X) = p([U|V])
2つの関数の引数の数を見比べましょう。
左の項の関数は2つ、右の項の関数は1つと、引数の数が左と右で異なっていますね。
なので、単一化ができない。×。
4. 最後に
今回は、論理プログラム(Prolog)におけるリスト構造の2つの表し方と、リスト構造の木構造化、そして2つのリストの単一化のしかたとその練習をまとめました。リストの単一化は慣れればパズルなので楽しくなりますよ!
次回はカットオペレーター!についてまとめてみようとおもいます!
関連広告・スポンサードリンク