スポンサードリンク
こんにちは、ももやまです!
今回は離散数学でよく使われる証明法である数学的帰納法についてまとめてみたいと思います!
離散数学と書いてありますが、数Bで習う帰納法と同じ書き方と大学数学用の書き方をわけているので高校生の皆さんもぜひ見てください!
数学的帰納法は数Bや数検2級でも出題されているので確実に理解できるようにしましょう!
目次
スポンサードリンク
1.数学的帰納法って何?
いきなりですが1つ例を示してみます。
\( n = 1 \) のとき \( 2^3 + 3^3 = 8 + 27 = 35 \)
\( n = 2 \) のとき \( 2^4 + 3^5 = 16 + 243 = 259 \)
\( n = 3 \) のとき \( 2^5 + 3^7 = 32 + 243 = 2219 \)
ただ答えを書くだけなら〇はもらえますが、記述式の試験の場合はよくて20%~30%の点数しかもらえません。\( n \) が4以上の場合でも7で割り切れるとは限らないからです。
そんなときに使うのが数学的帰納法です。
数学的帰納法は次の2つのステップを使って示すことができます。
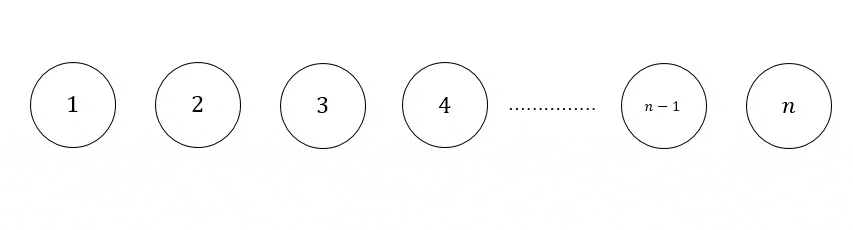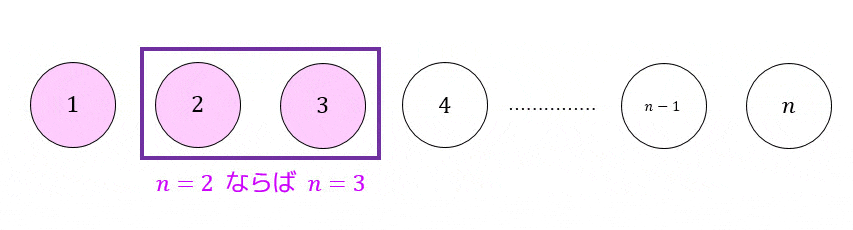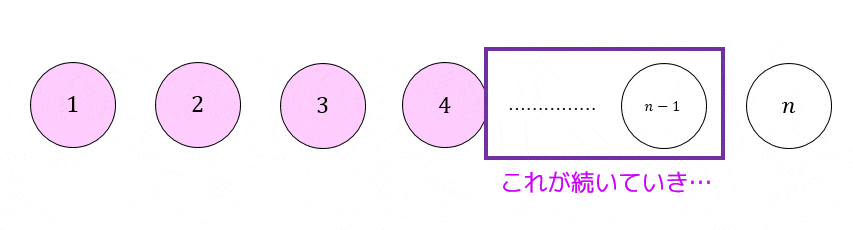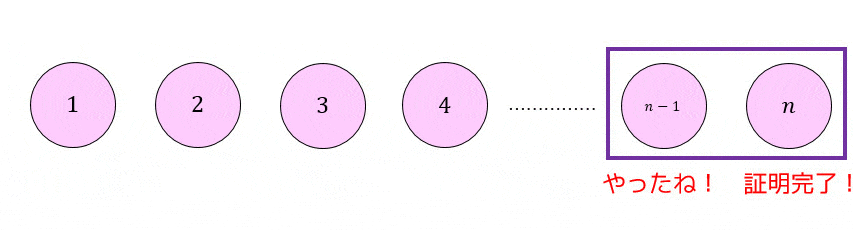
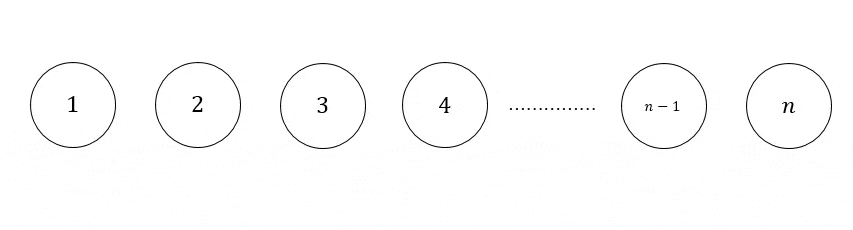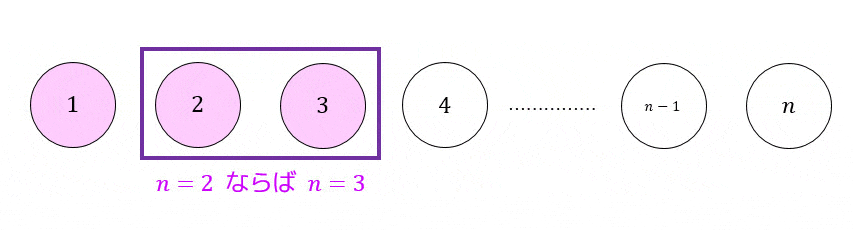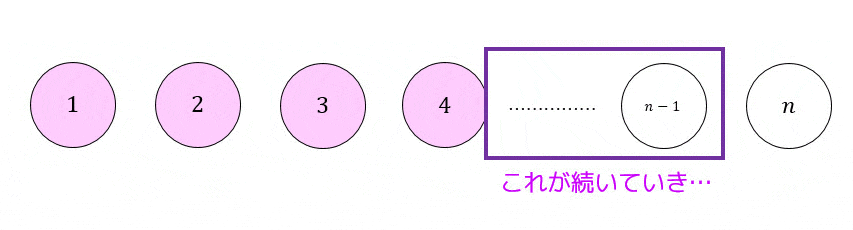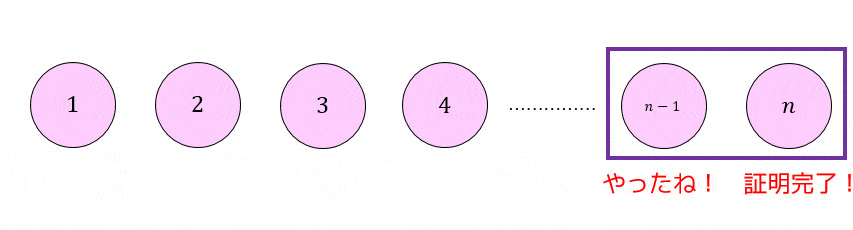
(1) \( n \) が一番小さいときの値(初期値、だいたい0か1)に成り立つことを示す
(2) \( n \) のときに成立すると仮定し \( n+1 \) で成立することを示す。
命題っぽく書くと:\( n \) で成立するならば \( n+1 \) で成立することを示す
\( n \) で成立すると仮定し、仮定した \( n \) をつかって \( n+1 \) で成立することを示すことにより、
(2) \( n = 1 \) で成立するので \( n = 2 \) でも成立
(3) \( n = 2 \) で成立するので \( n = 3 \) でも成立
(4) \( n = 3 \) で成立するので \( n = 4 \) でも成立
(以下略)
スポンサードリンク
2.数学的帰納法の答案の書き方
なるべく文字数を少なくした答案と、高校数学などでおすすめな書き方の2つを記してみます。
(答案ではmodを使って書かなくてももちろんOK)
数学的帰納法で示す。
(1) \( n = 1 \) のとき、\[ 2^3 + 3^3 = 35 = 7 \cdot 5 \equiv 0 \pmod{7} \] より、\( n = 1 \) のときは成立する。
ここまではどちらとも同じです。
ほとんどの場合、この \( n = 1 \) の初期値の場合は簡単に示すことができます。ここを示すだけで少し部分点を貰えるので、(2)がわからなくても最低限ここは書きましょう。
つぎに、\( n \) が成り立つならば \( n + 1 \) が成り立つ、つまり \( n = k \) の場合が成立すると仮定して \( n = k + 1 \) の場合が成り立つことを示します。
ここから文字数に差がでます、まずは高校数学おすすめの書き方から。

ここの変形が数学的帰納法の中で慣れないと難しいかもしれません。練習して慣れましょう。
今回の場合は、\( n = k \) のとき、つまり \( 2^{k+2} + 3^{(2k+1)} \) が7の倍数ならば(7の倍数になると仮定したら) \( n = k + 1 \) も7の倍数になることを示していますね。
かなり丁寧に書いている感じがしますね。では大学の授業でよく使われる文字数を減らしたバージョンも見てみましょう。

記述量が半分以下になっていますね。
とくに、\( k \) と仮定するところを「帰納法の仮定」1行で済ませてしまっているところが記述量を減らすのに貢献していますね。
大学の先生はいちいち分かり切ったことを書くことがめんどくさがるのでこのようによく省略することが結構あります。(もちろん意味が変わらない程度に)
高校のテストなどの答案では上のほうのきっちりと書いたほうで証明することをおすすめします。*1
ここから帰納法の例を4つ紹介するのですが、すべて高校のテストを想定した答案(きっちり丁寧に書く方)を書いていこうとおもいます。大学で帰納法を習う人は脳内で省略バージョンに変換してください。
スポンサードリンク
3.数学的帰納法が使える証明の例
ここからは帰納法が使える証明の例を紹介します。
(1) 等式を示す
まずは、等式を示す場合です。
数学的帰納法で示す。
(1) \( n = 1 \) のとき、\[ (左辺) = 1^2 = 1 \\ (右辺) = \frac{(1+2+3)}{6} = 1 \] より、(左辺)=(右辺)となり、\( n = 1 \) のときは成立する。
(2) \( n = k \) のとき、\[ 1^2 + 2^2 + 3^2 + \cdots + k^2 = \frac{k(k+1)(2k+1)}{6}\] が成立すると仮定する。
\( n = k + 1 \) のとき、\[ 1^2 + 2^2 + \cdots + k^2 + (k+1)^2 = \frac{(k+1)( (k+1)+1)(2(k+1)+1)}{6}\]が成立することを示す。\[
\begin{align*} (左辺) = & 1^2 + 2^2 + \cdots + k^2 + (k+1)^2 \\ = & \frac{k(k+1)(2k+1)}{6} + (k+1)^2 \ [仮定]\\ = & \frac{(k+1)(2k^2+k) + 6(k+1)^2}{6} \\ = & \frac{(k+1)(2k^2+k + 6k + 6)}{6} \\ = & \frac{(k+1)(2k^2+7k + 6)}{6} \\ = & \frac{(k+1)(2k+3)(k+2)}{6} \\ = & \frac{(k+1)( (k+1)+1)(2(k+1)+1)}{6}
\end{align*} \]となるので \( n = k+1 \) のときも成立。
(1),(2)より題意は満たされた。
ここまではどちらとも同じです。
帰納法の(2)を書く部分のポイントとして、\( n = k + 1 \) のときに目標を書いておくことです。
目標を書くことで答案が書きやすくなるし、採点者にもアピールができるので目標は書いておくことをおすすめします。大学の授業内の数学的帰納法で答案を省略する場合でも、問題用紙に目標をメモしておくといいです。大学の先生で記述省略したい人は「そんなの書くなよって言う人もいますが」…
(2) 不等式を示す
次は不等式を示します。等号のように仮定する式を直接代入するわけではないので、難易度は(1)と比べたら少し高くなります。
このような問題の場合、(左辺)と(右辺)の2つをそれぞれ比べるのは少し大変です。式変形をして、(左辺) - (右辺) > 0 を示す方が、1つの式が0より大きいかを比べるだけになるので、少し簡単に解くことができます。
数学的帰納法で示す。
(1) \( n = 2 \) のとき、\[ (左辺) = 3^2 = 9 \\ (右辺) = 2 \cdot 2^2 = 8\] より、(左辺)>(右辺)となり、\( n = 2 \) のときは成立する。
(2) \( n = k \ \ (k \geqq 2) \) のとき、\( 3^k \gt k 2^k \) 、つまり \( 3^k - k 2^k \gt 0 \) が成立すると仮定する。
\( n = k + 1 \) のとき、\( 3^{k+1} \gt (k+1)2^{k+1} \) 、つまり \( 3^{k+1} - (k+1)2^{k+1} \gt 0 \) が成立することを示す。\[ \begin{align*} &
3^{k+1} - (k+1)2^{k+1} \\ = & 3 \cdot 3^k - (2k +2) \cdot 2^k
\\ = & 3 \cdot 3^k - (2k +2) \cdot 2^k
\\ = & 3 \cdot 3^k - 3k \cdot 2^k + (k - 2) \cdot 2^k
\\ = & 3(3^k - k \cdot 2^k) + (k - 2) \cdot 2^k \gt 0
\end{align*} \]ここで、仮定より \( (3^k - 3k \cdot 2^k) \gt 0 \) である。
さらに、\( k \geqq 2 \) より、\( (k - 2) \cdot 2^k \geqq 0 \) である。
よって、 \( n = k+1 \) のときも成立。
(1),(2)より題意は満たされた。
スタートが \( n = 1 \) ではなく、\( n = 2 \) であることに気を付けてください。このように問題文によってはスタート地点が1とは限らないので注意して問題文を見ましょう。
不等式の場合は、何とかして (左辺) - (右辺) > 0 を示すのが目標となります。
ちなみに別解ですが(2)はこのような書き方でもOKです。
(2) \( n = k \) のとき、\( 3^k \gt k 2^k \) が成立すると仮定する。
\( n = k + 1 \) のとき、\( 3^{k+1} \gt (k+1)2^{k+1} \) 、つまり \( 3^{k+1} - (k+1)2^{k+1} \gt 0 \) が成立することを示す。\[ \begin{align*} &
3^{k+1} - (k+1)2^{k+1} \\ = & 3 \cdot 3^k - (2k +2) \cdot 2^k
\\ = & 3 \cdot 3^k - (2k +2) \cdot 2^k
\\ \gt & 3k \cdot 2^k - (2k +2) \cdot 2^k [仮定]\\ = & (k - 2) \cdot 2^k \geqq 0
\end{align*} \]
となるので \( n = k+1 \) のときも成立。
(1),(2)より題意は満たされた。
このように仮定を使う方法もOKです。しかし、\( = \) ではなく \( \gt \) を使い、最後は \( \geqq 0 \) になるところに要注意です。( \( k = 2 \) のときは0になってしまう、しかし途中に \( \gt \) が入っているため \( n = k + 1 \) でも問題なく示せる)
(3) 漸化式(差分方程式)の項を予測して証明する
a_3 = 3a_2 - 2 = 10 \\
a_4 = 3a_3 - 2 = 28 \\
a_5 = 3a_4 - 2 = 82 \\
a_6 = 3a_5 - 2 = 244 \]
こんな感じに解法を忘れてしまって推測して答えを出そうとするのはいい考えなのですが、この場合だと \( a_7 \) 以降が正しい答えになるのかが書かれていないため、記述式だとかなりの減点をくらってしまいます。
そんなときに役に立つのが帰納法です。答えを推測し、その答えが合っていることを帰納法で証明してしまえばいいのです! 今回は上の \( a_n = 3^{n-1} + 1 \) を証明してみましょう。
答えが \( a_n = 3^{n-1} +1 \) になることを数学的帰納法で示す。
(1) \( a_1 \) のとき、\( a_n = 3^0 +1 = 1 + 1 = 2 \) より成立する。
(2) \( a_k \) のとき、 \( a_k = 3^{k-1} +1 \) が成立すると仮定する。
\( a_{k+1} \) のとき、\( a_{k+1} = 3^{k} + 1 \) が成り立つことを示す。\[ \begin{align*} a_{k+1} = & 3a_{k} - 2 \\ = & 3 \cdot 3^{k - 1}+1 - 2 \ [仮定] \\ = & 3^{k} + 1 \\ = & 3^{(k - 1) + 1} + 1 \end{align*}\]より、\( a_{k+1} \) のときも成立。
(1),(2) より題意は満たされた。
(2) のときは、仮定した式 \( a_k = 3^{k-1} +1 \) に加えてもとの漸化式 \( a_n = 3^{n-1} +1 \) も使って \( a_{k+1} \) でも成立することを示しています。
このように記述すれば、\( n \) がどんな値でも \( a_n = 3^{n-1} +1 \) になることが示せるので記述式でも正しいといえる答案になりますね。
(4) 整数問題
数学Aの整数問題みたいな問題も帰納法で証明できてしまいます。
数学的帰納法で示す。
(1) \( n = 1 \) のとき、\[ 1 + 5 = 6 \equiv 0 \pmod{6} \] より、\( n = 1 \) のときは成立する。
(2) \( n = k \) のとき、\( k^3 + 5k \) が6で割り切れると仮定する。ここで、\( k^3 + 5k = 6m \) とする。
\( n = k + 1 \) のとき、\( (k+1)^3 + 5(k+1) \) が6で割り切れることを示せばよい。\[ \begin{align*} (k+1)^3 + 5(k+1) = & (k^3+ 3k^2+3k + 1) + 5k + 5 \\ = &
k^3 + 3k^2 + 8k + 6 \\ = & (k^3+5k) + 3k^2 + 3k + 6 \\ = & 6m + 3k(k+1) + 6 \ [仮定] \end{align*}\]
ここで、\( k(k+1) \) は、連続する2整数なため、2の倍数である。
よって \( 6m + 3k(k+1) + 6 \) は6の倍数と言うことができ、\( n = k + 1 \) のときも成立する。
(1),(2) より題意は満たされた。
このように整数問題も数学的帰納法を使って解くことができちゃいます。*2
また、大学に入学すると、数学的帰納法を数式以外にもリスト(集合)や木構造などの数字が出てこないものについても使う機会があるかもしれませんが、少し難しいので今回は紹介はやめときます。機会があればまたまとめようと思います。
4.さいごに
今回は数学的帰納法についてまとめました。
帰納法の証明は書き方を間違えると減点されてしまうことが多いため、苦手と思う人が多いかもしれませんが、慣れてしまえばワンパターンなため、形を覚えるまで練習しましょう。(特に不等式の帰納法が難易度高いので練習必須)
余談ですが、数学的帰納法はアンサイクロペディアの記事が結構面白かったのでぜひ見てください。
関連広告・スポンサードリンク