スポンサードリンク
修正:2019/6/10(Mon)
例題1-(2)の解答、解説を修正。
こんにちは、ももやまです!
大学数学になると、突然\[
\forall x \in \mathbb{N} \ \ \ \exists y \in \mathbb{N} , \ \ x < y
\]のように、\( \forall \), \( \exists \) や、集合などを用いた難しい表現で書かれた命題(論理式)が出てきて、難しいなと思う人も多いと思います。
そこで、今日は大学数学で出てくるこれらの記号 \( \forall \), \( \exists \) が含まれる式の読み方について、一緒に勉強していきましょう。
前回(第2羽)の「命題・真理値表編」はこちらから↓
目次
スポンサードリンク
1.動画での解説はこちら!
本記事の内容は、動画でも解説しております。動画でご覧いただきたい方は、以下の動画をご覧ください。
スポンサードリンク
2.∀・∃で書かれた式を読むために必要な3つのルール
\( \forall \), \( \exists \) が出てくる述語論理で書かれた式は、たった以下の3つのルールさえ理解すれば、基本的な述語論理は読めるようになります!
- 記号 \( \forall \), \( \exists \) の読み方
- 否定 \( \neg \) が出てくる式の書き換え
- 複数の変数が登場する場合の読み方
この3つのルールさえ理解できれば、あとは練習あるのみです!
スポンサードリンク
3.述語論理の記号
ここで、述語論理に使われる記号をいくつか紹介しましょう。
(1) \( \forall \) for all 全称記号
この記号は、"領域(定義域)内であればどんな値でも条件を満たす" ことを表します。
"どんな値でも" なので、1個でも条件を満たさないものがあれば、その時点でアウト(偽)です。
For All の A を逆さまにしてできた記号 \( \forall \) と頭に入れておくのがおすすめです。
ここからは、実際に \( \forall \) を使った表記例を、2つほど見ていきましょう。
すべての工業大学生は、賢い。\[
\textcolor{red}{\forall} \textcolor{purple}{x \in A} , \ \ \ \textcolor{limegreen}{P(x)}
\]
\( A \): 工業大学生を集めた集合
\( P(x) \): \( x \) は賢い
すべての自然数 \( x \)に対して、\( x \) は1以上。\[
\textcolor{red}{\forall} \textcolor{purple}{x \in \mathbb{N}} , \ \ \ \textcolor{limegreen}{x \geqq 1}
\]
\( \mathbb{N} \): 自然数全体の集合(この記事では、0は自然数とはしない)
(2) \( \exists \) there exists 存在記号
この記号は、"領域(定義域)内のうち、ある1つ以上の値が条件を満たす" ことを表します。
"ある1つ以上の値" なので、1個でも条件を満たすものがあれば、その時点で条件式クリア (真) です。
there Existsの E を逆さまにしてできた記号 \( \exists \) と頭に入れておくのがおすすめです。
ここからは、実際に \( \exists \) を使った表記例を、2つほど見ていきましょう。
ある(1人以上の)ての工業大学生は、賢い。\[
\textcolor{blue}{\exists} \textcolor{purple}{x \in A} , \ \ \ \textcolor{limegreen}{P(x)}
\]
\( A \): 工業大学生を集めた集合
\( P(x) \): \( x \) は賢い
ある(1つ以上の)整数 \( x \)に対して、\( x \) は1以上。\[
\textcolor{blue}{\exists} \textcolor{purple}{x \in \mathbb{Z}} , \ \ \ \textcolor{limegreen}{x \geqq 1}
\]
\( \mathbb{Z} \): 整数全体の集合
(3) 例題で確認!
では、全称記号 \( \forall \) と存在記号 \( \exists \) の使い方が理解できているか、例題で確認してみましょう。
つぎの述語論理で表される式(1), (2)の真偽を答えなさい。
(1)\[
\forall x \in \mathbb{Z} , \ \ x^2 > 0
\]
(2)\[
\exists x \in \mathbb{Z} , \ \ x^2 > 0
\]
※ \( \mathbb{Z} \): 整数全体の集合(つまり \( x \) は整数)
[解説1]
まずは、全称記号 \( \forall \) と存在記号 \( \exists \) の特徴を振り返り、さらに少し特徴を言い換えてみましょう。
全称記号 \( \forall \)
領域内すべての \( x \) で条件を満たす場合に使われる
→ 1つでも成り立たない例(反例)を見つければ、偽と言える。
存在記号 \( \exists \)
領域内のある1つ以上の \( x \) で条件を満たす場合に使われる
→ 1つでも成り立つ例を見つければ、正と言える。
特徴を振り返ったところで、早速問題を解いていきましょう。
(1) \( \forall x \in \mathbb{Z} , \ \ x^2 > 0 \)
式の意味:すべての整数 \( x \) において、\( x^2 > 0 \)
「すべての~」なので、まず反例がないか考えてみましょう。すると、\( x = 0 \) において条件 \( x^2 > 0 \) を満たさないことがわかりますね。
よって、(1)の式は偽となります。
(2) \( \exists x \in \mathbb{Z} , \ \ x^2 > 0 \)
式の意味:ある1つ(以上)の整数 \( x \) において、\( x^2 > 0 \)
「ある1つ(以上)の~」なので、まず条件を満たす例がないか考えてみましょう。すると、いくらでも出てきますね。
例えば、\( x = 2 \) において条件 \( x^2 = 4 > 0 \) を満たしますね。
よって、(2)の式は真となります。
(4) 領域の表し方は様々です!
この章で述語論理について説明する際には、領域を下のように集合を使って表現しましたね。\[
\textcolor{red}{\exists n \in \mathbb{N}} , \ \ n^2 > 0
\]
実は、領域は集合以外の形式で表現することもできます。
[例1] 等式・不等式を用いた表現\[\textcolor{red}{\exists n \geqq 1} , \ \ n^2 > 0
\] [例2] 式外で領域を表現し、式内では省略。\[
\textcolor{red}{\exists n} , \ \ n^2 > 0
\]※ \( n \) は自然数(領域は自然数全体)
(5) s.t. (such that) の使い方も覚えておこう!
先生・参考書によっては、述語論理で論理式を表現する際に、s.t. (such that) を使って、以下のように表現することがあります。\[
\exists n \in \mathbb{N} \ \ \textcolor{red}{\mathrm{s.t.}} \ \ n^2 > 0
\]
この、s.t. は「~が成り立つような」や「~を満たすような」という意味を持ちます。
例えば、上の式であれば「ある \( n \) において、\( n^2 > 0 \) を満たすような \( n \) が存在する。」なります。
4.述語論理記号の変形
ここからは、述語論理内に否定が出てくる式の書き換え方についてみていきましょう。
(1) 全称記号∀(すべての~)の書き換え
例えば、こんな式があったとしましょう。\[
\neg \left( \forall x \in A , \ \ P(x) \right)
\]この式は、「すべての \( A \) に属する \( x \) において、\( P(x) \) が成り立つ」の否定を表していますね。
ここで、元の述語論理式が偽になることを言う(=この式の否定が成立する)ためには、\( P(x) \) を満たさない例を1つ見つければOKでしたね。
そのため、次のような書き換えが成立します。\[
\neg \left( \forall x \in A , \ \ P(x) \right) \Leftrightarrow \exists x \in A , \ \ \neg P(x)
\]※ \( \lnot P(x) \) は、\( P(x) \) が偽になる(=成立しない)ことを表します。
ここで、具体的な書き換えの例も見てみましょう。
「\( A \) に属するすべての \( x \) に対し、\( x \) は5以上」の否定は、「ある \( A \) に属する1つ以上の \( x \) において、\( x \) は5未満」となる。
\[
\neg \left( \forall x \in A , \ \ x \geqq 5 \right) \Leftrightarrow \exists x \in A , \ \ x < 5
\]
※ \( \lnot (x \geqq 5 ) \) を \( x < 5 \) と言い換えている。
(2) 存在記号∃(ある1つの~)の書き換え
先ほどと似た、こんな式があったとしましょう。\[
\neg \left( \exists x \in A , \ \ P(x) \right)
\]この式は、「 \( A \) に属するある1つ以上の \( x \) において、\( P(x) \) が成り立つ」の否定を表していますね。
ここで、元の述語論理式が偽になることを言う(=この式の否定が成立する)ためには、領域内のすべてで \( P(x) \) を満たさないことを確認する必要があります[1]1つでも \( P(x) \) を満たしてしまう \( x \) があると、条件式 \( P(x) \) が成立してしまうため。。
そのため、次のような書き換えが成立します。\[
\neg \left( \exists x \in A , \ \ P(x) \right) \Leftrightarrow \forall x \in A , \ \ \neg P(x)
\]
こちらも、具体的な書き換えの例も見てみましょう。
「\( A \) に属するある1つ以上の \( x \) に対し、\( x \) は0未満である。」の否定は、「\( A \) に属するすべての \( x \) において、\( x \) は0以上である。」となる。
\[
\neg \left( \exists x \in A , \ \ x < 0 \right) \Leftrightarrow \exists x \in A , \ \ x \geqq 0
\]
※ \( \lnot (x < 0 ) \) を \( x \geqq 0 \) と言い換えている。
5.述語論理記号の組み合わせ
(1) 複数変数を使った述語論理の表し方
述語論理を用いて式を表す際には、次のように2つ以上の変数を組み合わせて使うことができます。\[
\forall x \in A \ \ \exists y \in B , \ \ \ P(x,y)
\]
ここで、2つ以上の変数を組み合わせて使う場合に非常に重要になってくるのが、領域を表す際に使う変数の列挙順序です。
というのも、次の2つの式では意味が全く変わってくるからです。\[
\forall x \in A \ \ \exists y \in B , \ \ \ P(x,y)
\]\[
\exists y \in B \ \ \forall x \in A , \ \ \ P(x,y)
\]
ここからは、実際にどう変わってくるかを、例を使ってみていきましょう。
(2) 述語論理は順番が命!
ここからは、変数の列挙順序を変えると、意味が大きく変わることを身をもって体験してもらいましょう。
まず、
- \( A \) … 男性グループ {はやて, りょう, はると}
- \( B \) … 女性グループ {ゆうき, めい, みく}
- \( P(x,y) \) … 2人はお付き合いしている(=恋愛関係にある)
と定義します。
この状態で、\[
\forall x \in A \ \ \exists y \in B , \ \ \ P(x,y)
\]\[
\exists y \in B \ \ \forall x \in A , \ \ \ P(x,y)
\]の式の意味を考えてみましょう。
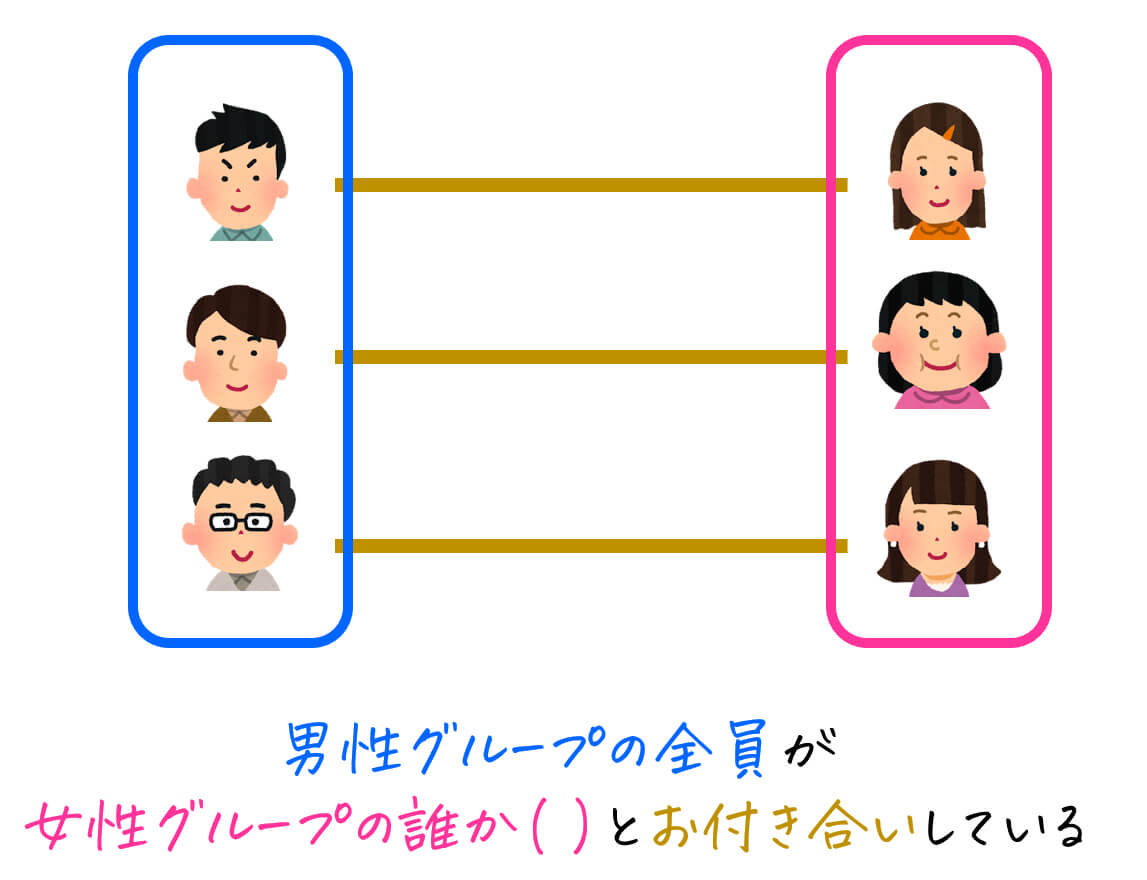
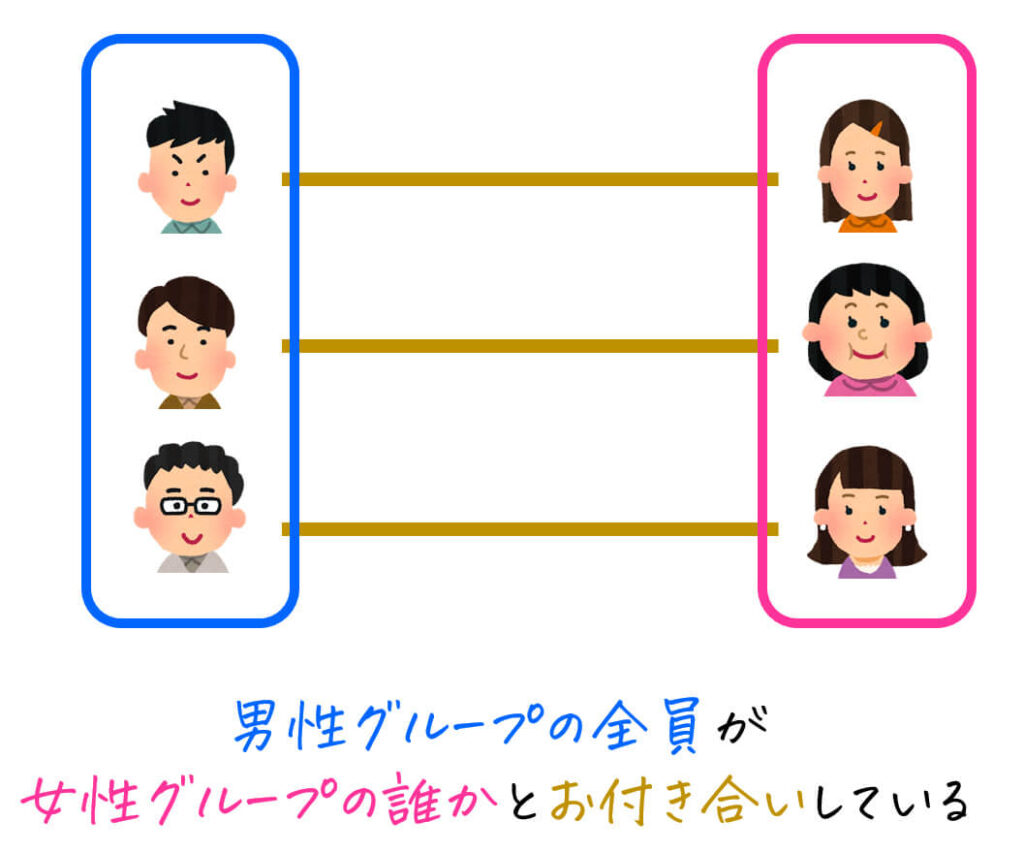
パターン1: \( \forall x \in A \ \ \exists y \in B , \ \ \ P(x,y) \)
意味:\( A \) に属するすべての ( x \) に対して、\( P(x,y) \) が成り立つ、ある1つ以上の \( B \) に属する \( y \) が存在する。
この場合は、\( P(x,y) \) が真になるためには、すべての \( x \) に対して、\( P(x,y) \) を満たす \( y \) を1つ以上持ってくればOKですね。
なので、この式は「男性グループの全員が、女性グループの誰か[2]述語論理的には、2人以上付き合っていても成立しますが、リアルではあまりよくないので、ここでは1人とだけお付き合いしていることとします。とお付き合いしている」という意味になります。
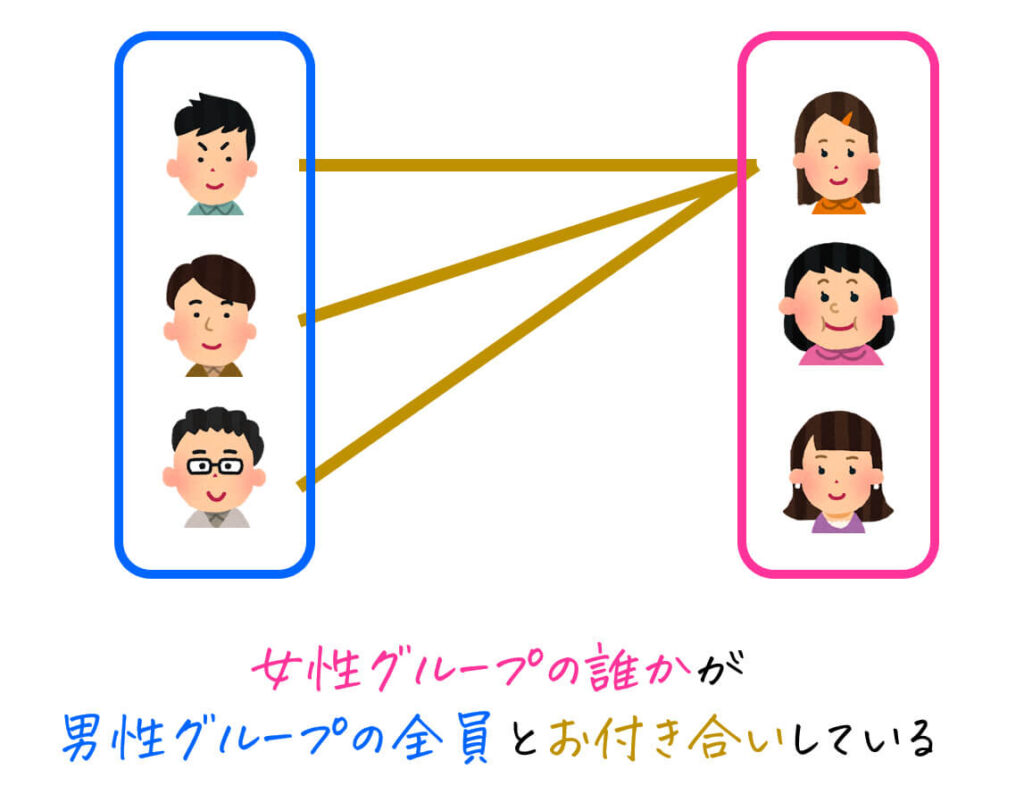
パターン2: \( \exists y \in B \ \ \forall x \in A , \ \ \ P(x,y) \)
意味:\( B \) に属するある1つ以上の ( y \) に対して、すべての \( A \) に属する \( x \) において \( P(x,y) \) が成立する。
この場合は、\( P(x,y) \) が真になるためには、ある1つ以上の \( y \) に対して、すべての \( x \) が成立する必要があります。
そのため、この式は「女性グループの中の誰か1人が、男性グループ全員とお付き合いしている」という超ハーレム状態な意味となってしまいます。
このように、述語論理は順番を変えてしまうと全く違う意味になってしまうのです。
(3) 例題で確認!
複数の変数が出てくる述語論理は、大学数学を学ぶ上でも、離散数学のテストを受けるためにも非常に重要です。
なので、理解できているかを例題で確認しましょう。
つぎの述語論理で表される式(1), (2)の真偽を答えなさい。ただし、\( x \), \( y \) の領域は整数範囲とする。
(1)\[
\forall x \exists y , x = y
\]
(2)\[
\exists y \forall x , x = y
\]
※ \( \mathbb{Z} \): 整数全体の集合(つまり \( x \) は整数)
[解説2]
(1) \( \forall x \exists y \ (x = y) \)
この場合、「どんな \( x \) に対しても、条件 \( x = y \) が成り立つような \( y \) が1つでも存在する」ことが言えればOKですね。
例えば、\( y = x \)(\( y \) が \( x \) と等しい値)のときは、どんな \( x \) であろうとも、必ず条件式 \( x = y \) が成立しますね。
なので、この式は真と言えます。
(2) \( \exists y \forall x \ (x = y) \)
この場合、「ある1つ以上の \( y \) に対して、すべての \( x \) において条件 \( x = y \) が成り立つ」ことが言えればOKですね。
しかし、\( y \) がどんな値であろうとも、条件 \( x = y \) が成り立つのは、\( y \) と \( x \) が等しいときだけですね。
なので、\( y \) の値に関わらず、すべての \( x \) に対して条件式 \( x = y \) が成り立つとは言えないため、この式は偽ですね。(反例: \( y \) と \( x \) の値が異なるとき)
6.領域を変えただけで真偽が変わる!?
実は、領域を変えるだけで述語論理の式の真偽が変わることがあります。
実際に例題を踏まえて、確認していきましょう。
つぎの述語論理で表される式(1), (2)の真偽を答えなさい。ただし、\( S = \{ 1,2, 3 \} \) とします。
(1)\[
\forall x \in S \ \ \exists y \in S , x < y
\]
(2)\[
\forall x \in \mathbb{N} \ \ \exists y \in \mathbb{N} , x < y
\]
※ \( \mathbb{N} \): 自然数全体の集合(つまり(2)の \( x, y \) は自然数)
[解説3]
(1), (2)の式の意味としては、どちらも「どんな \( x \) に対しても、\( x < y \) を満たす \( y \) が1つ以上存在する」となります。
これを踏まえて、問題を解いていきましょう。
(1) \( \forall x \in S \ \ \exists y \in S , x < y \)
この述語論理では、\( x \), \( y \) が取りうる値の最大値は3ですね。
ここで、\( x \) が3(最大値)のときは、これよりも大きい \( y \) を取ってくることができません。
そのため、\( x \) が3のとき、\( x < y \) を満たす \( y \) が1つも存在しないため、答えは偽となります。
(1) \( \forall x \in S \ \ \exists y \in S , x < y \)
この述語論理では、\( x \), \( y \) が自然数なので、\( x \), \( y \) の値を無限に大きくすることができます。(言い換えると、\( x \), \( y \) には最大値がありません。)
そのため、\( x \) の値がいくらであろうが、\( y \) を \( x \) よりも1大きい値とすることで、必ず 条件 \( x < y \) を満たすような \( y \) を求められますね。
そのため、\( y = x + 1 \) のとき「すべての \( x \) に対して、条件 \( x < y \) を満たす \( y \) が存在する」ことが言えるため、答えは真となります。
7.そもそも述語論理がなぜ必要なの?
※ この部分は離散数学(情報数学)を習っている向けの内容です。
「最後に、そもそも述語論理が何故必要なの?」というのを、簡単に書いていきます。
例えば、こんな三段論法を考えてみましょう。
- うさぎは猫よりもかわいい
(かわいさ:猫 < うさぎ) - 私はうさぎよりかわいい
(かわいさ:うさぎ < 私) - よって、私は猫よりかわいい
(かわいさ:猫 < 私)
この三段論法は、常に成立しますよね。
(私がかわいいかどうかはおいておくとして、)
では、これを命題論理で表してみましょう。
まず、
- 猫 < うさぎ → p
- うさぎ < 私 → q
- 猫 < 私 → r
とします。
すると、この三段論法は、\( (p \land q) \to r \) と表すことができます。

つぎに、\( (p \land q) \to r \) も常に正しいとは言えるでしょうか。実際に真理値表を書いてみましょう。
| \( p \) | \( q \) | \( r \) | \( p \land q \) | \( p \land q \to r \) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
あれ、 \( (p,q,r) = (1,1,0) \) のときは0 (False) になってしまうぞ!
実は命題論理の場合、不等式で出てきた関連する各変数 (猫, うさぎ, 私) が考慮されないため、正しい命題が表せないことがあります。
そこで、関連する変数を指定して命題の真偽を判定できる概念として登場したのが、述語論理です。
8.動画のQuizの答えと解説
「領域 \( A \) に属する自然数 \( x \) はすべて3の倍数である。」を述語論理で書いた式として、最も適切なものはどれ?
- \( \forall x \in A \ \ \forall n \in \mathbb{N}, \ \ x = 3n \)
- \( \forall x \in A \ \ \exists n \in \mathbb{N}, \ \ x = 3n \)
- \( \exists n \in \mathbb{N} \ \ \forall x \in A, \ \ x = 3n \)
- \( \exists n \in \mathbb{N} \ \ \forall x \in A, \ \ x = 3n \)
[解説]
正解: 2
「領域 \( A \) に属する自然数 \( x \) はすべて3の倍数である。」を少し言い換えると、「領域 \( A \) に属する自然数 \( x \) に対し、必ずある3の倍数の値 (3, 6, 9, 12, …) をどれか1つ取る」と言い換えることができます。
そのため、答えは2の\[
\forall x \in A \ \ \exists n \in \mathbb{N}, \ \ x = 3n
\]となります。
9.練習問題
最後に少しだけ練習してみましょう。
例題1
つぎの(1),(2)の論理式の (a) \( S= \{1,2,3\} \) の領域 (b) 自然数 \( \mathbb{N} \) の領域 (c) 整数 \( \mathbb{Z} \) の領域 における真偽を判定しなさい。
(1) \( \forall x \forall y \exists z \exists w \ \ (x \lt z) \lor (y \lt w \land x = z) \)
(2) \( \exists x \exists y \forall z \forall w \ \ (x \lt z) \lor (y \lt w \land x = z) \)
解答1
(a),(b),(c) の領域の最小値と最大値を表す。
| 最小値 | 最大値 | |
| (a) | 1 | 3 |
| (b) | 1 | なし |
| (c) | なし | なし |
(1)
\( \forall x \forall y \exists z \exists w \) ということは、すべての範囲 \( x,y \) に対して、それぞれ1つ以上の \( z,w \) を満たせばOK。
(a) のとき、\( (x,y,z) = (3,3,3) \) のとき、3が最大値なため、3より大きい数を満たす \( w \) が1つも存在しない。よって偽。
(b) のとき、最大値がないため、すべての \( x \) において、\( x \) より1だけ大きい数も存在する。よって \( z \) の値は1つ以上存在する。よって真。
(c) のときも最大値がないため (b) と同様に真。
(2)
\( \exists x \exists y \forall z \forall w \) ということは、ある1つ以上の \( x,y \) が、すべての範囲で \( z,w \) を満たせばOK。
(a),(b),(c)
(i) \( x \lt z \) を考えます。ある \( x \) に対して、\( z = x \) とします。このとき、\( x \lt z \) なので、どのような \( x \) に対しても必ず \( x = z \) においては成立しませんね。
(ii) \( y \lt w \land x = z \) の場合を考えます。たとえ \( x = z \) だとしても、\( y \lt w \) の場合も(i)と同様にある \( y \) に対して、\( w = y \) とします。このとき、\( y \lt w \) なので、どのような \( y \) に対しても必ず \( y = w \) においては成立しませんね。
なので、ある \( x,y \) に対して、\( z = x \), \( w = y \) とするとき、どの領域においても必ず1つ以上成り立たない \( z,w \) が存在するので、 (a),(b),(c)どの範囲においても偽になります。
| (a) | (b) | (c) | |
| (1) | 偽 | 真 | 真 |
| (2) | 偽 | 偽 | 偽 |
10.確認テスト
最後に、今回の記事や動画で勉強した内容が、理解できているかどうかをどうかを確認するための小テストを作りました!
理解度確認に是非チャレンジしてみてください!
※ 回答フォームに入力後、自動採点 & 自動解説表示が行われます。
11.さらなる練習問題
確認テストじゃ物足りない、、という人のため、述語論理の読み方の練習問題を集めた記事を作成しました!
述語論理について、もっと練習したい人は、こちらにもチャレンジしてみてください!
12.さいごに
今回は、変数を用いた命題、述語論理についてまとめてみました。
次回は二項関係についてまとめていきたいとおもいます。
第4羽「二項関係」はこちらから↓
関連広告・スポンサードリンク