うさぎでもわかる離散数学　第4羽　二項関係編

2019年4月14日 2024年8月8日 76分9秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

"関係" というのは、日常生活にもなじみのある概念ですが、離散数学で出てくる関係である "二項関係" について習うと、「なんやねんこれ」と思う人も多いと、思います。

そこで今回は、離散数学の世界で出てくる二項関係について、分かりやすく復習をしていきましょう。

スポンサードリンク

1. 動画での解説はこちら！

本記事の内容は、動画でも解説しております。動画でご覧いただきたい方は、以下の動画をご覧ください。

スポンサードリンク

2. 二項関係のいろは

(1) 二項関係とは何か

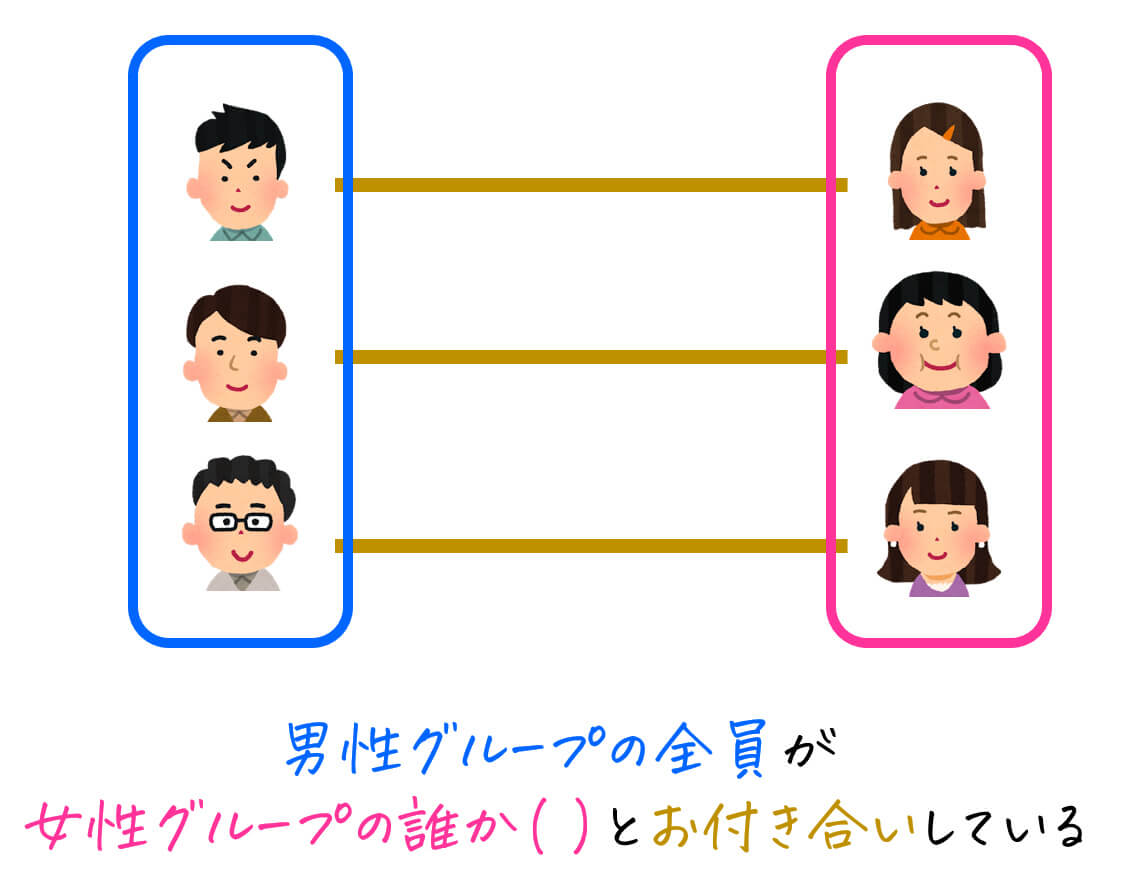
日常生活に出てくる "関係" には様々なものがありますが、その中の1つに "人間関係" がありますね。

その人間関係を細分化すると、"友達関係" や "恋愛関係" など様々なあります。

例えば、恋愛関係に出てくる "関係"は、「ある2人が付き合っているときに成立する関係」と考えることができます。

[関係の具体的な例]

翔くんと祐希さんは付き合っている
→ 翔くんと祐希さんに対しては、関係が成立している
怜音くんと凛さんは付き合っていない
→ 翔くんと祐希さんに対しては、関係が成立していない

こんな感じに、ある2つの物事に対して、関係が成立するかしないかを考えるというのは、数学の世界にも登場し、二項関係と呼ばれます！

もう少し具体的に説明すると、数学の世界に出てくる二項関係 $R$ は、"ある集合の要素間や、数値同士の関係性を、どんなペアで成り立ち、どんなペアでは成り立たないかを、具体例の列挙や、数式を用いて定義したもの" と言えます。

(2) 実は小学3年生でもわかる二項関係がある！？

二項関係って、なんだか難しそうですよね。

でも実は、小学3年生レベルでもわかる二項関係があるのです！

例えば、次の記号 $<$ で書かれた式は見たことありますよね。 $a < b$ この記号は、" $a$ が $b$ よりも大きい関係" であることを表す記号です。

言い換えると、この記号は " $a$ が $b$ よりも大きいときに関係が成立する" 二項関係と言えますね！

離散数学で出てくる二項関係は、このような記号（＝, ≠, >, <, ≧, ≦など）の関係を、自由気ままに定義できる道具みたいなもの、だと思ってください！

高校数学と大学数学と二項関係

[高校数学までの二項関係]

$a = b, a < b$ のように、等号・不等号を使った関係を表すときに使われる。

[大学数学 (離散数学) での二項関係] $a R b$ とし、 $R$ の関係を自由気ままに定義する。

(3) 二項関係の定義の仕方

二項関係を用いて、ペアごとに関係 $R$ を定義する方法は2つあります。

集合の形で、関係が成り立つペアを列挙する方法
関係が成り立つ条件を、数式を使って定義する方法

ここからは、2つの方法をそれぞれ詳しくみていきましょう。

(i) 集合の形で、関係が成り立つペアを定義する方法

二項関係 $R$ は、集合を用いて関係が成り立つペアを以下のように列挙します。 $R = {(1, 1), (1, 2), (2, 2)}$ ※ $R$ は、 $S = {1, 2}$ 上での二項関係とします。

この場合、成り立つ関係のペアと成り立たない関係のペアは以下の通りです。

成り立つ関係: (1,1), (1,2), (2,2)
成り立たない関係: (2,1)

※ 上の例（ (1,2) と (2,1) ）のように、関係 (a,b) が成り立っていても、a, bを入れ替えた (b,a) は、必ず関係が成り立つとは限らないので注意です。また、関係 (a,b) が成り立っていなくて、a, bを入れ替えた関係 (b,a) が成り立つこともあります。

Tips1. 関係の有無の表記法

ここで、ある要素が関係が成り立つか否かを表す際には、以下のような表記が使われます。

関係が成り立つとき: $(1, 1) \in R$ , $1 R 1$
関係が成り立たないとき: $(2, 1) \notin R$ , $2 R̸ 1$ , $(2, 1) \in R$ でない、 $2 R 1$ でない

※ 複数表記法があるので、どれも使えるようになっておきましょう。

Tips2. 二項関係と直積集合

関係が成り立つペア（＝二項関係 $R$ の要素）の書き方ですが、見覚えはありませんか？ $R = {(1, 1), (1, 2), (2, 2)}$

この書き方は直積集合の書き方 $S \times S = {(1, 1), (1, 2), (2, 1), (2, 2)}$ とそっくりですね^[1]直積集合 $A \times B$ は、集合 $A$ , $B$ から1つずつ要素を取り出して、( $A$ から取り出した要素, $B$ から取り出した要素 ) … Continue reading。

ここで、二項関係 $R$ というのは、「集合 $S$ から1つずつ要素を取り出してできるペアを全て列挙した集合（直積集合 $S \times S$ ）」から、関係が成り立つペアを抜き出して列挙した集合ですよね。

さらに、元の集合の要素をいくつか抜き出して作った集合は、部分集合と呼ばれますよね。

そのため、二項関係 $R$ は、必ず元の直積集合 $S \times S$ の部分集合、つまり $R \subseteq S \times S$ となることが分かりますね。

(ii) 関係が成り立つ条件を、数式や述語論理を使って定義する方法

領域が自然数領域、整数領域のように、無限に大きい値 (小さい値) が取れるような領域のときは(i) の集合の形でいちいち関係を列挙していたら、キリがありません。

そういうときに使われるのが、次のように2つ目のような数式や述語論理を使って定義する方法です。 $x R y \Leftrightarrow \exists n \in N s . t . x + y = 2 n$ 例えばこの式では、「 $x$ と $y$ が2の倍数（ある2の倍数の値を取る）」関係と言えますね^[2] $\exists n \in N s . t . x + y = 2 n$ を日本語に直すと「整数 $x + y$ の和が、ある2の倍数の値 (2,4,6,8, …) となる。」となりますね。。

ここで、関係 $R$ を定義する際に使われる記号 $\Leftrightarrow$ ですが、先生によっては定義であることを強調するために矢印の上に、def (definition・定義の略) と書いて $\overset{def}{\Leftrightarrow}$ と書く先生もいるので、頭に入れておきましょう。

実際に、defを使った定義例はこんな感じですね。 $x R y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x + y = 2 n$

※ 述語論理の読み方については、こちらの記事にて詳しく説明しておりますので、必要であれば以下のリンク先をご覧ください！

スポンサードリンク

3. 二項関係で重要な4つの関係 + おまけ2つ

ここからは、離散数学の期末試験で非常に重要である、二項関係で重要な4つの関係

反射性
対称性
反対称性
推移性

について、お勉強していきましょう！

おまけで、同値関係と比較可能な関係についても説明しています。

(1) 反射性

[述語論理を用いた定義] $\forall x \in A, x R x$ $\forall x \in A, (x, x) \in R$ 意味: 値が等しいペアのとき、必ず関係が成立する。（定義域 $A$ において）

反射性は、鏡の反射のように、二項関係において要素が自分自身と関係している性質です。

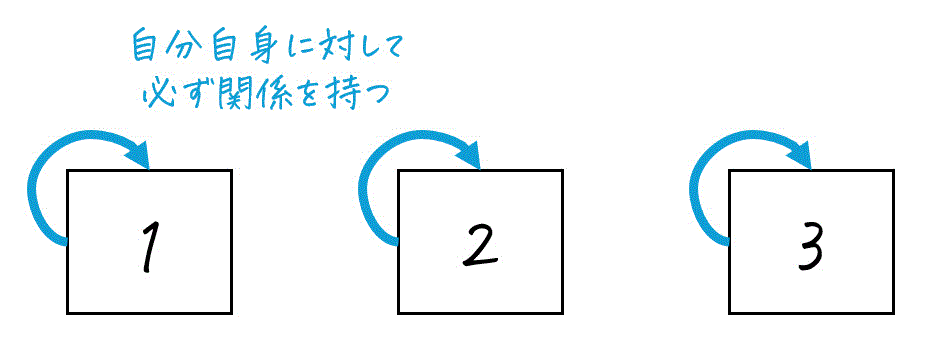
具体的に言うと、反射性を満たす二項関係とは、"定義域内において、値が等しいペアであれば、必ず関係が成り立つ" 二項関係のことを言います。

言い換えると、定義内において、1つでも値が等しいときに関係が成り立たなければ、反射性を満たすとは言えません。

[反射性を満たす例]

(1) 等号 $=$ , 不等号 $≦$ , $≧$

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{1}$ $R_{1} = {(1, 1), (2, 2), (3, 3), (1, 2), (3, 1)}$ ※ 赤色の関係 $(1, 1), (2, 2), (3, 3)$ が反射性を満たすための必須条件。必須条件以外のペアは、あってもなくても反射性を満たすか満たさないかには関係

(1) 自然数 $N$ 上において、2つのペアの和が偶数となる二項関係 $R_{2}$ $x R_{2} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x + y = 2 n$ ※ 自然数 $t$ を $t = x = y$ とすると、和が偶数 $2 t$ となるため。

[反射性を満たさない例]

(1) 不等号 $<$ , $>$ , 否定等号 $\neq$

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{3}$ $R_{3} = {(1, 1), (2, 2), (1, 3), (3, 1)}$ ※ 反例: $(3, 3) \notin R_{3}$ 。1つでも、値が等しいペアにおいて関係が成り立たなければ、そのペアが反例となり、反射性を満たさない。

(2) 自然数 $N$ 上において、2つのペアの積が、2の倍数となる二項関係 $R_{2}$ $x R_{4} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x y = 2 n$ ※ 反例: $1 {R̸}_{4} 1$ など。値が奇数のとき、値が等しいペアにおいて関係が成り立たない。

(2) 対称性

[述語論理を用いた定義] $\forall x \in A \forall y \in A, x R y \to y R x$ $\forall x \in A \forall y \in A, (x, y) \in R \to (y, x) \in R$ 意味: ペア $(x, y)$ に対して関係が成立するならば、必ずペアの順番を入れ替えた $(y, x)$ も関係が成立する。

対称性とは、ペア $(x, y)$ の関係が成り立っているとき、そのペアを入れ替えて $(y, x)$ としても、関係が必ず成り立つ性質を表します。

簡単に説明すると、対称性は

美玖さんにとって祐希さんはお友達の関係
→ 祐希さんにとっても美玖さんはお友達の関係成立

のように、関係が成立しているペアの順番を入れ替えても、関係が成立している性質です。

反対に、

祐希さんにとって瑠香さんはお友達の関係
→ 瑠香さんにとっては祐希さんはお友達の関係は成立していない

のような組み合わせが1つでもあれば、対称性を満たしません。
（この組み合わせが対称性を満たさない反例となります。）

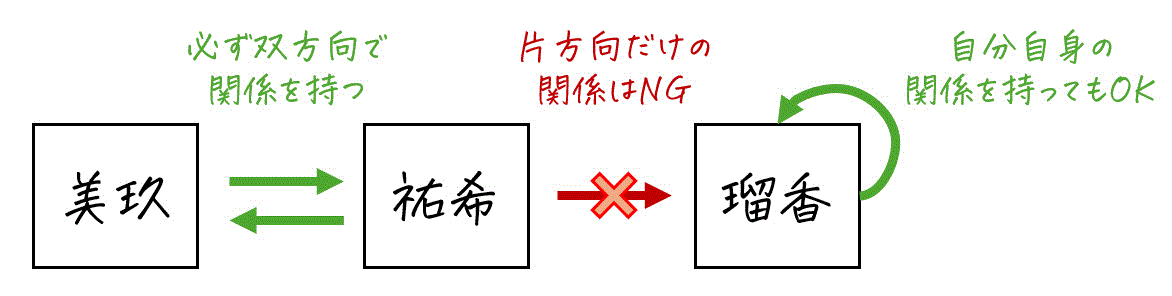
また、関係が成立しているペアが1つもない場合（つまり $R = ϕ$ のとき) は、そもそも前提条件（あるペアに対して関係が成立するとき～）が成立していないため、対称性が成立するという点にも注意です^[3]条件A → … Continue reading。

[対称性を満たす例]

(1) 等号 $=$ , 否定等号 $\neq$

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{1}$ $R_{1} = {(3, 1), (1, 2), (3, 3), (1, 3), (2, 1)}$ ※ 色が対応している関係（ $(1, 3), (3, 1)$ と $(1, 2), (2, 1)$ ）がペアになっている点に着目。また、2つの値が等しいペア $(3, 3)$ は入れ替えても一緒なので、単独でペアになる点に要注意。

(3) 自然数 $N$ 上において、2つのペアの和が偶数となる二項関係 $R_{2}$ $x R_{2} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x + y = 2 n$ ※ $x$ と $y$ を入れ替えても和は変わらないため、 $x R_{2} y$ （ $x + y$ の和が2の倍数）であれば、必ず $y R_{2} x$ （ $y + x$ の和も2の倍数）と言える。

[対称性を満たさない例]

(1) 各種不等号 $<$ , $>$ , $≦$ , $≧$
→ 例えば、 $1 < 2$ が成り立つとき、 $2 < 1$ は成り立ちませんよね。

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{3}$ $R_{3} = {(3, 2), (1, 3), (1, 1), (2, 3)}$ ※ 反例: 「 $(1, 3) \in R_{3}$ だが $(3, 1) \in R_{3}$ 」。 $(3, 2), (2, 3)$ と $(3, 3)$ にはペアを入れ替えた仲間がいるが、 $(1, 3)$ にはペアを入れ替えた仲間がいない仲間外れ。よってこれが反例となる。

(3) 自然数 $N$ 上において、2つのペアの差が、正の偶数となる関係 $R_{4}$ $x R_{4} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x - y = 2 n$ ※ 反例: $3 {R̸}_{4} 1$ など。元のペア $(x, y)$ の差 $x - y$ が正の偶数であっても、値を入れ替えると正負が入れ替わってしまい、関係をみたさなくなる。よって、対称性が成り立たない。

(3) 反対称性

[述語論理を用いた定義] $\forall x \in A \forall y \in A, x R y \land y R x \to x = y$ $\forall x \in A \forall y \in A, (x, y) \in R \land (y, x) \in R \to x = y$ 意味: 関係が成立するペアを入れ替えても関係が成立するならば、ペア内の値は等しい。

反対称性のイメージは、「異なるもの同士が、必ず双方向に関係を持たない」関係だと思ってください。（元の定義の対偶を取ったものです）

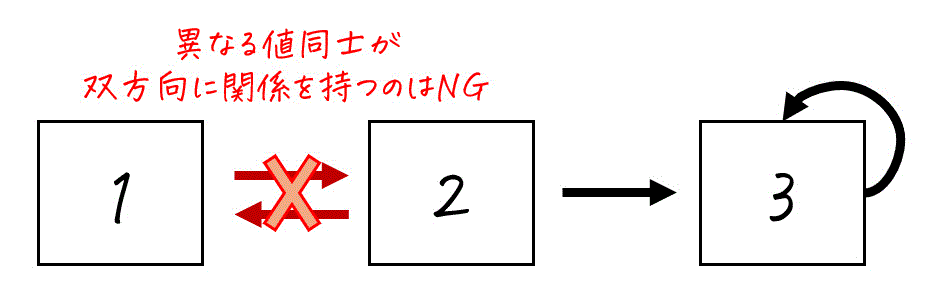
教科書によっては、対偶を取った形で定義を記載している参考書もあります。 $\forall x \in A \forall y \in A, x R y \land x \neq y \to \neg y R x$ 意味: 関係が成り立つペア $(x, y)$ のペア内の値が等しくない ( $x \neq y$ ) とき、そのペアの値を入れ替えたペア $(y, x$ には関係が絶対に成り立たない。

としている参考書もあります。

ここで、注意ポイントが2つあります。

まず1つ目は、「対称性を満たすか否か」と「反対称性を満たすか否か」は、独立しているということです。

言い換えると、

対称性を満たす（満たさない）からと言って、必ず反対称性を満たさない（満たす）とは限らない
反対称性を満たす（満たさない）からと言って、必ず反対称性を満たさない（満たす）とは限らない

ということが言えます。例えば、 $R = {(1, 1), (2, 2), (3, 3)}$ のように、2つの値が同じペアでのみ条件を満たす関係は、対称性・反対称性ともに成り立ちますね^[4](1,1), (2,2), (3,3) … Continue reading。

2つ目は、対称性のときと同じく、関係が成立しているペアが1つもない場合（つまり $R = {(1, 2)}$ のように、 $(x, y) \in R \land (y, x) \in R$ となるペアの組がないとき) は、そもそも前提条件（あるペアに対して関係が成立するとき～）が成立していないため、反対称性が成立するという点にも注意です。

[反対称性を満たす例]

(1) 等号 $=$ , 各種不等号 $<$ , $>$ , $≦$ , $≧$

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{3}$ $R_{3} = {(3, 2), (1, 3), (1, 1)$

$(1, 1)$
→ 値を入れ替えても $(1, 1)$ なので関係成立。さらに、 $(1 = 1$ なのでOK。
$(3, 2)$ , $(1, 3)$ は、ペアを入れ替えた仲間（ $(2, 3), (3, 1)$ がいない仲間外れ。なので、前提条件を満たしていないため、OK。

(3) 自然数 $N$ 上において、2つのペアの差が、正の偶数となる関係 $R_{2}$ $x R_{4} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x - y = 2 n$ [(3)が成り立つ理由]

関係が成り立つ全てのペアは、 $x - y$ は正の偶数
ペアの値を入れ替えて $(y, x)$ とすると、 $y - x = - (x - y)$ となり、正負が入れ替わる。よって、関係は絶対に成り立たない。
よって、関係が成り立つ全てのペアにおいて、ペアの値を入れ替えると関係が成り立たなくなることが言える。
→ 反対称性が成り立つ。

[反対称性を満たさない例]

(1) 否定等号 $\neq$

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{3}$ $R_{3} = {(1, 2), (3, 3), (1, 3), (2, 1)}$ 反例: $(1, 2) \in R$ かつ $(2, 1) \in R$ だが $1 \neq 2$ 。

色が対応している関係 $(3, 3)$ と $(1, 2) (2, 1)$ が前提条件である $(x, y) \in R \land (y, x) \in R$ （元のペアと、その値を入れ替えたペアの両方において、関係が成立する）を満たす組である。

しかし $(1, 2) (2, 1)$ は、前提条件を満たしているにも関わらず、ペア内の値が $1 \neq 2$ と異なるため、これが反例となる。

(3) 自然数 $N$ 上において、2つのペアの和が、正の偶数となる関係 $R_{4}$ $x R_{4} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x + y = 2 n$ 反例: $1 R 3$ かつ $3 R 1$ だが、 $1 \neq 3$ など

※ $x$ と $y$ を入れ替えても和は変わらないため、 $x$ と $y$ が等しくなくても前提条件 $(x, y) \in R \land (y, x) \in R$ （元のペアと、その値を入れ替えたペアの両方において、関係が成立する）を満たすペアが大量に存在する。

(4) 推移性

[述語論理を用いた定義] $\forall x \in A \forall y \in A \forall z \in A, x R y \land y R z \to x R z$ $\forall x \in A \forall y \in A \forall z \in A, (x, y) \in R \land (y, z) \in R \to (x, z) \in R$ 意味: ペア $(x, y)$ と $(y, z)$ がともに関係が成り立つならば、必ず $(x, z)$ も関係をが成り立つ。

推移性とは、ペア $(x, y)$ と $(y, z)) がともに関係が成り立つとき、ペア \((x, z)$ も関係を満たす性質のことを言います。

簡単に説明すると、推移性は

美玖さんと祐希さんはお友達の関係成立
祐希さんと大樹さんもお友達の関係成立
→ 美玖さんと大樹さんもお友達の関係成立

みたいな三段論法的が、常に成立する性質です。

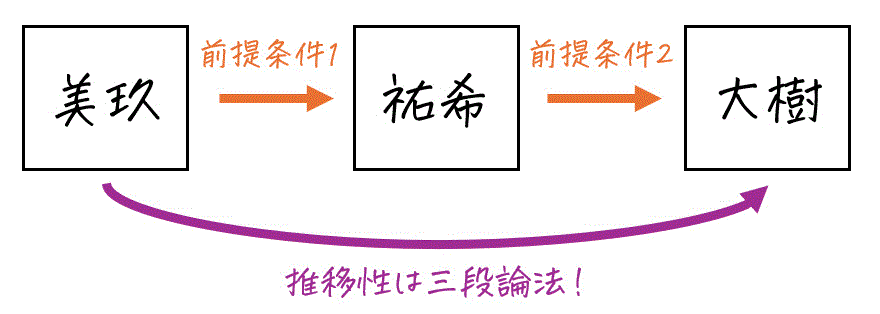
こちらも対称性のときと同じく、関係が成立しているペアが1つもない場合（つまり $R = {(1, 2), (3, 2)}$ のように、 $(x, y) \in R \land (y, z) \in R$ となるペアの組がないとき) は、そもそも前提条件（あるペアに対して関係が成立するとき～）が成立していないため、推移性が成立するという点にも注意です。

推移性は、前提条件が割と複雑なため、結構反例を逃しがちなので、反例を探す練習をしましょう。

[推移性を満たす例]

(1) 等号 $=$ , 各種不等号 $<$ , $>$ , $≦$ , $≧$
→ 例えば、 $a < b$ と $b < c$ が共に成立する場合、 $a < c$ も必ず言えますよね。

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{3}$ $R_{1} = {(1, 2), (2, 3), (1, 3),}$

(3) 自然数 $N$ 上において、2つのペアの和が、正の偶数となる関係 $R_{2}$ $x R_{2} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x + y = 2 n$ [(3)が成り立つ理由] 2つのペアの和が偶数になるためには、(偶数,偶数) もしくは (奇数,奇数) である必要がある^[5]偶数 + 偶数 = 偶数，奇数 + 奇数 = 偶数，偶数 + 奇数 = 奇数，奇数 + 偶数 = 奇数。

ここで、推移性の前提条件ごとに場合分けすると、

(偶数,偶数) かつ (偶数,偶数) → (偶数,偶数) [OK]
(奇数,奇数) かつ (奇数,奇数) → (奇数,奇数) [OK]

となるため、必ず $R_{2}$ は推移性を満たすと言える。

[推移性を満たさない例]

(1) 否定等号 $\neq$
→ $1 \neq 2$ かつ $2 \neq 1$ ですが、 $1 = 1$ になってしまいますね。

(2) $S = {1, 2, 3}$ としたときの、二項関係 $R_{3}$ $R_{3} = {(1, 2), (3, 1), (2, 2)}$ 反例: $(3, 1) \in R$ かつ $(1, 2) \in R$ \) だが、( \textcolor{deepskyblue}{3}, \textcolor{limegreen}{2} ) \notin R \)

※ この例のように、見つかりにくいように反例が隠されていることもあるので注意！　前提条件を見つけるコツは、あるペアの右側の値 $(x, y$ とあるペアの左側の値 $(y, z$ が等しい組かつ、2つの値が等しくないペアに着目^[6]2つの値が等しいペアに着目すると、\[\textcolor{deepskyblue}{x}R \textcolor{magenta}{x} \land \textcolor{magenta}{x} R \textcolor{limegreen}{y} \to \textcolor{deepskyblue}{x} R … Continue readingすること！

(3) 自然数 $N$ 上において、2つのペアの積が、偶数となる関係 $R_{4}$ $x R_{4} y \overset{def}{\Leftrightarrow} \exists n \in N s . t . x y = 2 n$ 反例: $1 R 2$ かつ $2 R 3$ だが、 $2 R 3$ など。

[(3)が成り立つ理由] 2つのペアの積が偶数になるためには、(奇数,奇数) 以外のペアであればなんでもよい。すると、(奇数,偶数) かつ (偶数,奇数) → (奇数,奇数) というパターンで、前提条件を満たし、なおかつ条件を満たさないような例（反例）を作れる。

二項関係の4つの性質

ある集合 $A$ 上の二項関係 $R$ に対して、以下の4つの重要な性質はテストに頻出なので覚えておきましょう！

(1) 反射性(反射律): $\forall x \in A, x R x$
→ ペア内の値が同じときは常に関係が成り立つ。

(2) 対称性(対称律): $\forall x \in A \forall y \in A, \forall x R y \to y R x$
→ 関係 $x R y$ が成り立つとき、ペア内の変数 $x$ , $y$ を入れ替えて $y R x$ としても常に関係が成り立つ。

(3) 反対称性: $\forall x \in A \forall y \in A, x R y \land y R x \to x = y$
→ 2つの変数 $x$ , $y$ を入れ替えても常に関係が成り立つとき、その2つの変数 $x$ , $y$ の値は常に同じである。

(4) 推移性(推移律): $\forall x \in A \forall y \in A \forall z \in A, x R y \land y R z \to x R z$
→ $x$ と $y$ の関係が成り立ち、 $y$ と $z$ の関係が成り立てば、三段論法のように $x$ と $z$ の関係が成り立つ。

おまけ1. 同値関係

離散数学の第01羽では、「同値関係 $x \equiv y$ は、2つの値 $x$ , $y$ が同じグループに属することを表す」と説明しました。

ですが、今回の二項関係の知識を使うことで、同値関係は、

反射性（反射律）
→ 同じ値同士は、必ず同値関係となること。
対称性（対称律）
→ ペア内の順番を入れ替えても、同値関係の成立／不成立は変わらないこと。
（例えば同値関係 $a \equiv b$ が成立していれば、必ず $b \equiv a$ も成立している。）
推移性（推移律）
→ 三段論法的な関係があること。

の3つを全て満たすもの、と厳密に定義できるようになります。

おまけ2. 比較可能

[述語論理を用いた定義] $\forall x \in A \forall y \in A, x R y \lor y R x$ $\forall x \in A \forall y \in A, (x, y) \in R \lor (y, x) \in R$ 意味: どんな $x$ , $y$ に対してでも、 $(x, y)$ もしくは $(y, x)$ のどちらか一方／両方に関係が成り立つ。

二項関係における比較可能とは、領域内にあるすべての値に対して、その値の "大小 " や "等しい／等しくない" が関係の成立／不成立だけで比べられるような関係です。

例えば、皆さんが日常的に使っている記号 $≦$ であれば、 $a ≦ b$ の $a$ , $b$ にどんな値を入れても、 $a$ , $b$ の大小が分かりますよね。そのため、 $≦$ には比較可能であることがわかります。

ここで、比較可能の定義の仕組みを $≦$ を用いて説明しましょう。

まず、 $x$ , $y$ の大小によって二項関係 $x ≦ y$ が

関係	$x ≦ y$	$y ≦ x$
xよりyの方が大きい	成立	不成立
xよりyの方が小さい	不成立	成立
xがyと等しい	成立	成立

この表から、

あるペア $(x, y)$ および値を入れ替えたペア $(y, x)$ のうち、どちらか片方が成立することで、大小関係が分かる
あるペア $(x, y)$ および値を入れ替えたペア $(y, x)$ のうち、両方が成立することで、等しいことが分かる

ことが分かります。

よって、領域内のどの2つの値 $x$ , $y$ を取ってきても、"大小関係" や "等しい／等しくない" かどうかを判別するためには、「どんな $x$ , $y$ に対してでも、 $(x, y)$ もしくは $(y, x)$ のどちらか一方／両方に関係が成り立つ」必要があることがわかります。

例えば、 $S = {1, 2, 3, 4}$ とします。このとき、比較可能性を満たすためには、

色なし部分は必ず成立させる
色あり部分は、同じ色がついた要素の中から少なくとも1つ成立させる

すればOKです。

(1,1)	(1,2)	(1,3)	(1,4)
(2,1)	(2,2)	(2,3)	(2,4)
(3,1)	(3,2)	(3,3)	(3,4)
(4,1)	(4,2)	(4,3)	(4,4)

例えば、

R = {(1,1),(1,2),(1,3),(1,4),(2,2),(2,3),(2,4),(3,3),(3,4),(4,4)}

は完全性を持ちます。

（色の部分が対応しています）

おまけ3. 半順序関係

※ 詳しい内容は、離散数学の第5羽にて説明します。

半順序関係とは、与えられた集合の要素の一部分において、順序付けができるような関係のことを表します。

厳密にいうと、以下の3つの関係性が成り立っている関係が半順序関係です。

反射性
反対称性
推移性

例えば、A = {翔くん, 祐希さん, 怜音くん} とし、足が速いという関係 $R$ を考えます。

翔くんは、祐希さん以上に足が速い
怜音くんは、祐希さん以上に足が速い

という関係が成立していたとき、「翔くんと祐希さんの足の速さの関係」は、上の関係から分かりますが、「翔くんと怜音くんの足の速さの関係」は、上の関係からでは分かりませんよね。

このように、与えられた要素の一部分だけが順序付けができるような関係のことを、半順序関係と呼びます。

おまけ4. 全順序関係

※ 詳しい内容は、離散数学の第5羽にて説明します。

全順序関係とは、与えられた集合の要素のどの要素を比べても、順序付けができるような関係のことを表します。

厳密にいうと、半順序関係の条件（反射性・反対称性・推移性）に加えて比較可能性が成立していることが、全順序関係が成立する条件です。

例えば、数学の世界で使われる関係 $≦$ は、どんな実数を与えても、必ずどちらが大きい（or 同じ）かが出てきますよね。

そのため、 $≦$ は実数領域上で、全順序関係を持つ二項関係ということができます。

4. 例題で確認！

では、ここからは「ある関係が反射性、対称性、反対称性、推移性を満たすかどうか」を判定するための練習として、例題を解いてみましょう！

例題1

二項関係 $R_{1}$ , $R_{2}$ が(1), (2)で示される領域上において定義されている。

(1) 領域: $S = {1, 2, 3}$ 上の関係 $R_{1}$ $R_{1} = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1)}$

(2) 領域: 0以上の整数 $N^{+} = N \cup {0}$ 上の関係 $R_{2}$ $x R_{2} y \overset{def}{\Leftrightarrow} \exists n \in N^{+} s . t . x y = n^{2}$

このとき、 $R_{1}$ , $R_{2}$ が(i)反射性、(ii)対称性、(iii)反対称性、(iv)推移性の各性質を満たすかどうか答え、満たさない場合は反例を1つ挙げなさい。

[略解1]

※ 各性質を満たす場合は〇を、満たさない場合は反例を1つ挙げている。

関係	(i) 反射性	(ii) 対称性	(iii) 反対称性	(iv) 推移性
$R_{1}$	$(2, 2) \notin R_{1}$	$(3, 2) \in R_{1}$ だが $(2, 3) \notin R_{1}$	$(1, 3) \in R_{1}$ かつ $(3, 1) \in R_{1}$ だが $1 \neq 3$	$(1, 3) \in R_{1}$ かつ $(3, 2) \in R_{1}$ だが $(1, 2) \notin R_{1}$
$R_{2}$	〇	〇	$1 R_{2} 4$ かつ $4 R_{2} 1$ だが $1 \neq 4$	$1 R_{2} 0$ かつ $0 R_{2} 2$ だが $1 {R̸}_{2} 2$

[解説1]

(1) 関係 $R_{1} = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1)}$

(1-i) [反射性] 満たさない。反例: $(2, 2) \notin R_{1}$

$S = {1, 2, 3}$ なので、 $(1, 1), (2, 2), (3, 3)$ の全てのペアで関係が成り立つ必要があるが、 $(2, 2)$ では関係が成り立っていないため、これが反例となる。

(1-ii) [対称性] 満たさない。反例: $(3, 2) \in R_{1}$ だが $(2, 3) \notin R_{1}$

関係 $R_{1}$ が成立しているペアを、色付けしてグループ分けしてみる $R_{1} = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1)}$ ※ 同じ色のグループは、元のペア $(x, y)$ と、値を入れ替えたペア $(y, x)$ の対応があることを表す。

すると、関係が成り立つペア $(3, 2)$ を入れ替えたペア $(2, 3)$ は $R_{1}$ の中に含まれておらず（＝関係 $R_{1}$ が成り立たず）、仲間外れである。よって、これがが反例となる。

(1-iii) [反対称性] 満たさない。反例: $(1, 3) \in R_{1}$ かつ $(3, 1) \in R_{1}$ だが $1 \neq 3$

先ほどの色分けしたグループ分けに着目する。すると、前提条件として、 $(1, 3) \in R_{1}$ と $(3, 1) \in R_{1}$ となっていることが分かる（共に関係を持つ）。しかし、1と3は等しくないため、これが反例となる。

(1-iv) [推移性] 満たさない。反例: $(1, 3) \in R_{1}$ かつ $(3, 2) \in R_{1}$ だが $(1, 2) \notin R_{1}$

反例を探すのが難しいが、 $(1, 3), (3, 2)$ に着目すると、 $(1, 3)$ と $(3, 2)$ は共に関係が成り立っているが、 $(1, 2)$ が $R_{1}$ にない（＝関係が成り立たない）ことがわかるだろう。よって、これが反例となる。

(2) 関係 $R_{2}$ 0以上の整数 $x$ , $y$ の積が平方数。

(2-i) [反射性] 満たす。

$t = x = y$ のとき、 $x y = t^{2}$ となるため、必ず平方数となる。

(2-ii) [対称性] 満たす。

$x R_{2} y$ → $x y$ が平方数
$y R_{2} x$ → $y x$ が平方数

ここで、 $x y = y x$ （順番を入れ替えても2つの積は変わらない）なので、 $x R_{2} y$ であれば、必ず $y R_{2} x$ も成り立つ。

よって、対称性もOK。

(2-iii) [反対称性] 満たさない。反例: $1 R_{2} 4$ かつ $4 R_{2} 1$ だが $1 \neq 4$

$x y$ が平方数になるためには、 $x = y$ である必要があると思うが、実は $x = 1$ , $y = 4$ としても、平方数になる。

ここで、(ii) より、 $x y = y x$ （順番を入れ替えても2つの積は変わらない）ので、「 $1 R_{2} 4$ かつ $4 R_{2} 1$ だが $1 \neq 4$ のような反例が出せる。」

よって、反対称性は満たさない。

(2-iv) [推移性] 満たさない。反例: $1 R_{2} 0$ かつ $0 R_{2} 2$ だが $1 {R̸}_{2} 2$

「 $x y$ が平方数」かつ「 $y z$ が平方数」だけど、「 $x z$ が平方数ではない」ような組み合わせを探せばOK。

見た目的に反例がなさそうだなと思うかもしれないが、油断するのはダメ。

反例がなさそうだなと思ったら、極端な例として0を代入するというのをやってみよう^[8]0というのは、何を掛けても0という特殊な数なので、0を入れると反例が割と出てくることがある。。
（※ 領域に0が含まれていることを確認しましょう。）

すると、以下の [前提条件] を満たすけど、 $1 {R̸}_{2} 2$ という反例を見つけられます。

[前提条件]

$1 R_{2} 0$
$0 R_{2} 2$

反例を見つけるコツ

反射性、対称性、反対称性、推移性が成り立つかどうかを考える際には、成り立つ理由を考える前に、まず身近な例で反例が見つからないかを調べる。特に0が許容されている場合には、0を代入することで反例が見つかることも多い。

関係 $x R y$ の反例は、下のようにして探すのがよい。

反射性: $x = y$ 以外のときに反例が見つかるかどうか
対称性: $x$ , $y$ を入れ替えたときの値の変化を見る
反対称性: 対称性が成り立つ場合で、 $x \neq y$ となるような $x, y$ を探す
推移性: $x R y$ と $y R z$ が成り立つのに $x R z$ で成り立たないものを調べる。反射性が成り立たない場合は、 $x R y$ と $y R x$ で成り立つのに $x R x$ となるようなものを探すのもあり。

5. 二項関係と閉包 [応用]

閉包とは「（反射性、対称性、推移性などの条件を満たしていない）二項関係に対して、条件を満たすためには、最低限の要素としてどんな要素を追加すれば良いか」を追加した後の二項関係で表したものです。

ここで、閉包の中でも、試験によく出てくる閉包はこの3つです。

反射閉包 $r (R)$
→ 関係 $R$ に最低限の要素を追加し、反射性を満たすようにした関係
対称閉包 $s (R)$
→ 関係 $R$ に最低限の要素を追加し、対称性を満たすようにした関係
推移閉包 $t (R)$
→ 関係 $R$ に最低限の要素を追加し、推移性を満たすようにした関係

閉包の求め方については、実際に例題（関係は例題1の $R_{1}$ と同じ）で確認していきましょう。

例題2

領域: $S = {1, 2, 3}$ 上の関係 $R$ $R = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1)}$ が定義されている。

(1) 反射閉包 $r (R)$ を求めなさい。
(2) 対称閉包 $s (R)$ を求めなさい。
(3) 推移閉包 $t (R)$ を求めなさい。

[解答2]

(1) $r (R) = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1), (2, 2), (3, 3)}$

(2) $s (R) = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1), (2, 3)}$

(3) $t (R) = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1), (1, 2)}$

※ ピンク色の要素が、関係を成り立たせるために最低限補った要素である。

[解説2]

(1) 反射閉包 $r (R)$

反射性を満たすためには、領域 $S = {1, 2, 3}$ 上において、値が同じペア (1,1), (2,2), (3,3) で関係が成り立つ必要がありましたね。

しかし、与えられた $R$ は、ペア (2,2) と (3,3) が不足しています。なので、(2,2), (3,3) を補った関係が、反射閉包 $r (R)$ となります。 $\begin{aligned} r (R) & = R \cup {(2, 2), (3, 3)} \\ = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1), (2, 2), (3, 3)} \end{aligned}$ ※ 赤色の要素は、反射性を満たすために必要な要素を表す。

(2) 対称閉包 $s (R)$

対称性を満たすためには、「関係が成立しているペア $(x, y)$ を入れ替えて $(y, x)$ としても、必ず関係が成立している」必要があります。

ここで、「元のペア $(x, y)$ と、入れ替えたペア $(y, x)$ 」を1つの組として、関係 $R$ の要素を、色ごとに分けてみましょう。 $R = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1)}$ すると、 $(3, 2)$ だけが、入れ替えたペア $(2, 3)$ の関係が成り立っておらず、仲間外れです。

なので、元の関係 $R$ に $(2, 3)$ を補ってあげて、仲間外れを解消してあげれば、対称閉包が求まります。 $\begin{aligned} s (R) & = R \cup {(2, 3)} \\ = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1), (2, 3)} \end{aligned}$

(3) 推移閉包 $t (R)$

推移閉包は、補い漏れが発生しやすいため、慎重に見ていきましょう。

補い漏れを防ぐためには、関係が成立しているあるペアの右側の値 $(x, y$ とあるペアの左側の値 $(y, z$ が等しく、2つの値が等しくないペアを全て列挙するのがおすすめです。

今回の場合は、次の3つを確認します。

$(1, 3)$ と $(3, 2) がともに関係成立 \to \((1, 2)$ が $R$ にあるかを確認。
→ ないため、 $(1, 2)$ を補う必要あり。
$(1, 3)$ と $(3, 1) がともに関係成立 \to \((1, 1)$ が $R$ にあるかを確認。
→ あるため、何もしなくてOK。
$(3, 1)$ と $(1, 3) がともに関係成立 \to \((3, 3)$ が $R$ にあるかを確認。
→ あるため、何もしなくてOK。

よって、推移閉包は $(1, 2)$ を補い、 $\begin{aligned} t (R) & = R \cup (1, 2) \\ = {(1, 3), (3, 3), (3, 2), (1, 1), (3, 1), (1, 2)} \end{aligned}$ と求まります。

6. 二項関係の数え上げ [応用]

最後に、今回お勉強した二項関係の知識を使って、少し難易度の高い数え上げにチャレンジしてみましょう！

例題3

集合 $A = {1, 2, 3}$ がある。(1)～(5)の問いに答えなさい。

(1) 直積集合 $A \times A$ の要素数を答えなさい。
(2) 集合 $A$ の二項関係の総数を答えなさい。
(3) 集合 $A$ の二項関係のうち、反射性を満たす二項関係の総数を答えなさい。
(4) 集合 $A$ の二項関係のうち、対称性を満たす二項関係の総数を答えなさい。
(5) 集合 $A$ の二項関係のうち、反射性、対称性をともに満たす二項関係の総数を答えなさい。

[解答3]

(1) 9
(2) 512 [ $2^{9}$ ]
(3) 64 [ $2^{6}$ ]
(4) 64 [ $2^{6}$ ]
(5) 8 [ $2^{3}$ ]

[解説3]

(1) 答え: 9個

直積集合の要素数を数えるときは、こんな感じに表を書きましょう。

A ＼ A	1	2	3
1	(1,1)	(1,2)	(1,3)
2	(2,1)	(2,2)	(2,3)
3	(3,1)	(3,2)	(3,3)

すると、直観的に 3×3 = 9 だな、というのが分かります！

(2) 答え: 512通り

二項関係 $R$ は、直積集合の要素 $A \times A$ の中から、何個か要素を取り出して作るものでしたね。

つまり、 $R$ は $A \times A$ の部分集合 $R \subseteq A \times A$ という関係式が成り立ちます。

よって、二項関係 $R$ の総数は、「 $A \times A$ の各要素に対して、選ぶ／選ばないの2通りを組み合わせた数」だけ存在します。

ここで、 $A \times A$ の要素数は(1)より 9 だったため、二項関係の総数は、 $\underset{9 個分}{\underset{⏟}{2 \times 2 \times \dots \times 2}} = 512$ と求められます。

A ＼ A	1	2	3
1	(1,1)	(1,2)	(1,3)
2	(2,1)	(2,2)	(2,3)
3	(3,1)	(3,2)	(3,3)

(3) 答え: 64通り

二項関係 $R$ において反射性が成り立つためには、「領域内において、値が等しいペアは必ず関係が成立する」必要があります。

今回の領域は、 $A = {1, 2, 3}$ なので、 $(1, 1), (2, 2), (3, 3)$ の3ペアは必ず関係が成立している必要があります。

一方、その他のペア（9 - 3 = 6ペア）は、関係が成り立っていようが成り立っていなかろうが、反射性を満たすか否かには関係ありません。

そのため、6ペアに対して、関係を成立させるかさせないかの2通りを組み合わせた数 $\underset{6 個分}{\underset{⏟}{2 \times 2 \times \dots \times 2}} = 64$ だけ、反射性が成立する二項関係 $R$ が存在します。

A ＼ A	1	2	3
1	(1,1)	(1,2)	(1,3)
2	(2,1)	(2,2)	(2,3)
3	(3,1)	(3,2)	(3,3)

※ 赤い関係 → 必ず成立する必要あり
※ それ以外 → 成立していてもいなくてもどちらでもOK

(4) 答え: 64通り

二項関係 $R$ において対称性が成り立つためには、「関係が成立しているペア $(x, y)$ を入れ替えて $(y, x)$ としても、必ず関係が成立している」必要があります。

ただし、(1,1), (2,2), (3,3) のように、値が等しいペアについては、ペアの (x,y) の値を入れ替えて (y,x) の形にしても (1,1), (2,2), (3,3) と変わらないため、単独で成立している／成立していないを考えても問題ありません。

一方、値が異なる残りの6ペアについては、ペア $(x, y)$ と、入れ替えたペア $(y, x)$ の関係は、共に成立している／成立していないのどちらかである必要があるため、「元のペア $(x, y)$ と、入れ替えたペア $(y, x)$ 」は、組単位で成立している／していないを考える必要があります。

よって今回の場合、6ペアを2ペアごとに1組とするため、3組について、成立している／成立していないを考えることができます。

※ 本当に3ペアかどうか、値が等しくない ( $x \neq y$ ) ペアについて、 $(x, y)$ と、入れ替えたペア $(y, x)$ ごとにグループで色分けしてみましょう。

A ＼ A	1	2	3
1	(1,1)	(1,2)	(1,3)
2	(2,1)	(2,2)	(2,3)
3	(3,1)	(3,2)	(3,3)

※ 色ありの関係 → 同じ色ごとに、成立している／成立していない、を考える [3組]
※ 色なしの関係 → 成立している／成立していないを単独で考えてOK [3ペア]

よって、対称性を満たす二項関係は、以下をすべて組み合わせた数だけ存在します。

(1,2) と (2,1) の組の関係が共に成立しているか否かの2通り
(1,3) と (3,2) の組の関係が共に成立しているか否かの2通り
(2,3) と (3,2) の組の関係が共に成立しているか否かの2通り
(1,1), (2,2), (3,3) それぞれのペアの関係が成立しているか否かの2通り

二項関係 $R$ において対称性が成り立つような関係の数は $2 \times 2 \times 2 \times \underset{3 ペア分}{\underset{⏟}{2 \times 2 \times 2}} = 64$ と求められます。

(5) 答え: 8通り

二項関係 $R$ において対称性と反射性を成り立たせるためには、まず、反射性を成り立たせるために「領域内において、値が等しいペアは必ず関係が成立する」必要がありますね。

そのため、今回の例だと (1,1), (2,2), (3,3) は常に関係が成立している必要があります。

さらに、対称性を成り立たせるためには、あるペア $(x, y)$ と、入れ替えたペア $(y, x)$ の関係は、共に成立している／成立していないのどちらかである必要があるため、「元のペア $(x, y)$ と、入れ替えたペア $(y, x)$ 」は組単位で成立している／していないを考える必要があります。

そのため、反射性・対称性をともに満たすような二項関係の総数は、

(1,2) と (2,1) の組の関係が共に成立しているか否かの2通り
(1,3) と (3,2) の組の関係が共に成立しているか否かの2通り
(2,3) と (3,2) の組の関係が共に成立しているか否かの2通り

を組み合わせた数だけあるため、 $2 \times 2 \times 2 = 8$ 通りだけ存在します。

「元のペア $(x, y)$ と、入れ替えたペア $(y, x)$ 」は組単位で成立している／していないを考える櫃ようがあります。

7. 確認テスト

最後に、今回の記事や動画で勉強した内容が、理解できているかどうかをどうかを確認するための小テストを作りました！

理解度確認に是非チャレンジしてみてください！

※ 回答フォームに入力後、自動採点 & 自動解説表示が行われます。

問題ダウンロードはこちら！！

回答フォームはこちら！！

8. さいごに

今回は、離散数学に出てくる二項関係について、色々お勉強していきました。

反射性、対称性、反対称性、推移性は離散数学のテストによく出てくるとても重要な概念なので、理解をしておきましょう！

次回は、半順序関係についてお勉強していきましょう。

注釈[+]

注釈
↑1	直積集合 $A \times B$ は、集合 $A$ , $B$ から1つずつ要素を取り出して、( $A$ から取り出した要素, $B$ から取り出した要素 ) とペアの形にしたときに、できるペアをすべて集めて要素とした集合を表します。
↑2	$\exists n \in N s . t . x + y = 2 n$ を日本語に直すと「整数 $x + y$ の和が、ある2の倍数の値 (2,4,6,8, …) となる。」となりますね。
↑3	条件A → 条件B、を偽と言うためには、条件Aが成立しているにも関わらず、条件Bが成立していないことを言う必要がある。しかし、その条件Ａを満たす例がないため、「条件A → 条件Ｂ」を偽と言うことは出来ない。よって、条件Aを満たす例が1つもないとき、「条件A → 条件Ｂ」は必ず真となってしまう。
↑4	(1,1), (2,2), (3,3) はすべて2つの値が同じペアなため、単独で対称性の条件を満たしますね。さらに、3つのペアはともに、反対称性「元のペアと、値を入れ替えたペアが共に関係が成りたっている」の前提条件を満たしており、なおかつ、どのペアも2つの値が同じになっていますね。なので、反対称性の条件も満たしています。
↑5	偶数 + 偶数 = 偶数，奇数 + 奇数 = 偶数，偶数 + 奇数 = 奇数，奇数 + 偶数 = 奇数
↑6	2つの値が等しいペアに着目すると、 $x R x \land x R y \to x R y$ $x R y \land y R y \to y R y$ となり、常に正しい式になってしまうため。
↑7	偶数 × 偶数 = 偶数，奇数 × 奇数 = 奇数，偶数 × 奇数 = 偶数，奇数 × 偶数 = 偶数
↑8	0というのは、何を掛けても0という特殊な数なので、0を入れると反例が割と出てくることがある。