スポンサードリンク
こんにちは、ももやまです。
今回はグラフの点、辺に関する連結度についてまとめていきたいと思います。
前回の離散数学(第15羽)の記事はこちら!
最大フロー、最小カットを求める方法についてまとめています!
目次
スポンサードリンク
0.復習(グラフの連結とは)
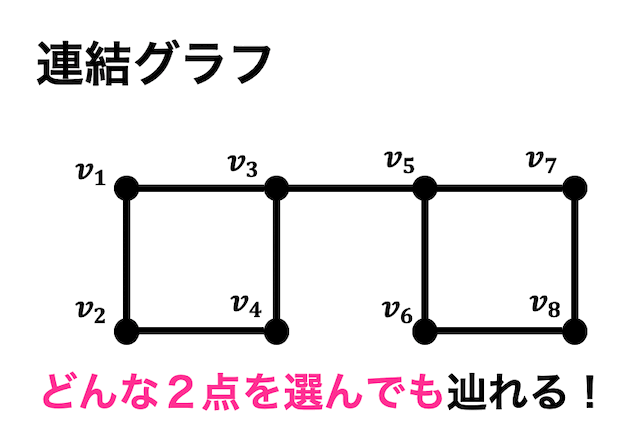
どの2点の間にも道が存在するようなグラフを連結グラフと呼びます。
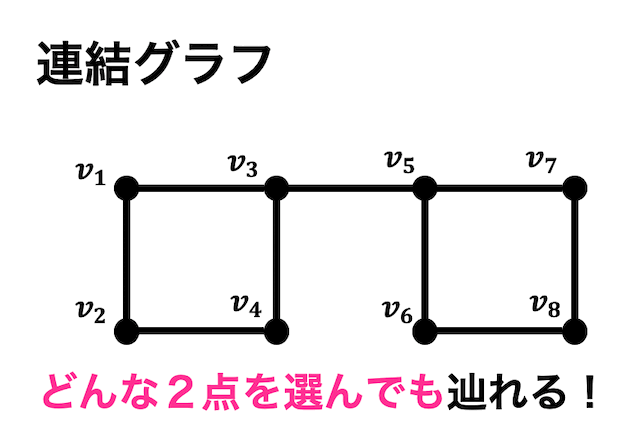
例えば上のグラフは \( v_1 \) から \( v_7 \) のどの点を選んでも必ず道が1つ以上存在しますね。なので連結グラフとなります。
また、連結ではないグラフのことを非連結グラフと呼びます。
グラフの連結についてはこちらの記事にまとめているので、もし忘れてしまったのであればこちらの記事をご覧ください。
スポンサードリンク
1.点に関する連結の強さ
(1) k-連結グラフ(k-頂点連結グラフ)
ある連結グラフから頂点を \( k \) より少ない数(\( k - 1 \) 個)取り除いても連結な(非連結にならない)グラフのことをk-連結グラフと呼びます。
下のグラフを例に考えてみましょう。
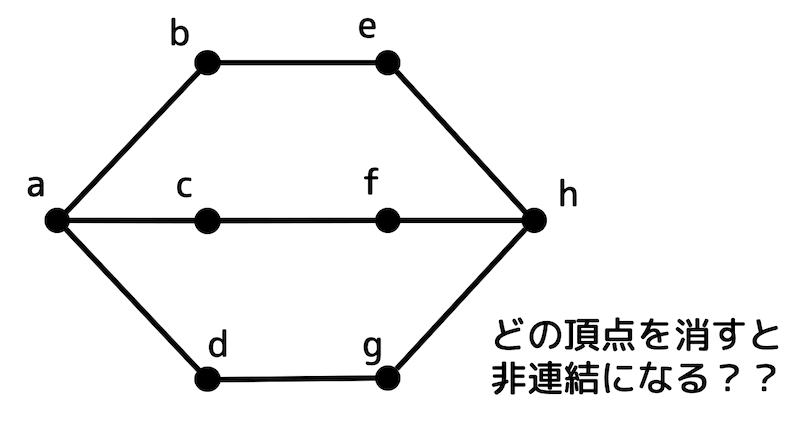
見た感じ、1個頂点を取っただけではどのグラフも連結そうですね…*1。
1個取り除いても連結なので、このグラフは2-連結グラフですね。
なので \( b, h \) と2つ点を取ってみましょう。
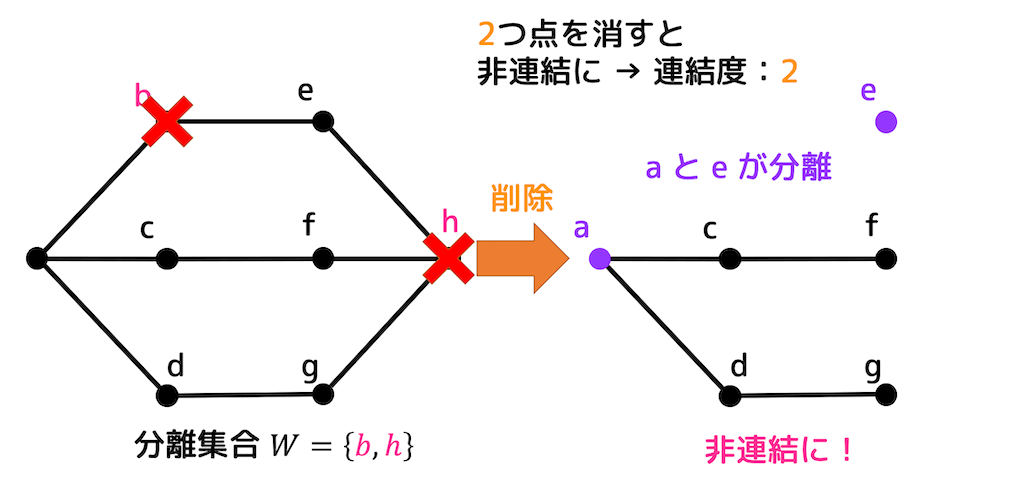
すると、\( e \) が分離されて非連結になりましたね。
2個の点を取ってしまうと連結ではなくなる可能性があるので3-連結グラフではありませんね。なので2-連結グラフ止まりです。
あるグラフから何個か( \( k - 1 \) 個 )点を取り除いても必ず連結グラフであれば、より少ない数( \( k - 2 \) 個 )取り除いても必ず連結グラフですよね。
なので、k-連結グラフであるものは (k-1)-連結グラフとなります*2。
ある連結グラフ \( G \) の \( k \) より少ない数、つまりどの \( k-1 \) 点を削除しても連結グラフであるとき、k-連結グラフと呼ぶ。
また、連結グラフであれば必ず1-連結グラフである。
(2) 連結度(点連結度)
k-連結グラフ \( G \) の \( k \) の最大値のことを連結度(点連結度)と呼び、\( \kappa ( x ) \) で表します。
つまり、とある連結グラフを非連結にするために取り除く必要のある頂点の数が連結度となります。
先程のグラフの場合、2個の頂点を取り除くことで非連結にできますよね。なので連結度は2となります。
連結度はグラフの連結の強さを表すものと思っていただけたらOKです。
(3) 分離集合(点分離集合)
連結グラフを非連結グラフにするために消した点の集合 \( W \) を分離集合(点分離集合)と呼びます。
上の例の場合、非連結にするために点 \( b \), \( h \) の2点を消したので、分離集合は\[
W = \{ b, h \}
\]となります。
ある連結グラフ \( G \) を非連結にするために消す必要のある点の最小数のことを連結度(点連結度)と呼ぶ。
また、非連結にするために消した点の集合 \( W \) のことを分離集合と呼ぶ。
スポンサードリンク
2.辺に関する連結の強さ
1では点に関する連結の強さについてやっていきましたね。
辺についても説明していきましょう。
(1) k-辺連結グラフ(k-頂点連結グラフ)
ある連結グラフから辺を \( k \) より少ない数(\( k - 1 \) 個)取り除いても連結な(非連結にならない)グラフのことをk-辺連結グラフと呼びます。
点のときと同じグラフを例に考えてみましょう。

見た感じ、1個辺を取っただけではどのグラフも連結そうですね…*3。
1辺取り除いても連結なので、このグラフは2-辺連結グラフですね。
なので2辺を取ってみましょう。
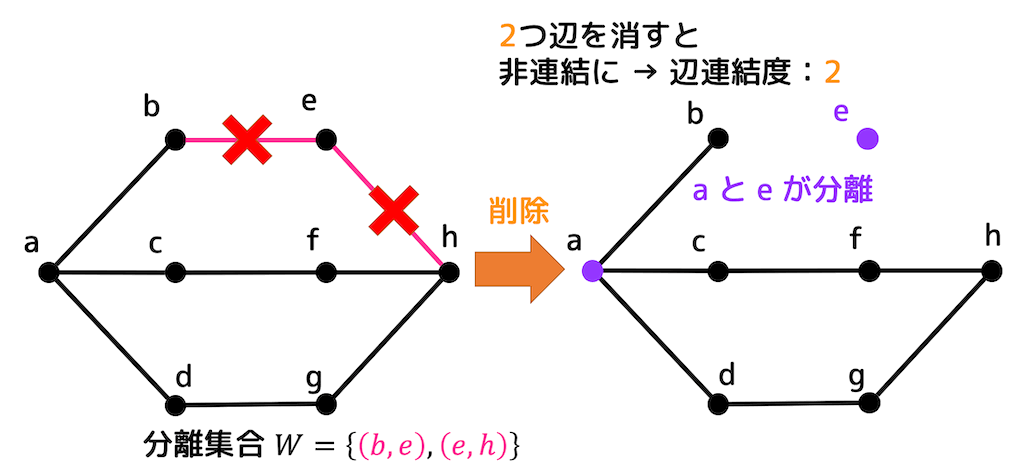
すると、\( e \) が分離されて非連結になりましたね。
2個の辺を取ってしまうと連結ではなくなる可能性があるので3-辺連結グラフではありませんね。なので2-辺連結グラフ止まりです。
k-連結グラフと同様にあるグラフから何個か( \( k - 1 \) 個 )辺を取り除いても必ず連結グラフであれば、より少ない数( \( k - 2 \) 個 )取り除いても必ず連結グラフですよね。
なので、k-辺連結グラフであるものは (k-1)-辺連結グラフとなります*4。
ある連結グラフ \( G \) の \( k \) より少ない数、つまりどの \( k-1 \) 辺を削除しても連結グラフであるとき、k-辺連結グラフと呼ぶ。
また、連結グラフであれば必ず1-辺連結グラフである。
(2) 辺連結度
k-辺連結グラフ \( G \) の \( k \) の最大値のことを辺連結度と呼び、\( \lambda ( G ) \) で表します。
つまり、とある連結グラフを非連結にするために取り除く必要のある辺の数が辺連結度となります。
先程のグラフの場合、2個の辺を取り除くことで非連結にできますよね。なので辺連結度は2となります。
辺連結度も(点)連結度と同じグラフの連結の強さを表すものと思っていただけたらOKです。
(3) 分離集合(辺分離集合)
連結グラフを非連結グラフにするために消した辺の集合 \( W \) を分離集合と呼びます。
上の例の場合、非連結にするために辺 \( (b,e) \), \( (e,h) \) の2辺を消したので、分離集合は\[
W = \{ (b,e) , (e,h) \}
\]となります。
ある連結グラフ \( G \) を非連結にするために消す必要のある辺の最小数のことを辺連結度と呼ぶ。
また、非連結にするために消した辺の集合 \( W \) のことを分離集合(辺分離集合)と呼ぶ。
3.連結度・辺連結度・最小次数の関係
あるグラフ \( G \) における連結度 \( \kappa (G) \)、辺連結度 \( \lambda (G) \)、最小次数 \( \delta (G) \) には\[
\kappa (G) \leqq \lambda(G) \leqq \delta (G)
\]という関係式が常に成立します。
[簡単な理由]
下の図のように、最小次数の点の周りの辺をすべて消すと最小次数の点は孤立点となり、非連結になりますよね。
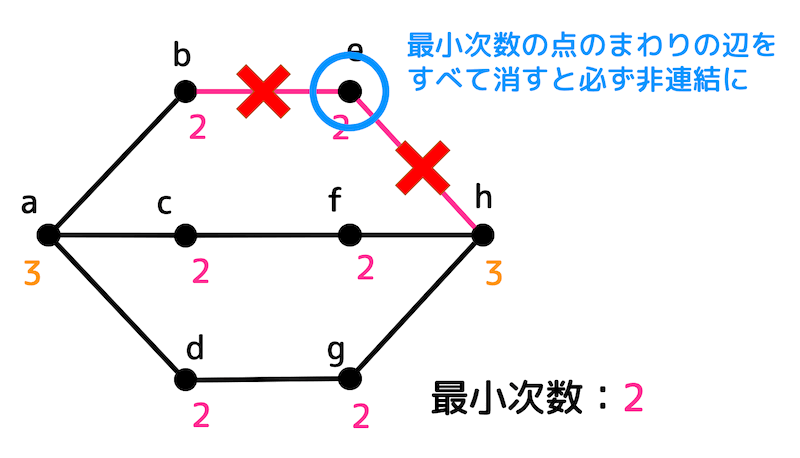
なので、辺連結度は必ず最小次数以下となります。
また、点連結度が辺連結度以下になるイメージですが*5、辺を消した場合、必ず消した1辺以外には影響が出ませんが、点を消した場合、辺を消した場合に比べてより多くの辺に影響がでますよね。
(点を消すと消した点の周りの辺が消えるので、1辺だけでなく2辺以上消える可能性もある)
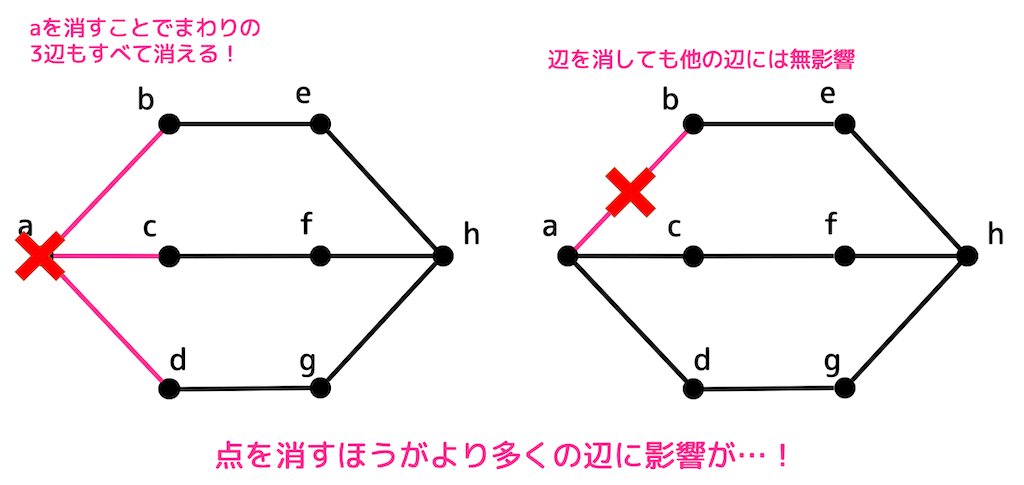
なので点のほうがより少ない数でグラフを非連結にすることができるのです。
4.橋・カット点(関節点)
(1) 関節点(カット点)
あるグラフ \( G \) にある点のうち、削除すると連結成分の数が増える点のことを関節点(カット点)と呼びます。
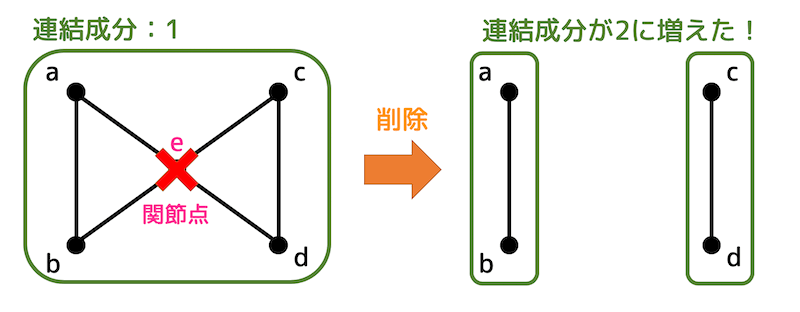
例えば、上のグラフの場合、点 \( e \) を削除すると連結成分が1つ増えますね。なので、点 \( e \) は関節点となりますね。
(2) 橋(橋辺)
あるグラフ \( G \) にある辺のうち、削除すると連結成分の数が増える辺のことを橋(橋辺)と呼びます。
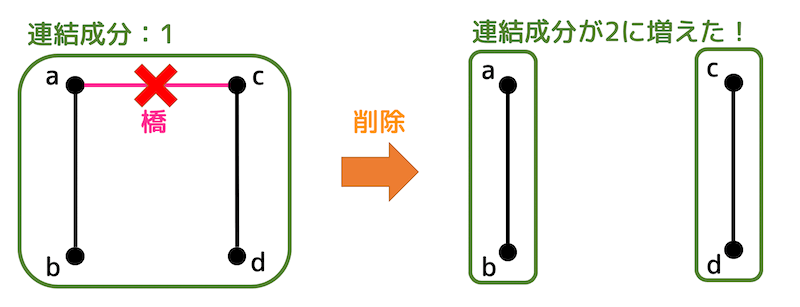
例えば、上のグラフの場合、\( a \) と \( c \) を結んでいる辺 \( (a,c) \) を削除すると連結成分が1つ増えますね。なので、辺 \( (a,c) \) は橋ですね。
削除すると連結成分が増える点のことを関節点、削除すると連結成分が増える辺のことを橋と呼ぶ。
もともと非連結なグラフであっても関節点・橋は存在するので注意しましょう。
5.点素・辺素
点素・辺素はともに2本(以上)の道に対する関係を表します。
(1) 点素(内素)
2本の道が始点と終点以外で同じ点を通っていないとき互いに点素(内素)であるといいます。
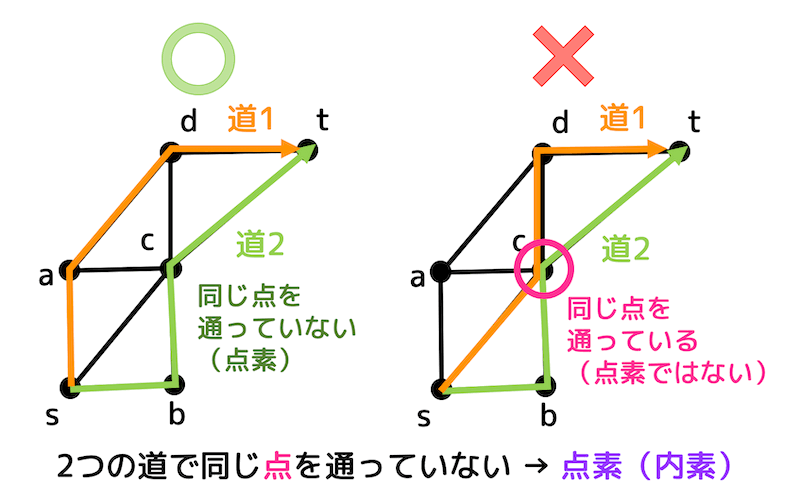
上の2つのグラフは始点 \( s \) から終点 \( t \) までの道を表しています。
左側のグラフは \( s \), \( t \) 以外で同じ点を通っていませんね。なので互いに点素です。
一方右側のグラフは \( s \), \( t \) 以外にも点 \( c \) を通っていますね。なので互いに点素ではありません。
(2) 辺素
2本の道が同じ辺を通っていないとき互いに辺素(辺素)であるといいます。
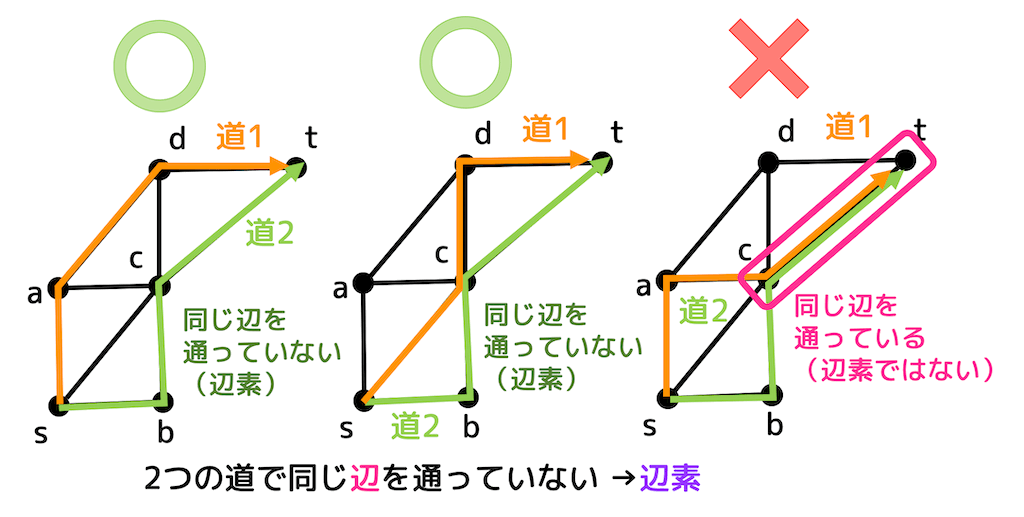
上の3つのグラフは始点 \( s \) から終点 \( t \) までの道を表しています。
左側のグラフは同じ辺を通っていませんね。なので互いに辺素です。
真ん中のグラフは同じ点 \( c \) を通っていますが同じ辺は取っていませんね。なので左のグラフと同じように互いに辺素です。
一方右側のグラフは同じ辺 \( (c,t) \) を通っているので互いに点素ではありません。
2本以上の道においてスタート点 \( s \), ゴール点 \( t \) 以外に同じ点を通っていないような道のことを互いに点素と呼ぶ。
また、2本以上の道において同じ辺を通っていないような道のことを互いに辺素と呼ぶ。
6.メンガーの定理
(1) 2点を分離するための最小分離点数
2点 \( s \), \( t \) を分離するために消す必要がある点の最小数は、\( s \), \( t \) 間の点素な道の数に等しくなります。
また、そのとき*6の分離集合 \( W \) はそれぞれの道の中から(\( s \), \( t \) 以外の)1点ずつ選んだ点集合から構成されます。この分離集合のことを最小分離集合と呼びます。
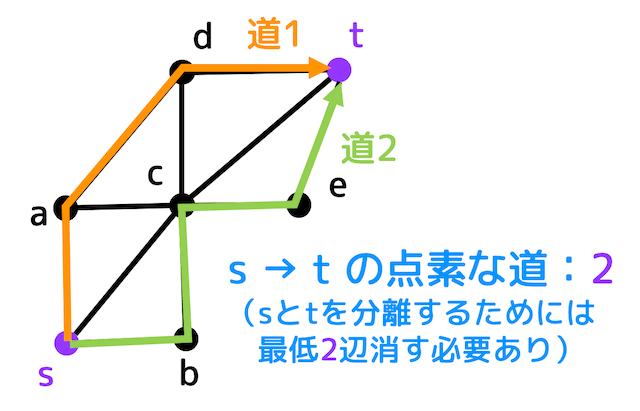
[訂正]
最低2辺 → 最低2点、です。申し訳ございません。
例えば、上のようなグラフの場合、\( s,t \) 間の点素な道は2つ存在します。
なので、\( s \), \( t \) を分離するために最低2点を消す必要があることがわかります。
また、2点の選び方としては、例えば道1から1つ (a)、道2から1つ (c) 選べばいいので、最小分離集合 \( W \) は \( W = \{a,c\} \) となります。
2点 \( s \), \( t \) を分離するために消す必要のある点の数は、\( s \), \( t \) 間に存在する点素な道の数に等しい。
また、そのとき消す必要のある点はそれぞれの点素な道から1つずつ選ぶ方法が存在する。
(2) 2点を分離するための最小分離辺数
2点 \( s \), \( t \) を分離するために消す必要がある辺の最小数は、\( s \), \( t \) 間の辺素な道の数に等しくなります。
また、そのときの分離集合 \( W \) はそれぞれの道の中から1辺ずつ選んだ辺集合から構成されます。この分離集合のことを最小分離集合(最小辺分離集合)と呼びます。
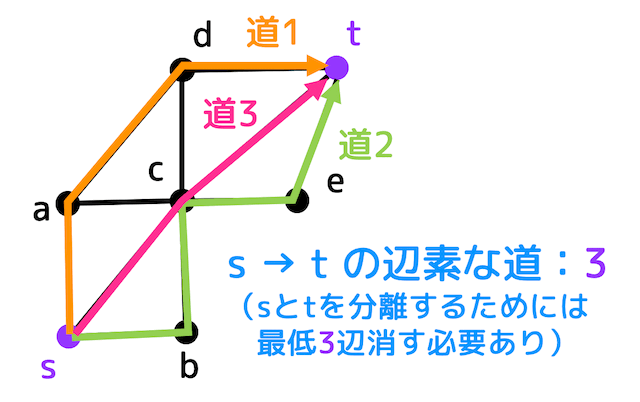
例えば、上のようなグラフの場合、\( s,t \) 間の辺素な道は3つ存在します。
なので、\( s \), \( t \) を分離するために最低3辺を消す必要があることがわかります。
また、3点の選び方としては、例えば道1から1つ (a,d)、道2から1つ (b,c)、道3から1つ (c,t) 選べばいいので、最小分離集合 \( W \) は \( W = \{ (a,d), (b,c), (c,t) \} \) となります。
2点 \( s \), \( t \) を分離するために消す必要のある辺の数は、\( s \), \( t \) 間に存在する辺素な道の数に等しい。
また、そのとき消す必要のある辺はそれぞれの辺素な道から1つずつ選べばよい。
7.メンガーの定理の応用
先程のメンガーの定理を応用することで \( s,t \) 間だけでなく、グラフ全体の連結度、辺連結度も辺素・内素な道の数から求めることができます。
(1) 点連結度と道
点連結度は、あるグラフを非連結にするために消す必要のある点の最小数を表していましたね。
メンガーの定理を応用すると、点連結度は、あるグラフにおける2点間の点素な道の数のうち最も小さいものが点連結度となりますね。
(あるグラフの点 \( s,t \) が分離されると当然グラフは非連結になりますよね。なので、ある2点間の中で最も「分離するために消す必要のある点の数」が少ないものがそのまま点連結度となります。)
(2) 辺連結度と道
辺連結度は、あるグラフを非連結にするために消す必要のある辺の最小数を表していましたね。
同じようにメンガーの定理を応用すると、辺連結度は、あるグラフにおける2点間の辺素な道の数のうち最も小さいものが辺連結度となりますね。
(あるグラフの点 \( s,t \) が分離されると当然グラフは非連結になりますよね。なので、ある2点間の中で最も「分離するために消す必要のある辺の数」が少ないものがそのまま辺連結度となります。)
グラフ \( G \) のあらゆる2点間の中で、
- 最小分離点数が最も少ないものが点連結度
- 最小分離辺数が最も少ないものが辺連結度
となる。
8.練習問題
では、2問ほど練習してみましょう。
練習1
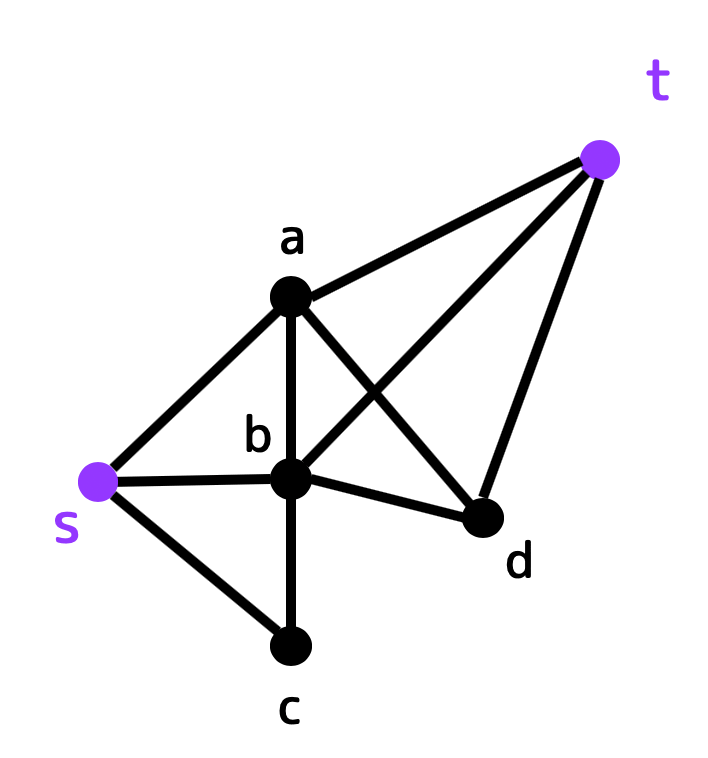
つぎのグラフ \( G \) について、(1), (2)の問いに答えなさい。
(1) 点 \( s \) と点 \( t \) を分離するために消す必要な点の個数およびそのときの最小分離集合を求めなさい。
(2) 点 \( s \) と点 \( t \) を分離するために消す必要な辺の個数およびそのときの最小分離集合を求めなさい。
練習2
つぎのグラフ \( G \) について、(1)〜(3)の問いに答えなさい。
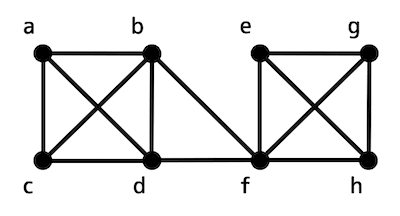
(1) グラフ \( G \) の最小次数 \( \delta(G) \) を求めなさい。
(2) グラフ \( G \) の点連結度 \( \kappa(G) \) を求めなさい。
(3) グラフ \( G \) の辺連結度 \( \lambda(G) \) を求めなさい。
9.練習問題の答え
解答1
(1)
s-t間の点素な道は、下の合計2個となる。
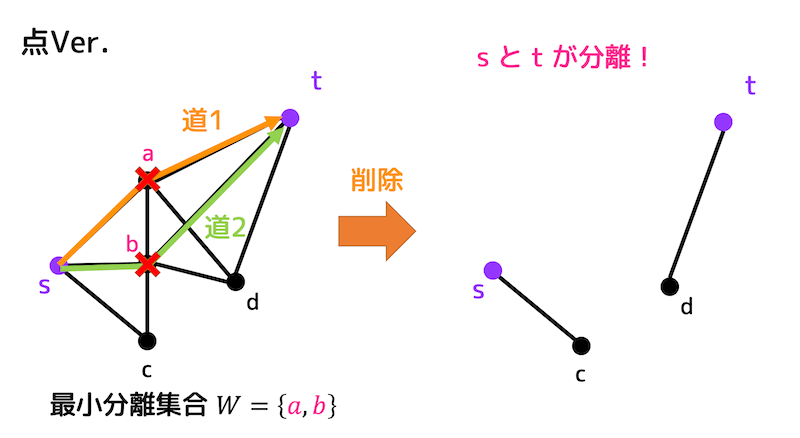
なので、\( s \), \( t \) を分離するためには最低2点を消す必要がある。
また、最小分離集合 \( W \) は道1から \( a \)、道2から \( b \) を選ぶことで \( W = \{a, b\} \) となる。
解答2
(2)
s-t間の辺素な道は、下の合計3個となる。
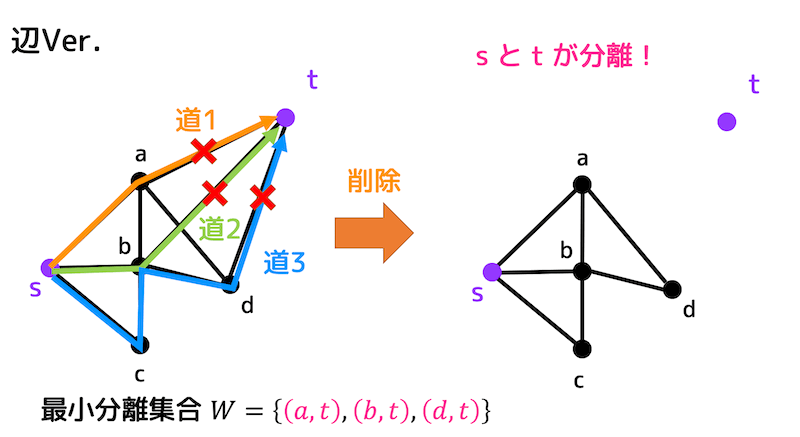
なので、\( s \), \( t \) を分離するためには最低3辺を消す必要がある。
また、最小分離集合 \( W \) は道1から \( (a,t) \)、道2から \( (b,t) \)、道3から \( (d,t) \) を選ぶことで \[ W = \{ (a,t), (b,t), (d,t) \} \] となる。
解答2
(1)
それぞれの点の次数は下のようになる。
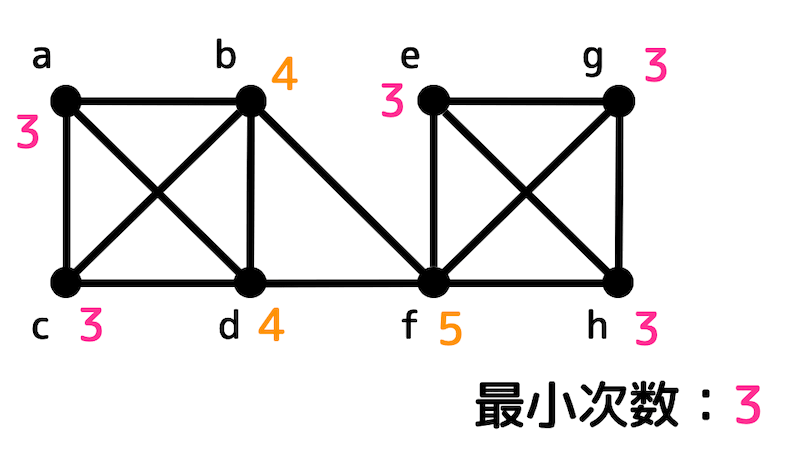
よって最小次数は3となる。
(2)
例えば点 \( d \), \( e \) を分離することを考える。
点 \( d \) から点 \( e \) への点素な道は、図のように1つしか存在しない。
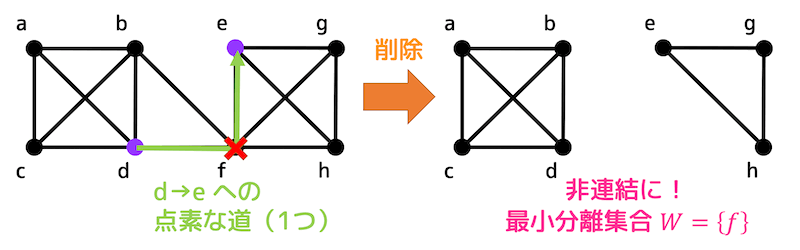
よって、d-e道の間の点 \( f \) を削除することで点 \( d \) と点 \( e \) を分離することができる。
点 \( d,e \) が分離されるということは、当然グラフは非連結となる。なので点連結度は1となる。
(3)
(2)と同じように点 \( d \), \( e \) を分離することを考える。
点 \( d \) から点 \( e \) への辺素な道は、図のように2つ存在する。
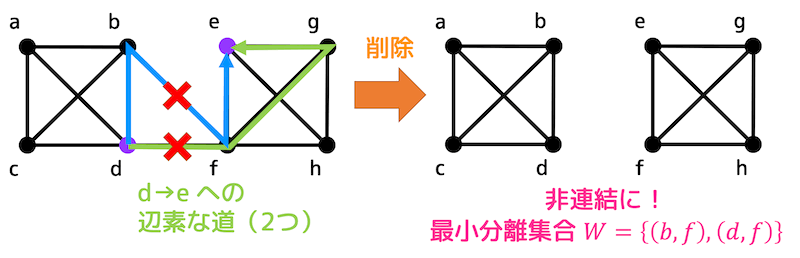
よって、d-e道の間の辺 \( (b,f) \) と辺 \( (d,f) \) の2つを削除することで点 \( d \) と点 \( e \) を分離することができる。
点 \( d,e \) が分離されるということは、当然グラフは非連結となる。なので辺連結度は2となる。
10.さいごに
今回はグラフの点、辺に関する連結度についてまとめていきました。
連結度は、あるネットワークや道路などが壊れてもどれくらい連結性を維持できるか、つまりネットワークの故障に対する強さを表す重要な項目の1つとなります。
次回は「2人組を作る際にできるだけ多くのペアを作る方法」や「できるだけ多くのカップルを組むためにはどのようにカップルを組めばいいのか」などを離散数学(グラフ理論)的に説明していきたいと思います。
関連広告・スポンサードリンク