スポンサードリンク
こんにちは、ももやまです。
今回は離散数学・グラフ理論におけるマッチングについてまとめていきたいと思います。
マッチングを使うことで例えばこのような問題を解くことができます。
A君〜F君はとある授業で2人組を組むことになった。
A君〜F君の友達関係は下のようになっている。
- A君とB君は仲良し
- A君とE君は仲良し
- A君とF君は仲良し
- B君とC君は仲良し
- B君とE君は仲良し
- C君とD君は仲良し
- C君とE君は仲良し
- E君とF君は仲良し
このとき、仲良しの人同士で2人組を組むことはできますか? また、できる場合はどのように2人組を組めばいいか答えなさい。
前回の記事(第16羽)はこちら!
グラフの連結性や連結度についてまとめています!
目次
スポンサードリンク
1.グラフ理論におけるマッチングとは
(1) マッチングとは
皆さんは「マッチング」という言葉を聞いたことはありますか? おそらくどこかしらで聞いたことがある人が多いかと思います。
最近は「マッチングアプリ」*1なんてものも流行ってますよね。
離散数学、グラフ理論におけるマッチングとは、2つの頂点を1本の辺で結んだ部分グラフを表します。
実世界の場合、辺で結ばれた点(人)同士がカップルであったりペア(2人組)であったりします。
しかし、マッチングでは1つの頂点に結ぶことができる辺は1つまでで、2つ以上を結ぶことはできません。
実世界でも2人組を2つ掛け持ちすることや2人以上の人とお付き合いすることはできませんよね*2。
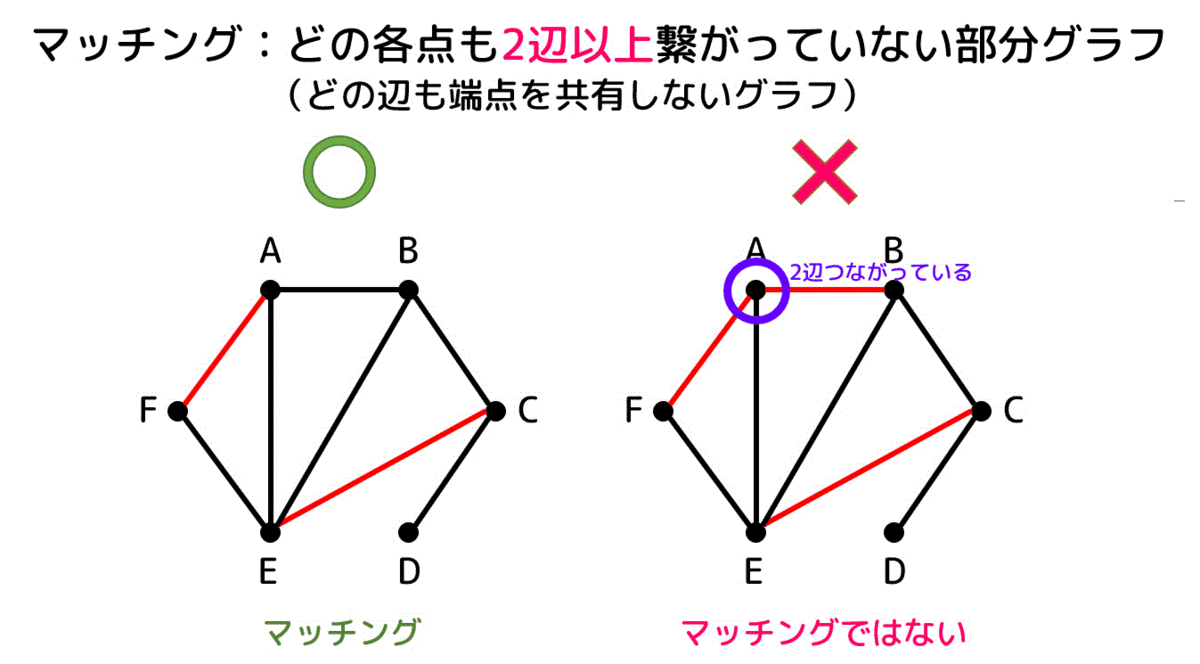
まずはマッチングの例をみてみましょう。
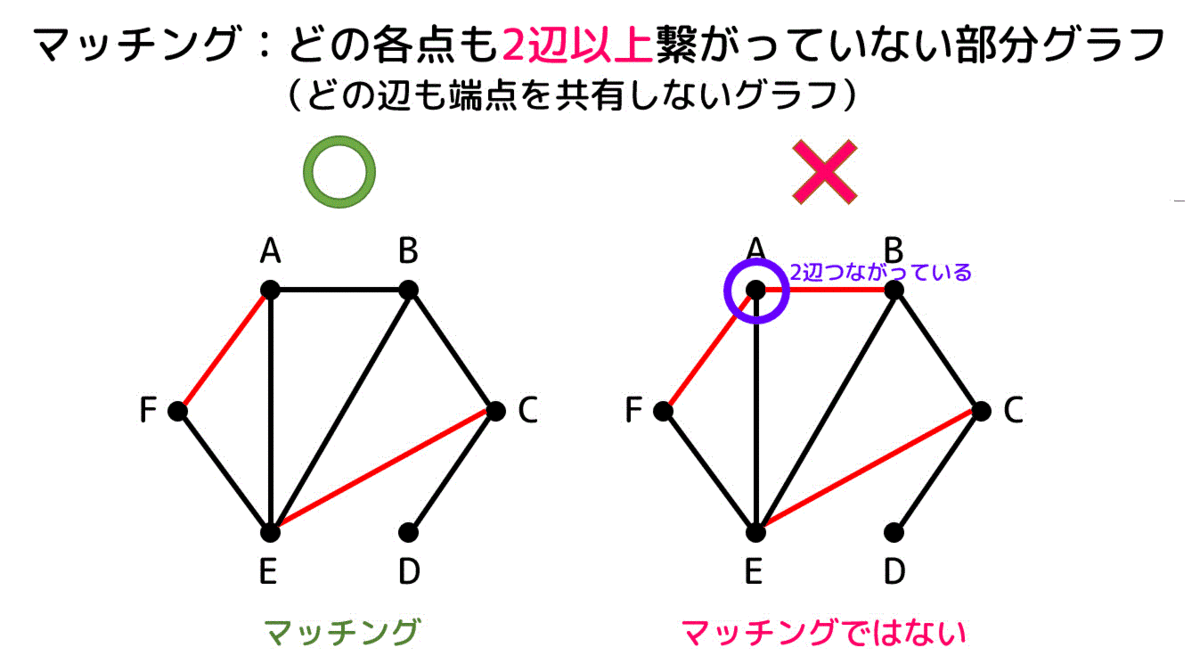
グラフの赤色の辺がマッチング(ペア)を表します(以後共通)。
左側のグラフは2辺以上つながっている点がないのでマッチングですね。一方右側のグラフは点Aにおいて2辺がつながってしまっているため、マッチングとは言えませんね。
(2) 極大マッチングとは
現在のマッチングからもう辺を増やせない状態のマッチングのことを極大マッチングと呼びます。
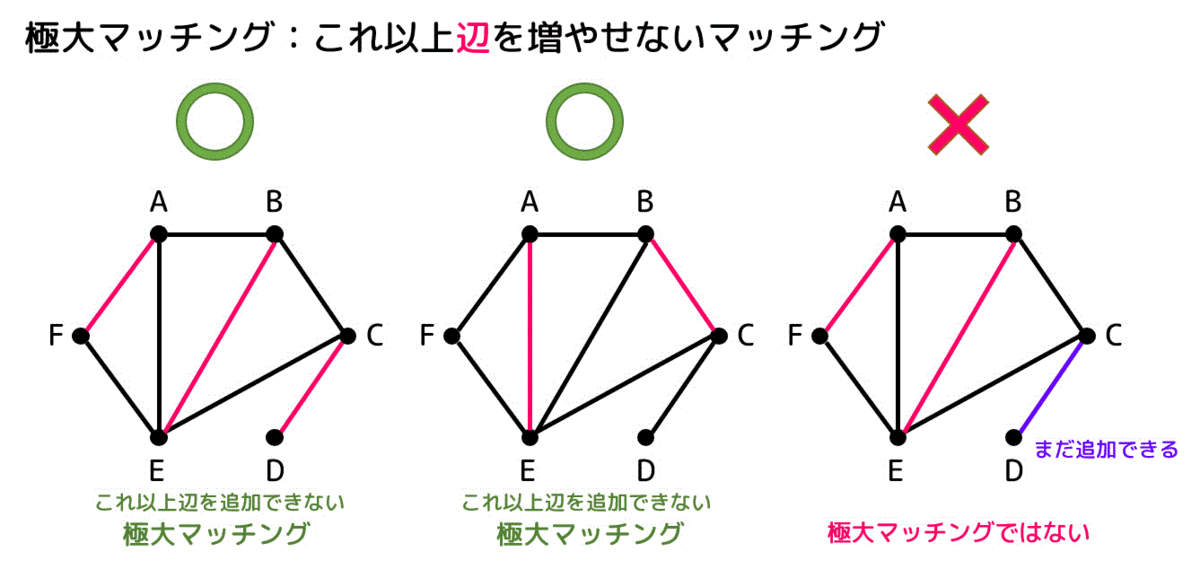
例えば左と真ん中のグラフはどこに辺を追加しようとしても2辺以上つながってしまう点ができてしまうため、これ以上辺を追加することができません。なので極大マッチングですね。
一方右のグラフは、まだ紫色で示された辺を追加することができますね。なので極大マッチングではありません。
(3) 最大マッチングとは
あるグラフにおいて追加できるだけ辺(ペア)を追加したようなマッチングのことを最大マッチングと呼びます。
(言い換えるとあるグラフに追加できるペアの上限数だけ追加したマッチングが最大マッチングとなります。)
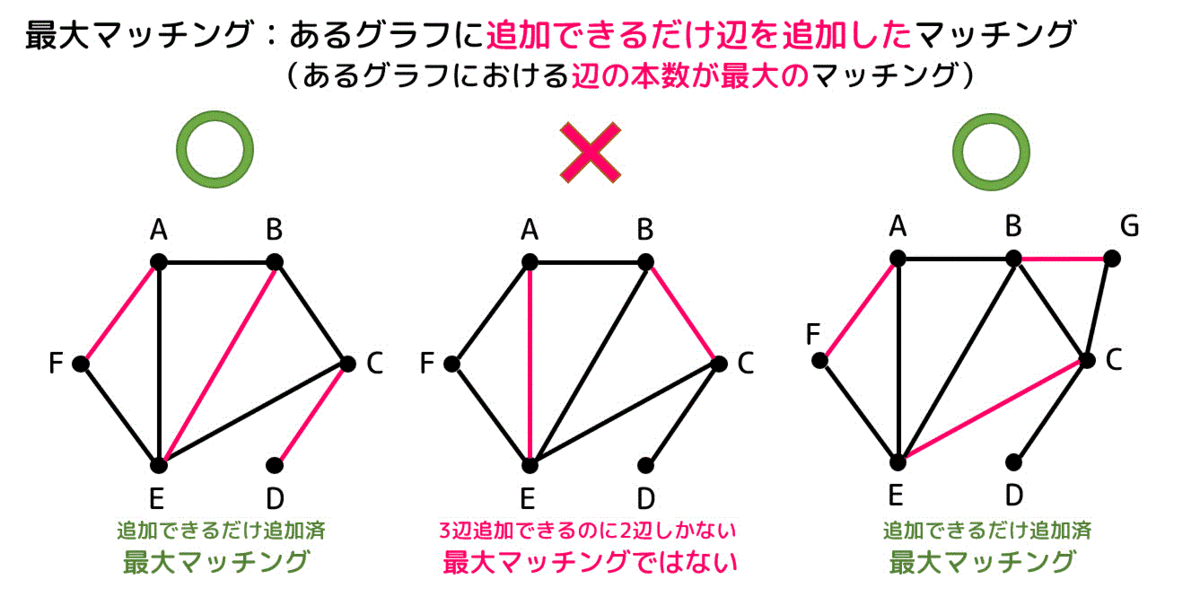
例えば左側のグラフは追加できるだけ辺を追加している(3辺追加*3できるグラフに3辺追加できている)ので最大マッチングと言うことができます。
また、右側のグラフも追加できるだけ辺を追加している*4ので最大マッチングとなります。
しかし真ん中のグラフはどうでしょうか。左側のように3辺追加しようと思えば3辺追加できるのに2辺しか追加されていませんよね。なので最大マッチングではありませんね。
(4) 完全マッチングとは
どの点にも辺がつながっているマッチングのことを完全マッチングと呼びます。
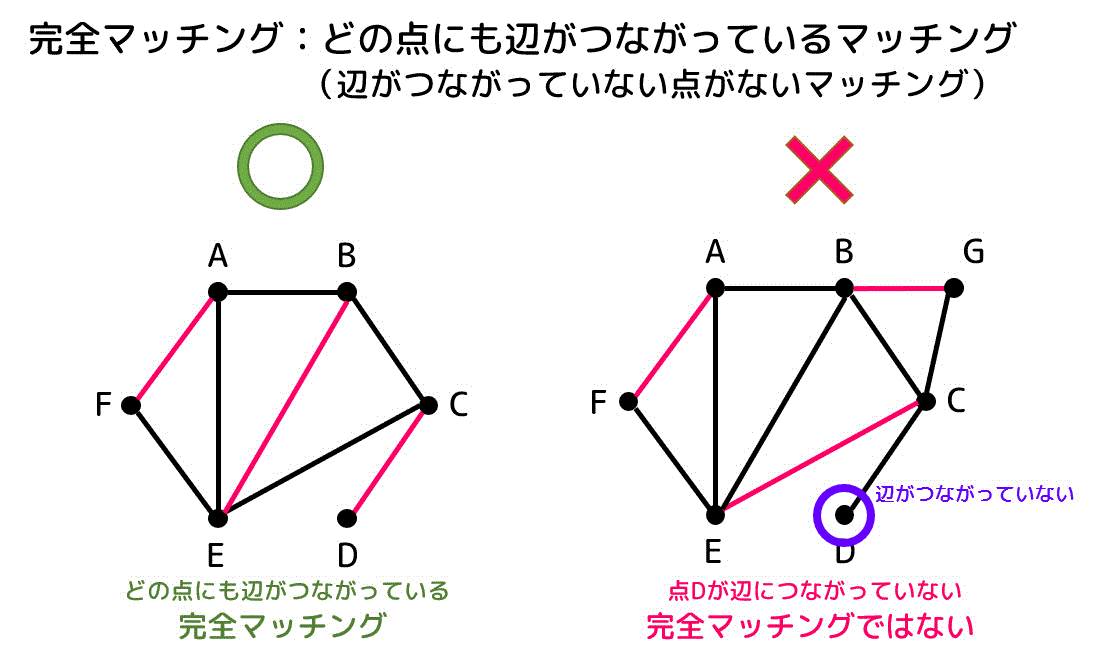
例えば左側のグラフはどの点にも辺がつながっていますね。なので完全マッチングといえます。
一方右側のグラフは点Dがどの辺ともつながっていないため、完全グラフとはいえませんね。
また、あるマッチングが完全マッチングであるかを確かめるにはマッチング(ペア)の数 \( m \) と頂点の数 \( n \) だけで確認することができます。
1つの辺(ペア)を作るためには点の数は必ず2つ必要ですね。さらに完全マッチングの場合、\( n \) 個すべての頂点に対してペアがありますよね。なので、ペアの数 \( m \) とグラフの頂点数 \( n \) が\[
m = \frac{1}{2} n
\]を満たすとき、マッチングが完全マッチングになりますよね。
マッチング:あるグラフの部分グラフにおいて、それぞれの点に2辺以上がつながっていないような部分グラフ
極大マッチング:マッチングの中でこれ以上辺(ペア)を追加できないもの
最大マッチング:あるグラフに追加できる上限数分の辺(ペア)を追加したもの
(最大マッチングであるものは必ず極大マッチングであるが、極大マッチングだからといって最大マッチングであるとは限らない*5。)
完全マッチング:どの点にも辺がつながっている(ペアになっている)マッチング
(完全マッチングであれば必ず最大マッチングとなる)
なお、極大マッチングや最大マッチングはどのグラフであっても必ず存在しますが、完全マッチングは必ず存在するとは限りません。
(5) 極大マッチングと最大マッチング
最大マッチングであれば極大マッチングとなりますが、極大マッチングだからといって最大マッチングとは限りません。
なので最大マッチングではない極大マッチングを最大マッチングにする方法を考えましょう。
(i) 増大道
増大道とは、どの辺ともつながっていない(フリーな)点同士が始点・終点となっていて、交互にペアが存在するような道を表します(交互道と呼ぶこともあります)。

たとえば、下のグラフの場合、緑色の部分が増大道となります。
(増大道の辺の数は必ず奇数になります。また、辺の数が \( 2k + 1 \) 本のとき、ペアとなっている辺は \( k \) 本、それ以外の辺が \( k + 1 \) 本となります。
(ii) 極大マッチングを最大マッチングにする方法
増大道のペアになっている部分をもとに戻し、ペアでない部分をペアに入れ替えることで、増大道のペアを1辺増やすことができますね*6。
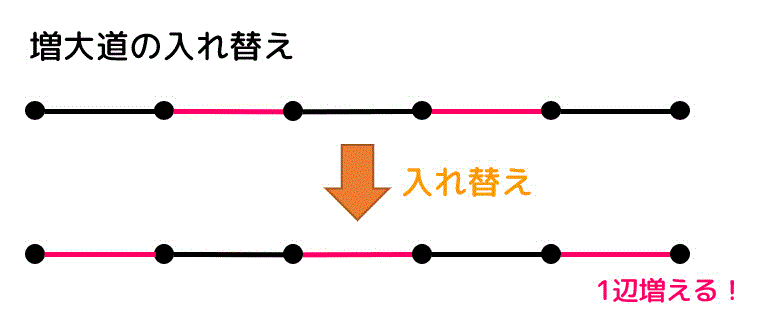
「増大道を見つけ、入れ替える」ステップを増大道がなくなるまで行うことで極大マッチングを最大マッチングにすることができます。
言い換えると、増大道がないような極大マッチングは最大マッチングであるといえます!
最大マッチングでない極大マッチングでも、
- 増大道を見つける
- 増大道のペアの辺をペアでなくし、ペアでない辺をペアに入れ替える
- 1,2を増大道がなくなるまで行う
のステップで最大マッチングにすることができる。
極大マッチングから最大マッチングにする方法
極大マッチングではないマッチングから最大マッチングを求める場合は、まず辺を追加し、極大マッチング(これ以上辺が追加できない)にしてから最大マッチングを求めていきましょう。
スポンサードリンク
2.実世界の問題をマッチングで解く
さて、最初に紹介した問題をマッチングを使って解いてみましょう。
問題をもう1度おさらいしましょう。
A君〜F君の友達関係が、
- A君とB君は仲良し
- A君とE君は仲良し
- A君とF君は仲良し
- B君とC君は仲良し
- B君とE君は仲良し
- C君とD君は仲良し
- C君とE君は仲良し
- E君とF君は仲良し
のとき、A君〜F君の6人は友達同士で2組を組むことができるだろうか。また、できるときはどのように2人組を組めばよいか。
この問題を先程説明したマッチングで解いてみましょう。
まずは、仲良し(ペアとなりえる)な人(点)同士で辺を結んでいきましょう。
すると、下のようなグラフとなりますね。
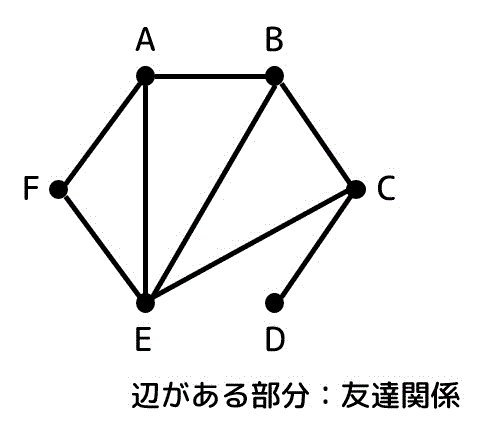
あれ、先程の例と同じグラフになりましたね*7!
このグラフの辺がある部分が友達関係となります。
問題は「6人全員が友達の誰かとペアを組めるか」でしたね。
全員が誰かとペアを組むということは、すべての頂点がどこからしらと辺で結ばれていると言い換えることができますね。
なので、この問題は上のグラフの完全マッチングを求めるような問題となりますね。
上のグラフの完全マッチングとして、下のように辺を選ぶことで完全マッチングとなります(完全マッチングは2通りあります)。
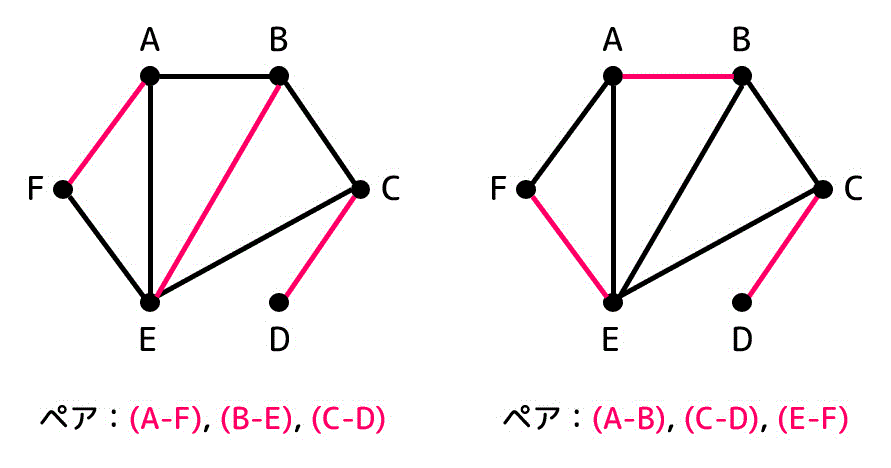
完全マッチングが存在するので、6人全員が友達の誰かしらとペアを組むことができることがわかりましたね。
また、完全マッチングの辺を見ることで6人全員がペアを組めるときのそれぞれのペアも求めることができますね。
(例えば左側の辺の場合、A-F、B-E、C-Dとペアを組むと6人全員が友達同士のペアとなり、右側の辺の場合、A-B、C-D、E-Fとペアを組むと全員が友達同士のペアとなります。)
スポンサードリンク
2.2部グラフにおけるマッチング
(1) 2部グラフとは(復習)
2部グラフについて軽く復習しておきましょう。
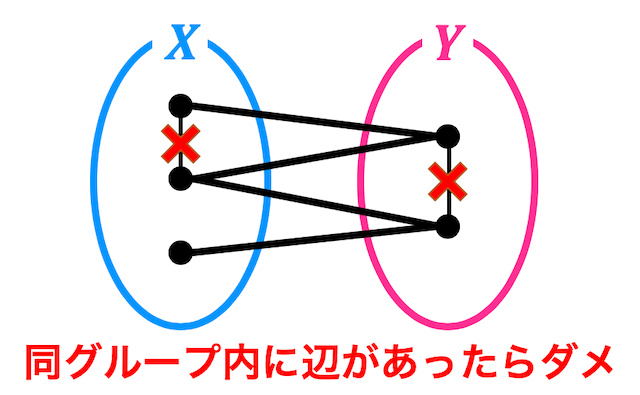
グラフ \( G \) の点を \( X \), \( Y \) の2つのグループに分けた際に \( X \) 同士の点、\( Y \) 同士の点それぞれに辺がないようなグラフを2部グラフと呼び、\[
G = (X \cup Y, E)
\]と表します。
2部グラフについての詳しい説明はこちらに書いてあるのでご覧ください。
(2) 2部グラフにおけるマッチングとは
2部グラフはそれぞれの点を2つのグループに分け、同じグループ同士には辺がないようなグラフでしたね。
2部グラフのマッチングでは、\( X \) 側のグループの人と \( Y \) 側のグループの人をペアにしていくことを考えます。
2部グラフのマッチングを使うことで、
- 男性と女性のカップルマッチング(男性 / 女性)
- 生徒と教授のゼミ(研究室)マッチング(生徒 / 研究室)
- バイトのシフト決め問題(従業員 / シフト)
などを解くことができます。
(3) 2部グラフにおける最大マッチングの求め方
2部グラフの最大マッチングは最大フロー問題を用いることでより簡単に求めることができます。
(最大フロー問題を解く方法についてわかりやすくまとめた記事があるので、解法についてはこちらの記事をご覧ください。)
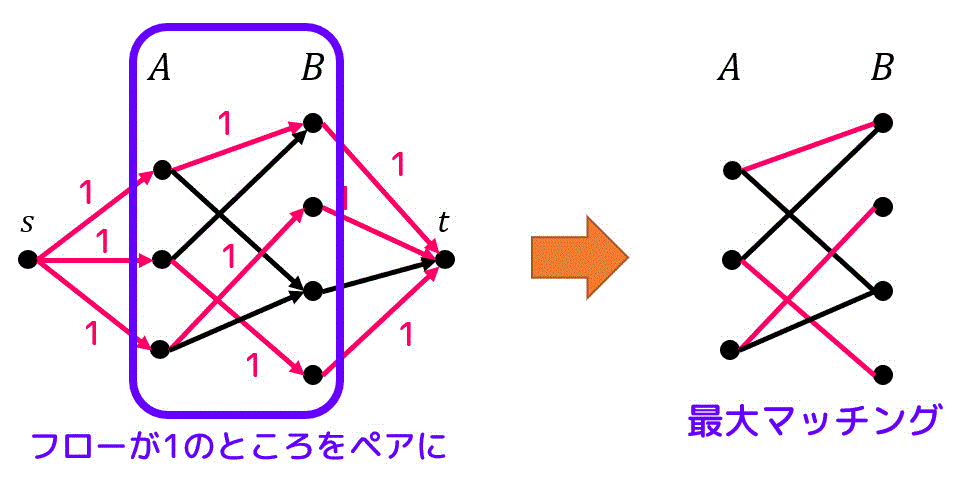
つぎの2部グラフを例に最大マッチングを最大フロー問題を解いてみましょう。
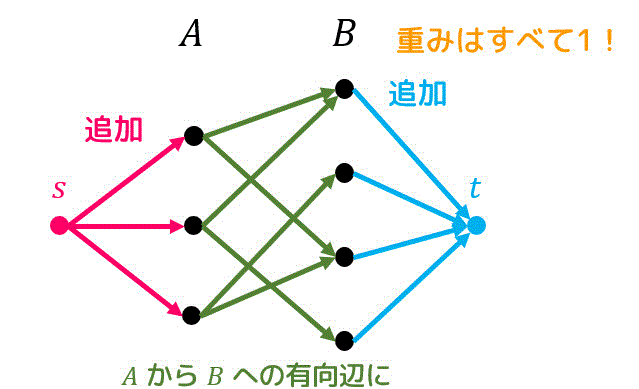
まず、フローの始点 \( s \) と終点 \( t \) を用意します。
つぎに、\( s \) からグループAに属するすべての点をつなぐ有向辺*8と、グループBに属するすべての点から \( t \) をつなぐ有向辺を用意します。
最後にAからBにつながれているすべての辺をAからBへの有向辺にします。
つぎに作ったグラフの最大フローを求めます。今回の場合だと、左下の色がついている3つの増大道を考えることで、右下のようなフローを求めることができます。
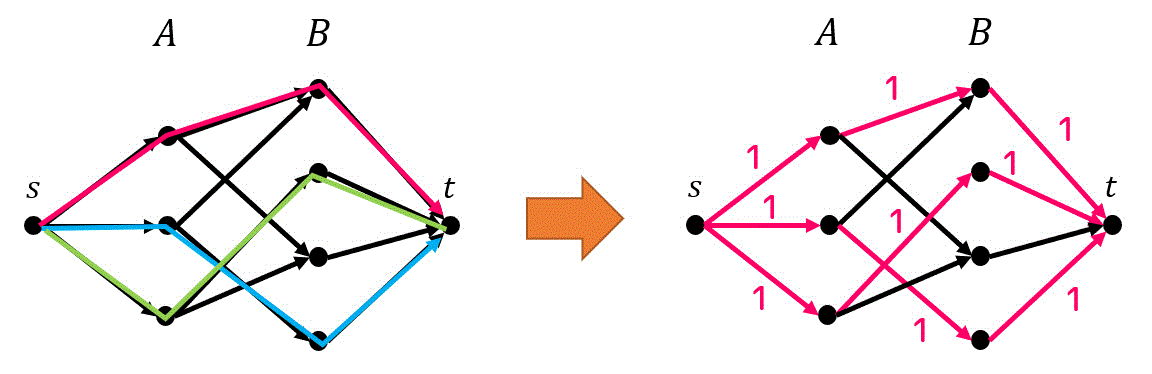
求めた最大フローのフローが1の部分をすべてペアとすることで最大マッチングを求めることができます。
(4) 2部グラフにおける完全マッチング
2部グラフのA側のすべての点が、B側のどこからしらの点とペアになっているような状態のことをAからBへの完全マッチングと呼びます。
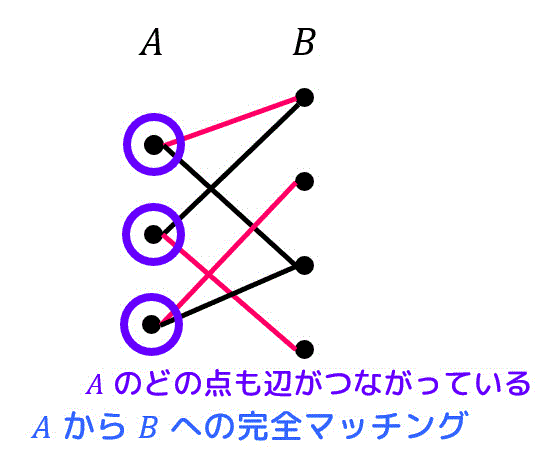
実世界における2部グラフのAからBへの完全マッチングの例としては学生グループA、教授グループBがあったとして、学生全員が誰かしらの教授グループとマッチング(研究室配属やゼミなど)できることを表します*9。
3.マッチングにおける有名な定理
2部グラフ、一般グラフそれぞれのマッチングにおける有名な定理を紹介したいと思います。
この2つの定理は両方とも完全マッチングを作れないことを示すのに役に立ちます。
(1) ホールの結婚定理
ホールの結構定理は2部グラフにおけるAからBの完全マッチングが存在するための条件を記した公式です。
結婚定理を説明する前に、記号の説明をしておきましょう。
\( N(S) \) とは、グループA側の点集合 \( S \) からたどれるグループB側のすべての点を集合で表したものを表します。
例えば、\( S = \{ 1 \} \) であれば、1からたどれる点はa, cの2つなので \( N(S) = \{a,c \} \) となります。
同様に \( S = \{2,3\} \) であれば、1,2からたどれる点はa,b,c,dのすべてなので \( N(S) = \{a,b,c,d\} \) となります。
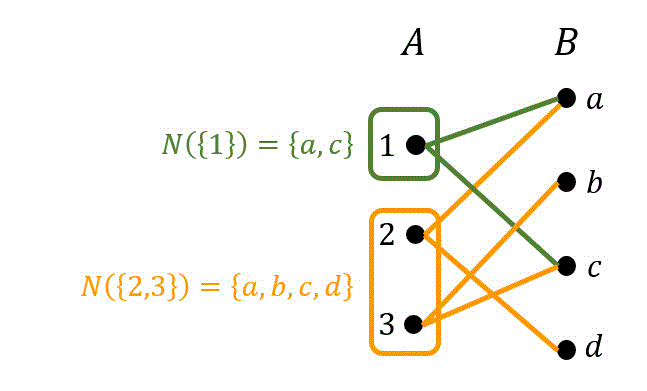
では記号の説明が終わったのでホールの結婚定理を紹介したいと思います。
2部グラフ \( G = (A \cup B, E) \) に対し、\( A \) から \( B \) への完全マッチングが存在するための必要十分条件は、どのような \( S \)(ただし \( S \subseteq A \))であっても\[
|S| \leqq |N(S)|
\]が成立することである。
ホールの定理の \( |S| \leqq |N(S)| \) は、集合 \( S \) から何個か(\( n \) 個とします)点を取ったときに、集合 \( S \) にある点のすべてからたどれる点 \( N(S) \) は必ず \( n \) 個以上あることを示しています。
これを言い換えると、ある1つの \( S \)(ただし \( S \subseteq A \))でも\[
|S| > |N(S)|
\]となるような \( S \) が見つけることができればホールの定理は成立せず、グラフに完全マッチングが存在しないことを示すことができますね。
(1つでもホールの結婚定理が成り立たないような \( S \) を見つけることで完全マッチングがないことを示すことができる!)
ホールの結婚定理が成立しない、つまり \( A \) から \( B \) への完全マッチングが成立しないような例を1つ考えてみましょう。
例えば、下のグラフを考えてみます。
\( S = \{ 1,3 \} \) とします。すると、1, 3からいけるグループBの点はaだけですよね。
すると、\( |S| = 2 \) に対し、\( |N(S)| = |{a}| = 1 \) となりますね。
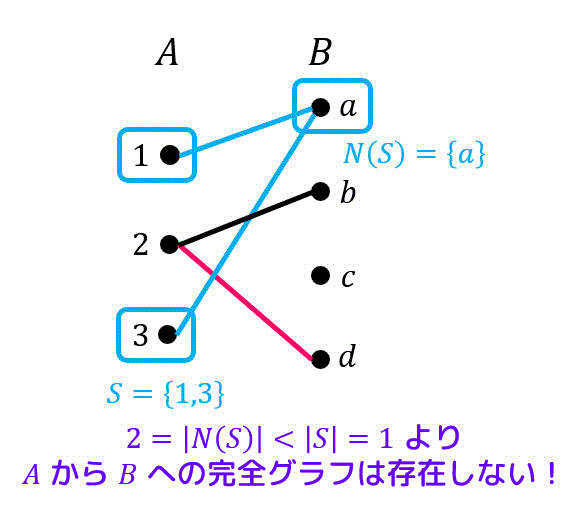
もし完全マッチングであればAから適当に2点選べば、選んだ点からいけるグループBの点は2点以上あるはずですよね*10。
しかし、Aから1,3の2点を選ぶと、1,3から行けるBの点はaの1点しかありませんよね。
なので完全マッチングということはできませんよね。
このように、ホールの結婚定理はある2部グラフ \( G \) に完全マッチングが存在しないことを示せる便利な定理なのです!
(ちなみに完全マッチングが存在することを示すためには、完全マッチングとなるペアの選び方を1つ書くだけでOKなので、ホールの結婚定理は不要です。)
(2) タットの定理
ホールの定理を2部グラフでない普通のグラフでも使えるように拡張したのがタットの定理です。
タットの定理を説明するまえに再び記号や用語の説明をしましょう。
あるグラフ \( X \) に存在する奇成分*11の数を \( o(X) \) で表します。
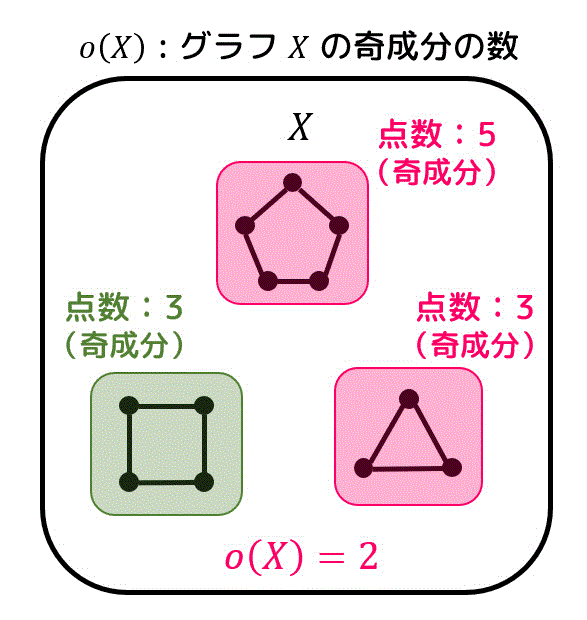
上のグラフの例で行くと、奇成分が2つあるので、\( o(X) = 2 \) となります。
記号の説明が終わったのでタットの定理を紹介したいと思います。
グラフ \( G = (V, E) \) の完全マッチングが存在するための必要十分条件は、どのような \( S \)(ただし \( S \subseteq V \))であっても\[
o(G-S) \leqq |S|
\]が成立することである。
タットの定理の \( o(G-S) \leqq |S| \) は、集合 \( S \) から何個か(\( n \) 個とします)点を取ったときに、グラフ \( G \) から \( S \) の点をすべて削除したグラフの奇成分の数が必ず削除した点以下になることを表しています。
これを言い換えると、ある1つの \( S \)(ただし \( S \subseteq V \))でも\[
o(G-S) > |S|
\]となるような \( S \) が見つかればタットの定理は成立せず、グラフに完全マッチングが存在しないことを示すことができますね。
(タットの定理が成り立たない1つの例を示せば完全グラフでないことを示せる!)
タットの定理が成立しない例を具体的に1つ見ていきましょう。
例えば次のグラフ \( G \) から1つ点を消したとします。(消した点の集合が \( S \) となります。)
すると、グラフ \( G-S \) は3つの奇成分にわかれますね。なので \( o(G-S) = 3 \) となります。
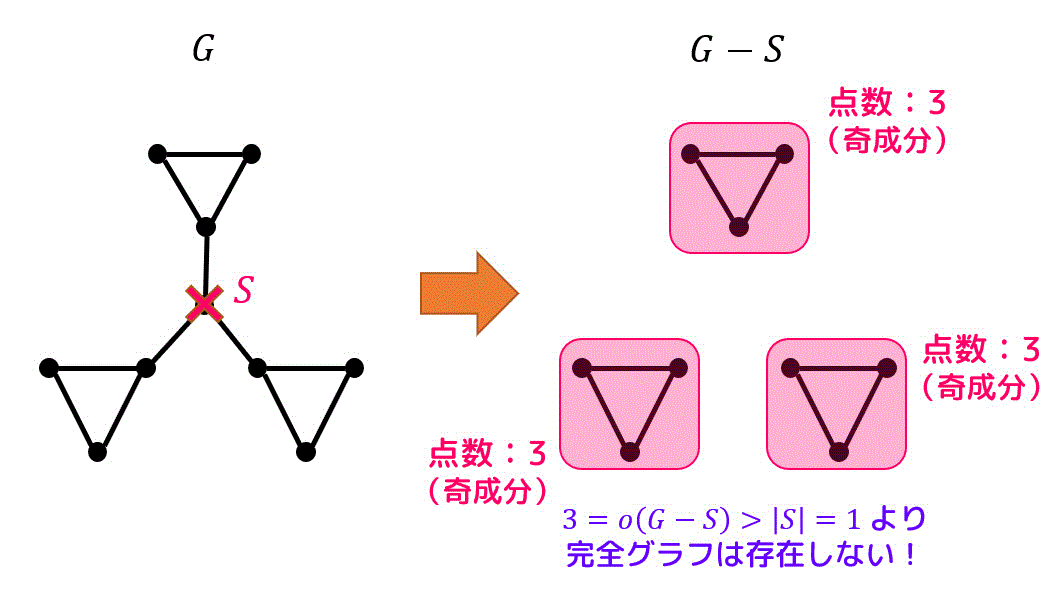
しかし、1つしか点を消していないので \( |S| = 1 \) ですよね。
なので、\( o(G-S) \gt |S| \) となり、完全マッチングがないことを証明することができます。
このように、タットの定理はあるグラフ \( G \) に完全マッチングが存在しないことを示せる便利な定理なのです!
(ちなみに完全マッチングが存在することを示すためには、完全マッチングとなるペアの選び方を1つ書くだけでOKなので、タットの定理は不要です。)
4.練習問題
では、4問ほど練習しましょう。
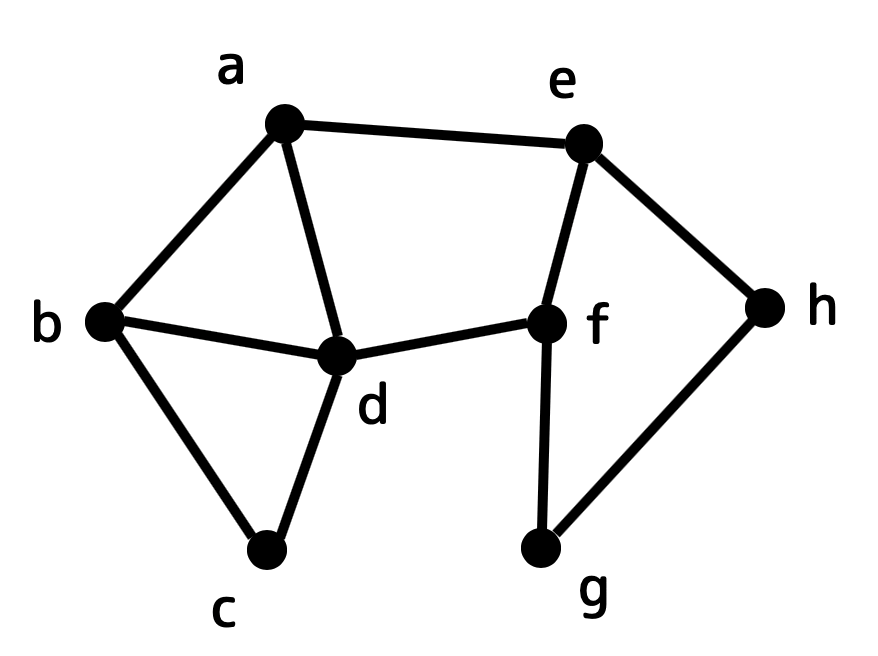
練習1
次のグラフが完全マッチングを持つならば完全マッチングを答え、完全マッチングを持たないのであればその理由を答えなさい。
練習2
あるクラスにいるA君〜F君はとある授業で2人組を作ることになった。
しかし、このクラスは大変治安が悪く、つぎの2人でペアを作ると授業どころではなくなってしまう(以後このペアのことを事案ペアと呼ぶ)。
- a君とc君
- a君とd君
- a君とf君
- b君とd君
- b君とf君
- c君とd君
- c君とf君
- d君とf君
なるべく問題が起こらないように6人全員が2人組を組むことはできるだろうか。
(言い換えると、上で示した2人組にならないように2人組を組むことはできるだろうか。)
つぎの(1)〜(3)の問いに答えなさい。
(1) A君〜F君を点、それぞれの事案ペアを辺としてグラフ \( X \) を描きなさい。
(2) 上の問題をグラフ理論(離散数学)の問題としてどのように解けばいいか答えなさい。
(3) 6人全員が問題が起こらないように2人組を組むことができるのかどうかを理由とともに答えなさい。
練習3
とあるサークルには男性4人(m君、n君、o君、p君)と女性4人(xさん、yさん、zさん、wさん)の4人がいる。
このサークルの恋愛事情について、とある4人がこのように言っている。
- 「xさんはo君かp君と付き合っている」
- 「m君はyさんかzさんと付き合っている」
- 「p君はxさんかzさんと付き合っている」
- 「n君はyさんかwさんと付き合っている」
この4人の証言が正しいとき、8人(男性4人、女性4人)がそれぞれ付き合っているペアを答えなさい。
練習4
a君〜e君の5人は文化祭で屋台(模擬店)を開くことになった。当日模擬店を営業するためには少なくとも1人が店にいる必要がある。
そこで、5人に当日の店番のシフトを聞いたところ、a君〜e君が働ける時間は下のようになった。
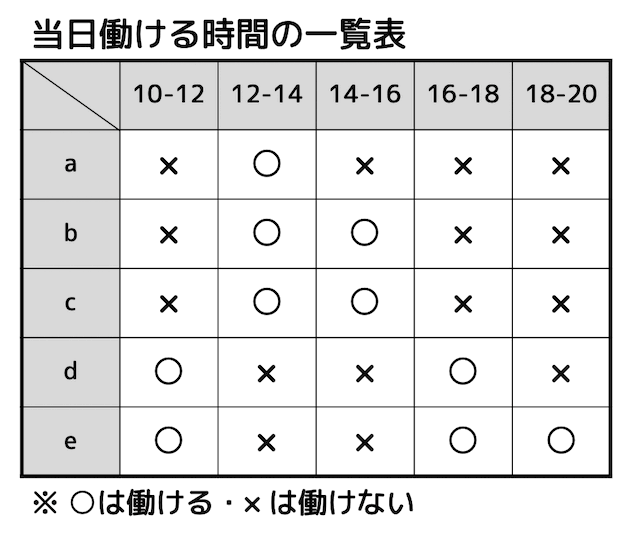
a君〜e君がそれぞれ2時間ずつ働くようなシフトを組むことができるだろうか。理由とともに答えなさい。
5.練習問題の答え
解答1
例えば、下のような完全マッチングをつくることができる。
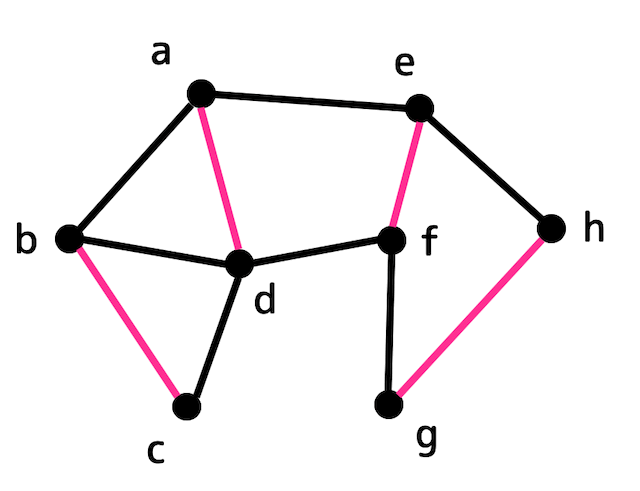
解答2
(1)
次のようなグラフ \( X \) を作ることができる。
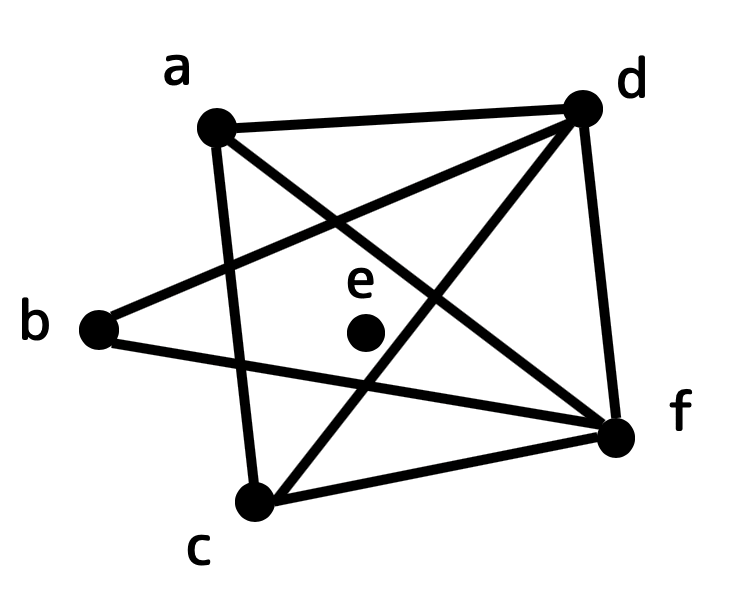
(2)
事案ペアではないようなペアは、グラフ \( X \) の補グラフ \( G \) の辺で表される。
つまり、グラフ \( X \) の補グラフ \( G \) における完全マッチングがあるかどうかを判定することで、6人全員が事案ペアとはならない2人組を組むことができるかどうかを判定できる。
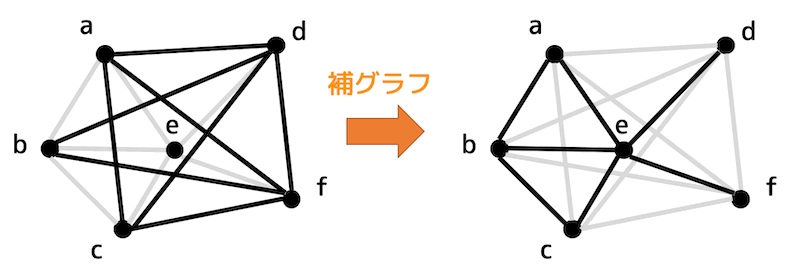
(3)
解答:できない
理由
もし、6人全員が事案ペアを含まないように2人組を組むことができるのであれば、グラフ \( G \) の完全マッチングが存在し、タットの定理 \( o(G-S) \leqq S \) が成立する。
例えば、\( S = e \) とすると、グラフ \( G - S \) は3つの奇成分からなるグラフとなる。なので、\( o(G-S) = 3 \) となる。ここで、\( o(G-S) \gt |S| \) となるため、タットの定理が成立しない。
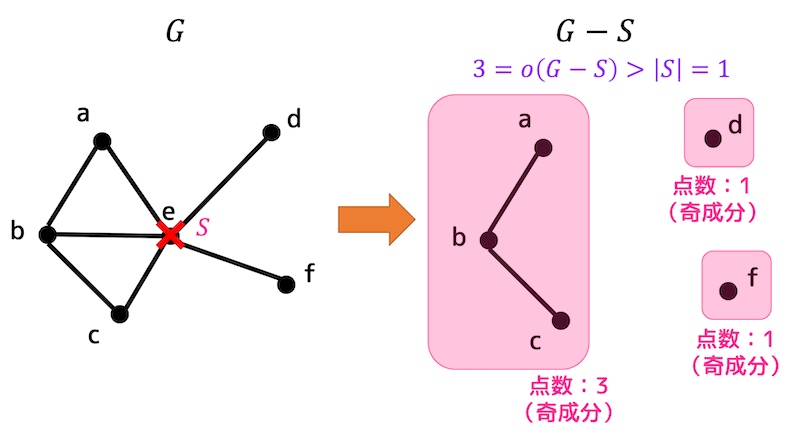
なので、グラフ \( G \) の完全マッチングは存在しないので6人全員が事案ペアを含まないような2人組を組むことができないことが示された。
解答3
それぞれの4人の証言から付き合っている可能性のあるペアの点に辺を結んでいくと、下のような2部グラフとなる。
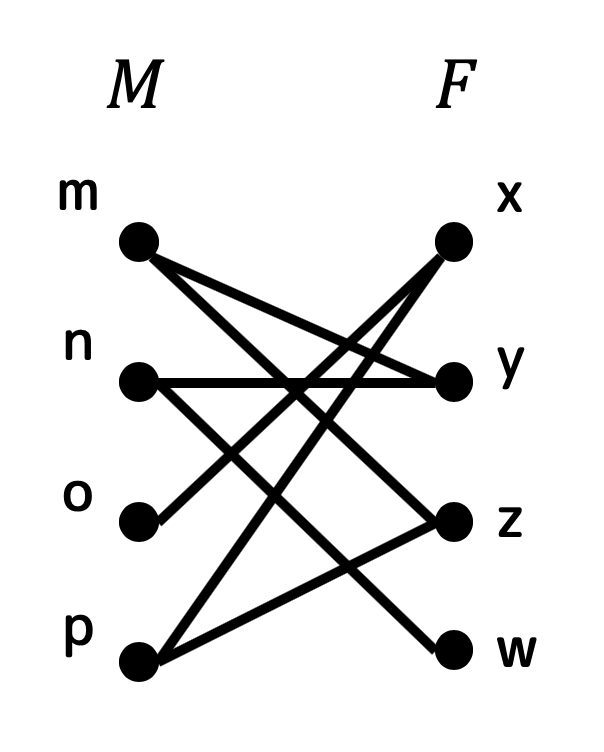
あとは上の2部グラフの最大マッチングを求めればよい。
始点、始点から \( M \) の点をつなぐ有向辺、 \( F \) の点から終点をつなぐ有向辺、終点を書き足し、\( M \) から \( F \) の辺を有向辺を変え、最大フローを求める。
すると、下のようなフローを得ることができる。(色がある部分が1、それぞれの色はどの増大道から求めたフローかを表す)
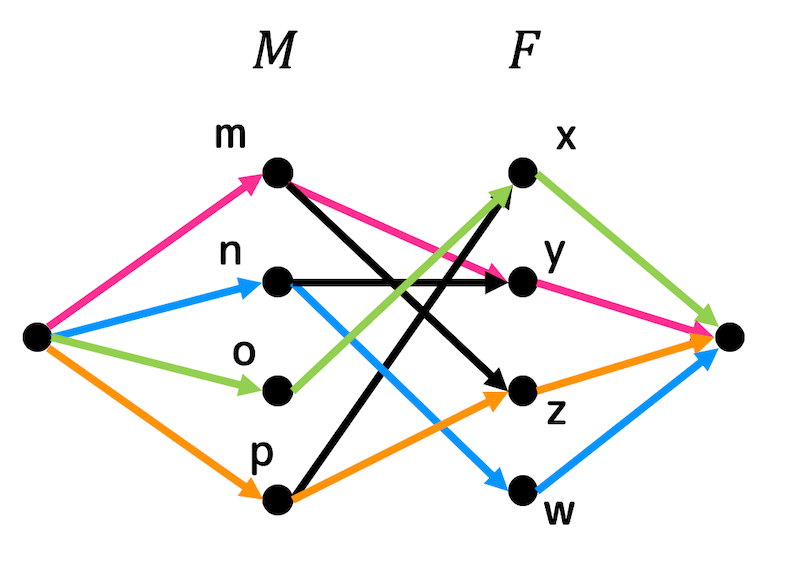
あとは、フローが1になっている部分をペアとすることで最大マッチングを求めることができる。
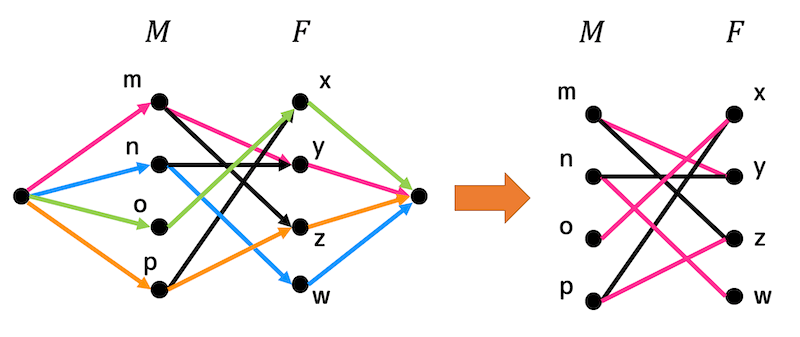
よって、付き合っているペアはそれぞれ「mくんとyさん」、「nくんとwさん」、「oくんとxさん」、「oくんとzさん」となる。
解答4
a君〜e君の5人を人の点集合 \( P \)、それぞれのシフトの時間を時間の点集合 \( T \) とし、それぞれの5人が働ける可能性のある時間を辺で結んでいくと、下のような2部グラフが出来上がる。
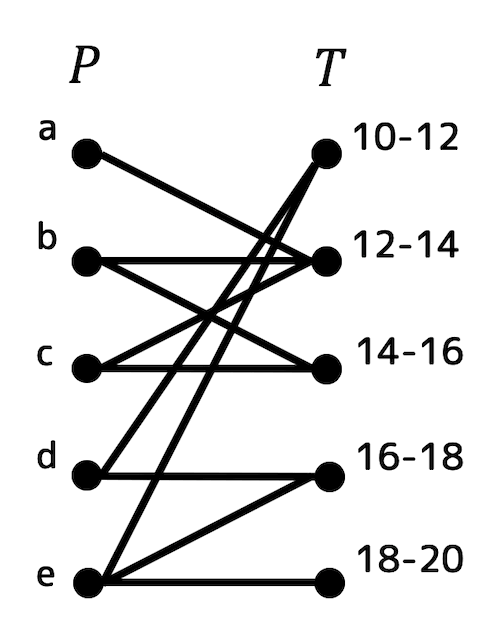
あとは上のグラフ \( G \) が \( P \) から \( T \) への完全マッチングを持つかどうかを判定すればよい。
(完全マッチングが存在すればa君〜e君がそれぞれ2時間ずつ働くようなシフトを組むことができ、存在しなければ組むことができない)
しかし、上のグラフは完全マッチングを持たない。
(完全マッチングを持たない理由)
2部グラフ \( G \) が \( P \) から \( T \) への完全マッチングを持つと仮定する。すると、ホールの定理より、どのような \( S \)(ただし \( S \subseteq P \))であっても \( S \leqq N(S) \) が成立する。
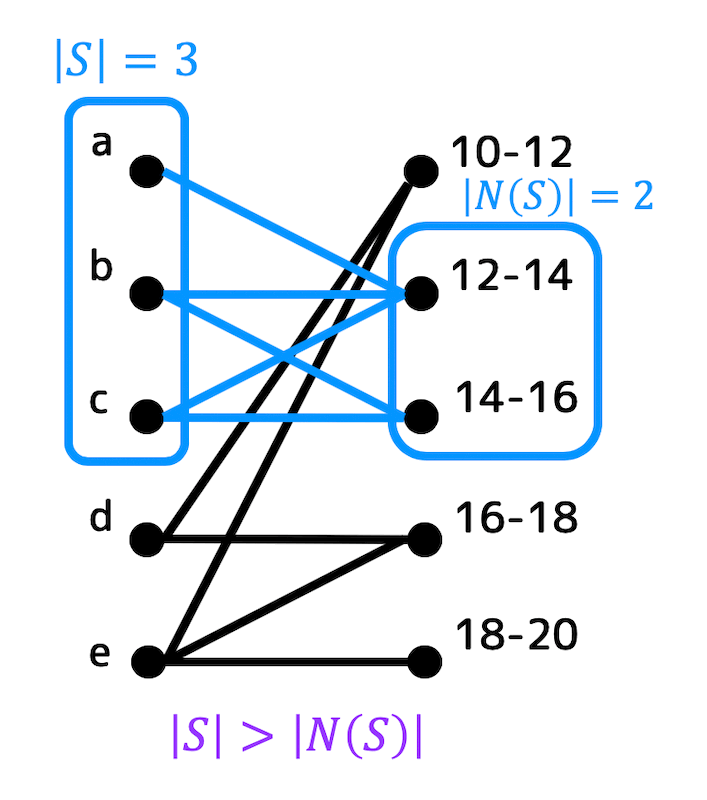
しかし、例えば \( S = \{a,b,c\} \) とすると、\( |S| = 3 \)、\( | N(S)| = 2 \) となるので \( |S| \gt | N(S) | \) となってしまい、ホールの定理が成立しない。
ホールの定理が成り立たないので、2部グラフ \( G \) は \( P \) から \( T \) への完全マッチングも持たない。
なのでa君〜e君がそれぞれ2時間ずつ働くようなシフトを組めないことが示された。
6.さいごに
今回は離散数学、グラフ理論におけるマッチングについてまとめていきました。
マッチングはグラフ理論にかかわらず、日常生活の問題(パズル)にも応用することができるのでぜひ覚えておきましょう!
次回は平面グラフについてまとめていきたいとおもいます。
(最終話まであと2記事なのでがんばりましょう!)
*1:マッチングアプリは、お付き合いがしたい男性と女性を結びつけるようなアプリです。詳しくはググってください。
*2:たまに2人以上と付き合っているやばい人がいるのですが、今回は除外します。良い子のみんなはちゃんと1人を愛しましょう。
*3:1つのペアを作るためには点が2つ必要ですよね。なので位数(頂点数)が6の左側と真ん中のグラフ、7の右側グラフともに3ペアのマッチングは作れるかのせいはありますが、点が足りないのでどうがんばっても4ペア以上マッチングさせることはできませんよね。
*4:頂点数が7なので作れるとしても3ペアしか追加できない。
*5:最大マッチングが極大マッチングと違うところは、極大マッチングは現在のペアの状態からどこにも辺を加えられないようなマッチングであるのに対し、最大マッチングは辺(ペア)をどのように変えてもさらにペアを追加できないようなマッチングを表します。
*6:増大道全体の辺の数 \( 2k + 1 \) に対し、\( k \) 本がペアなので入れ替えるとペアの数が \( k + 1 \) 本になり1ペア増えますね
*7:偶然ではなく、僕がそうしただけです。気にしないでください。
*8:向きがある辺のことです。向きの方向を矢印で示しています。逆に向きがない辺のことを無向辺と呼びます。
*9:他の例でいくとAを男性グループ、Bを女性グループとするとAをからBへの完全マッチングは男性グループ全員が女性グループの誰かしらとお付き合いできることを表します。
*10:1つの点につなぐことのできる辺、ペアは1つまでなので、スタート点が2点あれば当然ゴール点も2点以上ないとA側のすべての点を辺でつなぐことはできませんよね。
*11:位数(点の数)が偶数の連結成分を偶成分、位数(点の数)が奇数の連結成分のことを奇成分と呼びます。
関連広告・スポンサードリンク








![[基本情報・応用情報] うさぎでもわかる情報理論 第3羽 ハフマン符号化](https://www.momoyama-usagi.com/wp-content/uploads/joho3-2-3-150x150.jpg)