スポンサードリンク
こんにちは、ももやまです。
今日は、確率・統計分野の中で出てくる指数分布と、指数分布を使った確率を求める計算方法を紹介していきます。
※ 本記事では、確率・統計分野の確率密度関数、累積分布関数の知識を使用します。未学習の人や、復習したい人は、以下のリンク先の記事にて復習することをお勧めします。
目次
スポンサードリンク
1. 指数分布とは
指数分布は、「つぎに事象が発生するまでの時間」をモデル化した分布です。
指数分布を使うことで、つぎのような問題を解くことができます。
桃山工場で生産しているご飯盛り付け機(以後、機械と表記する。)がある。この機械は、過去のデータから、故障するまでの平均日数が1,000日であることが判明している。このとき、つぎの(1), (2)の問いに答えなさい。
(1) 機械が500日以内に故障する確率を求めなさい。
(2) 機械が少なくとも1,500日間正常に稼働し続ける(=故障が発生しない)確率を求めなさい。
スポンサードリンク
2. 指数分布の公式(累積分布関数)導出
ある事象が指数分布に従う(ことを仮定できる)場合、「つぎに事象が発生するまでの時間」を以下の公式で簡単に求めることができます。
ある事象が単位時間あたりに、平均して \( \lambda \) 回発生するとする。
このとき、次に事象が発生するまでの時間が \( t \) 以内となる確率 \( F(t) \) は、つぎの式で計算できる。\[
F(t) = 1 - e^{- \lambda t }
\]
ここで、\( t \) は単位時間に対する経過時間を、単位時間に対する倍率で示した変数である。例えば、単位時間が10分で、次に事象が発生する時間が30分の場合、\( t = \frac{30}{10} = 3 \) となる。
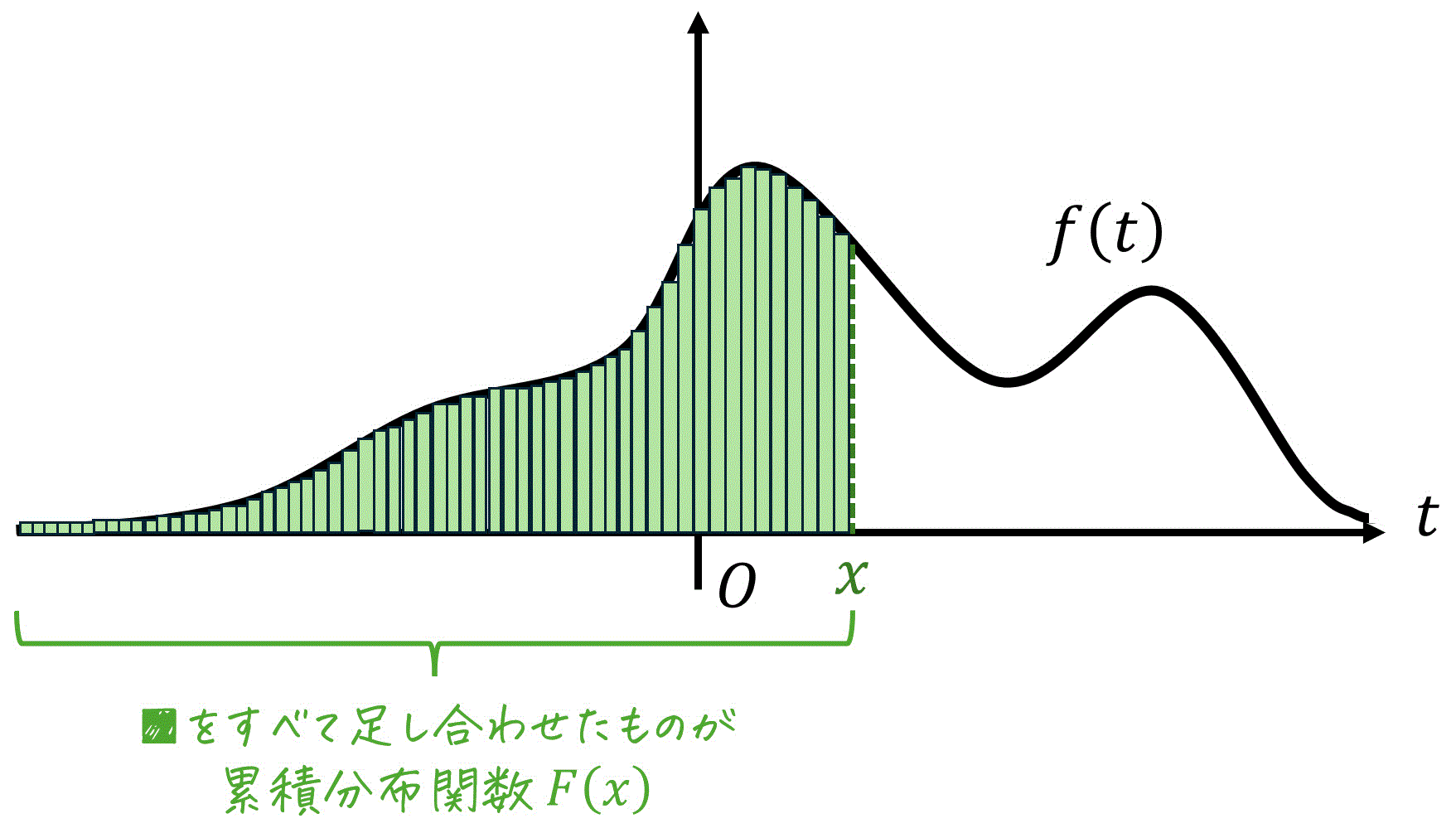
また、この \( F(t) \) は指数分布の累積分布関数となる[1]累積分布関数とは、ある確率変数が特定の値以下になる確率を表す関数です。
累積分布関数の導出は、ポアソン分布を使って導出することができます。
※ ポアソン分布の復習は以下の記事から出来ます。まだ未履修な人や、ポアソン分布を忘れてしまった人はご覧ください。
公式の導出
指数分布は「つぎに事象が発生するまでの時間が \( t \) 以内となる確率」を表しています。
この表現を言い換えると、「ある時間 \( t \) が経過するまでに、少なくとも事象が1回が発生する確率 \( P(X \geqq 1) \)」言えます。この確率は、ポアソン分布の公式から計算することができます。
この確率は、「ある時間 \( t \) が経過するまでに、事象が1回も発生しない \( P(X = 0) \) 」の補集合に相当します。つまり、つぎのように表すことが出来ます。\[
P( X \geqq 1 ) = 1 - P(X=0)
\]
ここで、ある事象が単位時間あたりに平均して \( \lambda \) 回発生するとします。このとき、\( X \) がポアソン分布に従う場合、事象が単位時間以内に \( k \) 回発生する確率は、次のように表されます。\[
P(X = \textcolor{blue}{ k } ) = \frac{\textcolor{red}{ \lambda }^{\textcolor{blue}{ k } } }{\textcolor{blue}{ k } !} e^{ - \textcolor{red}{ \lambda } }
\]
ここで、単位時間 → 時間 \( t \) におきかえてみましょう。すると、経過時間 \( t \) において事象の発生する確率は \( \lambda t \) となります。そのため、事象が \( t \) 以内に \( k \) 回発生する確率 \( P(X=k) \) は、つぎのように表されます。\[
P(X = \textcolor{blue}{ k } ) = \frac{\textcolor{red}{ \lambda t }^{\textcolor{blue}{ k } } }{\textcolor{blue}{ k } !} e^{ - \textcolor{red}{ \lambda t } }
\]
事象が1回も発生しない確率 \( P(X=0) \) が欲しいので、1つ前の式に \( k = 0 \) を代入することで、つぎのように求められます。\[\begin{align*}
P(X = \textcolor{blue}{ k } ) & = \frac{\textcolor{red}{ \lambda t }^{\textcolor{blue}{ 0 } } }{\textcolor{blue}{ 0 } !} e^{ - \textcolor{red}{ \lambda t } }
\\ & = e^{- \lambda t}
\end{align*}\]
よって、「ある時間 \( t \) が経過するまでに、少なくとも事象が1回が発生する確率 \( P(X \geqq 1) \)」がつぎのように導出できます。\[\begin{align*}
P( X \geqq 1 ) & = 1 - P(X=0)
\\ & = 1 - e^{- \lambda t}
\end{align*}\]この式が、指数分布の累積分布関数となります。
スポンサードリンク
3. 例題で確認
ここからは、実際の問題例を通じて、指数分布の理解度を深めていきましょう。
桃山工場で生産しているご飯盛り付け機(以後、機械と表記する。)がある。この機械は、過去のデータから、故障するまでの平均日数が1,000日であることが判明している。このとき、つぎの(1), (2)の問いに答えなさい。答えは小数第2位まで記すこと。
(1) 機械が500日以内に故障する確率を求めなさい。
(2) 機械が少なくとも1,500日間正常に稼働し続ける(=故障が発生しない)確率を求めなさい。
※ 必要であれば、以下の表で与えられる指数関数の値を用いてもよい。
| \( x \) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
|---|---|---|---|---|---|---|
| \( e^x \) | 1.649 | 2.718 | 4.482 | 7.389 | 12.182 | 20.086 |
(1)
まず、機械の故障までの平均日数が1,000日であることから、1,000日を1単位時間としましょう。
この場合、単位時間(=1,000日)ごとに平均1回の故障が発生するので、\( \lambda = \textcolor{red}{1} \) となります。
今回求めたい確率は、500日(=0.5単位時間)以内に故障する確率なので、\( t = \textcolor{blue}{0.5} \) となります。
あとは、指数分布の累積分布関数\[
F(t) = 1 - e^{- \lambda t}
\]に、\( \lambda = 1 \), \( t = 0.5 \) を代入すればOKです。\[\begin{align*}
F(0.5) & = 1 - e^{- 1 \cdot 0.5}
\\ & = 1 - e^{-0.5}
\\ & = 1 - \frac{1}{e^{0.5}}
\\ & \fallingdotseq 1 - \frac{1}{1.649}
\\ & = 1 - 0.606
\\ & = 0.394
\end{align*}\]
したがって、機械が500日以内に故障する確率は 0.39 と求められます。
(2)
機械が少なくとも1,500日正常に稼働し続ける(=故障しない)確率を求めていきます。
この確率は、1から「1,500日以内(=1.5単位時間)に機械が壊れる確率」から引くことで求めることができます。(余事象)
1,500日以内に機械が壊れる確率は、指数分布の累積分布関数\[
F(t) = 1 - e^{- \lambda t}
\]に、\( \lambda = \textcolor{red}{1} \), \( t = \textcolor{blue}{1.5} \) を代入すれば求めることが出来ます。\[\begin{align*}
F(1.5) & = 1 - e^{- 1 \cdot 1.5}
\\ & = 1 - e^{-1.5}
\\ & = 1 - \frac{1}{e^{1.5}}
\end{align*}\]※ 指数関数は、最後に近似します。
よって、少なくとも1,500日機械が稼働する確率は、次のように計算できます。\[\begin{align*}
1 - F(1.5) & = 1 - \left( 1 - \frac{1}{e^{1.5}} \right)
\\ & = \frac{1}{e^{1.5}}
\\ & \fallingdotseq \frac{1}{4.482}
\\ & = 0.223
\end{align*}\]
したがって、機械が少なくとも1,500日正常に稼働し続ける確率は 0.22 と求められます。
4. 指数分布の確率密度関数
指数分布の累積分布関数は、次のように表されるのでしたね。\[
F(t) = 1 - e^{- \lambda t} \ \ \ (t \geqq 0)
\]
確率密度関数 \( f(t) \) は、この累積分布関数 \( F(t) \) を時間 \( t \) で微分することで求めることができます。
実際に微分すると、\[\begin{align*}
f(t) & = \frac{d}{dt} F(t)
\\ & = \frac{d}{dt} \left( 1 - e^{- \lambda t} \right)
\\ & = \lambda e^{- \lambda t}
\end{align*}\]と導出することができます。
指数分布の確率密度関数 \( f(t) \) は、以下の通りである。ただし、\( t \geqq 0 \) である。\[
f(t) = e^{- \lambda t}
\]※ \( t < 0 \) のとき、\( f(t) = 0 \)。
5. 指数分布の期待値・分散
指数分布で表される確率変数 \( X \) の期待値 \( E(X) \)、分散 \( V(X) \) は以下の通りである。\[
E(X) = \frac{1}{ \lambda} , \ \ \ V(X) = \frac{1}{ \lambda^2 }
\]
指数分布の確率密度関数\[
\lambda e^{- \lambda t} \ \ \ (t \geqq 0)
\]から、期待値と分散を導出していきましょう。
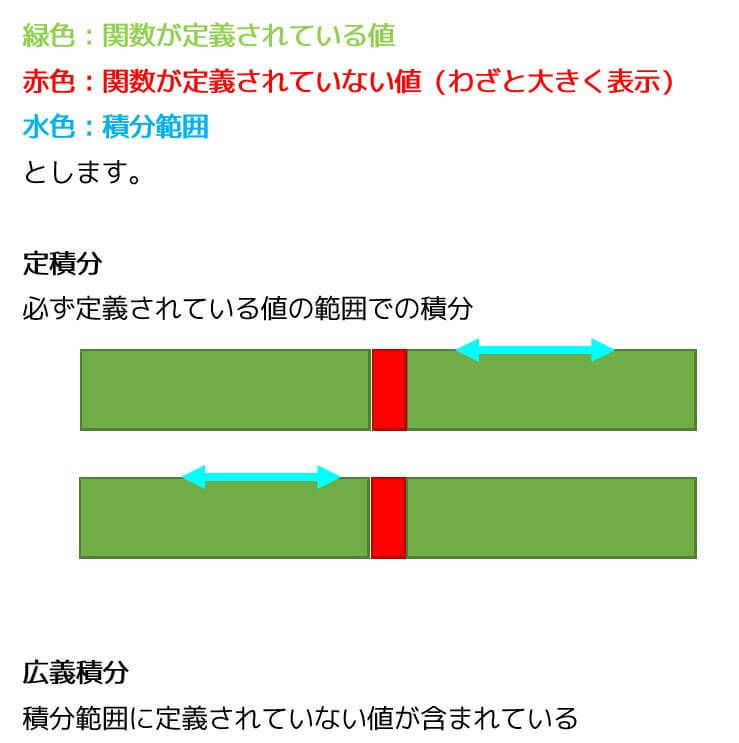
※ 導出の途中で、解析学の知識(部分積分、ロピタルの定理、広義積分)を使います。復習したい方は、以下の記事にて学習ができます。
(1) 期待値
確率密度関数 \( f(t) \) で表される確率変数 \( X \) の期待値 \( E(X) \) は、次のように計算できるのでしたね。\[
E(X) = \int^{\infty}_{- \infty} t f(t) \ dt
\]
実際に、指数分布をこの式に代入して計算してみましょう。\[\begin{align*}
E(X) & = \int^{\infty}_{- \infty} t f(t) \ dt
\\ & = \int^{\infty}_{0} t\lambda e^{- \lambda t} \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} t \lambda e^{- \lambda t} \ dt
\\ & = \lim_{R \to \infty} \left[ - t e^{- \lambda t} \right]^{R}_{0} - \int^{R}_{0} - e^{- \lambda t} \ dt
\\ & = \lim_{R \to \infty} - R e^{- \lambda R} - \left( 0 \cdot e^{- \lambda \cdot 0} \right) - \int^{R}_{0} - e^{- \lambda t} \ dt
\\ & = \lim_{R \to \infty} - R e^{- \lambda R} - \left[\frac{1}{ \lambda} e^{- \lambda t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} - R e^{- \lambda R} - \left( \frac{1}{ \lambda} e^{- \lambda R} - \frac{1}{ \lambda} e^{- \lambda \cdot 0} \right)
\\ & = \lim_{R \to \infty} - R e^{- \lambda R} - \frac{1}{ \lambda} e^{- \lambda R} + \frac{1}{ \lambda} \cdot 1
\\ & = \lim_{R \to \infty} - \frac{R}{ e^{ \lambda R} } - \frac{1}{ \lambda e^{ \lambda R} } + \frac{1}{ \lambda} \cdot 1
\\ & = \lim_{R \to \infty} - \frac{ \lambda R + 1 }{\lambda e^{\lambda R}} + \frac{1}{ \lambda }
\\ & = \frac{1}{ \lambda } - \underbrace{ \lim_{R \to \infty} \frac{ \lambda R + 1 }{\lambda e^{\lambda R} } }_{ \mathrm{ロピタルの定理} }
\\ & = \frac{1}{ \lambda } - \underbrace{ \lim_{R \to \infty} \frac{ \lambda }{\lambda^2 e^{\lambda R}} }_{0}
\\ & = \frac{1}{ \lambda }
\end{align*}\]と導出できます。
よって、指数分布の期待値を\[
E(X) = \frac{1}{ \lambda }
\]と導出することができます。
(2) 分散
確率密度関数 \( f(t) \) の分散は、次のように計算できるのでしたね。\[\begin{align*}
V(X) & = E(X^2) - \left\{ E(X) \right\}^2
\\ & = \int^{\infty}_{- \infty} t^2 f(t) \ dt - \left\{ E(X) \right\}^2
\end{align*}\]
実際に、\( E(X^2) \) を計算してみましょう。\[\begin{align*}
E(X) & = \int^{\infty}_{- \infty} t^2 f(t) \ dt
\\ & = \int^{\infty}_{0} t^2 \lambda e^{- \lambda t} \ dt
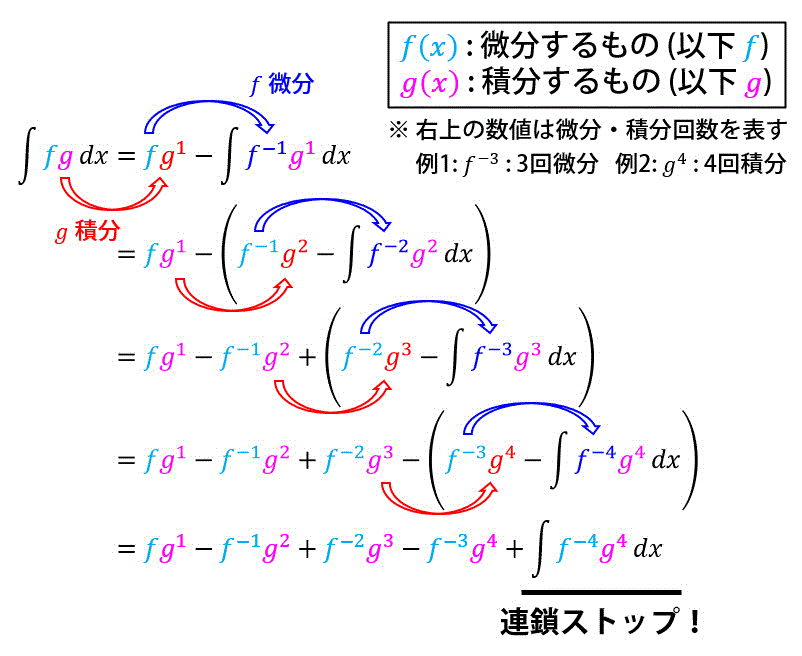
\\ & = \lim_{R \to \infty } \int^{\infty}_{0} \lambda \textcolor{blue}{ \underbrace{ t^2 }_{ \mathrm{微分} } } \textcolor{red}{ \underbrace{ e^{- \lambda t} }_{ \mathrm{積分} } } \ dt
\\ & = \lim_{R \to \infty } \lambda \left[ \textcolor{blue}{ t^2 } \textcolor{red}{ \left( - \frac{1}{\lambda} e^{- \lambda t} \right) } - \textcolor{blue}{2t} \textcolor{red}{ \left( \frac{1}{\lambda^2} e^{- \lambda t} \right) } + \textcolor{blue}{2} \textcolor{red}{ \left( - \frac{1}{\lambda^3} e^{- \lambda t} \right) } \right]^{R}_{0}
\\ & = \lambda \lim_{R \to \infty} \left[ - \frac{t^2 \lambda^2 + 2t \lambda + 2}{\lambda^3 e^{\lambda t}} \right]^{R}_{0}
\\ & = \lambda \lim_{R \to \infty} - \frac{R^2 \lambda^2 + 2R \lambda + 2}{\lambda^3 e^{\lambda R}} - \left( - \frac{0^2 \lambda^2 + 2 \cdot 0 \lambda + 2}{\lambda^3 e^{\lambda \cdot 0}} \right)
\\ & = \lambda \lim_{R \to \infty} - \frac{R^2 \lambda^2 + 2R \lambda + 2}{\lambda^3 e^{\lambda R}} + \frac{2}{ \lambda^3}
\\ & = \frac{2}{ \lambda^3} \cdot \lambda - \lambda \underbrace{ \lim_{R \to \infty} \frac{R^2 \lambda^2 + 2R \lambda + 2}{\lambda^3 e^{\lambda R}} }_{_{ \mathrm{ロピタルの定理} }}
\\ & = \frac{2}{ \lambda^2} - \lambda \underbrace{ \lim_{R \to \infty} \frac{2R \lambda^2 + 2 \lambda }{\lambda^4 e^{\lambda R}} }_{ \mathrm{ロピタルの定理} }
\\ & = \frac{2}{ \lambda^2} - \lambda \underbrace{ \lim_{R \to \infty} \frac{2\lambda^2 }{\lambda^5 e^{\lambda R}} }_{0}
\\ & = \frac{2}{ \lambda^2}
\end{align*}\]※ 部分積分をする際に、省略公式(ブンブン積分)を使用しています。
よって、確率密度関数 \( f(t) \) の分散を、つぎの通りに導出できます。\[\begin{align*}
V(X) & = E(X^2) - \left\{ E(X) \right\}^2
\\ & = \frac{2}{ \lambda^2} - \left( \frac{1}{ \lambda} \right)^2
\\ & = \frac{2}{ \lambda^2} - \frac{1}{ \lambda^2}
\\ & = \frac{1}{ \lambda^2}
\end{align*}\]
指数分布で表される確率変数 \( X \) の期待値 \( E(X) \)、分散 \( V(X) \) は以下の通りである。\[
E(X) = \frac{1}{ \lambda} , \ \ \ V(X) = \frac{1}{ \lambda^2 }
\]
6. 練習問題にチャレンジ
最後に、練習問題を解いて理解が出来ているか確かめましょう。
桃山先生が営んでいるカフェ「喫茶モモ」では、10分あたり平均1人の来店がある。このとき、(1)~(4)の問いに答えなさい。
(1) 15分以内に客が来店する確率を求めなさい。
(2) 少なくとも30分間、1人も客が来店しない確率を求めなさい。
(3) つぎの客が来るまでの時間に関する期待値 [分] と、分散 [分2]を答えなさい。
(4) つぎの客が来るまでの時間に関する中央値 [分] 、第1四分位数 [分] 、第3四分位数 [分] を答えなさい。
※1 必要であれば、以下の表で与えられる指数関数の値を用いてもよい。
| \( x \) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
|---|---|---|---|---|---|---|
| \( e^x \) | 1.649 | 2.718 | 4.482 | 7.389 | 12.182 | 20.086 |
※2 必要であれば、\( \log 2 = 0.693 \), \( \log 3 = 1.099 \) を用いてもよい。ただし、\( \log \) は \( e \) を底とする対数である。
7. 練習問題の答え
今回は、(3),(4)で [分] 単位で答える問題があるので、1単位時間を1分としましょう。
ここで、10分(=10単位時間)あたり平均1人来店があるので、1単位時間あたりの来店人数は平均0.1人となります。つまり、\( \lambda = \textcolor{red}{0.1} \) となります。
(1)
15分(=15単位時間)に客が来店する確率は、指数分布の累積分布関数\[
F(t) = 1 - e^{- \lambda t}
\]に、\( t = \textcolor{blue}{15} \) を代入したときの値 \( F(15) \) を求めればOKです。
実際に計算すると、つぎのように計算できます。\[\begin{align*}
F(15) & = 1 - e^{- 0.1 \cdot 15}
\\ & = 1 - e^{1.5}
\\ & = 1 - \frac{1}{e^{1.5}}
\\ & \fallingdotseq 1 - \frac{1}{4.482}
\\ & = 1 - 0.223
\\ & = 0.777
\end{align*}\]
よって、15分以内に客が来店する確率は 0.78 となります。
(2)
少なくとも30分間(=30単位時間)、1人も客が来店しない確率は、\( t = \textcolor{blue}{30} \) での累積分布関数 \( F(30) \) の補集合、つまり \( 1 - F(30) \) で計算できます。
ここで、\( \lambda = 0.1 \), \( t = 30 \) を累積分布関数\[
F(t) = 1 - e^{- \lambda t}
\]に入れて計算してみましょう。
すると、つぎのように計算ができます。\[\begin{align*}
F(30) & = 1 - e^{- 0.1 \cdot 30}
\\ & = 1 - e^{-3}
\\ & = 1 - \frac{1}{e^3}
\end{align*}\]
よって、\[\begin{align*}
1 - F(30) & = 1 - \left( 1 - \frac{1}{e^3} \right)
\\ & = \frac{1}{e^3}
\\ & \fallingdotseq \frac{1}{20.086}
\\ & = 0.050
\end{align*}\]と計算できるため、少なくとも30分間、1人も客が来店しない確率は0.05と求められます。
(3)
確率変数 \( X \) が指数分布に従う場合、期待値 \( E(X) \), 分散 \( V(X) \) は次のように計算ができます。\[
E(X) = \frac{1}{\lambda}, \ \ \ V(X) = \frac{1}{\lambda^2}
\]
この式に \( \lambda = 0.1 \) を代入すると、つぎの客が来るまでの期待値と分散を求めることができます。
実際に代入すると、\[\begin{align*}
E(X) & = \frac{1}{ \lambda }
\\ & = \frac{1}{ 0.1 }
\\ & = 10
\end{align*}\]\[\begin{align*}
V(X) & = \frac{1}{ \lambda^2 }
\\ & = \frac{1}{ 0.1^2 }
\\ & = \frac{1}{0.01}
\\ & = 100
\end{align*}\]となるため、期待値は 10[分]、分散は100[分2]と求められます。
(4)
中央値
累積分布関数が以下の値となるときの \( t \) の値を求めればOKです。\[
F(t) = \frac{1}{2}
\]
実際に、\( \lambda = 0.1 \) を累積分布関数に入れて \( t \) の値を計算していきましょう。\[
1 - e^{- \lambda t} = \frac{1}{2}
\]\[
- e^{- \lambda t } = - \frac{1}{2}
\]\[
e^{- \lambda t} = \frac{1}{2}
\]\[
\log e^{- \lambda t} = \log \frac{1}{2}
\]\[
- \lambda t = - \log 2
\]\[\begin{align*}
t & = \frac{1}{\lambda} \log 2
\\ & = \frac{1}{0.1} \log 2
\\ & = 10 \log 2
\\ & \fallingdotseq 10 \cdot 0.693
\\ & = 6.93
\end{align*}\]
よって、中央値は6.93[分]となります。
第1四分位数
累積分布関数が以下の値となるときの \( t \) の値を求めればOKです。\[
F(t) = \frac{1}{4}
\]
中央値のときと同じように、\( \lambda = 0.1 \) を累積分布関数に入れて \( t \) の値を計算していきましょう。\[
1 - e^{- \lambda t} = \frac{1}{4}
\]\[
- e^{- \lambda t } = - \frac{3}{4}
\]\[
e^{- \lambda t} = \frac{3}{4}
\]\[
\log e^{- \lambda t} = \log \frac{3}{4}
\]\[
- \lambda t = \log 3 - \log 4
\]\[\begin{align*}
t & = \frac{1}{\lambda} ( \log 4 - \log 3 )
\\ & = \frac{1}{0.1} ( 2 \log 2 - \log 3)
\\ & = 10 ( 2 \log 2 - \log 3)
\\ & \fallingdotseq 10 ( 2 \cdot 0.693 - 1.099)
\\ & = 10 \cdot 0.287
\\ & = 2.87
\end{align*}\]
よって、第1四分位数は2.87[分]となります。
第3四分位数
累積分布関数が以下の値となるときの \( t \) の値を求めればOKです。\[
F(t) = \frac{3}{4}
\]
同じように、\( \lambda = 0.1 \) を累積分布関数に入れて \( t \) の値を計算していきましょう。\[
1 - e^{- \lambda t} = \frac{3}{4}
\]\[
- e^{- \lambda t } = - \frac{1}{4}
\]\[
e^{- \lambda t} = \frac{1}{4}
\]\[
\log e^{- \lambda t} = \log \frac{1}{4}
\]\[
- \lambda t = - \log 4
\]\[\begin{align*}
t & = \frac{1}{\lambda} \log 4
\\ & = \frac{1}{0.1} 2 \log 2
\\ & = 20 \log 2
\\ & \fallingdotseq 20 \cdot 0.693
\\ & = 13.86
\end{align*}\]
よって、第3四分位数は13.86[分]となります。
注釈
| ↑1 | 累積分布関数とは、ある確率変数が特定の値以下になる確率を表す関数です |
|---|
関連広告・スポンサードリンク