スポンサードリンク
こんにちは、ももやまです。
今回が双曲線関数としては最終回となります。なので、もうひと踏ん張りです。
最終回となる今回は、逆双曲線関数(双曲線関数の逆関数)について勉強していきましょう。
過去の双曲線関数の記事の内容を読みたい方は、下のリンクをご覧ください。
[双曲線関数の1回目] 双曲線関数のいろは目次
(1) 双曲線の逆三角関数とは
三角関数の場合、逆関数(逆三角関数)を \( \sin^{-1} x \), \( \cos^{-1} x \), \( \tan^{-1} x \) のように-1乗表記で表すことができるのでしたね[1] \( ( \sin x )^{-1} \) と間違えないために \( \arcsin x \), \( \arccos x \), \( \arctan x \) のように arc 表記で逆三角関数を表記することもあります。。
例えば、\( y = \sin^{-1} x \) は、\( x = \sin y \) と同じ式を表します。
同じように双曲線関数 \( \sinh x \), \( \cosh x \), \( \tanh x \) の逆関数も、三角関数のときと同じように \( \sinh^{-1} x \), \( \cosh^{-1} x \), \( \tanh^{-1} x \) と-1乗表記で表現され、逆双曲線関数と呼ばれます。
表記例を見てみましょう。\[\begin{align*}
y = \sinh^{-1} x \ \ \ & \Leftrightarrow \ \ \ x = \sinh y \\
y = \cosh^{-1} x \ \ \ & \Leftrightarrow \ \ \ x = \cosh y \\
y = \tanh^{-1} x \ \ \ & \Leftrightarrow \ \ \ x = \tanh y
\end{align*}\]
※ \( ( \sinh x)^{-1} \) などと読み間違えを防ぐために \( \sinh^{-1} x \), \( \cosh^{-1} x \), \( \tanh^{-1} x \) を \( \arcsin x \), \( \arccos x \), \( \arctan x \) などと表記することもあります。
(2) 逆双曲線関数の定義域・値域
逆三角関数のときと同じように、逆双曲線関数でも定義域、値域の範囲を考える必要があります[2]例えば \( \sinh^{-1} x \) であれば、\( x \) が取りうる値の範囲を定義域、\( \sinh^{-1} x \) が取りうる値の範囲が値域となります。。
そのために、まずは双曲線関数の定義域と値域を考えましょう。
まず双曲線関数の定義域ですが、これは\[\begin{align*}
\sinh x & = \frac{ e^{x} - e^{-x} }{2} \\
\cosh x & = \frac{ e^{x} + e^{-x} }{2} \\
\tanh x & = \frac{ \sinh x }{ \cosh x }
\\ & = \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} }
\end{align*}\]であることから、(実数範囲の)どのような \( x \) でも双曲線関数 \( \sinh x \), \( \cosh x \), \( \tanh x \) の値が定義されることがわかりますね[3]\( \tanh x \) は分母が0になる \( x \) がないかを確かめる必要がありますが、\( e^{x} + e^{-x} \) が0になることはないので \( \tanh x \) … Continue reading。
ただし、\( y = \cosh^{-1} x \), つまり \( x = \cosh y \) については \( y \geqq 0 \), \( y \leqq 0 \) で場合分けをしないと、\( y \) の値が1つに確定しません。
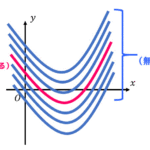
ここで、\( x = \cosh y \) のグラフを描写してみました。このグラフで「\( y \) の値が1つに確定しない例」を見てみましょう。
例えば、\( x = 6 \) の場合、\( x = \cosh y \) を満たす \( y \) は \( y \geqq 0 \) に1つ、\( y \leqq 0 \) に1つ、合計2つありますね。
そのため、\( \cosh^{-1} x \) だけは定義域を \( x \geqq 0 \) と制限します。制限することにより、\( x \) と対応する \( y \) の値を1つにすることができます。
つぎに、逆双曲線関数の値域はグラフを考えると非常にわかりやすいです。
(\( \sinh^{-1} x \) がピンク色、 \( \cosh^{-1} x \) が水色、\( \tanh^{-1} x \) が緑色です。)
グラフより、\( \sinh x \) の値域は実数範囲すべて、\( \cosh x \), \( \tanh x \) の値域はそれぞれ\[
1 \leqq \cosh x
\]\[
-1 < \tanh x < 1
\]となることがわかります。
よって、逆双曲線関数\[\begin{align*}
y = \sinh^{-1} x \ \ \ & \Leftrightarrow \ \ \ x = \sinh y \\
y = \cosh^{-1} x \ \ \ & \Leftrightarrow \ \ \ x = \cosh y \\
y = \tanh^{-1} x \ \ \ & \Leftrightarrow \ \ \ x = \tanh y
\end{align*}\]の定義域、値域は下の表の通りになります。
| 逆双曲線関数 | 定義域 | 値域 |
|---|---|---|
| \( y = \sinh^{-1} x \) | 実数全体 | 実数全体 |
| \( y = \cosh^{-1} x \) | \( 1 \leqq x \) | \( 0 \leqq x \) |
| \( y = \tanh^{-1} x \) | \( -1 < x < 1 \) | 実数全体 |
(3) 逆双曲線関数の書き換え
つぎに、逆双曲線関数 \( \sinh^{-1} x \), \( \cosh^{-1} x \), \( \tanh^{-1} x \) を皆さんが知っている他の関数で書きかえてみましょう。
\( \sinh^{-1} x \) の書き換え
\( y = \sinh^{-1} x \) とおきましょう。
すると、\( x = \sinh y \) となりますね。つまり、\[\begin{align*}
x & = \sinh y
\\ & = \frac{ e^y - e^{-y} }{2}
\end{align*}\]となります。
この式を、\[\begin{align*}
x & = \frac{e^y - e^{-y}}{2} \\
2e^{y} \cdot x & = 2e^{y} \cdot \frac{e^y - e^{-y}}{2} \\
2 x e^{y} & = e^{2y} - 1 \\
e^{2y} - 2x e^{y} + 1 & = 0
\end{align*}\]としたうえで、\( t = e^y \) とおきます。
( \( t > 0 \) に注意 )
すると、\[
t^2 - 2x t + 1 = 0
\]となり、\( t \) に関する2次方程式になりますね。
( \( x \) は2次方程式を解き終わるまで定数だと思ってください)
あとはこれを解の公式[4]連立方程式 \( ax^2 + bx + c = 0 \) の解を\[
x = \frac{-b \pm \sqrt{ b^2 - 4ac} }{2a}
\]と機械的に求められる公式。で解くことで\[
t = x \pm \sqrt{x^2 + 1}
\]と求められますね。さらに \( t > 0 \) より、\[\begin{align*}
t & = x + \sqrt{x^2 + 1} \\
e^y & = x + \sqrt{x^2 + 1} \\
y & = \log (x + \sqrt{x^2 + 1} )
\end{align*}\]となるため、\[\begin{align*}
y & = \sinh^{-1} x
\\ & = \log (x + \sqrt{x^2 + 1} )
\end{align*}\]と書き変えることができます。
\( \cosh^{-1} x \) の書き換え
※ 基本的な導出手順は \( \sinh^{-1} \) のときと同じですが、\( \cosh^{-1} x \) の定義域が \( x \geqq 1 \)、値域が \( y \geqq 0 \) であることに注意しましょう。
\( y = \cosh^{-1} x \) とおくと、\( x = \cosh y \) となりますね。
つまり、\[\begin{align*}
x & = \cosh y
\\ & = \frac{ e^y + e^{-y} }{2}
\end{align*}\]と変形できますね。
この式を、\[\begin{align*}
x & = \frac{e^y + e^{-y}}{2} \\
2e^{y} \cdot x & = 2e^{y} \cdot \frac{e^y + e^{-y}}{2} \\
2 x e^{y} & = e^{2y} + 1 \\
e^{2y} + 2x e^{y} + 1 & = 0
\end{align*}\]としたうえで、\( t = e^y \) とおきます。
( \( y \geqq 0 \) より、\( t \geqq 1 \) である。)
すると、\[
t^2 + 2x t + 1 = 0
\]となり、\( t \) に関する2次方程式になりますね。
( \( x \) は2次方程式を解き終わるまでは定数)
あとはこれを解の公式で解くことで\[
t = x \pm \sqrt{x^2 - 1}
\]と求められますね。
ここで、\( x - \sqrt{x^2 - 1 } \) が解であると仮定しましょう。すると、\[\begin{align*}
x - \sqrt{x^2 - 1} & \geqq 1 \\
x - 1 & \geqq \sqrt{x^2 - 1 } \\
(x-1)^2 & \geqq x^2 - 1 \\
x^2 - 2x + 1 & \geqq x^2 - 1 \\
-2x & \geqq -2 \\
x & \leqq 1
\end{align*}\]となり、\( x \leqq 1 \) を満たしている必要がありますね。
しかし、\( x \leqq 1 \) の場合、\( x = 1 \) のときを除き、定義域 \( x \geqq 1 \) を満たしておりません[5]\( x = 1 \) のときも、最後に \( \log 0 \) が出てきてしまうため、どっちにしろ \( x - \sqrt{x^2 - 1 } \) は解になりえません。。そのため、\( x - \sqrt{x^2 - 1} \) は解ではありません。(仮定が誤り)
したがって、\( t = x + \sqrt{x^2 - 1} \) となり、\[\begin{align*}
t & = x + \sqrt{x^2 - 1} \\
e^y & = x + \sqrt{x^2 - 1} \\
y & = \log (x + \sqrt{x^2 - 1} )
\end{align*}\]となるため、\[\begin{align*}
y & = \cosh^{-1} x
\\ & = \log (x + \sqrt{x^2 - 1} )
\end{align*}\]と書き変えることができます。
\( \tanh^{-1} x \) の書き換え
\( y = \tanh^{-1} x \) とおくと、\( x = \tanh y \) となりますね。
つまり、\[\begin{align*}
x & = \tanh y
\\ & = \frac{ e^y - e^{-y} }{e^y + e^{-y}}
\\ & = \frac{ e^{2y} - 1 }{ e^{2y} + 1 }
\end{align*}\]と変形できますね。
この式を、\[\begin{align*}
x & =\frac{ e^{2y} - 1 }{ e^{2y} + 1 } \\
(e^{2y} + 1)x & = e^{2y} - 1\\
e^{2y} x - e^{2y} & = -1 - x \ \ \ (e^{2y} \ \mathrm{の項を左辺、それ以外を右辺に}) \\
(x - 1) e^{2y} & = -1 - x \\
e^{2y} & = \frac{-1 - x}{x - 1 }
\\ & = \frac{1+x}{1-x}
\end{align*}\]となりますね。
よって、\[\begin{align*}
2y & = \log \frac{1+x}{1-x} \\
y & = \frac{1}{2} \log \frac{1+x}{1-x}
\end{align*}\]となり、\[\begin{align*}
y & = \tanh^{-1} x
\\ & = \frac{1}{2} \log \frac{1+x}{1-x}
\end{align*}\]を導出することができます。
双曲線関数 \( \sinh x \), \( \cosh x \), \( \tanh x \) の逆関数をそれぞれ \( \sinh^{-1} x \), \( \cosh^{-1} x \), \( \tanh^{-1} x \) と表記する。
この逆双曲線関数 \( \sinh^{-1} x \), \( \cosh^{-1} x \), \( \tanh^{-1} x \) の定義域、および値域は次の表の通りである。
| 逆双曲線関数 | 定義域 | 値域 |
|---|---|---|
| \( y = \sinh^{-1} x \) | 実数全体 | 実数全体 |
| \( y = \cosh^{-1} x \) | \( 1 \leqq x \) | \( 0 \leqq y \) |
| \( y = \tanh^{-1} x \) | \( -1 < x < 1 \) | 実数全体 |
また、逆双曲線関数は\[\begin{align*}
\sinh^{-1} x & = \log \left( x + \sqrt{ x^2 + 1 } \right) \\
\cosh^{-1} x & = \log \left( x + \sqrt{ x^2 - 1 } \right) \\
\tanh^{-1} x & = \frac{1}{2} \log \frac{1+x}{1-x}
\end{align*}\]と自然対数 \( \log \) を用いた形に変形することができる。
逆三角関数 \( \sin^{-1} x \), \( \cos^{-1} x \), \( \tan^{-1} x \) では、定義域のほかに値域も制限されている。
| 逆三角関数 | 定義域 | 値域 |
|---|---|---|
| \( y = \sin^{-1} x \) | \( -1 \leqq x \leqq 1 \) | \[ - \frac{\pi}{2} \leqq y \leqq \frac{\pi}{2} \] |
| \( y = \cos^{-1} x \) | \( -1 \leqq x \leqq 1 \) | \[ 0 \leqq y \leqq \pi \] |
| \( y = \tan{-1} x \) | 実数全体 | \[ - \frac{\pi}{2} < y < \frac{\pi}{2} \] |
(4) 実際に例題を解いてみよう
それでは、実際に例題を解くことで逆双曲線関数に慣れていきましょう。
つぎの(1), (2), (3) の [ ] に当てはまる値を答えなさい。
(1)\[
\sinh 3 = \log [ \ \ \ \ \ \ ]
\]
(2)\[
\cosh 3 = \log [ \ \ \ \ \ \ ]
\]
(3)\[
\tanh \frac{1}{2} = \log [ \ \ \ \ \ \ ]
\]
[解説1]
(1)
\[
\sinh x = \log \left( x + \sqrt{ x^2 + 1 } \right)
\]で \( \log \) の形に直す。
\[\begin{align*}
\sinh 3 & = \log \left( 3 + \sqrt{ 3^2 + 1 } \right)
\\ & = \log \left( \textcolor{red}{3 + \sqrt{10}} \right)
\end{align*}\]※ 赤色の部分が [ ] となる。
(2)
\[
\cosh x = \log \left( x + \sqrt{ x^2 - 1 } \right)
\]で \( \log \) の形に直す。
\[\begin{align*}
\cosh 3 & = \log \left( 3 + \sqrt{ 3^2 - 1 } \right)
\\ & = \log \left( 3 + \sqrt{8} \right)
\\ & = \log \left( \textcolor{red}{3 + 2 \sqrt{2}} \right)
\end{align*}\]※ 赤色の部分が [ ] となる。
(3)
\[
\tanh x = \frac{1}{2} \log \frac{1+x}{1-x}
\]で \( \log \) の形に直す。
\[\begin{align*}
\tanh 3 & = \frac{1}{2} \log \frac{1+\frac{1}{2}}{1-\frac{1}{2}}
\\ & = \frac{1}{2} \log \frac{\frac{3}{2}}{\frac{1}{2}}
\\ & = \frac{1}{2} \log 3
\\ & = \log \textcolor{red}{ \sqrt{3} }
\end{align*}\]※ 赤色の部分が [ ] となる。
スポンサードリンク
2. 逆双曲線関数の微分
それでは、逆双曲線関数の微分公式を見ていきましょう。
(逆三角関数と比較も載せています。)
(1) 逆双曲線関数の微分公式
★ ベースの公式\[\begin{align*}
\frac{d}{dx} \sinh^{-1} x & = \frac{1}{ \sqrt{x^2 + 1} } \\
\frac{d}{dx} \cosh^{-1} x & = \frac{1}{ \sqrt{x^2 - 1} } \\
\frac{d}{dx} \tanh^{-1} x & = \frac{1}{1-x^2}
\end{align*}\]
★ 公式拡張Ver\[\begin{align*}
\frac{d}{dx} \sinh^{-1} f(x) & = \frac{f'(x)}{ \sqrt{ \left\{ f(x) \right\}^2 + 1} } \\
\frac{d}{dx} \cosh^{-1} f(x) & = \frac{f'(x)}{ \sqrt{ \left\{ f(x) \right\}^2 - 1} } \\
\frac{d}{dx} \tanh^{-1} f(x) & = \frac{f'(x)}{1 - \left\{ f(x) \right\}^2}
\end{align*}\]※ \( a \) は定数
※ 合成関数の微分を使えば簡単に「公式拡張Ver」を導出できるので、ベースの公式で頭に入れてもOK
★ ベースの公式\[\begin{align*}
\frac{d}{dx} \sin^{-1} x & = \frac{1}{ \sqrt{1 - x^2} } \\
\frac{d}{dx} \cos^{-1} x & = - \frac{1}{ \sqrt{1 - x^2} }\\
\frac{d}{dx} \tan^{-1} x & = \frac{1}{1 + x^2}
\end{align*}\]
★ 公式拡張Ver\[\begin{align*}
\frac{d}{dx} \sin^{-1} f(x) & = \frac{f'(x)}{ \sqrt{1 - \left\{ f(x) \right\}^2 } } \\
\frac{d}{dx} \cos^{-1} f(x) & = - \frac{f'(x)}{ \sqrt{1 - \left\{ f(x) \right\}^2 } } \\
\frac{d}{dx} \tan^{-1} f(x) & = \frac{f'(x)}{1 + \left\{ f(x) \right\}^2}
\end{align*}\]
(2) 公式の導出
\( \sinh^{-1} f(x) \) の導出
まずは、\( \sinh^{-1} x \) の微分を求める。
\[\begin{align*}
\frac{d}{dx} \sinh^{-1} x & = \frac{d}{dx} \log \left( x + \sqrt{ x^2 + 1 } \right)
\\ & = \frac{1 + \frac{1}{2} \cdot 2x \cdot \frac{1}{ \sqrt{x^2+1} } }{x + \sqrt{ x^2 + 1 }}
\\ & = \frac{\frac{x + \sqrt{x^2 + 1} }{ \sqrt{x^2+1} } }{x + \sqrt{ x^2 + 1 }}
\\ & = \frac{1}{ \sqrt{x^2+1} }
\end{align*}\]
つぎに \( \sinh^{-1} f(x) \) の微分を求めるために、\( t = f(x) \) とおく。
すると、\( y = \sinh^{-1} t \) となり、\[
\frac{dt}{dx} = f'(x) , \ \ \ \frac{dy}{dt} = \frac{1}{ \sqrt{t^2 + 1} }
\]となる。
よって、\[\begin{align*}
\frac{d}{dx} \sinh^{-1} f(x) & = \frac{dy}{dt} \cdot \frac{dt}{dx}
\\ & = f'(x) \cdot \frac{1}{ \sqrt{t^2 + 1} }
\\ & = \frac{f'(x)}{ \sqrt{ t^2 + 1 } }
\\ & = \frac{f'(x)}{ \sqrt{ \left\{ f(x) \right\}^2 + 1 } }
\end{align*}\]と求められる。
\( \cosh^{-1} f(x) \) の導出
\( \sinh^{-1} x \) のときと同じく、まずは、\( \cosh^{-1} x \) の微分を求める。
\[\begin{align*}
\frac{d}{dx} \cosh^{-1} x & = \frac{d}{dx} \log \left( x + \sqrt{ x^2 - 1 } \right)
\\ & = \frac{1 + \frac{1}{2} \cdot 2x \cdot \frac{1}{ \sqrt{x^2-1} } }{x + \sqrt{ x^2 - 1 }}
\\ & = \frac{\frac{x + \sqrt{x^2 - 1} }{ \sqrt{x^2-1} } }{x + \sqrt{ x^2 - 1 }}
\\ & = \frac{1}{ \sqrt{x^2-1} }
\end{align*}\]※符号以外は計算過程は \( \sinh^{-1} x \) のときと全く同じ
つぎに \( \cosh^{-1} f(x) \) の微分を求めるために、\( t = f(x) \) とおく。
すると、\( y = \cosh^{-1} t \) となり、\[
\frac{dt}{dx} = f'(x) , \ \ \ \frac{dy}{dt} = \frac{1}{ \sqrt{t^2 - 1} }
\]となる。
よって、\[\begin{align*}
\frac{d}{dx} \cosh^{-1} f(x) & = \frac{dy}{dt} \cdot \frac{dt}{dx}
\\ & = f'(x) \cdot \frac{1}{ \sqrt{t^2 - 1} }
\\ & = \frac{f'(x)}{ \sqrt{ t^2 - 1 } }
\\ & = \frac{f'(x)}{ \sqrt{ \left\{ f(x) \right\}^2 - 1 } }
\end{align*}\]と求められる。
\( \tanh^{-1} f(x) \) の導出
今までと同じように \( \tanh^{-1} x \) の微分を求める。
\[\begin{align*}
\frac{d}{dx} \tanh^{-1} x & = \frac{d}{dx} \frac{1}{2} \log \frac{1+x}{1-x}
\\ & = \frac{d}{dx} \frac{1}{2} \log (1+x) - \frac{1}{2} \log (1-x)
\\ & = \frac{1}{2} \cdot \frac{1}{1+x} - \frac{1}{2} \cdot \frac{-1}{1-x}
\\ & = \frac{1}{2} \cdot \frac{(1-x) + (1+x)}{(1+x)(1-x)}
\\ & = \frac{1}{2} \cdot \frac{2}{1-x^2}
\\ & = \frac{1}{1-x^2}
\end{align*}\]
つぎに \( \tanh^{-1} f(x) \) の微分を求めるために、\( t = f(x) \) とおく。
(ここからは \( \sinh^{-1} x \), \( \cosh^{-1} x \) と同じ流れ)
すると、\( y = \tanh^{-1} t \) となり、\[
\frac{dt}{dx} = f'(x) , \ \ \ \frac{dy}{dt} = \frac{1}{ 1 - t^2 }
\]となる。
よって、\[\begin{align*}
\frac{d}{dx} \tanh^{-1} f(x) & = \frac{dy}{dt} \cdot \frac{dt}{dx}
\\ & = f'(x) \cdot \frac{1}{ \sqrt{1 - t^2} }
\\ & = \frac{f'(x)}{ \sqrt{1 - t^2} }
\\ & = \frac{f'(x)}{ \sqrt{1 - \left\{ f(x) \right\}^2} }
\end{align*}\]と求められる。
(3) 例題で実際に計算してみよう
それでは、実際に例題で実際に計算練習をしてみましょう。
つぎの(1), (2) で表される関数 \( f(x) \) の導関数を求めなさい。
(1)\[
f(x) = \tanh^{-1} 3x
\]
(2)\[
f(x) = \sinh^{-1} x^2
\]
[解説2]
(1)
公式\[
\frac{d}{dx} \tanh^{-1} g(x) = \frac{g'(x)}{1- \left\{ g(x) \right\}^2}
\]に、\( f(x) = 3x \) を代入すればOK。
(問題文の \( f(x) \) と紛らわしくなるので、公式内は \( g(x) \) で表記しています。)
ここで、\( g'(x) = 3 \) なので、\[\begin{align*}
f(x) & = \tanh^{-1} 3x
\\ & = \frac{3}{1- \left( 3x \right)^2}
\\ & = \frac{3}{1 - 9x^2}
\end{align*}\]と計算できる。
(2)
公式\[
\frac{d}{dx} \sinh^{-1} g(x) = \frac{g'(x)}{ \sqrt{ \left\{ g(x) \right\}^2 + 1} }
\]に \( f(x) = x^2 \) を代入すればOK。
(問題文の \( f(x) \) と紛らわしくなるので、公式内は \( g(x) \) で表記しています。)
ここで、\( g'(x) = 2x \) なので、\[\begin{align*}
f'(x) & = \sinh^{-1} x^2
\\ & = \frac{2x}{ \sqrt{ \left( x^2 \right)^2 + 1 } }
\\ & = \frac{2x}{ \sqrt{ x^4 + 1 } }
\end{align*}\]と計算できる。
スポンサードリンク
3. 逆双曲線関数の積分
(1) 積分すると逆双曲線関数になる関数
2章「逆双曲線関数の微分」の公式から、逆双曲線関数を使うことで、高校数学では非常に難しい積分であった\[
\int \frac{1}{ \sqrt{x^2 + a^2} } \ dx , \ \ \ \int \frac{1}{ \sqrt{x^2 - a^2} } \ dx
\]を瞬時に計算できるようになります。
★ ベースの公式\[\begin{align*}
\int \frac{1}{ \sqrt{ x^2 + 1} } \ dx & = \sinh^{-1} x + C
\\ & = \log \left( x + \sqrt{x^2 + 1} \right) + C' \\
\int \frac{1}{ \sqrt{ x^2 - 1} } \ dx & = \cosh^{-1} x + C
\\ & = \log \left( x + \sqrt{x^2 - 1} \right) + C' \ \ \ ( x \geqq 0 ) \\
\int \frac{1}{1 - x^2} \ dx & = \tanh^{-1} x + C
\\ & = \log \frac{1+x}{1-x} \ \ \ (-1 < x < 1)
\end{align*}\]
★ 公式拡張 Ver\[\begin{align*}
\int \frac{1}{ \sqrt{ x^2 + a^2} } \ dx & = \sinh^{-1} \frac{x}{a} + C
\\ & = \log \left( x + \sqrt{x^2 + a^2} \right) + C' \\
\int \frac{1}{ \sqrt{ x^2 - a^2} } \ dx & = \cosh^{-1} \frac{x}{a} + C
\\ & = \log \left( x + \sqrt{x^2 - a^2} \right) + C' \ \ \ ( x \geqq 0 ) \\
\int \frac{a}{a^2 - x^2} \ dx & = \tanh^{-1} \frac{x}{a} + C
\\ & = \log \frac{a+x}{a-x} \ \ \ (-1 < x < 1)
\end{align*}\]※ \( a \) は正の定数
※1 \( C \), \( C' \) は積分定数
(逆双曲線関数から \( \log \) の形に直す際に、積分定数をおきなおすため、\( C \), \( C' \) の2種類の積分定数を用いている)
※2 積分の条件となっている \( x \geqq 0 \) もしくは \( -1 < x < 1 \) を取り除きたい場合、\( \log \) の中身が負になってしまう可能性があるため、\[\begin{align*}
\int \frac{1}{ \sqrt{ x^2 - a^2} } \ dx & = \log \left| x + \sqrt{x^2 - a^2} \right| + C'\\
\int \frac{a}{a^2 - x^2} \ dx & = \log \left| \frac{a+x}{a-x} \right| + C
\end{align*}\]と絶対値表記を付ける必要があります。
(条件を取った場合、逆双曲線関数の定義域を満たさなくなるため、逆双曲線関数による表記は不可能になる)
※3 積分の条件がない\[
\int \frac{1}{ \sqrt{ x^2 + a^2} } \ dx = \log \left( x + \sqrt{x^2 + a^2} \right) + C'
\]は \( \log \) の中身が負になることがない[6]常に \( \sqrt{x^2+a^2} > x \)、つまり \( \sqrt{x^2 +1} - x > 0 \) が成立するからです。ため、絶対値表記は不要です。
[導出]
微分公式\[\begin{align*}
\frac{d}{dx} \sinh^{-1} x & = \frac{1}{ \sqrt{x^2 + 1} } \\
\frac{d}{dx} \cosh^{-1} x & = \frac{1}{ \sqrt{x^2 - 1} } \\
\frac{d}{dx} \tanh^{-1} x & = \frac{1}{1-x^2}
\end{align*}\]より、積分定数 \( C \) を用いた次の2つの式も成立する。\[\begin{align*}
\int \frac{1}{ \sqrt{x^2 + 1} } \ dx & = \sinh^{-1} x + C
\\ & = \log \left(x + \sqrt{x^2 + 1} \right) \\
\int \frac{1}{ \sqrt{x^2 - 1 } } \ dx & = \cosh^{-1} x + C
\\ & = \log \left(x + \sqrt{x^2 - 1} \right) \\
\int \frac{1}{1-x^2} \ dx & = \tanh^{-1} x + C
\\ & = \log \frac{1+x}{1-x}
\end{align*}\]
ここで、\( x = ay \), つまり \( y = \frac{x}{a} \) とおく。すると、\( dx = a \ dy \) が成立する。
よって、\[\begin{align*}
\int \frac{1}{ \sqrt{x^2 + a^2} } \ dx & = \int \frac{1}{ \sqrt{(ax)^2 + a^2} } \cdot a \ dy
\\ & = \int \frac{a}{ \sqrt{ a^2 (x^2 + 1) } } \ dy
\\ & = \int \frac{a}{ a \sqrt{ x^2 + 1 } } \ dy
\\ & = \int \frac{1}{ \sqrt{ y^2 + 1 } } \ dy
\\ & = \sinh^{-1} y + C
\\ & = \sinh^{-1} \frac{x}{a} + C
\end{align*}\]
\[\begin{align*}
\int \frac{1}{ \sqrt{x^2 - a^2} } \ dx & = \int \frac{1}{ \sqrt{(ax)^2 - a^2} } \cdot a \ dy
\\ & = \int \frac{a}{ \sqrt{ a^2 (x^2 - 1) } } \ dy
\\ & = \int \frac{a}{ a \sqrt{ x^2 - 1 } } \ dy
\\ & = \int \frac{1}{ \sqrt{ y^2 - 1 } } \ dy
\\ & = \cosh^{-1} y + C
\\ & = \cosh^{-1} \frac{x}{a} + C
\end{align*}\] と導出できる。
\[\begin{align*}
\int \frac{a}{ a^2 - x^2 } \ dx & = \int \frac{a}{ a^2 - (ay)^2 } \cdot a \ dy
\\ & = \int \frac{a^2}{ a^2 (1 - y^2) } \ dy
\\ & = \int \frac{1}{ 1-y^2 } \ dy
\\ & = \tanh^{-1} y + C
\\ & = \tanh^{-1} \frac{x}{a} + C
\end{align*}\] と導出できる。
次に、計算結果を \( \log \) の形に変える。
\[\begin{align*}
\sinh^{-1} \frac{x}{a} + C & = \log \left( \frac{x}{a} + \sqrt{ \left( \frac{x}{a} \right)^2 + 1} \right) + C
\\ & = \log \left( \frac{ x }{ a } + \sqrt{ \frac{x^2}{a^2} + 1 } \right)
\\ & = \log \left( \frac{ x }{ a } + \frac{1}{a} \sqrt{a^2 \left( \frac{x^2}{a^2} + 1 \right) } \right) + C
\\ & = \log \left( \frac{ x }{ a } + \frac{1}{a} \sqrt{ x^2 + a^2 } \right) + C
\\ & = \log \frac{ x + \sqrt{x^2 + a^2} }{a} + C
\\ & = \log ( x + \sqrt{x^2 + a^2} ) - \underbrace{ \log a + C }_{ - C' \ \mathrm{とおく} }
\\ & = \log ( x + \sqrt{x^2 + a^2} ) + C'
\end{align*}\]
\[\begin{align*}
\cosh^{-1} \frac{x}{a} + C & = \log \left( \frac{x}{a} + \sqrt{ \left( \frac{x}{a} \right)^2 - 1} \right) + C
\\ & = \log \left( \frac{ x }{ a } + \sqrt{ \frac{x^2}{a^2} - 1 } \right)
\\ & = \log \left( \frac{ x }{ a } + \frac{1}{a} \sqrt{a^2 \left( \frac{x^2}{a^2} - 1 \right) } \right) + C
\\ & = \log \left( \frac{ x }{ a } + \frac{1}{a} \sqrt{ x^2 - a^2 } \right) + C
\\ & = \log \frac{ x + \sqrt{x^2 - a^2} }{a} + C
\\ & = \log ( x + \sqrt{x^2 - a^2} ) - \underbrace{ \log a + C }_{ - C' \ \mathrm{とおく} }
\\ & = \log ( x + \sqrt{x^2 - a^2} ) + C'
\end{align*}\]
\[\begin{align*}
\tanh^{-1} \frac{x}{a} + C & = \log \frac{1 + \frac{x}{a}}{1 - \frac{x}{a}} + C
\\ & = \log \frac{\frac{a+x}{a}}{\frac{a-x}{a}} + C
\\ & = \log \frac{a+x}{a-x} + C
\end{align*}\]※ 積分定数 \( C \) をおきなおしていないため、\( C' \) は出てこない。
よって、2つの積分定数 \( C \), \( C' \) を用いて積分公式\[\begin{align*}
\int \frac{1}{ \sqrt{ x^2 + a^2} } \ dx & = \sinh^{-1} \frac{x}{a} + C
\\ & = \log \left( x + \sqrt{x^2 + a^2} \right) + C'
\end{align*}\]\[\begin{align*}
\int \frac{1}{ \sqrt{ x^2 - a^2} } \ dx & = \cosh^{-1} \frac{x}{a} + C
\\ & = \log \left( x + \sqrt{x^2 - a^2} \right) + C'
\int \frac{a}{ a^2 - x^2 } \ dx & = \tanh^{-1} \frac{x}{a} + C
\\ & = \log \frac{a+x}{a-x} + C
\end{align*}\]を導出できる。
(2) \( \sqrt{ x^2 \pm a^2} \) の積分公式導出
逆双曲線関数は、高校数学最難関の公式\[\begin{align*}
\int \sqrt{x^2 + a^2} \ dx & = \frac{1}{2} \left\{ x \sqrt{x^2 + a^2} + a^2 \log \left( x + \sqrt{ x^2 + a^2 } \right) \right\} \\
\int \sqrt{x^2 - a^2} \ dx & = \frac{1}{2} \left\{ x \sqrt{x^2 - a^2} - a^2 \log \left( x + \sqrt{ x^2 - a^2 } \right) \right\}
\end{align*}\]と大きなつながりを持ちます[7]厳密には、\( x + \sqrt{x^2 + a^2} \), \( x + \sqrt{x^2 - a^2} \) が負になる可能性があるので\[\begin{align*}\int \sqrt{x^2 + a^2} \ dx & = \frac{1}{2} \left( x \sqrt{x^2 + a^2} … Continue reading。
実際に導出することで確認していきましょう。
\( \sqrt{ x^2 + a^2 } \) の積分
\[\begin{align*}
\int \sqrt{x^2 + a^2} \ dx & = x \sqrt{x^2 + a^2} - \int x \cdot \frac{1}{2} \cdot \frac{2x}{ \sqrt{x^2 + a^2}}
\\ & = x \sqrt{x^2 + a^2} - \int \frac{x^2}{ \sqrt{ x^2 + a^2 } } \ dx
\\ & = x \sqrt{x^2 + a^2} - \int \frac{(x^2 + a^2) - a^2}{ \sqrt{ x^2 + a^2 } } \ dx
\\ & = x \sqrt{x^2 + a^2} - \left( \int \sqrt{x^2 + a^2} \ dx - \int \frac{a^2}{ \sqrt{x^2 + a^2} } \ dx \right)
\\ & = x \sqrt{x^2 + a^2} - \int \sqrt{x^2 + a^2} \ dx + a^2 \int \frac{1}{ \sqrt{x^2 + a^2} } \ dx
\end{align*}\]となるので、積分定数 \( C \), \( C' \) を用いて\[\begin{align*}
2 \int \sqrt{x^2 + a^2} \ dx & = x \sqrt{x^2 + a^2} + a^2 \int \frac{1}{ \sqrt{x^2 + a^2} } \ dx
\\ & = x \sqrt{x^2 + a^2} + a^2 \sinh^{-1} \frac{x}{a} + C
\\ & = x \sqrt{x^2 + a^2} + a^2 \log \left( x + \sqrt{x^2 + a^2} \right) + C'
\end{align*}\]の関係式が導ける。
最後に積分定数を \( C'' \), \( C''' \) とつけかえたら\[\begin{align*}
\int \sqrt{x^2 + a^2} \ dx & = \frac{1}{2} \left( x \sqrt{x^2 + a^2} + a^2 \sinh^{-1} \frac{x}{a} \right) + C''
\\ & = \frac{1}{2} \left\{ x \sqrt{x^2 + a^2} + a^2 \log \left( x + \sqrt{x^2 + a^2} \right) \right\} + C'''
\end{align*}\]となり、導出完了。
\( \sqrt{ x^2 - a^2 } \) の積分
\[\begin{align*}
\int \sqrt{x^2 - a^2} \ dx & = x \sqrt{x^2 - a^2} - \int x \cdot \frac{1}{2} \cdot \frac{2x}{ \sqrt{x^2 - a^2}}
\\ & = x \sqrt{x^2 - a^2} - \int \frac{x^2}{ \sqrt{ x^2 - a^2 } } \ dx
\\ & = x \sqrt{x^2 - a^2} - \int \frac{(x^2 - a^2) + a^2}{ \sqrt{ x^2 - a^2 } } \ dx
\\ & = x \sqrt{x^2 - a^2} - \left( \int \sqrt{x^2 + a^2} \ dx + \int \frac{a^2}{ \sqrt{x^2 - a^2} } \ dx \right)
\\ & = x \sqrt{x^2 - a^2} - \int \sqrt{x^2 + a^2} \ dx - a^2 \int \frac{1}{ \sqrt{x^2 - a^2} } \ dx
\end{align*}\]となるので、積分定数 \( C \), \( C' \) を用いて\[\begin{align*}
2 \int \sqrt{x^2 - a^2} \ dx & = x \sqrt{x^2 + a^2} - a^2 \int \frac{1}{ \sqrt{x^2 - a^2} } \ dx
\\ & = x \sqrt{x^2 - a^2} - a^2 \cosh^{-1} \frac{x}{a} + C
\\ & = x \sqrt{x^2 - a^2} - a^2 \log \left( x + \sqrt{x^2 - a^2} \right) + C'
\end{align*}\]の関係式が導ける。
最後に積分定数を \( C'' \), \( C''' \) とつけかえたら\[\begin{align*}
\int \sqrt{x^2 - a^2} \ dx & = \frac{1}{2} \left( x \sqrt{x^2 - a^2} - a^2 \cosh^{-1} \frac{x}{a} \right) + C''
\\ & = \frac{1}{2} \left\{ x \sqrt{x^2 - a^2} - a^2 \log \left( x + \sqrt{x^2 - a^2} \right) \right\} + C'''
\end{align*}\]となり、導出完了。
\[\begin{align*}
\int \sqrt{x^2 + a^2} \ dx & = \frac{1}{2} \left( x \sqrt{x^2 + a^2} + a^2 \sinh^{-1} \frac{x}{a} \right) + C
\\ & = \frac{1}{2} \left\{ x \sqrt{x^2 + a^2} + a^2 \log \left( x + \sqrt{x^2 + a^2} \right) \right\} + C'
\end{align*}\]\[\begin{align*}
\int \sqrt{x^2 - a^2} \ dx & = \frac{1}{2} \left( x \sqrt{x^2 - a^2} - a^2 \cosh^{-1} \frac{x}{a} \right) + C
\\ & = \frac{1}{2} \left\{ x \sqrt{x^2 - a^2} - a^2 \log \left( x + \sqrt{x^2 - a^2} \right) \right\} + C' \ \ \ (x \geqq 1)
\end{align*}\]
※1: \( C \), \( C' \) は積分定数。
※2: \( a \) は正の定数、つまり \( a > 0 \) とする。
※3: 1番目の積分は、常に\( \log \) の中身が正となるため[8]常に \( \sqrt{x^2+a^2} > x \)、つまり \( \sqrt{x^2 +1} - x > 0 \) が成立するからです。、\( \log \) の中身を絶対値表記する必要はない。
※4: 2番目の積分は、\( x \geqq 1 \) という条件を取る場合は、\[
\int \sqrt{x^2 - a^2} \ dx = \frac{1}{2} \left\{ x \sqrt{x^2 + a^2} - a^2 \log \left( x - \sqrt{ x^2 + 1 } \right) \right\} + C'
\]のように \( \log \) の中身を絶対値にする必要がある。
(条件を取った場合、逆双曲線関数の定義域を満たさなくなるため、逆双曲線関数による表記は不可能になる)
\( \sqrt{ x^2 \pm a^2 } \) の積分の計算練習
\[
\int \frac{1}{ \sqrt{x^2 \pm a^2} } \ dx , \ \ \ \int \sqrt{x^2 \pm a^2} \ dx
\]の計算練習を実際にやってみたい人は、下の記事をご覧ください。
(3) 逆双曲線関数の積分
つぎは、逆双曲線関数の積分を見ていきましょう。
いつも通り、公式を紹介してから導出方法を解説していきます。
★ 基本パターン\[\begin{align*}
\int \sinh^{-1} x \ dx & = x \sinh^{-1} x - \sqrt{x^2 + 1} + C \\
\int \cosh^{-1} x \ dx & = x \cosh^{-1} x - \sqrt{x^2 - 1} + C \\
\int \tanh^{-1} x \ dx & = x \tanh^{-1} x + \frac{1}{2} \log ( 1 - x^2 ) + C
\end{align*}\]
★ 拡張Ver\[\begin{align*}
\int \sinh^{-1} ax \ dx & = x \sinh^{-1} ax - \frac{1}{a} \sqrt{(ax)^2 + 1} + C \\
\int \cosh^{-1} ax \ dx & = x \cosh^{-1} ax - \frac{1}{a} \sqrt{(ax)^2 - 1} + C \\
\int \tanh^{-1} ax \ dx & = x \tanh^{-1} ax + \frac{1}{2a} \log ( 1 - x^2 ) + C \\
\end{align*}\]
※1: \( C \) は積分定数
※2: \( a \) は定数、ただし \( a \not = 0 \)。
※3: 3つとも部分積分で簡単に導出できるため、暗記不要
[導出]
(1) \( \sinh^{-1} x \), \( \sinh^{-1} ax \) の積分
まずは、\( \sinh^{-1} x \) の積分を求める。\[\begin{align*}
\int \sinh^{-1} x \ dx & = x \sinh^{-1} x - \int \frac{x}{ \sqrt{x^2+1} } \ dx
\\ & = x \sinh^{-1} x - \frac{1}{2} \int \frac{2}{ \sqrt{x^2+1} } \ dx
\\ & = x \sinh^{-1} x - \frac{1}{2}\cdot 2 \sqrt{x^2 + 1} + C
\\ & = x \sinh^{-1} x - \sqrt{x^2 + 1} + C
\end{align*}\]
同じように \( \sinh^{-1} ax \) も\[\begin{align*}
\int \sinh^{-1} ax \ dx & = x \sinh^{-1} ax - \int x \cdot \frac{a}{ \sqrt{(ax)^2+1} } \ dx
\\ & = x \sinh^{-1} ax - \int \frac{ax}{ \sqrt{a^2 x^2+1} } \ dx
\\ & = x \sinh^{-1} ax - \frac{1}{2a} \int \cdot \frac{2a^2 x}{ \sqrt{a^2 x^2+1} } \ dx
\\ & = x \sinh^{-1} ax - \frac{1}{2a} \cdot 2 \sqrt{a^2 x^2 + 1} + C
\\ & = x \sinh^{-1} ax - \frac{1}{a} \sqrt{(ax)^2 + 1} + C
\end{align*}\]と部分積分で求められる。
(2) \( \cosh^{-1} x \), \( \cosh^{-1} ax \) の積分
まずは、\( \cosh^{-1} x \) の積分を求める。\[\begin{align*}
\int \cosh^{-1} x \ dx & = x \cosh^{-1} x - \int \frac{x}{ \sqrt{x^2-1} } \ dx
\\ & = x \cosh^{-1} x - \frac{1}{2} \int \frac{2x}{ \sqrt{x^2-1} } \ dx
\\ & = x \cosh^{-1} x - \frac{1}{2}\cdot 2 \sqrt{x^2 - 1} + C
\\ & = x \cosh^{-1} x - \sqrt{x^2 - 1} + C
\end{align*}\]
同じように \( \cosh^{-1} ax \) も\[\begin{align*}
\int \cosh^{-1} ax \ dx & = x \cosh^{-1} ax - \int x \cdot \frac{a}{ \sqrt{(ax)^2-1} } \ dx
\\ & = x \cosh^{-1} ax - \int \frac{ax}{ \sqrt{a^2 x^2-1} } \ dx
\\ & = x \cosh^{-1} ax - \frac{1}{2a} \int \cdot \frac{2a^2 x}{ \sqrt{a^2 x^2-1} } \ dx
\\ & = x \cosh^{-1} ax - \frac{1}{2a} \cdot 2 \sqrt{a^2 x^2 - 1} + C
\\ & = x \cosh^{-1} ax - \frac{1}{a} \sqrt{(ax)^2 - 1} + C
\end{align*}\]と部分積分で求められる。
(3) \( \tanh^{-1} x \), \( \tanh^{-1} ax \) の積分
まずは \( \tanh^{-1} x \) から。\[\begin{align*}
\int \tanh^{-1} x \ dx & = x \tanh^{-1} x - \int \frac{x}{1 - x^2} \ dx
\\ & = x \tanh^{-1} x + \frac{1}{2} \int \frac{-2x}{1 - x^2} \ dx
\\ & = x \tanh^{-1} x + \frac{1}{2} \log ( 1 - x^2 ) + C
\end{align*}\]
同じように \( \tanh^{-1} ax \) も\[\begin{align*}
\int \tanh^{-1} ax \ dx & = x \tanh^{-1} ax - \int x \cdot \frac{a}{1 - (ax)^2} \ dx
\\ & = x \tanh^{-1} ax - \int \frac{ax}{1 - a^2 x^2 } \ dx
\\ & = x \tanh^{-1} ax + \frac{1}{2a} \int \frac{- 2a^2 x }{ 1 - a^2 x^2} \ dx
\\ & = x \tanh^{-1} ax + \frac{1}{2a} \log (1 - a^2 x^2 ) + C
\\ & = x \tanh^{-1} ax + \frac{1}{2a} \log \left\{ 1 - (ax)^2 \right\} + C
\end{align*}\]と部分積分で求められる。
※ \( -1 < x < 1 \) なので、\( \log \) の中身は必ず正。なので絶対値は不要。
(3) 例題で実際に計算してみよう
つぎの(1), (2) で表される関数の不定積分を求めなさい。
(1)\[
\int \frac{x^2}{x^2-1} \ dx
\]※ できれば計算結果を逆双曲線関数で表してみましょう。
(2)\[
\sinh^{-1} 3x \ dx
\]
[解説]
(1)\[\begin{align*}
\frac{x^2}{x^2-1} \ dx & = \frac{(x^2-1)+1}{x^2-1}
\\ & = 1 + \frac{1}{x^2-1}
\end{align*}\]に気づけるかがポイント。
気づけてしまえば、あとは\[
\int \frac{1}{1 - x^2} \ dx = \tanh^{-1} x + C
\]の形に楽勝で持ち込める。
よって、積分定数を \( C \) として\[\begin{align*}
\frac{x^2}{x^2-1} \ dx & = \int 1 \ dx + \int \frac{1}{x^2 - 1} \ dx
\\ & = x - \int \frac{1}{1 - x^2} \ dx
\\ & = x - \tanh^{-1} x + C
\\ & \left( = x - \log \frac{1+x}{1-x} \right)
\end{align*}\]となる。
(2)
逆双曲線関数の積分は、部分積分をすればOK。
せっかくなので、公式を使わずに自力で計算してみましょう。
\[\begin{align*}
\sinh^{-1} 3x \ dx & = x \sinh^{-1} 3x - \int x \cdot \frac{3}{ \sqrt{(3x)^2 + 1 } } \ dx
\\ & = x \sinh^{-1} 3x - \int \frac{3x}{ \sqrt{9x^2 + 1 } } \ dx
\\ & = x \sinh^{-1} 3x - \frac{1}{6} \int \frac{18x}{ \sqrt{9x^2 + 1 } } \ dx
\\ & = x \sinh^{-1} 3x - \frac{1}{6} \cdot 2 \sqrt{ 9x^2 + 1 } + C
\\ & = x \sinh^{-1} 3x - \frac{1}{3} \sqrt{ 9x^2 + 1 } + C
\end{align*}\]となる。
スポンサードリンク
4. さいごに
今回、前回、前々回と3回に分けて、逆双曲線関数の様々な内容
- 双曲線関数ってなに?
- 双曲線関数のグラフ
- 双曲線関数の基本変形公式
- 双曲線関数の加法定理
- 双曲線関数の2倍角・3倍角公式
- 双曲線関数の積和公式
- 双曲線関数の微分
- 双曲線関数の積分
- 双曲線関数の極限
- 双曲線関数のマクローリン展開
- 双曲線関数の逆関数
を説明していきました。
分量が多めだったので、双曲線関数について復習する場合は、
- ピンク色の単元
- 水色の単元
- 黒色の単元
の順番に復習していくことをおすすめします。
3回にわたり、双曲線関数の記事をお読みいただきありがとうございました!
注釈
| ↑1 | \( ( \sin x )^{-1} \) と間違えないために \( \arcsin x \), \( \arccos x \), \( \arctan x \) のように arc 表記で逆三角関数を表記することもあります。 |
|---|---|
| ↑2 | 例えば \( \sinh^{-1} x \) であれば、\( x \) が取りうる値の範囲を定義域、\( \sinh^{-1} x \) が取りうる値の範囲が値域となります。 |
| ↑3 | \( \tanh x \) は分母が0になる \( x \) がないかを確かめる必要がありますが、\( e^{x} + e^{-x} \) が0になることはないので \( \tanh x \) も定義域は実数範囲全域となります。 |
| ↑4 | 連立方程式 \( ax^2 + bx + c = 0 \) の解を\[ x = \frac{-b \pm \sqrt{ b^2 - 4ac} }{2a} \]と機械的に求められる公式。 |
| ↑5 | \( x = 1 \) のときも、最後に \( \log 0 \) が出てきてしまうため、どっちにしろ \( x - \sqrt{x^2 - 1 } \) は解になりえません。 |
| ↑6, ↑8 | 常に \( \sqrt{x^2+a^2} > x \)、つまり \( \sqrt{x^2 +1} - x > 0 \) が成立するからです。 |
| ↑7 | 厳密には、\( x + \sqrt{x^2 + a^2} \), \( x + \sqrt{x^2 - a^2} \) が負になる可能性があるので\[\begin{align*} \int \sqrt{x^2 + a^2} \ dx & = \frac{1}{2} \left( x \sqrt{x^2 + a^2} + a^2 \log \left| x + \sqrt{ x^2 + 1 } \right| \right) \\ \int \sqrt{x^2 - a^2} \ dx & = \frac{1}{2} \left( x \sqrt{x^2 - a^2} - \frac{a^2}{2} \log \left| x + \sqrt{ x^2 - 1 } \right| \right) \end{align*}\]と \( \log \) の中身が正になるように絶対値をつけたほうがよい。 |
関連広告・スポンサードリンク