スポンサードリンク
こんにちは、ももやまです。
今回は、
- 中学入試
- 高校入試
- 共通テスト(大学入試)
- SPI(就職試験)
- 基本情報
など、様々な場面で出てくる場合の数、特に「順列と組み合わせの違い」に注目して説明していきます。
目次
スポンサードリンク
0.困ったら数えあげ
「~の作り方は何通りですか。」という問題が出てどうにもならないときは、まずは何通りか書き出してみましょう。
書き出しているうちに法則が見つかるかもしれません*1。
例えば、1, 2, 3枚のカードを使って3桁の数字を作ることを考えましょう。
このとき、3桁の数字の作り方は何通りあるかを全部列挙してみます。
すると、
123, 132, 213, 231, 312, 321
の6通りとなりますね。
全部列挙していく際には、下のような樹形図で列挙していくことをおすすめします。
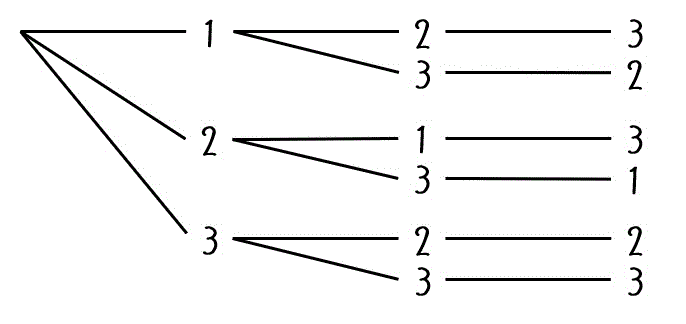
今回は6通りなのであっという間に列挙できました。
しかし、答えが1000通りとかになったらどうでしょう。列挙していたら日が暮れてしまいます。
ということで、ここからは組み合わせの総数を求めるための重要な計算パターンについていくつか紹介していきたいと思います。
スポンサードリンク
1.階乗計算の意味
ここでは、階乗計算の復習をしておきましょう。
階乗なんてもうわかっているよ、という人は読み飛ばしてOKです。

上の1, 2, 3のカードを使って作れる3桁の数字の組み合わせの総数をもう少し賢く求める方法を考えてみましょう。
(1) 考え方
まず、1枚目(一番左の桁)として選ぶカードについて考えましょう。
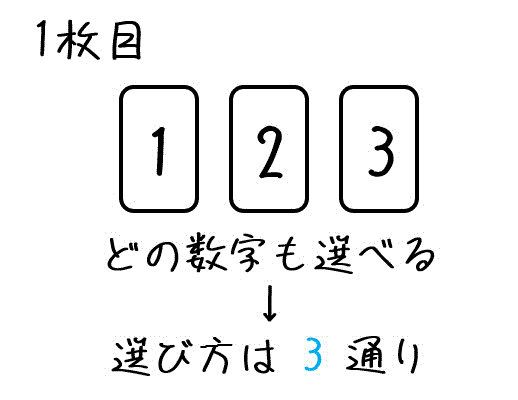
1, 2, 3どの数字も選べるので、選び方は全部で3通りですね。
今回は1枚目として「1」を選んでみましょう。
つぎに、2枚目について考えましょう。
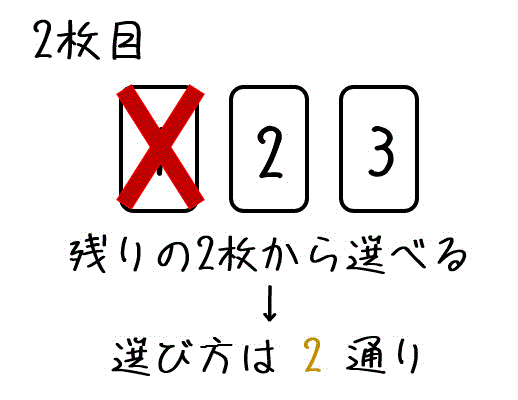
1枚目に選んだカード以外の2枚(2と3)から選べるので、選び方は2通りですね。
今回は2枚目として「2」を選んでみましょう。
最後に3枚目について考えましょう。
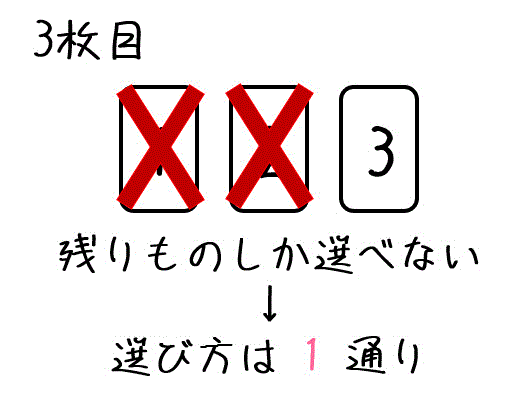
1, 2枚目に選んだカード以外からしか選べないので、残り物しか選べません。選び方は1通りですね。
ここで、2枚目までの選び方が何通りあるかを求めてみましょう。
2枚目までの選び方は、「1枚目に選んだ3通り」それぞれに対し、「2枚目に選んだ2通り分」だけ存在します。
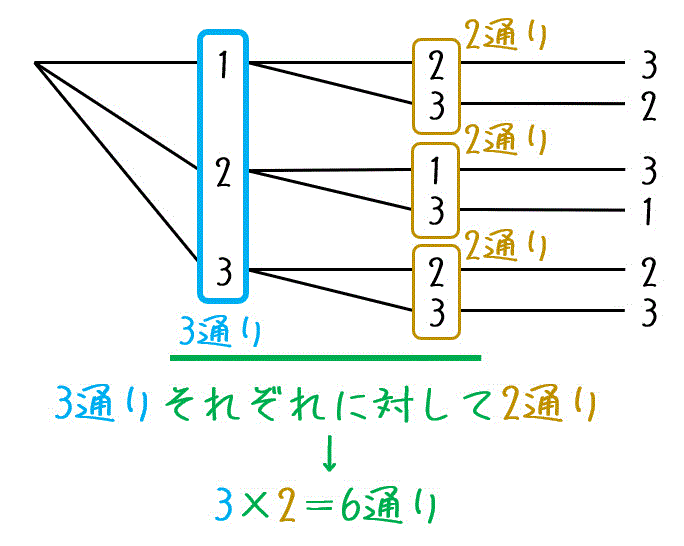
そのため、\[
3 \times 2 = 6
\]より、2枚目までの選び方は合計6通りと計算できます。
同じようにして、3枚目までの選び方、つまり3桁の数字の組み合わせの総数を求めてみましょう。
3枚目までの選び方は、「2枚目までの3×2=6通り」それぞれに対し、「3枚目に選んだ1通り分」だけ存在します。
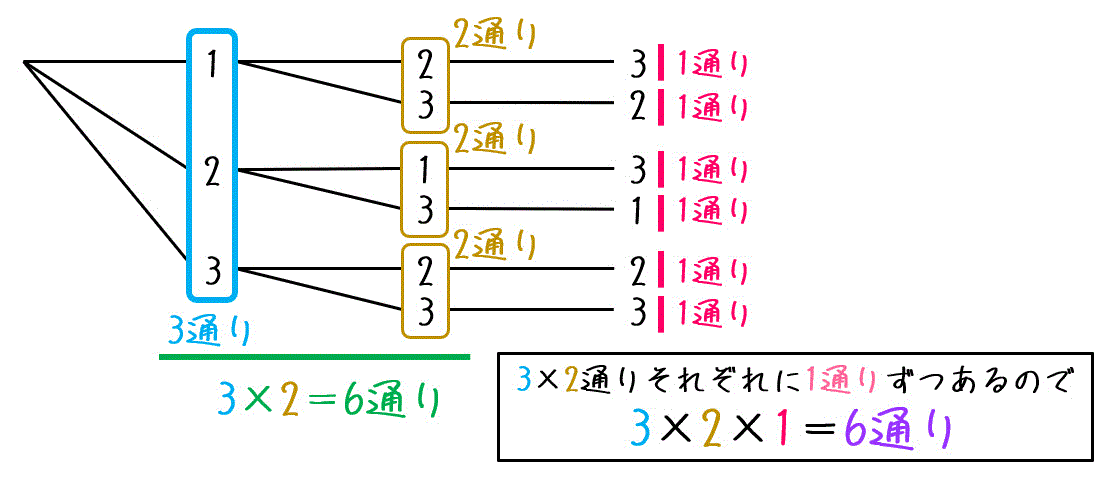
よって、\[
3 \times 2 \times 1 = 6
\]より3桁の数字の組み合わせの総数*2は合計6通りと計算できます。
(2) 階乗 ! とは
上の例のような \( n \) 個の異なるものを並び替えることで作れる数字の組み合わせは下のように計算することができ、\( n! \) と表記されます。

びっくりですね。!だけに。
例えば、\( 5! \) であれば、
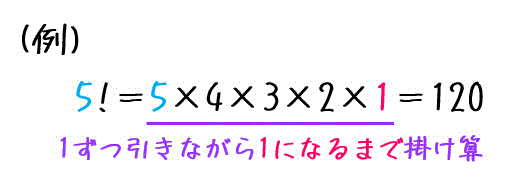
のように計算することができます。
スポンサードリンク
2.順列の総数の求め方
3枚では少し物足りないので、ここからはカードの枚数を1枚増やし、4枚で考えていきましょう。
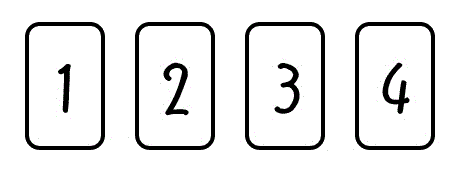
上の1, 2, 3, 4のカードの中から2枚使ったときに作れる2桁の数字の総数を求めてみましょう。
(1) 考え方
とは言っても考え方は階乗のときとほぼ同じです。
まずは、1枚目(一番左の桁)として選ぶカードについて考えましょう。
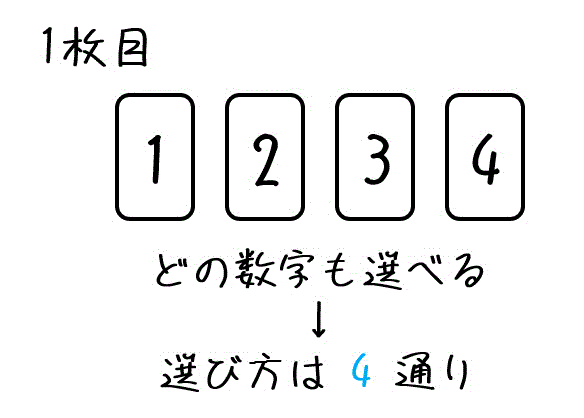
1, 2, 3, 4どの数字も選べるので選び方は4通りですね。
次に、2枚目のカードについて考えましょう。
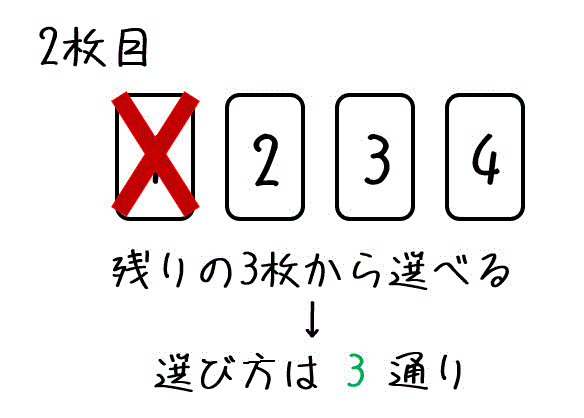
1枚目に選んだ数字なら選べるので選び方は3通りですね。
そのため、2桁の数字の選び方の総数は「1枚目に選んだ4通り」それぞれに対し、「2枚目に選んだ3通り分」だけ存在します。
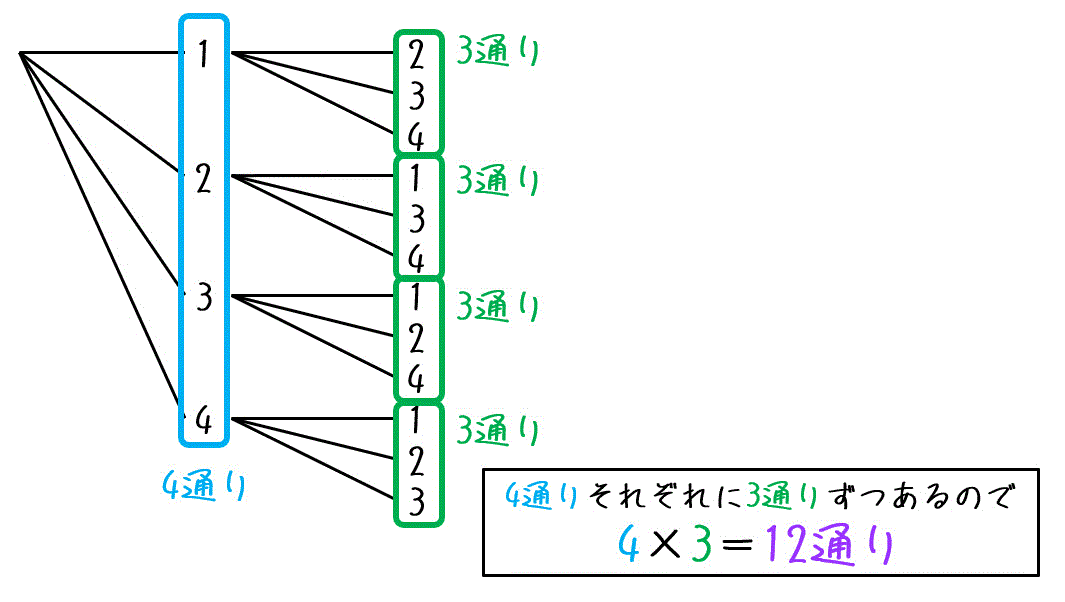
よって、\[
4 \times 3 = 12
\]より2桁の数字の組み合わせの総数は合計12通りと計算できます。
(2) 順列の記号 P
上の例のような \( n \) 個の異なるものから \( r \) 個とったときの並べ方の総数は下のように計算することができ、 \( {}_n \mathrm{P}_r \) と表記されます。

例えば、 \( {}_6 \mathrm{P}_3 \) であれば、下のように計算することができます。
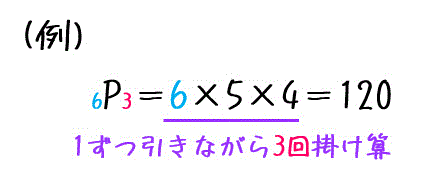
上で説明した「すべてのものを並び替えるときの数え方」は、この
3.重複順列の総数の求め方
重複を許した順列についても考えてみましょう。

1, 2, 3, 4の数字を使って作れる2桁の数が全部で何通りあるのかを考えてみましょう。
(1) 考え方
重複を許すということは、何枚目だろうが選べるカードは4通りですね。
そのため、選び方は「1枚目に選べる4通り」それぞれに対し、「2枚目に選べる4通り」だけ存在します。
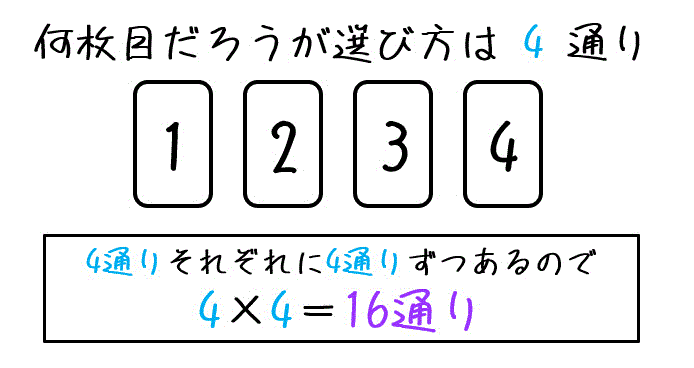
よって、組み合わせの総数は16通りとなります。
(2) 公式化
重複を許した場合の順列の総数を \( n \) や \( r \) の文字を使って表すと、下のような式で表せます。
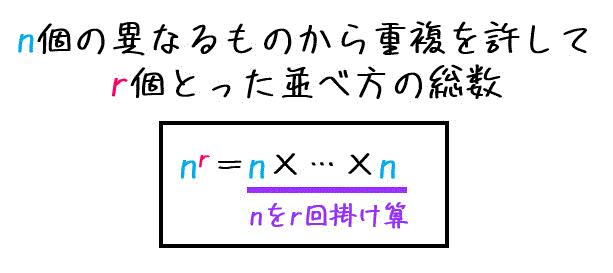
4.組み合わせの総数の求め方
つぎに組み合わせの総数についても求めてみましょう。

上の1, 2, 3, 4のカードの中から2枚を取り出し方たときの組み合わせの総数を求めてみましょう。
(1) 順列と組み合わせの違い
まずは、順列と組み合わせの違いについて確認しておきましょう。
(i) 順列(並び順が関係ある場合)
順列は、並び順(選んだ順番)を考慮して数え上げていきます。
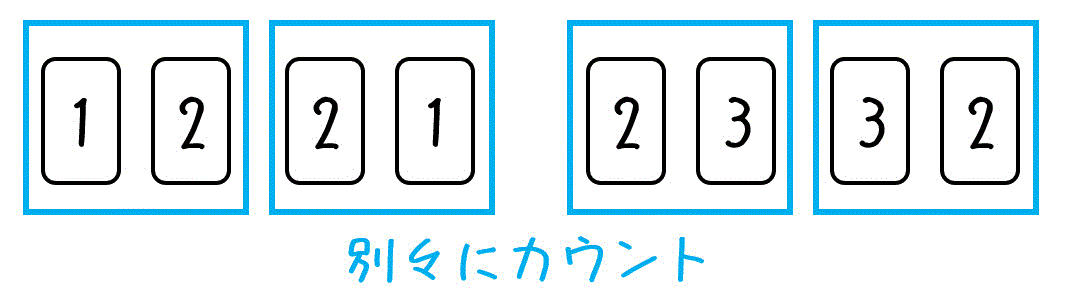
上のように、並び順が異なるものは別々にカウントされます。
順列の例としては、
- 何枚かのカードを並び替えて作れる数字の総数
- リレーのランナーの走者順
などがあります。
(ii) 組み合わせ(並び順が関係ない場合)
順列は、並び順(選んだ順番)を考慮せずに数え上げていきます。
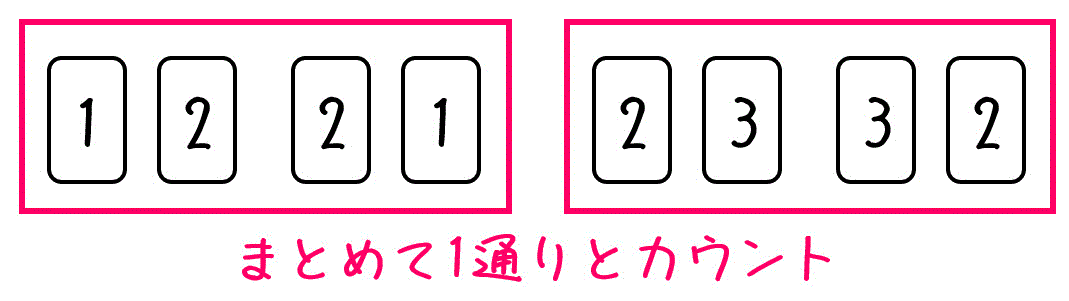
上のように、組み合わせが同じで順序が違うものがまとめて1通りとカウントされます。
組み合わせの例としては、「カードの中から何枚か取り出したときの組み合わせ数」などがあります。
順列と組み合わせの違いをまとめると、下のようになります。
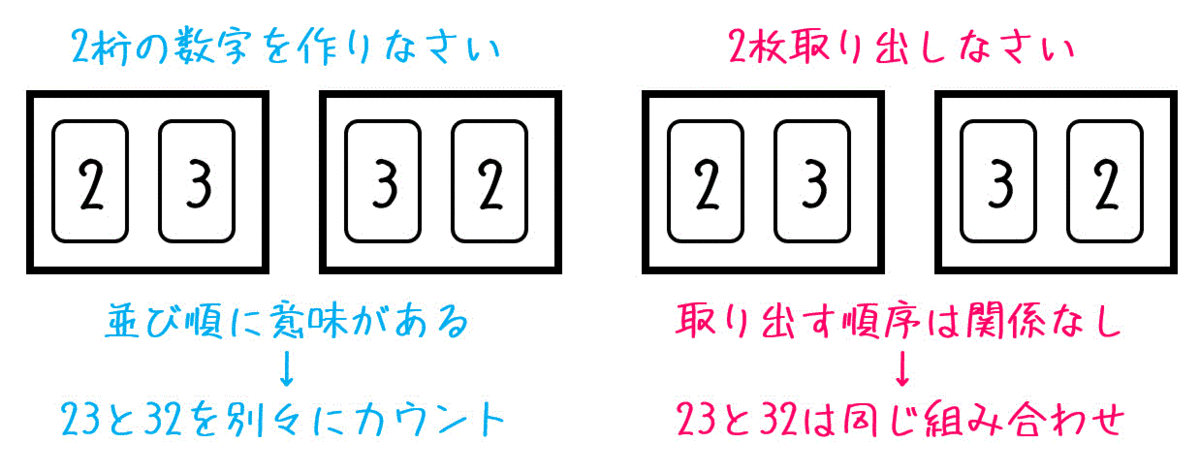
(2) 組み合わせの考え方
組み合わせが順列と異なる点は、選んだ順番を考慮しないところでしたね。
具体歴な例で「選んだ順番を考慮しない」ことが組み合わせの数にどう影響するかを見ていきましょう。
例えば、下のように2枚のカードを選んだ場合を考えます。
この場合、2枚を並び替えたときにできる2通りの並べ方を1つの組み合わせとカウントする必要があります。
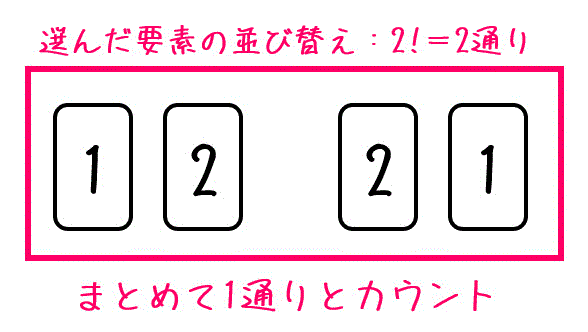
同じように3枚の場合は、3枚を並び替えたときにできる6通りの並べ方を1つの組み合わせとカウントする必要があります。
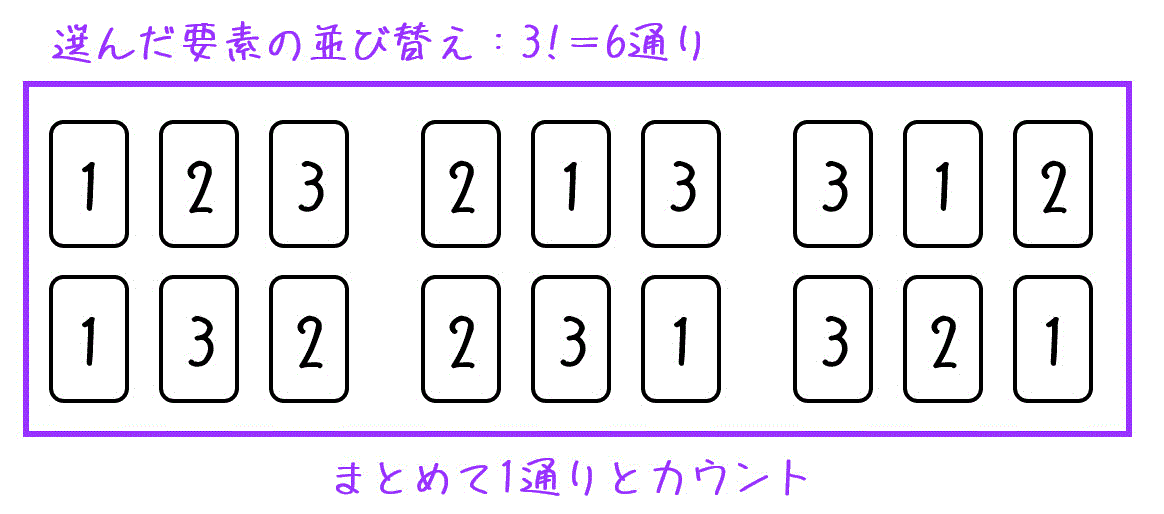
組み合わせの総数を求める際には、並び替えてできるペアをすべて1通りと数え上げればOKです。
具体的には、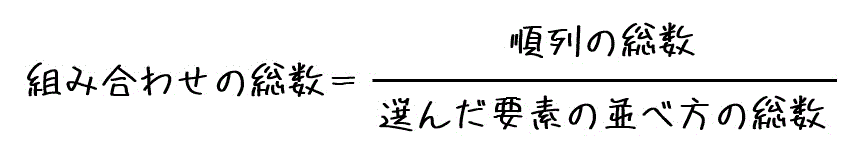
の計算をすることで求めることができます。
例えば、1, 2, 3, 4枚の中から2枚選ぶ組み合わせの総数を考えてみましょう。

まず、順番を考える場合、\( 4 \times 3 = 12 \) 通りの選び方がありますね。
しかし、組み合わせなので1,2と2,1のように重複する組み合わせのペアを1通りと数える必要があります。
よって、組み合わせの総数は\[
12 \div 2 = 6
\]となり、6通りとなります。
(3) 組み合わせの記号 C
上の例のような \( n \) 個の異なるものから \( r \) 個選んだ組み合わせ総数は下のように計算することができ、 \( {}_n \mathrm{C}_r \) と表記されます。
例えば、 \( {}_6 \mathrm{C}_3 \) であれば、下のように計算することができます。
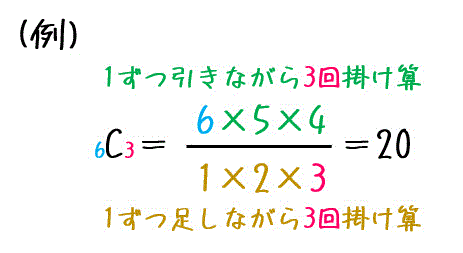
4.練習問題
では、4問ほど簡単に練習してみましょう。
少し応用問題も入れています。
練習1
うさぎ塾にはオス5匹とメス3匹、合計8匹の先生がいる。この中から明日の早番を3匹選びたい。
(1) 早番3匹を全員オスから選ぶ場合、選び方は何通りあるか。
(2) 早番3匹をオスの中から2匹、メスの中から1匹から選ぶ場合、選び方は何通りあるか。
練習2
「うさぎの記念撮影」をするために、まろん、きなこ、るか、そら、ももやまの5匹の並べ方を考えたい。
(1) 並べ方は全部で何通りですか。
(2) 右端が「るか」となる並べ方は全部で何通りですか。
(3) 「まろん」と「きなこ」が隣同士となる並べ方は全部で何通りですか。
練習3
1, 2, 3, 4, 5の5つの数字の中から3つ選び、3桁の数を作る。
このとき、偶数となる組み合わせは全部で何通りか。
練習4 応用
男子3人、女子5人の中から3人を選ぶとき、男子が少なくとも1人含まれる選び方は何通りか。
[基本情報技術者平成18年秋期 午前問7]
5.練習問題の答え
解答1
(1) [答え:10通り]
早番は、オス5匹の中から3匹選べばいいので、\[\begin{align*}
{}_5 \mathrm{C}_3 & = \frac{5 \cdot 4 \cdot 3}{1 \cdot 2 \cdot 3}
\\ & = 10
\end{align*}\]で計算でき、10通りとなる。
(ただ単に選ぶだけなので、順列ではない点に注意。)
(2) [答え:30通り]
条件を満たす組み合わせの総数は、「オス5匹の中から2匹選ぶパターン」それぞれに「メス3匹の中から1匹選ぶパターン」の数だけ組み合わせがあるので、2つの組み合わせの積が答えとなる。
オス5匹の中から2匹選ぶパターンの総数は、\[\begin{align*}
{}_5 \mathrm{C}_2 & = \frac{5 \cdot 4}{1 \cdot 2}
\\ & = 10
\end{align*}\]となり、10通りとなる。
メス3匹の中から1匹選ぶパターンの総数は、\[\begin{align*}
{}_3 \mathrm{C}_1 & = \frac{3}{1}
\\ & = 3
\end{align*}\]となり、3通りとなる。
よって、オス2匹、メス1匹が早番となるパターンは\[
10 \times 3 = 30
\]で計算でき、30通りと求められる。
解答2
(1) [答え:120通り]
5匹の並べ方なので、順番を考える必要がある。よって、パターン数は\[
5! = 120
\]で計算でき、120通りである。
(2) [答え:24通り]
右端が「るか」なので、右端は固定されてしまう。
よって、残り4匹の並び方を考えればよい。よってパターン数は\[
4! = 24
\]で計算でき、24通りと求められる。
(3) [答え:48通り]
「まろん」と「きなこ」が隣同士なので、いったん2匹を縛って*31匹として考える。
つまり、4匹分の並び方を考えればよい。しかし、4匹分の並び方それぞれに対し、「まろん・きなこ」と「きなこ・まろん」の2パターンの隣りあわせが考えられるので、\[
4! \times 2 = 24 \times 2 = 48
\]で計算でき、48通りと求められる。
解答3
答え:50通り
偶数ということは、1の位が2, 4でなければならないため、1の位だけは2通りしか選び方がない。
しかし、10の位と100の位は1~5すべての数字が使えるため、全部で5通りの選び方がある。
よって、答えは\[
5 \times 5 \times 2 = 50
\]となり、50通りとなる。
解答4
答え:46通り
「少なくとも1人含まれる」選び方の総数は、全体の総数から「誰1人も含まれない」選び方の総数を引いたほうが早く求められる。(余事象)
男子が少なくとも1人含まれる選び方の総数は、「8人の中から3人を選ぶ選び方の総数」から「8人の中から3人を選んだ際に男子が1人も選ばれない選び方の総数」から求められる。
8人の中から3人を選ぶ選び方は、\[\begin{align*}
{}_8 \mathrm{C}_3 & = \frac{8 \cdot 7 \cdot 6}{1 \cdot 2 \cdot 3}
\\ & = 56
\end{align*}\]より、56通り。
また、「男子が1人も選ばれない選び方」というのは、「全員女子を選ぶ選び方」と言い換えられる。つまり、女子5人の中から3人選ぶ組み合わせの総数\[\begin{align*}
{}_5 \mathrm{C}_3 & = \frac{5 \cdot 4 \cdot 3}{1 \cdot 2 \cdot 3}
\\ & = 10
\end{align*}\]より、10通り。
よって答えは \( 56 - 10 = 46 \) 通りとなる。
6.さいごに
今回は、場合の数の中でも基本となる
- 順列(順番を考慮した数え上げ)
- 重複順列
- 組み合わせ(順番を考慮しない数え上げ)
の3つについて説明していきました。
大事なのは、「どうしてこの数え上げの式になるんだろう」というのが自分の頭の中で理解できることです。
(ただ公式を覚えるだけではあまり意味がありません。)
ぜひ、数え上げの仕方を理解し、場合の数マスターになりましょう!
関連広告・スポンサードリンク