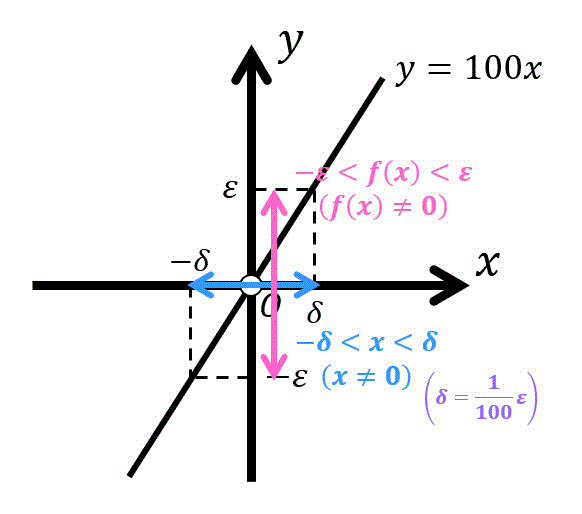
スポンサードリンク
※ 修正内容
2022/03/17 … 数式の改行が行われていない問題点を
こんにちは、ももやまです。
大学生の「解析学」で最初に出てくる「極限」の中で出てくる
- \( \varepsilon - \delta \) 論法(関数に関する極限で登場)
- \( \varepsilon - N \) 論法(数列に関する極限で登場)
って高校までの極限と全然違ってて「あれ??」となる人が多いかと思います。
ということで、今回はそんな \( \varepsilon - \delta \) 論法、\( \varepsilon - N \) 論法についてうさぎでもわかるようにわかりやすく説明していきたいと思います。
※ 私ももやま自身も今回初めて \( \varepsilon - \delta \), \( \varepsilon - N \) 論法について勉強したため、ミスがあるかもしれません。そのときはコメントなどでご指摘いただけたら幸いです。
目次
スポンサードリンク
1.ε-δ論法とは
今まで数3や解析学で極限を習った人であれば\[
\lim_{x \to 0} 100x
\]を計算すると、\[
\lim_{x \to 0} 100x = 0
\]になることはすぐにわかるでしょう。
しかし、「本当に0に近づくか」疑問に思ってしまう人が出てしまいました。
その疑問が「ε-δ論法」のきっかけなのです。
ここからは「ε-δ論法」がどんなものなのかを下の例題を踏まえて説明していきましょう。
(1)
0.01より小さくしたいということは、\[
100x < 0.1 \]\[
x < 0.001
\]となる \( x \) を1つ答えればよい。
そのような \( x \) の例として、\[
x = 0.0009
\]がある。
(2)
0.001より小さくしたいということは、\[
100x < 0.01 \]\[
x < 0.0001
\]となる \( x \) を1つ答えればよい。
そのような \( x \) の例として、\[
x = 0.00009
\]がある。
(3)
0.0001より小さくしたいということは、\[
100x < 0.001 \]\[
x < 0.00001
\]となる \( x \) を1つ答えればよい。
そのような \( x \) の例として、\[
x = 0.000009
\]がある。
(4)
微小な値 \( \varepsilon \) より小さくしたいということは、\[
100x <\varepsilon \]\[
x < \frac{1}{100} \varepsilon
\]となる \( x \) を1つ答えればよい。
そのような \( x \) の例として、\[
x = \frac{1}{101} \varepsilon
\]がある。
(4)より、\( x < \frac{1}{100} \varepsilon \) であれば、\( 100x \) は微小な数 \( \varepsilon \) に近づくことがわかりますね。
実は上のように「どんなに0に近い値 \( \varepsilon \) に対しても、必ず \( 100x \lt \varepsilon \) を満たすような \( x \) を0近くにすることができる」がまさに \( \varepsilon - \delta \) 論法の仕組みなのです!
スポンサードリンク
2.ε-δ論法で極限を示してみよう
(1) 証明の目標・流れ
\( x \) が負になる場合も踏まえて、\[
\lim_{x \to \textcolor{red}{0}} 100x = \textcolor{blue}{0}
\]を \( \varepsilon - \delta \) 論法で示すときの流れをもう詳しく説明しましょう。
\( \varepsilon - \delta \) 論法による証明の手順としては、
- どんなに \( 100x \) が \( \textcolor{blue}{0} \) に近くても
- すべての1に対し、極限値を実現できるような \( \textcolor{red}{0} \) に近い \( x \) が存在することを示す
の2ステップで証明できます。
まず、1の部分では、\( 100x \) が \( \textcolor{blue}{0} \) に近いことを小さな正の値 \( \varepsilon \) で表します。
すると、\[
- \varepsilon < 100x < \varepsilon \ \ (\varepsilon \not = 0) \]\[
| 100x | < \varepsilon
\]となります。
(ただし、\( \varepsilon \not = 0 \) に注意! 極限値はあくまでも近づく値であり、実際の値ではありません!)
※ \( \varepsilon \) は極限値 \( \textcolor{blue}{0} \) と \( f(x) \) との差を表していると考えるとわかりやすいかと思います。
つぎに、すべての1の部分、つまり\[
| 100x | < \varepsilon \tag{1}
\]を満たすようなすべての \( \varepsilon \) に対し、極限値を満たす \( \textcolor{red}{0} \) に近い \( x \) が存在することを、\[
- \delta < x < \delta \]\[
0 < |x| < \delta
\]となる小さな正の値 \( \delta \) が1つ以上存在することで確認します。
(こちらも \( \delta \not = 0 \) に注意! あくまでも \( x \) を0に近づけるだけで、0を代入するわけではありません。)
※ \( \delta \) は近づける値 \( \textcolor{red}{0} \) と \( x \) との差を表していると考えるとわかりやすいかと思います。
今回の場合、(1)の式を100で割り、\[
| x | < \frac{1}{100} \varepsilon
\]となるので、\[
\delta = \frac{1}{100} \varepsilon
\]とすることで2の部分を示すことができます。
(実際に \( \delta \) に代入するのがポイント!)
さらに図を用いて説明すると、
- \( \varepsilon \) がどんな値であったとしても
(赤色矢印がどんな長さだったとしても) - \( \delta \) の値をうまいこと選び、青色矢印の中に \( x \) が入ることを示す
のが \( \varepsilon - \delta \) 論法となります。
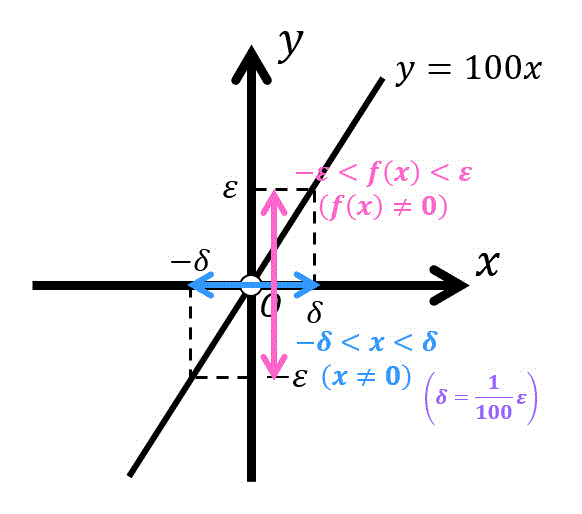
(2) 定義の紹介
ここで、\( \varepsilon - \delta \) 論法を用いた極限\[
\lim_{x \to \textcolor{red}{a}} f(x) = \textcolor{blue}{b}
\]の定義を確認しましょう。
どんな小さな \( \varepsilon \) に対しても、\[
0 < |x-\textcolor{red}{a}| < \delta \ \ ならば \ \ | f(x) - \textcolor{blue}{b} | < \varepsilon
\]となるようなある1つの小さな値 \( \delta \) が存在することがいえるとき、極限\[
\lim_{x \to \textcolor{red}{a}} f(x) = \textcolor{blue}{b}
\]が成立する。
さらに図を用いて定義を確認してみましょう。
極限値 \( b \) と \( f(x) \) の誤差 \( \varepsilon \)(ピンク矢印部分)がどんな値であったとしても、必ず \( x \) と \( a \) の誤差 \( \delta \)(青矢印部分)となるような \( \delta \) が存在することがいえれば、\[
\lim_{x \to \textcolor{red}{a}} f(x) = \textcolor{blue}{b}
\]が示せます。
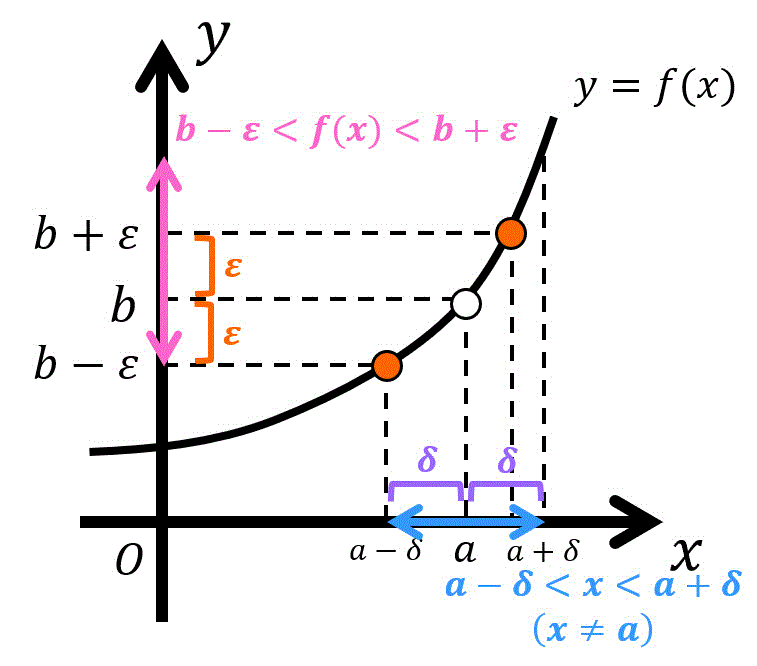
もう少し数学用語を使って堅く定義を書いてみましょう。
極限が\[
\lim_{x \to \textcolor{red}{a}} f(x) = \textcolor{blue}{b}
\]となることは、任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
|x-\textcolor{red}{a}| < \delta \ \Rightarrow \ | f(x) - \textcolor{blue}{b} | < \varepsilon
\]が成り立つことと同値である。
ここで、謎の記号 \( \Rightarrow \) が出てきましたね。
この記号は、「ならば」を表します。
\( A \Rightarrow B \) を例にしてもう少し丁寧に説明しましょう。
「ならば」の左側(Aの部分)は前提条件を表します。つまり、Aは仮定を表しています。
「ならば」の右側(Bの部分)は結論、つまり証明したい部分を表します。

\( A \Rightarrow B \) を証明する場合には、前提条件Aが成立するときに結論Bも成立することを示せばOKです。
(3) ∀や∃を用いた式の表し方(述語論理)
この記事では \( \forall \) や \( \exists \) を用いた述語論理形式による表し方はしませんが、教科書や一部の先生は述語論理式で定義を表すのがいるので、この記事でも簡単に述語論理式の読み方について説明しましょう。
なお、より詳しく \( \forall \) や \( \exists \) を用いた述語論理形式での表し方についてお勉強したい人は、以下に記事や動画を用意したので、是非ご覧ください。
[記事]
[動画]
(i) 述語論理の読み方
任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
|x-\textcolor{red}{a}| < \delta \ \Rightarrow \ | f(x) - \textcolor{blue}{b} | < \varepsilon
\]が成り立つ、というのは述語論理で表すと下のようになります。

まず、\( \textcolor{red}{\forall} \varepsilon \gt 0 \) で「すべての正の実数 \( \varepsilon \)」を表します。
つぎに、\( \textcolor{blue}{\exists} \varepsilon \gt 0 \) で「ある(1つ以上)の正の実数 \( \delta \)」を表します。
さらに、s.t は such that(~の条件を満たすような)を表します。(書かない先生も多いです。)
(ii) 述語論理は順番に気をつけろ!
述語論理では、順番が大切になってきます。
例えば、\[
\forall x , \exists y \ \ \mathrm{s.t.} \ \ x = y \]\[
\exists y, \forall x \ \ \mathrm{s.t.} \ \ x = y
\]の2つが正しい式なのかを考えてみましょう。
前者\[
\forall x , \exists y \ \ \mathrm{s.t.} \ \ x = y
\]を日本語訳すると「すべての \( x \) に対し、ある1つの \( y \) が存在し、\( x = y \) が成立する」となります。
つまり、どんな \( x \) であったとしても、必ず \( y \) と等しくなるような \( x \) が1つ以上存在することを表します。
もちろん、この文章は正しいです。
相手がどんな数字を言ってきた \( x \) としても(すべての \( x \) に対し)、その数字をそのままあなたが言い返す \( y \) ことはできます(ある1つの \( y \) に対して成り立つ)よね。
一方後者は\[
\exists y , \forall x \ \ \mathrm{s.t.} \ \ x = y
\]を日本語訳すると「ある1つ(以上)の \( y \) に対し、すべての \( x \) について \( x = y \) が成立する」となります。
つまり、1つの \( y \) でいいから、固定した \( y \) に対し、どんな \( x \) でも \( x = y \) 成立することを表します。
日本語訳すると、この文章は無茶苦茶なことがわかりますよね。
例えばですが、\( y = 2 \) のとき、\( x = 3 \) だと \( x = y \) にはなりませんよね。
そのため、後者の述語論理式は誤っていることがわかります。
このように、述語論理を読み書きする際には順番に大きく気を付ける必要があるのです。
(4) 例題を解いてみよう
※ 2023/02/08:例題の解説の途中過程で、大幅な式変形のミスをしていたものを修正しました。ご迷惑をおかけし、申し訳ございません。
解説1
極限\[
\lim_{x \to \textcolor{red}{2}} x^2 = \textcolor{blue}{4}
\]を示すためには、任意の正の実数 \( \varepsilon \) に対し、ある正の実数 \( \delta \) が存在し、\[
0 < |x-\textcolor{red}{2}| < \delta \ \ ならば \ \ | x^2 - \textcolor{blue}{4} | < \varepsilon
\]となることを示せばよい。
ここで、\[
0 < |x-\textcolor{red}{2}| < \delta
\]を \( x \) に関する不等式に変形する。
\[
0 < |x-\textcolor{red}{2}| < \delta \]\[
- \delta < x - 2 < \delta \]\[
2 - \delta < x < 2 + \delta
\]となる。(ただし \( x \not = 2 \))
同じように\[
| x^2 - \textcolor{blue}{4} | < \varepsilon
\]も \( x \) に関する不等式に変形する。\[
- \varepsilon < x^2 - 4 < \varepsilon \]\[
4 - \varepsilon < x^2 < 4 + \varepsilon \]と変形でき、さらに \( x \to 2 \) より \( x \) は正と考えてよい。よって\[
\sqrt{4 - \varepsilon} < x < \sqrt{4 + \varepsilon}
\]と変形できる。
つまり、すべての \( \varepsilon \) に対し、\[
2 - \delta < x < 2 + \delta \Rightarrow \sqrt{4 - \varepsilon} < x < \sqrt{4 + \varepsilon}
\]を満たすような \( \delta \) を1つ見つければよい。
そのためには、\[
2 - \delta = \sqrt{4 - \varepsilon} \Leftrightarrow \delta = 2 - \sqrt{4 - \varepsilon} \]\[
2 + \delta = \sqrt{4 + \varepsilon} \Leftrightarrow \delta = \sqrt{4 + \varepsilon } - 2 \]\[
\]の2つのうち、小さい方を \( \delta \) してとればよい*1。
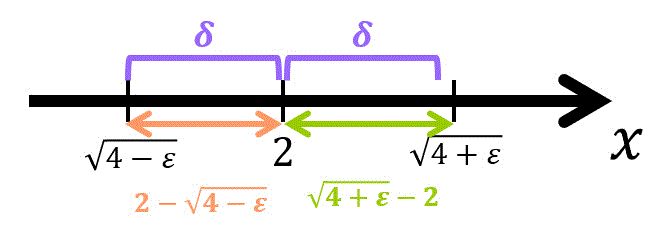
ここで、\( \min (A,B) \) を A, Bの2つのうち、小さい方を表すとすると、\[
\delta = \min ( 2 - \sqrt{4 - \varepsilon}, \sqrt{4 + \varepsilon } - 2 )
\]とすることで、\[
2 - \delta < x < \delta - 2 \Rightarrow \sqrt{4 - \varepsilon} < x < \sqrt{\varepsilon - 4}
\]を成立させることができる。
(※具体的にどっちが小さいかを求める必要はありません。)
よって、任意の正の実数 \( \varepsilon \) に対し、ある正の実数 \( \delta \) が存在し、\[
0 < |x-\textcolor{red}{2}| < \delta \ \ ならば \ \ | x^2 - \textcolor{blue}{4} | < \varepsilon
\]となるので、\[
\lim_{x \to 2} x^2 = 4
\]が示された。
(5) 証明のテンプレート
最初は、\( \varepsilon - \delta \) 論法の証明に慣れないと思うので、証明のテンプレートを用意してみました。
証明をする際の参考にしてください。

スポンサードリンク
3.x→∞のときのε-δ論法
つぎに \( x \to \infty \) にしたときの極限\[
\lim_{x \to \infty} f(x) = \textcolor{blue}{b}
\]を \( \varepsilon - \delta \) 論法で示す方法を見ていきましょう。
極限が\[
\lim_{x \to \infty} f(x) = \textcolor{blue}{b}
\]となることは、任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
x > \delta \ \Rightarrow \ | f(x) - \textcolor{blue}{b} | < \varepsilon
\]が成り立つことと同値である。
日本語で証明の流れを簡単に説明すると、
- どんな小さな正の数 \( \varepsilon \) を取ったとしても
- 1に対して\[
x > \delta \ \Rightarrow \ | f(x) - b | \varepsilon
\]を満たすような \( \delta \) を1つ以上ある
ことを示せば、\( \varepsilon - \delta \) 論法で\[
\lim_{x \to \infty} f(x) = \textcolor{blue}{b}
\]を示すことができます。
とは言っても、基本的には \( x \to a \) のときと同じく、すべての \( \varepsilon \) に対して、条件を満たすような \( \delta \) を \( \varepsilon \) を用いて表すだけです。
例題を解いてみましょう。
解説2
極限\[
\lim_{x \to \infty} \frac{2x}{2x+1}= \textcolor{blue}{1}
\]を示すためには、任意の正の実数 \( \varepsilon \) に対し、ある正の実数 \( \delta \) が存在し、\[
x > \delta \ \Rightarrow \ \left| \frac{2x}{2x+1} - \textcolor{blue}{1} \right| < \varepsilon
\]となることを示せばよい。
ここで、\( x \to \infty \) なので、\( x \gt 0 \) と考えてよい。
そのため、\[\begin{align*}
\frac{2x}{2x+1} - 1 & = \frac{2x - (2x+1)}{2x+1}
\\ & = - \frac{1}{2x+1} < 0
\end{align*}\]変形できる。
さらに、\[\begin{align*}
& \left| \frac{2x}{2x+1} - \textcolor{blue}{1} \right| < \varepsilon
\\ \Leftrightarrow \ & 1 - \frac{1}{2x+1} < \varepsilon
\\ \Leftrightarrow \ & \frac{1}{2x+1} < \varepsilon
\\ \Leftrightarrow \ & 2x+1 > \frac{1}{\varepsilon}
\end{align*}\]となるので、\[
2x > \frac{1}{\varepsilon} - 1 \]\[
x > \frac{1}{2\varepsilon} - \frac{1}{2}
\]とすることで \( x \) に関する関係式に変形ができる。
つまり、すべての \( \varepsilon \) に対し、\[
x > \delta \Rightarrow x > \frac{1}{2\varepsilon} - \frac{1}{2}
\]を満たすような \( \delta \) を1つ見つければよい。
ここで、\( \delta \) を\[
\delta = \frac{1}{2\varepsilon} - \frac{1}{2}
\]とすれば、\[
x > \delta = \frac{1}{2\varepsilon} - \frac{1}{2} \Rightarrow x > \frac{1}{2\varepsilon} - \frac{1}{2}
\]となり、すべての \( \varepsilon \) に対して条件\[
x > \delta \ \Rightarrow \ \left| \frac{2x}{2x+1} - \textcolor{blue}{1} \right| < \varepsilon
\]を満たす。
よって、\[
\lim_{x \to \infty} \frac{2x}{2x+1}= 1
\]が示された。
証明のテンプレート(x→∞のとき)
\( x \to \infty \) での \( \varepsilon - \delta \) 論法による証明のテンプレートも用意しました。
こちらも参考までにどうぞ。

4.ε-N論法とは(ε-δ論法の数列Ver)
数3や解析学では、ある数列 \( a_n \) の極限\[
\lim_{n \to infty} a_n
\]を求めましたね。
早速 \( \varepsilon - N \) 論法の定義を確認しましょう。
数列 \( a_n \) の極限が\[
\lim_{n \to \infty} a_n = \textcolor{blue}{\alpha}
\]となることは、任意の正の実数 \( \varepsilon \) に対して、ある正の自然数 \( N \) が存在し、\[
n > N \ \Leftrightarrow \ | a_n - \textcolor{blue}{\alpha} | < \varepsilon
\]が成り立つことと同値である。
とはいっても、3章で出てきた \( x \to \infty \) のときの \( \varepsilon - \delta \) 論法の「実数 \( \delta \) が自然数 \( N \) に変わっている」だけなので、理解は難しくありません!
念のため日本語で簡単に説明すると、
- どんな小さな正の数 \( \varepsilon \) を取ったとしても
- 1に対して\[
x > \delta \ であれば \ | f(x) - b | \varepsilon
\]を満たすような自然数 \( N \) を1つ以上ある
ことを示せば、\( \varepsilon - N \) 論法で\[
\lim_{n \to \infty} a_n = \textcolor{blue}{\alpha}
\]を示すことができます。
また例題を解いてみましょう。
解説3
極限\[
\lim_{n \to \infty} \frac{2n}{2n+1}= \textcolor{blue}{1}
\]を示すためには、任意の正の実数 \( \varepsilon \) に対し、ある正の自然数 \( N \) が存在し、\[
n > N \ \Rightarrow \ \left| \frac{2n}{2n+1} - \textcolor{blue}{1} \right| < \varepsilon
\]となることを示せばよい。
ここで、\( n \to \infty \) なので、\( n \gt 0 \) と考えてよい。
そのため、\[\begin{align*}
\frac{2n}{2n+1} - 1 & = \frac{2n - (2n+1)}{2n+1}
\\ & = - \frac{1}{2n+1} < 0
\end{align*}\]と変形できる。
さらに、\[\begin{align*}
& \left| \frac{2n}{2n+1} - \textcolor{blue}{1} \right| < \varepsilon
\\ \Leftrightarrow \ & 1 - \frac{1}{2n+1} < \varepsilon
\\ \Leftrightarrow \ & \frac{1}{2n+1} < \varepsilon
\\ \Leftrightarrow \ & 2n+1 > \frac{1}{\varepsilon}
\end{align*}\]となるので、\[
2n > \frac{1}{\varepsilon} - 1 \]\[
n > \frac{1}{2\varepsilon} - \frac{1}{2}
\]とすることで \( n \) に関する関係式となる。
つまり、すべての \( \varepsilon \) に対し、\[
n > N \Rightarrow n > \frac{1}{2\varepsilon} - \frac{1}{2}
\]を満たすような自然数 \( N \) を1つ見つければよい。
ただし、\( N \) は自然数なので、そのまま\[
N = \frac{1}{2\varepsilon} - \frac{1}{2}
\]とすることはできない。
そこで、\( N \) を\[
N > \frac{1}{2\varepsilon} - \frac{1}{2}
\]を満たす自然数とする。すると、\[
n > N > \frac{1}{2\varepsilon} - \frac{1}{2}
\]となるので、すべての \( \varepsilon \) に対し、条件\[
n > N > \frac{1}{2\varepsilon} - \frac{1}{2} \ \Rightarrow \ \left| \frac{2n}{2n+1} - \textcolor{blue}{1} \right| < \varepsilon
\]を満たす。
よって、\[
\lim_{n \to \infty} \frac{2n}{2n+1}= 1
\]が示された。
[補足:ガウス記号を用いた \( N \) の表し方]
\( \varepsilon - N \) 論法では、\( N \) が1つでも存在することを示せばいいので、具体的な \( N \) の値を求める必要はありません。
しかし、実際に \( N \) を求めたいのであればガウス記号*2を用いて表すことができます。
今回の場合は、\[
N > \frac{1}{2\varepsilon} - \frac{1}{2}
\]とすればよいので、\[
N = \left[ \frac{1}{2\varepsilon} - \frac{1}{2} \right] \textcolor{red}{+ 1}
\]と具体的に \( N \) の値を表せる。
(ガウス記号は、小数部分を取り除くが、小数部分は絶対に1未満なので、最後に1を足すことで必ず\[
\frac{1}{2\varepsilon} - \frac{1}{2}
\]より大きい自然数を表現できる。)
証明のテンプレート(x→∞のとき)
\( \varepsilon - N \) 論法も、最初は証明に慣れないと思うので、証明のテンプレートを用意してみました。
証明をする際の参考にしてください。

5.ε-δ論法の応用・関数の連続性
最後に、\( \varepsilon - \delta \) 論法を用いて関数の連続性を証明する方法について説明しましょう。
(1) 関数の連続 [復習]
ある関数 \( f(x) \) が \( x = \textcolor{red}{a} \) において連続かどうかを確認するためには\[
\lim_{x \to \textcolor{red}{a}} f(x) = \textcolor{blue}{f(a)}
\]が成り立つかどうか確認すればOKでしたね。
この極限を \( \varepsilon - \delta \) 論法で示す場合、任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
\textcolor{purple}{0 <} |x-\textcolor{red}{a}| < \delta\ \Leftrightarrow \ | f(x) - \textcolor{blue}{f(a)} | < \varepsilon
\]が成り立つことを示せばよさそうですね。
ですが、関数が連続である場合「\( (x,y) = (a,f(a) ) \) で途切れていないので、\( x = a \) の部分を除外する必要がありません。
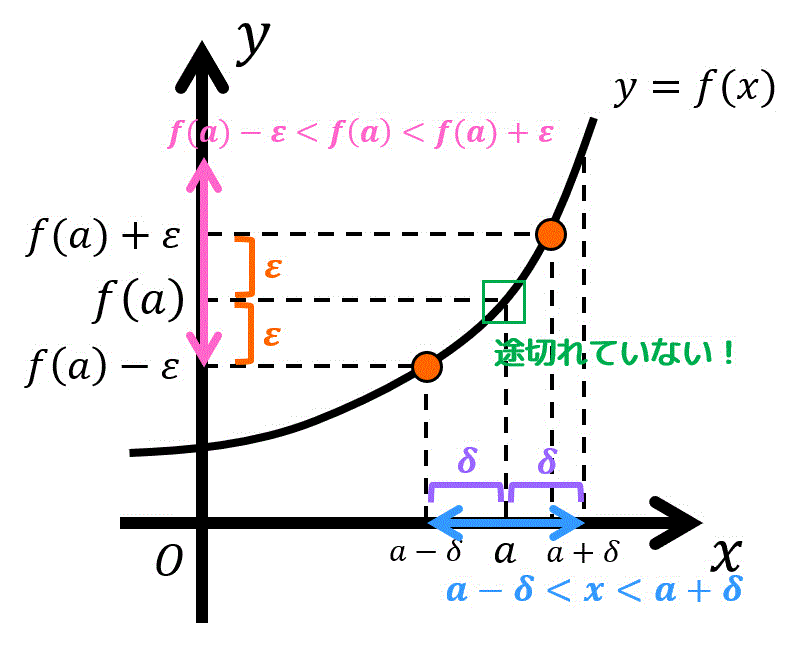
そのため、\( \textcolor{purple}{0 \lt} \) の部分を消し、\[
|x-\textcolor{red}{a}| < \delta\ \Leftrightarrow \ | f(x) - \textcolor{blue}{f(a)} | < \varepsilon
\]と書き換えることができ、この式が成立することを確かめることで \( \varepsilon - \delta \) 論法で関数の連続性を示すことができます。
ある関数 \( f(x) \) が \( x = \textcolor{red}{a} \) において連続であることと、任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
|x-\textcolor{red}{a}| < \delta\ \Leftrightarrow \ | f(x) - \textcolor{blue}{f(a)} | < \varepsilon
\]が成り立つことは同値である。
(2) 連続な関数のとき
では、簡単な例題で \( \varepsilon - \delta \) 論法による証明の流れを確認しましょう。
解説4
\( x = \textcolor{red}{0} \) のとき、\( f(\textcolor{red}{0}) = \textcolor{blue}{0} \) である。
ここで、\( x = \textcolor{red}{0} \) で連続であることを示すためには、任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
|x-\textcolor{red}{0}| < \delta \ \Leftrightarrow \ | f(x) - \textcolor{blue}{0} | < \varepsilon \]\[
|x| < \delta \ \Leftrightarrow \ | | x | | = |x| < \varepsilon
\]が成り立つことを示せばよい。
ここで、\[
\delta = \varepsilon
\]とすると、すべての \( \varepsilon \) に対して条件\[
|x-\textcolor{red}{0}| < \delta = \varepsilon \ \Leftrightarrow \ | f(x) - \textcolor{blue}{0} | < \varepsilon
\]を満たす。
よって、\( x = 0 \) で連続であることが示された。
\( f(x) \) が \( x = \textcolor{red}{a} \) で連続かどうかを示すときは、\[
\lim_{x \to \textcolor{red}{a}} f(x) = \textcolor{blue}{f(a)}
\]を \( \varepsilon - \alpha \) 論法で示す手順と同じようにすることで証明ができます。
(ただし \( x \not = a \) を除外する必要がないのが唯一の違うポイント)
(3) 連続ではない関数のとき
いつも連続になる関数ばかりが出題されるとは限りません。
ということで、連続ではない場合のパターンも確認しておきましょう。
解説5
連続ではないことを示す場合には、背理法を使います。222
つまり、いったん連続であることを仮定します。
\( x = \textcolor{red}{0} \) のとき、\( f(\textcolor{red}{0}) = \textcolor{blue}{1} \) である。
ここで、\( x = \textcolor{red}{0} \) で連続であると仮定する。
すると、任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
|x-\textcolor{red}{0}| < \delta \ \Rightarrow \ | f(x) - \textcolor{blue}{1} | < \varepsilon \]\[
|x| < \delta \ \Rightarrow \ | f(x)-1 | < \varepsilon
\]が成り立つ。
ここで、\( \varepsilon = 0.5 \) とする。
すると、\[
| f(x)-1 | < 0.5 \]\[
-0.5 < f(x) < 0.5 \]\[
0.5 < f(x) < 1.5 \tag {1}
\]と変形できる。
しかし、正の実数 \( \delta \) に対し、\[
|x| < \delta \]\[
- \delta < x < \delta
\]となるため、\( \delta \) の値がどんな値であったとしても範囲の中に \( x \lt 0 \) が含まれる。
よって、仮定は誤りとなり、\( x = \textcolor{red}{0} \) で連続ではないことが示された。
このように、連続ではないことを示す場合は一旦連続であると仮定してから成り立たない反例を見つけることで証明を行います。
反例を示す場合、ある1つの \( \varepsilon \) を固定し、固定された \( \varepsilon \) のとき、どんな \( \delta \) であったとしても\[
|x-\textcolor{red}{0}| < \delta \ \Rightarrow \ | f(x) - \textcolor{blue}{0} | < \varepsilon
\]が成立しないことを示せばOKです。
(どんな \( \delta \) でも上の式が成り立たないような \( \varepsilon \) を探せばOK!)
6.練習問題
では、
- \( \varepsilon - \delta \) 論法
- \( \varepsilon - N \) 論法
- 関数の連続性
に関する練習問題を1問ずつ、合計3問にチャレンジしてみましょう。
練習1
つぎの極限\[
\lim_{x \to 3} \sqrt{x-3} = 0
\]を \( \varepsilon - \delta \) 論法を用いて示しなさい。
練習2
つぎの極限\[
\lim_{n \to \infty} \frac{n^2}{3n^2 - 1} = \frac{1}{3}
\]を \( \varepsilon - N \) 論法を用いて示しなさい。
練習3
関数\[
f(x) = \frac{1}{x}
\]が \( x = 1 \) で連続かどうかを \( \varepsilon - \delta \) 論法を用いて確認しなさい。
7.練習問題の答え
解答1
極限\[
\lim_{x \to \textcolor{red}{3}} \sqrt{x-3} = \textcolor{blue}{0}
\]を示すためには、任意の正の実数 \( \varepsilon \) に対し、ある正の実数 \( \delta \) が存在し、\[
0 < |x-\textcolor{red}{3}| < \delta \ \ ならば \ \ | \sqrt{x-3} - \textcolor{blue}{0} | < \varepsilon \tag{1}
\]となることを示せばよい。
\( 0 \lt |x-\textcolor{red}{3}| \lt \delta \) は、\[
- \delta < x - 3 < \delta \]\[
3 - \delta < x < 3 + \delta \ (x \not = 3)
\]と変形できる。
また、\[
| \sqrt{x-3} - \textcolor{blue}{0} | < \varepsilon
\]の両辺を2乗すると、\[
0 \leqq x-3 < \varepsilon^2 \]\[
0 \leqq x < \varepsilon^2 + 3
\]となる。(2乗したことにより \( x \geqq 0 \) となる)
つまり、\[
3 - \delta < x < 3 + \delta \ (x \not = 3) \ \Rightarrow \ 0 \leqq x < \varepsilon^2 + 3
\]となることを示せばよい。
ここで、\[
3 + \delta = \varepsilon^2 + 3
\]より、\[
\delta = \varepsilon^2
\]とすると、すべての \( \varepsilon \) に対し、\[
3 - \varepsilon^2 < x < 3 + \varepsilon^2 \ (x \not = 3) \ \Rightarrow \ 0 \leqq x < \varepsilon^2 + 3
\]となるので、(1)も成立する。
よって、\[
\lim_{x \to \textcolor{red}{3}} \sqrt{x-3} = \textcolor{blue}{0}
\]が示された。
解答2
極限\[
\lim_{n \to \infty} \frac{n^2}{3n^2 - 1} = \textcolor{blue}{\frac{1}{3}}
\]を示すためには、任意の正の実数 \( \varepsilon \) に対し、ある正の自然数 \( N \) が存在し、\[
n > N \ \Rightarrow \ \left| \frac{n^2}{3n^2 - 1}- \textcolor{blue}{\frac{1}{3}} \right| < \varepsilon
\]となることを示せばよい。
ここで、\[\begin{align*}
\frac{n^2}{3n^2 - 1} - \frac{1}{3} & = \frac{3n^2 - (3n^2-1)}{3(3n^2-1)}
\\ & = \frac{1}{3(3n^2-1)} > 0
\end{align*}\]と変形できる。
(\( n \to \infty \) なので、\( 3n^2 - 1 \gt 0 \) と考えてよい。)
さらに、\[\begin{align*}
& \left| \frac{n^2}{3n^2 - 1}- \textcolor{blue}{\frac{1}{3}} \right|< \varepsilon
\\ \Leftrightarrow \ & \frac{1}{3(3n^2-1)} < \varepsilon
\\ \Leftrightarrow \ & 3(3n^2-1) > \frac{1}{\varepsilon}
\\ \Leftrightarrow \ & 3n^2-1 > \frac{1}{3 \varepsilon}
\\ \Leftrightarrow \ & 3n^2 > \frac{1}{3 \varepsilon} + 1
\\ \Leftrightarrow \ & n^2 > \frac{1}{9} \left( \frac{1}{\varepsilon} + 1 \right)
\end{align*}\]となるので、\[
n^2 > \frac{1}{9} \left( \frac{1}{\varepsilon} + 1 \right) \]\[
n > \frac{1}{3} \sqrt{ \frac{1}{ \varepsilon} + 1}
\]とすることで \( n \) に関する関係式となる。
つまり、すべての \( \varepsilon \) に対し、\[
n > N \Rightarrow n > \frac{1}{3} \sqrt{ \frac{1}{ \varepsilon} + 1}
\]を満たすような自然数 \( N \) を1つ見つければよい。
ここで、\( N \) を\[
N > \frac{1}{3} \sqrt{ \frac{1}{\varepsilon} + 1}
\]を満たす自然数とする。すると、\[
n > N > \frac{1}{3} \sqrt{ \frac{1}{ \varepsilon} + 1}
\]となるので、すべての \( \varepsilon \) に対し、条件\[
n > N > \frac{1}{3} \sqrt{ \frac{1}{ \varepsilon} + 1} \ \Rightarrow \ \left| \frac{2n}{2n+1} - \textcolor{blue}{1} \right| < \varepsilon
\]を満たす。
よって、\[
\lim_{n \to \infty} \frac{n^2}{3n^2 - 1} = \textcolor{blue}{\frac{1}{3}}
\]が示された。
解答3
\( x = \textcolor{red}{1} \) のとき、\( f(\textcolor{red}{1}) = \textcolor{blue}{1} \) である。
ここで、\( x = \textcolor{red}{1} \) で連続であると仮定する。
すると、任意の正の実数 \( \varepsilon \) に対して、ある正の実数 \( \delta \) が存在し、\[
|x-\textcolor{red}{1}| < \delta \ \Rightarrow \ \left| \frac{1}{x} - \textcolor{blue}{1} \right| < \varepsilon \tag{1}
\]が成り立つ。
ここで、\( |x-1| \lt \delta \) は\[
|x-1| < \delta \]\[
- \delta < x-1 < \delta \]\[
1 - \delta < x < 1 + \delta
\]と変形でき、\[
\left| \frac{1}{x} - 1 \right|
\]は\[
- \varepsilon < \frac{1}{x} - 1 < \varepsilon \]\[
1 - \varepsilon < \frac{1}{x} < 1 + \varepsilon \]\[
\frac{1}{1+\varepsilon} < x < \frac{1}{1-\varepsilon}
\]と変形ができる。
つまり、すべての \( \varepsilon \) に対し、\[
1 - \delta < x < 1 + \delta \Rightarrow \frac{1}{1+\varepsilon} < x < \frac{1}{1-\varepsilon}
\]を満たすような \( \delta \) を1つ見つければよい。
そのためには、\[
1 - \delta = \frac{1}{1+\varepsilon} \Leftrightarrow \delta = \frac{\varepsilon}{1+\varepsilon} \]\[
1 + \delta = \frac{1}{1-\varepsilon} \Leftrightarrow \delta = \frac{\varepsilon}{1-\varepsilon}
\]の2つのうち、小さい方を \( \delta \) してとればよい。
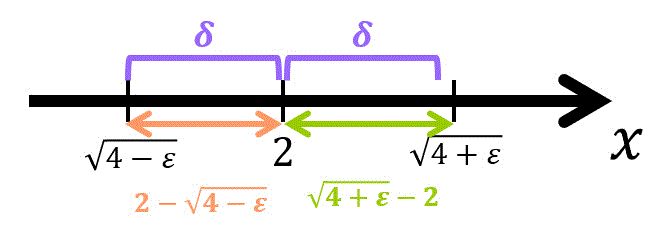
ここで、\( \min (A,B) \) を A, Bの2つのうち、小さい方を表すとすると、\[
\delta = \min ( \frac{\varepsilon}{1+\varepsilon}, \frac{\varepsilon}{1-\varepsilon} )
\]とすることで*3、\[
1 - \delta < x < 1 + \delta \Rightarrow \frac{1}{1+\varepsilon} < x < \frac{1}{1-\varepsilon}
\]を成立させることができるので、(1)も成立し、仮定が正しいことがわかる。
よって \( f(x) \) は \( x = 1 \) で連続である。
8.さいごに
今回は \( \varepsilon - \delta \) 論法、\( \varepsilon - N \) 論法をうさぎでもわかるようにわかりやすく説明していきました。
この記事を見て、\( \varepsilon - \delta \) 論法、\( \varepsilon - N \) 論法について少しでも理解していただけたら幸いです。
もし、機会があれば、
- はさみうちの定理の証明
- 極限の計算公式の一部*4
のような \( \varepsilon - \delta \) 論法、\( \varepsilon - N \) 論法を用いた応用例について紹介したいと思います。
*1:もし、大きい方を \( \delta \) にしてしまうと、前提条件のとき、必ず結論になると言うことができません。そのため、なるべく前提条件は小さくかつ結論の範囲を網羅するように取る必要があります。
*2:ガウス記号 \( [a] \) は、\( a \) の整数部分を表す。例えば、\( [3.14] \) であれば、3となる。
*3:今回の場合、\( \varepsilon \) が正なので、左側 \( \frac{\varepsilon}{1+\varepsilon} \) のほうが小さいことがわかる。なので、わざわざminをおかなくても、\[
\delta = \frac{\varepsilon}{1+\varepsilon}
\]としてあげてもOK。
*4:例えば、\[
\lim_{n \to \infty} a_n = a , \ \ \ \lim_{n \to \infty} b_n = b
\]ならば、\[
\lim_{n \to \infty} (a_n+b_n) = a+b
\]のような公式
関連広告・スポンサードリンク