スポンサードリンク
こんにちは、ももやまです。
全3回に及ぶノルムの記事ですが、1記事目の応用編第3羽では様々なベクトルのノルム、2記事目の応用編第4編では様々な行列のノルムについて勉強しましたね。
3記事目(最終)の第5羽では、「関数のノルム」、「ベクトルで表される連続時間信号のノルム」についてみていきましょう。
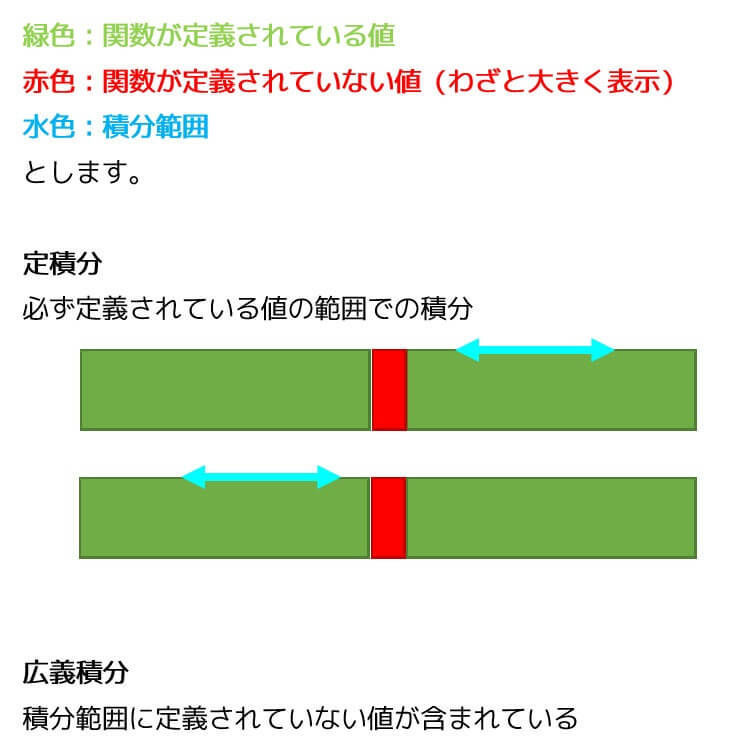
[注意] 本記事では広義積分が出てきます。もし、広義積分があやふやな人(or よくわからない人)は下の記事にて復習をしましょう。復習ができた or 広義積分なんて余裕!という人は、関数のノルムから勉強していきましょう!
スポンサードリンク
1. 関数のノルム
早速関数 \( f(x) \) の \( L_p \) ノルムの定義式を見てみましょう。
連続な関数 \( f(x) \) の \( L_p \) ノルム \( \| f(x) \|_p \) は次のように計算できる。\[
\| f(x) \|_p = \sqrt[p]{ \int^{\infty}_{- \infty}| f(x) |^p \ dx }
\]
定義式だけ出してもわかりずらいと思うので、よく出てくる \( p = 1 \), \( p = 2 \), \( p = \infty \) のときにどうなるかを例題も踏まえて見ていきましょう。
\( L^1 \) ノルム [p = 1]
\( p = 1 \) のときの関数の \( L^1 \) ノルムの計算公式は次のようになります。\[
\| f(x) \|_1 = \int^{\infty}_{- \infty} | f(x) | \ dx
\]
公式の使用例を例題で見てみましょう。
次の関数 \( f(x) \) の \( L^1 \) ノルムを求めなさい。\[
f(x) = \left\{ \begin{array}{cl} - x^2 + 2x + 3 & (-1 \leqq x \leqq 3) \\
0 & (x < -1, 3 < x)
\end{array}
\right.\]
[解説1]
\[
- x^2 + 2x + 3 = - (x+1)(x-3)
\]より、\( -1 \leqq x \leqq 3 \) のとき、\( f(x) \geqq 0 \) となる。
よって、\[\begin{align*}
\| f(x) \|_1 & = \int^{\infty}_{- \infty} | f(x) | \ dx
\\ & = \int^{-1}_{- \infty} \ 0 \ dx + \int^{3}_{-1} | -x^2 + 2x + 3 | \ dx + \int^{\infty}_{3} \ 0 \ dx
\\ & = \int^{3}_{-1} | -x^2 + 2x + 3 | \ dx
\\ & = \int^{3}_{-1} -x^2 + 2x + 3 \ dx \ \ \ (\because -1 \leqq x \leqq 3 \ \mathrm{において} \ x \geqq 0)
\\ & = \left[ - \frac{1}{3} x^3 + x^2 + 3x \right]^{3}_{-1}
\\ & = \left( -9 + 9 + 9 \right) - \left( \frac{1}{3} + 1 - 3 \right)
\\ & = 9 - \left( - \frac{5}{3} \right)
\\ & = \frac{32}{3}
\end{align*}\]と計算できる。
\( L^2 \) ノルム [p = 2]
\( p = 2 \) のときは、関数の \( L^2 \) ノルムの計算公式は次のようになります。\[
\| f(x) \|_2 = \sqrt{ \int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \ dx }
\]
ルート内に積分式を入れたくない人は、\[
\left( \| f(x) \|_2 \right)^2 = \sqrt{ \int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \ dx }
\]を計算してから\[
\| f(x) \|_2 = \sqrt{ \left( | f(x) \|_2 \right)^2 }
\]と求めてもOKです。
先ほどと同じように、公式の使用例を例題で確認しましょう。
次の関数 \( f(x) \) の \( L^2 \) ノルムを求めなさい。\[
f(x) = \left\{ \begin{array}{cl} x^2-1 & (-1 \leqq x \leqq 1) \\
0 & (x < -1, 1 < x)
\end{array}
\right.\]
\( L^2 \) ノルムは、次の計算をすることで求められるのでしたね。\[
\| f(x) \|_2 = \sqrt{ \int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \ dx }
\]
ここで、\[\begin{align*}
\int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \ dx & = \int^{1}_{-1} \left( x^2 - 1 \right)^2 \ dx
\\ & = \int^{1}_{-1} x^4 - 2x^2 + 1 \ dx
\\ & = 2 \int^{1}_{0} x^4 - 2x^2 + 1 \ dx
\\ & = 2 \left[ \frac{1}{5} x^5 - \frac{2}{3} x^3 + x \right]^{1}_{0}
\\ & = 2 \left( \frac{1}{5} - \frac{2}{3} + 1 \right)
\\ & = 2 \cdot \frac{8}{15}
\\ & = \frac{16}{15}
\end{align*}\]
となるので、\[\begin{align*}
\| f(x) \|_2 & = \sqrt{ \int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \ dx }
\\ & = \sqrt{ \frac{16}{15} }
\\ & = \frac{ 4 }{\sqrt{15}}
\\ & = \frac{ 4 \sqrt{15} }{15}
\end{align*}\]と計算できる。
\( L^{\infty} \) ノルム [p = ∞]
\( p = \infty \) のときの関数の \( L^{\infty} \) ノルムの公式は次のようになります。
\[\begin{align*}
\| f(x) \|_{\infty} & = \lim_{p \to \infty} \sqrt[p]{ \int^{\infty}_{- \infty}| f(x) |^p \ dx }
\\ & = \sup_{x \in (- \infty, \infty)} | f(x) |
\end{align*}\]
★ sup(上限)の計算方法
ここで、上限 \( \sup \) について少し確認しておきましょう。
上限\[
\sup_{x \in U} f(x) = A
\]とは、「定義域 \( U \) [1]大学数学では定義域を \( x \in U \) と集合表記で表すことがあります。ここで、\( U \) には \( x \in (- \infty, \infty) \) … Continue reading(\( x \) が取りうる値の範囲) の中で \( A \) より大きな数は存在しないという条件の中で、\( f(x) \) が最も小さくなるような \( A \) のことを指します。
例えば、\( -1 < x < 2 \) における \( |2x| \) の上限\[
\sup_{x \in (- 1, 2)} | 2x |
\]を考えてみましょう。
\( |2x| \) が取りうる値の範囲(値域)は \( 0 \leqq |2x| < 4 \) ですね。そのため、\( -1 < x < 2 \) において \( |2x| \) が4より大きくなることはありませんね。
また、4より小さい数は、\( |2x| \) が取りうる値 \( 0 \leqq |2x| < 4 \) に入ってしまいますね。そのため、\[
\sup_{x \in (- 1, 2)} | 2x | = 4
\]となります。
なお、範囲 \( x \in U \) における \( |f(x)| \) の最大値が存在すれば、その値がそのまま \( \sup_{x \in U} | f(x) | \) となります。つまり、\( \max_{x \in U} f(x) \) が存在する場合、必ず\[
\sup_{x \in U} f(x) = \max_{x \in U} f(x)
\]が成立しますね。
supの復習が終わりましたので、改めて例題で公式の使い方を確認しましょう。
次の関数 \( f(x) \) の \( L^{\infty} \) ノルムを求めなさい。\[
f(x) = \left\{ \begin{array}{cl} -x^2+2x+3 & (-1 \leqq x \leqq 3) \\
0 & (x < -1, 3 < x)
\end{array}
\right.\]
[解説3]
\( 0 \leqq x \leqq 3 \) のとき、\[\begin{align*}
f(x) & = - x^2 + 2x + 3
\\ & = - (x-1)^2 + 4
\end{align*}\]となるため、\( f(x) \) の最大値は4となる。
また、\( -1 \leqq x \leqq 3 \) における \( f(x) \) の最小値は0のため、\( |f(x)| \) の最大値も4となる。
ここで、最大値が存在するため、上限は最大値4と等しくなる。よって、ノルムは\[\begin{align*}
\| f(x) \|_{\infty} & = \sup_{x \in (- \infty, \infty)} | f(x) |
\\ & = 4
\end{align*}\]と計算できる。
\( p = 1 \) のとき(\( L^1 \) ノルム)\[
\| f (x) \|_1 = \int^{\infty}_{- \infty} | f(x) | \ dx
\]
\( p = 2 \) のとき (\( L^2 \) ノルム)\[\begin{align*}
( \| f(x) \|_2 )^2 & = \int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \\
\| f(x) \|_2 & = \sqrt{ \int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \ dx }
\end{align*}\]
\( p = \infty \) のとき(\(L^{\infty} \) ノルム)\[
\sup_{x \in (- \infty, \infty)} | f(x) |
\]
[\( L^{\infty} \) ノルムの求め方]
- 定義域 \( - \infty < x < \infty \) 内に最大値が存在すればその値が \( \| f(x) \|_{\infty} \) になる。
- 最大値が存在しない場合は、次の1, 2により \( \| f(x) \|_{\infty} \) を決定する
- 定義域 \( -x < \infty < x \) 内で、\( | f(x) | \) がとりうるどの値よりも大きい or 等しくなる値を考える
- 1を満たすような値のうち、最も小さい値が \( \| f(x) \|_{\infty} \) となる。
スポンサードリンク
2. 連続時間信号(成分に関数が含まれるベクトル)のノルム
信号処理の世界では、下のような連続時間信号(成分に時間 \( t \) の関数 \( f(t) \) が含まれるベクトル)のノルムを計算することがあります。\[
f(t) = \left( \begin{array}{ccc} t^2 \\ 3t \end{array} \right)
\]
ベクトルの成分に時間 \( t \) が含まれている連続時間信号\[
f(t) = \left( \begin{array}{ccc} f_1 (t) \\ f_2 (t) \\ \vdots \\ f_n (t) \end{array} \right)
\]の \( L ^p \) ノルムは次のように計算できる。\[\begin{align*}
\| f(t) \|_p & = \sqrt[p]{ \int^{\infty}_{- \infty} | f_1 (t) |^p + | f_2 (t) |^p + \cdots + | f_n (t) |^p \ dt }
\\ & = \sqrt[p]{ \int^{\infty}_{- \infty} \sum^{n}_{k = 1} | f_k (t) |^p \ dt }
\end{align*}\]
※1 ベクトルのノルム公式と関数のノルム公式をあわせたような形
※2 \( f(t) \) は \( n \) 次元ベクトルとなる
こちらも、よく(試験などで)出てくる \( L^1 \) ノルム、\( L^2 \) ノルム、\( L^{\infty} \) ノルムについて、それぞれ計算方法を確認しましょう。
(1) \( L^1 \) ノルム [p = 1]
( p = 1 \) のときの連続時間信号の \( L^1 \) ノルムの計算公式は次のようになります。\[\begin{align*}
|\| f(t) \|_1 & = \int^{\infty}_{- \infty} | f_1 (t) | + | f_2 (t) | + \cdots + | f_n (t) | \ dt
\\ & = \int^{\infty}_{- \infty} \sum^{n}_{k = 1} | f_k (t) | \ dt
\end{align*}\]
例題で計算公式の使い方を確認しましょう。
次の連続時間信号 \( f(t) \) の \( L^1 \) ノルム \( \| f(t) \|_1 \) を求めなさい。\[
f(t) = \left\{ \begin{array}{cl} \left( \begin{array}{ccc} t^2 - t \\ t^3-3t^2+2t \end{array} \right) & (0 \leqq t \leqq 1) \\
\left( \begin{array}{ccc} 0 \\ 0 \end{array} \right) & (t < 0, 1 < t)
\end{array}
\right.\]
[解説4]
\[
t^2 - t = t(t-1)
\]\[
t^3 - 3t^2 + 2t = t(t-1)(t-2)
\]より、\( 0 \leqq t \leqq 1 \) において、\( t^2 - t \leqq 0 \)、\( t^3-3t^2+2t \geqq 0 \) となる。
よって、連続時間信号 \( f(t) \) の\( L^{1} \) ノルムは\[\begin{align*}
\| f(t) \|_1 & = \int^{1}_{0} |t^2 - t| \ dt + \int^{1}_{0} | t^3 - 3t^2 + 2t | \ dt
\\ &= \int^{1}_{0} -t^2 + t \ dt + \int^{1}_{0} t^3 - 3t^2 + 2t \ dt
\\ & = \left[ - \frac{1}{3} t^3 + \frac{1}{2} t^2 \right]^{1}_{0} + \left[ \frac{1}{4} t^4 - t^3 + t^2 \right]^{1}_{0}
\\ & = \left( - \frac{1}{3} + \frac{1}{2} \right) + \left( \frac{1}{4} - 1 + 1 \right)
\\ & = \frac{1}{6} + \frac{1}{4}
\\ & = \frac{5}{12}
\end{align*}\]と計算できる。
(2) \( L^2 \) ノルム [p = 2]
\( p = 2 \) のときの連続時間信号の \( L^2 \) ノルムの計算公式も見ていきましょう。\[\begin{align*}
\| f(t) \|_2 & = \sqrt{ \int^{\infty}_{- \infty} \left\{ f_1 (t) \right\}^2 + \left\{ f_2 (t) \right\}^2 + \cdots + \left\{ f_n (t) \right\}^2 \ dt }
\\ & = \sqrt{ \int^{\infty}_{- \infty} \sum^{n}_{k = 1} \left\{ f_k (t) \right\}^2 \ dt }
\end{align*}\]
※ ルートの中に積分式を入れたくない人は、\[
ルート内に積分式を入れたくない人は、\[\begin{align*}
\left( \| f(t) \|_2 \right)^2 & = \int^{\infty}_{- \infty} \left\{ f_1 (t) \right\}^2 + \left\{ f_2 (t) \right\}^2 + \cdots + \left\{ f_n (t) \right\}^2 \ dt
\\ & = \int^{\infty}_{- \infty} \sum^{n}_{k = 1} \left\{ f_k (t) \right\}^2 \ dt
\end{align*}\]を計算してから\[
\| f(t) \|_2 = \sqrt{ \left( | f(t) \|_2 \right)^2 }
\]と求めてもOKです。
同じように例題で計算公式の使い方を確認しましょう。
次の連続時間信号 \( f(t) \) の \( L^2 \) ノルム \( \| f(t) \|_2 \) を求めなさい。\[
f(t) = \left\{ \begin{array}{cl} \left( \begin{array}{ccc} t^2 - t \\ t^3-t \end{array} \right) & (0 \leqq t \leqq 1) \\
\left( \begin{array}{ccc} 0 \\ 0 \end{array} \right) & (t < 0, 1 < t)
\end{array}
\right.\]
[解説5]
まずは、ノルムの2乗 \( \| f(t) \|_2 \) を求める。\[\begin{align*}
\left( \| f(t) \|_2 \right)^2 & = \int^{1}_{0} (t^2 - t)^2 \ dt + \int^{1}_{0} (t^3-t)^2 \ dt
\\ & = \int^{1}_{0} t^4 - 2t^3 + t^2 \ dt + \int^{1}_{0} t^6 - 2t^4 +t^2 \ dt
\\ & = \left[ \frac{1}{5} t^5 - \frac{1}{2} t^4 + \frac{1}{3} t^3 \right]^{1}_{0} + \left[ \frac{1}{7} t^7 - \frac{2}{5} t^5 + \frac{1}{3} t^3 \right]^{1}_{0}
\\ & = \left( \frac{1}{5} - \frac{1}{2} + \frac{1}{3} \right) + \left( \frac{1}{7} - \frac{2}{5} + \frac{1}{3} \right)
\\ & = \frac{1}{30} + \frac{8}{105}
\\ & = \frac{23}{210}
\end{align*}\]
よって、連続時間信号 \( f(t) \) の\( L^2 \) ノルムは\[\begin{align*}
\| f(t) \|_2 & = \sqrt{ ( \| f(t) \|_2 )^2 }
\\ & = \sqrt{ \frac{23}{210} }
\\ & = \frac{ \sqrt{23} }{ \sqrt{210} }
\\ & = \frac{ \sqrt{4830} }{210}
\end{align*}\]と計算できる。
(3) \( L^{\infty} \) ノルム [p = ∞]
\( p = \infty \) のときの関数の \( L^{\infty} \) ノルム公式は次のようになります。
\[\begin{align*}
\| f(x) \|_{\infty} & = \lim_{p \to \infty} \sqrt[p]{ \int^{\infty}_{- \infty} | f_1 (t) |^p + | f_2 (t) |^p + \cdots + | f_n (t) |^p \ dt }
\\ & = \sup_{t \in (- \infty, \infty)} \max ( |f_1 (t)|, | f_2 (t) | , \cdots, | f_n (t) | )
\\ & = \sup_{t \in (- \infty, \infty)} \max_{1 \leqq k \leqq n} | f_k (t) |
\end{align*}\]
求め方としては、\( f_1 (t) \), \( f_2 (t) \), …, \( f_n (t) \) の上限値(sup)を求め、それらの最大値を取ればOKです。
こちらも実際に例題の計算演習で確認してみましょう。
次の連続時間信号 \( f(t) \) の \( L^{\infty} \) ノルム \( \| f(t) \|_{\infty} \) を求めなさい。\[
f(t) = \left\{ \begin{array}{cl} \left( \begin{array}{ccc} - t^2 + t \\ - t^3 + t \end{array} \right) & (0 \leqq t \leqq 1) \\
\left( \begin{array}{ccc} 0 \\ 0 \end{array} \right) & (t < 0, 1 < t)
\end{array}
\right.\]
\( t^2 - t \), \( t^3 -t \) の最大値を求める。
\[\begin{align*}
- t^2 + t = - \left( t - \frac{1}{2} \right)^2 + \frac{1}{4}
\end{align*}\]となるため、最大値は \( t = 1/2 \) のとき、\( 1/4 \) となる。
また、\( -t^3 + t \) の最大値は微分をすることで求める。ここで \( g(t) = -t^3+t \) とすると、\[\begin{align*}
g'(t)& = -3t^2 + 1
\end{align*}\]となるため、\( 0 \leqq t \leqq 1 \) における極値は\[
t = \frac{ \sqrt{3} }{3}
\]となる。さらに増減表を書くと、下のようになる。
よって、最大値は\[
\frac{ 2 \sqrt{3} }{9}
\]と求められる。
ここで、\[
\frac{9}{36} < \frac{13.6}{36} < \frac{8 \sqrt{3}}{36} \]が成立するため、
\[\frac{1}{4} < \frac{ 2 \sqrt{3} }{9}
\]となる。\( L^{\infty} \) ノルムを\[\begin{align*}
\| f(x) \|_{\infty} & =\sup_{t \in (- \infty, \infty)} \max \left( f_1 (t), f_2 (t)\right)
\\ & = \max \left( \frac{ \sqrt{3} }{3}, \frac{ 2 \sqrt{3} }{9} \right)
\\ & = \frac{ 2 \sqrt{3} }{9}
\end{align*}\]と求めることができる。
なお、\( \| f(t) \|_{\infty} \) を計算する際には、下のようにグラフを書き、どの成分の関数の最大値が(ベクトル内の関数の中で)一番最大になるのかを把握するのがおすすめ。
\( n \) 次元ベクトルで表される連続時間信号 \( f(t) \) の \( p = 1, 2, \infty \) における \( L^{p} \) ノルムの計算方法は以下の通り。
\( p = 1 \) のとき(\( L^1 \) ノルム)\[\begin{align*}
|\| f(t) \|_1 & = \int^{\infty}_{- \infty} | f_1 (t) | + | f_2 (t) | + \cdots + | f_n (t) | \ dt
\\ & = \int^{\infty}_{- \infty} \sum^{n}_{k = 1} | f_k (t) | \ dt
\end{align*}\]
\( p = 2 \) のとき (\( L^2 \) ノルム)\[\begin{align*}
\left( | f(t) \|_2 \right)^2 & = \int^{\infty}_{- \infty} \left\{ f_1 (t) \right\}^2 + \left\{ f_2 (t) \right\}^2 + \cdots + \left\{ f_2 (t) \right\}^2 \ dt
\\ & = \int^{\infty}_{- \infty} \sum^{n}_{k = 1} \left\{ f_k (t) \right\}^2 \ dt
\end{align*}\]\[\begin{align*}
\| f(t) \|_2 & = \sqrt{ \int^{\infty}_{- \infty} \left\{ f_1 (t) \right\}^2 + \left\{ f_2 (t) \right\}^2 + \cdots + \left\{ f_n (t) \right\}^2 \ dt }
\\ & = \sqrt{ \int^{\infty}_{- \infty} \sum^{n}_{k = 1} \left\{ f_k (t) \right\}^2 \ dt }
\end{align*}\]
\( p = \infty \) のとき(\(L^{\infty} \) ノルム)\[\begin{align*}
\| f(x) \|_{\infty} & = \sup_{t \in (- \infty, \infty)} \max ( |f_1 (t)|, | f_2 (t) | , \cdots, | f_n (t) | )
\\ & = \sup_{t \in (- \infty, \infty)} \max_{1 \leqq k \leqq n} | f_k (t) |
\end{align*}\]
[\( L^{\infty} \) ノルムの求め方] \( f_1 (t) \), \( f_2 (t) \), …, \( f_n (t) \) の上限値(sup)を求め、それらの最大値を取ればOK。
スポンサードリンク
3. 練習問題
では、実際に関数ノルム・連続時間信号のノルムを計算する練習をしてみましょう。
練習1:関数の \( L^1 \), \( L^2 \) ノルム
次の関数 \( f(x) \) の \( L^1 \), \( L^2 \) ノルムを求めなさい。\[
f(x) = \left\{ \begin{array}{cl} e^{-x} & (0 \leqq x) \\
e^{x} & (x < 0)
\end{array}
\right.\]
練習2:関数の \( L^{\infty} \) ノルム
次の関数 \( f(x) \) の \( L^{\infty} \) ノルムを求めなさい。\[
f(x) = \left\{ \begin{array}{cl} x^2 & (0 < x < 4) \\
0 & (x \leqq 0 , 4 \leqq x)
\end{array}
\right.\]
練習3:連続時間信号の \( L^1 \), \( L^2 \) ノルム
次の連続時間信号 \( f(t) \) の \( L^1 \), \( L^2 \) ノルムを求めなさい。\[
f(t) = \left\{ \begin{array}{cl} \left( \begin{array}{ccc} e^{-3t} \\ -2e^{-4t} \end{array} \right) & (0 \leqq t ) \\
\left( \begin{array}{ccc} 0 \\ 0 \end{array} \right) & (t < 0)
\end{array}
\right.\]
練習4:連続時間信号の \( L^{\infty} \) ノルム
次の連続時間信号 \( f(t) \) の \( L^{\infty} \) ノルムを求めなさい。\[
f(t) = \left( \begin{array}{ccc} \cos t \\ 2 \sin t \\ 3 \cos t \end{array} \right)
\]
4. 練習問題の答え
練習1:関数の \( L^1 \), \( L^2 \) ノルム
(i) \( L^1 \) ノルム
\[\begin{align*}
\| f(x) \|_1 & = \int^{\infty}_{- \infty} |f(x)| \ dx
\\ & = \int^{0}_{- \infty} |e^x| \ dx + \int^{\infty}_{0} |e^{-x}| \ dx
\\ & = \lim_{R \to \infty} \int^{0}_{- R} e^x \ dx + \lim_{R \to \infty} \int^{R}_{0} e^{-x} \ dx
\end{align*}\]を計算すればOK[2]\( 0 \leqq x \) において、\( e^x \geqq 0 \), \( e^{-x} \geqq 0 \) となるため簡単に絶対値をはずせる。。
ここで、\[\begin{align*}
\lim_{R \to \infty} \int^{0}_{- R} e^x \ dx & = \left[ e^x \right]^{0}_{- R}
\\ & = \lim_{R \to \infty} 1 - e^{-R}
\\ & = 1 - \lim_{R \to \infty} \frac{1}{ e^R }
\\ &= 1
\end{align*}\]
\[\begin{align*}
\lim_{R \to \infty} \int^{R}_{0} e^{-x} \ dx & = \left[ -e^{-x} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} - e^{-R} + 1
\\ & = 1 - \lim_{R \to \infty} \frac{1}{ e^R }
\\ &= 1
\end{align*}\]と計算できるので、
\[\begin{align*}
\| f(x) \|_1 & = \lim_{R \to \infty} \int^{0}_{- R} e^x \ dx + \lim_{R \to \infty} \int^{R}_{0} e^{-x} \ dx
\\ & = 1 + 1
\\ & = 2
\end{align*}\]と計算できる。
(ii) \( L^2 \) ノルム
\[\begin{align*}
\left( \| f(x) \|_2 \right)^2 & = \int^{\infty}_{- \infty} \left\{ f(x) \right\}^2 \ dx
\\ & = \int^{0}_{- \infty} \left( e^x \right)^2 \ dx + \int^{\infty}_{0} \left( e^{-x} \right)^2 \ dx
\\ & = \lim_{R \to \infty} \int^{0}_{- R} e^{2x} \ dx + \lim_{R \to \infty} \int^{R}_{0} e^{-2x} \ dx
\end{align*}\]を計算してから、\( \| f(x) \|_2 = \sqrt{ \left( \| f(x) \|_2 \right)^2 } \) をすればOK。
ここで、\[\begin{align*}
\lim_{R \to \infty} \int^{0}_{- R} e^{2x} \ dx & = \left[ \frac{1}{2} e^{2x} \right]^{0}_{- R}
\\ & = \lim_{R \to \infty} \frac{1}{2} - \frac{1}{2} e^{-2R}
\\ & = \frac{1}{2} - \lim_{R \to \infty} \frac{1}{ 2e^{2R} }
\\ &= \frac{1}{2}
\end{align*}\]
\[\begin{align*}
\lim_{R \to \infty} \int^{R}_{0} e^{-2x} \ dx & = \left[ - \frac{1}{2} e^{-2x} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} - \frac{1}{2} e^{-2R} + \frac{1}{2}
\\ & = \frac{1}{2} - \lim_{R \to \infty} \frac{1}{ 2e^{2R} }
\\ &= \frac{1}{2}
\end{align*}\]と計算できるので、
\[\begin{align*}
\left( \| f(x) \|_2 \right)^2 & = \lim_{R \to \infty} \int^{0}_{- R} e^{2x} \ dx + \lim_{R \to \infty} \int^{R}_{0} e^{-2x} \ dx
\\ & = \frac{1}{2} + \frac{1}{2}
\\ & = 1
\end{align*}\]なので、\( L^2 \) ノルムは\[\begin{align*}
\| f(x) \|_2 & = \sqrt{\left( \| f(x) \|_2 \right)^2}
\\ & = \sqrt{1}
\\ & = 1
\end{align*}\]となる。
練習2:関数の \( L^{\infty} \) ノルム
\[\begin{align*}
\sup_{x \in (- \infty, \infty)} | f(x) | & = \sup_{x \in (0,4)} |x^2|
\\ & = A
\end{align*}\]を満たすような \( A \) を考える。
ここで、\( 0 < x < 4 \) のとき、値域は\( 0 < | x^2 | < 16 \) となる。
そのため、値域 \( 0 < | x^2 | < 16 \) に含まれるどの値よりも大きくなり、なおかつ \( A \) をできるだけ小さくするようにするためには、\( A = 16 \) とすればOK。
よって、\[\begin{align*}
\| f(x) \|_{\infty} & = \sup_{x \in (- \infty, \infty)} | f(x) |
\\ & = \sup_{x \in (0,4)} |x^2|
\\ & = 16
\end{align*}\]と計算できる。
練習3:連続時間信号の \( L^1 \), \( L^2 \) ノルム
(i) \( L^1 \) ノルム
\[\begin{align*}
\| f(t) \|_1 & = \int^{\infty}_{0} |e^{-3t}| \ dt + \int^{\infty}_{0} |-2e^{-4t}| \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} e^{-3t} dt + 2 \lim_{R \to \infty} \int^{R}_{0} e^{-4t} \ dt
\end{align*}\]を計算すればOK[3] \( 0 \leqq t \) において、\( e^{-3t} \geqq 0 \), \( - e^{-4t} \leqq 0 \) となるため、絶対値を簡単に外せる。。
ここで、\[\begin{align*}
\lim_{R \to \infty} \int^{R}_{0} e^{-3t} \ dt & = \left[ - \frac{1}{3} e^{-3t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} - \frac{1}{3} e^{-3R} + \frac{1}{3}
\\ & = \frac{1}{3} - \lim_{R \to \infty} \frac{1}{ 3e^{3R} }
\\ &= \frac{1}{3}
\end{align*}\]
\[\begin{align*}
\lim_{R \to \infty} \int^{R}_{0} e^{-4t} \ dx & = \left[ - \frac{1}{4} e^{-4t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} - \frac{1}{4} e^{-4R} + \frac{1}{4}
\\ & = \frac{1}{4} - \lim_{R \to \infty} \frac{1}{ 4e^{4R} }
\\ &= \frac{1}{4}
\end{align*}\]と計算できるので、\[\begin{align*}
\| f(t) \|_1 & = \lim_{R \to \infty} \int^{R}_{0} e^{-3t} dt + 2 \lim_{R \to \infty} \int^{R}_{0} e^{-4t} \ dt
\\ & = \frac{1}{3} + 2 \cdot \frac{1}{4}
\\ & = \frac{5}{6}
\end{align*}\]と計算できる。
(ii) \( L^2 \) ノルム
\[\begin{align*}
\left( \| f(t) \|_2 \right)^2 & = \int^{\infty}_{0} \left\{ e^{-3t} \right\}^2 \ dt + \int^{\infty}_{0} \left\{ -2 e^{-4t} \right\}^2 \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} e^{-6t} dt + 4 \lim_{R \to \infty} \int^{R}_{0} e^{-8t} \ dt
\end{align*}\]を計算し、\( \| f(t) \|_2 = \sqrt{ \left( \| f(t) \| \right)^2 } \) とすればOK。
ここで、\[\begin{align*}
\lim_{R \to \infty} \int^{R}_{0} e^{-6t} \ dt & = \left[ - \frac{1}{6} e^{-6t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} - \frac{1}{6} e^{-6R} + \frac{1}{6}
\\ & = \frac{1}{6} - \lim_{R \to \infty} \frac{1}{ 6e^{6R} }
\\ &= \frac{1}{6}
\end{align*}\]
\[\begin{align*}
\lim_{R \to \infty} \int^{R}_{0} e^{-8t} \ dx & = \left[ - \frac{1}{8} e^{-8t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} - \frac{1}{8} e^{-8R} + \frac{1}{8}
\\ & = \frac{1}{8} - \lim_{R \to \infty} \frac{1}{ 8e^{8R} }
\\ &= \frac{1}{8}
\end{align*}\]と計算できるので、\[\begin{align*}
( \| f(t) \|_2 )^2 & = \lim_{R \to \infty} \int^{R}_{0} e^{-6t} dt + 4 \lim_{R \to \infty} \int^{R}_{0} e^{-8t} \ dt
\\ & = \frac{1}{6} + 4 \cdot \frac{1}{8}
\\ & = \frac{2}{3}
\end{align*}\]と計算できる。
よって、\( L^2 \) ノルムは\[\begin{align*}
\| f(t) \|_2 & = \sqrt{\left( \| f(t) \|_2 \right)^2}
\\ & = \sqrt{ \frac{2}{3} }
\\ & = \frac{ \sqrt{2} }{ \sqrt{3} }
\\ & = \frac{ \sqrt{6} }{3}
\end{align*}\]となる。
練習4:連続時間信号の \( L^{\infty} \) ノルム
\( | \cos t | \leqq 1 \), \( | 2 \sin t | \leqq 2 \), \( | 3 \cos t | \leqq 3 \) である。
よって、\[
\max |\cos t| = 1
\]\[
\max | 2 \sin t | = 2
\]\[
\max | 3 \cos t | = 3
\]となる。
したがって、\( L^{\infty} \) ノルムは\[\begin{align*}
\| f(t) \|_{\infty} & = \sup_{t \in (- \infty, \infty)} \max ( |\cos t|, |2 \sin t |, |3 \cos t| )
\\ & = 3
\end{align*}\]と計算できる。
連続時間信号の \( L^{\infty} \) ノルムはグラフを書くと計算しやすいかもしれません。
5. さいごに
今回は、関数のノルム、およびベクトルで表される連続時間信号のノルムについて説明しました。
第3羽から3記事にわたったノルム、いかがだったでしょうか。
- 第3羽 様々なベクトルのノルム
- 第4羽 行列のノルム
- 第5羽 関数のノルム・ベクトルで表される連続時間信号のノルム ← この記事!
第3羽、第4羽のリンクで復習ができるので、復習をしたい方はリンクから飛んでください!
第6羽では、2次形式の(半)正定値、(半)負定値の判定方法についてみていきたいと思います!
注釈
| ↑1 | 大学数学では定義域を \( x \in U \) と集合表記で表すことがあります。ここで、\( U \) には \( x \in (- \infty, \infty) \) のように括弧を使って定義域を表します。 この括弧ですが、\( ( \) と \( ) \) がそれぞれ不等号 \( < \) と \( > \) に対応しており、\( [ \) と \( ] \) がそれぞれ \( \leqq \), \( \geqq \) に対応しています。 例えば、\( x \in (2,5] \) であれば、\( x \) の定義域(取りうる値の範囲)は \( 2 < x \leqq 5 \) となります。 |
|---|---|
| ↑2 | \( 0 \leqq x \) において、\( e^x \geqq 0 \), \( e^{-x} \geqq 0 \) となるため簡単に絶対値をはずせる。 |
| ↑3 | \( 0 \leqq t \) において、\( e^{-3t} \geqq 0 \), \( - e^{-4t} \leqq 0 \) となるため、絶対値を簡単に外せる。 |
関連広告・スポンサードリンク