うさぎでもわかる解析（高校数学・数3）　Part06　部分積分（部分積分の連鎖公式：ブンブン・瞬間部分積分）

こんにちは、ももやまです！
今日は積分の中でも計算量が特に多くなってしまう部分積分についてまとめを行います。

スポンサードリンク

１．部分積分の公式

2つの関数の積 \( f(x) \), \( g(x) \) には、つぎのような公式が成り立ちます。

公式の導出は、積の微分公式で導くことができます。

合成関数の微分は、\[ \left( f(x)g(x) \right)' = f'(x) g(x) + f(x) g'(x) \]でしたね。

両辺を積分すると、\[ \int ( f(x)(g(x) )' \ dx = f(x) g(x)  = \int f'(x) g(x)  \ dx + \int f(x) g'(x) \ dx \]となるのでこれを整理して、\[ \int f(x) g'(x)  \ dx = f(x) g(x) -   \int f'(x) g(x)  \ dx \]と求めることができます。

実際に積分をする際には、「後ろを積分、符号を変えて前を微分……」と心の中で言いながら積分していきましょう。

早速例題を1つ解いてみましょう。

例題1

不定積分\[ \int x \sin 2x \ dx \]を計算しなさい。

解説1

\( f(x) = x \), \( g(x) = \sin 2x \) として計算します。

基本的に前側（ \( f(x) \) のほう）に微分したら消えるものを用意するのが鉄則です。

\[\begin{align*} \int x \sin 2x \ dx & = - \frac{1}{2} x \cos 2x - \int - \frac{1}{2} \cos 2x \ dx
\\ & = - \frac{1}{2} x \cos 2x - \left( - \frac{1}{4} \sin 2x \right)
\\ & = - \frac{1}{2} x \cos 2x + \frac{1}{4} \sin 2x + C
\end{align*} \]と計算できます。

※ \( C \) は積分定数です。（以後、本記事では省略します。）

例題2

不定積分\[ \int \log x \ dx \]を計算しなさい。

解説2

ポイントとしては、\( \log x \) の前に 1 があると思いこむことです。
1を積分すると  \( x \) となります。

\[\begin{align*} \int \log x \ dx & = \int 1 \cdot \log x \ dx  \\ & = x \log x - \int x \cdot \frac{1}{x} \ dx \\ & = x \log x - \int 1 \ dx \\ & = x \log x - x + C
\end{align*} \]と計算できます。

（ \( \log x \) の積分は重要なのでできれば覚えちゃってください。）

部分積分は2回以上適用することもできます。

例題3

不定積分\[ \int x^3 \cos x \ dx \]を計算しなさい。

解説3

\( x^3 \) は微分し続けたら定数項になってくれるのでこちらを微分し、\( \sin x \) を積分する。

\[\begin{align*} \int x^3 \cos x \ dx & = x^3 \sin x - \int 3x^2 \sin x \ dx
\\ & = x^3 \sin x - \left( - 3x^2 \cos x - \int - 6x \cos x \ dx \right)
\\ & = x^3 \sin x + 3x^2 \cos x - 6x \sin x + \int 6 \sin x \ dx
\\ & = x^3 \sin x + 3x^2 \cos x - 6x \sin x - 6 \cos x + C
\end{align*} \]と計算できます。

スポンサードリンク

２．部分積分連鎖公式（ブンブン・瞬間部分積分）

しかし、いちいちインテグラルを書くのはめんどくさいですよね（特に複数回部分積分を適用する場合）。

なので、部分積分をドミノ倒しに適応させてしまおうというのが部分積分の連鎖公式です。

通称ブンブン・瞬間部分積分と呼ばれています。

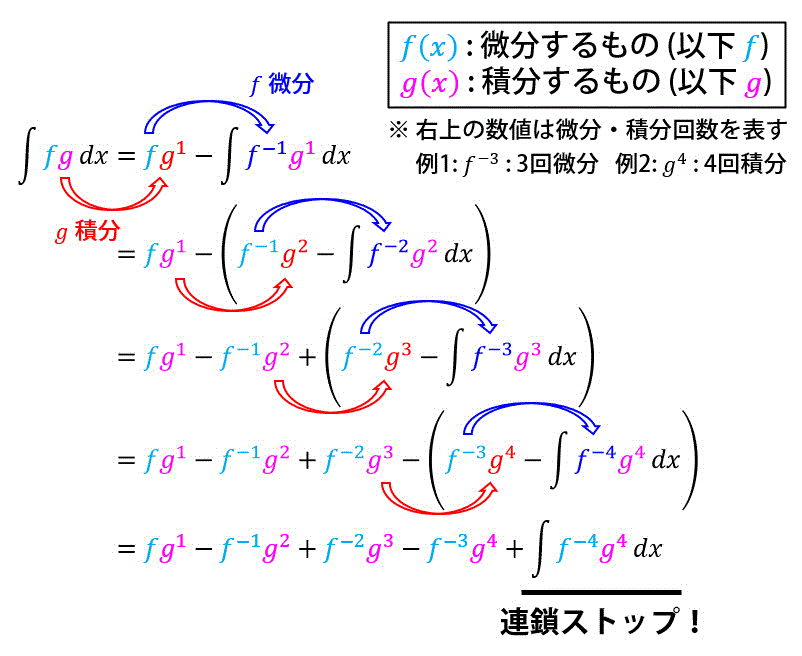
連鎖公式が成り立つ理屈を下のほうで紹介しておきます。

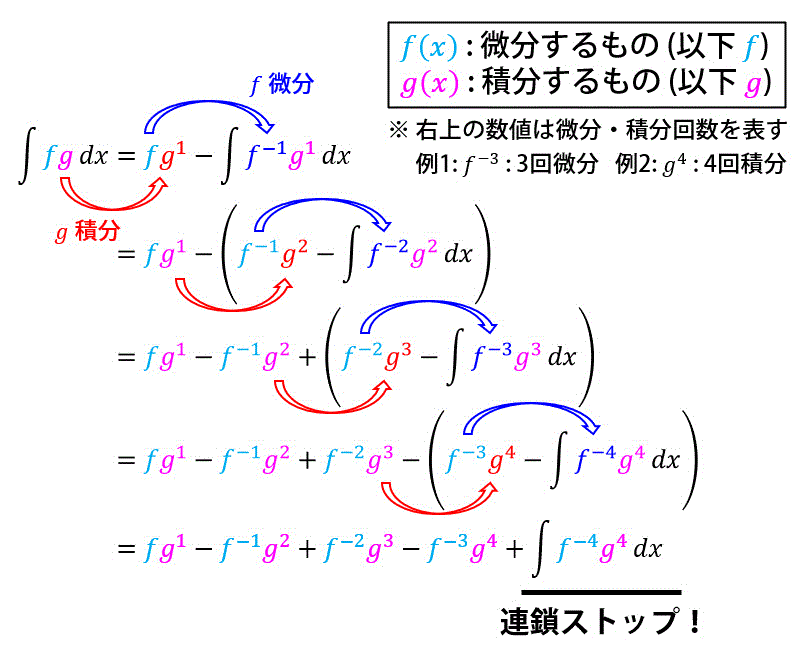
この公式をまとめると、

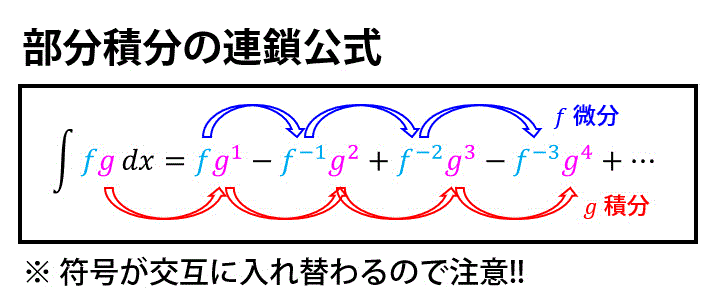
のようになります。

連鎖公式のステップとしては

1. 積分する側を1回積分
2. 符号を変え、微分する側を1回微分、積分する側を1回積分
3. 微分する側が消えるまで2を繰り返す*1

となります。

ただし、微分した際に分数が出てくる \( \log x \), \( \tan x \), \( \sin^{-1} x \),\( \cos^{-1} x \), \( \tan^{-1} x \) などには連鎖公式が使えないので注意してください。

先ほどの例題3を連鎖公式で解きましょう。\[\begin{align*}
& \int x^3 \cos x \ dx \\ = & x^3 \sin x - 3x^2 (- \cos x) + 6x (- \sin x) - 6 \cos x
\\ = & x^3 \sin x + 3x^2 \cos x - 6x \sin x - 6 \cos x + C
\end{align*} \]となります。

余計なインテグラルを一切書かなくていいのでごちゃごちゃせずに計算ができますね！

連鎖公式（通称：ブンブン）についてはこちらの記事を引用させていただきました。

saitei.net

引用：saitei.net　「瞬間部分積分とテーブル法にサヨナラよ」
2019年7月16日アクセス

連鎖公式の練習としてもう1問解いてみましょう。

例題4

不定積分\[ \int x^3  e^x  \ dx \]を計算しなさい。

解説4

連鎖公式でイチコロ
\[\begin{align*}
\int x^3 e^x \ dx & = x^3 e^x - 3x^2 e^x + 6x e^x - 6 e^x + C
\\ & = (x^3 - 3x^2 + 6x-6) e^x + C
\end{align*} \]となる。

連鎖公式はもちろん定積分でも使用が可能です。

例題5

定積分\[ \int^{\frac{\pi}{2}}_0 x^2  \sin x  \ dx \]を計算しなさい。

解説5

定積分の場合、最終的な答えが出せれば良いので、[   ] の中を整理する必要はまったくない。

\[\begin{align*}
& \int^{\frac{\pi}{2}}_0 x^2  \sin x  \ dx
\\ = & \left[ x^2 (-\cos x) - 2x (- \sin x) + 2 (\cos x)   \right]^{\frac{\pi}{2}}_0
\\ = & \pi -  2
\end{align*} \]

スポンサードリンク

３．部分積分を解くと元の式が登場するパターン

つぎのように、部分積分をしてたら元の部分積分の式が出てくるようなパターンがあります。

例題6

不定積分\[ \int e^x \sin x  \ dx \]を計算しなさい。

解説6

この問題の場合は \( e^x \), \( \sin x \) を微分側・積分側どちらに設定しても解くことができます。（下の式の場合は \( e^x \) 側を積分しています。）

\[\begin{align*} \int  e^x \sin x \ dx & =  e^x \sin x - \int e^x \cos x \ dx
\\ & = e^x \sin x - \left( e^x \cos x - \int - e^x \sin x \ dx \right)
\\ & = e^x \sin x - e^x \cos x - \int e^x \sin x \ dx
\end{align*} \]と計算すると、\[ \int e^x \sin x \ dx \] が右辺にも現れますね。これを左辺に移項すると、\[ 2 \int e^x \sin x \ dx = e^x \sin x - e^x \cos x \]となります。したがって、\[\int e^x \sin x \ dx =  \frac{1}{2} \left( e^x \sin x - e^x \cos x \right) + C\]と計算できます。

部分積分をしたらもとに戻るパターンの積分でも連鎖公式を使うこともできます。

しかし、注意しないと永久に連鎖公式が終わらないので \( \int e^x \sin x \ dx \) が見える1つ前の段階で連鎖公式をやめる必要がある。

連鎖公式を適用（ \( \sin x \) 側を積分している）すると、\[\begin{align*} & \int  e^x \sin x \ dx
\\ = & e^x (- \cos x) -  e^x (- \sin x) + \int e^x (- \sin x)
\\ = & - e^x \cos x + e^x \sin x - \int e^x \sin x dx
\end{align*} \]

連鎖公式をやめるときは、微分する側を1回微分（今回の場合は \( e^x \)）し、積分する側は積分しないようにすれば連鎖を切ることができます。

４．練習問題

では、練習していきましょう。

今回は定積分・不定積分をごちゃ混ぜで入れています。

練習

つぎの不定積分・定積分を求めなさい。

積分定数は \( C \) とすること。

(1) \[ \int^{e^2}_1 x \log x  \ dx \]

(2) \[\int  (2x - 3) e^{-3x} \ dx \]

(3) \[ \int (3x + 1) \sin 3x \ dx \]

(4) \[ \int (2x^2 + 3x - 4) e^x \ dx\]

(5)[大学数学用] \[ \int \tan^{-1} x \ dx \]

(6) \[ \int (x^2 - 3x + 4) \cos 2x \ dx \]

(7) \[ \int^{\pi}_0 (x^2-4x) \cos x \ dx \]

(8) \[ \int e^{3x} \cos 2x \ dx \]

５．練習問題の解答

(1)

\[\begin{align*}
\int^{e^2}_1 x \log x  \ dx & = \left[ \frac{1}{2} x^2 \log x \right]^{e^2}_1 - \int^{e^2}_1 \frac{1}{2} x^2 \cdot \frac{1}{x} \ dx
\\ & = e^4 - \int^{e^2}_1 \frac{1}{2} x \ dx
\\ & = e^4 - \left[ \frac{1}{4} x^2  \right]^{e^2}_1
\\ & = e^4 - \left( \frac{1}{4} e^4 -  \frac{1}{4} \right)
\\ & = \frac{3}{4} e^4 + \frac{1}{4}
\end{align*} \]

(2)

連鎖公式を使う。\[\begin{align*}
\int (2x - 3) e^{-3x} \ dx & = (2x - 3) \left(-\frac{1}{3} e^{-3x} \right) - 2 \left(\frac{1}{9} e^{-3x} \right) \\ & = \frac{1}{9} e^{-3x}  \left(-6x +7 \right) + C
\end{align*} \]

(3)

連鎖公式を使う。\[\begin{align*}
& \int (3x + 1) \sin 3x \ dx
\\ = & (3x + 1) \left(- \frac{1}{3} \cos 3x \right) - 3 \left(- \frac{1}{9} \sin 3x \right) + C
\\ = & \frac{1}{3} \left(\sin 3x -(3x+1) \cos 3x \right) + C
\end{align*} \]

(4)

これも連鎖公式。\[\begin{align*}
& \int (2x^2 + 3x - 4) e^x \ dx =
\\ = & (2x^2 + 3x -4) e^x - (4x + 3) e^x + 4 e^x
\\ = & (2x^2 - x - 3 ) e^x + C
\end{align*} \]

(5)

\( \log x \) の微分と同じく、1があると思いこむパターンの積分。

微分する側が微分すると分数が出てくるタイプの場合は連鎖公式が使えない。\[\begin{align*} \int \tan^{-1} x \ dx & =  x \tan^{-1} x - \int \frac{x}{1+x^2}
\\ & =  x \tan^{-1} x - \frac{1}{2} \int \frac{2x}{1+x^2}
\\ & =  x \tan^{-1} x - \frac{1}{2} \log(1 + x^2) + C
\end{align*} \]

(6)

連鎖公式を使う。\[\begin{align*}
& \int (x^2 - 3x + 4) \cos 2x \ dx
\\ = & (x^2 - 3x + 4) \left(\frac{1}{2} \sin 2x \right) - (2x -3) \left(-\frac{1}{4} \cos 2x \right) + 2 \left(-\frac{1}{8} \sin 2x \right) + C
\\ = & \frac{1}{4} \sin 2x \left( 2x^2 - 6x + 7 \right) + \frac{1}{4} \cos 2x (2x - 3) + C
\\ = & \frac{1}{4} \left(\sin 2x \left( 2x^2 - 6x + 7 \right) + \cos 2x (2x - 3) \right) + C
\end{align*} \]

(7)

こちらも連鎖。\[\begin{align*}
& \int^{\pi}_0 (x^2-4x) \cos x \ dx
\\ = & \left[ (x^2 - 4x) \sin x - (2x -4) (- \cos x) + 2 (- \sin x)  \right]^{\pi}_0
\\ = & (- 2 \pi + 4) - (-4) \\ = & 8 - 2 \pi
\end{align*} \]

(8)

\[\begin{align*}
& \int e^{3x} \cos 2x \ dx
\\ = & \frac{1}{2} e^{3x} \sin 2x - \int \frac{3}{2} e^{3x} \sin 2x \ dx
\\ = & \frac{1}{2} e^{3x} \sin 2x - \left(- \frac{3}{4} e^{3x} \cos 2x - \int - \frac{9}{4} e^{3x} \cos 2x \ dx \right)
\\ = & \frac{1}{2} e^{3x} \sin 2x + \frac{3}{4} e^{3x} \cos 2x - \int \frac{9}{4} e^{3x} \cos 2x \ dx
\end{align*} \]

と計算していくと、\[ \int e^{3x} \cos 2x \ dx \] が右辺にも現れる。

これを左辺に移項し、\[ \frac{13}{4} e^{3x} \cos 2x \ dx = \frac{1}{2} e^{3x} \sin 2x + \frac{3}{4} e^{3x} \cos 2x \]となります。したがって、\[\int e^{3x} \cos 2x \ dx =  \frac{2}{13} e^{3x} \sin 2x + \frac{3}{13} e^{3x} \cos 2x+ C\]と計算できます。

連鎖公式を使った場合

\[\begin{align*} & \int e^{3x} \cos 2x \ dx
\\ = & e^{3x} \left(\frac{1}{2} \sin 2x \right) -  3e^{3x} \left(-\frac{1}{4} \cos 2x \right) + \int 9 e^{3x} \left(-\frac{1}{4} \cos 2x \right)
\\ = & \frac{1}{4} e^{3x} \left( 2 \sin 2x + 3 \cos 2x \right) - \int \frac{9}{4} e^{3x} \cos 2x \ dx
\end{align*} \]となり、\[ \int e^{3x} \cos 2x \ dx \] が右辺にも現れる。ので、左辺に移項して答えが出せる。

６．さいごに

今回は、積分の中でも計算量が特に増える部分積分についてまとめました。

数3ではもちろんのこと、解析学でも様々場面で登場してくるため、ぜひ連鎖公式をマスターしましょう！！