スポンサードリンク
こんにちは、ももやまです。
「1年前期の線形代数でもう限界なのに、1年後期の線形代数難しすぎてもうわからない」ってなっている人もいるかと思います。
そこで、試験前でも4時間あれば総復習ができるように計11題の練習問題を作成しました!
※ 問題8~問題11は選択問題です。大学のテスト範囲などに合わせて1問を選択してください。
- 80分間で問題を解く。答えを回答フォームに入力する。
- 答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 時間があれば、合っている箇所も確認する。(青色と赤色の枠部分)
- 寝る。
時間がある人はじっくり、時間がない人は素早くこの記事にて1年後期の線形代数の復習をしましょう!
本記事では、練習問題の解説を載せております。さらに、要点を
- 試験で必要な知識:青色の枠
- 試験で必要な解き方:赤色の枠
- 試験で使える豆知識:オレンジ色の枠
- ワンポイントアドバイス:紫色の枠
などでまとめております。
※ この記事はフォーム式問題である、問題1~問題5の解説を載せております。問題6~問題11の記述式問題の解説は、別記事にて掲載しております。
目次
スポンサードリンク
問題1. 知識チェック
次の(1)〜(6)の小問にそれぞれ答えなさい。
(1) 線形独立と線形従属
3次元ベクトル空間 \( \mathbb{R}^3 \) のベクトル \( \boldsymbol{a}_1 \), \( \boldsymbol {a}_2 \), \( \boldsymbol{a}_3 \) がある。以下の (i), (ii) の問いに答えなさい。
(i) ベクトル \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) が線形独立であるとする。このとき、行列 \( A = ( \boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3 ) \) に対して必ず成り立つ関係式として正しいものを1~4の中から1つ選びなさい。解答番号: [ 01 ]
- \( |A| = 0 \)
- \( |A| \not = 0 \)
- \( |A| > 0 \)
- \( |A| < 0 \)
(ii) 次の1~5の命題の中から、必ず成立する文章を1つ選びなさい。 解答番号: [ 02 ]
- \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \) が線形独立ならば \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{0} \) は線形独立である。
- \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \) が線形独立ならば \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) は線形従属である。
- \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \) が線形従属ならば \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) は線形独立である。
- \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) が線形独立ならば \( 3 \boldsymbol{a}_1 \), \( 3 \boldsymbol{a}_2 \), \( 4 \boldsymbol{a}_3 \) は線形独立である。
- \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) が線形独立ならば \( 3 \boldsymbol{a}_1 \), \( 3 \boldsymbol{a}_2 \), \( 4 \boldsymbol{a}_3 \) は線形従属である。
★解答★
(1-i) 2 [2点] (1-ii) 4 [2点]
(i) 解答: 2 [2点]
まず、線形独立 or 線形従属であるかというと行列 \( A \) がどのように関係あるのかを復習しましょう。
\( n \) 次正方行列 \( A \) が正則であるというのは、次の1~5と同値である。
- \( \mathrm{Rank} \ A = n \)
- \( |A| \not = 0 \)
- \( A \) の逆行列 \( A^{-1} \) が存在する。
- 連立方程式 \( A \boldsymbol{x} = \boldsymbol{0} \) の解が自明な解 ( \( \boldsymbol{x} = \boldsymbol{0} \) ) 以外存在しない。
- \( A = (\boldsymbol{a}_1 , \boldsymbol{a}_2 , \cdots , \boldsymbol{a}_n) \) としたとき、\( \boldsymbol{a}_1 , \boldsymbol{a}_2 , \cdots , \boldsymbol{a}_n \) は線形独立(1次独立)である。
※ 1~4は1年前期の線形代数の復習です。
よって、答えは2の \( |A| \not = 0 \) です。
(ii) 解答: 4 [2点]
(i)の答えをヒントに、1つずつ選択肢を見ていきましょう。
- ゼロベクトル \( \boldsymbol{0} \) が入ると、\( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \) がどんなベクトルであろうと\[
\left| \boldsymbol{a}_1 , \boldsymbol{a}_2 , \boldsymbol{0} \right| = \left| \begin{array}{ccc} * & * & 0 \\ * & * & 0 \\ * & * & 0 \end{array} \right| = 0
\]となってしまうため、必ず線形従属となる。よって誤り。
(※ * には任意の数字が入る) - 例えば\[
\boldsymbol{a}_1 = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) , \ \
\boldsymbol{a}_2 = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) , \ \
\boldsymbol{a}_3 = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right)
\]とすると、\( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \) が線形独立だが、\( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) は線形従属とはならない[1]行列式 \( \left| \boldsymbol{a}_1 , \boldsymbol{a}_2 , \boldsymbol{0} \right| = 1 \)となるため。。よって、反例があるため誤り。 - もともと線形従属なベクトルの組に、ベクトルを追加したところで線形独立にはなりません。例えば階数1の行列に1行(1列)を追加しても階数3にはなりませんよね。よって、誤り。
- \( \boldsymbol{a}_1 , \boldsymbol{a}_2, \boldsymbol{a}_3 \) から作られる下の行列式を考えてみましょう。\[
\left| \boldsymbol{a}_1 , \boldsymbol{a}_2 , \boldsymbol{a}_3 \right| = \left| \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| \not = 0
\]ここで、この行列式に対し列を(0倍以外の)何倍かにする操作を考えましょう。
すると、もともと行列式が0でなければ、(0倍以外なら)何倍にしようが行列式は0にはなりませんよね。
よって、\[
\left| 3 \boldsymbol{a}_1 , 3 \boldsymbol{a}_2 , 4 \boldsymbol{a}_3 \right| = \left| \begin{array}{ccc} 3 a_{11} & 3 a_{12} & 4 a_{13} \\ 3 a_{21} & 3 a_{22} & 4 a_{23} \\ 3 a_{31} & 3 a_{32} & 4 a_{33} \end{array} \right| \not = 0
\]となるので、4は正しい。 - 4で作った行列式は、0倍にしない限り何倍をかけても0(線形従属)にならない。よって、誤り。
よって、答えは4です。
(2) ベクトルと内積
\( n \) 次元ベクトル空間 \( \mathbb{R}^3 \) のベクトル \( \boldsymbol{x} \), \( \boldsymbol{y} \) , \( \boldsymbol{z} \) がある。 次の(i)~(iii)の問いに答えなさい。
(i) 内積 \( \boldsymbol{x} \cdot \boldsymbol{y} \) の定義式として正しいものを1つ選びなさい。 解答番号: [ 03 ]
- \( \boldsymbol{x} + \boldsymbol{y} \)
- \( \boldsymbol{x} \ \boldsymbol{y} \)
- \( {}^t \boldsymbol{x} \ \boldsymbol{y} \)
- \( \boldsymbol{x} \ {}^t \boldsymbol{y} \)
- \( {}^t \boldsymbol{x} \ {}^t \boldsymbol{y} \)
(ii) ベクトル \( \boldsymbol{x} \), \( \boldsymbol{y} \) , \( \boldsymbol{z} \) の内積や大きさについて述べた以下の文章の中で正しい文章は何個あるか。個数を回答欄に入力しなさい。 解答番号: [ 04 ]
(例:正しい文章が2つ → 2と回答)
- \( \boldsymbol{x} \cdot \boldsymbol{y} = - \boldsymbol{y} \cdot \boldsymbol{x} \)
- \( (\boldsymbol{x} + \boldsymbol{y}) \cdot \boldsymbol{z} = \boldsymbol{x} \cdot \boldsymbol{y} + \boldsymbol{y} \cdot \boldsymbol{z} \)
- \( | \boldsymbol{x} \cdot \boldsymbol{y} | \geqq |\boldsymbol{x}| | \boldsymbol{y} | \)
- \( | \boldsymbol{x} - \boldsymbol{y} | \leqq | \boldsymbol{x} | - | \boldsymbol{y} | \)
- \( | \boldsymbol{x} + \boldsymbol{y} | \leqq | \boldsymbol{x} | + | \boldsymbol{y} | \)
(iii) 複素数を成分とするベクトル \( \boldsymbol{x} \), \( \boldsymbol{y} \) の内積(複素内積) \( \boldsymbol{x} \cdot \boldsymbol{y} \) を考える。このとき、次の(ア), (イ) の式がともに必ず成立するものになっているものを次の①~④の中から選びなさい。ただし \( c \) は複素数とし、\( \overline{c} \) は \( c \) の共役複素数を表す。解答番号: [ 05 ]
選択肢 (ア) (イ) ① \( \boldsymbol{x} \cdot \boldsymbol{y} = \boldsymbol{y} \cdot \boldsymbol{x} \) \( ( c \boldsymbol{x} ) \cdot \boldsymbol{y} = \overline{c} ( \boldsymbol{x} \cdot \boldsymbol{y} ) \) ② \( \boldsymbol{x} \cdot \boldsymbol{y} = \boldsymbol{y} \cdot \boldsymbol{x} \) \( \boldsymbol{x} \cdot (c \boldsymbol{y} ) = \overline{c} ( \boldsymbol{x} \cdot \boldsymbol{y} ) \) ③ \( \boldsymbol{x} \cdot \boldsymbol{y} = \overline{\boldsymbol{y} \cdot \boldsymbol{x}} \) \( ( c \boldsymbol{x} ) \cdot \boldsymbol{y} = \overline{c} ( \boldsymbol{x} \cdot \boldsymbol{y} ) \) ④ \( \boldsymbol{x} \cdot \boldsymbol{y} = \overline{\boldsymbol{y} \cdot \boldsymbol{x}} \) \( \boldsymbol{x} \cdot (c\boldsymbol{y} ) = \overline{c} ( \boldsymbol{x} \cdot \boldsymbol{y} ) \)
★解答★
No.03 3 [1点]
No.04 1 [1点]
No.05 4 [1点]
まずは、ベクトルの定義などについて軽くおさらいしておきましょう。
\( n \) 次元実ベクトル \( \boldsymbol{a} \), \( \boldsymbol{b} \) を\[
\boldsymbol{a} = \left( \begin{array}{ccc} a_{1} \\ a_{2} \\ \vdots \\ a_{n} \end{array} \right) , \ \ \boldsymbol{b} = \left( \begin{array}{ccc} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{array} \right)
\]とする。
(1) 内積 \( \boldsymbol{a} \cdot \boldsymbol{b} \) は以下の式で求めることができる。\[\begin{align*}
\boldsymbol{a} \cdot \boldsymbol{b} & = \left( \begin{array}{ccc} a_{1} \ a_{2} \ \cdots \ a_{n} \end{array} \right) \left( \begin{array}{ccc} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \end{array} \right)
\\ & = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n
\end{align*}\]となる。
- (2) ベクトル \( \boldsymbol{a} \) の大きさ \( |\boldsymbol{a}| \) は以下の式で求めることができる。\[\begin{align*}
| \boldsymbol{a} | & = \sqrt{ a_1^2 + a_2^2 + \cdots + a_n^2}
\\ & = \boldsymbol{a} \cdot \boldsymbol{a}
\end{align*}\]
(3) ベクトル \( \boldsymbol{a} , \boldsymbol{b} \) がなす角度を \( \theta \) とする。すると、以下の関係式が成立する。\[
\boldsymbol{a} \cdot \boldsymbol{b} = | \boldsymbol{a} | | \boldsymbol{b} | \cos \theta
\]
特に \( \theta = 90^{\circ} \) のとき、\( \boldsymbol{a} \) と \( \boldsymbol{b} \) は直交するといい、\( \boldsymbol{a} \perp \boldsymbol{b} \) と書く。また、このとき内積は \( \boldsymbol{a} \cdot \boldsymbol{b} = 0 \) となる。
次に、内積の計算法則について見ていきましょう。
- \( \boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{b} \cdot \boldsymbol{a} \)
- \( \boldsymbol{a} \cdot (k\boldsymbol{b}) \) = \( (k \boldsymbol{a}) \cdot \boldsymbol{b} = k ( \boldsymbol{a} \cdot \boldsymbol{b} ) \)
(i) 解答: 3 [1点]
縦ベクトルはn行1列の行列として考えることができます。
ここで、内積はスカラー(1行1列の行列)なので、答えをスカラーにするためには「1行n列×n行1列」の計算になるようなものを選べばOK。よって答えは3。
(ii) 解答: 1 [1点]
順番に選択肢を見ていきましょう。
- 誤り。正しくは \( \boldsymbol{x} \cdot \boldsymbol{y} = \boldsymbol{y} \cdot \boldsymbol{x} \)
- 誤り。正しくは \( (\boldsymbol{x} + \boldsymbol{y}) \cdot \boldsymbol{z} = \boldsymbol{x} \cdot \boldsymbol{z} + \boldsymbol{y} \cdot \boldsymbol{z} \)
- 誤り。内積の公式は \( \boldsymbol{x} \cdot \boldsymbol{y} = | \boldsymbol{x} | | \boldsymbol{y} | \cos \theta \) なので、\( -1 \leqq \cos \theta \leqq 1 \) より、\[
- | \boldsymbol{x} | | \boldsymbol{y} | \leqq \textcolor{red}{ \boldsymbol{x} \cdot \boldsymbol{y} \leqq | \boldsymbol{x} | | \boldsymbol{y} | }
\]となります。(不等号の向きを反対にすれば正しくなります。) - 誤り。例えば、\[
\boldsymbol{x} = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) , \ \ \
\boldsymbol{y} = \left( \begin{array}{ccc} -1 \\ -1 \end{array} \right)
\]のとき、\[
| \boldsymbol{x} - \boldsymbol{y} | = \left| \begin{array}{ccc} 2 \ 2 \end{array} \right| = 2 \sqrt{2}
\]\[\begin{align*}
| \boldsymbol{x} | - | \boldsymbol{y} | & = \sqrt{2} - \sqrt{2}
\\ & = 0
\end{align*}\]となるため、\[
2 \sqrt{2} \leqq 0
\]となり、これが反例となる。 - 正しい。三角不等式の定義です。
(1) 基本形\[
| \boldsymbol{a} + \boldsymbol{b} | \leqq | \boldsymbol{a} | + | \boldsymbol{b} |
\]
(2) 引き算型1[2]基本形に対し、\( \boldsymbol{b'} = \boldsymbol{a} + \boldsymbol{b} \) とおいてから \( \boldsymbol{b} = \boldsymbol{b}' - \boldsymbol{a} \) と代入し、最後に \( \boldsymbol{b} = … Continue reading\[
- | \boldsymbol{a} | + | \boldsymbol{b} | \leqq | - \boldsymbol{a} + \boldsymbol{b}|
\]
(3)引き算型2 [3]引き算型1に対し、\( \boldsymbol{a'} = - \boldsymbol{a} \) とおき、最後に \( \boldsymbol{a} = \boldsymbol{a}' \) とすることで導出できます。\( |- \boldsymbol{a} | = … Continue reading \[
- | \boldsymbol{a} | + | \boldsymbol{b} | \leqq | \boldsymbol{a} + \boldsymbol{b} |
\]
(iii)
まずは複素内積の定義を確認しましょう。
ある複素数範囲でのベクトル\[
\boldsymbol{a} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right) , \ \ \
\boldsymbol{b} = \left( \begin{array}{ccc} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right)
\]が存在する。
このとき、複素内積 \( \boldsymbol{a} \cdot \boldsymbol{b} \) は下のように計算できる。\[\begin{align*}
\boldsymbol{a} \cdot \boldsymbol{b} & = a_1 \overline{b_1} + a_2 \overline{b_2} + \cdots + a_n \overline{b_n}
\\ & = \sum^{n}_{k = 1} a_k \overline{b_k}
\end{align*}\]※ \( \overline{z} \) は \( z \) の共役複素数を表す。
次に、複素内積で成り立つ特別な計算法則も紹介しましょう。
- \( \boldsymbol{a} \cdot \boldsymbol{b} = \overline{ \boldsymbol{b} \cdot \boldsymbol{a}} \)
(内積の順序を入れ替えると、その値は共役複素数[4]複素数 \( k = a + bi \) に対し、共役複素数は \( \overline{k} = a - bi \) となる。をとった値となる。) - \( (k \boldsymbol{a} ) \cdot \boldsymbol{b} \) = \( (k \boldsymbol{a}) \cdot \boldsymbol{b} = k ( \boldsymbol{a} \cdot \boldsymbol{b} ) \)
( \( \boldsymbol{a} \) 側にある定数倍はそのまま外に出すことができる) - \( \boldsymbol{a} \cdot (k \boldsymbol{b}) \) = \( (k \boldsymbol{a}) \cdot \boldsymbol{b} = \overline{k} ( \boldsymbol{a} \cdot \boldsymbol{b} ) \)
( \( \boldsymbol{b} \) 側にある定数倍は複素共役を取ってから外に出すことができる)
※ 実際に上の3つの公式を忘れてしまったときは、適当に\[
\boldsymbol{a} = \left( \begin{array}{ccc} 2 + 2i \\ 1 \end{array} \right), \ \ \ \boldsymbol{b} = \left( \begin{array}{ccc} 1 \\ 2-2i \end{array} \right)
\]などとおいて、計算してから確かめましょう!
よって、答えは④。
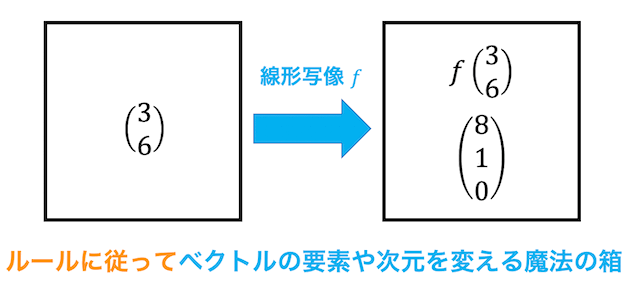
(3) 線形写像・線形変換
写像 \( f : \mathbb{R}^n \to \mathbb{R}^m \) がある。以下の(i)~(iii)の問いに答えなさい。
(i) \( f \) が線形写像である定義として正しいものはどれか。ただし、\( \boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^n \), \( k \in \mathbb{R} \) とする。 解答番号: [ 06 ]
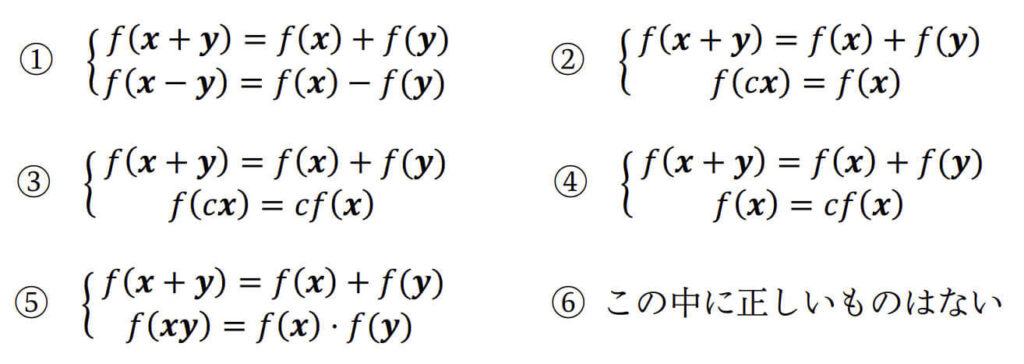
(ii) \( f \) を線形変換とし、条件 \( f(\boldsymbol{x}) \cdot f(\boldsymbol{y}) = \boldsymbol{x} \cdot \boldsymbol{y} \) を満たすとする。このときの線形変換 \( f \) をなんというか。正しいものを選びなさい。 解答番号: [ 07 ]
- 正規変換
- 対称変換
- 等価変換
- 固有変換
- 直交変換
(iii) \( f : \mathbb{R}^n \to \mathbb{R}^m \) を線形写像とする。核の次元 \( \dim \mathrm{Ker} \ f \)、像の次元 \( \dim \mathrm{Im} \ f \) について、必ず成立する式を1つ選びなさい。 解答番号: [ 08 ]
- \( n = \dim \mathrm{Ker} \ f + \dim \mathrm{Im} \ f \)
- \( m = \dim \mathrm{Ker} \ f + \dim \mathrm{Im} \ f \)
- \( 0 = \dim \mathrm{Ker} \ f + \dim \mathrm{Im} \ f \)
- \( n = | \dim \mathrm{Ker} \ f - \dim \mathrm{Im} \ f | \)
- \( m = | \dim \mathrm{Ker} \ f - \dim \mathrm{Im} \ f | \)
- \( 0 = | \dim \mathrm{Ker} \ f - \dim \mathrm{Im} \ f | \)
★解答★
No.06 3 [1点]
No.07 5 [1点]
No.08 1 [2点]
(i) 解答: 3 [1点]
線形写像の定義を復習しましょう。
- ある写像 \( f \) が次の1, 2を満たすとき、線形写像となる。
(1) 足し算の分離が可能\[
f( \boldsymbol{x} + \boldsymbol{y} ) = f( \boldsymbol{x} ) + f ( \boldsymbol{y} )
\]
(2) 定数倍の分離が可能\[
f( c \boldsymbol{x}) = k f ( \boldsymbol{x} )
\]
※ \( \boldsymbol{x} \), \( \boldsymbol{y} \) はn次元ベクトル、\( k \) は実数です
(ii) 解答: 5 [1点]
ここでは、線形変換について復習しましょう。
線形写像 \( f \) の前後で、ベクトルの次元が変わらない変換のことを線形変換と呼ぶ。
(線形写像 \( f : \mathbb{R}^n \to \mathbb{R}^m \) に対し、\( n = m \) となる線形写像を線形変換と呼ぶ。)
また、ベクトル \( \boldsymbol{x} \), \( \boldsymbol{y} \) に線形変換 \( f \) を施したときに、変換の前後で内積が変化しない変換を直交変換と呼ぶ。
( \( f(\boldsymbol{x}) \cdot f(\boldsymbol{y}) = \boldsymbol{x} \cdot \boldsymbol{y} \) を満たす変換を直交変換と呼ぶ)
(iii) 解答: 1 [1点]
まずは、線形写像の表現行列と、核と像の関係について復習しましょう。
線形写像\( f : \mathbb{R}^n \to \mathbb{R}^m \) を線形写像とする。
(1) \( f \) の表現行列 \( A \) は \( m \) 行 \( n \) 列となる。
※ \( m \) と \( n \)
(2) 核 \( \mathrm{Ker} \ f \) の次元と基底は下のようになる。
次元: \( \dim \mathrm{Ker} \ f = n - \mathrm{Rank} \ A \)
基底: 連立方程式 \( A \boldsymbol{x} = \boldsymbol{0} \) の解空間
(3) 像 \( \mathrm{Im} \ f \) の次元と基底下のようになる。
次元: \( \dim \mathrm{Im} \ f = \mathrm{Rank} \ A \)
基底: \( A = (\boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_m) \) としたときの線形独立なベクトルの最大組。
よって、\[\begin{align*}
\textcolor{red}{\dim \mathrm{Ker} \ f} + \textcolor{blue}{ \dim \mathrm{Im} \ f } & =
\textcolor{red}{ n - \mathrm{Rank} \ A } + \textcolor{blue}{\mathrm{Rank} \ A}
\\ & = n
\end{align*}\]となり、解答は1となる。
(4) 直交行列
直交行列について、(i)~(iii)の問いに答えなさい。
(i) \( n \) 次正方行列 \( A \) を直交行列とする。このとき、必ず成り立つ式を1~4、5~8からそれぞれ1つずつ選びなさい。 1~4の回答番号: [ 09 ] 5~8の 回答 番号: [ 10 ]
- \( {}^t A = A \)
- \( {}^t A A = A \ {}^t A = O \)
- \( {}^t A A = A \ {}^t A = E \)
- \( {}^t A A = A \ {}^t A = A \)
- \( \mathrm{Rank} \ A = 0 \)
- \( \mathrm{Rank} \ A = 1 \)
- \( |A| = 0 \)
- \( |A| = \pm 1 \)
(ii) 次の1~8の行列のうち、直交行列であるものを1-4, 5-8からそれぞれ1つずつ選びなさい。
1~4の回答番号:[ 11 ], 5~8の回答番号:[ 12 ]
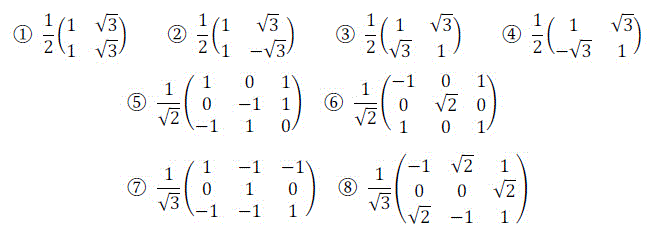
★解答★
No.09 3 [1点]
No.10 8 [1点]
No.11 4 [1点]
No.12 6 [1点]
(4-i) 解答: 3-8 [1点×2]
直交行列の大切な性質を確認していきましょう。
ある行列 \( U \) が直交行列のとき、以下の性質が成立する。
(1) 直交行列とその転値の積(順不同)は必ず単位行列となる\[
{}^t U U = U \ {}^t U = E
\]
(2) 直交行列を転置させたものは逆行列となる\[
{}^t U = U^{-1}
\]
(3) 直交行列の行列式は1か-1のいずれかである\[
|U| = \pm 1
\]
(4) ある直交行列 \( U \) を下のような縦ベクトルで分解する。\[
U = ( \boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n )
\]このとき、これらのベクトルを基底 \( \{ \boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_n \} \)としたものは、正規直交基底となる。
今回の選択肢の中で、正しいものは
- \( {}^t A A = A \ {}^t A = E \)
- \( |A| = \pm 1 \)
の2つとなり、答えは3-8となる。
(ii) 解答: 4-6 [1点×2]
真面目に \( {}^t U U = U \ {}^t U = E \) や \( {}^t U = U^{-1} \) で確認すると時間がかかってしまい、非常にもったないです。
ここは、\( U = ( \boldsymbol{u}_1, \boldsymbol{u}_2 ) \) としてから、各ベクトルが正規直交基底となっているかで確認する方法をおすすめします。
具体的には、
- \( | \boldsymbol{u}_1 | = | \boldsymbol{u}_2 | = | \boldsymbol{u}_3 | = 1 \)
- \( \boldsymbol{u}_1 \cdot \boldsymbol{u}_2 = \boldsymbol{u}_1 \cdot \boldsymbol{u}_3 = \boldsymbol{u}_2 \cdot \boldsymbol{u}_3 = 0 \)
の2つをそれぞれの行列に対して調べていけばOKです。
- \( | \boldsymbol{u}_2 | \not = 1 \) より×
- \( | \boldsymbol{u}_2 | \not = 1 \) より×
- \( | \boldsymbol{u}_1 | = | \boldsymbol{u}_2 | = 1 \) だけど \( \boldsymbol{u}_1 \cdot \boldsymbol{u}_2 \not = 0 \) なので×
- \( | \boldsymbol{u}_1 | = | \boldsymbol{u}_2 | = 1 \) かつ \( \boldsymbol{u}_1 \cdot \boldsymbol{u}_2 = 0 \) となるので○
- \( | \boldsymbol{u}_1 | = | \boldsymbol{u}_2 | = | \boldsymbol{u}_3 | = 1 \) だけど \( \boldsymbol{u}_1 \cdot \boldsymbol{u}_3 \not = 0 \) なので×
- \( | \boldsymbol{u}_1 | = | \boldsymbol{u}_2 | = | \boldsymbol{u}_3 | = 1 \) かつ \( \boldsymbol{u}_1 \cdot \boldsymbol{u}_2 = \boldsymbol{u}_1 \cdot \boldsymbol{u}_3 = \boldsymbol{u}_2 \cdot \boldsymbol{u}_3 = 0 \) なので○
- \( | \boldsymbol{u}_1 | \not = 1 \) より×
- \( | \boldsymbol{u}_3 | \not = 1 \) より×
となるので、直交行列となるのは4-6。
大きさ1、内積0のどちらか一方を満たしていない時点で直交行列でないことが確定するので、すぐ次の行列の判定にうつりましょう。
また、内積0を判定する際には分母を無視してから計算すると計算効率をあげられます!
(5) 直交行列による対角化
次の1~6の行列のうち、直交行列で対角化可能な行列は何個あるか。個数を回答欄に入力しなさい。(例: 2つ → 2 と回答)回答番号: [ 13 ]
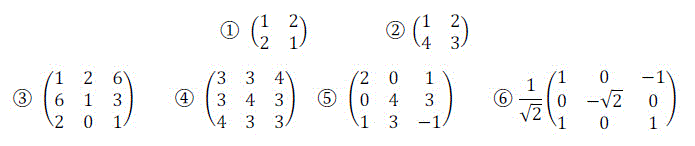
解答: 3 [2点]
まずは、直交行列で対角化可能ために必要な条件を見ていきましょう。
ある行列 \( A \) の行と列を転置させても変わらない行列、つまり \( {}^t A = A \) が成立する行列に対しては、直交行列を用いて対角化をすることができる。
また、 \( {}^t A = A \) を満たす行列のことを実対称行列(対称行列)と呼ぶ。
実際に \( {}^t A = A \) が成立するかを試してみると、1, 4, 5が実対称行列となる。よって、答えは3。
(6) 2次形式
\( n \) 次実対称行列 \( A \) により定められる2次形式 \( q( \boldsymbol{x} ) = {}^t \boldsymbol{x} A \boldsymbol{x} \ ( \boldsymbol{x} = \boldsymbol{0 } ) \) があるとする。
(i) 任意の \( \boldsymbol{x} \) に対し、\( q( \boldsymbol{x} ) > 0 \) を満たすことをなんというか。回答番号: [ 14 ]
(ii) (i) のとき、行列 \( A \) の固有値 \( \lambda_1 , \lambda_2 , \cdots , \lambda_n \) に対して常に成り立つ関係として正しいものを1つ選びなさい。回答番号: [ 15 ]
- \( \lambda_1 + \lambda_2 + \cdots + \lambda_n > 0 \)
- \( \lambda_1 \lambda_2 \cdots \lambda_n > 0 \)
- \( \lambda_1 > 0, \lambda_2 > 0 , \cdots, \lambda_n > 0 \)
★解答★
No.14 7 [2点]
No.15 3 [1点]
2次形式では、以下の2つのことを覚えておきましょう。
\( n \) 次実対称行列 \( A \) により、2次形式 \( q( \boldsymbol{x} ) = {}^t \boldsymbol{x} A \boldsymbol{x} \ ( \boldsymbol{x} = \boldsymbol{0 } ) \) を定める。
(1) \( q( \boldsymbol{x} ) > 0 \) のとき
→ 正定値と呼ばれる
→ すべての固有値が0より大きい ( \( \lambda_1 > 0, \lambda_2 > 0 , \cdots, \lambda_n > 0 \) )
(2) \( q( \boldsymbol{x} ) \geqq 0 \) のとき
→ 半正定値と呼ばれる
→ すべての固有値が0以上 ( \( \lambda_1 \geqq 0, \lambda_2 \geqq 0 , \cdots, \lambda_n \geqq 0 \) )
スポンサードリンク
問題2. 線形写像
(1) 線形写像(基礎)
線形写像に関する文章を読み、空欄に入る整数として正しいものをそれぞれ入力しなさい。
(i) \( \mathbb{R}^2 \to \mathbb{R}^2 \) への線形写像 \( f \) が\[
f \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) = \left( \begin{array}{ccc} -1 \\ 3 \end{array} \right) , \ \ \
f \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 3 \\ 2 \end{array} \right)
\]を満たすとする。このときの表現行列 \( A \) は\[
A = \left( \begin{array}{ccc} \left[ \ \ 16 \ \ \right] & \left[ \ \ 17 \ \ \right] \\ \left[ \ \ 18 \ \ \right] & \left[ \ \ 19 \ \ \right] \end{array} \right)
\]となる。
(ii) \( \mathbb{R}^3 \to \mathbb{R}^3 \) への線形写像 \( f \) が\[
f \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 1 \\ 3 \end{array} \right) , \ \ \ f \left( \begin{array}{ccc} 1 \\ 3 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 \\ -1 \\ 1 \end{array} \right) , \ \ \ f \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 1 \\ 1 \end{array} \right)
\]を満たすとする。このときの表現行列 \( B \) は、\[
B= \left( \begin{array}{ccc} \left[ \ \ 20 \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ 21 \ \ \right] \\ \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] \\ \left[ \ \ 22 \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ 23 \ \ \right] \end{array} \right)
\]となる。
(iii) \( \mathbb{R}^5 \to \mathbb{R}^4 \) への線形写像 \( f \) の表現行列 \( C \) は [ 24 ] 行 [ 25 ] 列となる。
この分野に該当するうさぎ塾の記事はこちら ↓↓
まずは、表現行列の求め方を確認しましょう。
表現行列は、下のように各基本ベクトルに対して線形写像 \( f \) を適用したベクトルを並べたものである。\[
A = \left( \begin{array}{ccc} f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \end{array} \right)
\]
ここで \( f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) \) などを求める際には、加減算 \( f( \boldsymbol{x} + \boldsymbol{y} ) = f( \boldsymbol{x} ) + f( \boldsymbol{y} ) \) や定数倍 \( f( k \boldsymbol{x} ) = k f ( \boldsymbol{x} ) \)を駆使して基本ベクトルを作り出せばよい。
※1 \( \mathbb{R}^3 \) で例をしめしていますが、次元に関係なく同じ方法で求めることができます。
※2 逆行列を使って求める方法もありますが、個人的にはあまりおすすめではありません。
(i)
No.16 2 [1点]
No.17 5 [1点]
No.18 5 [1点]
No.19 7 [1点]
★解法1★
\[\begin{align*}
f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) & =
f \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) + f \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 \\ 3 \end{array} \right) + \left( \begin{array}{ccc} 3 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 \\ 5 \end{array} \right)
\end{align*}\]
\[\begin{align*}
f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) & =
f \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right) + f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 \\ 2 \end{array} \right) + \left( \begin{array}{ccc} 2 \\ 5 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 5 \\ 7 \end{array} \right)
\end{align*}\]
となるので、表現行列 \( A \) は、\[\begin{align*}
A & = \left( \begin{array}{ccc} f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & 5 \\ 5 & 7 \end{array} \right)
\end{align*}\]と計算できる。
★解法2★
\[\begin{align*}
\left( f \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) , f \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right) \right) & = \left( f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \right)
\\ & = \left( \begin{array}{ccc} 2 & -1 \\ -1 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 & 3 \\ 3 & 2 \end{array} \right)
\end{align*}\]が成立することを利用して、表現行列を求める。
\[\begin{align*}
A & = \left( \begin{array}{ccc} f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 & 3 \\ 3 & 2 \end{array} \right) \left( \begin{array}{ccc} 2 & -1 \\ -1 & 1 \end{array} \right)^{-1}
\\ & = \left( \begin{array}{ccc} -1 & 3 \\ 3 & 2 \end{array} \right) \left( \begin{array}{ccc} 1 & 1 \\ 1 & 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & 5 \\ 5 & 7 \end{array} \right)
\end{align*}\]
※1 \( AX = Y \) から \( A \) を求める際には、右側に \( X^{-1} \) をかけて \( AXX^{-1} = Y X^{-1} \) として、\( A = Y X^{-1} \) とすることに注意。
※2 2次正方行列 \( A \) とその逆行列 \( A^{-1} \) の関係は \[ A = \left( \begin{array}{ccc} a & b \\ c & d \end{array} \right) , \ \ \ A^{-1} = \frac{1}{|A|} \left( \begin{array}{ccc} d & -b \\ -c & a \end{array} \right) \] となる。特に \( |A| = -1 \) のときに行列式で割り忘れるミスが頻発するので要注意!!
表現行列 \( A \) を求めたあとは、\( f( \boldsymbol{x} ) = A \boldsymbol{x} \) の性質を使って検算をしよう。
例えば、今回の問題であれば\[\begin{align*}
f \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) & =
A \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & 5 \\ 5 & 7 \end{array} \right) \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 \\ 3 \end{array} \right)
\end{align*}\]のような検算が可能だ。
※ 時間がもったいないので、与えられた変換法則のうちの1つを試せばOK。
(ii)
No.20 -4 [1点]
No.21 -1 [1点]
No.22 5 [1点]
No.23 2 [1点]
(i)と同じように計算していけばOK。
★解法1★
\[\begin{align*}
f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) & =
f \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) - f \left( \begin{array}{ccc} 1 \\ 3 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 \\ 1 \\ 3 \end{array} \right) - \left( \begin{array}{ccc} 1 \\ -1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 \\ 2 \\ 2 \end{array} \right)
\end{align*}\]
\[\begin{align*}
f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) & =
f \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) - f \left( \begin{array}{ccc} 1 \\ 3 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 \\ 1 \\ 3 \end{array} \right) - \left( \begin{array}{ccc} 1 \\ -1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 \\ 2 \\ 2 \end{array} \right)
\end{align*}\]
\[\begin{align*}
f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) & =
f \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) - f \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \end{array} \right) - 2 f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 \\ 1 \\ 3 \end{array} \right) - \left( \begin{array}{ccc} 0 \\ 1 \\ 1 \end{array} \right) - 2 \left( \begin{array}{ccc} -1 \\ 2 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 \\ -4 \\ -2 \end{array} \right)
\end{align*}\]
\[\begin{align*}
f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) & =
f \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \end{array} \right) - 2 f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 \\ 1 \\ 1 \end{array} \right) - 2 \left( \begin{array}{ccc} 2 \\ -4 \\ -2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -4 \\ 9 \\ 5 \end{array} \right)
\end{align*}\]
となるので、表現行列 \( B \) は、\[\begin{align*}
B & = \left( \begin{array}{ccc} f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{-4} & 2 & \textcolor{red}{-1} \\ 9 & -4 & 2 \\ \textcolor{red}{5} & -2 & \textcolor{red}{2} \end{array} \right)
\end{align*}\]となる。
★解法2★
\[\begin{align*}
\left( f \left( \begin{array}{ccc} 1 \\ 3 \\ 2 \end{array} \right) , f \left( \begin{array}{ccc} 1 \\ 3 \\ 1 \end{array} \right) , f \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \end{array} \right) \right) & = \left( f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \right)
\\ & = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 3 & 3 & 2 \\ 2 & 1 & 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 1 \\ 3 & 1 & 1 \end{array} \right)
\end{align*}\]が成立することを利用して、表現行列を求める。
\[\begin{align*}
B & = \left( f \left( \begin{array}{ccc} 1 \\ 0\\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \right)
\\ & = \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 1 \\ 3 & 1 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 1 & 1 \\ 3 & 3 & 2 \\ 2 & 1 & 0 \end{array} \right)^{-1}
\\ & = \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 1 \\ 3 & 1 & 1 \end{array} \right) \left( \begin{array}{ccc} 2 & -1 & 1 \\ -4 & 2 & -1 \\ 3 & -1 & 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{-4} & 2 & \textcolor{red}{-1} \\ 9 & -4 & 2 \\ \textcolor{red}{5} & -2 & \textcolor{red}{2} \end{array} \right)
\end{align*}\]
(iii)
No.24 4 [1点]
No.25 5 [1点]
\( \mathbb{R}^5 \to \mathbb{R}^4 \) への線形写像とは、下のように5次元ベクトルを4次元ベクトルに変換する線形写像である。\[
f \left( \begin{array}{ccc} * \\ * \\ * \\ * \\ * \end{array} \right) =
\left( \begin{array}{ccc} * \\ * \\ * \\ * \end{array} \right)
\]
さらに表現行列 \( C \) は、この変換を5つ並べた下のような形で表現できる。\[\begin{align*}
C & = \left( f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{array} \right) \right)
\\ & = \left( \begin{array}{ccc} * & * & * & * & * \\ * & * & * & * & * \\ * & * & * & * & * \\ * & * & * & * & * \end{array} \right)
\end{align*}\]
よって、\( C \) は4行5列の行列となる。
\( \mathbb{R}^n \to \mathbb{R}^m \) への線形写像 \( f \) の表現行列は、\( m \) 行 \( n \) 列となる。
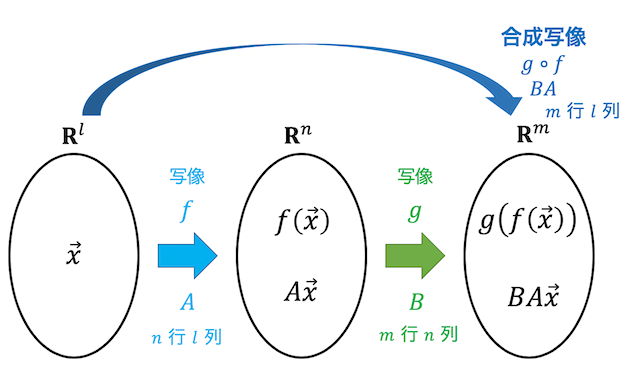
(2) 線形写像(発展・合成写像)
次の線形写像 \( f \), \( g \) \[
f \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{ccc} 2 x_1 + 3x_2 \\ 3x_1 + x_2 + 3x_3 \end{array} \right) , \ \ \
g \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) = \left( \begin{array}{ccc} x_1 + x_2 \\ 3x_1 + 2x_2 \\ -x_1 - x_2 \end{array} \right)
\]がある。(i)~(iii)の問いに答えなさい。
(i) \( f \) の表現行列を \( A \)、\( g \) の表現行列を \( B \) とする。すると、 \[
A = \left( \begin{array}{ccc} \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ 26 \ \ \right] \\ \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] \end{array} \right)
\]\[
B = \left( \begin{array}{ccc} \left[ \ \ 27 \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] \\ \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] \\ \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] \end{array} \right)
\]と求められる。
(ii) 合成写像 \( f \circ g \) の表現行列を \( C \)、\( g \circ f \) の表現行列を \( D \) とする。すると、\[
C = \left( \begin{array}{ccc} \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ 28 \ \ \right] \\ \left[ \ \ 29 \ \ \right] & \left[ \ \ 30 \ \ \right] \end{array} \right)
\]\[
D = \left( \begin{array}{ccc} \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] \\ \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] & \left[ \ \ \ \ \ \ \ \ \right] \\ \left[ \ \ 31 \ \ \right] & \left[ \ \ 32 \ \ \right] & \left[ \ \ 33 \ \ \right] \end{array} \right)
\]となる。
(iii) 合成写像 \( f \circ g \), \( g \circ f \) に逆変換は存在するか。正しい文章を1~4から選び、番号で解答しなさい。回答番号:[ 34 ]
- \( f \circ g \), \( g \circ f \) ともに逆変換は存在する。
- \( f \circ g \) には逆変換が存在するが、\( g \circ f \) には逆変換が存在しない。
- \( g\circ f \) には逆変換が存在するが、\( f \circ g \) には逆変換が存在しない。
- \( f \circ g \), \( g \circ f \) ともに逆変換は存在しない。
この分野に該当するうさぎ塾の記事はこちら ↓↓
(i)
No.26 0 [1点]
No.27 1 [1点]
\[\begin{align*}
A & = \left( f \left( \begin{array}{ccc} 1 \\ 0\\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \right)
\\ & = \left( \begin{array}{ccc} 2 & 3 & \textcolor{red}{0} \\ 3 & 1 & 3 \end{array} \right)
\end{align*}\]
\[\begin{align*} B & = \left( f \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) , f \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{1} & 1 \\ 3 & 2 \\ -1 & -1 \end{array} \right)
\end{align*}\]
(ii)
No.28 8 [1点]
No.29 3 [1点]
No.30 2 [1点]
No.31 -5 [1点]
No.32 -4 [1点]
No.33 -3 [1点]
合成写像の表現行列は、行列を掛ける順番に要注意です。
ただ、幸いなことに今回は行列のサイズが問題文に与えられているため、掛ける順番のミスは発生しないようになっています。(記述式の場合要注意!!)
\[\begin{align*}
C & = AB
\\ & = \left( \begin{array}{ccc} 2 & 3 & 0 \\ 3 & 1 & 3 \end{array} \right) \left( \begin{array}{ccc} 1 & 1 \\ 3 & 2 \\ -1 & -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 11 & \textcolor{red}{8} \\ \textcolor{red}{3} & \textcolor{red}{2} \end{array} \right)
\end{align*}\]
\[\begin{align*}
D & = BA
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ 3 & 2 \\ -1 & -1 \end{array} \right) \left( \begin{array}{ccc} 2 & 3 & 0 \\ 3 & 1 & 3 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 5 & 4 & 3 \\ 12 & 11 & 6 \\ \textcolor{red}{-5} & \textcolor{red}{-4} & \textcolor{red}{-3} \end{array} \right)
\end{align*}\]
\( \mathbb{R}^n \to \mathbb{R}^m \) への線形写像 \( f \) の表現行列を \( A \)、\( \mathbb{R}^{m'} \to \mathbb{R}^{m'} \) への線形写像 \( g \) の表現行列を \( B \) とする。
すると \( n =m' \) のとき、合成写像 \( f \circ g \) の表現行列は \( AB \) と計算できる。
※ \( n \not= m' \) のときは行列 \( AB \) の演算ができないので合成写像は定義されない。
(iii)
No.34 2 [2点]
ある写像 \( f \) に逆変換が存在するかどうかは、
(a) 写像 \( f \) の表現行列が正方行列である
(b) 写像 \( f \) の表現行列が逆行列を持つ(表現行列が正則である)
の2つを確認すればOKです。
今回は、\( C \), \( D \) どちらの表現行列ともに(a)を満たしていますね。
なので、(b)を満たすかどうかを行列式で確かめていきましょう[5]行列の階数で判定する方法もあるのですが、行列式の方が早く計算ができると思います。。
\[\begin{align*}
|C| & = \left| \begin{array}{ccc} 11 & 8 \\ 3 & 2 \end{array} \right|
\\ & = 22 - 24
\\ & = -2 \not = 0
\end{align*}\]
\[\begin{align*}
|D| & = \left| \begin{array}{ccc} 5 & 4 & 3 \\ 12 & 11 & 6 \\ -5 & -4 & -3 \end{array} \right|
\\ & = \left| \begin{array}{ccc} 5 & 4 & 3 \\ 12 & 11 & 6 \\ 0 & 0 & 0 \end{array} \right|
\\ & = 0
\end{align*}\]
となるので、\( C \) は \( |C| = -2 \not = 0 \) より逆行列を持つが、\( D \) は \( |D| = 0 \) なので逆行列を持ちません。
よって、\( f \circ g \) は逆変換を持つが、\( g \circ f \) は逆変換を持たないので答えは2となる。
表現行列が \( X \) である線形写像 \( f \) の逆変換が存在するかどうかは、次の(a), (b)を確認すればOK。
(a) \( X \) が正方行列である
(b) \( X \) が逆行列を持つ。(\( |X| \not = 0 \) である)
また逆変換を持つ場合、その逆変換 \( f^{-1} \) は \( X \) の逆行列 \( X^{-1} \) となる。
ちなみに、余裕がある人は \( f \circ g \) の逆変換の表現行列も求めてみましょう[6]答えは\[ \frac{1}{2} \left( \begin{array}{ccc} -2 & 8 \\ 3 & -11 \end{array} \right) \]です。。
スポンサードリンク
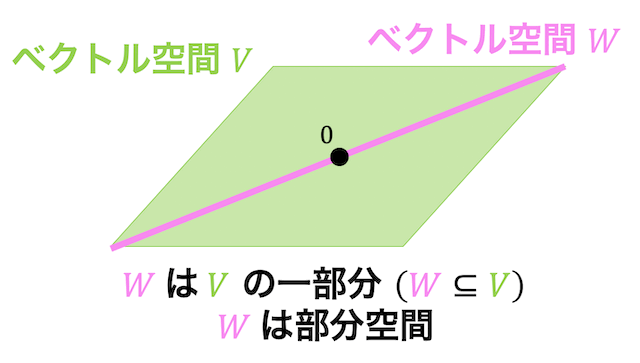
問題3. 部分空間
この分野に該当するうさぎ塾の記事はこちら ↓↓
(1) 部分空間の定義
つぎの(a), (b) の集合は \( \mathbb{R}^3 \) の部分空間か。正しい選択肢を1~4の中から1つ選びなさい。回答番号:[ 35 ]
(a)\[
\left\{ \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) \middle| \ 6 x_1 = 3x_2 + 4x_3 \right\}
\]
(b)\[
\left\{ \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) \middle| \ 6 x_1 \geqq 3x_2 + 4x_3 \right\}
\]
- (a), (b) ともに \( \mathbb{R}^3 \) の部分空間である。
- (a) は \( \mathbb{R}^3 \) の部分空間だが、(b)は \( \mathbb{R}^3 \) の部分空間ではない。
- (b) は \( \mathbb{R}^3 \) の部分空間だが、(a)は \( \mathbb{R}^3 \) の部分空間ではない。
- (a), (b)ともに \( \mathbb{R}^3 \) の部分空間ではない。
解答: 2 [5点]
(a) 部分空間である
部分空間の式を変形すると、以下のような式となる。\[
\left\{ \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) \middle| \ 6 x_1 - 3x_2 + 4x_3 = 0 \right\}
\]これは連立方程式の解空間となるため、部分空間となる。
(b) 部分空間ではない
(b)が部分空間だと仮定する。例えば、\[
\left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{ccc} 3 \\ 1 \\ 1 \end{array} \right)
\]は、\( 18 \geqq 3 + 4 \) より部分空間である。
また、ある \( \boldsymbol{x} \) が部分空間であると、それを \( k \) 倍した \( k \boldsymbol{x} \) も部分空間である。つまり、\[
\left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = -1 \left( \begin{array}{ccc} 3 \\ 1 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = \left( \begin{array}{ccc} -3 \\ -1 \\ -1 \end{array} \right)
\]も部分空間となる。
しかし、\( -18 \geqq -3 - 4 = -7 \) となるため、矛盾。
よって、部分空間だという仮定は誤りとなり、答えは2。
部分空間の定義は重要なので、見直しておきましょう。
次の 1, 2 を満たす集合が部分空間 \( W \) となる。
- \( \boldsymbol{x}, \boldsymbol{y} \) が部分空間であるならば、\( \boldsymbol{x} + \boldsymbol{y} \) も部分空間である。\[
\boldsymbol{x}, \boldsymbol{y} \in W \to \boldsymbol{x} + \boldsymbol{y} \in W
\] - \( \boldsymbol{x} \) が部分空間であるならば、それを \( k \) 倍した \( k \boldsymbol{x} \) も部分空間である。\[
\boldsymbol{x} \in W \to k \boldsymbol{x} \in W
\]
(2) 部分空間の次元[1]
つぎの \( \mathbb{R}^4 \) のベクトル \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \), \( \boldsymbol{a}_4 \) が生成する部分空間の次元はいくらか。次元を回答欄に入力しなさい。回答番号:[ 36 ]\[
\boldsymbol{a}_1 = \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \\ 1 \end{array} \right), \ \ \ \boldsymbol{a}_2 = \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ 3 \end{array} \right) , \ \ \ \boldsymbol{a}_3 = \left( \begin{array}{ccc} 0 \\ -1 \\ -1 \\ 1 \end{array} \right), \ \ \ \boldsymbol{a}_4 = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \\ 4 \end{array} \right)
\]
解答: 3 [5点]
行列 \( A \) を \( A = ( \boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3, \boldsymbol{a}_4 ) \) とする。
ここで、ベクトルが生成する部分空間の次元は行列 \( A \) の階数に一致する。
そこで、行列 \( A \) に行基本変形を施すことで階数を求める。\[\begin{align*}
A & = \left( \begin{array}{ccc} 1 & 1 & 0 & 1 \\ 2 & 0 & -1 & -1 \\ 3 & 1 & -1 & 0 \\ 1 & 3 & 1 & 4 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & 0 & 1 \\ 0 & -2 & -1 & 1 \\ 0 & -2 & -1 & -3 \\ 0 & 2 & 1 & 3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & 0 & 1 \\ 0 & 2 & 1 & 3 \\ 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}\]
となるので、行列 \( A \) の階数は3となるので、ベクトルが生成する部分空間の次元も3となる。
よって答えは3。
あるベクトル \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), …, \( \boldsymbol{a}_n \) が生成する部分空間の次元は、\[
A = ( \boldsymbol{a}_1 , \boldsymbol{a}_2 , \cdots , \boldsymbol{a}_n )
\]としたときの行列 \( A \) の階数に一致する。
(3) 部分空間の次元[2]
つぎの \( \mathbb{R}^4 \) のベクトル \( \boldsymbol{b}_1 \), \( \boldsymbol{b}_2 \), \( \boldsymbol{b}_3 \), \( \boldsymbol{b}_4 \) が生成する部分空間の次元が3となるような \( c \) の値を求め、回答欄に \( c \) の値を入力しなさい。回答番号:[ 36 ]\[
\boldsymbol{b}_1 = \left( \begin{array}{ccc} 1 \\ 3 \\ -2 \\ c \end{array} \right), \ \ \ \boldsymbol{b}_2 = \left( \begin{array}{ccc} 5 \\ 1 \\ 1 \\ 2c \end{array} \right) , \ \ \ \boldsymbol{b}_3 = \left( \begin{array}{ccc} 1 \\ 3 \\ -5 \\ 2 \end{array} \right), \ \ \ \boldsymbol{b}_4 = \left( \begin{array}{ccc} 3 \\ 2 \\ -2 \\ 3 \end{array} \right)
\]
解答: 2 [5点]
行列 \( B \) を \( B = ( \boldsymbol{b}_1, \boldsymbol{b}_2, \boldsymbol{b}_3, \boldsymbol{b}_4 ) \) とし、行列の階数を求める。
\[\begin{align*}
B & = \left( \begin{array}{ccc} 1 & 5 & 1 & 3 \\ 3 & 1 & 3 & 2 \\ -2 & 1 & -5 & -2 \\ c & 2c & 2 & 3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 5 & 1 & 3 \\ 0 & -14 & 0 & -7 \\ 0 & 11 & 0 & 4 \\ c-2 & 2c-10 & 0 & -3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 5 & 1 & 3 \\ 0 & 2 & 0 & 1 \\ 0 & 11 & 8 & 4 \\ c-2 & 2c-10 & 0 & -3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 5 & 1 & 3 \\ 0 & 2 & 0 & 1 \\ 0 & 11 & 8 & 4 \\ c-2 & 2c-4 & 0 & 0 \end{array} \right)
\end{align*}\]となる。
よって、\( c = 2 \) のときに行列 \( B \) の階数が3となり、部分空間の次元も3となることがわかる。
[別解]行列式で確認をすることも一応できる。\[\begin{align*}
|B| & = \left| \begin{array}{ccc} 1 & 5 & 1 & 3 \\ 3 & 1 & 3 & 2 \\ -2 & 1 & -5 & -2 \\ c & 2c & 2 & 3 \end{array} \right|
\\ & = \left| \begin{array}{ccc} 1 & 5 & 1 & 3 \\ 0 & -14 & 0 & -7 \\ 0 & 11 & 0 & 4 \\ c-2 & 2c-10 & 0 & -3 \end{array} \right|
\\ & = -1 \left| \begin{array}{ccc} 0 & -14 & -7 \\ 0 & 11 & 4 \\ c-2 & 2c-10 & -3 \end{array} \right|
\\ & = -1 (c-2) \left| \begin{array}{ccc} -14 & -7 \\ 11 & 4 \end{array} \right|
\\ & = -1 (c-2) (-56+77)
\end{align*}\]となるので、\( c \not = 2 \) のときに次元が4になることがわかるので、残りの \( c = 2 \) のときが次元3となる。
(ただし、この方法では \( c \not = 2 \) のときに次元が4になることだけしかわからないので、あまりおすすめはできません。)
問題4. 正規直交基底の作成
次の \( \mathbb{R}^3 \) のベクトル \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) がある。\[
\boldsymbol{a}_1 = \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right) , \ \
\boldsymbol{a}_2 = \left( \begin{array}{ccc} 1 \\ 0 \\ 2 \end{array} \right) , \ \
\boldsymbol{a}_3 = \left( \begin{array}{ccc} -3 \\ -2 \\ 2 \end{array} \right)
\]このベクトルに対してグラム・シュミットの直交化法を順に適用する。
すると、以下のベクトル \( \boldsymbol{u}_1 \), \( \boldsymbol{u}_2 \), \( \boldsymbol{u}_3 \) からなる正規直交基底 \( \{ \boldsymbol{u}_1, \boldsymbol{u}_2, \boldsymbol{u}_3 \} \) を得ることができる。\[
\boldsymbol{u}_1 = \frac{1}{\sqrt{ \left[ \ \ 38 \ \ \right] } } \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right) , \ \
\boldsymbol{u}_2 = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} \left[ \ \ 39 \ \ \right] \\ \left[ \ \ 40 \ \ \right] \\ \left[ \ \ 41 \ \ \right] \end{array} \right) , \ \
\boldsymbol{u}_3 = \frac{1}{\sqrt{ \left[ \ \ 42\ \ \right] } } \left( \begin{array}{ccc} \left[ \ \ 43 \ \ \right] \\ \left[ \ \ 44 \ \ \right] \\ \left[ \ \ 45 \ \ \right] \end{array} \right)
\]ここで、本当にグラム・シュミットの直交化法を行うと正規直交基底になるかを確認しよう。すると、\( | \boldsymbol{u}_1 | = | \boldsymbol{u}_2 | = | \boldsymbol{u}_3 | = \left[ \ \ 46 \ \ \right] \)、\( \boldsymbol{u}_1 \cdot \boldsymbol{u}_2 = \boldsymbol{u}_1 \cdot \boldsymbol{u}_3 = \boldsymbol{u}_2 \cdot \boldsymbol{u}_3 = \left[ \ \ 47 \ \ \right] \) となるので、たしかに正規直交基底であることが確認できる。
この分野に該当するうさぎ塾の記事はこちら ↓↓
まずは、グラムシュミットの直交化法による正規直交基底の求め方を確認しましょう。
ベクトル \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) に対して、以下の演算を行うことで正規直交基底 \( \{ \boldsymbol{u}_1, \boldsymbol{u}_2, \boldsymbol{u}_3 \} \) を得ることができる。
\[
\boldsymbol{u}_1 = \frac{ \boldsymbol{a}_1 }{ | \boldsymbol{a}_1 | }
\]\[
\boldsymbol{b}_2 = \boldsymbol{a}_2 - ( \boldsymbol{a}_2 \cdot \boldsymbol{u}_1 ) \boldsymbol{u}_1 , \ \ \ \boldsymbol{u}_2 = \frac{ \boldsymbol{b}_2 }{ | \boldsymbol{b}_2 | }
\]\[
\boldsymbol{b}_3 = \boldsymbol{a}_3 - ( \boldsymbol{a}_3 \cdot \boldsymbol{u}_1 ) \boldsymbol{u}_1 - ( \boldsymbol{a}_3 \cdot \boldsymbol{u}_2 ) \boldsymbol{u}_2 , \ \ \ \boldsymbol{u}_3 = \frac{ \boldsymbol{b}_3 }{ | \boldsymbol{b}_3 | }
\]
また、この公式を一般化したものを示す。
\[\begin{align*}
\boldsymbol{b}_n & = \boldsymbol{a}_n - ( \boldsymbol{a}_n \cdot \boldsymbol{u}_1 ) \boldsymbol{u}_1 - ( \boldsymbol{a}_n \cdot \boldsymbol{u}_2 ) - \cdots
\\ & = \boldsymbol{a}_n - \sum^{n-1}_{k = 1} ( \boldsymbol{a}_n \cdot \boldsymbol{u}_k ) \boldsymbol{u}_k
\end{align*}\]\[
\boldsymbol{u}_n = \frac{ \boldsymbol{b}_n }{ | \boldsymbol{b}_n | }
\]
では、実際に計算していきましょう。
(i) \( \boldsymbol{u}_1 \) の計算
No.38 3 [1点]
\[\begin{align*}
\boldsymbol{u}_1 & = \frac{\boldsymbol{a}_1}{ | \boldsymbol{a}_1| }
\\ & = \frac{1}{ \sqrt{3} } \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\end{align*}\]
(ii) \( \boldsymbol{u}_2 \) の計算
No.39 0 [1点]
No.40 -1 [1点]
No.41 1 [1点]
まずは、\( \boldsymbol{b}_2 \) を求める。
\[\begin{align*}
\boldsymbol{b}_2 & = \boldsymbol{a}_2 - ( \boldsymbol{a}_2 \cdot \boldsymbol{u}_1 )
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \\ 2 \end{array} \right) - \sqrt{3} \cdot \frac{1}{ \sqrt{3} } \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right)
\end{align*}\]
あとは \( \boldsymbol{u}_2 \) を正規化するだけ。\[\begin{align*}
\boldsymbol{u}_2 & = \frac{ \boldsymbol{b}_2 }{ | \boldsymbol{b}_2 | }
\\ & = \frac{1}{\sqrt{2}} \\ & = \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right)
\end{align*}\]
(ii) \( \boldsymbol{u}_2 \) の計算
No.39 0 [1点]
No.40 -1 [1点]
No.41 1 [1点]
まずは、\( \boldsymbol{b}_2 \) を求める。
\[\begin{align*}
\boldsymbol{b}_2 & = \boldsymbol{a}_2 - ( \boldsymbol{a}_2 \cdot \boldsymbol{u}_1 )
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \\ 2 \end{array} \right) - \sqrt{3} \cdot \frac{1}{ \sqrt{3} } \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right)
\end{align*}\]
あとは \( \boldsymbol{b}_2 \) を正規化するだけ。\[\begin{align*}
\boldsymbol{u}_2 & = \frac{ \boldsymbol{b}_2 }{ | \boldsymbol{b}_2 | }
\\ & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right)
\end{align*} \]
\( \boldsymbol{b}_2 \) の計算を間違えてしまうと、それ以降の計算がすべて狂ってしまいます。
なので、この段階で \( \boldsymbol{u}_1 \cdot \boldsymbol{b}_2 = 0 \) の検算を必ずしてください。
10秒の検算で救われる単位がある!
(iii) \( \boldsymbol{u}_3 \) の計算
まずは、\( \boldsymbol{b}_3 \) を求める。
\[\begin{align*}
\boldsymbol{b}_3 & = \boldsymbol{a}_3 - ( \boldsymbol{a}_3 \cdot \boldsymbol{u}_1 ) \boldsymbol{u}_1 - ( \boldsymbol{a}_3 \cdot \boldsymbol{u}_2 ) \boldsymbol{u}_2
\\ & = \left( \begin{array}{ccc} -3 \\ -2 \\ 2 \end{array} \right) - ( - \sqrt{3} ) \cdot \frac{1}{\sqrt{3}} \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right) - 2 \sqrt{2} \cdot \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -3 \\ -2 \\ 2 \end{array} \right) + \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right) - 2 \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -2 \\ 1 \\ 1 \end{array} \right)
\end{align*}\]
あとは \( \boldsymbol{b}_3 \) を正規化するだけ。\[\begin{align*}
\boldsymbol{u}_3 & = \frac{ \boldsymbol{b}_3 }{ | \boldsymbol{b}_3 | }
\\ & = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} -2 \\ 1 \\ 1 \end{array} \right)
\end{align*}\]
\( \boldsymbol{b}_3 \) の計算ができた段階で、\( \boldsymbol{u}_1 \cdot \boldsymbol{b}_3 = 0 \) と \( \boldsymbol{u}_2 \cdot \boldsymbol{b}_3 = 0 \) の検算を必ずしてください。
正規直交基底の確認
No.46 1 [1点]
No.47 0 [1点]
この問題は、
- グラム・シュミットで出てくるベクトルはどんなベクトルなのか
- 絶対に検算してよね!!
という2つのメッセージを込めて作成しております。
あるベクトル \( \boldsymbol{u}_1, \boldsymbol{u}_2, \boldsymbol{u}_3, \cdots \) が正規直交基底 \( \{ \boldsymbol{u}_1, \boldsymbol{u}_2, \boldsymbol{u}_3, \cdots \} \) を成している。このとき、次の(1)~(3)の性質が重要である。
(1) どのベクトルの大きさも1である(大きさ1に正規化されている)。\[
| \boldsymbol{u}_1 | = | \boldsymbol{u}_2 | = | \boldsymbol{u}_3 | = \cdots = 1
\]
(2) 正規直交基底から2本を選んで、その内積を取ると必ず0になる(直交している)。\[
\boldsymbol{u}_1 \cdot \boldsymbol{u}_2 = \boldsymbol{u}_1 \cdot \boldsymbol{u}_3 = \boldsymbol{u}_2 \cdot \boldsymbol{u}_3 = \cdots = 0
\]
(3) 正規直交基底を並べて作った行列 \( U \) は直交行列となる。\[
U = ( \boldsymbol{u}_1, \boldsymbol{u}_2, \boldsymbol{u}_3 , \cdots )
\]
問題5. 固有値・固有ベクトル・対角化
(1) 知識問題
次の固有値、固有ベクトルに関する(i)~(iii)の問題に答えなさい。
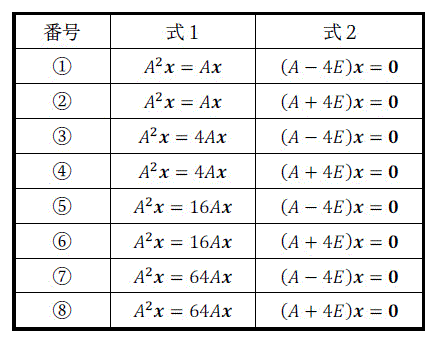
(i) ある正方行列 \( A \) の固有値に4が含まれており、さらに固有値4の固有ベクトルの1つが \( \boldsymbol{x} \) である。このとき、式1、式2がともに成立する式となっている番号を1~8の中から1つ選びなさい。回答番号:[ 48 ]
(ii) 固有値、固有ベクトルに関する記述として最も適切なものを1つ選びなさい。回答番号:[ 49 ]
- 固有値に0が含まれる行列は絶対に対角化不可能である。
- 固有値に重解が含まれない行列は必ず対角化できる。
- ある固有値に対し、1つも固有ベクトルが存在しないことがある。
- 相異なる固有値に対する固有ベクトルが線形従属になることがある。
(iii) ある \( n \) 次正方行列(ただし \( n \geqq 3 \))の固有値は \( \lambda_1 \), \( \lambda_2 \), \( \lambda_3 \) の3つで、さらに正則行列 \( P \) を用いて \( P^{-1} AP \) と対角化することができる。このとき、必ず成立する式はどれか。1つ選び、番号で答えなさい。回答番号:[ 50 ]
- \( \dim V( \lambda_1 ) + \dim V( \lambda_2 ) + \dim V( \lambda_3 ) = 0 \)
- \( 1 \leqq \dim V( \lambda_1 ) + \dim V( \lambda_2 ) + \dim V( \lambda_3 ) \leqq n-1 \)
- \( \dim V( \lambda_1 ) + \dim V( \lambda_2 ) + \dim V( \lambda_3 ) = n \)
- \( \dim V( \lambda_1 ) = \dim V( \lambda_2 ) = \dim V( \lambda_3 ) = 1 \)
- \( \dim V( \lambda_1 ) = \dim V( \lambda_2 ) = \dim V( \lambda_3 ) = n \)
この分野に該当するうさぎ塾の記事はこちら ↓↓
(1)
最初に固有値・固有ベクトル・固有空間に関して軽く復習をしましょう。
ある正方行列 \( A \) の固有値を \( \lambda \)、固有ベクトルを \( \boldsymbol{x} \) とする。このとき、以下の関係式が成立する。\[
A \boldsymbol{x} = \lambda \boldsymbol{x}
\]
また、固有空間 \( V( \lambda ) \) は、ある固有値 \( \lambda \) に対する固有ベクトルの基底となる。
ある \( n \) 次正方行列 \( A \) の固有値を \( \lambda \)、固有ベクトルを \(\boldsymbol{x} \) は次のように求める。
(1) 固有値は \( |A - \lambda E | = 0 \) となるような \( \lambda \) を求める。
(2) 固有ベクトルは連立方程式 \( (A - \lambda E) \boldsymbol{x} = \boldsymbol{0} \) を解くことによって求められる。
ただし、求める際に以下の注意が必要である。
- \( \boldsymbol{x} \not = \boldsymbol{0} \) である。
- 固有ベクトルの数は最小で1本、最大で重解の数だけ存在する。
- ある固有値に対する固有ベクトルの数は \( n - \mathrm{Rank} \ (A - \lambda E) \) 本である
- 固有ベクトルが複数ある場合、それらのベクトルは必ず線形独立になるように取る必要がある。
(i) 解答: 3 [1点]
まずは、定義 \( A \boldsymbol{x} = \lambda \boldsymbol{x} \)、および固有ベクトルの計算式 \( (A - \lambda E ) \boldsymbol{x} = \boldsymbol{0} \) を使う問題です。
ここで、固有値が4なので、\( A \boldsymbol{x} = 4 \boldsymbol{x} \)、および \( (A - 4 E ) \boldsymbol{x} = \boldsymbol{0} \) が成立しますね。
さらに、\[\begin{align*}
A^2 \boldsymbol{x} & = A (A \boldsymbol{x})
\\ & = A( 4 \boldsymbol{x} )
\\ & = 4 A \boldsymbol{x}
\end{align*}\]と変形できますね。
よって、両方とも成立する組み合わせになっているのは3です。
(ii)
解答: 2 [1点]
選択肢を1つずつ見ていきましょう。
- 誤り。反例は今回の問題7。固有値が0でも対角化ができることはある。
- 正しい。\( |A - \lambda E| = 0 \) なため、\( (A - \lambda E) \boldsymbol{x} = \boldsymbol{0} \) を満たす \( \boldsymbol{x} ( \not = \boldsymbol{0} ) \) は最低1つ存在する。よって、固有値に重解がなければ、\( n \) 次正方行列に対し、\( n \) 個のベクトルが存在するので正しい。
- 誤り。\( (A - \lambda E) \boldsymbol{x} = \boldsymbol{0} \) を満たす \( \boldsymbol{x} ( \not = \boldsymbol{0} ) \) は最低1つ存在するため、1つも固有ベクトルが存在しないことはありえない。ありえるとしたらそれは「あなたが計算ミスをしているときだけ」だ。
- 誤り。相異なる固有値に対する固有ベクトルは必ず線形独立となる。もし線形従属になったら、固有ベクトルを並べて行列 \( P \) を作る際に \( P \) が正則行列ではなくなってしまう。
よって、答えは2。
\( k \) 重解の固有値 \( \lambda \) に対する固有ベクトルの数は、最低1個存在し、最大で重解の数まで存在する。つまり、\[
1 \leqq \dim V( \lambda ) \leqq k
\]である。
また、ある行列 \( A \) の固有値に重解がすべて含まれない場合、必ず対角化をすることができる。
(iii)
解答: 3 [1点]
対角化ができるということは、\( n \) 次正方行列に対して合計 \( n \) 本の固有ベクトルを得ることができたと言い換えることができる。
これを固有空間で言い換えると、\[
\dim V( \lambda_1 ) + \dim V( \lambda_2 ) + \dim V( \lambda_3 ) = n
\]となる。よって答えは3。
(ちなみに選択肢4は、\( n = 3 \) であれば正しいですが、\( n > 3 \) のときは必ずしも成立する選択肢ではありません。なので誤りです。)
ある \( n \) 次正方行列 \( A \) に対し、合計 \( n \) 本の固有ベクトルを計算することができるとき、対角化が可能である。
この条件を固有空間の次元で表現すると、\[
\dim V( \lambda_1 ) + \dim V( \lambda_2 ) + \dim V( \lambda_3 ) +\cdots = n
\]となる。
※ \( \dim V( \lambda_1 ), \dim V( \lambda_2 ) , \cdots \) は行列 \( A \) の固有値を表す
(2) 対角化(誘導あり)
行列\[
A = \left( \begin{array}{ccc} 1 & 1 & -1 \\ 2 & 2 & 1 \\ 2 & -1 & 4 \end{array} \right)
\]に対して対角化を行う。
(i) \( A \) の固有値は 3 と [ 51 ] である。また、固有値3に対する重複度は [ 52 ] である。
(ii) 固有値3に対する固有ベクトルとして、以下の2本が得られる。\[
\boldsymbol{p}_1 = \left( \begin{array}{ccc} 1 \\ 0 \\ \left[ \ \ 53 \ \ \right] \end{array} \right), \ \ \ \boldsymbol{p}_2 = \left( \begin{array}{ccc} 1 \\ 2 \\ \left[ \ \ 54 \ \ \right] \end{array} \right)
\]また、固有値 [ 51 ] に対する固有ベクトルとして、以下の1本が得られる。\[
\boldsymbol{p}_3 = \left( \begin{array}{ccc} \left[ \ \ 55 \ \ \right] \\ 1 \\ 1 \end{array} \right)
\]
(iii) ここで、正則な行列 \( P \) を\[
P = ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 ) = \left( \begin{array}{ccc} 1 & 1 & \left[ \ \ 55 \ \ \right] \\ 0 & 2 & 1 \\ \left[ \ \ 53 \ \ \right] & \left[ \ \ 54 \ \ \right] & 1 \end{array} \right)
\]とおく。すると、[ 56 ]。
- \( P^{-1} AP = D \) を用いて対角化することができる。ただし、\( D \) は以下の行列である。\[
D = \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{array} \right)
\] - \( P^{-1} AP = D \) を用いて対角化することができる。ただし、\( D \) は以下の行列である。\[
D = \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & \left[ \ \ 51 \ \ \right] \end{array} \right)
\] - \( P^{-1} AP = D \) を用いて対角化することができる。ただし、\( D \) は以下の行列である。\[
D = \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & \left[ \ \ 51 \ \ \right] & 0 \\ 0 & 0 & 3 \end{array} \right)
\] - \( P^{-1} AP = D \) を用いて対角化することができる。ただし、\( D \) は以下の行列である。\[
D = \left( \begin{array}{ccc} \left[ \ \ 51 \ \ \right] & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{array} \right)
\] - 対角化ができないことがわかる。
この分野に該当するうさぎ塾の記事はこちら ↓↓
(i) 固有値計算
No.51 1 [3点]
No.52 2 [2点]
普通に \( |A - \lambda E| = 0 \) を計算しましょう。サラスでごり押しするよりも、余因子展開を使って計算することをおすすめします。\[\begin{align*}
|A - \lambda E| & = \left| \begin{array}{ccc} 1 - \lambda & 1 & -1 \\ 2 & 2 - \lambda & 1 \\ 2 & -1 & 4 - \lambda \end{array} \right|
\\ & = \left| \begin{array}{ccc} 1 - \lambda & 1 & -1 \\ 2 & 2 - \lambda & 1 \\ 0 & \lambda - 3 & 3 - \lambda \end{array} \right|
\\ & = (3 - \lambda)\left| \begin{array}{ccc} 1 - \lambda & 1 & -1 \\ 2 & 2 - \lambda & 1 \\ 0 & -1 & 1 \end{array} \right|
\\ & = (3 - \lambda) \left| \begin{array}{ccc} 1 - \lambda & 0 & 0 \\ 2 & 3 - \lambda & 0 \\ 0 & -1 & 1 \end{array} \right|
\\ & = (3 - \lambda) \left| \begin{array}{ccc} 1 - \lambda & 0 \\ 2 & 3 - \lambda \end{array} \right|
\\ & = ( 3 - \lambda)^2 ( 1 - \lambda) = 0
\end{align*}\]
となるので、固有値は1と、3(2重解)と求まります。
固有値の総和は行列の対角成分の和に一致しているので、検算に大変便利です。
今回の場合は、対角成分の和は\[
\left( \begin{array}{ccc} \textcolor{red}{1} & 1 & -1 \\ 2 & \textcolor{red}{2} & 1 \\ 2 & -1 & \textcolor{red}{4} \end{array} \right)
\]は、1 + 2 + 4 = 7ですね。
確かに固有値の和は 1 + 3 + 3 = 7 と一致していますね!
(重解の場合は重解の数だけカウントしてください)
(ii) 固有ベクトルの計算
No.53 -2 [2点]
No.54 0 [2点]
No.55 -1 [1点]
固有値3に対する固有ベクトル \( \boldsymbol{p} \) は、連立方程式 \( (A - 3E) \boldsymbol{p} = \boldsymbol{0} \) を解けばOK。
行基本変形をすると\[\begin{align*}
A - 3E & = \left( \begin{array}{ccc} -2 & 1 & -1 \\ 2 & -1 & 1 \\ 2 & -1 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 2 & -1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]
となる。\( A - 3E \) の階数は1なので、固有ベクトルは3 - 1 = 2本存在する。
ここで、行基本変形より、連立方程式 \( ( A - 3E) \boldsymbol{p} = \boldsymbol{0} \) の解は \( 2x - y + z = 0 \) の解と同じ。ここで、任意定数を \( s, t \) とおくと、解は\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = s \left( \begin{array}{ccc} 1 \\ 0 \\ -2 \end{array} \right) + t \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \end{array} \right)
\]と表せる。
固有値3の固有ベクトルは、この解の中から線形従属な固有ベクトル2本なので、\( (s,t) = (1,0), (0,1) \) のときを固有ベクトル \( \boldsymbol{p}_1 \), \( \boldsymbol{p}_2 \) とする。\[
\boldsymbol{p}_1 = \left( \begin{array}{ccc} 1 \\ 0 \\ \textcolor{red}{-2} \end{array} \right) , \ \ \
\boldsymbol{p}_2 = \left( \begin{array}{ccc} 1 \\ 2 \\ \textcolor{red}{0} \end{array} \right)
\]
固有値1に対する固有ベクトルは、\( (A-E) \boldsymbol{p} = \boldsymbol{0} \) を解けばOK。
行基本変形をすると、\[\begin{align*}
A - E & = \left( \begin{array}{ccc} 0 & 1 & -1 \\ 2 & 1 & 1 \\ 2 & -1 & 3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 1 & -1 \\ 2 & 0 & 2 \\ 2 & 0 & 2 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 1 & -1 \\ 1 & 0 & 1 \\ 0 & 0 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]
となる。\( A - E \) の階数は2なので、固有ベクトルは3 - 2 = 1本存在する。
ここで、行基本変形より、連立方程式 \( ( A - E) \boldsymbol{p} = \boldsymbol{0} \) の解は\[
\begin{array}{l} x + z = 0 \\ y - z = 0 \end{array}
\]の解と同じ。ここで、任意定数を \( k \) とおくと、解は\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} -1 \\ 1 \\ 1 \end{array} \right)
\]と表せる。
この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_3 \) とする。\[
\boldsymbol{p}_3 = \left( \begin{array}{ccc} \textcolor{red}{-1} \\ 1 \\ 1 \end{array} \right)
\]
(iii)
No.56 2 [3点]
正則行列 \( P \) を\[\begin{align*}
P & = ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 )
\\ & = \left( \begin{array}{ccc} 1 & 1 & -1 \\ 0 & 2 & 1 \\ -2 & 0 & 1 \end{array} \right)
\end{align*}\]とすると、\[\begin{align*}
AP & = A ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 )
\\ & = (A \boldsymbol{p}_1,A \boldsymbol{p}_2,A \boldsymbol{p}_3 )
\\ & = (3 \boldsymbol{p}_1, 3 \boldsymbol{p}_2, \boldsymbol{p}_3 )
\\ & = ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 ) \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{array} \right)
\\ & = P \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{array} \right)
\\ & = PD
\end{align*}\]となるので、\( AP = PD \) が成り立つ。さらに、両辺に左側から \( P^{-1} \) を掛けることで、\[
P^{-1} AP = D = \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{array} \right)
\]と対角化を行うことができる。よって答えは2。
注釈
| ↑1 | 行列式 \( \left| \boldsymbol{a}_1 , \boldsymbol{a}_2 , \boldsymbol{0} \right| = 1 \)となるため。 |
|---|---|
| ↑2 | 基本形に対し、\( \boldsymbol{b'} = \boldsymbol{a} + \boldsymbol{b} \) とおいてから \( \boldsymbol{b} = \boldsymbol{b}' - \boldsymbol{a} \) と代入し、最後に \( \boldsymbol{b} = \boldsymbol{b}' \) としたら導出できます。 |
| ↑3 | 引き算型1に対し、\( \boldsymbol{a'} = - \boldsymbol{a} \) とおき、最後に \( \boldsymbol{a} = \boldsymbol{a}' \) とすることで導出できます。\( |- \boldsymbol{a} | = | \boldsymbol{a} | \) に注意。 |
| ↑4 | 複素数 \( k = a + bi \) に対し、共役複素数は \( \overline{k} = a - bi \) となる。 |
| ↑5 | 行列の階数で判定する方法もあるのですが、行列式の方が早く計算ができると思います。 |
| ↑6 | 答えは\[ \frac{1}{2} \left( \begin{array}{ccc} -2 & 8 \\ 3 & -11 \end{array} \right) \]です。 |
関連広告・スポンサードリンク





![うさぎでもわかる画像処理 Part02 トーンカーブと画像処理 [Python・MATLABコード付き]](https://www.momoyama-usagi.com/wp-content/uploads/ip1-18-150x150.jpg)
![うさぎでもわかる計算機システム Part04 桁落ち・情報落ち・丸め誤差・打ち切り誤差について [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612150639-1-150x150.jpg)
![[基本情報・応用情報] うさぎでもわかる情報理論 第3羽 ハフマン符号化](https://www.momoyama-usagi.com/wp-content/uploads/joho3-2-3-150x150.jpg)