うさぎでもわかる解析　Part23　2重積分の基礎・積分範囲の交換

こんにちは、ももやまです。

今回から2重積分を数回にわけて説明していきたいと思います。

まずは2重積分の基礎についてと、積分範囲の交換についてです。

前回の記事はこちら！
（Part22　院関数表記で表された関数の極値を求める方法についてです。）

www.momoyama-usagi.com

スポンサードリンク

１．2重積分とは

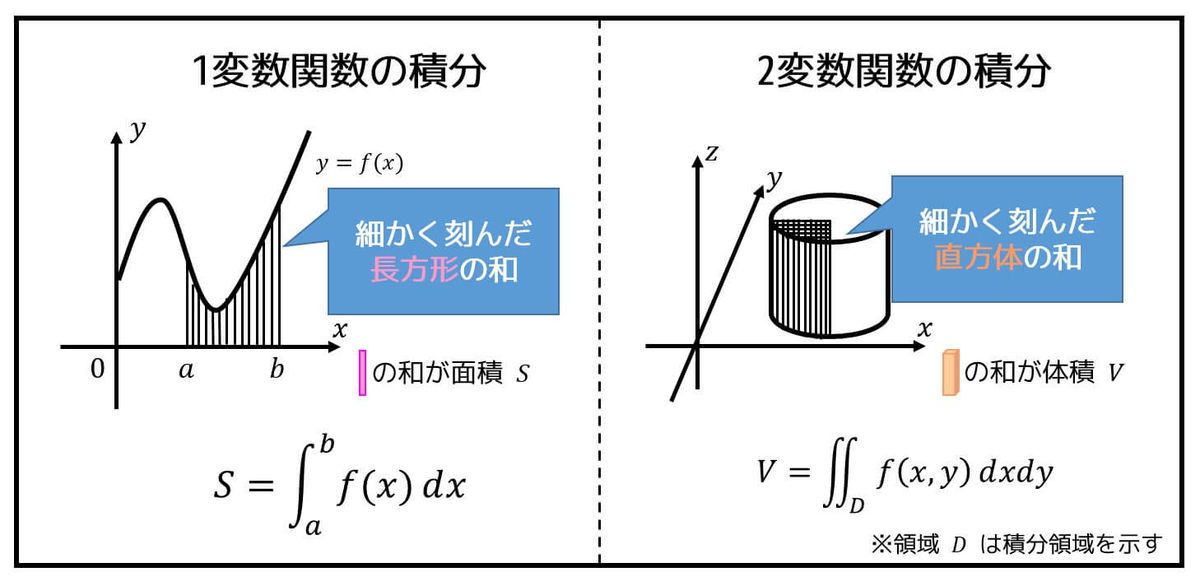
まずは2重積分とはどんなものかを説明していきましょう。

今まで習った1変数の関数の積分のイメージは積分区間を細かく刻み、細かく刻んだ部分の長方形の面積をすべて足したものでしたね。

では、2変数関数、つまり2重積分の場合だとどうなるでしょうか。

2変数関数の積分（2重積分）の考え方も1変数関数の場合と似ていて積分領域を細かく刻み、細かく刻んだ部分の立方体の体積をすべて足したものとなります。

しかし、2変数関数の場合は \( x \) 軸を細かく刻む区間と \( y \) 軸を細かく刻む区間の2つを考える必要があります。なので積分範囲は平面 \( D \) で表されます。

この平面 \( D \) のことを積分領域と呼びます。

スポンサードリンク

２．2重積分の計算法則

まずは2重積分の計算法則を3つほど紹介しましょう。

ですが、ほとんど1変数の場合と同じなので戸惑うことはないと思います。

(1) 2重積分の基本計算

まずは2重積分をどうやって計算するかについてまとめていきたいと思います。

このように2重積分の領域を \( x \) 軸による積分、\( y \) 軸による積分の2つに分解することで積分結果を求めることができます。

図で表すと下のようになります。
（※以降黄緑色で塗りつぶされた部分は積分領域 \( D \) を表します。）

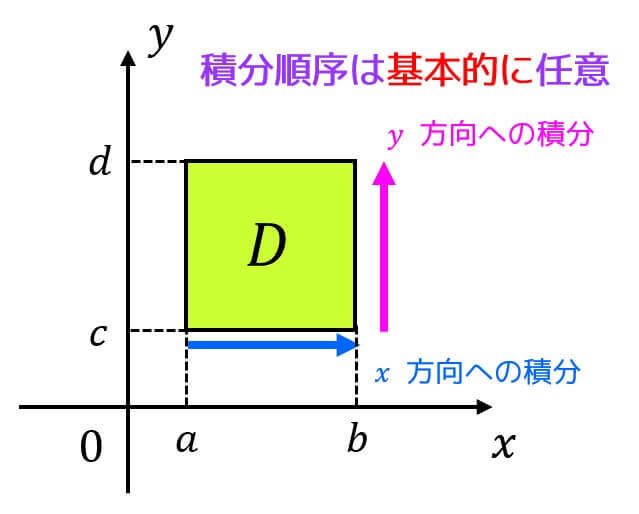
イメージとしては、\( x \) 方向にまず積分することにより領域 \( D \) を千切りにし、さらに \( y \) 方向に積分することでさらに細かくする、と考えるとわかりやすいかと思います。

この積分区間の変数 \( a \), \( b \), \( c \), \( d \) には定数以外にも自分自身以外の積分変数であっても構いません*1。ただし、（自分自身以外の）積分変数を入れる場合、必ず変数が入っている方を先に積分してください*2。
（1つあとの章の例題でも説明します。）

また、\( f(x,y) \) が \( x \) だけの関数 \( g(x) \) および \( y \) だけの関数 \( h(y) \) に分解できる場合は以下のように計算しても構いません。

(2) 定数倍の分離

2重積分に出てくる積分変数とは関係ない定数はインテグラルの外に出すことができます。

例えば、\[
\iint_D 4x^2 + 2y^2 \ dxdy = 2 \iint_D 2x^2 + y^2 \ dxdy
\]のように適用することができます。

(3) 和（差）の分離

1変数積分と同じように2つの和で表された関数の2重積分を２つに分割することができます。

例えば、\[
\iint_D 4x^2 + 2y^2 \ dxdy = \iint_D 4x^2  \ dxdy +  \iint_D 2y^2  \ dxdy
\]のように適用することができます。さらに(1)と組み合わせると\[
\iint_D 4x^2 + 2y^2 \ dxdy = 4 \iint_D x^2  \ dxdy + 2 \iint_D y^2  \ dxdy
\]とすることもできます。

(4) 領域の分割

2重積分の積分領域を分配（分割）することができます。

2つの領域への分配を図で表すと下のようになります。

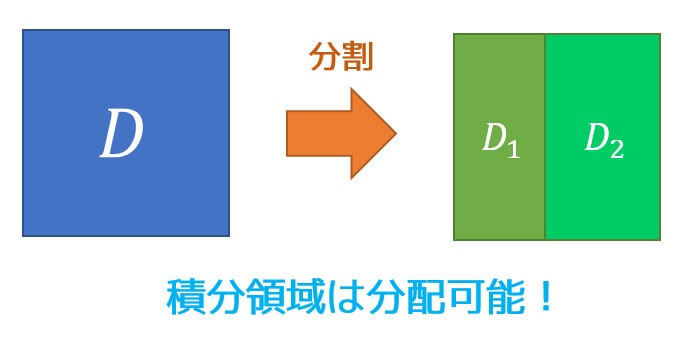
1変数関数の積分区間の分割\[
\int^c_a f(x) \ dx = \int^b_a f(x) \ dx + \int^c_b f(x) \ dx
\]を2変数に拡張したもんだと思ってもらってOKです。

スポンサードリンク

３．2重積分の例・基本パターン

では、2つのパターンにわけて2重積分の計算方法を例題を含めながら解説をしていきましょう。

(1) 積分領域に変数 x,y が含まれない場合（長方形）

まずは2重積分の中でも最も基本的な、積分範囲に \( x \), \( y \) が含まないパターンの2重積分の求め方を例題を踏まえながら説明していきたいと思います。

このパターンの場合、\( x \), \( y \) どちらから先に積分しても答えを出すことができます。計算しやすい方で計算をしましょう。

例題1

つぎの重積分\[
\iint_D x^2 + y^2 \  dxdy  \]\[  D = \{ (x,y) \mid 1 \leqq x \leqq 2, \ 0 \leqq y \leqq 1  \ \}
\]を計算しなさい。

解説1

今回の積分領域 \( D \) を見てみると \( x \), \( y \) ともに定数となっていますね。

なので \( x \) 方向から積分しても \( y \) 方向から積分してもどちらでもOKですね。

(a) \( x \) から先に積分する場合

\( x \) を先に積分する場合、\[
\iint_D x^2 + y^2 \  dxdy = \int^1_0 \left( \int^2_1 x^2 + y^2 \ dx \right) \ dy
\]を計算すればよい。

あとは1変数の積分と同じように積分するだけです。

\[\begin{align*}
\int^2_1 x^2 + y^2 \ dx & = \left[ \frac{1}{3} x^3 + xy^2 \right]^2_1
\\ & = \frac{8}{3} + 2y^2 - \left( \frac{1}{3} + y^2 \right)
\\ & = \frac{7}{3} + y^2
\end{align*} \]より、\[\begin{align*} &
\int^1_0 \left( \int^2_1 x^2 + y^2 \ dx \right) \ dy
\\ = & \int^1_0 \frac{7}{3} + y^2  \ dy
\\ = & \left[ \frac{7}{3} y + \frac{1}{3} y^3 \right]^1_0
\\ = & \ \frac{7}{3} + \frac{1}{3}
\\ = & \ \frac{8}{3}
\end{align*} \]となる。

(b) \( y \) から先に積分する場合

\( x \) を先に積分する場合、\[
\int_D x^2 + y^2 \  dxdy = \int^2_1 \left( \int^1_0 x^2 + y^2 \ dy \right) \ dx
\]を計算すればよい。

\[\begin{align*}
\int^1_0 x^2 + y^2 \ dy & = \left[ yx^2 + \frac{1}{3} y^3 \right]^1_0
\\ & = x^2 + \frac{1}{3}
\end{align*} \]より、\[\begin{align*} &
\int^2_1 \left( \int^1_0 x^2 + y^2 \ dy \right) \ dx
\\ = & \int^2_1 x^2 + \frac{1}{3}  \ dx
\\ = & \left[ \frac{1}{3} x^3 + \frac{1}{3} x \right]^2_1
\\ = & \ \frac{8}{3} + \frac{2}{3} - \left( \frac{1}{3} - \frac{1}{3} \right)
\\ = & \ \frac{8}{3}
\end{align*} \]となる。

このように積分範囲に積分する変数（今回は \( x,y \) ）が範囲に含まれていない場合は \( x \), \( y \) どちらから積分しても答えを得ることができます。

(2) 積分領域に変数 x,y が含まれる場合

積分領域を\[
D = \{ (x,y) \mid 0 \leqq x \leqq 1, \ 0 \leqq y \leqq x \ \}
\]の \( 0 \leqq y \leqq x \) のような、積分範囲に積分する変数を含めることもできます。

しかし、積分範囲に積分する変数が含まれている場合、先に変数が含まれている方を積分する必要があります。

例題2

つぎの重積分\[
\iint_D e^{2x-y} \  dxdy  \]\[  D = \{ (x,y) \mid 0 \leqq x \leqq 1, \ 0 \leqq y \leqq x \}
\]を計算しなさい。

解説2

\( y \) の積分範囲（ \( 0 \leqq y \leqq x \) ）を見てみると、積分区間に積分変数である \( x \) が含まれていますね。

なので、必ず \( y \) から積分しなければなりません。なので、\[
\iint_D e^{2x-y} \  dxdy  = \int^1_0 \left( \int^x_0 e^{2x-y} \ dy \right) \ dx
\]を計算すればよい。

\[\begin{align*}
\int^x_0 e^{2x-y} \ dy & = \left[ - e^{2x-y} \right]^x_0
\\ & = - e^x + e^{2x}
\end{align*} \]より、\[\begin{align*} &
\int^1_0 \left( \int^x_0 e^{2x-y} \ dy \right) \ dx
\\ = & \int^1_0 e^{2x} - e^x  \ dx
\\ = & \left[ \frac{1}{2} e^{2x} - e^x \right]^1_0
\\ = & \ \frac{1}{2} e^2 - e - \left( \frac{1}{2} - 1 \right)
\\ = & \ \frac{1}{2} e^2 - e + \frac{1}{2}
\\ = & \ \frac{1}{2} (e-1)^2
\end{align*} \]となる。

４．積分順序の交換

積分範囲に積分する変数が含まれている場合、先に変数が含まれている方を積分する必要がありましたね。

しかし、中には先に変数が含まれている方を先に積分しようとしてもできない or 非常に複雑な計算が必要な二重積分があります。

このような場合、積分範囲を書き換えることにより、積分順序を入れ替えます。

実際に例題で1問見てみましょう。

例題3

つぎの重積分\[
\iint_D x e^{y^2} \  dxdy  \]\[  D = \{ (x,y) \mid 0 \leqq x \leqq 1, \ x^2 \leqq y \leqq 1 \ \}
\]を計算しなさい。

解説3

\( y \) の積分範囲（ \( x^2 \leqq y \leqq 1 \) ）に積分区間に積分変数である \( x \) が含まれています。

なので必ず \( y \) から積分する必要があります。しかし\[
\int e^{y^2} \ dy
\]を積分することはできません。

なので、\( x \) から先に積分できるように積分順序を入れ替えてみましょう。

今回は \( x \) から先に積分したいため、\( x \) の積分範囲を \( y \) を用いて表し、\( y \) の積分範囲は定数で表すようにします。

積分順序を入れ替えを考える際には、下の図のように積分領域を実際に図示してから入れ替えることをおすすめします*3。

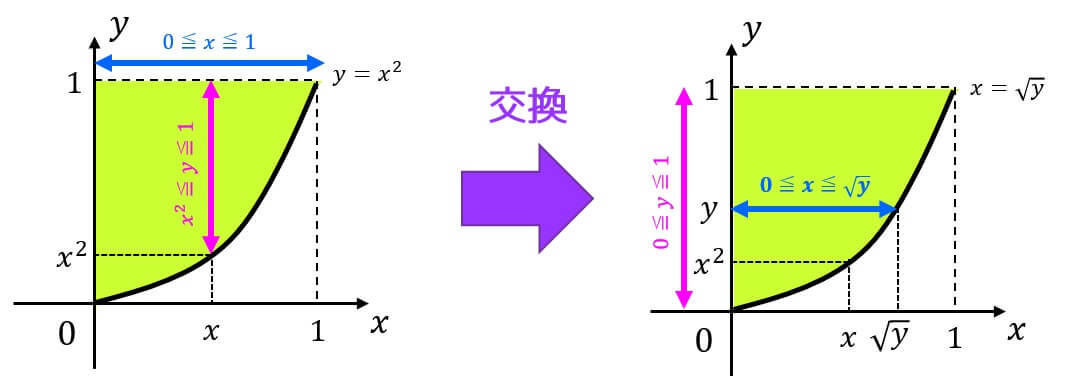
すると、\[
D = \{ (x,y) \mid  0 \leqq y \leqq 1, \ 0 \leqq x \leqq \sqrt{y} \}
\]と書き換えることができますね。なので、\[
\iint_D x e^{y^2} \  dxdy = \int^1_0 \left( \int^{\sqrt{y}}_0 x e^{y^2} \ dx \right) \ dy
\]を計算すればよい。

あとは積分計算するだけです。ここで、\[\begin{align*}
\int^{\sqrt{y}}_0 x e^{y^2} \ dx & = \left[ \frac{1}{2} x^2 e^{y^2} \right]^{\sqrt{y}}_0
\\ & = \frac{1}{2} y e^{y^2}
\end{align*} \]と計算できるので、積分結果は\[\begin{align*} &
\int^1_0 \left( \int^{\sqrt{y}}_0 x e^{y^2} \ dx \right) \ dy
\\ = & \int^1_0 \frac{1}{2} y e^{y^2}  \ dy
\\ = & \ \frac{1}{4} \int^1_0 2 y e^{y^2}  \ dy
\\ = & \ \frac{1}{4} \left[ e^{y^2} \right]^1_0
\\ = & \ \frac{1}{4} e - \frac{1}{4}
\end{align*} \]となる。

５．練習問題

では、4問ほど練習しましょう。

練習1

つぎの重積分\[
\iint_D \sin (x+y) \  dxdy  \]\[  D = \{ (x,y) \mid 0 \leqq x \leqq \frac{\pi}{2}, \ 0 \leqq y \leqq \frac{\pi}{2}  \ \}
\]を計算しなさい。

練習2

つぎの重積分\[
\iint_D (y-x)^3 \  dxdy  \]\[  D = \{ (x,y) \mid 0 \leqq x \leqq 2, \ x \leqq y \leqq 3x \ \}
\]を計算しなさい。

練習3

つぎの2重積分\[
\int^1_0 \left( \int^{x}_{x^2} f(x,y) \ dy \right) \ dx
\]の積分順序を交換しなさい。

練習4

つぎの重積分\[
\iint_D \sin x \sin^3 y \  dxdy  \]\[  D = \{ (x,y) \mid 0 \leqq x \leqq \frac{\pi}{2}, \ 0 \leqq y \leqq x \ \}
\]を計算しなさい。

６．練習問題の答え

解答1

積分範囲がともに定数なのでどちらから積分してもOK。

今回は \( x \) から積分するバージョンでやってみます。よって、\[
\iint_D \sin (x+y) \  dxdy = \int^{ \frac{\pi}{2} }_0 \left( \int^{ \frac{\pi}{2} }_0 \sin (x+y) \ dx \right) \ dy
\]を計算すればOK。

\[\begin{align*}
\int^{ \frac{\pi}{2} }_0 \sin (x+y) \ dx & = \left[ - \cos (x+y) \right]^{\frac{\pi}{2}}_0
\\ & = - \cos \left( y + \frac{\pi}{2} \right) + \cos y
\\ & = \sin y + \cos y
\end{align*} \]より、\[\begin{align*} &
\int^{ \frac{\pi}{2} }_0 \left( \int^{\frac{\pi}{2}}_0 \sin (x+y) \ dy \right) \ dx
\\ = & \int^{\frac{\pi}{2}}_0 \sin y + \cos y \ dx
\\ = & \left[ - \cos y + \sin y \right]^{\frac{\pi}{2}}_0
\\ = & \ 1 - (-1)
\\ = & \ 2
\end{align*} \]となる。

解答2

\( y \) の積分範囲（ \( x \leqq y \leqq 3x \) ）を見てみると、積分区間に積分変数である \( x \) が含まれていますね。

なので、必ず \( y \) から積分しなければなりません。なので、\[
\iint_D (y-x)^3 \  dxdy  = \int^2_0 \left( \int^{3x}_{x} (y-x)^3 \ dy \right) \ dx
\]を計算すればよい。

\[\begin{align*}
\int^{3x}_x (y-x)^3 \ dy & = \left[ \frac{1}{4} (y-x)^4 \right]^{3x}_x
\\ & = \frac{1}{4} (2x)^4
\\ & = 4 x^4
\end{align*} \]より、\[\begin{align*} &
\int^2_0 \left( \int^{3x}_x (y-x)^3 \ dy \right) \ dx
\\ = & \int^{2}_0 4 x^4 \ dx
\\ = & \int^{2}_0 \frac{4}{5} x^5 \ dx
\\ = & \ \frac{128}{5}
\end{align*} \]となる。

解答3

積分順序の交換するために、積分範囲を図示しましょう。

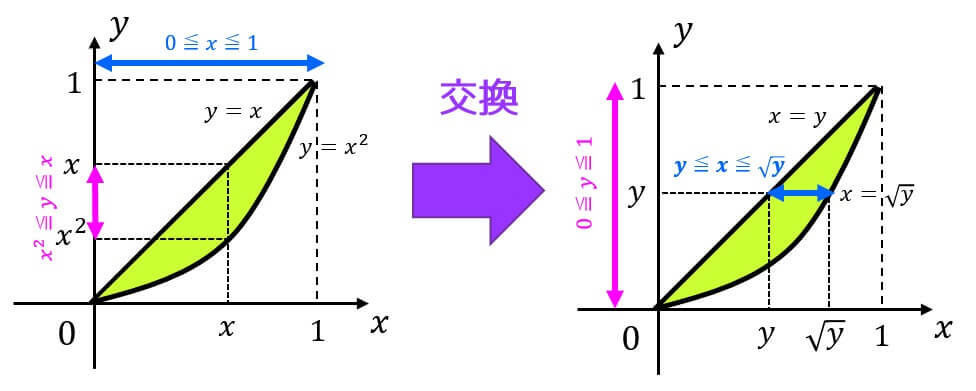
今回の場合は \( 0 \leqq x \leqq 1 \) における \( y = x^2 \) および \( y = x \) の囲まれた部分になりますね。

積分順序を交換するためには、\( y \) を定数範囲で（ \( 0 \leqq y \leqq 1 \) ）で表した際に \( x \) の積分範囲が \( y \) を用いてどう表されるかを考えればいいですね。

\( y = x \), \( y = x^2 \) の逆関数を取ると \( x = y \), \( x = \sqrt{y} \)*4となるので、積分領域 \( D \) は\[
D = \{ (x,y) \mid 0 \leqq y \leqq 1, \ y \leqq x \leqq \sqrt{y} \  \}
\]と交換することできます。

よって、\[
\int^1_0 \left( \int^{\sqrt{y}}_{y} f(x,y) \ dx \right) \ dy
\]となります。

解答4

\( y \) の積分範囲に \( x \) が含まれているため \( y \) から先に積分しなければならない。しかし、\( \sin^3 y \) の積分は少ししんどいですね（3倍角の公式を使えばできないことはないが…）。

なので、積分範囲を入れ替えることを考える。

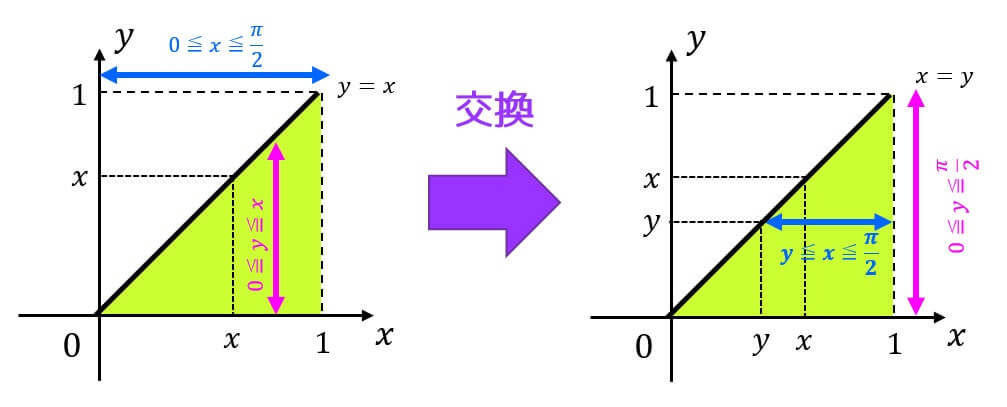
と図示することで積分範囲 \( D \) を\[
D = \{ (x,y) \mid 0 \leqq y \leqq \frac{\pi}{2}, \ y \leqq x \leqq \frac{\pi}{2}  \ \}
\]と交換する。

よって、\[
\iint_D \sin x \sin^3 y \  dxdy = \int^{\frac{\pi}{2}}_0 \left( \int^{\frac{\pi}{2}}_y \sin x \sin^3 y \ dx \right) \ dy
\]を計算すればよい。

ここで \[\begin{align*}
\int^{\frac{\pi}{2}}_y \sin x \sin^3 y \ dx & =  \sin^3 y \left[ - \cos x \right]^{\frac{\pi}{2} }_y
\\ & = \sin^3 y \cos y
\end{align*} \]より、\[\begin{align*} &
\int^{\frac{\pi}{2}}_0 \left( \int^{\frac{\pi}{2}}_y \sin x \sin^3 y \ dx \right) \ dy
\\ = & \int^{\frac{\pi}{2}}_0  \sin^3 y \cos y \ dy
\end{align*} \]となる。

ここで \( \sin y = t \) とおくと、

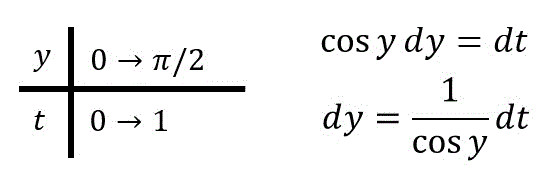
となるので、\[\begin{align*} &
\int^{\frac{\pi}{2}}_0  \sin^3 y \cos y \ dy
\\ = & \int^1_0 t^3 \ dt
\\ = & \left[ \frac{1}{4} t^4 \right]^1_0
\\ = & \ \frac{1}{4}
\end{align*} \]と計算できる。

７．さいごに

今回は2重積分の基礎、および積分範囲の交換についてまとめていきました。

2重積分というと難しいイメージがあるかもしれませんが、実際には1変数の積分が2回するだけなのでそこまで難しくはありません。（ただし計算量は多くなりますが…）

次回は2重積分の置換積分についてまとめていきたいと思います。