スポンサードリンク
※ 動的システムではなく、ディジタルシステムについて(伝達関数、インパルス応答、ステップ応答の求め方など)知りたい人は、こちらの記事ではなく、下のリンク先の記事をご覧ください。
こんにちは、ももやまです!
今回からは、動的システムの振る舞いについて書いていきます。
前編となる第06羽では、下の5つの内容についてみていきましょう。
- 動的システムとは何か
- 動的システムを見るために必要なラプラス変換の復習
- 伝達関数の定義と求め方
- 単位インパルス関数と単位ステップ関数について
- インパルス応答とステップ応答の求め方
目次
スポンサードリンク
1. 静的システムと動的システム
最初に動的システムとはどのようなシステムかについて、対になる静的システムと比べながら見ていきましょう。
(1) 静的システム
静的システムとは、時間 \( t \) に関係なく、常に出力 \( y(t) \) が一定になるようなシステムのことをいいます。
言い換えると、ある入力 \( u(t) \) に対して、常に同じ出力 \( y(t) \) を返す関数のようなシステムと言えますね。
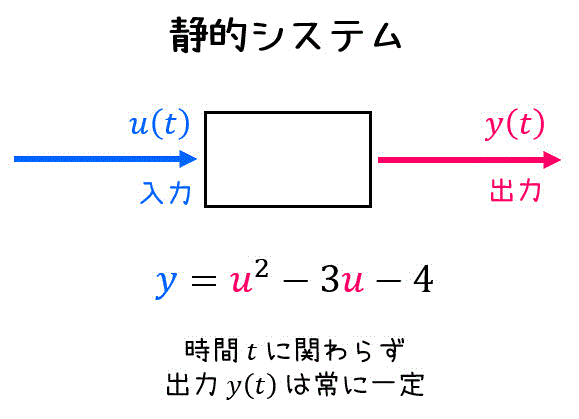
高校物理で習う物理公式の中で、時間 \( t \) が出てこない公式はほぼすべて静的システムと言えます。
例えば、力学分野で出てくるフックの法則 \( F = kx \) では、ばねの伸び \( x \) を入力すると、力 \( F \) を出力するシステムと言えます。同じように電磁気分野だと、オームの法則 \( V = IR \) では、電流 \( I \) を入力すると、電圧 \( V \) を出力するシステムと言えますね。
静的システムは簡単に解ける!
静的システムの大きな特徴に、ある入力 \( u(t) \) に対して、代入を行ったり、方程式を解くだけで簡単に出力 \( y(t) \) を求めることができるというのがあります。
例えば、上の例で示したシステム \( y = u^2 - 3u - 4 \) であれば、入力 \( u \) の値が分かれば簡単に出力 \( y \) の値を求められますね。例えば、\( u = 3 \) であれば、出力は下のように代入をするだけで求められます。\[\begin{align*}
y & = 3^2 - 3 \cdot 3 - 4
\\ & = 9 - 9 - 4
\\ & = -4
\end{align*}\]また、仮に \( y^2 - 3y - 4 = u \) のような式であったとしても、中3レベルの数学力さえあれば[1]方程式を解くだけならのお話です。例えば、数式に \( \log_2 x \) などの対数関数が入ると高校数学の数2レベルに、\( e \) が入ると数3レベルに、\( … Continue reading簡単に解くことができます。例えば、入力 \( u = 6 \) とすると、\[\begin{align*}
y^2 - 3y - 4 & = 6
\\ y^2 - 3y - 10 & = 0
\\ (y+2)(y-5) & = 0
\end{align*}\]と変形して、\( y = -2 , 5 \) と簡単に求めることができます。
このように、静的システムは中学数学レベルでも入出力関係がわかる簡単なシステムと言えるのです!
(2) 動的システム
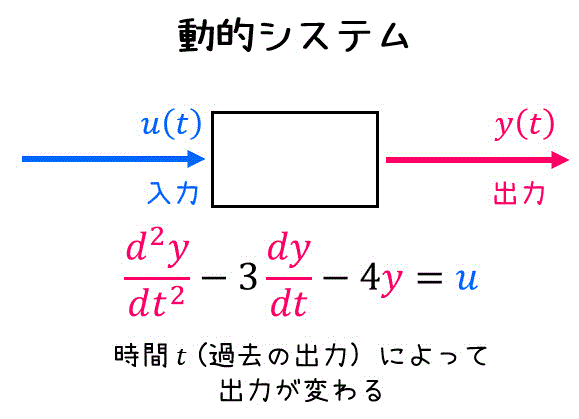
動的システムとは、時間 \( t \) によって、出力 \( y(t) \) が変化するようなシステムのことをいいます。
言い換えると、入力 \( u(t) \) が同じでも、過去の入出力によって出力 \( y(t) \) が変換するようなようなシステムと言えますね。

動的システムは、微積が頻繁に出てくる大学物理で登場し、微分方程式の形で表されます。
例えば、ある加速度 \( a \) に対しての落下運動を表す式は\[
m \frac{d^2 y}{dt^2} = - ma
\]と表せます。これは、ある加速度 \( a = a(t) \) を入力すると、物体の位置 \( y = y(t) \) を返すシステムと言えますね。
動的システムは難しい!
動的システムの振る舞いは、先ほども説明した通り微分方程式の形で表されます。そのため、中3レベルの方程式を解くだけでよかった静的システムに比べて、入出力関係を把握するための難易度が一気に上昇します。
例えば上で出てきたシステム\[
\frac{d^2 y}{dt^2} - 3 \frac{dy}{dt} - 4y = u
\]であれば、まず同次(斉次)方程式\[
\frac{d^2 y}{dt^2} - 3 \frac{dy}{dt} - 4y = 0
\]を解いてから、次に特殊解(題意の微分方程式を満たす1つの解)を1つ求め、その和(同次式の解+題意を満たす特殊解)を求め、最後に初期条件を代入する必要があります。
どう考えても静的システムより解く難易度が高いです。
そこで、動的システムをより簡単に解く方法について、次の章から説明していきましょう!
スポンサードリンク
2. 動的システムを解読する魔法・ラプラス変換
※ 「ラプラス変換をまだ習っていない or 習っているけど理解があいまいだ」という人は、下の2つの記事にて内容を確認してからこちらの内容に戻ることをおすすめします。
ラプラス変換と微分方程式
微分方程式はラプラス変換という道具を使うことで、微分方程式という難しい問題から中3レベルの方程式を解く簡単な問題に持ち込むことができるのでしたね。
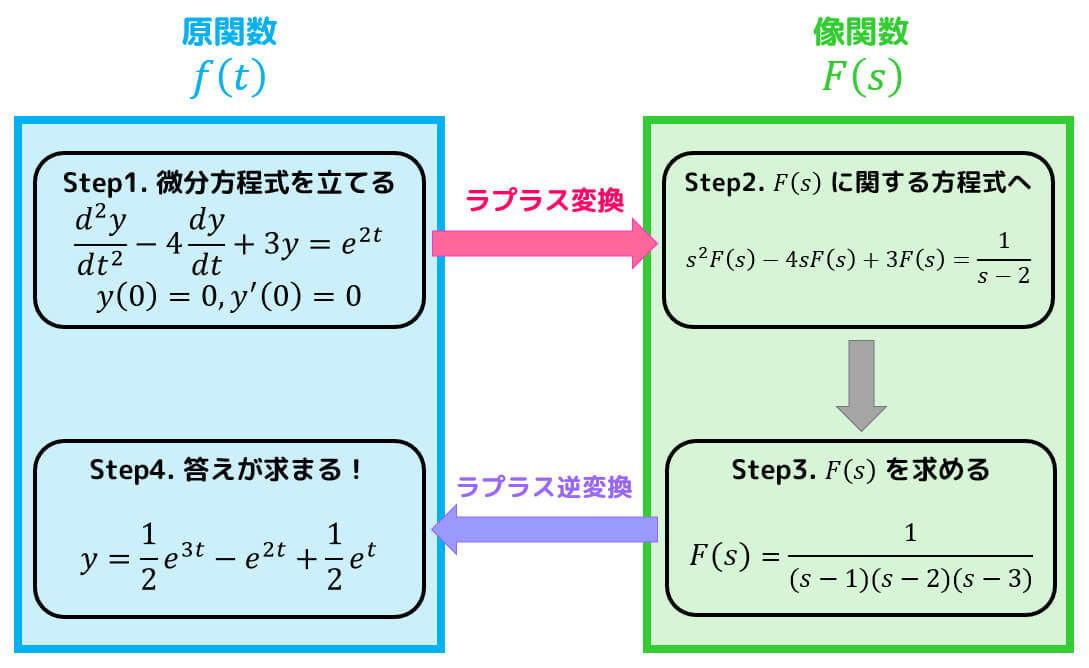
そのため、「微分方程式で振る舞いが表されている動的システム」もラプラス変換を使うことで、簡単に解くことができそうですね。
そこで、第2章では動的システムを解くために必要なラプラス変換の知識について復習しましょう。
(1) ラプラス変換の基本法則
まずは、ラプラス変換で使える法則について軽く復習しましょう。
ただし、微分の法則については少し補足があります。

★ 動的システムで使う微分方程式の初期値は…?
微分方程式の解を解くためには、下のように初期値が与えられますね。\[
\frac{d^2 y }{dt^2} - 4 \frac{dy}{dt} + 3 y = e^{2t}
\]\[
y(0) = 0, \ \ \ y'(0) = 0
\]
動的システムの振る舞いを考える場合でも同じように初期値を考える必要がありますが、将来的にどのような振る舞いをするかを調べればOKです。
ここで、十分先の未来においては初期値の値が少しくらい変わったところでほとんど影響がなさそうですね。そのため、動的システムの振る舞いを考える際には、基本的にすべての初期条件 \( y(0) , y'(0), y''(0), \cdots \) を0とみなして考えます。
そのため、ラプラス変換の微分の法則を下のように簡略化することができます。
動的システムの振る舞いを考える際は、初期条件 \( y(0), y'(0), y''(0), \cdots \) をすべて0として考える。
そのため、ラプラス変換の微分の法則を以下のように簡略化できる。\[\begin{align*}
\mathcal{L} \left[ f'(t) \right] & = s F(s) \\
\mathcal{L} \left[ f''(t) \right] & = s^2 F(s) \\
\mathcal{L} \left[ f'''(t) \right] & = s^3 F(s) \\
& \vdots \\
\mathcal{L} \left[ f^{(n)}(t) \right] & = s^n F(s)
\end{align*}\]
※ \( f(t) \) を1回微分すると、ラプラス変換の結果が \( s \) 倍になる!
(2) 基本的なラプラス変換・ラプラス変換表
(i) 最低限頭に入れておいたほうがいい公式
魔法の技だって言われても、それを発動する方法がわからければ使いませんね。
同じように、ラプラス変換も最低限の公式を頭に入れておかないと実際に使うことはできません。
そこで、最低限覚える必要がある公式を紹介します。
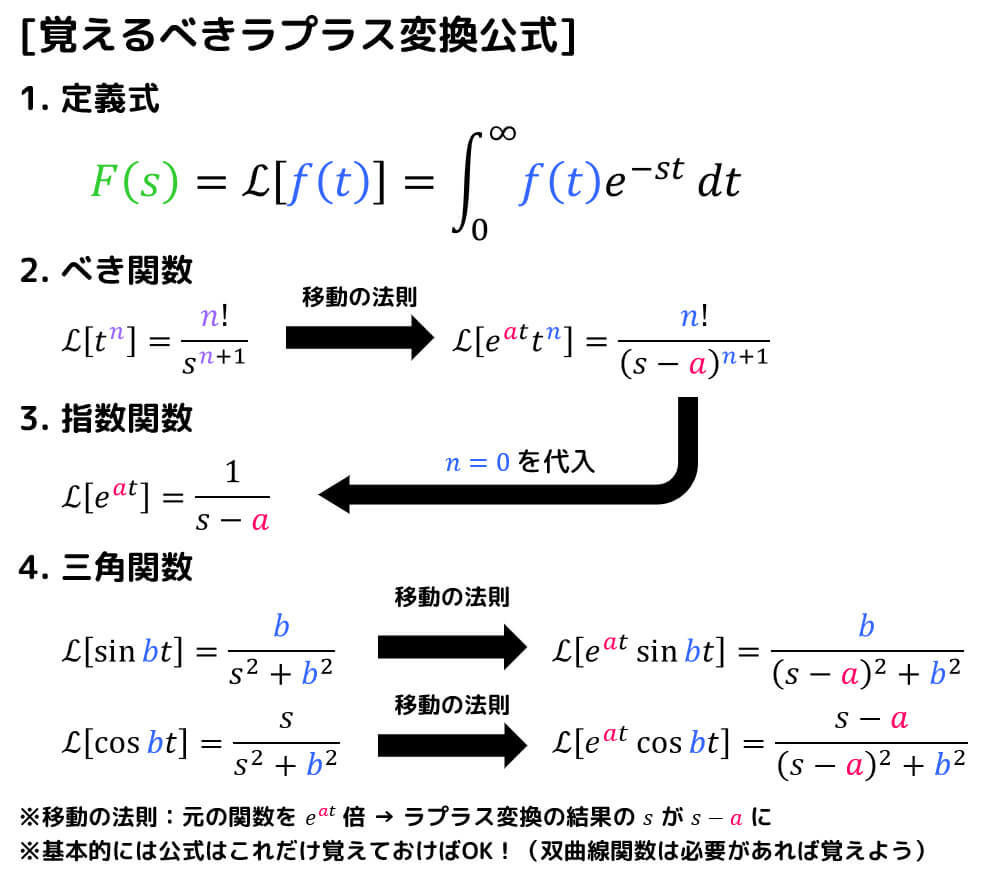
例えば、\( f(t) = e^{\textcolor{red}{2}t} \sin \textcolor{blue}{3} t \) をラプラス変換する場合、上の公式にある\[
\mathcal{L} \left[ e^{\textcolor{red}{a}t} \sin \textcolor{blue}{b} t \right] = \frac{ \textcolor{blue}{b} }{ (s- \textcolor{red}{a} )^2 + \textcolor{blue}{b}^2 }
\]に対して、\( \textcolor{red}{a = 2} , \ \textcolor{blue}{b = 3} \) を代入して、\[
F(s) = \frac{ \textcolor{blue}{3} }{ (s - \textcolor{red}{2} )^2 + \textcolor{blue}{3}^2 }
\]と求めることができます。
(ii) ラプラス変換表の使い方
また、試験によっては下のようにラプラス変換表が与えられていることがあります。
この場合、それぞれの関数 \( f (t) \) をラプラス変換をすると、どのような値になるかを覚える必要はありません。
| 時間関数 \( f(t) \) | ラプラス変換 \( F(s) \) | 時間関数 \( f(t) \) | ラプラス変換 \( F(s) \) |
|---|---|---|---|
| \( 1 \) | \[ \frac{1}{s} \] | \( e^{ \textcolor{red}{a} t} \) | \[ \frac{1}{s- \textcolor{red}{a} } \] |
| \( t^{\textcolor{purple}{n}} \) | \[ \frac{ \textcolor{purple}{n} !}{s^{ \textcolor{ purple }{n} +1}} \] | \( e^{ \textcolor{red}{a} t} t^{\textcolor{ purple }{n} }\) | \[ \frac{ \textcolor{ purple }{n} ! }{ (s- \textcolor{red}{a} )^{ \textcolor{ purple }{n} + 1 } } \] |
| \( \sin \textcolor{blue}{b} t \) | \[ \frac{ \textcolor{blue}{b} }{s^2 + \textcolor{blue}{b}^2 } \] | \( e^{ \textcolor{red}{a} t} \sin \textcolor{blue}{b} t \) | \[ \frac{ \textcolor{blue}{b} }{ (s- \textcolor{red}{a} )^2 + \textcolor{blue}{b}^2 } \] |
| \( \cos \textcolor{blue}{b} t \) | \[ \frac{ s }{s^2 + \textcolor{blue}{b}^2 } \] | \( e^{ \textcolor{red}{a} t} \cos \textcolor{blue}{b} t \) | \[ \frac{ s - \textcolor{red}{a} }{ (s- \textcolor{red}{a} )^2 + \textcolor{blue}{b}^2 } \] |
ただし、試験前にラプラス変換表の使い方は確認しておきましょう。
例えば、上の表から \( f(t) = t^3 \) のラプラス変換を求める場合、 \( f(t) \) から \( t^{ \textcolor{purple}{n} } \) を探し、その右隣にある値に \( \textcolor{purple}{n = 3} \) を代入して\[\begin{align*}
F(s) & = \frac{ \textcolor{purple}{3} !}{s^{ \textcolor{ purple }{3} +1}}
\\ & = \frac{6}{s^4}
\end{align*}\] と求めることができます。
なお、PDF版のラプラス変換表がもしほしい方がいらっしゃれば、下からダウンロードをしてください!
スポンサードリンク
3. 動的システムと伝達関数
動的システムの入出力をラプラス変換上の値で表現したものを伝達関数と呼びます。
といきなり日本語で言われてもよくわからないと思うので、伝達関数がどのように定義されているかを、例題を使いながら見ていきましょう!
下の式で表されるような振る舞いをする動的システムがある。\[
\frac{d^2 y}{dt^2} - 4 \frac{dy}{dt} + 3y = u
\]ここで、入力を \( u = u(t) \)、出力を \( y = y(t) \) とする。このときの伝達関数 \( H(z) \) を求めなさい。
[解説1]
まずは、両辺をラプラス変換しましょう。ここで、入力 \( u = u(t) \) をラプラス変換した結果を \( U(s) \)、出力 \( y = y(t) \) をラプラス変換した結果を \( Y(s) \) とおきます。
さらに、左辺、右辺の項を線形の法則を用いてバラバラにします。\[\begin{align*}
\mathcal{L} \left[ \frac{d^2 y}{dt^2} - 4 \frac{dy}{dt} + 3y \right] & = \mathcal{L} \left[ u \right] \\
\mathcal{L} \left[ \frac{d^2 y}{dt^2} \right] - 4 \mathcal{L} \left[ \frac{d y}{dt } \right] + 3 \mathcal{L} \left[ y \right] & = \mathcal{L} \left[ u \right] \\
s^2 Y(s) - 4 s Y(s) + 3 Y(s) & = U(s) \\
(s^2 - 4s + 3) Y(s) & = U(s)
\end{align*}\]
最後に、\( Y(s) = \cdots \) の関係にしましょう。\[
Y(s) = \frac{1}{s^2 - 4s + 3} U(s)
\]
どうでしょう、元々は微分方程式という難しい方程式で表されていた動的システムが、ラプラス変換上では \( Y(s) = \cdots \) のように、ただの方程式で表すことができましたね!
ここで、ラプラス変換上で表される出力 \( Y(s) \) に対して、入力 \( U(s) \) との関係を表現した関数のことを伝達関数と呼び、\( G(s) \) で表されます。

ラプラス変換上にて、出力 \( Y(s) \) に対する入力 \( U(s) \) との関係を下のように表した関数を伝達関数と呼び、\( G(s) \) で表す。\[
Y(s) = G(s) U(s) , \ \ \ G(s) = \frac{Y(s)}{U(s)}
\]
4. インパルス応答とステップ応答
3章では、ラプラス変換上による入力 \( U(s) \) と出力 \( Y(s) \) の関係を表す伝達関数 \( G(s) \) について見ていきました。
ただし、ラプラス変換上にて入出力の関係を表されても、少しよくわかりませんよね。我々が知りたいのはラプラス変換する前の世界線(実世界線上と呼びましょう)における入力 \( u(t) \) と出力 \( y(t) \) の関係ですよね[2] … Continue reading。
そこで、動的システムの振る舞いをラプラス変換上でなく、実世界線上の値で把握するために使われるインパルス応答とステップ応答について見ていきましょう。
(1) インパルス応答
まずは、インパルス応答から見ていきましょう。
(i) (単位)インパルス関数 [デルタ関数] とは
インパルス応答では、下のように定義されるちょっと不思議な関数である(単位)インパルス関数(別名:デルタ関数)\( \delta (t) \) を使います。高校数学ではもちろん、大学1年生の解析学でも登場しない不思議な関数です。\[
\int^{\infty}_{- \infty} \delta(t) g(t) = g(0)
\]
この(単位)インパルス関数は、下のように \( t = 0 \) のときに非常に大きな値を取り、それ以外のときは0になる関数のことです。
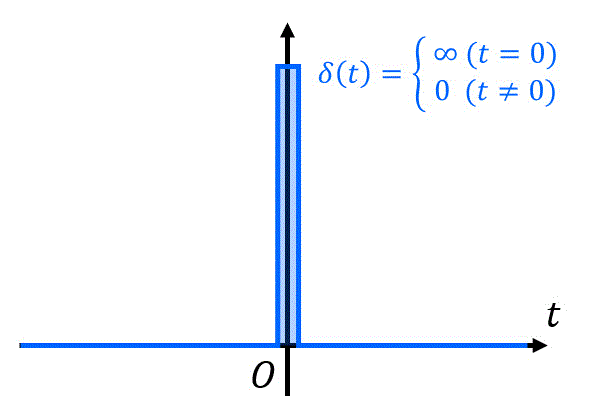
この関数の大きな特徴として、実数領域全体(負の無限大から正の無限大まで)積分をすると、1になるという特徴があります。
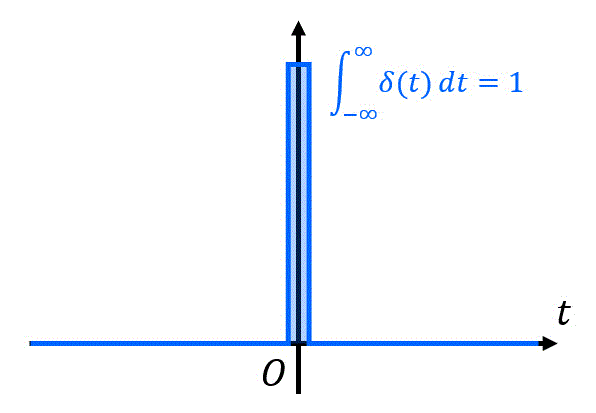
なお、積分範囲は \( t = 0 \) が含まれていれば \( - \infty \to \infty \) でなくてもOKです。例えば微小な正の値を \( \varepsilon \) として、\[
\int^{\varepsilon}_{- \varepsilon} \delta (t) = 1
\]なども成り立ちます。
(ii) (単位)インパルス関数をラプラス変換すると…
次に(単位)インパルス関数をラプラス変換してみましょう。
ラプラス変換の定義は\[
F(s) = \int^{\infty}_{0} f(t) e^{-st} \ dt
\]でしたね。
ここで、\( \textcolor{magenta}{ f(t) = \delta (t) } \), \( \textcolor{deepskyblue}{g(t) = e^{-st} } \) とし、微小な正の数を \( \varepsilon \) としてから計算をしましょう。
すると、\[\begin{align*}
F(s) & = \int^{\infty}_{0} \textcolor{magenta}{f(t)} \textcolor{deepskyblue}{ e^{-st} } \ dt
\\ & = \lim_{ \varepsilon \to +0} \int^{\infty}_{- \varepsilon} \textcolor{magenta}{\delta (t) } \textcolor{deepskyblue}{ g(t) } \ dt
\\ & = g(0)
\\ & = e^{-s \cdot 0}
\\ & = e^0
\\ & = 1
\end{align*}\]と計算できますね。
つまり、(単位)インパルス関数は、ラプラス変換をすると1になる不思議な関数であることが確認できましたね!
(iii) インパルス応答の計算方法
単位インパルス応答とは、入力 \( u(t) \) に単位インパルス関数を入れたときの出力される値 \( y(t) \) を指しています。
ここで、単位インパルス関数 \( u(t) = \delta (t) \) をラプラス変換すると \( U(s) = 1 \) となるため、\[\begin{align*}
Y(s) & = G(s) U(s)
\\ & = G(s)
\end{align*}\]となり、出力 \( Y(s) \) は伝達関数 \( G(s) \) と全く同じになるといえますね。
そのため、\( G(s) \) を逆ラプラス展開して実世界線上に戻してあげることで、出力 \( y(t) \)、つまりインパルス応答がわかります。
単位インパルス関数 \( \delta (t) \) は、ラプラス変換の結果が1となる不思議な関数である。
また、この(単位)インパルス関数 [デルタ関数] \( \delta (t) \) を入力 \( u(t) \) としたときの出力 \( y(t) \) をインパルス応答と呼び、伝達関数 \( G(s) \) を逆ラプラス変換することで求めることができる。
(2) ステップ応答
続いてステップ応答も見てきましょう。
(i) (単位)ステップ応答
(単位)ステップ関数は、下のように \( t \) が正(or 0)のときは1、それ以外(負)のときは0を持つ関数で、\( u_s (t) \) と書きます[3] \( u(t) \) と書くと、入力変数 \( u(t) \) と間違えてしまうため、添え字 \( s \) を加えて \( u_s (t) \) と表記しています。。
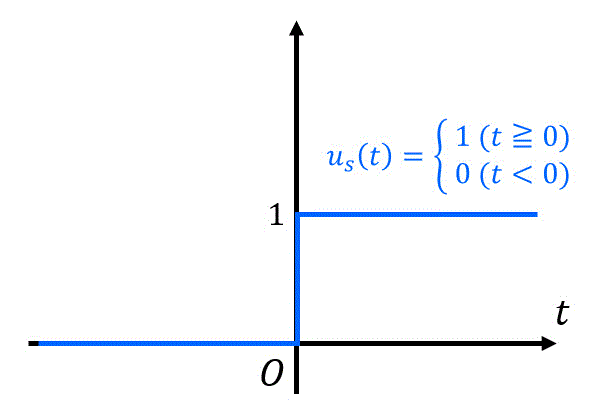
単位ステップ応答 \( f(t) = u_s (t) \) のラプラス変換 \( F(s) \) は、定義に従って下のように計算することができます。\[\begin{align*}
F(s) &= \int^{\infty}_{0} f(t) e^{-st} \ dt
\\ & = \int^{\infty}_{0} u_s (t) e^{-st} \ dt
\\ & = \int^{\infty}_{0} 1 \cdot e^{-st} \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} e^{-st} \ dt
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{s} e^{-st} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left( - \frac{1}{s} ( \underbrace{e^{-sR}}_{ \mathrm{0} \ に収束 } - 1 ) \right)
\\ & = \frac{1}{s}
\end{align*}\]
(ii) ステップ応答の計算方法
ステップ応答とは、入力 \( u(t) \) に(単位)ステップ関数を入れたときの出力される値 \( y(t) \) を指しています。
ここで、(単位)ステップ関数 \( ( u(t) = u_s (t) \) をラプラス変換すると、\( U(s) = 1/s \) となるのでしたね。よって、\[\begin{align*}
Y(s) & = G(s) U(s)
\\ & = \frac{1}{s} G(s)
\end{align*}\]となるため、出力 \( Y(s) \) は、伝達関数 \( G(s) \) を \( s \) で割ったものに等しくなりますね。
そのため、\( G(s)/s \) を計算し、逆ラプラス変換を行うことでステップ応答をを求めることができます。
単位ステップ関数 \( u_s (t) \) は、負のときに値を持たず、0もしくは正のときに値が1となる関数であり、ラプラス変換を行うと \( 1/s \) となる。
また、この(単位)ステップ関数 \( u_s (t) \) を入力 \( u(t) \) としたときの出力 \( y(t) \) をステップ応答と呼び、伝達関数を \( s \) で割ったもの \( G(s)/s \) を逆ラプラス変換することで求めることができる。
(3) (単位)ランプ応答
(i) (単位)ランプ応答
(単位)ランプ関数は、下のように \( t \) が正(or 0)のときは1、それ以外(負)のときは0を持つ関数で、\( r (t) \) と書きます。
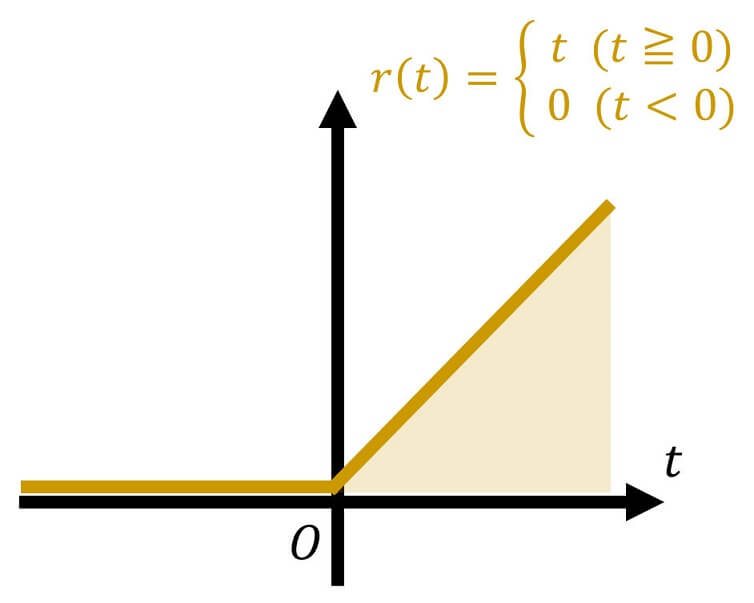
単位ランプ応答のラプラス変換 \( F(s) \) は定義に従って計算することもできますが、素直にラプラス変換表の\[
\mathcal{L} [ t^{ \textcolor{purple}{n}} ] = \frac{ \textcolor{purple}{n} !}{s^{ \textcolor{ purple }{n} +1}}
\]に、\( n = 1 \) を代入してから、\[\begin{align*}
F(s) &= \int^{\infty}_{0} r(t) e^{-st} \ dt
\\ & = \frac{\textcolor{purple}{1} !}{ s^{\textcolor{purple}{1}} +1}
\\ & = \frac{1}{s^2}
\end{align*}\]と求めた方がより早く単位ランプ応答のラプラス変換を求めることができます。
(ii) ランプ応答の計算方法
ランプ応答とは、入力 \( u(t) \) に(単位)ランプ関数を入れたときの出力される値 \( y(t) \) を表します。
ここで、(単位)ランプ関数 \( ( u(t) = r (t) \) をラプラス変換すると、\( U(s) = 1/s^2 \) となるのでしたね。
よって、\[\begin{align*}
Y(s) & = G(s) U(s)
\\ & = \frac{1}{s^2} G(s)
\end{align*}\]となるため、出力 \( Y(s) \) は、伝達関数 \( G(s) \) を \( s^2 \) で割ったものに等しくなりますね。
そのため、\( G(s)/s^2 \) を計算し、逆ラプラス変換を行うことでランプ応答をを求めることができます。
(4) 例題で確認!
インパルス応答とステップ応答についてさらに理解を深めるため、ここで例題を見ていきましょう。
以下の伝達関数 \( G(s) \) の振る舞いをする動的システムがある。\[
G(s) = \frac{1}{s^2 - 4s + 3}
\]次の(1), (2)の問いに答えなさい。
(1) インパルス応答を求めなさい。
(2) ステップ応答を求めなさい。
(3) ランプ応答を求めなさい。
[解答2]
(1) [インパルス応答]
インパルス応答なので、単位インパルス関数を入力としたときの出力を求めればOK。ここで、単位インパルス関数のラプラス変換は1、つまり \( U(s) = 1 \) なので、出力をラプラス変換したもの \( Y(s) \) は、\[\begin{align*}
Y(s) & = G(s) U(s)
\\ & = G(s)
\\ & = \frac{1}{s^2 - 4s + 3}
\\ & = \frac{1}{(s-1)(s-3)}
\end{align*}\]となる。この \( Y(s) \) を逆ラプラス変換すれば出力を求めることができる。
ここで、\[
\frac{1}{(s-1)(s-3)} = \frac{a}{s-1} + \frac{b}{s-3}
\]と部分分数分解をすることを考える。両辺を \( (s-1)(s-3) \) 倍すると、\[
1 = a (s-3) + b (s-1)
\]となる。ここで、片方の括弧の中身を0にしてから \( a \), \( b \) の値を求める。
- \( s = 1 \) を代入 → \( 1 = -2a \) より、\( a = -1/2 \)
- \( s = 3 \) を代入 → \( 1 = 2b \) より、\( b = 1/2 \)
と係数を求めることができるため、\[\begin{align*}
\frac{1}{(s-1)(s-3)} & = \frac{ - \frac{1}{2} }{s-1} + \frac{ \frac{1}{2} }{s-3 }
\\ & = \frac{1}{2} \cdot \frac{1}{s-3} - \frac{1}{2} \cdot \frac{1}{s-1}
\end{align*}\]と部分分数分解ができる。
よって、インパルス応答は\[\begin{align*}
y(t) & = \mathcal{L}^{-1} \left[ Y(s) \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{s^2 - 4s + 3} \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{2} \cdot \frac{1}{s-3} - \frac{1}{2} \cdot \frac{1}{s-1} \right]
\\ & = \frac{1}{2} \mathcal{L}^{-1} \left[ \frac{1}{s-\textcolor{red}{3}} \right] - \frac{1}{2} \mathcal{L}^{-1} \left[ \frac{1}{s-\textcolor{red}{1}} \right]
\\ & = \frac{1}{2} e^{\textcolor{red}{3}t} + \frac{1}{2} e^{\textcolor{red}{1}t}
\\ & = \frac{1}{2} e^{3t} - \frac{1}{2} e^{t}
\end{align*}\]と求められる。
※ 最後に初期条件 \( y(0) = 0 \) を確認することで、あっているかを検算することができます。
(2) [ステップ応答]
ステップ応答なので、単位ステップ関数を入力としたときの出力を求めればOK。ここで、単位ステップ関数のラプラス変換は \( 1/s \) 、つまり \( U(s) = 1/s \) なので、出力をラプラス変換したもの \( Y(s) \) は、\[\begin{align*}
Y(s) & = G(s) U(s)
\\ & = \frac{1}{s} G(s)
\\ & = \frac{1}{s(s^2 - 4s + 3)}
\\ & = \frac{1}{s(s-1)(s-3)}
\end{align*}\]となる。この \( Y(s) \) を逆ラプラス変換すれば出力を求めることができる。
ここで、\[
\frac{1}{s(s-1)(s-3)} = \frac{a}{s} + \frac{b}{s-1} + \frac{c}{s-3}
\]と部分分数分解をすることを考える。両辺を \( s(s-1)(s-3) \) 倍すると、\[
1 = a(s-1)(s-3) + b s(s-3) + c s(s-1)
\]となる。ここで、 1つの項以外の値を0にしてから \( a \), \( b \), \( c \) の値を求める。
- \( s = 0 \) を代入 → \( 1 = 3a \) より、\( a = 1/3 \)
- \( s = 1 \) を代入 → \( 1 = -2b \) より、\( b = -1/2 \)
- \( s = 3 \) を代入 → \( 1 = 6c \) より、\( c = 1/6 \)
と係数を求めることができるため、\[\begin{align*}
\frac{1}{s(s-1)(s-3)} & = \frac{ \frac{1}{3} }{s} + \frac{ - \frac{1}{2} }{s-1} + \frac{ \frac{1}{6} }{s-3 }
\\ & = \frac{1}{3} \cdot \frac{1}{s} - \frac{1}{2} \cdot \frac{1}{s-1} + \frac{1}{6} \cdot \frac{1}{s-3}
\end{align*}\]と部分分数分解ができる。
よって、ステップ応答は\[\begin{align*}
y(t) & = \mathcal{L}^{-1} \left[ Y(s) \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{s(s^2 - 4s + 3)} \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{3} \cdot \frac{1}{s} - \frac{1}{2} \cdot \frac{1}{s-1} + \frac{1}{6} \cdot \frac{1}{s-3} \right]
\\ & = \frac{1}{3} \mathcal{L}^{-1} \left[ \frac{1}{s} \right] - \frac{1}{2} \mathcal{L}^{-1} \left[ \frac{1}{s-\textcolor{red}{1}} \right] + \frac{1}{6} \mathcal{L}^{-1} \left[ \frac{1}{s-\textcolor{red}{3}} \right]
\\ & = \frac{1}{3} - \frac{1}{2} e^{\textcolor{red}{1}t} + \frac{1}{6} e^{\textcolor{red}{3}t}
\\ & = \frac{1}{3} - \frac{1}{2} e^{t} + \frac{1}{6} e^{3t}
\end{align*}\]と求められる。
(3) [ランプ応答]
ランプ応答なので、単位ランプ関数 \( r(t) \) を入力としたときの出力を求めればOK。
ここで、単位ランプ関数のラプラス変換は \( 1/s^2 \) 、つまり \( U(s) = 1/s^2 \) となる。
よって、出力をラプラス変換したもの \( Y(s) \) は、\[\begin{align*}
Y(s) & = G(s) U(s)
\\ & = \frac{1}{s^2} G(s)
\\ & = \frac{1}{s^2(s^2 - 4s + 3)}
\\ & = \frac{1}{s^2(s-1)(s-3)}
\end{align*}\]となる。この \( Y(s) \) を逆ラプラス変換すれば出力を求めることができる。
ここで、\[
\frac{1}{s^2(s-1)(s-3)} = \frac{a}{s} + \frac{b}{s^2} + \frac{c}{s-1} + \frac{d}{s-3}
\]と部分分数分解をすることを考える。両辺を \( s^2(s-1)(s-3) \) 倍すると、\[
1 = a \ s(s-1)(s-3) + b \ (s-1)(s-3) + c s^2(s-3) + d s^2 (s-1)
\]となる。ここで、 1つの項以外の値を0にしてから \( a \), \( b \), \( c \), \( d \) の値を求める。
- \( s = 0 \) を代入 → \( 1 = 3b \) より、\( b = 1/3 \)
- \( s = 1 \) を代入 → \( 1 = -2c \) より、\( c = -1/2 \)
- \( s = 3 \) を代入 → \( 1 = 18c \) より、\( d = 1/18 \)
- \( a \) だけはどう頑張っても消せないので、仕方なしに \( s = 2 \) を代入。
すると、\[\begin{align*}
1 & = -2a - b - 4c + 4d
\\ & = -2a - \frac{1}{3} + 2 + \frac{2}{9}
\\ & = -2a + \frac{17}{9}
\end{align*}\]となるため、\( 2a = 8/9 \) となり、\( a = 4/9 \)
と係数を求めることができるため、\[\begin{align*}
\frac{1}{s^2(s-1)(s-3)} & = \frac{ \frac{4}{9} }{s} + \frac{ \frac{1}{3} }{s^2} + \frac{ - \frac{1}{2} }{s-1} + \frac{ \frac{1}{18} }{s-3}
\\ & = \frac{4}{9} \cdot \frac{1}{s} + \frac{1}{3} \cdot \frac{1}{s^2} - \frac{1}{2} \cdot \frac{1}{s-1} + \frac{1}{18} \cdot \frac{1}{s-3}
\end{align*}\]と部分分数分解ができる。
よって、ランプ応答は\[\begin{align*}
y(t) & = \mathcal{L}^{-1} \left[ Y(s) \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{s^2(s^2 - 4s + 3)} \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{4}{9} \cdot \frac{1}{s} + \frac{1}{3} \cdot \frac{1}{s^2} - \frac{1}{2} \cdot \frac{1}{s-1} + \frac{1}{18} \cdot \frac{1}{s-3} \right]
\\ & = \frac{4}{9} \mathcal{L}^{-1} \left[ \frac{1}{s} \right] + \frac{1}{3} \mathcal{L}^{-1} \left[ \frac{1}{s^2} \right] - \frac{1}{2} \mathcal{L}^{-1} \left[ \frac{1}{s-\textcolor{red}{1}} \right] + \frac{1}{18} \mathcal{L}^{-1} \left[ \frac{1}{s-\textcolor{red}{3}} \right]
\\ & = \frac{4}{9} + \frac{1}{3} t - \frac{1}{2} e^{\textcolor{red}{1}t} + \frac{1}{18} e^{\textcolor{red}{3}t}
\\ & = \frac{4}{9} + \frac{1}{3} t - \frac{1}{2} e^{t} + \frac{1}{18} e^{3t}
\end{align*}\]と求められる。
※ 最後に初期条件 \( y(0) = 0 \) を確認することで、あっているかを検算することができます。
※ 部分分数分解の計算に慣れていない人は、こちらの記事にて練習をすることをお勧めします。
(5) インパルス応答、ステップ応答、ランプ応答の関係
インパルス応答、ステップ応答、ランプ応答のすべてを計算すると結構な時間がかかりますよね。そこで、計算量を減らすための工夫をしましょう。
まず、ある関数 \( y(t) \) のラプラス変換を \( F(s) \) とします。すると、\( y(t) \) を \( t \) で1回微分した関数 \( y'(t) \) のラプラス変換は、微分の法則により \( s F(s) \) となるのでしたね。
さらに、\( t \) で2回微分した関数 \( y''(t) \) のラプラス変換は、微分の法則により \( s^2 F(s) \) となるのでしたね。
よって、\[\begin{align*}
\mathcal{L} \left[ y(t) \right] & = F(s) \\
\mathcal{L} \left[ y'(t) \right] & = s F(s) \\
\mathcal{L} \left[ y''(t) \right] & = s^2 F(s)
\end{align*}\]の関係式が成り立ちますね。
さらに、伝達関数を \( G(s) = s^2 F(s) \) としてからインパルス応答、ステップ応答を \( y(t) \) を用いて表してみましょう。
まず、インパルス応答は \( Y(s) = G(s) \) で求められるため、\[\begin{align*}
\mathcal{L}^{-1} \left[ Y(s) \right] & = \mathcal{L}^{-1} \left[ G(s) \right]
\\ & = \mathcal{L}^{-1} \left[ s^2 F(s) \right]
\\ & = y''(t)
\end{align*}\]となりますね。
つぎにステップ応答は \( Y(s) = G(s)/s \) で求められるため、 \[\begin{align*}
\mathcal{L}^{-1} \left[ Y(s) \right] & = \mathcal{L}^{-1} \left[ \frac{1}{s} G(s) \right]
\\ & = \mathcal{L}^{-1} \left[ s F(s) \right]
\\ & = y'(t)
\end{align*}\] となりますね。
さらにランプ応答は \( Y(s) = G(s)/s^2 \) で求められるため、 \[\begin{align*}
\mathcal{L}^{-1} \left[ Y(s) \right] & = \mathcal{L}^{-1} \left[ \frac{1}{s^2} G(s) \right]
\\ & = \mathcal{L}^{-1} \left[ F(s) \right]
\\ & = y(t)
\end{align*}\] となりますね。
この2つに着目すると、
- ランプ応答 \( y(t) \) を時間 \( t \) で微分 → ステップ応答 \( y'(t) \)
- ステップ応答 \( y'(t) \) を時間 \( t \) で微分 → インパルス応答 \( y''(t) \)
となることが分かります。
言い換えると、
- インパルス応答 \( y''(t) \) を時間 \( t \) で積分 → ステップ応答 \( y'(t) \)
- ステップ応答 \( y'(t) \) を時間 \( t \) で積分 → ランプ応答 \( y(t) \)
となります!
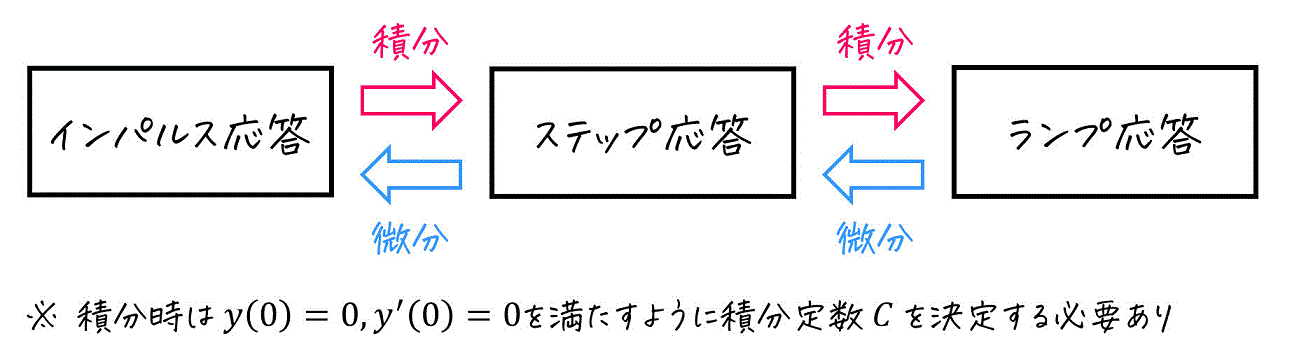
この微分、積分の関係を使うことで、ステップ応答、インパルス応答、ランプ応答のうちの1つを求めることができれば、いちいち部分分数分解しなくても簡単に残りの2つを求めることができるということですね!
※ 積分してステップ応答、ランプ応答を求める際には積分定数 \( C \) の存在に注意! 積分後に \( y(0) = 0 \) となるように積分定数 \( C \) の値を決定する必要があります。
(1) ランプ応答 \( y(t) \) を \( t \) で微分することで、ステップ応答 \( y'(t) \) を得ることができる。また、ステップ応答 \( y'(t) \) を \( t \) で微分することで、インパルス応答 \( y''(t) \) を得ることができる。
(2) インパルス応答 \( y''(t) \) を \( t \) で積分し、初期条件 \( y'(0) = 0 \) に合うように積分定数 \( C \) の値を決定することでステップ応答 \( y'(t) \) を得ることができる。また、ステップ応答 \( y'(t) \) を \( t \) で積分し、初期条件 \( y(0) = 0 \) に合うように積分定数 \( C \) の値を決定することでランプ応答 \( y(t) \) を得ることができる。
以下の伝達関数 \( G(s) \) の振る舞いをする動的システムがある。\[
G(s) = \frac{1}{s^2 - 4s + 3}
\]このシステムのインパルス応答 \( f(t) \) は\[
f(t) = \frac{1}{2} e^{3t} - \frac{1}{2} e^{t}
\]であった。またステップ応答 \( g(t) \) は\[
g(t) = \frac{1}{3} - \frac{1}{2} e^{t} + \frac{1}{6} e^{3t}
\]であった。次の(1), (2), (3)に答えなさい。
(1) ステップ応答を \( t \) で微分するとインパルス応答になることを確認しなさい。
(2) インパルス応答を \( t \) で積分し、初期条件 \( g(0) = 0 \) から積分定数 \( C \) を決定するとステップ応答になることを確認しなさい。
(3) この動的システムのランプ応答を求めなさい。
[解説3]
(1) ステップ応答 \( g(t) \) を \( t \) で微分する。すると、\[\begin{align*}
g'(t) & = - \frac{1}{2} e^t + \frac{1}{2} e^{3t}
\\ & = f(t)
\end{align*}\]となるため、確かに成立することが確認できた。
(2) インパルス応答 \( f(t) \) を \( t \) で積分する。すると、積分定数 \( C \) を用いて\[\begin{align*}
\int f(t) \ dt & = \int \frac{1}{2} e^{3t} - \frac{1}{2} e^{t} \ dt
\\ & = \frac{1}{6} e^{3t} - \frac{1}{2} e^t + C
\end{align*}\]となる。
ここで、\[
\frac{1}{6} e^{3t} - \frac{1}{2} e^t + C = g(t)
\]が成立することを確認すればOK。
\( g(0) = 0 \) なので \( t = 0 \) を代入し、\[\begin{align*}
\frac{1}{6} e^0 - \frac{1}{2} e^0 + C & = g(0)
\\ \frac{1}{6} - \frac{1}{2} + C & = 0
\\ C & = \frac{1}{3}
\end{align*}\]となるため、\[
\frac{1}{6} e^{3t} - \frac{1}{2} e^t + \frac{1}{3} = g(t)
\]がなり、確かに題意が成り立つことが確認できた。
(3) ランプ応答は、
- ステップ応答を1回積分
- \( t = 0 \) を代入したときに \( r(0) = 0 \) を満たすように積分定数 \( C \) を代入すること
で求めることができる。
実際にステップ応答 \( g(t) \) を積分すると、積分定数 \( C \) を用いて\[\begin{align*}
\int g(t) \ dt & = \int \frac{1}{3} - \frac{1}{2} e^{t} + \frac{1}{6} e^{3t} \ dt
\\ & = \frac{1}{3} t - \frac{1}{2} e^t + \frac{1}{18} e^{3t} + C
\end{align*}\]と求められる。
あとは、\( r(0) = 0 \) を満たすような積分定数 \( C \) を求めればOK。よって、\[
0 = - \frac{1}{2} + \frac{1}{18} + C
\]より、\[\begin{align*}
C & = + \frac{1}{2} - \frac{1}{18}
\\ & = \frac{8}{18}
\\ & = \frac{4}{9}
\end{align*}\]と決定される。
よって、ランプ応答は、\[
r(t) = \frac{1}{3} t - \frac{1}{2} e^t + \frac{1}{18} e^{3t} + \frac{4}{9}
\]と求められる。(先ほどの例題2の(3)と同じ答えになっていますね)
ステップ応答さえも求まっていれば、積分を用いることでランプ応答を少し簡単に求めることができることがわかりましたね。
5. 練習問題
では、実際に練習問題を解いて、今回の内容を復習しましょう。
下の式で表されるような振る舞いをする動的システムがある。\[
\frac{d^2 y}{dt^2} + 4 \frac{dy}{dt} + 13y = \frac{du}{dt} - 7u
\]ここで、入力を \( u = u(t) \)、出力を \( y = y(t) \) とする。次の問いに答えなさい。
(1) 伝達関数 \( G(s) \) を求めなさい。
(2) 入力を単位インパルス関数 \( u(t) = \delta (t) \) としたときの出力(インパルス応答)を求めなさい。
(3) 入力を単位ステップ関数 \( u(t) = u_s (t) \) としたときの出力(ステップ応答)を求めなさい。
(1)
両辺をラプラス変換して、\( Y(s) = G(s) U(s) \) の形にしましょう。
\[\begin{align*}
\mathcal{L} \left[ \frac{d^2 y}{dt^2} + 4 \frac{dy}{dt} + 13y \right] & = \mathcal{L} \left[ \frac{du}{dt} - 7 \right] \\
\mathcal{L} \left[ \frac{d^2 y}{dt^2} \right] + 4 \mathcal{L} \left[ \frac{dy}{dt} \right] + 13 \mathcal{L} \left[ y \right] & = \mathcal{L} \left[ \frac{du}{dt} \right] - 7 \mathcal{L} \left[ y \right] \\
s^2 Y(s) + 4 s Y(s) + 13 Y(s) & = s U(s) - 7 U(s) \\
(s^2 + 4s + 13) Y(s) & = (s-7) U(s)
\end{align*}\]となるため、\[
Y(s) = \frac{s-7}{s^2 + 4s + 13} U(s)
\]と変形できる。よって、伝達関数 \( G(s) \) は、\[
G(s) = \frac{s-7}{s^2 + 4s + 13}
\]と求められる。
(2)
単位インパルス関数を入力とするので、\( U(s) = 1 \) のときの出力 \( Y(s) = G(s) \) を逆ラプラス変換すればOK。
最初に \( s^2 + 4s + 13 \) を因数分解しようと考えるが、うまく因数分解ができないので方針を変える。
ここで\[\begin{align*}
G(s) & = \frac{s-7}{s^2 + 4s + 13}
\\ & = \frac{s-7}{(s+2)^2 + 9}
\\ & = \frac{s-7}{(s+2)^2 + 3^2}
\\ & = \frac{\textcolor{orange}{s+2} }{(\textcolor{orange}{s+2})^2 + 3^2} - \frac{\textcolor{green}{3^2}}{(s+2)^2 + \textcolor{green}{ 3^2 }}
\\ & = \frac{ s-(\textcolor{red}{-2}) }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } - 3 \cdot \frac{ \textcolor{blue}{3} }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 }
\end{align*}\]と変形できる。
さらに、\[
\mathcal{L}^{-1} \left[ \frac{ s-(\textcolor{red}{-2}) }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right] = e^{\textcolor{red}{-2}t} \cos \textcolor{blue}{3} t
\]\[
\mathcal{L}^{-1} \left[ \frac{ \textcolor{blue}{3} }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right] = e^{\textcolor{red}{-2}t} \sin \textcolor{blue}{3} t
\]と逆ラプラス変換が計算できることを利用する。
よって、\[\begin{align*}
y(t) & = \mathcal{L}^{-1} \left[ Y(s) \right]
\\ & = \mathcal{L}^{-1} \left[ G(s) \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{s-7}{s^2 + 4s + 13} \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{ s-(\textcolor{red}{-2}) }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } - 3 \cdot \frac{ \textcolor{blue}{3} }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{ s-(\textcolor{red}{-2}) }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right] - 3 \mathcal{L}^{-1} \left[ \frac{ \textcolor{blue}{3} }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right]
\\ & = e^{\textcolor{red}{-2}t} \cos \textcolor{blue}{3} t - 3 e^{\textcolor{red}{-2}t} \sin \textcolor{blue}{3} t
\\ & = e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) \end{align*}\]と計算できる。
(3)
[方針1:普通に計算する]
単位ステップ関数を入力とするので、\( U(s) = 1/s \) のときの出力 \( Y(s) = G(s)/s \) を逆ラプラス変換すればOK。
ここで、\[
\frac{s-7}{s(s^2 + 4s + 13)} = \frac{a}{s} + \frac{bs + c}{s^2+4s+13}
\]と部分分数分解をすることを考える。両辺を \( s(s^2 + 4s + 13) \) 倍すると、\[
s-7 = a (s^2 + 4s + 13) + (bs+c) s \tag{a}
\]となる。ここで、 1つの項以外の値を0にしてから \( a \), \( b \), \( c \) の値を求める。
- \( s = 0 \) を代入 → \( -7 = 13a \) より、\( a = -7/13 \)
ここで、(a)式の両辺を微分を微分しても恒等式は成立する。実際に微分をすると、\[
1 = a (2s+4) + 2bs + c
\]となる。
- \( s = 0 \) を代入 → \( 4a + c = 1 \) → \( c = 1-4a = 41/13 \)
- \( s = -2 \) を代入 → \( -4b + c = 1 \) → \( b = (c-1)/4 = 7/13 \)
と係数を求めることができるため、\[\begin{align*}
\frac{1}{s(s^2+4s+13)} & = \frac{- \frac{7}{13} }{s} + \frac{ \frac{7}{13} s + \frac{41}{13} }{s^2+4s+13}
\\ & = - \frac{7}{13} \cdot \frac{1}{s} + \frac{1}{13} \cdot \frac{7s+41}{s^2+4s+13}
\\ & = - \frac{7}{13} \cdot \frac{1}{s} + \frac{1}{13} \cdot \frac{7(s+2)}{(s+2)^2+3^2} + \frac{1}{13} \cdot \frac{27}{(s+2)^2+3^2}
\\ & = - \frac{7}{13} \cdot \frac{1}{s} + \frac{7}{13} \cdot \frac{\textcolor{orange}{s+2}}{(\textcolor{orange}{s+2})^2+3^2} + \frac{9}{13} \cdot \frac{\textcolor{green}{3}}{(s+2)^2+ \textcolor{green}{3}^2}
\end{align*}\]と分解ができる。
よって、\[\begin{align*}
y(t) & = \mathcal{L}^{-1} \left[ Y(s) \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{s} G(s) \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{s-7}{s(s^2 + 4s + 13)} \right]
\\ & = \mathcal{L}^{-1} \left[ - \frac{7}{13} \cdot \frac{1}{3} + \frac{7}{13} \frac{ s-(\textcolor{red}{-2}) }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } + \frac{9}{13} \cdot \frac{ \textcolor{blue}{3} }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right]
\\ & = - \frac{7}{13} \mathcal{L}^{-1} \left[ \frac{1}{s} \right] + \frac{7}{13} \mathcal{L}^{-1} \left[ \frac{ s-(\textcolor{red}{-2}) }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right] + \frac{9}{13} \mathcal{L}^{-1} \left[ \frac{ \textcolor{blue}{3} }{ (s - (\textcolor{red}{-2}) )^2 + \textcolor{blue}{3}^2 } \right]
\\ & = - \frac{7}{13} + \frac{7}{13} e^{\textcolor{red}{-2}t} \cos \textcolor{blue}{3} t + \frac{9}{13} e^{\textcolor{red}{-2}t} \sin \textcolor{blue}{3} t
\\ & = \frac{1}{13} e^{-2t} \left( 7 \cos 3 t + 9 \sin 3t - 7 \right) \end{align*}\]と計算できる。
[方針2:インパルス応答を積分する]
インパルス応答を積分し、初期条件 \( y(0) = 0 \) を満たすように積分定数 \( C \) を決定すればステップ応答が求められることを利用する。
ここで、インパルス応答を \( y'(t) \) とすると、\[
y'(t) = e^{-2t} \left( \cos 3 t - 3 \sin 3t \right)
\]となる。
これを積分したものがステップ応答 \( y(t) \) となる。
ここで部分積分を2回適用する。\[\begin{align*}
y(t) & = \int e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) \ dt
\\ & = \frac{1}{-2} e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) - \int \frac{1}{-2} e^{-2t} \left( - 3 \sin 3 t - 9 \cos 3t \right) \ dt
\\ & = - \frac{1}{2} e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) + \int \frac{-3}{2} e^{-2t} \left( \sin 3 t + 3 \cos 3t \right) \ dt
\\ & = - \frac{2}{4} e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) + \frac{3}{4} e^{-2t} \left( \sin 3 t + 3 \cos 3t \right) - \int \frac{3}{4} e^{-2t} \left( 3 \cos 3 t - 9 \sin 3t \right) \ dt
\\ & = \frac{1}{4} \left( 9 \sin 3x + 7 \cos 3x \right) - \frac{9}{4} \int e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) \ dt
\end{align*}\]すると、\[
\frac{13}{4} \int e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) \ dt = \frac{1}{4} \left( 9 \sin 3x + 7 \cos 3x \right)
\]の関係式が成り立つため、積分結果は以下のようになる。\[\begin{align*}
\int e^{-2t} \left( \cos 3 t - 3 \sin 3t \right) \ dt & = \frac{1}{13} e^{-2t} \left( 9 \sin 3x + 7 \cos 3x \right) + C
\\ & = y(t)
\end{align*}\]※ただし \( C \) は積分定数。
ここで、初期条件 \( y(0) = 0 \) を満たすような \( C \) を求める。すると、\[\begin{align*}
\frac{1}{13} e^{-2 \cdot 0 } \left( 9 \sin 0 + 7 \cos 0 \right) + C & = 0 \\
\frac{7}{13} + C & = 0 \\
C & = - \frac{7}{13}
\end{align*}\]となるため、ステップ応答 \( y(t) \) は、\[
y(t) = \frac{1}{13} e^{-2t} \left( 9 \sin 3x + 7 \cos 3x \right) - \frac{7}{13}
\]となる。
6. さいごに
今回は、動的システムの振る舞いを確認する手段の中でも、伝達関数、インパルス応答、ステップ応答の3つを中心に説明しました。
次回は、動的システムの安定性について見ていきましょう。それではさようなら。
注釈
| ↑1 | 方程式を解くだけならのお話です。例えば、数式に \( \log_2 x \) などの対数関数が入ると高校数学の数2レベルに、\( e \) が入ると数3レベルに、\( \tan^{-1} x \) などの逆三角関数が入ると大学数学レベルにはなります…。 |
|---|---|
| ↑2 | 例えば、「この商品は10,000ドンです」と言われてもピンときませんよね。できれば、「この商品は50円です」のように、馴染みの深い単位で知りたいですよね。 |
| ↑3 | \( u(t) \) と書くと、入力変数 \( u(t) \) と間違えてしまうため、添え字 \( s \) を加えて \( u_s (t) \) と表記しています。 |
関連広告・スポンサードリンク