うさぎでもわかる信号処理　第05羽　ディジタルシステムの周波数特性・振幅特性・位相特性

2022年5月15日 2022年6月23日 53分28秒

ももうさ

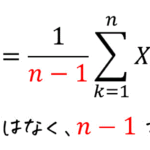
スポンサードリンク

※ ディジタルシステムではなく、動的システムの周波数特性、振幅特性、位相特性について知りたい人は、こちらの記事ではなく、下のリンク先の記事をご覧ください。

うさぎでもわかる信号処理　第05羽　ディジタルシステムの周波数特性・振幅特性・位相特性

こんにちは、ももやまです。

第03羽ではディジタルシステムの基礎として、

ディジタルシステムとはなにか
伝達関数
インパルス応答
任意の入力から出力を求める方法

を勉強しました。（以下のリンクから第03羽の復習ができます。）

また、第04羽では、

ディジタルシステムの極と零点
ディジタルシステムの安定性

を勉強しました。（以下のリンクから第04羽の復習ができます。）

ディジタルシステムに関する記事の最終回である第05羽では、

周波数特性・振幅特性・位相特性について
極、零点と振幅特性の関係
総合演習問題（第03羽～第05羽の復習）

の3種類を勉強していきましょう。

スポンサードリンク

1. 複素数平面の復習

(1) 基本的な複素数計算

周波数特性・振幅特性・位相特性の算出には数3の複素数平面、および応用数学（複素解析）の知識が不可欠です。

なので、1回復習しましょう。

複素数と絶対値・位相

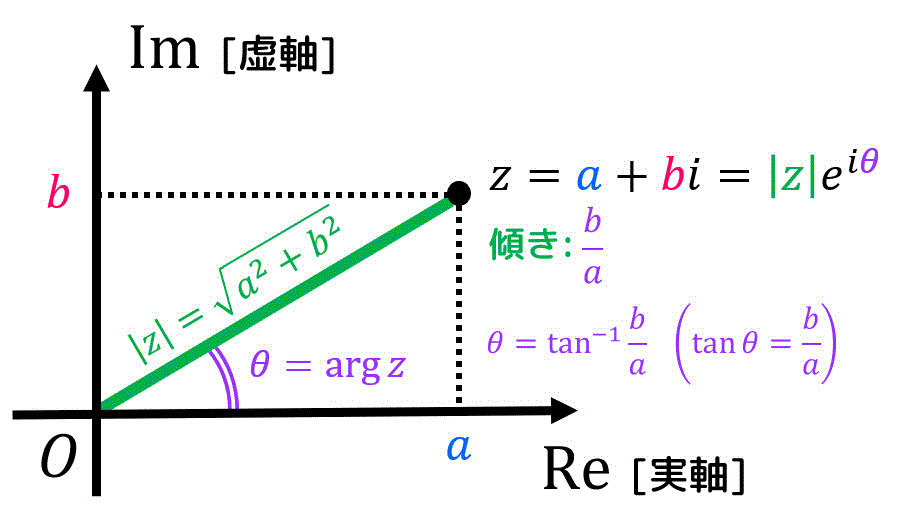
ある複素数 \( z = \textcolor{deepskyblue}{a} + \textcolor{magenta}{b} i \) を下の複素数平面上に図示することを考える。

(1) 絶対値 \( |z| \) \[
|z| = \sqrt{ \textcolor{deepskyblue}{a}^2 + \textcolor{magenta}{b}^2} \geqq 0
\]

(2) 偏角 \( \theta = \arg z \) \[
\tan \theta = \frac{\textcolor{magenta}{b}}{\textcolor{deepskyblue}{a}} , \ \ \ \left( \theta = \tan^{-1} \frac{ \textcolor{magenta}{b} }{ \textcolor{deepskyblue}{a} } \right)
\]

(3) \( e^{i \theta} \) を用いた表現\[
z =|z| e^{i \theta}
\]

(2) 特性を計算する際によく使うテクニック

2つの複素数の積 \( z_1 z_2 \) や商 \( \frac{z_1}{z_2} \)、および逆数 \( \frac{1}{z_1} \) 自体を計算するのは少ししんどいですが、絶対値や偏角であれば簡単に計算ができます。

複素数計算テクニック

ある複素数 \( z_1 \) , \( z_2 \) がある。

[積]\[\begin{align*}
|z_1 z_2| & = |z_1| |z_2| \\
\arg z_1 z_2 & = \arg z_1 + \arg z_2
\end{align*}\] [商]\[\begin{align*}
\left| \frac{z_1}{z_2} \right| & = \frac{ |z_1| }{ | z_2| } \\
\arg \frac{z_1}{z_2} & = \arg z_1 - \arg z_2
\end{align*}\] [逆数]\[\begin{align*}
\left| \frac{1}{z_1} \right| & = \frac{1}{ |z_1| } \\
\arg \frac{1}{z_1} & = - \arg z_1
\end{align*}\]

復習用に問題を1つ用意してみたので、チャレンジしてみましょう。

復習問題1

複素数 \( z_1 = \sqrt{3} + i \) がある。次の(1), (2)の問いに答えなさい。

(1) \( |z_1| \) を求めなさい。
(2) \( \arg z_1 \) を求めなさい。
(3) \( z_1 \) を \( re^{i \theta} \) の形で書きなさい。
(4) \( \arg \frac{1}{z_1} \) を求めなさい。

さらに、複素数 \( z_2 = 1 - i \) とする。

(5) \( |z_1 z_2| \) を計算しなさい。
(6) \( \arg z_1 z_2 \) を計算しなさい。
(7) \( \arg \frac{z_1}{z_2} \) を計算しなさい。

[解説]

(1) \[\begin{align*}
|z_1| & = \sqrt{(\textcolor{deepskyblue}{\sqrt{3}})^2 + \textcolor{magenta}{1}^2}
\\ & = 2
\end{align*}\]

(2) \[\begin{align*}
\arg z_1 & = \tan^{-1} \frac{\textcolor{magenta}{1}}{ \textcolor{deepskyblue}{\sqrt{3}} }
\\ & = \frac{\pi}{6} \left( = 30^{\circ} \right)
\end{align*}\]

(3) \[\begin{align*}
z_1 & = |z_1| e^{i \cdot \arg z}
\\ & = 2 e^{\frac{\pi}{6} i }
\end{align*}\]

(4) \[\begin{align*}
\arg \frac{1}{z_1} & = - \arg z_1
\\ & = - \frac{\pi}{6} \left( = - 30^{\circ} \right)
\end{align*}\]

※ 間違ってもこんなめんどくさい計算しないように。\[\begin{align*}
\frac{1}{\sqrt{3} - i} & = \frac{1(\sqrt{3}-i)}{( \sqrt{3} + i ) ( \sqrt{3} - i ) }
\\ & = \frac{ \sqrt{3} - i }{4}
\end{align*}\]より……。

(5)\[\begin{align*}
|z_2| & = \sqrt{\textcolor{deepskyblue}{1}^2 + \textcolor{magenta}{(-1)}^2}
\\ & = \sqrt{2}
\end{align*}\]より、\[\begin{align*}
|z_1 z_2| & = |z_1| |z_2|
\\ & = 2 \sqrt{2}
\end{align*}\]

(6) \[\begin{align*}
\arg z_2 & = \tan^{-1} \frac{\textcolor{magenta}{-1}}{\textcolor{deepskyblue}{1}}
\\ & = - \frac{\pi}{4} \left( = - 45^{\circ} \right)
\end{align*}\]

より、\[\begin{align*}
\arg z_1 z_2 & = \arg z_1 + \arg z_2
\\ & = - \frac{\pi}{12} \left( = - 15^{\circ} \right)
\end{align*}\]

(7)

\[\begin{align*}
\arg \frac{z_1}{z_2} & = \arg z_1 - \arg z_2
\\ & = \frac{5}{12} \pi \left( = 75^{\circ} \right)
\end{align*}\]

「複素数やオイラーの公式関連の計算をもう少ししたい！」という人は、こちらの記事をご覧ください。

スポンサードリンク

2. 周波数特性と振幅

(1) 周波数特性とは？

ある未知の数列 \( x_n \) があるとします。

この数列がどんな感じのふるまいをするかは、\( n \) に数字を代入していくとある程度予測することができます。例えば、

\( n = 1 \) を代入 → \( x_1 = 1 \)
\( n = 2 \) を代入 → \( x_2 = 3 \)
\( n = 3 \) を代入 → \( x_3 = 5 \)
\( n = 4 \) を代入 → \( x_4 = 7 \)

という結果が得られたとします。すると、この数列 \( x_n \) は、「初項1、交差2の等差数列だな」と予測することができますね。

ディジタルシステムの世界でも同じように、ある値を代入したときの結果からシステムの振る舞いを予測するということをします。

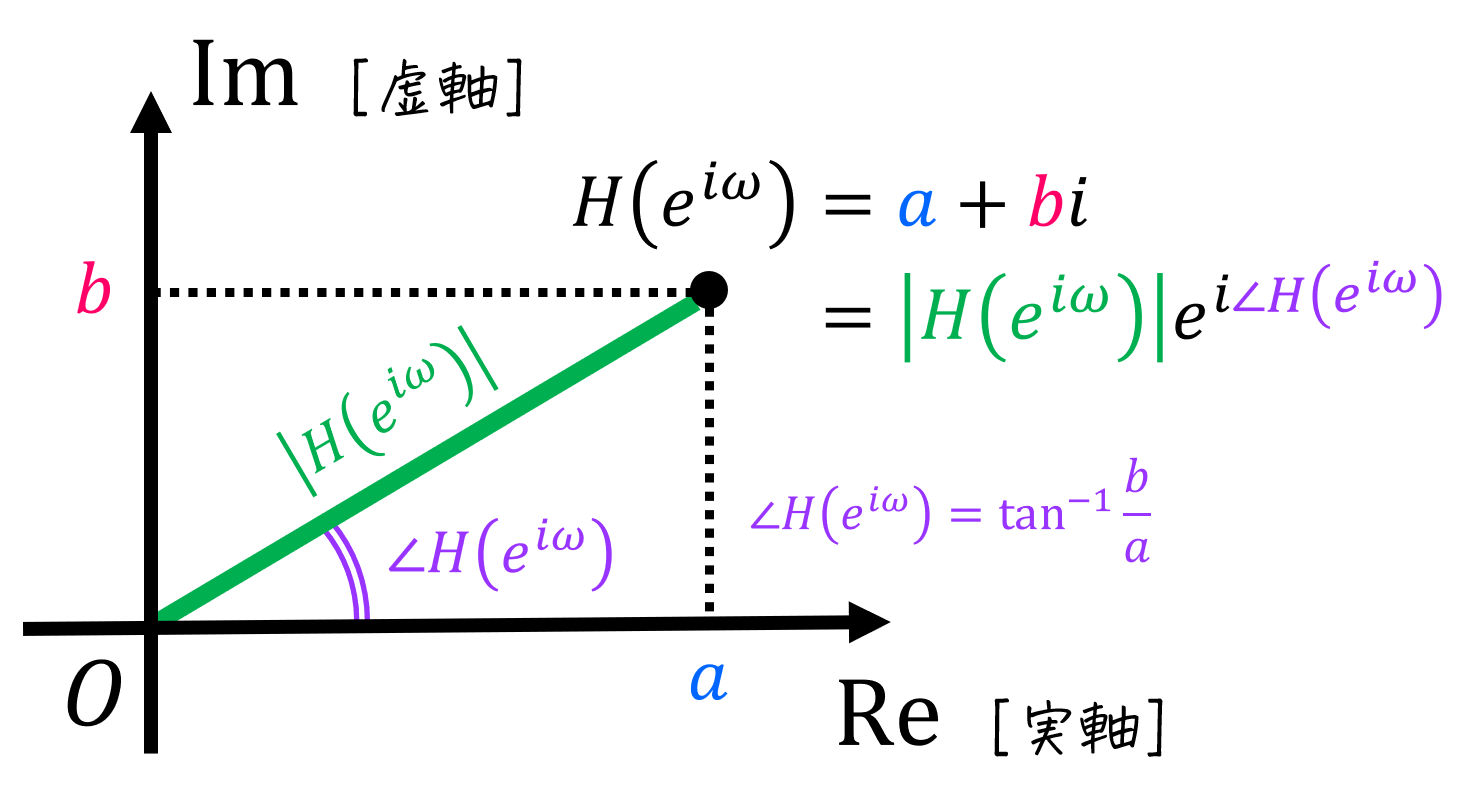
具体的には、伝達関数 \( H(z) \) に大きさ1の周期関数 \( z = e^{i \omega} \) が入力されたときのディジタルシステムの振る舞い、および「振る舞いの強弱」、「振る舞いの位相^[1]1周期の中で、どのタイミングにいるのかを表す。」を調べます。

この、\( z = e^{i \omega} \) が代入された値のことを周波数特性と呼び、ディジタルシステムの振る舞いを表します。

なお、周波数特性は \( H( e^{i \omega}) \) で表記されます。

(2) 振幅特性と位相特性

ディジタルシステムの振る舞い \( H(e^{i \omega} ) \) は、複素数 \( e^{i \omega} \) を代入することにより得られた値なので、実部 \( a \)、虚部 \( b \) に分解した形 \( H(e^{i \omega} ) = a + bi \) で表すことができます。
（※ ただし \( a \), \( b \) は実数）

ここで、ある複素数 \( z = a + bi \) の大きさ \( |z| \)、偏角 \( \angle z \) は\[\begin{align*}
|z| = \sqrt{ a^2 + b^2} \\
\angle z = \tan^{-1} \frac{b}{a} \ \ \ \left( \tan \angle z = \frac{b}{a} \right)
\end{align*}\]で求められるのでしたね。

この \( z \) を \( \( H(e^{i \omega} ) \) に置き換えることで、振る舞いの大きさ \( \( | H(e^{i \omega} ) \) | \) 、および振る舞いの位相 \( \angle H( e^{i \omega} \) を表すことができ、それぞれ振幅特性、位相特性と呼びます。

周波数特性・振幅特性・位相特性

伝達関数 \( H(z) \) に、\( z = e^{i \omega} \) を代入したものを周波数特性と呼び、\( G ( i \omega ) \) で表す。

また、周波数特性を実部 \( a \) と虚部 \( b \) に分解し、\( G ( i \omega ) = a + bi \) とすることで、振幅特性 \( |H ( e^{i \omega} )| \) と位相特性 \( \angle H (e^{i \omega} ) \) に下の計算式で分解できる。\[
|H ( e^{i \omega} )| = \sqrt{ a^2 + b^2}
\]\[
\angle H (e^{i \omega} ) = \tan^{-1} \frac{b}{a} \ \ \ \left( \tan \angle z = \frac{b}{a} \right)
\]

※ 振幅特性は \( |H(e^{i \omega} )| \geqq 0 \) なので、必ず0以上となる
※ 振幅特性、位相特性が \( \omega \) の関数であることを強調するために、振幅特性を \( H ( \omega ) \)、位相特性を \( \angle H ( \omega \) や \( \theta ( \omega ) \) と表記することもあります。

[注意] 不安定なシステムにおいては、周波数特性を考えることができないので注意してください。ただし、期末試験に出てくるディジタルシステムは、ほぼ確実に安定なシステム（周波数特性を考えることができるシステム）なので、単位を取るだけであればそこまで深く考えなくてOKです。

(3) 実際に例題で計算してみよう！

それでは、例題で実際に周波数特性、振幅特性、位相特性を計算してみましょう！

例題1

あるシステム\[
y_n = \frac{1}{3} \left( x_n + x_{n-1} + x_{n-2} \right)
\]について次の問いに答えなさい。

(1) 伝達関数 \( H(z) \) を求めなさい。（第03羽の復習）
(2) 周波数特性 \( H(e^{i \omega}) \) を求めなさい。
(3) 振幅特性 \( \left| H(e^{i \omega}) \right| \)、位相特性 \( \angle H(e^{i \omega}) \) を求めなさい。
(4) 横軸を \( \omega \)、縦軸を \( \left| H(e^{i \omega}) \right| \) とし、\( \omega \) と振幅特性に関するグラフを書きなさい。ただし、図示範囲は \( - \pi \leqq \omega \pi \) の範囲とする。
(5) 横軸を \( \omega \)、縦軸を \( \angle H(e^{i \omega}) \) とし、\( \omega \) と位相に関するグラフを書きなさい。ただし、図示範囲は \( - \pi \leqq \omega \pi \) の範囲とする。

[解説1]

(1)

\( y_n \) をz変換すると、\[\begin{align*}
Y(z) & = \mathcal{Z} \left[ y_n \right]
\\ & = \mathcal{Z} \left[ \frac{1}{3} \left( x_n + x_{n-1} + x_{n-2} \right) \right]
\\ & = \frac{1}{3} \left( \mathcal{Z} \left[ x_n \right] + \mathcal{Z} \left[ x_{n-1} \right] + \mathcal{Z} \left[ x_{n-2} \right] \right)
\\ & = \frac{1}{3} \left( X(z) + z^{-1} X(z) + z^{-2} X(z) \right)
\end{align*}\]

となる。ここで、\[\begin{align*}
Y(z) & = \frac{1}{3} \left( X(z) + z^{-1} X(z) + z^{-2} X(z) \right)
\\ & = \frac{1}{3} \left( 1+z^{-1}+z^{-2} \right)
\end{align*}\]となるため、伝達関数 \( H(z) \) は\[
H(z) = \frac{1}{3} \left( 1+z^{-1}+z^{-2} \right)
\]となる。

(2)

伝達関数に \( z = e^{i \omega} \) を代入するだけ。

ここで \( z^{-1} = e^{- i \omega} \) となるので^[3]ある複素数 \( z \) に対して、\( z^{-1} = \frac{1}{z} \) の偏角は-1倍されるため。もししっくりこない人は実際に複素数平面に図示してみよう。、\[\begin{align*}
H ( e^{i \omega } ) & = \frac{1}{3} \left( 1 + e^{- i \omega} + e^{- 2i \omega} \right)
\\ & = \frac{1}{3} \left( e^{i \omega} + 1 + e^{-i \omega} \right) e^{- i \omega}
\\ & = \frac{1}{3} \left( e^{i \omega} + e^{-i \omega} + 1 \right) e^{- i \omega}
\\ & = \frac{1}{3} ( 2 \cos \omega + 1 ) e^{- i \omega}
\end{align*}\]と計算できる。

※1 次の(3)のために「(実部) \( \times e^{i \theta \)」になるような変形にしております。

※2 オイラーの公式 \( e^{i \theta} = \cos \theta + i \sin \theta \) から以下の2つの式が出てくることは覚えておきましょう。\[
\cos \theta = \frac{1}{2} \left( e^{i \theta} + e^{- i \theta} \right)
\]\[
\sin \theta = \frac{1}{2i} \left( e^{i \theta} - e^{- i \theta} \right)
\]

(3)

(i) [振幅特性 \( |H ( e^{i \omega} )| \) ]

わざわざ \( H ( e^{i \omega} ) = a + bi \) で計算するよりも、\( \left| e^{- i \omega} \right| = 1 \) を使った方が早く求められる。

\[\begin{align*}
\left |H ( e^{i \omega} ) \right| & = \left| \frac{1}{3} ( 2 \cos \omega + 1 ) e^{- i \omega} \right|
\\ & = \frac{1}{3} \left| 2 \cos \omega + 1 \right| \left| e^{- i \omega} \right|
\\ & = \frac{1}{3} \left| 2 \cos \omega + 1 \right|
\end{align*}\]と変形できる。

なお、絶対値を外す場合は「振幅特性 ≧ 0」で場合分けすればOK。

どっちみち(ii)の計算やグラフを書く際に「振幅特性 ≧ 0」か「振幅特性 < 0」で場合分けをすることになるので、ここで計算をしておきましょう。

\[\begin{align*}
\frac{1}{3} ( 2 \cos \omega + 1 ) & \geqq 0 \\
2 \cos \omega + 1 & \geqq 0 \\
\cos \omega & \geqq - \frac{1}{2}
\end{align*}\]より、\( - 2 \pi / 3 \leqq \omega \leqq 2 \pi / 3 \) で \( H ( e^{i \omega} ) \) が正になり、それ以外の範囲（\( - \pi \leqq \omega < - 2 \pi / 3 \), \( 2 \pi / 3 < \omega \leqq \pi \) ）で負となる。

よって、絶対値を外す場合、振幅特性は\[
| H ( e^{i \omega} ) | = \left\{ \begin{array}{ccc} \frac{1}{3} ( 2 \cos \omega + 1 ) & \left( - \frac{2}{3} \pi \leqq \omega \leqq \frac{2}{3} \pi \right) \\
- \frac{1}{3} ( 2 \cos \omega + 1 ) & \left( - \pi \leqq \omega < - \frac{2}{3} \pi, \ \frac{2}{3} \pi < \omega \leqq \pi \right)
\end{array} \right.
\]と書ける。

(ii) [位相特性 \( \angle H ( e^{i \omega} ) \) ]

\( \angle \textcolor{magenta}{z_1} \textcolor{deepskyblue}{z_2} = \angle \textcolor{magenta}{z_1} + \angle \textcolor{deepskyblue}{z_2} \) を使って周波数特性を2つに分解する。

\[\begin{align*}
\angle H \left( e^{i \omega} \right) & = \angle \textcolor{magenta}{\frac{1}{3} ( 2 \cos \omega + 1 )} + \angle \textcolor{deepskyblue}{e^{- i \omega}}
\\ & = \angle \frac{1}{3} ( 2 \cos \omega + 1 ) - \omega
\end{align*}\]となる。

ここで、\[
\frac{1}{3} ( 2 \cos \omega + 1 )
\]は実数なので、0以上であれば位相は0、0未満であれば位相は \( \pi \) ずれて \( \pi \) となる^[4]\( - \pi \) でもOK。位相が \( \pi \) がずれるのがイマイチよくわからない人は、2と-2をそれぞれ複素数平面上に図示してみましょう。。

よって、\[
\angle \frac{1}{3} ( 2 \cos \omega + 1 ) = \left\{ \begin{array}{ccc} 0 & \left( - \frac{2}{3} \pi \leqq \omega \leqq \frac{2}{3} \pi \right) \\
\pi & \left( - \pi \leqq \omega < - \frac{2}{3} \pi, \ \frac{2}{3} \pi < \omega \leqq \pi \right)
\end{array} \right.
\]となるため、位相特性 \( \sigma H( e^{i \omega}) \) は\[
\angle H ( e^{i \omega} ) = \left\{ \begin{array}{ccc} - \omega & \left( - \frac{2}{3} \pi \leqq \omega \leqq \frac{2}{3} \pi \right) \\
\pi- \omega & \left( - \pi \leqq \omega < - \frac{2}{3} \pi, \ \frac{2}{3} \pi < \omega \leqq \pi \right)
\end{array} \right.
\]と計算できます。

\[
- \pi \leqq \omega < - \frac{2}{3} \pi, \ \frac{2}{3} \pi < \omega \leqq \pi
\]において、\[
\frac{1}{3} ( 2 \cos \omega + 1 ) < 0
\]となるため、位相が \( \pi \) ずれる^[5]\( - \pi \) でもOK。。

(4)

\( - \pi \leqq \omega \pi \) の範囲で\[
| H( e^{i \omega} ) | = \frac{1}{3} \left| 2 \cos \omega + 1 \right|
\]を図示しましょう。

(2)で絶対値を外していない人は、\[
H ( e^{i \omega} ) | = \left\{ \begin{array}{ccc} \frac{1}{3} ( 2 \cos \omega + 1 ) & \left( - \frac{2}{3} \pi \leqq \omega \leqq \frac{2}{3} \pi \right) \\
- \frac{1}{3} ( 2 \cos \omega + 1 ) & \left( - \pi \leqq \omega < - \frac{2}{3} \pi, \ \frac{2}{3} \pi < \omega \leqq \pi \right)
\end{array} \right.
\]のように絶対値を外すと図示しやすくなるかもしれません。

(5)

(3)で求めた位相\[
\angle H ( e^{i \omega} ) = \left\{ \begin{array}{ccc} - \omega & \left( - \frac{2}{3} \pi \leqq \omega \leqq \frac{2}{3} \pi \right) \\
\pi- \omega & \left( - \pi \leqq \omega < - \frac{2}{3} \pi, \ \frac{2}{3} \pi < \omega \leqq \pi \right)
\end{array} \right.
\]を（グラフがきれいになるように）少し書き換えましょう^[6]位相は \( 2 \pi \) ずらしても同じ位相になるので、\( - \pi \leqq \omega < - \frac{2}{3} \pi \) となっている部分に \( 2 \pi \) 引いて、\( \frac{2}{3} \pi < \omega … Continue reading。

すると、\[
\angle H ( e^{i \omega} ) = \left\{ \begin{array}{ccc} - \omega & \left( - \frac{2}{3} \pi \leqq \omega \leqq \frac{2}{3} \pi \right) \\
- \pi- \omega & \left( - \pi \leqq \omega < - \frac{2}{3} \pi \right) \\
\pi - \omega & \left( \frac{2}{3} \pi < \omega \leqq \pi \right)
\end{array} \right.
\]と書き換えられます。

あとは、これを \( - \pi \leqq \omega \leqq \pi \) の範囲で横軸 \( \omega \), 縦軸 \( \angle H \left( e^{i \omega} \right) \) のグラフを書けばOKです。

[補足] 振幅特性の定義の仕方の違い

今回の記事では、\( H( e^{i \omega} \) の絶対値 \( | H e^{i \omega} | \) を振幅特性と定義しています。

しかし、この方法で定義すると、例題1(4), (5)のように位相を答える際に場合分けが複雑になり、めんどくさくなることがあります。

そこで、参考書によっては振幅特性に負を認めた\[
H e^{i \omega} = \textcolor{green}{ A (e^{i \omega}) } \angle e^{i \omega}
\]の \( A e^{i \omega} \) を振幅特性として定義しているものもあります。

この方法で定義した場合、例題1の振幅特性 \( A (e^{i \omega}) \)、位相特性 \( \angle H (e^{i \omega} ) \) を\[\begin{align*}
A (e^{i \omega}) & = \frac{1}{3} ( 2 \cos \omega + 1 ) \\
\angle H (e^{i \omega} ) & = - \omega
\end{align*}\]と場合分けなしで答えることができます。

スポンサードリンク

3. 振幅特性と極、零点

(1) 極と零点の復習

振幅特性をいちいち計算するのはちょっとしんどいですが、極と零点を求めることである程度振幅特性を予測することができます。

その前に、まずは極と零点の復習からしましょうか。

復習問題2

つぎの伝達関数\[
H(z) = \frac{1+z^{-2}}{1 + 0.8 z^{-1} + 0.64 z^{-2}}
\]で示されるディジタルシステムがある。

このシステムの極と零点をすべて求め、\( r e^{i \theta} \) の形で表しなさい。

まずは、\( z \) のマイナスの項を消しましょう。\[
\frac{1+z^{-2}}{1 + 0.8 z^{-1} + 0.64 z^{-2}} = \frac{\textcolor{blue}{z^2 + 1}}{\textcolor{red}{z^2 + 0.8 z + 0.64} }
\] [極] 伝達関数の分母部分 \( \textcolor{red}{z^2 + 0.8z + 0.64z} = 0 \) を満たす \( z \)

両辺を25倍し、\( 25z^2 + 20 + 16 = 0 \) を解きます。すると、\[\begin{align*}
z & = \frac{-10 \pm \sqrt{100 - 400}}{25}
\\ & = \frac{-10 \pm \ 10 \sqrt{3} }{25}
\\ & = \frac{4}{5} \left( - \frac{1}{2} \pm \sqrt{3}{2} \right)
\\ & = \frac{4}{5} \cos \left( \pm \frac{2}{3} \pi \right) + i \sin \left( \pm \frac{2}{3} \pi \right)
\\ & = \frac{4}{5} e^{ \pm \frac{2 \pi}{3} i }
\end{align*}\]と求まり、これが極となる。

[零点] 伝達関数の分子部分 \( \textcolor{blue}{z^2 +1} = 0 \) を満たす \( z \)

\( z^2 + 1 = 0 \) は、\( z^2 = -1 \) となりますね。そのため、\[\begin{align*}
z & = \pm i
\\ & = e^{\pm \frac{\pi}{2} i}
\end{align*}\]となり、これが零点となりますね。

極と零点

伝達関数\[
H(z) = \frac{ \textcolor{blue}{ N(z) }{ \textcolor{red}{ D(z) }
\]の極、零点は次のように計算できる。

　極：\( \textcolor{red}{ D(z) } = 0 \) を満たす \( z \)
零点：\( \textcolor{blue}{ N(z) } = 0 \) を満たす \( z \)

※ \( H(z) \) を既約分数の形にしてから極・零点を求めること。例えば、\[
\frac{ z^2 - 1 }{ z^2 - 3z + 2 }
\]であれば、\[\begin{align*}
\frac{ z^2 - 1 }{ z^2 - 3z + 2 } & = \frac{(z+1)(z-1)}{(z-1)(z-2)}
\\ & = \frac{z+1}{z-2}
\end{align*}\]とすること。

(2) 振幅特性と極・零点

例題4に出てくるディジタルシステム\[
H(z) = \frac{1+z^{-2}}{1 + 0.8 z^{-1} + 0.64 z^{-2}}
\]を機械的に図示すると、下のような形になります^[7]実際に計算すると、\[ | H( e^{i \omega} ) | = \frac{ 2 | \cos \omega | }{ \sqrt{ (0.8 \sin \omega + 0.64 \sin 2 \omega )^2 + ( 0.8 \cos \omega + 0.64 \cos 2 \omega + 1)^2 } } … Continue reading。

このグラフと、復習問題で求めた極、零点をもとに「振幅特性と極・零点の関係」を見ていきましょう。

(i) 極

極は \(
\frac{4}{5} e^{ \textcolor{magenta}{ \pm \frac{2 \pi}{3} i } }
\) でしたね。

ここで、\( \omega = \textcolor{magenta}{ \frac{2 \pi}{3} i } \) を見てみると、下の紫の線と黒い線が \( \omega = \pm 2 \pi /3 \) となります。

実際に極となっている \( \omega \) の部分を見てみると、\( | H(e^{i \omega}) | \) がほかの \( \omega \) よりも大きな値（最大とは限らない）となっていますね。

つまり、極を調べることで振幅特性 \( | H(e^{i \omega}) | \) が大きくなる \( \omega \) の位置がある程度予測できるのです！

(ii) 零点

零点は \(
e^{ \textcolor{magenta}{\pm \frac{\pi}{2} } i}
\) でしたね。

ここで、\( \omega = \textcolor{magenta}{ \pm \frac{\pi}{2} i } \) を見てみると、下の紫の線と黒い線が \( \omega = \pm \pi /2 \) となります。

実際に零点となっている \( \omega \) の部分を見てみると、\( | H(e^{i \omega}) | \) が0となっていますね。

つまり、零点を調べることで振幅特性 \( | H(e^{i \omega}) | \) が0になる \( \omega \) の位置が予測できるのです！

振幅特性と極・零点

[極がわかると…]
振幅特性 \( | H (e^{i \omega}) | \) が大きくなるような \( \omega \) をある程度予測できる。

[零点がわかると…]
振幅特性 \( | H (e^{i \omega}) | \) が0になる \( \omega \) をがわかる。

4. 練習問題（総合演習）

では、周波数特性、振幅特性、位相特性を計算する練習をしてみましょう！

さらに、第03羽（伝達関数、インパルス応答）と第04羽（極やゼロ点、システムの安定性）の復習も兼ねています。

練習問題

あるディジタルシステム\[
y_n = \frac{1}{4} y_{n-1} + 2 x_n
\]について次の問いに答えなさい。

(1) 伝達関数 \( H(z) \) を求めなさい。
(2) インパルス応答 \( h_n \) を求めなさい。（ここまで第03羽の復習）
(3) 極、零点があれば求めなさい。複数あればすべて答えること。
(4) このシステムは安定か不安定か。理由と共に答えなさい。（ここまで第04羽の復習）

(5) 周波数特性 \( H(e^{i \omega}) \) を求めなさい。
(6) 振幅特性 \( | H ( e^{i \omega} ) \) を求めなさい。
(7) 位相特性 \( \angle H ( e^{i \omega} ) \) を求めなさい。

5. 練習問題の答え

※ 例題に比べて若干解説を省略気味にしております。ご了承ください。

(1) 伝達関数の計算

いつものように、両辺を \( z \) 変換して、\[
Y(z) = H(z) X(z)
\]の形に持ち込みましょう。

両辺を \( z \) 変換すると、\[\begin{align*}
Y(z) & = \frac{1}{4} z^{-1} Y(z) + 2 X(z) \\
\left( 1 - \frac{1}{4} z^{-1} \right) Y(z) & = 2 X(z) \\
Y(z) & = \underbrace{ \frac{ 2 }{ 1 - \frac{1}{4} z^{-1} } }_{H(z)} X(z)
\end{align*}\]と計算できる。

よって、伝達関数は\[
H(z) = \frac{ 2 }{ 1 - \frac{1}{4} z^{-1} }
\]となる。

(2) インパルス応答の計算

インパルス応答は、伝達関数 \( H(z) \) を逆z変換すればOKですね。

実際に計算すると、\[\begin{align*}
h_n & = \mathcal{Z}^{-1} \left[ H(z) \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{ 2 }{ 1 - \frac{1}{4} z^{-1} } \right]
\\ & = 2 \mathcal{Z}^{-1} \left[ \frac{ 1 }{ 1 - \textcolor{red}{ \frac{1}{4} } z^{-1} } \right]
\\ & = 2 \cdot \left( \textcolor{red}{\frac{1}{4} }\right)^n

\end{align*}\]と計算できる。（ただし \( n \geqq 0 \)）

よって、インパルス応答 \( h_n \) は\[
h_n = \left\{ \begin{array}{ccc} 2 \cdot \left( \frac{1}{4} \right)^n & ( n \geqq 0 ) \\
0 & ( n < 0 )
\end{array} \right.
\]となる。

※ \( n \geqq 0 \) を書きたくない人（場合分けをしたくない人）は、単位インパルス関数 \( u_n \) を用いて\[
h_n = 2 \cdot \left( \frac{1}{4} \right)^n h_n
\]と答えてもOK。

(3) 極・ゼロ点

まず、\( z \) のマイナス乗を消し、さらに分子分母ともに分数が入らないようにする。

すると、\[\begin{align*}
H (z) & = \frac{ 2 }{ 1 - \frac{1}{4} z^{-1} }
\\ & = \frac{ 2z }{ z - \frac{1}{4} }
\\ & = \frac{8z}{4z - 1}
\end{align*}\]となる。

(i) 極

極は、伝達関数 \( H(z) \) の分母部分がとなる \( z \) なので、\( 4z - 1 = 0 \) より、\( z = \frac{1}{4} \) となる。

(ii) 零点

零点は、伝達関数 \( H(z) \) の分子部分がとなる \( z \) なので、\( 8z = 0 \) より、\( z = 0 \) となる。

(4) システムの安定性

すべての極が \( |z| < 1 \) にあるので、安定である。

[余談] 実際にインパルス応答に対して \( n \to \infty \) の極限を取ると\[
\lim_{n \to \infty} h_n = 0
\]となり、たしかに0に収束する。よって安定であることがわかる。

(5) 周波数応答

周波数応答 \( H (e^{i \omega} ) \) は、伝達関数 \( z \) に \( z = e^{i \omega} \) を代入すれば求められる。

よって、\[\begin{align*}
H (e^{i \omega} ) & = \frac{ 2 }{ 1 - \frac{1}{4} z^{-1} }
\\ & = \frac{ 2 }{ 1 - \frac{1}{4} e^{- i \omega} }
\\ & = \frac{ 2 }{ 1 - \frac{1}{4} e^{- i \omega} }
\\ & = \frac{ 2 }{ 1 - ( \frac{1}{4} \cos \omega - \frac{1}{4} i \sin \omega ) }
\\ & = \frac{ 2 }{ (1 - \frac{1}{4} \cos \omega) + \frac{1}{4} \sin \omega i }
\end{align*}\]となる。

※ 振幅特性、位相特性の計算をするために(5)の段階で \( e^{- i \omega} = \cos \omega - \sin \omega \) としています。

(6) 振幅特性

\( H (e^{i \omega} = a + bi )\) の形にしてから \( b/a \) を計算してもいいですが、\( H ( e^{i \omega} ) \) が分数の形になっている場合は\[
\left| \frac{z_1}{z_2} \right| = \frac{ | z_1 | }{ | z_2 | }
\]が成立するので、分子 \( z_1 \) と分母 \( z_2 \) をばらしてから計算するのがおすすめです。

ここで、周波数特性\[
H (e^{i \omega} ) = \frac{\textcolor{blue}{ 2} }{ \textcolor{red}{(1 - \frac{1}{4} \cos \omega) + \frac{1}{4} \sin \omega i }}
\]の分子部分を \( \textcolor{blue}{z_1} \), 分母部分を \( \textcolor{red}{z_2} \) とする。

すると、\[\begin{align*}
|z_1| & = |2|
\\ & = 2
\end{align*}\]

\[\begin{align*}
|z_2| & = \left|\textcolor{magenta}{\left(1 - \frac{1}{4} \cos \omega \right)} + \textcolor{deepskyblue}{ \frac{1}{4} \sin \omega } i \right|
\\ & = \sqrt{ \textcolor{magenta}{ \left(1 - \frac{1}{4} \cos \omega \right)}^2 + \left( \textcolor{deepskyblue}{ \frac{1}{4} \sin \omega } \right)^2 }
\\ & = \sqrt{ 1 - \frac{1}{2} \cos \omega + \frac{1}{16} \cos^2 \omega + \frac{1}{16} \sin^2 \omega }
\\ & = \sqrt{ \frac{17}{16} - \frac{1}{2} \cos \omega }
\end{align*}\]となるので、

\[\begin{align*}
| H (e^{i \omega} ) | & = \left| \frac{z_1}{z_2} \right|
\\ & = \frac{ | z_1 | }{ | z_2 | }
\\ & = \frac{2}{ \sqrt{ \frac{17}{16} - \frac{1}{2} \cos \omega } }
\\ & = \frac{8}{ \sqrt{ 17 - 8 \cos \omega } }
\end{align*}\]となる。

(7) 位相特性

位相特性を求める際にも、\( H ( e^{i \omega} ) \) が分数の形になっている場合は(6)のように\[
\angle \frac{z_1}{z_2} = \angle z_1 - \angle z_2
\]が成立するので、分子 \( z_1 \) と分母 \( z_2 \) をばらしてから計算しましょう。

(6)と同じく周波数特性\[
H (e^{i \omega} ) = \frac{\textcolor{blue}{ 2} }{ \textcolor{red}{(1 - \frac{1}{4} \cos \omega) + \frac{1}{4} \sin \omega i }}
\]の分子部分を \( \textcolor{blue}{z_1} \), 分母部分を \( \textcolor{red}{z_2} \) とする。

すると、\[\begin{align*}
\angle z_1 & = \angle 2
\\ & = 0
\end{align*}\]

\[\begin{align*}
\angle z_2 & = \angle \left\{ \textcolor{magenta}{\left(1 - \frac{1}{4} \cos \omega \right)} + \textcolor{deepskyblue}{ \frac{1}{4} \sin \omega } i \right\}
\\ & = \tan^{-1} \frac{ \textcolor{deepskyblue}{ \frac{1}{4} \sin \omega } }{ \textcolor{magenta}{1 - \frac{1}{4} \cos \omega } }
\\ & = \tan^{-1} \frac{ \sin \omega }{ 4 - \cos \omega }
\end{align*}\]となる。

よって、位相特性 \( \angle H ( e^{i \omega} ) \) は、\[\begin{align*}
\angle H ( e^{i \omega} ) & = \angle \frac{z_1}{z_2}
\\ & = \angle z_1 - \angle z_2
\\ & = 0 - \tan^{-1} \frac{ \sin \omega }{ 4 - \cos \omega }
\\ & = - \tan^{-1} \frac{ \sin \omega }{ 4 - \cos \omega }
\\ & = \tan^{-1} \left( - \frac{ \sin \omega }{ 4 - \cos \omega } \right)
\\ & = \tan^{-1} \frac{ \sin \omega }{ \cos \omega - 4}
\end{align*}\]となる。

※ 基本的に\[
\angle H ( e^{i \omega} ) = - \tan^{-1} \frac{ \sin \omega }{ 4 - \cos \omega }
\]の形が出せていればOKなので、計算が苦手な人はここで変形を止めましょう。なお、ここからの変形は、\( \tan^{-1} x = - \tan^{-1} (-x) \) を使っています。

6. さいごに

第03羽～第05羽にかけて、ディジタルシステムを解読するために使う様々な道具

伝達関数
インパルス応答
極と零点
システムの安定性
周波数特性、振幅特性、位相特性

を学んできました。

この3つの記事が、ディジタルシステム（信号処理）の理解の助けのきっかけになると中の人も大きく喜びます。

（実は中の人は信号処理未履修でした。この記事を書くにあたって、初見で信号処理の本などを参考にわかりやすく色などを付けてまとめたり、例題や練習問題を作成したりしました。）

注釈[+]

注釈
↑1	1周期の中で、どのタイミングにいるのかを表す。
↑2	周波数特性を考える際には、大きさ1の複素数 \( z = e^{i \omega} \) を代入するのですが、不安定なシステムの場合、\( \|z\| = 1 \) が収束領域に入っていないため、発散してしまい、正しい値をえれなくなってしまうのが、不安定なシステムにおいて周波数を考えられない理由です。（この分野は勉強したてなので、もし理由が誤っているとかあれば教えてください）
↑3	ある複素数 \( z \) に対して、\( z^{-1} = \frac{1}{z} \) の偏角は-1倍されるため。もししっくりこない人は実際に複素数平面に図示してみよう。
↑4	\( - \pi \) でもOK。位相が \( \pi \) がずれるのがイマイチよくわからない人は、2と-2をそれぞれ複素数平面上に図示してみましょう。
↑5	\( - \pi \) でもOK。
↑6	位相は \( 2 \pi \) ずらしても同じ位相になるので、\( - \pi \leqq \omega < - \frac{2}{3} \pi \) となっている部分に \( 2 \pi \) 引いて、\( \frac{2}{3} \pi < \omega \leqq \pi \) となっている部分に \( 2 \pi \) 足せばOKです。
↑7	実際に計算すると、\[ \| H( e^{i \omega} ) \| = \frac{ 2 \| \cos \omega \| }{ \sqrt{ (0.8 \sin \omega + 0.64 \sin 2 \omega )^2 + ( 0.8 \cos \omega + 0.64 \cos 2 \omega + 1)^2 } } \]となるので、とても人間が計算し、書けるグラフではありません。