うさぎでもわかる線形代数　補充2　平面・空間上における直線の方程式（ベクトル方程式の基礎）

こんにちは、ももやまです。

今回は、数Bのベクトルや、線形代数で出てくる

• ベクトル方程式
• 平面内や空間内における直線の方程式

について説明していきたいと思います。

 

 

※「線形代数」の単元となっていますが、数Bの「ベクトル」のお話しなので、高校生の方も是非ご覧ください！

 

スポンサードリンク

１．ベクトルを用いた直線の表し方（ベクトル方程式）

まずはベクトルを用いて直線を表す方法を確認していきましょう。

 

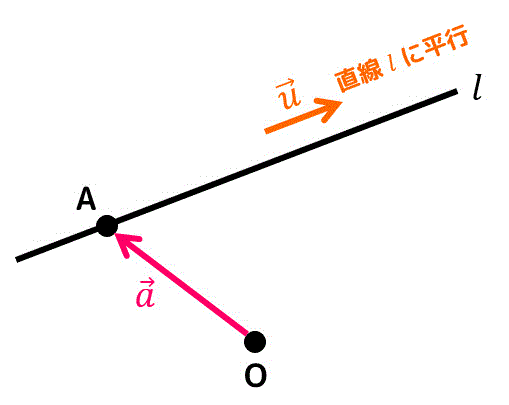
下のように、点A（位置ベクトル \( \vec{a} \)）を通るある直線 \( l \) があるとします。

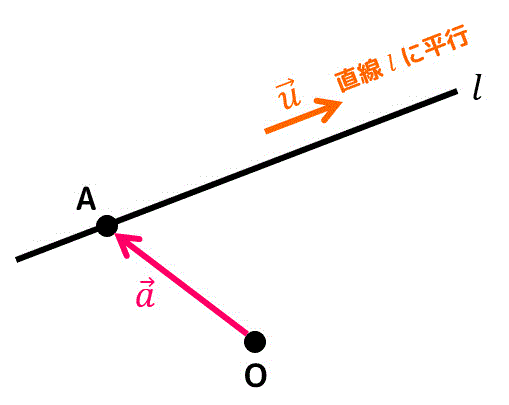
また、直線 \( l \) はベクトル \( \vec{u} \) に平行とします。

（つまり \( \vec{u} \) は直線 \( l \) の傾きを表した方向ベクトル*1となる）

 

ここで、直線 \( l \) を通る点Pを考えます。

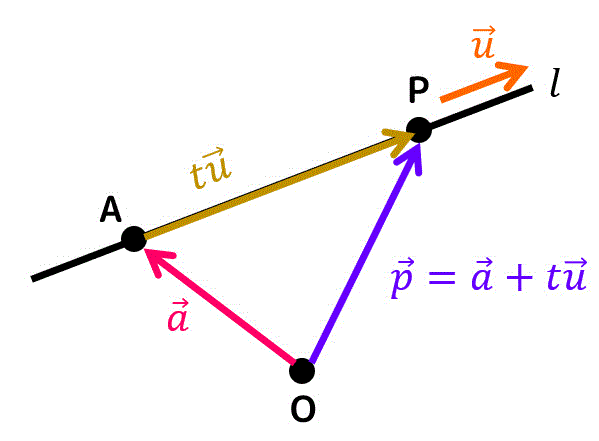
すると、ベクトル \(  \overrightarrow{AP} \) はある実数 \( t \) を用いて\[
\overrightarrow{AP} = t \vec{u}
\]と表せますね*2。

 

よって、点Pの位置ベクトル \( \vec{p} \) は、\[
\overrightarrow{OP} = \overrightarrow{OA} + \overrightarrow{AP} \\
\vec{p} = \vec{a} + t \vec{u}
\]と表すことができ、この \( \vec{p} \) の式を、直線 \( l \) のベクトル方程式と呼びます。

（ちなみに実数 \( t \) のことを媒介変数、もしくはパラメータというのでこちらも覚えておきましょう。）

 

スポンサードリンク

２．直線が平面上にあるとき（3パターン）

まずは、直線が平面上（2次元）にあるときに、ベクトル方程式を用いて直線の方程式を求めてみましょう。

パターンとしては3パターンあるので、パターンごとに説明していきたいと思います。

 

その1　1点と直線に平行なベクトルから求める

まずは、最も基本的なパターンである、

• 直線上にある1点
• 直線に平行なベクトル \( \vec{u} \)

の2つから直線の方程式を実際に求める練習をしてみましょう。

 例題1  

点A (2,-3) を通り、\[
\vec{u} = \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]に平行な直線 \( l \) を考える。

 

(1) 直線 \( l \) の方程式を媒介変数 \( t \) を用いて答えなさい。

(2) 直線 \( l \) の方程式を \( ax + by + c = 0 \) の形で表しなさい。

 

解説1

(1)

点Pをある直線 \( l \) 上におく。

すると、\(  \overrightarrow{OP} \) は、媒介変数 \( t \) を用いて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} 2 \\ -3 \end{array} \right) + t \vec{u}
\\ & = \left( \begin{array}{ccc} 2 \\ -3 \end{array} \right) + t \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} t+2 \\ 2t-3 \end{array} \right)
\end{align*}\]と求められる。

 

ここで、点Pの座標を \( (x,y) \) とすると、\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} t+2 \\ 2t-3 \end{array} \right)
\]となるので、直線 \( l \) の方程式は媒介変数 \( t \) を用いて\[
\left\{ \begin{array}{l} x = t + 2 \\ y = 2t - 3 \end{array}\right.
\]となる。

 

(2)

媒介変数表示\[
\left\{ \begin{array}{l} x = t + 2 \\ y = 2t - 3 \end{array}\right.
\]で表された式の \( t \) を削除すればよい。

 

\( t = x-2 \) を \( y = 2t - 3 \) に代入し、\[\begin{align*}
y & = 2(x-2)-3
\\ & = 2x-7
\end{align*}\]となるので、\( ax+by+c=0 \) の形にすると、\[
2x - y - 7 =0 
\]となる。

（点A (2,-3) を代入して式が成り立つか必ず確認しましょう。）

 

 一般化して公式にしておきましょう。

 

 

その2　2点から求める

つぎに、ある直線 \( l \) 上のある2点から直線の方程式を求めてみることを考えましょう。

ある2点を点A（位置ベクトル \( \vec{a} \)）、点B（位置ベクトル \( \vec{b} \)）とし、\(  \overrightarrow{AB} = \vec{u} \) とおきましょう。

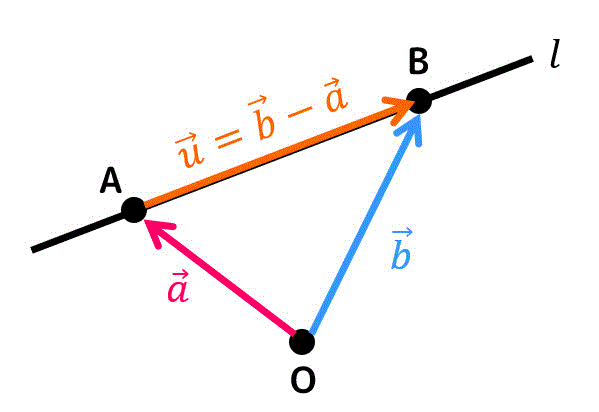
すると、\[
\vec{u} = \vec{b} - \vec{a}
\]となり、\( \vec{u} \) は直線 \( l \) に平行なベクトルとなりますね。

 

あとは、「その1（例題1）」と同じように直線上に点Pをおき、点Pの位置ベクトル \( \vec{p} \) を\[
\vec{p} = \vec{a} + t \vec{u}
\]とすることで直線の方程式を求めることができます。

 

 例題2  

2点 A(-1,-2), B(1,1) を通るような直線 \( l \) を考える。つぎの(1), (2)の問いに答えなさい。

 

(1) 直線 \( l \) の方程式を媒介変数 \( t \) を用いて答えなさい。

(2) 直線 \( l \) の方程式を \( ax + by + c = 0 \) の形で表しなさい。

 

解説2

(1)

まずは、直線 \( l \) に平行なベクトルを求める。

（※直線 \( l \) に平行なベクトルであれば長さはどうでもいい）

 

点A, B は直線 \( l \) を通るので \(  \overrightarrow{AB} \) は直線 \( l \) に平行なベクトルとなり、成分は\[\begin{align*}
\overrightarrow{AB} & = \overrightarrow{OB} - \overrightarrow{OA
}
\\ & =  \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) - \left( \begin{array}{ccc} -1 \\ -2 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} 2 \\ 3 \end{array} \right)
\end{align*}\]となる。

 

ここで、直線 \( l \) 上に点Pをおく。

すると、点Bと点Pはともに直線 \( l \) 上にあるので\[ \overrightarrow{AP} = t \overrightarrow{AB}\]の関係が成り立つ。

 

よって、\(  \overrightarrow{OP} \) は、媒介変数 \( t \) を用いて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} -1 \\ -2 \end{array} \right) + t \overrightarrow{AB}
\\ & = \left( \begin{array}{ccc} -1 \\ -2 \end{array} \right) + t \left( \begin{array}{ccc} 2 \\ 3 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2t-1 \\ 3t-2 \end{array} \right)
\end{align*}\]と求められる。

（点Bを通ると考えて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OB} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) + t \overrightarrow{AB}
\\ & = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) + t \left( \begin{array}{ccc} 2 \\ 3 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2t+1 \\ 3t+1 \end{array} \right)
\end{align*}\]としてももちろんOK。）

 

ここで、点Pの座標を \( (x,y) \) とすると、\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 2t-1 \\ 3t-2 \end{array} \right)
\]となるので、直線 \( l \) の方程式は媒介変数 \( t \) を用いて\[
\left\{ \begin{array}{l} x = 2t-1\\ y = 3t-2 \end{array}\right.
\]となる。

（点Bを通ると考えた場合は\[
\left\{ \begin{array}{l} x = 2t+1 \\ y = 3t+1 \end{array}\right.
\]となる。）

 

(2)

媒介変数表示\[
\left\{ \begin{array}{l} x = 2t-1 \\ y = 3t-2 \end{array}\right.
\]で表された式の \( t \) を削除すればよい。

 

\[\begin{align*}
6t = 3x + 3 \\
6t = 2y+4
\end{align*}\]となるので、\( ax+by+c=0 \) の形にすると、\[
3x + 3 = 2y + 4 \\
3x - 2y - 1 = 0
\]となる。

（点A(-1,-2)や点B(1,1)を代入して式が成り立つか必ず確認しましょう。）

 

[余談]

本当はベクトルで計算しなくても、傾き \( t \) を\[
t = \frac{1-(-2)}{1-(-1)} = \frac{3}{2}
\]と計算してから、\[\begin{align*}
y & = t(x-1) + 1
\\ & = \frac{3}{2}(x-1)+1
\\ & = \frac{3}{2}x - \frac{1}{2}
\end{align*}\]として、\[
\frac{3}{2}x - y - \frac{1}{2} = 0 \\
3x - 2y - 1 = 0
\]と求めることができます。

 

今回は、直線が空間上にある場合における方程式も求めたいので、その前段階としてベクトルを用いた方法で説明しています。

その3　1点と直線の法線ベクトルから求める

その1と同じように点A（位置ベクトル \( \vec{a} \)）を通るある直線 \( l \) があるとします。

さらに直線 \( l \) に垂直なベクトル \( \vec{n} \) を考えましょう。

（\( \vec{n} \) のことを法線ベクトルと呼びます）

 

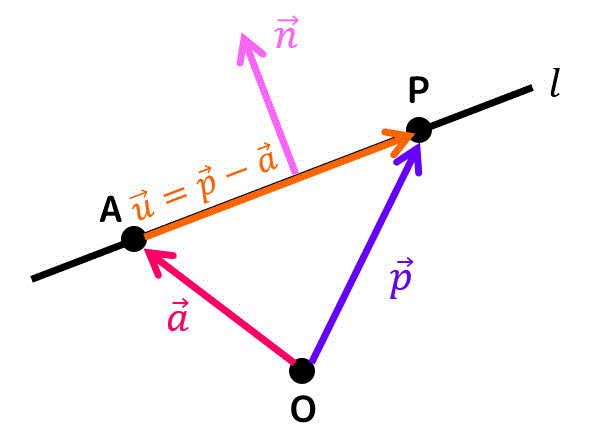
ここで、直線 \( l \) 上に点Pをおき、さらに \(  \overrightarrow{OP} = \vec{p} \) としましょう。（点Pの位置ベクトルに相当）

さらに、\(  \overrightarrow{AP} = \vec{u} \) とすると、\[\begin{align*}
\overrightarrow{AP} & = \overrightarrow{OP} - \overrightarrow{OA}
\\ & = \vec{p} - \vec{a}
\\ & = \vec{u}
\end{align*}\]となるので、\( \vec{u} = \vec{p} - \vec{a} \) と表せます。

 

ベクトル \( \vec{u} \) は直線 \( l \) に平行なので、法線ベクトル \( \vec{n} \) と直交しますね。

そのため、\[\begin{align*}
\vec{u} \cdot \vec{n} & = 0
\\ ( \vec{p} - \vec{a} ) \cdot \vec{n} & = 0 
\end{align*}\]が成立しますね。

 

ここで、点Pの座標を \( (x,y) \) とすると、\[
\vec{p} = \left( \begin{array}{ccc} x \\ y \end{array} \right) 
\]となります。さらに、\[
\vec{a} = \left( \begin{array}{ccc} x_0 \\ y_0 \end{array} \right) , \ \ \ 
\vec{n} =  \left( \begin{array}{ccc} p \\ q \end{array} \right) 
\]とすると、\[\begin{align*}
( \vec{p} - \vec{a} ) \cdot \vec{n} & =  0 \\
\left( \begin{array}{ccc} x - x_0 \\ y - y_0 \end{array} \right)  \cdot \left( \begin{array}{ccc} p \\ q \end{array} \right) 
\end{align*}\]となるので、\[
p (x - x_0) + q (y - y_0) = 0
\]の関係式が成り立ちますね。

 

 

 

また、上の公式から \( ax + by + c = 0 \) の係数がわかれば法線ベクトル \( \vec{n} \) も下のようにあっという間に求められることがわかりますね。

 

 

では、実際に例題で確認してみましょう。

 例題3  

点A (1,3) を通り、法線ベクトル \( \vec{n} \) が\[
\vec{n} =  \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) 
\]となる直線 \( l \) を考える。

このときの直線 \( l \) の方程式を答えなさい。

 

解説3

(1)

直線 \( l \) を通る点Pをおき、その座標を \( (x,y) \) とする。

すると、\[\begin{align*}
\overrightarrow{AP} & = \overrightarrow{OP} - \overrightarrow{OA}
\\ & = \left( \begin{array}{ccc} x \\ y \end{array} \right) - \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) 
\\ & = \left( \begin{array}{ccc} x-2 \\ y+1 \end{array} \right)  
\end{align*}\]となる。

 

ここで、\( \overrightarrow{AP} \) は直線 \( l \) に平行なので、法線ベクトル \( \vec{n} \) と直交する。

そのため、\[\begin{align*}
 \overrightarrow{AP} \cdot \vec{n} & = 0 \\
\left( \begin{array}{ccc} x-1 \\ y-3 \end{array} \right)  \cdot \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)  
\end{align*}\]が成立する。

 

よって、\[
2(x-1) - 1(y-3) = 0 \\
2x - y + 1 = 0
\]と直線の方程式を求めることができる。

（点A(1,3)を代入して式が成り立つか必ず確認しましょう。）

 

スポンサードリンク

３．直線が空間上にあるとき（2パターン）

先程は、平面上にある直線の方程式を求める方法について説明しましたね。

平面上での直線の方程式を求めるときと同じような手順で、空間上にある直線の方程式も求めることができるのです！

 

2パターンあるので、パターンごとに説明していきたいと思います。

その1　1点と直線に平行なベクトルから求める方法

まずは、

• 直線を通るある1点
• 直線に平行なベクトル \( \vec{u} \)

から空間上にある直線の方程式を求める方法を例題を踏まえながら説明しましょう。

 例題4  

点A (1, 2, 3) を通り、\[
\vec{u} = \left( \begin{array}{ccc} 2 \\ -3 \\ 1 \end{array} \right)
\]に平行な直線 \( l \) を考える。

 

(1) 直線 \( l \) の方程式を媒介変数 \( t \) を用いて表しなさい。

(2) 直線 \( l \) の方程式を媒介変数を用いずに表しなさい。

 

解説4

(1)

点Pをある直線 \( l \) 上におく。

すると、\(  \overrightarrow{OP} \) は、媒介変数 \( t \) を用いて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \end{array} \right) + t \vec{u}
\\ & = \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \end{array} \right) + t \left( \begin{array}{ccc} 2 \\ -3 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2t+1 \\ -3t+2 \\ t+3 \end{array} \right)
\end{align*}\]と求められる。

 

ここで、点Pの座標を \( (x,y,z) \) とすると、\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = \left( \begin{array}{ccc} 2t+1 \\ -3t+2 \\ t+3 \end{array} \right)
\]となるので、直線 \( l \) の方程式は媒介変数 \( t \) を用いて\[
\left\{ \begin{array}{l} x = 2t+1 \\ y = -3t+2 \\ z = t+3 \end{array}\right.
\]となる。

 

(2)

媒介変数表示\[
\left\{ \begin{array}{l} x = 2t+1 \\ y = -3t+2 \\ z = t+3 \end{array}\right.
\]で表された式の \( t \) を削除すればよい。

 

\[\begin{align*}
t = \frac{x-1}{2} \\ 
t = \frac{y-2}{-3} \\
t = \frac{z-3}{1} 
\end{align*}\]となるので、\( t \) を消去すると\[
\frac{x-1}{2} = \frac{y-2}{-3} = \frac{z-3}{1} \\
\frac{x-1}{2} = - \frac{y-2}{3} = z-3
\]となる。

（最後に点A (1, 2, 3)を代入して成立するか確かめましょう。また、空間内における直線を表す際には、分母のマイナスを残しておくことが多いですが、気持ち悪いなと思った人は変形して分母を正にしておいてもOKです。 ）

 

では、一般化して公式化しておきましょう。

 

「＝」が2つあってちょっと違和感ある式ですよね。

図示をして、上の式の意味を確認しておきましょう。

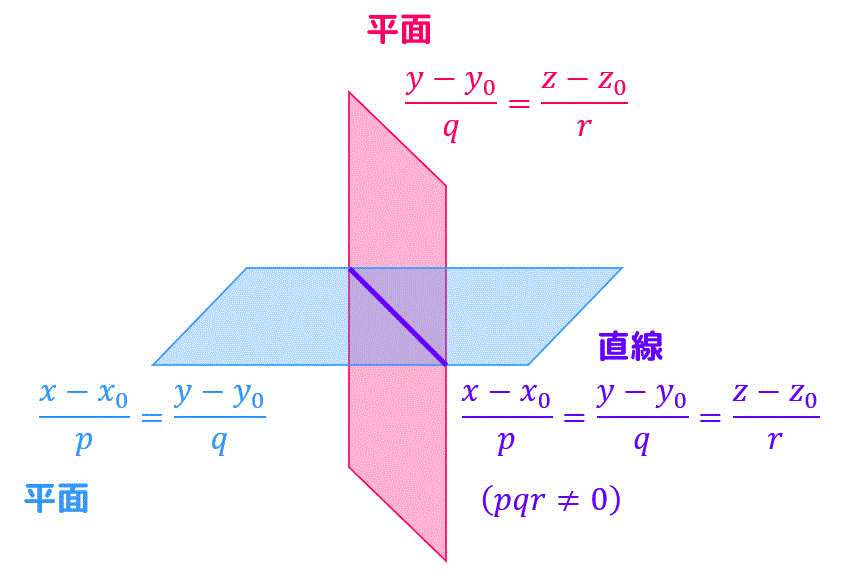
2つの平面の式が合わさって1つの直線の式になっているのです！

ただし、直線に平行なベクトル \( \vec{u} \) が\[
\vec{u} = \left( \begin{array}{ccc} 2 \\ 3 \\ \color{red}{0} \end{array} \right)
\]のように、0の成分が入っているときは上の公式が使えないので注意が必要です。

 

例えば平行なベクトル \( \vec{u} \) に \( z \) 成分に0が入っているときは \[
\left\{ \begin{array}{l} x = pt + x_0 \\ y = qt + y_0 \\ z = z_0 \end{array}\right.
\]のようにしてから、\[
t = \frac{x-x_0}{p} \\ 
t = \frac{y-y_0}{q}
\]の2式を \( t = \) の形に変形し、\[
\frac{x-x_0}{p} = \frac{y-y_0}{q}, \ \ z = z_0
\]と2つの式に分離して答えましょう。

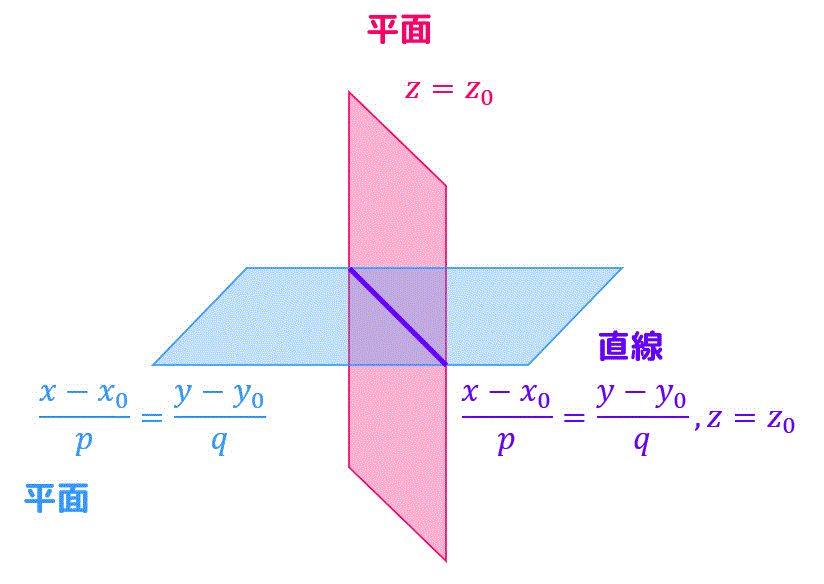
その2　2点から求める方法

では、空間内にある直線上の2点から方程式を求める方法も確認しておきましょう。

こちらも平面内にあるときと同じように求めることができます。

 例題5  

2点 A(-1,2,4), B(1,2,0) を通るような直線 \( l \) を考える。つぎの(1), (2)の問いに答えなさい。

 

(1) 直線 \( l \) の方程式を媒介変数 \( t \) を用いて表しなさい。

(2) 直線 \( l \) の方程式を媒介変数を用いずに表しなさい。

 

 

(1)

まずは、直線 \( l \) に平行なベクトルを求める。

（※向きが平行なベクトルであれば長さはどうでもいい）

 

点A, B は直線 \( l \) を通るので \(  \overrightarrow{AB} \) は直線 \( l \) に平行なベクトルとなり、成分は\[\begin{align*}
\overrightarrow{AB} & = \overrightarrow{OB} - \overrightarrow{OA
}
\\ & =  \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \end{array} \right) - \left( \begin{array}{ccc} -1 \\ 2 \\ 4 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} 2 \\ 0 \\ -4 \end{array} \right)
\end{align*}\]となる。

 

ここで、直線 \( l \) 上に点Pをおく。

すると、点Bと点Pはともに直線 \( l \) 上にあるので\[ \overrightarrow{AP} = t \overrightarrow{AB}\]の関係が成り立つ。

 

よって、\(  \overrightarrow{OP} \) は、媒介変数 \( t \) を用いて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} -1 \\ 2 \\ 4 \end{array} \right) + t \overrightarrow{AB}
\\ & = \left( \begin{array}{ccc} -1 \\ 2 \\ 4 \end{array} \right) + t \left( \begin{array}{ccc} 2 \\ 0 \\ -4 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2t-1 \\ 2 \\ -4t+4 \end{array} \right)
\end{align*}\]と求められる。

（点Bを通ると考えてもOK）

 

ここで、点Pの座標を \( (x,y,z) \) とすると、\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = \left( \begin{array}{ccc} 2t-1 \\ 2 \\ -4t+4 \end{array} \right)
\]となるので、直線 \( l \) の方程式は媒介変数 \( t \) を用いて\[
\left\{ \begin{array}{l} x = 2t-1\\ y = 2 \\ z = -4t+4 \end{array}\right.
\]となる。

 

(2)

媒介変数表示\[
\left\{ \begin{array}{l} x = 2t+1 \\ y = 2 \\ z = -4t+4 \end{array}\right.
\]で表された式の \( t \) を削除すればよい。

 

\[\begin{align*}
t = \frac{x-1}{2} \\ 
t = \frac{z-4}{-4}
\end{align*}\]となるので、\( t \) を消去すると\[
\frac{x-1}{2} = \frac{z-4}{-4} , \ \ y = 2
\]となる。

（もとの2点を代入して成立するか確かめましょう）

 

４．練習問題

では、2問ほど練習してみましょう。

1問は平面上、もう1問が空間上での直線の方程式に関する問題となっております。

練習1

点A (-1,4) を通り、\[
\vec{u} = \left( \begin{array}{ccc} 4 \\ -3 \end{array} \right)
\]に平行な直線 \( l \) を考える。

 

(1) 直線 \( l \) の方程式を媒介変数 \( t \) を用いて答えなさい。

(2) 直線 \( l \) の方程式を \( ax + by + c = 0 \) の形で表しなさい。

(3) 直線 \( l \) の法線ベクトル \( \vec{n} \) を求めなさい。

練習2

2点 A(-1,1,4), B(4,-1,5) を通るような直線 \( l \) を考える。つぎの(1), (2)の問いに答えなさい。

 

(1) 直線 \( l \) の方程式を媒介変数 \( t \) を用いて表しなさい。

(2) 直線 \( l \) の方程式を媒介変数を用いずに表しなさい。

 

５．練習問題の答え

練習1

(1)

点Pをある直線 \( l \) 上におく。

すると、\(  \overrightarrow{OP} \) は、媒介変数 \( t \) を用いて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} -1 \\ 4 \end{array} \right) + t \vec{u}
\\ & = \left( \begin{array}{ccc} -1 \\ 4 \end{array} \right) + t \left( \begin{array}{ccc} 4 \\ -3 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 4t-1 \\ -3t+4 \end{array} \right)
\end{align*}\]と求められる。

 

ここで、点Pの座標を \( (x,y) \) とすると、\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 4t-1 \\ -3t+4 \end{array} \right)
\]となるので、直線 \( l \) の方程式は媒介変数 \( t \) を用いて\[
\left\{ \begin{array}{l} x = 4t-1 \\ y = -3t+4 \end{array}\right.
\]となる。

 

(2)

媒介変数表示\[
\left\{ \begin{array}{l} x = 4t-1 \\ y = -3t+4 \end{array}\right.
\]で表された式の \( t \) を削除すればよい。

 

両辺を \( 12t \) に合わせると、\[\begin{align*}
12t = 3x + 3 \\
12t = 4y - 16
\end{align*}\]となるので、\( ax+by+c=0 \) の形にすると、\[
3x + 3 = 4y - 16 \\
3x - 4y + 19 = 0
\]となる。

（点A (-1,4) を代入して式が成り立つか必ず確認しましょう。）

 

(3)

\( \color{red}{3} x  \color{blue}{-4} y + 19 = 0 \) なので、法線ベクトル \( \vec{n} \) は\[
\vec{n} = \left( \begin{array}{ccc} \color{red}{3} \\ \color{blue}{-4} \end{array} \right)
\]となる。

 

練習2

(1)

まずは、直線 \( l \) に平行なベクトルを求める。

 

点A, B は直線 \( l \) を通るので \(  \overrightarrow{AB} \) は直線 \( l \) に平行なベクトルとなり、成分は\[\begin{align*}
\overrightarrow{AB} & = \overrightarrow{OB} - \overrightarrow{OA
}
\\ & =  \left( \begin{array}{ccc} 4 \\ -1 \\ 5 \end{array} \right) - \left( \begin{array}{ccc} -1 \\ 1 \\ 4 \end{array} \right)
\\ & =  \left( \begin{array}{ccc} 5 \\ -2 \\ 1 \end{array} \right)
\end{align*}\]となる。

 

ここで、直線 \( l \) 上に点Pをおく。

すると、点Bと点Pはともに直線 \( l \) 上にあるので\[ \overrightarrow{AP} = t \overrightarrow{AB}\]の関係が成り立つ。

 

よって、\(  \overrightarrow{OP} \) は、媒介変数 \( t \) を用いて\[\begin{align*}
\overrightarrow{OP} & = \overrightarrow{OA} + \overrightarrow{AP}
\\ & = \left( \begin{array}{ccc} -1 \\ 1 \\ 4 \end{array} \right) + t \overrightarrow{AB}
\\ & = \left( \begin{array}{ccc} -1 \\ 1 \\ 4 \end{array} \right) + t \left( \begin{array}{ccc} 5 \\ -2 \\ 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 5t-1 \\ -2t+1 \\ t+4 \end{array} \right)
\end{align*}\]と求められる。

（点Bを通ると考えてもOK）

 

ここで、点Pの座標を \( (x,y,z) \) とすると、\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = \left( \begin{array}{ccc} 5t-1 \\ -2t+1 \\ t+4 \end{array} \right)
\]となるので、直線 \( l \) の方程式は媒介変数 \( t \) を用いて\[
\left\{ \begin{array}{l} x = 5t-1 \\ y = -2t+1 \\ z = t+4 \end{array}\right.
\]となる。

 

(2)

媒介変数表示\[
\left\{ \begin{array}{l} x = 5t-1 \\ y = -2t+1 \\ z = t+4 \end{array}\right.
\]で表された式の \( t \) を削除すればよい。

 

\[\begin{align*}
t = \frac{x+1}{5} \\
t = \frac{y-1}{-2} \\
t = z-4
\end{align*}\]となるので、\( t \) を消去すると\[
\frac{x+1}{5} = \frac{y-1}{-2} = z-4
\]となる。

（2点A(-1,1,4), B(4,-1,5)を代入して成り立つか確認しましょう）

 

６．さいごに

今回は、

• ベクトル方程式とはなにか
• 平面内や空間内にある直線の方程式の求め方

について説明していきました。

補充3では、空間内における平面の求め方について説明していくので、興味がある方はぜひご覧ください！