スポンサードリンク
こんにちは、ももやまです!
今回は部分空間についてのまとめです。
部分空間とはどんなものなのか、部分空間の中でも特に出題頻度の高い解空間、生成系の次元や基底の求め方をまとめています!
前回の線形代数のまとめ(基底について)はこちらから!
基底についてまだよく理解できていない人はこちらをご覧ください!
スポンサードリンク
1.部分空間
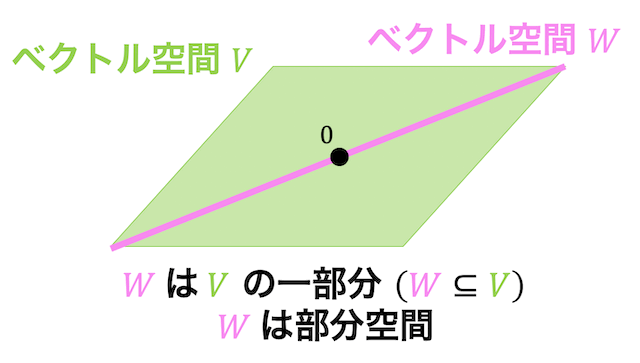
例えば次の図のような2次元ベクトル空間 \( V \) があるとします。
さらに、2次元ベクトルの中にベクトル空間 \( W \) があるとします。
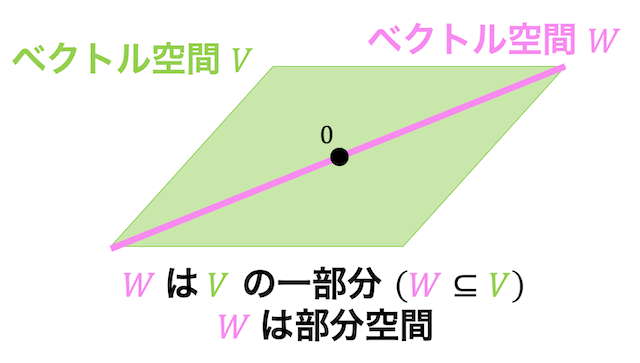
このとき、空間 \( W \) は空間 \( V \) の一部分(部分集合)となっているのがわかりますね。
このようにあるベクトル空間 \( V \) の一部分 \( W \) を取ったものもベクトル空間となっているとき、\( W \) は \( V \) の線形部分空間(以下部分空間と呼びます)であると呼びます。
部分空間となるためには、つぎの3つを満たす必要があります。
ベクトル空間 \( V \) の部分集合 \( W \) が、
- \( \vec{0} \in W \)
(原点において部分空間であること) - \( \vec{x}, \vec{y} \in W \) ならば \( \vec{x} + \vec{y} \in W \)
(部分空間同士のベクトルを足しても部分空間であること) - \( \vec{x} \in W \) ならば \( k \vec{x} \in W \)(ただし \( k \) は実数)
(部分空間のベクトルを何倍かしても部分空間であること)
この3つをすべて満たすとき、\( W \) は部分空間となる。
(ただし1の \( \vec{0} \in W \) は3の \( \vec{x} \in W \) ならば \( k \vec{x} \in W \) の \( k = 0 \) に相当するため省略OK。)
まずは、部分空間かどうかを判定するような問題を解いてみましょう。
例題1
つぎの3次元ベクトル空間 \( \mathbb{R}^3 \) 上のベクトル空間 \( W_1 \), \( W_2 \), \( W_3 \) は \( \mathbb{R}^3 \) 上の部分空間であるか判定しなさい。
(1) \[ W_1 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle| \ x - 3y + 5z = 0 \right\} \]
(2) \[ W_2 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle| \ 2x + 5y - z = 1 \right\} \]
(3) \[ W_3 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle| \ xyz = 0 \right\} \]
(4) \[ W_4 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle| x - 2y + 3z \leqq 0 \right\} \]
解説1
部分空間であることを示すには、
(a) 原点において式を満たすこと
(b) 部分空間同士のベクトルの和も部分空間となること
(c) 部分空間のベクトルを何倍かしても部分空間であること
の3つをすべて示す必要があります。
逆に(a), (b), (c)のうち1つでも満たさないものがあれば部分空間とはいえません。
(1)
(a) 原点において式を満たすか
明らかに満たすので \( \vec{0} \in W_1 \) である。
(b) 部分空間同士のベクトルの和も部分空間になるか
\( W \) の要素 \( \vec{x}, \vec{y} \) を \[ \vec{x} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ a_3 \end{array} \right) \ \ \
\vec{y} = \left( \begin{array}{ccc} b_1 \\ b_2 \\ b_3 \end{array} \right) \]とする。すると、\[
a_1 - 3 a_2 + 5 a_3 = 0 \\
b_1 - 3 b_2 + 5 b_3 = 0
\]が成立します。このとき、\( \vec{x} + \vec{y} \) も \( W \) の要素であることを示せばよい。\[
\vec{x} + \vec{y} = \left( \begin{array}{ccc} a_1 + b_1 \\ a_2 + b_2 \\ a_3 + b_3 \end{array} \right)
\]なので連立方程式に代入すると、\[\begin{align*} &
(a_1 + b_1) - 3 (a_2 + b_2) + 5(a_3 + b_3) \\ = &
a_1 - 3 a_2 + 5 a_3 + b_1 - 3 b_2 + 5 b_3 = 0
\end{align*} \]となり、\( \vec{x} + \vec{y} \) も \( W \) の要素であることが示せます。
なので(b)も成立です。
(c) 部分空間のベクトルを何倍かしても部分空間か。
\( W \) の要素 \( \vec{x} \) を \[ \vec{x} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ a_3 \end{array} \right) \]とする。すると、\[
a_1 - 3 a_2 + 5 a_3 = 0
\]が成立します。このとき、\( k \) 倍した \( k \vec{x} \) も部分空間であることを示せばよい。\[
k\vec{x} = \left( \begin{array}{ccc} k a_1 \\ k a_2 \\ ka_3 \end{array} \right)
\]なので連立方程式に代入すると、\[\begin{align*} &
k a_1 - 3 k a_2 + 5k a_ 3 \\ = &
k(a_1 - 3a_2 + 5a_3) = 0
\end{align*} \]となり、\( k \vec{x} \) も \( W \) の要素となることが示せますね。
(a), (b), (c) がすべて成立するので \( W_1 \) は部分空間といえます。
このように、1次の同次式( [1次式] = 0の形 )の解は部分空間となることがわかります。
同次式は今回は1つでしたが連立1次同次式( [1次式] = 0 and [1次式] = 0 and … )の解も部分空間となります。
(2)
(a) 原点において式を満たすか
\( (x,y,z) = (0,0,0) \) を代入すると、\( 0 = 1 \) となってしまい、成立しません。
よって \( W_2 \) は部分空間ではありません。
このように、( 方程式 ) ≠ 0 のような非同次の解は部分空間にはならないことがわかりますね。
(3)
(b) 部分空間同士のベクトルの和も部分空間になるか
ここで問題が発生します。
例えば、\[ \vec{x} = \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right) \ \ \
\vec{y} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \]とする。
このとき、\( \vec{x}, \vec{y} \) はともに \( xyz = 0 \) を満たすので \( W \) の要素といえますが、\[ \vec{x} + \vec{y} = \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right) \]となり、\( xyz = 1 \not = 0 \) となってしまい、\( W \) の要素とはなりません。
よって部分空間ではありません。
このように2次式以上の場合はたとえ同次式 (=0) の形であっても部分空間とはなりません。
(4)
(c) 部分空間のベクトルを何倍かしても部分空間か。
ここで問題が発生します。
例えば、\[ \vec{x} = \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right) \]とします。
このとき、\( x - 2y + 3z = -1 \leqq 0 \) を満たします。
しかし、\[ -1 \vec{x} = \left( \begin{array}{ccc} -1 \\ -1 \\ 0 \end{array} \right) \]とすると、このとき、\( x - 2y + 3z = 1 \leqq 0 \) となってしまい、\( W \) の要素となりません。
よって部分空間ではありません。
このように不等式の形であっても部分空間とはならないことがわかりますね。
部分空間の表し方には主に2パターンあるので、今回はその2パターンについて例題を加えながら説明をしていきたいと思います。
スポンサードリンク
2.解空間
2パターンのうちの1パターン目をまずは説明したいと思います。
先程例題で「1次式 = 0」の形が部分空間となることを確認しましたね。
「1次式 = 0」のような \( n \) 元同次式 \( A\vec{x} = \vec{0} \) を要素とする集合\[
W = \left\{ \vec{x} \in \mathbb{R}^n \ \middle| \ A \vec{x} = \vec{0} \right\}
\]は \( \mathbb{R}^n \) の部分空間となり、解空間と呼ばれます。
未知数が \( n \) 個ある同次連立方程式 \( A \vec{x} = \vec{0} \) の解を要素とする集合\[
V = \left\{ \vec{x} \in \mathbb{R}^n \ \middle| \ A \vec{x} = \vec{0} \right\}
\]の基底は、連立方程式 \( A \vec{x} = \vec{0} \) の基本解*1を集めたもの。
また、解空間の次元 \( \dim V \) は \[ \dim V = n - \mathrm{Rank} \ A \]で表される。
解空間の次元と基底
例題2
行列 \( A \) を \[
A = \left( \begin{array}{ccc} 1 & -1 & 1 & -3 \\ 2 & -2 & 5 & -3 \\ -1 & 1 & -3 & 1 \end{array} \right)
\]とする。このとき、次の部分空間 \( V \) の基底と次元を求めなさい。\[
V = \left\{ \vec{x} \in \mathbb{R}^3 \ \middle| \ A \vec{x} = \vec{0} \right\}
\]
解説2
まずは、連立方程式を解くために行列 \( A \) を掃き出します。\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & -1 & 1 & -3 \\ 2_{-2} & -2_{+2} & 5_{-2} & -3_{+6} \\ -1_{+1} & 1_{-1} & -3_{+1} & 1_{-3} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 1_{-1} & -3_{-1} \\ 0_{\div 3} & 0_{\div 3} & 3_{\div 3} & 3_{\div 3} \\ 0 & 0 & -2_{+2} & -2_{+2} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 & -4 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]となるので、\[
\left\{ \begin{array}{l} x-y-4w = 0 \\ z + w = 0 \end{array}\right.
\]と同じ連立方程式となることがわかる。
ここで、\( y = s \), \( w = t \) とすると \( x = s+4t \), \( z = -t \) となることがわかる。ベクトルで書くと\[ \vec{x} =
\left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right)
= s \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \\ 0 \end{array} \right)
+ t \left( \begin{array}{ccc} 4 \\ 0 \\ -1 \\ 1 \end{array} \right)
\]となる。
つまり、解ベクトル \( \vec{x} \) を表現するためには、\[ \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \\ 0 \end{array} \right) \ , \ \ \left( \begin{array}{ccc} 4 \\ 0 \\ -1 \\ 1 \end{array} \right) \]の2つのベクトルが必要となります(この2つのベクトルを基本解と呼びます)。よって、\[
V = \left\{\ \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \\ 0 \end{array} \right), \left( \begin{array}{ccc} 4 \\ 0 \\ -1 \\ 1 \end{array} \right) \ \right\}
\]となり、\( \dim V = 2 \) (2次元)となります。
なお、解空間の次元は、行列 \( A \) の階数を用いても判定することができるので、基底の次元だけを求めたい場合は行列 \( A \) を行基本変形して階数を求めたほうが早いです。
今回の場合だと、\[
\dim V = n - \mathrm{Rank} \ A = 4 - 2 = 2
\]と求められます。
スポンサードリンク
3.生成系の部分空間
つぎに生成系の部分空間の紹介をします。
ベクトル空間 \( W \) 内の \( \mathbb{R}^n \) ベクトルの組 \( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) に対し、ベクトルの組の1次結合\[
c_1 \vec{a_1} + c_2 \vec{a_2} + \cdots + c_n \vec{a_n}
\]で表せるベクトルの集合は \( W \) の部分空間となり、\[
V = \left< \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \right>
\]と書く。
この部分空間 \( V \) のことを \( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) によって生成する空間、もしくは張られる空間と呼ばれる。
(\( \vec{a_1} \), \( \vec{a_2} \), … \( \vec{a_n} \) は \( V \) の生成系という)
部分空間 \( V \) のベクトルの組すべてが基底になるとは限りません。
基底となるためには、互いのベクトルが1次独立になる必要があります。
ベクトル空間 \( W \) 内から取ってきた部分空間\[
V = \left< \vec{a_1}, \vec{a_2}, \cdots, \vec{a_n} \right>
\]の基底は \( V \) 内のベクトルから選べる1次独立な最大組となる。
また、生成系の部分の次元 \( \dim V \) は \[ \dim V = \mathrm{Rank} \ A \]で表される。
生成系の部分空間の次元
例題3
つぎの \( \mathbb{R}^n \) のベクトルが生成する部分空間の次元と基底を求めなさい。\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ -3 \\ 3 \end{array} \right) \ \ \
\vec{a_2} = \left( \begin{array}{ccc} 3 \\ 7 \\ -1 \end{array} \right) \ \ \
\vec{a_3} = \left( \begin{array}{ccc} 2 \\ 2 \\ 1 \end{array} \right) \ \ \
\vec{a_4} = \left( \begin{array}{ccc} -3 \\ 1 \\ 3 \end{array} \right) \ \ \
\]
解説3
生成系の部分空間の基底と次元は、ベクトル内の中から選び出せる1次独立な最大組と最大数となる。
1次独立な最大組を求めるために行列 \( A \) を\[
A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3}, \vec{a_4} \right)
\]とする。行基本変形を行うと、\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & 3 & 2 & -3 \\ -3_{+3} & 7_{+9} & 2_{+6} & 1_{-9} \\ 3_{-3} & -1_{-9} & 1_{-6} & 3_{+9} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 3 & 2 & -3 \\ 0 & 16 & 8 & -8 \\ 0 & -10_{\times 8} & -5_{\times 8} & 12_{\times 8} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 3 & 2 & -3 \\ 0 & 16 & 8 & -8 \\ 0 & -80_{+80} & -40_{+40} & 96_{-40} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 3 & 2 & -3 \\ 0 & 16 & 8 & -8 \\ 0 & 0 & 0 & 56 \end{array} \right)
\end{align*}
\]と階段行列に変形できるので、下の0の数に注目して場合分けを行い、最大組は \( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_4} \) となり、
\( \dim V = 3 \) (3次元)となります。
なお、生成系の次元も解空間の次元と同様に行列 \( A \) の階数を用いても判定することができるので、基底の次元だけを求めたい場合は行列 \( A \) を行基本変形して階数を求めたほうが早いです(ただし解空間の次元と公式が違うので注意)。
今回の場合だと、\[
\dim V = \mathrm{Rank} \ A = 3
\]と求められます。
4.練習問題
では、実際に練習してみましょう!
練習1
つぎの3次元ベクトル空間 \( \mathbb{R}^3 \) 上のベクトル空間 \( W_1 \), \( W_2 \), \( W_3 \), \( W_4 \) は \( \mathbb{R}^3 \) 上の部分空間であるか判定しなさい。
(証明は不要です。)
(1) \[ W_1 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle| \ \left\{ \begin{array}{l} \ 3x - \ \ y + 2z = 0 \\ -x - 3y - 5z = 0 \end{array}\right. \right\} \]
(2) \[ W_2 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle| (x-2y+z)(2x-3y+4z) = 0 \right\} \]
(3) \[ W_3 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle| (3x-5y+z)^2 + (2x+7y-2z)^2 = 0 \right\} \]
(4) \[ W_4 = \left\{ \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) \in \mathbb{R}^3 \ \middle|
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right)
= s \left( \begin{array}{ccc} 1 \\ 1 \\ 2 \end{array} \right)
+ t \left( \begin{array}{ccc} 3 \\ 0 \\ -1 \end{array} \right) , \ s,t \in \mathbb{R}
\right\}
\]
練習2
行列 \( A \) を \[
A = \left( \begin{array}{ccc} 1 & 1 & -1 & 1 \\ -2 & -1 & 0 & 1 \\ 3 & 1 & 1 & -3 \end{array} \right)
\]とする。このとき、次の部分空間 \( V \) の基底と次元を求めなさい。\[
V = \left\{ \vec{x} \in \mathbb{R}^4 \ \middle| \ A \vec{x} = \vec{0} \right\}
\]
練習3
つぎの \( \mathbb{R}^n \) のベクトルが生成する部分空間の次元が3となるような \( x \) の値とそのときの基底を求めなさい。\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 2 \end{array} \right) \ \ \
\vec{a_2} = \left( \begin{array}{ccc} 2 \\ 3 \\ -1 \\ -1 \end{array} \right) \ \ \
\vec{a_3} = \left( \begin{array}{ccc} 0 \\ -1 \\ 1 \\ 0 \end{array} \right) \\
\vec{a_4} = \left( \begin{array}{ccc} 4 \\ x \\ 2 \\ 3 \end{array} \right) \ \ \
\vec{a_5} = \left( \begin{array}{ccc} -2 \\ -3 \\ 1 \\ 1 \end{array} \right)
\]
5.練習問題の答え
解答1
(1) 部分空間である
「1次式 = 0」が2つある連立型ですね。
なので部分空間となります。
(2) 部分空間ではない
分解をすると「1次式 = 0」or「1次式 = 0」のような形で部分空間になりそうに見えるのですが、実は部分空間とはなりません。
反例をあげてみると、\[ \vec{x} = \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right) \ \ \
\vec{y} = \left( \begin{array}{ccc} 1 \\ 2 \\ 1 \end{array} \right) \]とする。
このとき、\( \vec{x}, \vec{y} \) はともに \( = 0 \) を満たすので \( W \) の要素といえますが、\[ \vec{x} + \vec{y} = \left( \begin{array}{ccc} 2 \\ 3 \\ 4 \end{array} \right) \]となり、\( (与式) = -6 \not = 0 \) となってしまい、\( W \) の要素とはなりません。
なので部分空間とはいえません。
「1次式 = 0」and「1次式 = 0」は部分空間となりますが、「1次式 = 0」or「1次式 = 0」は部分空間にならないことを頭の片隅にいれておくといいでしょう。
(3) 部分空間である。\[
(3x-5y+z)^2 + (2x+7y-2z)^2 = 0
\]は分解をすると、\[
\left\{ \begin{array}{l} 3x-5y+ \ \ z = 0 \\ 2x+7y-2z = 0 \end{array}\right.
\]となり、連立1次同次方程式となるため、部分空間となります。
(4) 部分空間である。
今までのような式ではなく、解が直接書かれていて少し驚くかもしれませんが、\[
W_4 = \left< \left( \begin{array}{ccc} 1 \\ 1 \\ 2 \end{array} \right) , \left( \begin{array}{ccc} 3 \\ 0 \\ -1 \end{array} \right) \right>
\]という生成系の部分空間パターンに落とし込めるので明らかに部分空間である。
解答2
まずは \( A \vec{x} = \vec{0} \) の解を求めましょう。
行列 \( A \) を行基本変形すると、\[
\begin{align*} &
\left( \begin{array}{ccc} 1 & 1 & -1 & 1 \\ -2_{+2} & -1_{+2} & 0_{-2} & 1_{+2} \\ 3_{-3} & 1_{-3} & 1_{+3} & -3_{-3} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1_{-1} & -1_{+2} & 1_{-3} \\ 0 & 1 & -2 & 3 \\ 0 & -2_{+2} & 4_{-4} & -6_{+6} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & 1 & -2 \\ 0 & 1 & -2 & 3 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]と変形できるので、\[
\dim V = n - \mathrm{Rank} \ A = 4 - 2 = 2
\]と求められます。
また、連立方程式の解は\[
\left\{ \begin{array}{l} x + z - 2w \\ y - 2z + 3w = 0 \end{array}\right.
\]を解くと求められる(自由度は2)。
ここで、\( z = s \), \( w = t \) とおくと、\( x = -s + 2t \), \( y = 2s - 3t \) となるので、\[
\vec{x} =
\left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right)
= s \left( \begin{array}{ccc} -1 \\ 2 \\ 1 \\ 0 \end{array} \right)
+ t \left( \begin{array}{ccc} 2 \\ -3 \\ 0 \\ 1 \end{array} \right)
\]となり、\( V \) の基底は\[
V = \left\{\ \left( \begin{array}{ccc} -1 \\ 2 \\ 1 \\ 0 \end{array} \right), \left( \begin{array}{ccc} 2 \\ -3 \\ 0 \\ 1 \end{array} \right) \ \right\}
\]となります(基底は基本解の組み合わせ)。
解答3
生成系の部分空間の次元は、最大数となる。
今回は次元が3となればいいので、1次独立なベクトルの最大数が3となればよい。
1次独立な最大組を求めるために行列 \( A \) を\[
A = \left( \vec{a_1}, \vec{a_2}, \vec{a_3}, \vec{a_4}, \vec{a_5} \right)
\]とする。この行列の階数が3となるような \( x \) の値を求める。
行基本変形を行うと、\[
\begin{align*} A = &
\left( \begin{array}{ccc} 1 & 2 & 0 & 4 & -2 \\ 2_{-2} & 3_{-4} & -1 & x_{-8} & -3_{+4} \\ 0 & -1 & 1 & 2 & 1 \\ 2_{-2} & -1_{-4} & 0 & 3_{-8} & 1_{+4} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc}1 & 2 & 0 & 4 & -2 \\ 0 & -1_{+1} & -1_{-1} & x-8_{-2} & 1_{-1} \\ 0 & -1 & 1 & 2 & 1 \\ 0 & -5_{+5} & 0_{-5} & -5_{-10} & 5_{-5} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc}1 & 2 & 0 & 4 & -2 \\ 0 & 0 & -2 & x-10 & 0 \\ 0 & -1 & 1 & 2 & 1 \\ 0 & 0 & -5 & -15 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 2 & 0 & 4 & -2 \\ 0 & 0 & -2_{+2} & x-10_{+6} & 0 \\ 0 & -1 & 1 & 2 & 1 \\ 0 & 0 & -5 & -15 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 2 & 0 & 4 & -2 \\ 0 & -1 & 1 & 2 & 1 \\ 0 & 0 & -5 & -15 & 0 \\ 0 & 0 & 0 & x-4 & 0 \end{array} \right)
\end{align*}
\]と階段行列に変形できる。
ここで、行列 \( A \) の階数が3となるためには、\( x - 4 = 0 \)、つまり \( x = 4 \) であればよい。
さらに \( x = 4 \) のとき、1次独立なベクトルの最大組は行基本変形の結果より、\( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) となる。
よって基底は\[
\left\{ \
\left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 2 \end{array} \right) , \
\left( \begin{array}{ccc} 2 \\ 3 \\ -1 \\ -1 \end{array} \right) , \
\left( \begin{array}{ccc} 0 \\ -1 \\ 1 \\ 0 \end{array} \right) \
\right\}
\]となる。
6.さいごに
今回は部分空間についてのまとめを行いました。
解空間の次元と基底の求め方と生成系の次元と基底の求め方を逆にしてしまう人がたまにいるので気をつけましょう。
次回は部分空間の和空間、共通空間についてまとめたいと思います。
*1:基本解は連立方程式の解をすべて表現するために必要な1次独立なベクトルの組のことを表します。
関連広告・スポンサードリンク




![PROGテストについて [就活に活かせ!!]](https://www.momoyama-usagi.com/wp-content/themes/diver/images/noimage.gif)