スポンサードリンク
こんにちは、ももやまです。
前回は
- 順序回路に関する基礎知識(フリップフロップなど)
- 順序回路の読み方
など、順序回路を「よむ」練習をしましたね。
今回からは、いよいよ順序回路を「つくる」側にチャレンジしてみましょう! しかし、いきなり順序回路を書くのは少し難しいです。
なので、今回は順序回路を設計するために与えられた問題を状態遷移図や状態遷移表に落とし込む練習を例題2問、練習問題2問でしてみましょう!
※ 状態遷移図や状態遷移表の書き方はわかるから、DフリップフロップやJKフリップフロップを使って順序回路を書く方法が知りたいという人は、下のリンクへどうぞ。
スポンサードリンク
[例題1] カウンタの設計
まずは、順序回路の中でも最も基本的なパターンでもある「カウンタ」に関する回路を設計する例題で、順序回路の設計で使う状態遷移図・状態遷移表の書き方を説明していきます。
1が3回入力されるごとに「1」が出力され、それ以外のときに「0」が出力されるアップカウンタ回路を考える。このとき、(1)〜(5)の問いに答えなさい。
(1) 入力変数、出力変数は最低何個必要か答えなさい。
(2) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために定義する必要がある状態は最低何個か?)
(3) 状態遷移図を書きなさい。
(4) 状態遷移表を書きなさい。
(5) このアップカウンタを作るためには、最低何個のフリップフロップが必要か答えなさい。
[解説1]
(1) 必要な入力変数・出力変数を考えよう
順序回路を設計する上で最初に考えることは、与えられた問題から必要な入力変数・出力変数を考えることです。
今回の問題は、「1が3回入力されるごとに1を出力されるアップカウンタ」でしたね。
この問題を詳しく言い換えると、「1つの変数の入力が0か1かどうかを判定し、『3回1と判定されるごとに1を、それ以外のときに0』を1つの変数から出力する回路」と言えますね。
よって、入力変数は最低1個、出力変数も最低1個必要なことがわかります。
※ この後状態遷移図を考えるために、入力変数を \( x \)、出力変数を \( z \) として定義しましょう。
(2) 必要な内部状態を考えよう
必要な入力変数・出力変数を考えた後は、順序回路を表現するために必要な内部状態を考えます。
ここで、必要な内部状態というのは「順序回路を表現するために必要な記憶すべき状態」だと思っていただけたらOKです。
今回は「1が3回入力されるごとに1を出力する」回路を作りたいため、最後に1が出力されてからの入力の数を記憶する必要があります。そのため、
- 最後に1が出力されてから1が0回入力された状態
(1が入力されていない状態) - 最後に1が出力されてから1が1回入力された状態
- 最後に1が出力されてから1が2回入力された状態
を記憶する必要があります[1] … Continue reading。
※ 「最後に1が出力されてから1が3回入力された状態」も必要では? と思うかもしれませんが、1が3回入力された状態のときは1が出力されるため、「最後に1が出力されてから1が3回入力された状態」を記憶する必要はありません。
そのため、必要な内部状態は
- 最後に1が出力されてから1が0回入力された状態
- 最後に1が出力されてから1が1回入力された状態
- 最後に1が出力されてから1が2回入力された状態
の3個とわかります。
(3) 状態遷移図を書いてみよう
必要な内部状態を考えた後は、いよいよ状態遷移図を書いていきましょう[2] … Continue reading。
その前に、状態遷移図の書き方について確認しましょう。
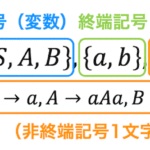
状態遷移図の書き方
[1] 各状態を〇で表し、〇の中に状態名をつける

[2] 現状態から次状態への変化を該当する入力、出力とともに矢印で書く
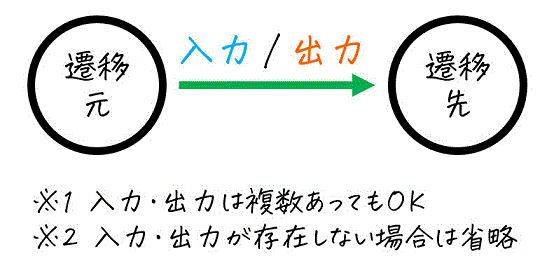
(例) 現状態 \( q_0 \) から \( \textcolor{deepskyblue}{x = 1} \) を入力した際に、\( \textcolor{magenta}{q_1} \) に遷移し、出力が \( \textcolor{orange}{z = 0} \) であることを書く場合
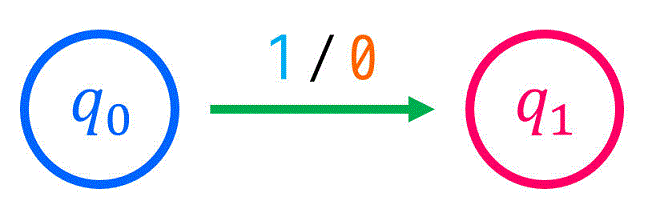
[3] 各状態(現状態)の全ての入力に対しての遷移先を書く
例えば、入力が \( x \) の1変数であれば、各状態ごとに \( x = 0 \) のとき、\( x = 1 \) のときの遷移先を書きます。ただし、定義されない入力に対しての遷移先は省略OKです[3]例えば、\( (x,y) = (1,1) \) の状態が定義されない場合は、\( (x,y) = (0,0), (0,1), (1,0) \) の3パターンを書けばOK。。
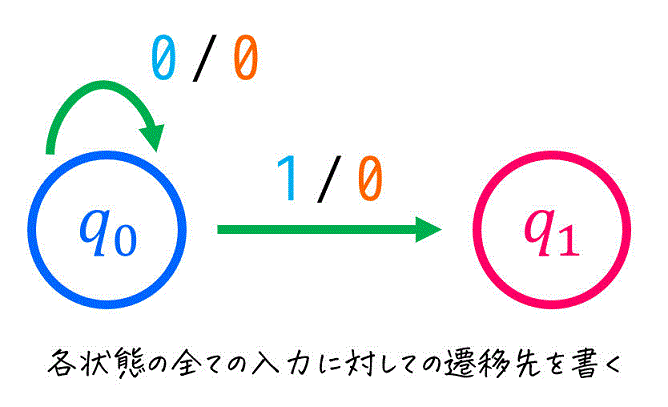
[4] 各状態の各入力に対する遷移先は必ず1つ
(遷移先が1つに特定できない書き方をしたらダメ)
下の例の場合、現状態 \( q_0 \) に対して、\( \textcolor{deepskyblue}{x = 1} \) に対する遷移先が \( q_1 \), \( q_2 \) の2つになっています。こんな書き方をしてはいけません。
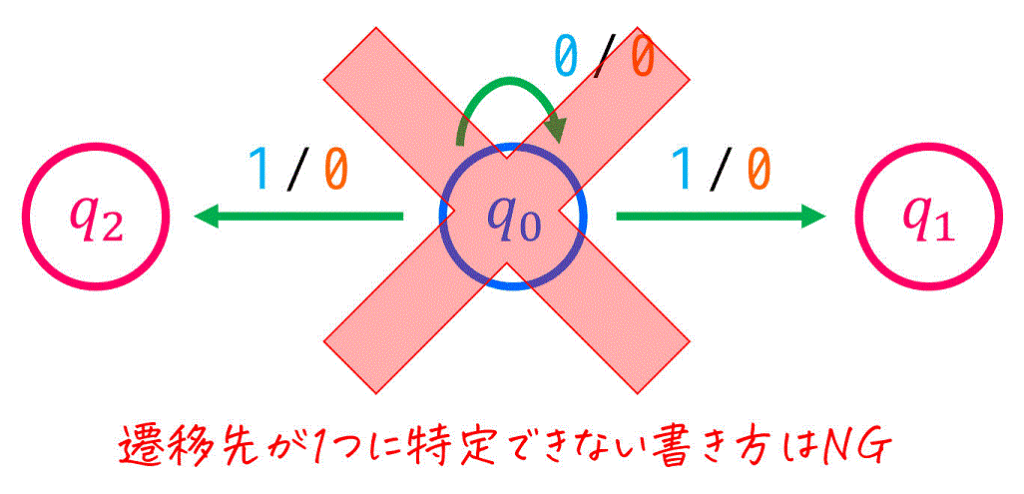
もう1度言います。各状態の各入力に対する遷移先は必ず1つです。2つ以上になったり、遷移先なしみたいなことはできません。
実際に状態遷移図にチャレンジ!
説明が終わったので、実際に状態遷移図を書いていきましょう。
まず、(2)で考えた状態に名前をつけましょう。名前はなんでもいいですが今回は、
- 最後に1が出力されてから1が0回入力された状態: \( q_0 \)
- 最後に1が出力されてから1が1回入力された状態: \( q_1 \)
- 最後に1が出力されてから1が2回入力された状態: \( q_2 \)
としましょうか。
名前を付けたら、まずは下のように考えた状態を配置しましょう。
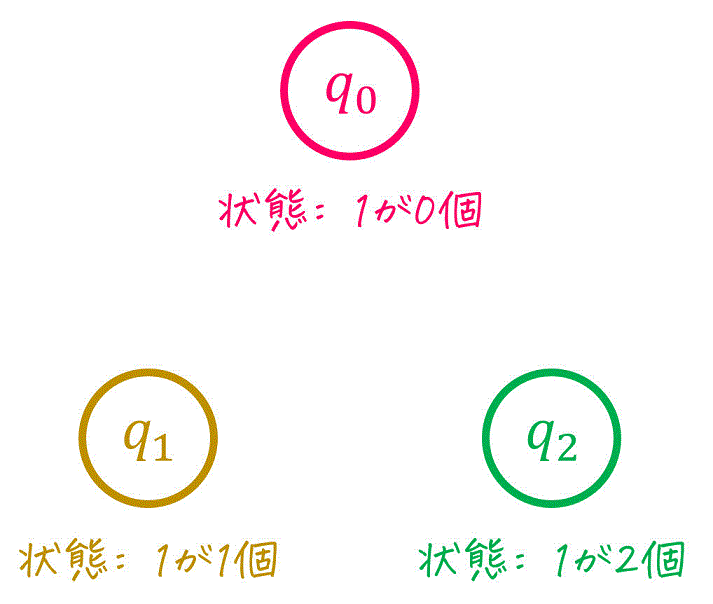
状態を配置したら、各状態ごとに各入力 \( x = 0 \), \( x = 1 \) ごとの遷移先を考えます。
[1] \( x = 0 \) のとき
\( x = 0 \) のときは、1の数が増えることはありませんよね。また、1の数が増えないため、出力 \( z \) が1になることもありませんよね。
そのため、\( x = 0 \) が入力された際は次状態は現状態と同じ(=状態が変化しない)で、出力は \( z = 0 \) となると言えます。
なので、状態遷移図に入力が \( x = 0 \) のときの遷移先と、出力が \( z = 0 \) である矢印を足しましょう。
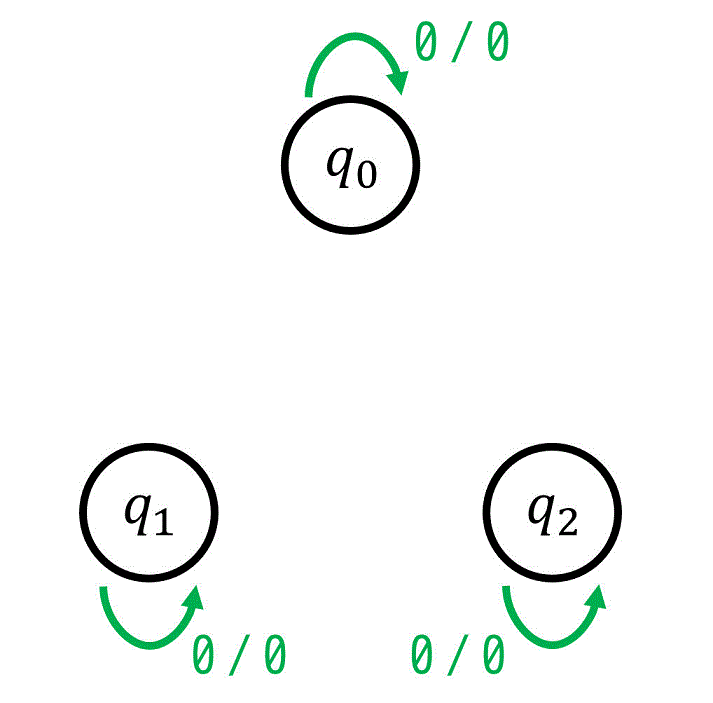
[2] \( x = 1 \) のとき
\( x = 1 \) のときは、1が入力された回数が1回増えますね。
そのため、
- \( q_0 \)(1が0回)のときは \( q_1 \)(1が1回)に遷移
- \( q_1 \)(1が0回)のときは \( q_2 \)(1が2回)に遷移
することがわかります。また、\( q_0 \), \( q_1 \) のときは1が入力された回数が3回に達しないため、出力は \( z = 0 \) となります。
つぎに、\( q_2 \)(1が2回入力された状態)のときに1が入力されると、1が入力された回数が3回に達するため、出力が \( \textcolor{purple}{ z = 1} \) となります。
さらに、最後に1が入力されてから1が入力された回数は0にリセットされるため、状態は \( q_0 \) となります。
これらを状態遷移図に加えると、下のようになります。
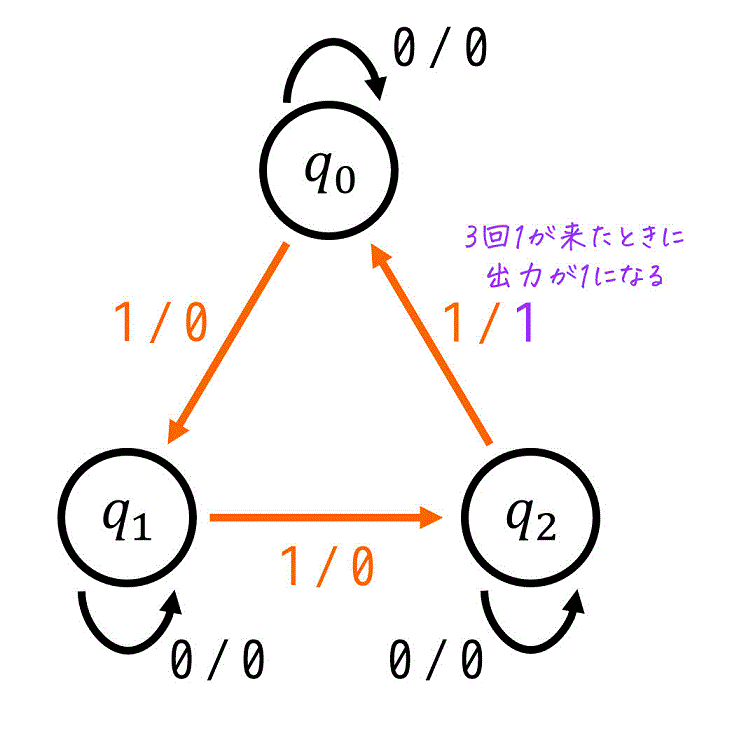
これで、各状態ごとに各入力 \( x = 0 \), \( x = 1 \) ごとの遷移先と出力を状態遷移図に書くことができましたね。よって状態遷移図の完成です!
(4) 状態遷移表を書いてみよう
状態遷移表は、状態遷移図を作れば機械的に作ることができます。
まずは、
- 現状態
- 次状態(入力ごと)
- 出力(入力ごと)
の3つの情報を書ける表を書きましょう。
※ 行数は、作った状態の数だけあればOKです。今回は3つなので3行分用意しました。
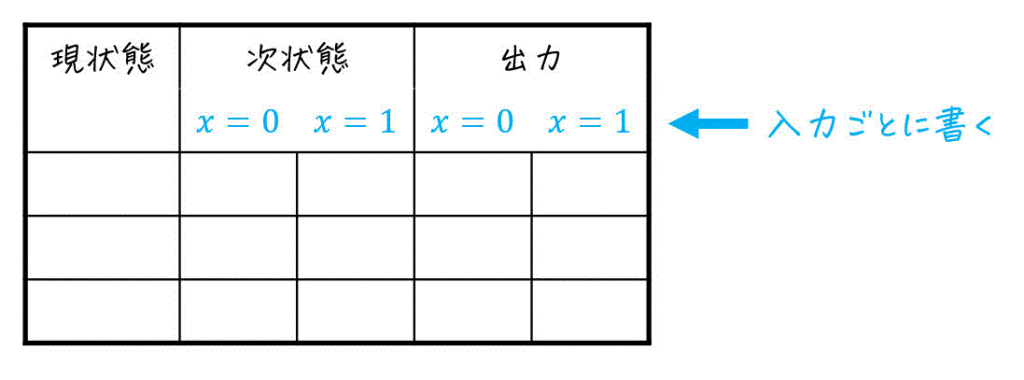
(状態遷移表の書き方は様々です)
つぎに、作った表の現状態の部分に、作った状態をすべて並べていきましょう。
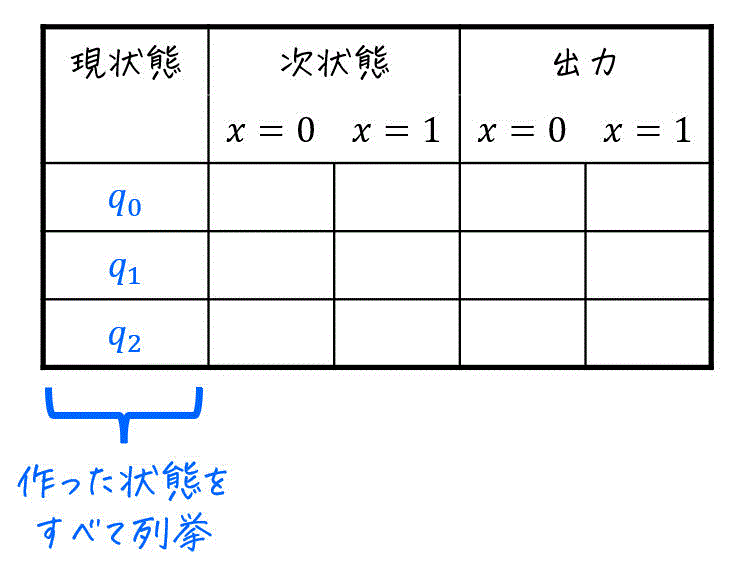
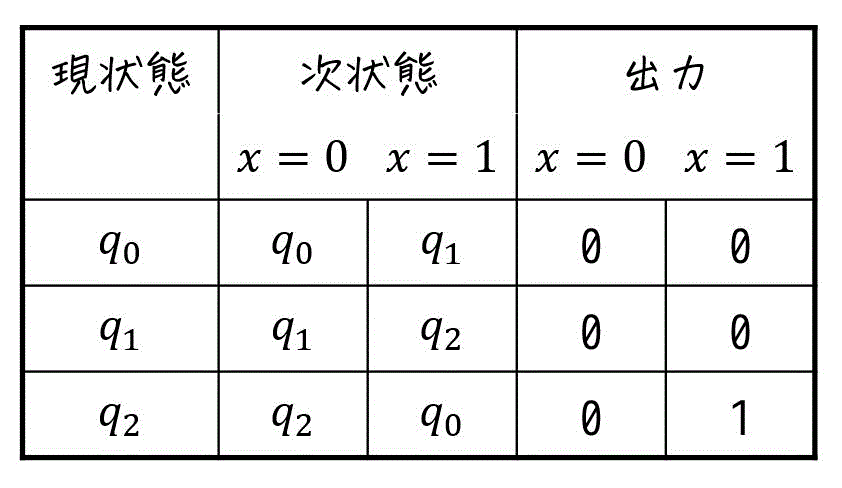
あとは、下のように各現状態ごとに各入力(今回は \( x = 0 \), \( x = 1 \))ごとの次状態(遷移先のこと)、および出力を書いていけばOKです。
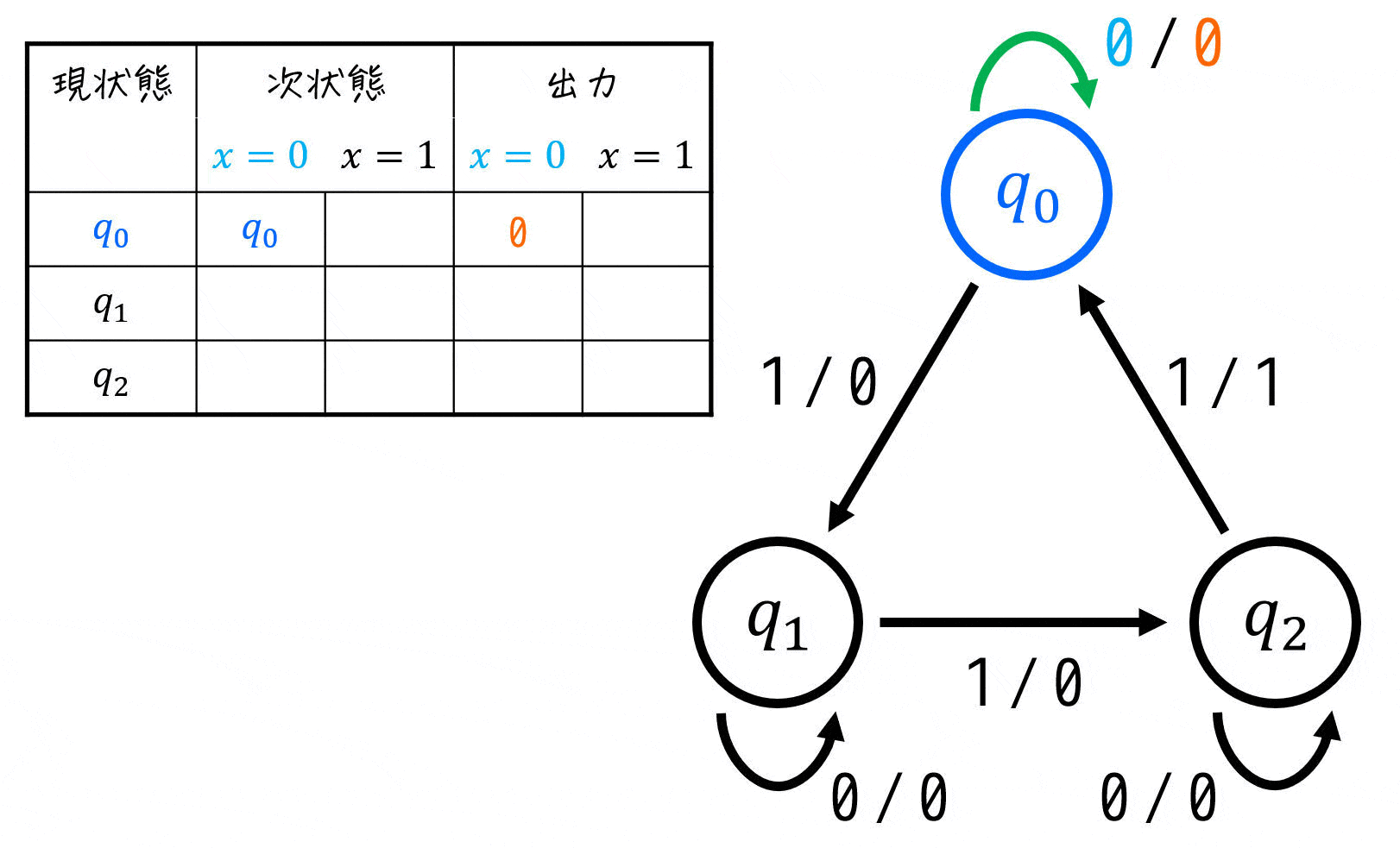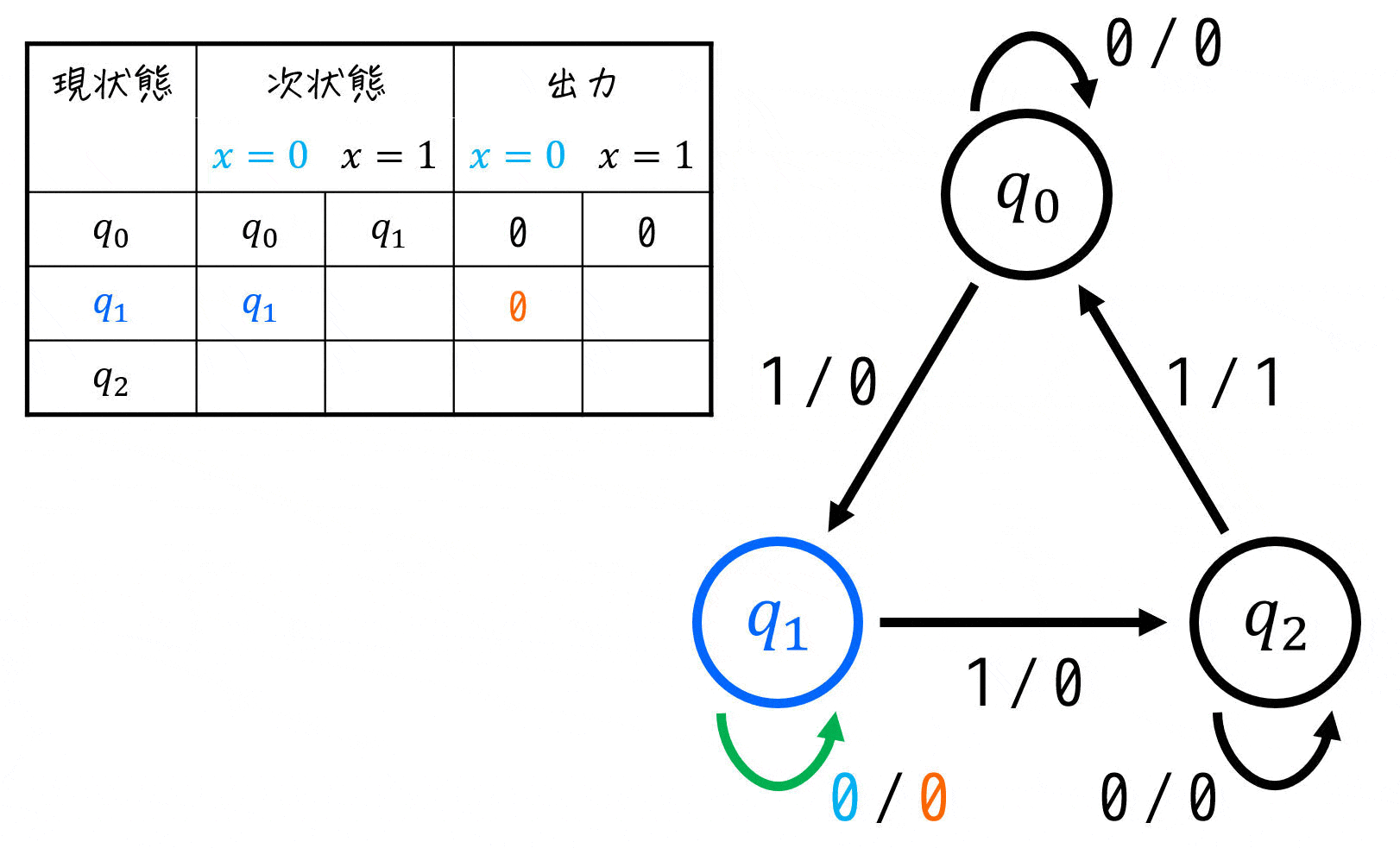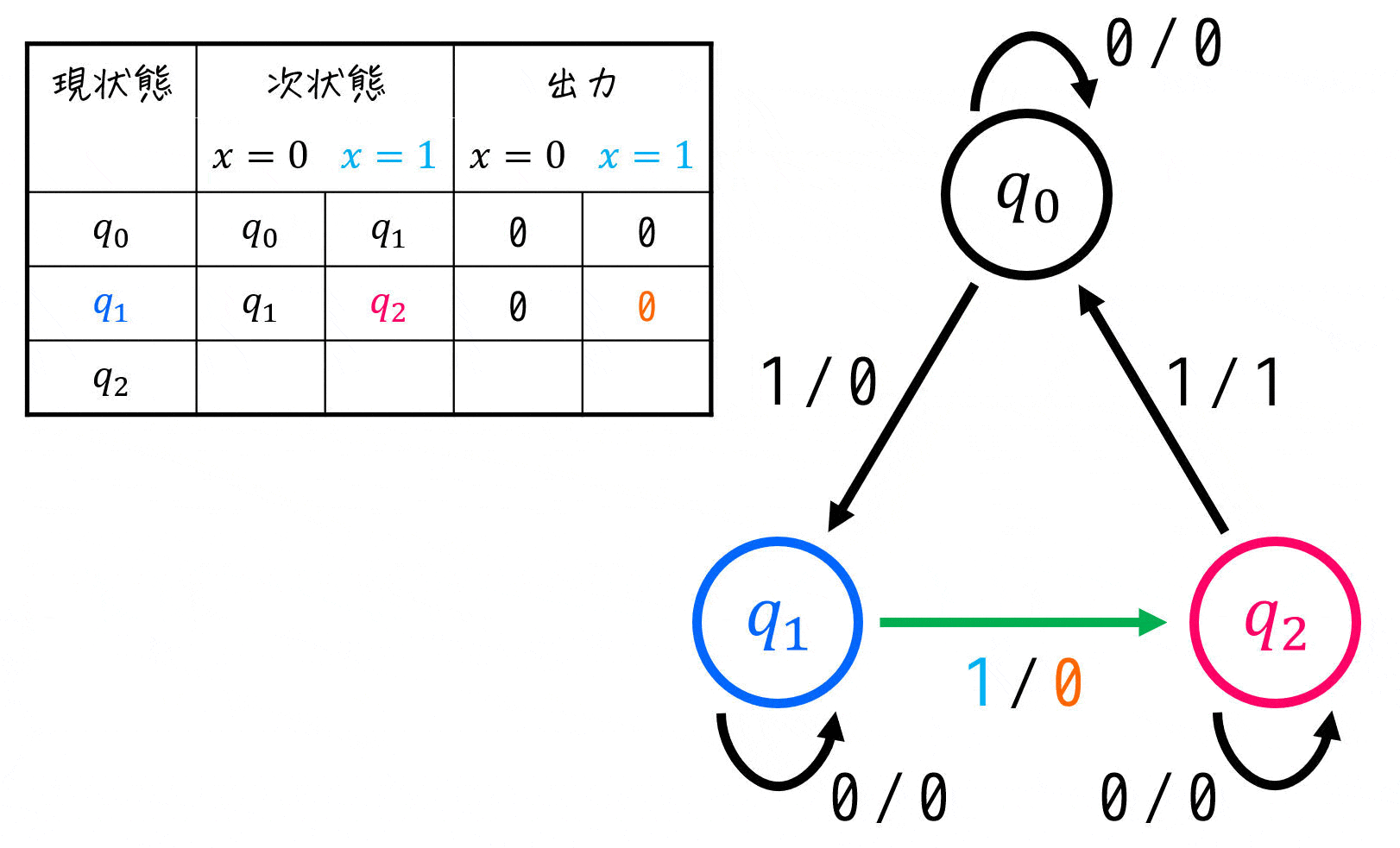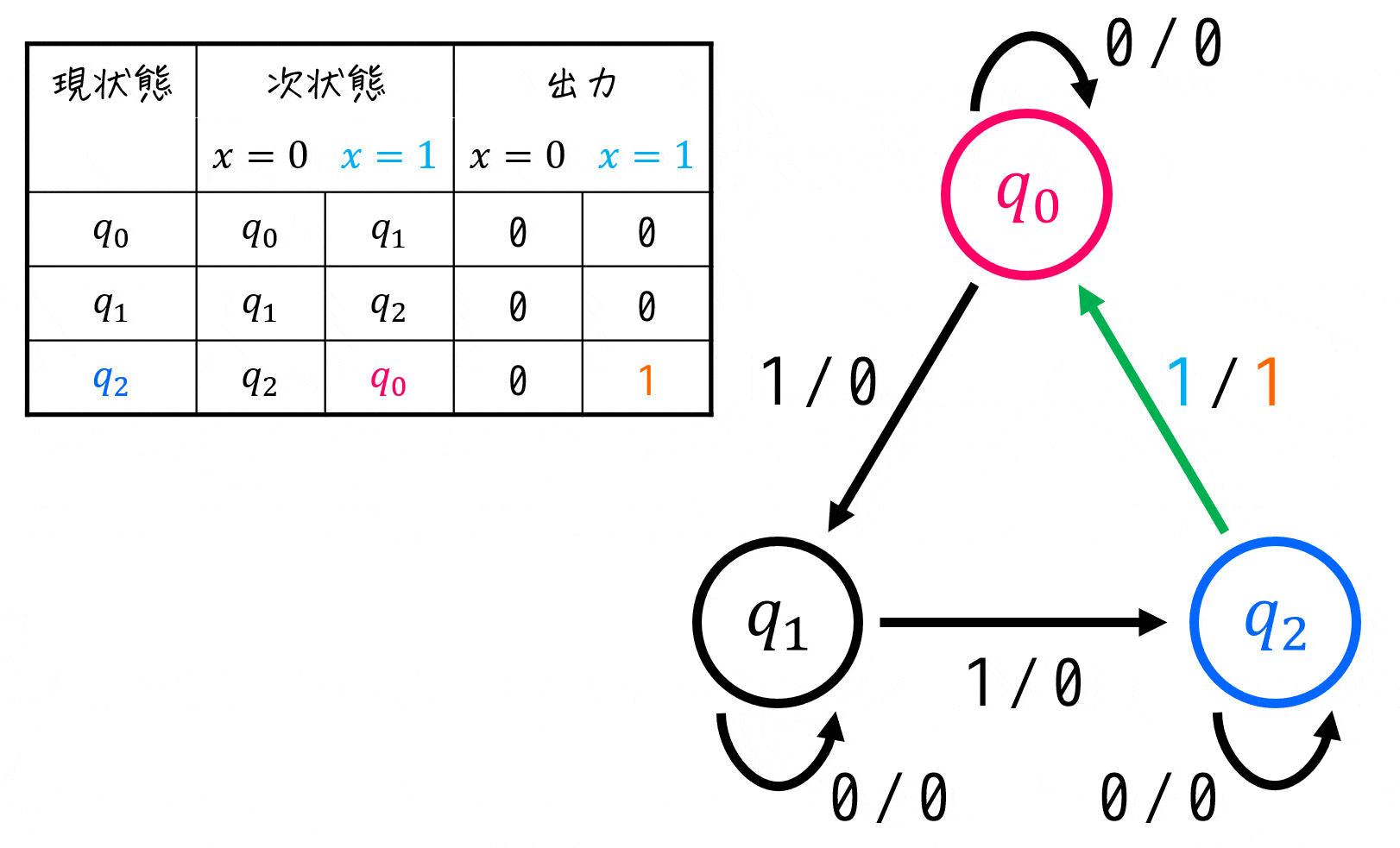
すべて埋め終われば、状態遷移表の完成です!
(5) 必要なフリップフロップの数を考えよう
1つのフリップフロップ(FF)は、0, 1の2つ(1ビット)の状態を記憶することができますね。
そのため、フリップフロップを1つ増やすと記憶できる状態の数は2倍になりますね。
(実際に樹形図を書くと2倍になっていくことがわかりやすいです。)
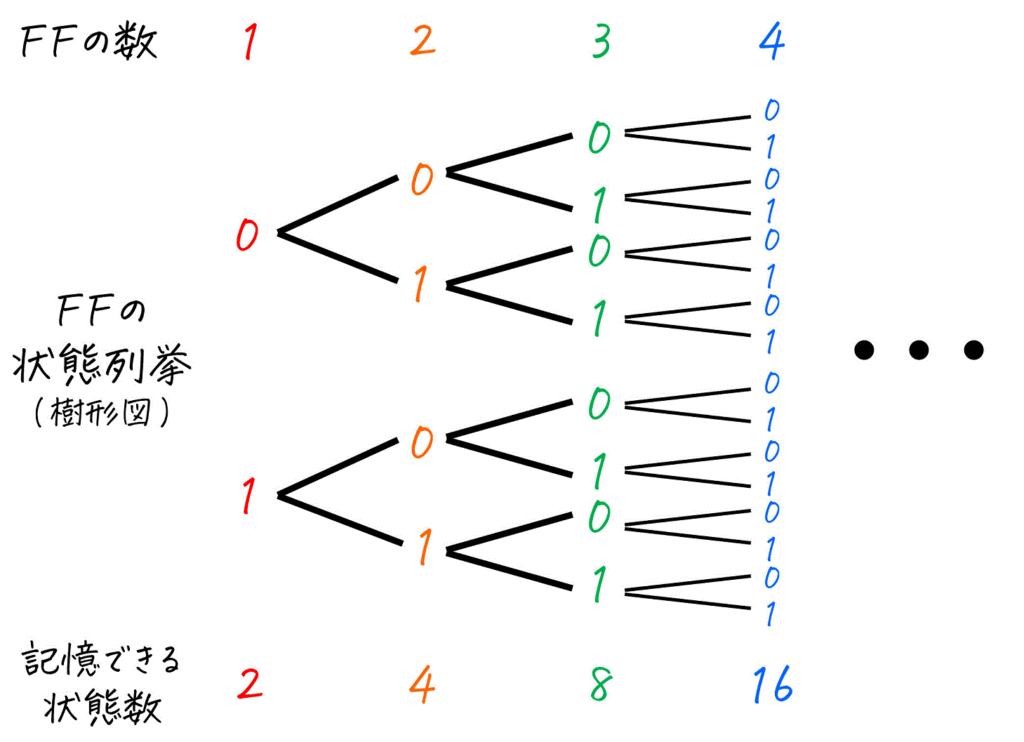
今回は、状態が3つあるので1つのフリップフロップでは記憶ができませんが、2つのフリップフロップがあれば最大で4つの状態を記憶できますね。
よって、「1が3回入力されたときに1を出力する回路」を作るためには、最低でも2つのFFが必要なことがわかります。
※ 数学っぽく解くのであれば、\[
2^{n-1} < 3 \leqq 2^n
\]を満たす \( n \) を求めることができます[4]\( n \) 個のフリップフロップで与えられた回路が記憶できるとき、\( n -1 \) … Continue reading
フリップフロップ(D-FF, T-FF, JK-FF, SR-FFの種類は問わない)の個数と、記憶できる状態の最大数の関係を表にしたものを下に記す。
| FFの個数 | 記憶できる状態数 |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| ︙ | ︙ |
| \( n \) | \( 2^n \) |
また、ある \( a \) 個の状態を記憶するために必要なフリップフロップの数 \( n \) は、\[
\textcolor{red}{2^{n-1}} < a \leqq \textcolor{blue}{2^{n}}
\]を満たすような不等式を満たすような \( n \) を求めることでも求められる。
\( 2^{n-1} \) … フリップフロップが1個不足してギリギリ回路が記憶できない場合
\( 2^{n} \) … フリップフロップがギリギリ足りている場合
[数学っぽい解き方] \( 2^{\textcolor{red}{6}-1} < 50 \leqq 2^{\textcolor{red}{6}} \) より、最低数は6個。
※ フリップフロップの個数とそのときに記憶できる状態数を表にしたものを下においておくので、もしよければ参考にしてください。
スポンサードリンク
[例題2] 自動販売機の設計
順序回路の問題で頻出なのが「自動販売機の設計」です。
なので、今度は自動販売機の設計を状態遷移図・状態遷移表を書くことで体験しましょう。
つぎの[仕様]を満たす300円のおもちゃを販売するガチャガチャ(自動販売機)の回路を設計したい。
[仕様]- 100円硬貨のみを受け付け、投入金額が300円になると商品が出てくる。
- 返却ボタンを搭載する。返却ボタンを押すと、投入された硬貨がすべて返却され、投入金額がリセットされる。
- 商品が出たかどうか、硬貨が返却されたかどうかをこの回路で判定すること。
- 1度に2枚以上の硬貨が投入されることは考えなくてよい。
- 硬貨の投入と、返却ボタンを押す動作が同時に生じることは考えなくてよい。
次の(1)~(5)の問いに答えなさい。
(1) 入力変数、出力変数は最低何個必要か答えなさい。
(2) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために最低何個の状態が必要?)
(3) 状態遷移図を書きなさい。
(4) 状態遷移表を書きなさい。
(5) この回路を設計するためには、最低何個のフリップフロップが必要か答えなさい。
(1) 必要な入力変数・出力変数を考えよう
まずは、回路を設計する際に必要な入力変数と出力変数を考えましょう。
- 入力変数(2個)
- 100円硬貨が投入されたかを表す変数 \( x \)
(投入されていない → 0、投入された → 1) - 返却ボタンが押されたかを表す変数 \( y \)
(押されていない → 0、押された → 1)
- 100円硬貨が投入されたかを表す変数 \( x \)
- 出力変数(2個)
- 商品が出たかを表す変数 \( z \)
(出なかった → 0、出た → 1) - 硬貨が返却されたかを表す変数 \( r \)
(返却されなかった → 0、返却された → 1)
- 商品が出たかを表す変数 \( z \)
※ 0と1の割り当ては逆にすることもできます。
(例: 100円硬貨が投入された状態を0、投入されていない状態を1)
よって、答えは
- 入力変数: 2個
- 出力変数: 2個
となります。
(2) 必要な内部状態を考えよう
内部状態は、「回路を表すために必要な記憶」の状態を表すのでしたね。
今回は、最後に商品が出てから投入された合計金額を100円単位[5]100円硬貨以外の硬貨は入ってこないため、合計金額は必ず100円単位となる。で記憶すればOKですね。
(さらに商品が出る or 返却ボタンが押されると、投入金額の合計は0円にリセットされる)
そのため、
- 最後に商品が出てから合計0円投入された状態(硬貨が投入されていない状態)
- 最後に商品が出てから合計100円投入された状態
- 最後に商品が出てから合計200円投入された状態
の3種類の状態を記憶すれば、回路が表せますね。
よって、必要な内部状態は最低3個であることがわかります。
※ 合計300円投入すると商品が出てくるため、「最後に商品が出てから合計300円投入された状態」を記憶する必要はない。
(3) 状態遷移図を書いてみよう
まずは、(2)で考えた状態に名前を付けましょう。
今回は、最後に商品が出てから
- 合計0円投入された状態 → \( q_0 \)
- 合計100円投入された状態 → \( q_1 \)
- 合計200円投入された状態 → \( q_2 \)
とつけることにします。
つぎに、名前を付けた状態を並べましょう。
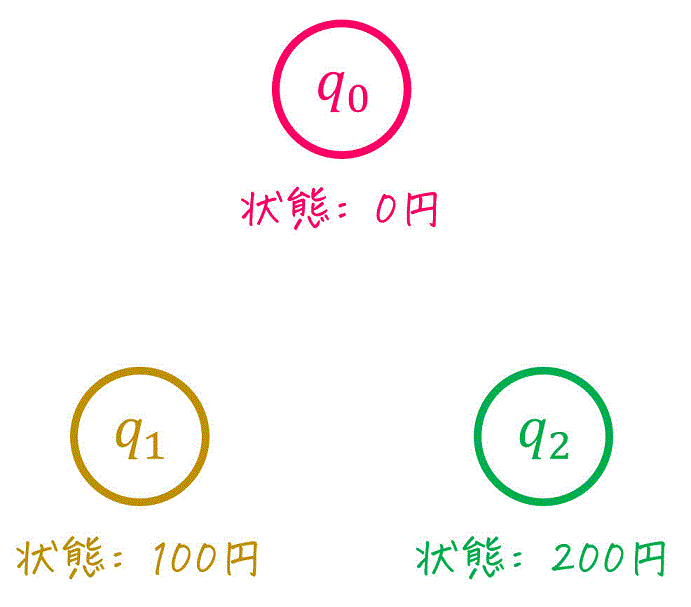
ここからは、(1)で考えた
- 入力変数
- 100円硬貨が投入されたかを表す変数 \( x \)
(投入されていない → 0、投入された → 1) - 返却ボタンが押されたかを表す変数 \( y \)
(押されていない → 0、押された → 1)
- 100円硬貨が投入されたかを表す変数 \( x \)
- 出力変数
- 商品が出たかを表す変数 \( z \)
(出なかった → 0、出た → 1) - 硬貨が返却されたかを表す変数 \( r \)
(返却されなかった → 0、返却された → 1)
- 商品が出たかを表す変数 \( z \)
を使いながら状態遷移図を書いていきましょう。
今回は、入力も出力も2変数あるので、状態遷移図に入力・出力変数をどの順番で書くかも考えましょう。素直に \( xy \) / \( zr \) としますか[6]例えば入力が \( x = 0 \), \( y = 1 \) で、出力が \( z = 1 \), \( r = 0 \) であれば 01 / 10 と表記されます。。
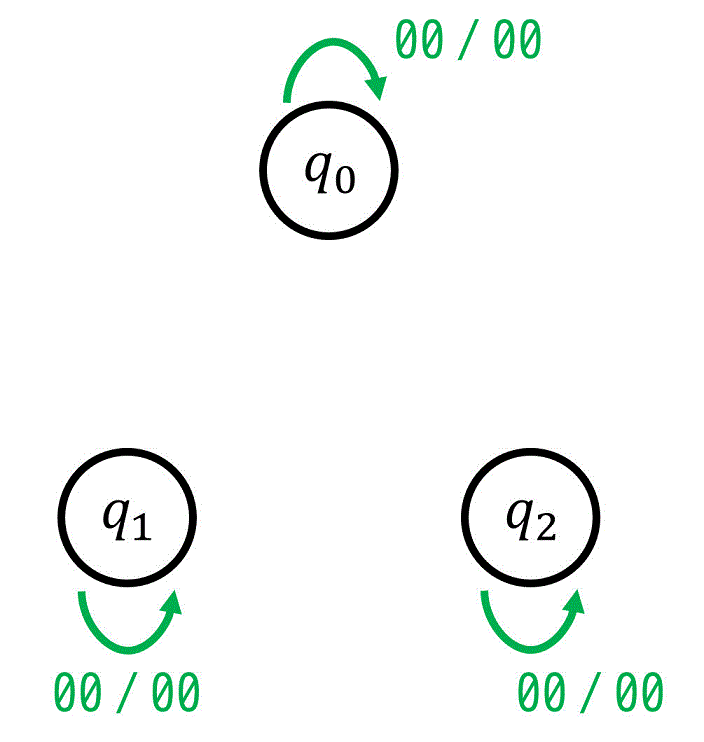
[1] 入力: \( x = 0 \), \( y = 0 \) のとき
100円玉も投入されておらず、返却ボタンが押されていない状態を考えましょう。
このときは、状態は変化しませんね。(つまり次状態は現状態と等しくなる。)
また、100円玉を投入しないため、300円に達することもありません(つまり \( z = 0 \) )し、返却ボタンも押されていないため、コインが返却されることもありません(つまり \( r = 0 \))。
これらを踏まえることで、各状態ごとに \( (x,y) = (0,0) \) のときの遷移先と出力が下のように状態遷移図に追記できます。
[2] 入力: \( x = 1 \), \( y = 0 \) のとき
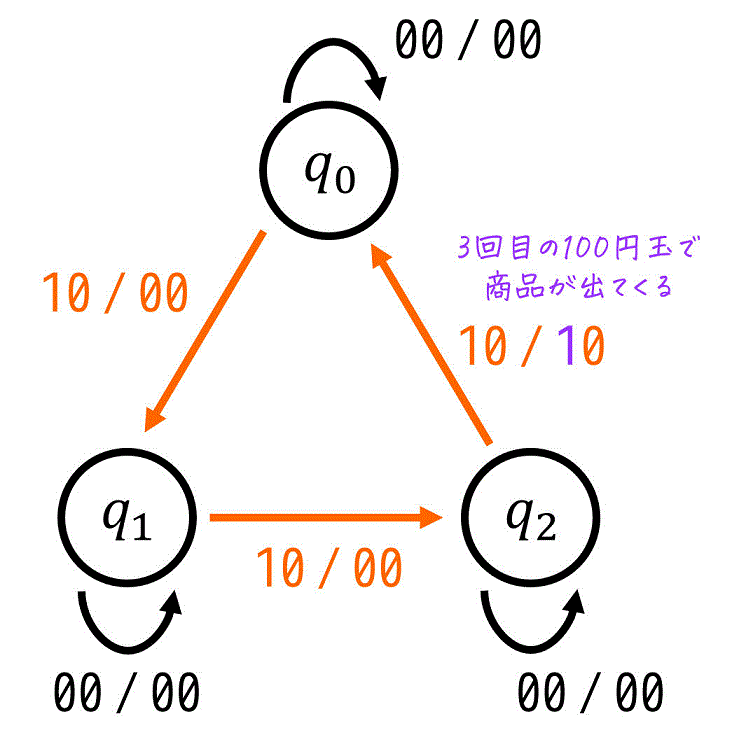
つぎは、100円玉が投入され、返却ボタンが押されていない状態を考えましょう。
このときは
- \( q_0 \)(0円)のとき → \( q_1 \)(100円)
※ 商品は出てこない \( z = 0 \) - \( q_1 \) (100円)のとき → \( q_2 \)(200円)
※ 商品は出てこない \( z = 0 \) - \( q_2 \) (200円)のとき → 商品が出てくる + 金額リセット \( q_0 \)(0円)
※ 商品が出てくる \( z = 1 \)
となりますね。
また、返却ボタンは押されていないため、硬貨は返却されません。
(つまり \( r = 0 \)
これらを踏まえることで、各状態ごとに \( (x,y) = (1,0) \) のときの遷移先と出力が下のように状態遷移図に追記できます。
[3] 入力: \( x = 0 \), \( y = 1 \) のとき
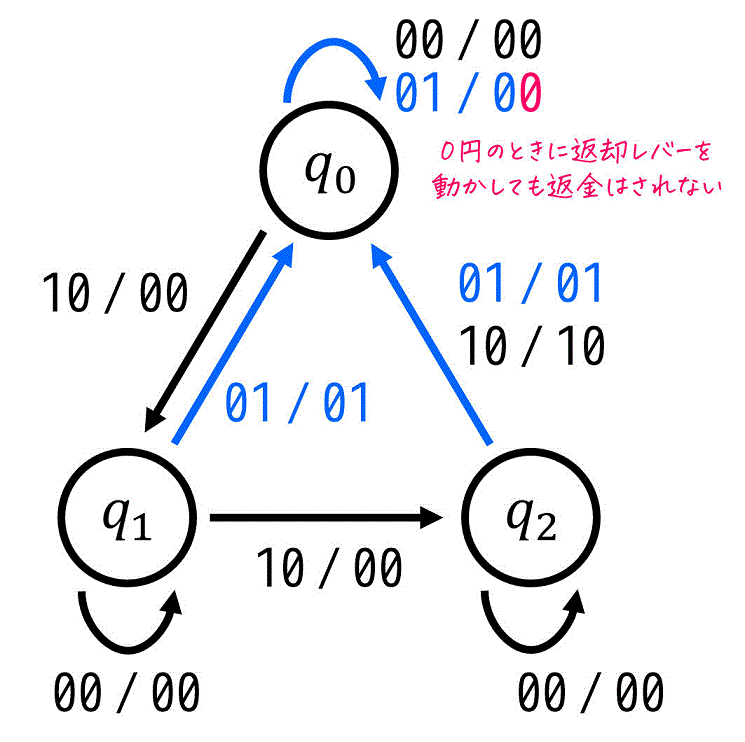
最後に、返却ボタンが押されたとき(かつ硬貨が投入されなかったとき)を考えましょう。
返却ボタンが押されるということは、投入された金額は0円にリセットされますよね。つまり、どの状態であろうが次状態は \( q_0 \)(投入金額0円)になりますね。
さらに、返却ボタンを押された際に投入金額が100円以上だった場合は、硬貨(投入金)が返却されますね(つまり \( r = 1 \))。
※ 0円のときは返却される硬貨がないので、\( r = 0 \) な点に注意!
これらを踏まえることで、各状態ごとに \( (x,y) = (0,1) \) のときの遷移先と出力が下のように状態遷移図に追記できます。
\( (x,y) = (1,1) \) は考えなくてOK
\( (x,y) = (1,1) \) のときは考えなくてOKなので、これで状態遷移図の完成です!
(4) 状態遷移表を書いてみよう
まずは、
- 現状態
- 次状態(入力ごと)
- 出力(入力ごと)
の3つの情報を書ける表を書きましょう。
さらに、作った現状態をすべて列挙してしまいましょう。
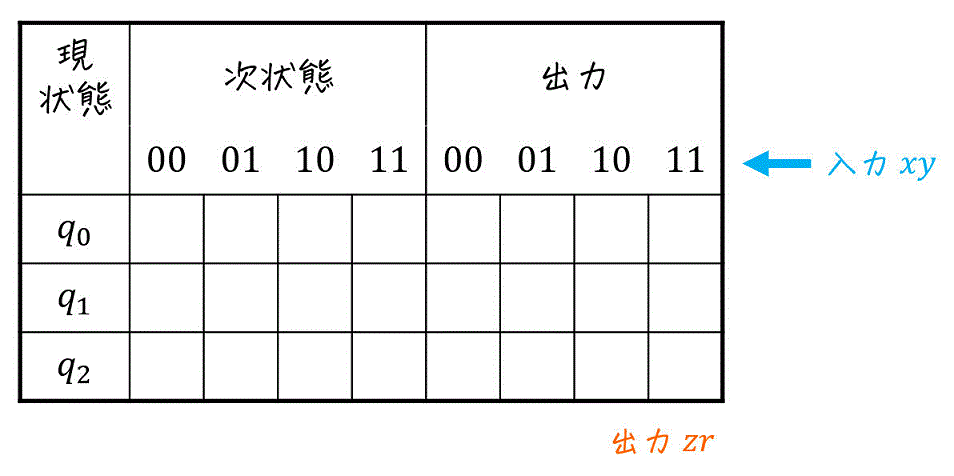
※ 入力部分でいちいち \( (x,y) = (0,0) \), \( (x,y) = (0,1) \), … と書いていると列幅がでかくなるので、今回は \( (x,y) = \) の部分を省略して表記しています。
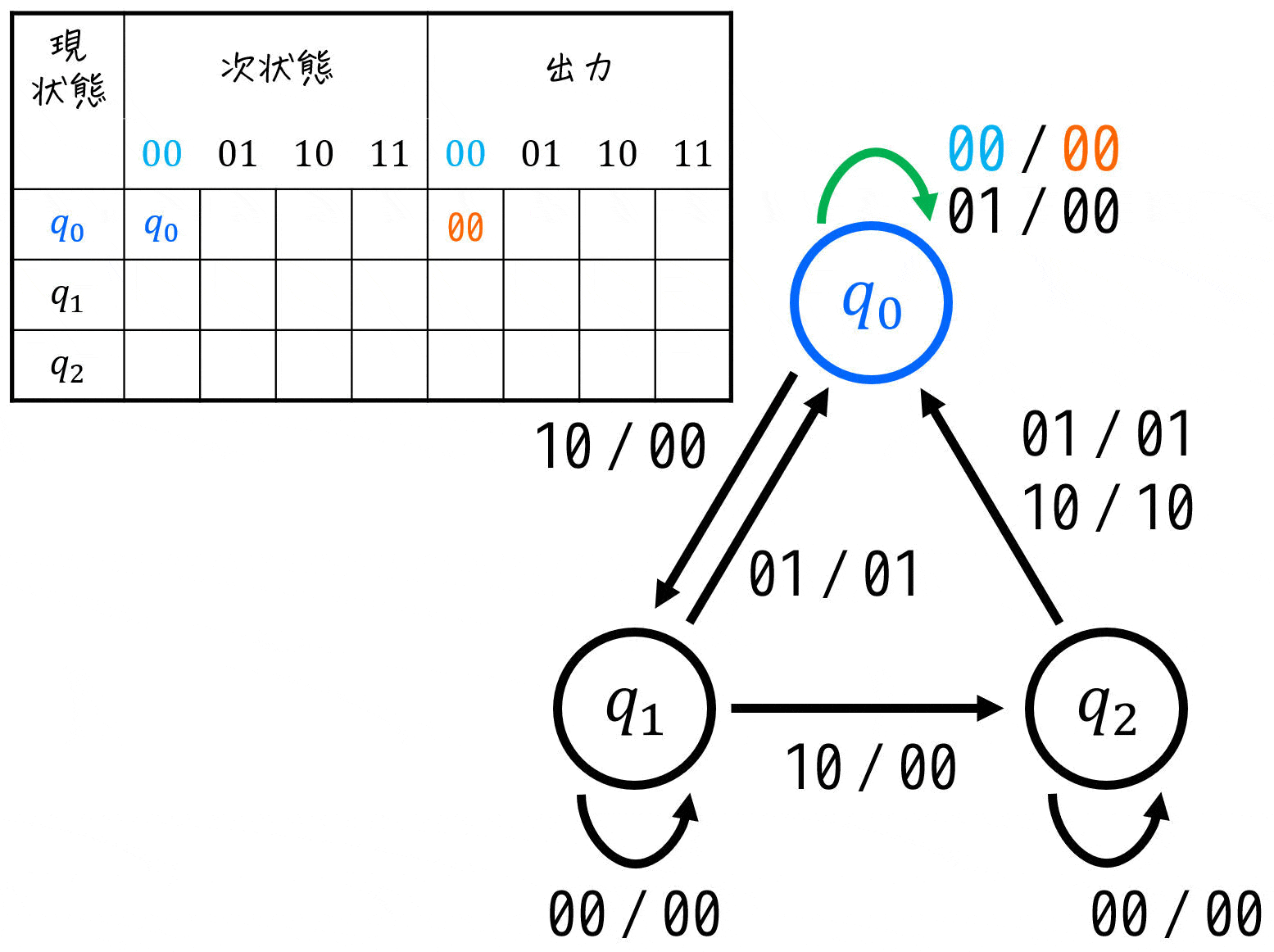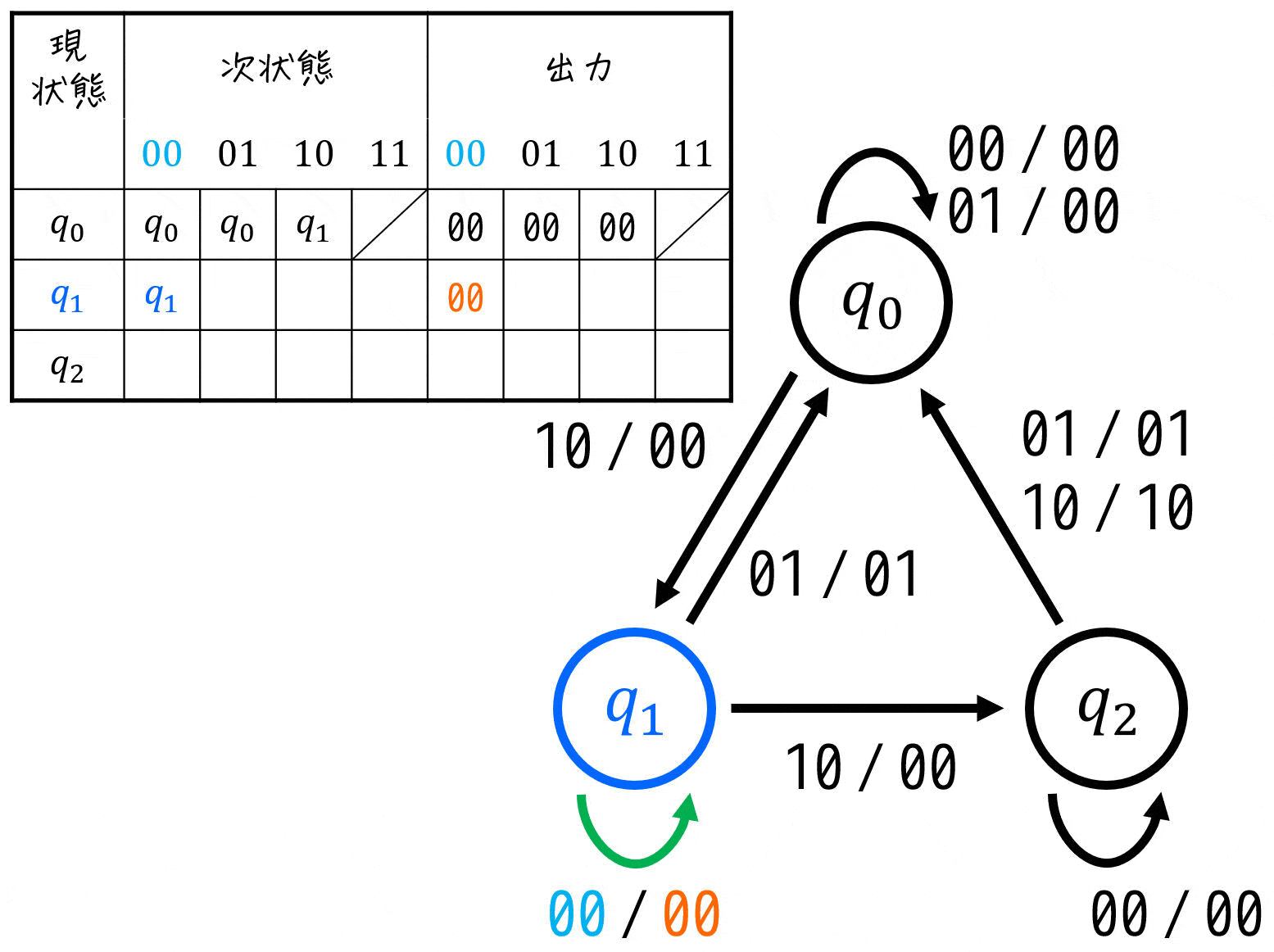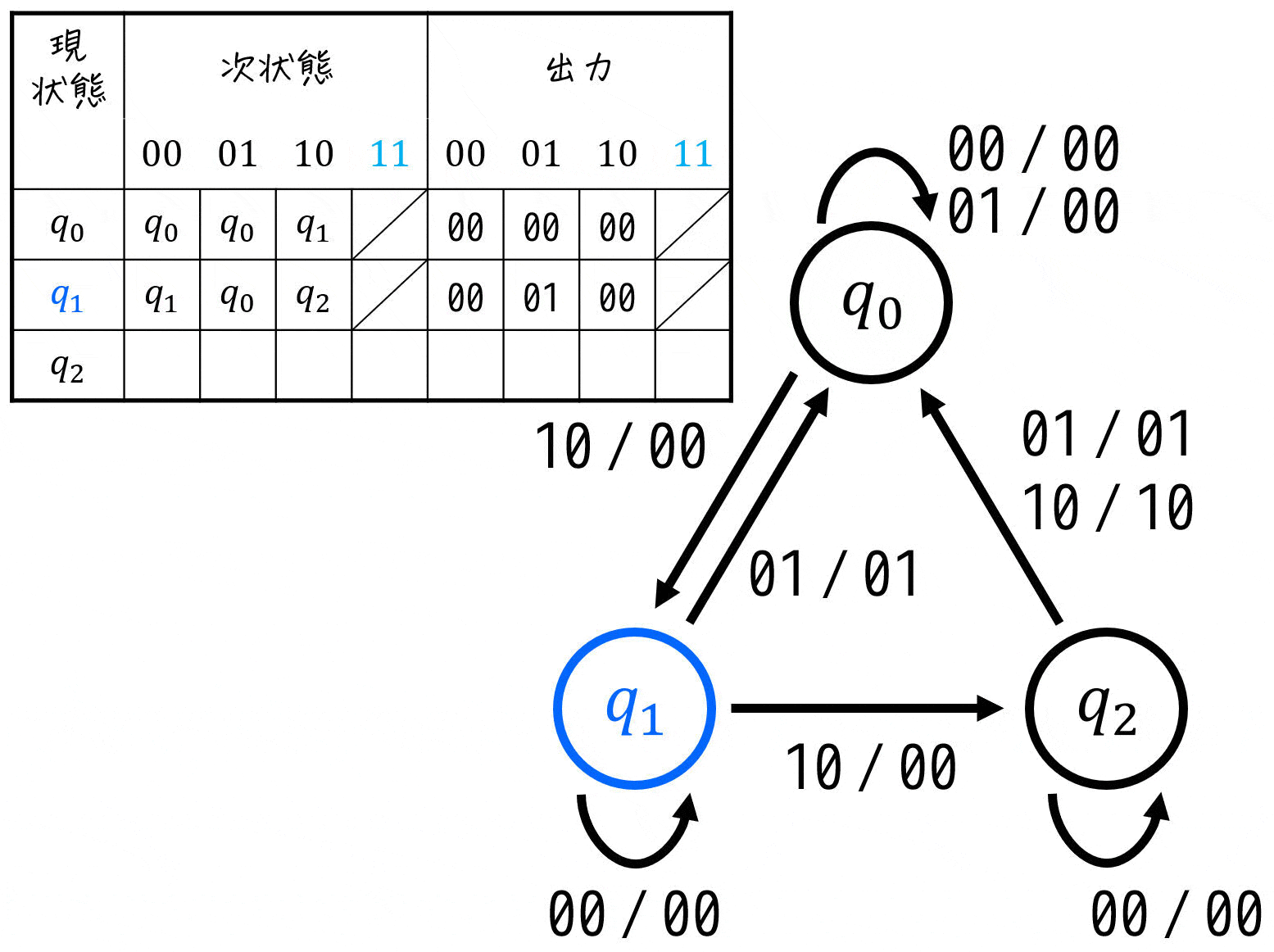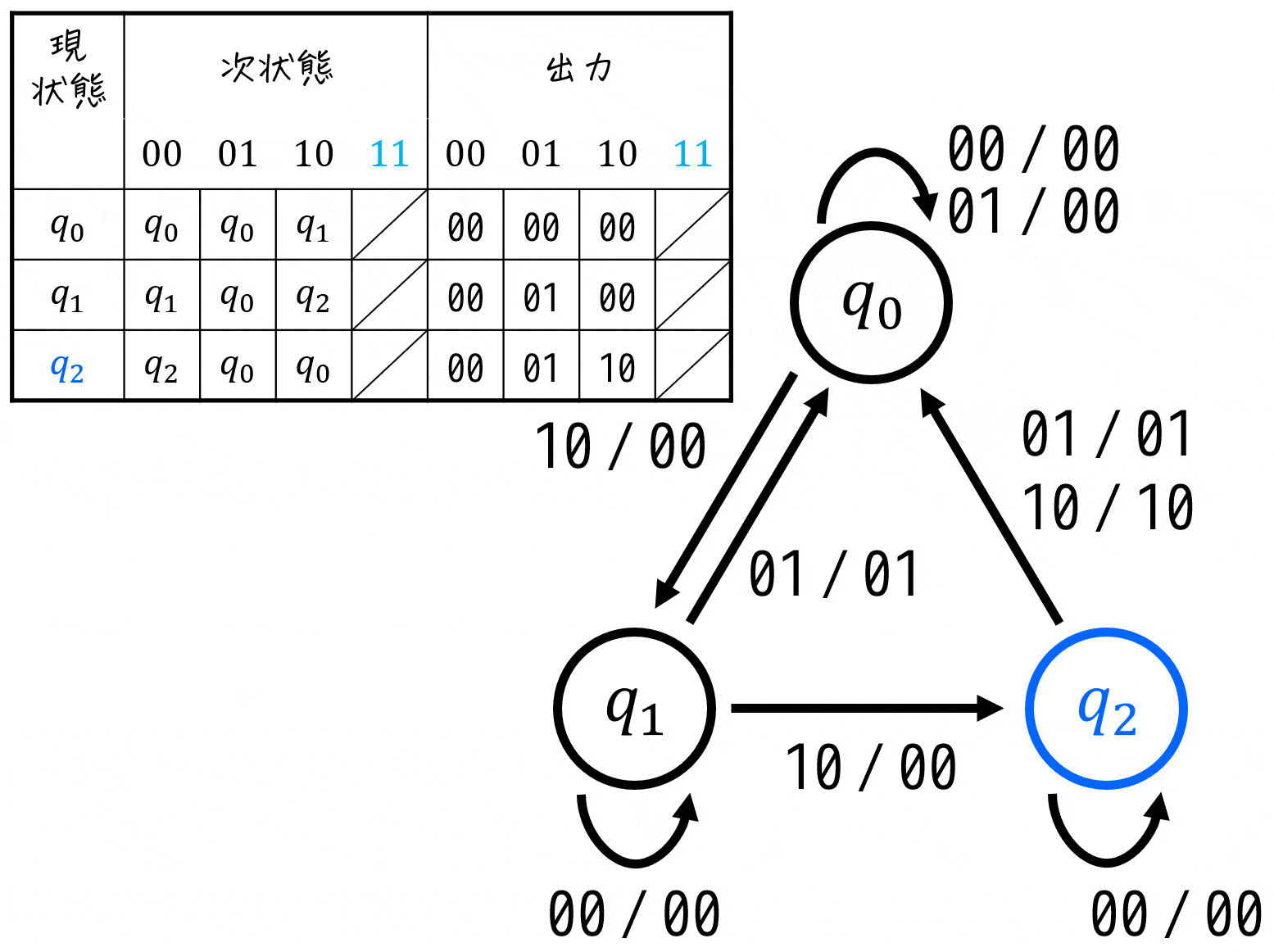
よって、状態遷移表は下のように求められる。
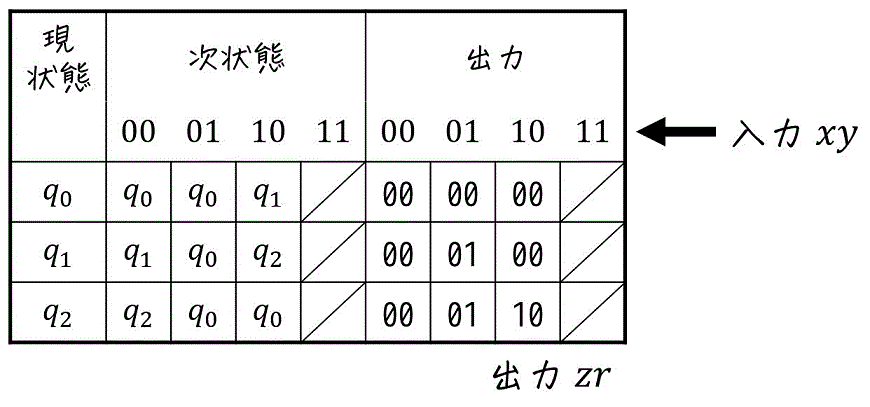
(入力を \( xy \)、出力は \( zr \) の順で記した)
(5) 必要なフリップフロップの数を考えよう
状態が3つあるので、1つのフリップフロップ(最大2個の状態を記憶可)では記憶できませんが、2つフリップフロップ(最大4個の状態を記憶可)があれば、[仕様]を満たす回路を作成することができますね。
よって、答えは2個です。
スポンサードリンク
[練習問題1] カウンタの設計
ここからは、例題と同じ難易度~若干難しめの問題を解くことで、順序回路の設計で使う状態遷移図や状態遷移表を書く練習をしていきましょう。
1が5回入力されるごとに「1」が出力され、それ以外のときに「0」が出力されるアップカウンタ回路を考える。このとき、(1)〜(4)の問いに答えなさい。
(1) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために最低何個の状態が必要?)
(2) 状態遷移図を書きなさい。
(3) 状態遷移表を書きなさい。
(4) このアップカウンタを作るためには、最低何個のフリップフロップが必要か答えなさい。
問題を解く前に、入力変数(この変数が5回入力されると1を出力し、それ以外のときは0を出力する)を \( x \)、出力する変数を \( z \) とおいておきましょう。
(1) 必要な内部状態の定義
必要な入力変数・出力変数を考えたので、順序回路を表現するために必要な内部状態を考えます。
今回は「1が5回入力されるごとに1を出力する」回路を作りたいので、最後に1が出力されてからの入力の数を記憶する必要(=内部状態として定義する必要)があります。
よって、必要な内部状態は
- 最後に1が出力されてから1が0回入力された状態
(1が入力されていない状態) - 最後に1が出力されてから1が1回入力された状態
- 最後に1が出力されてから1が2回入力された状態
- 最後に1が出力されてから1が3回入力された状態
- 最後に1が出力されてから1が4回入力された状態
の5個となります。
※ 「最後に1が出力されてから1が4回入力された状態」を記憶している際に1を入力すると、1の入力が5回となり、出力が1になるため、「最後に1が出力されてから1が5回入力された状態」を記憶する必要はない(このときは「1が0回入力された状態」を記憶すればOK)。
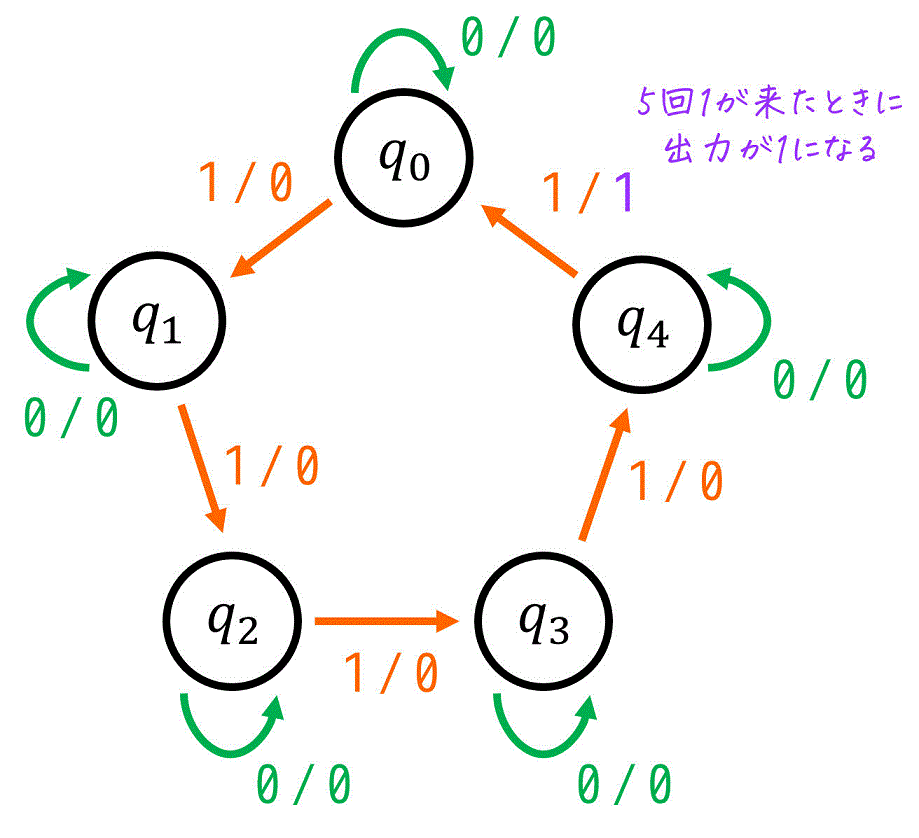
(2) 状態遷移図の設計
まずは(1)で作った内部状態を配置します。

あとは、各状態からの遷移先(次状態)と、そのときの入出力を矢印で表せばOKです。
今回の場合は、内部状態に対し
- 0が入力された場合:1が入力された回数が変化しないため、状態が変わらず、出力は0
(現状態と次状態が同じ) - 1が入力された場合:
- \( q_0 \) ~ \( q_3 \): 1の数が1個増えた状態に遷移
- \( q_4 \): 1の数が5個になるので、1を出力し、1の回数を0回にリセット。
を満たすように、矢印を追加すれば状態遷移図の完成です。

(3) 状態遷移表の設計
作ったすべての状態(現状態とする)に対して、各入力 \( x = 0 \), \( x = 1 \) ごとの「遷移先(次状態)」、および出力を表にすればOKです。
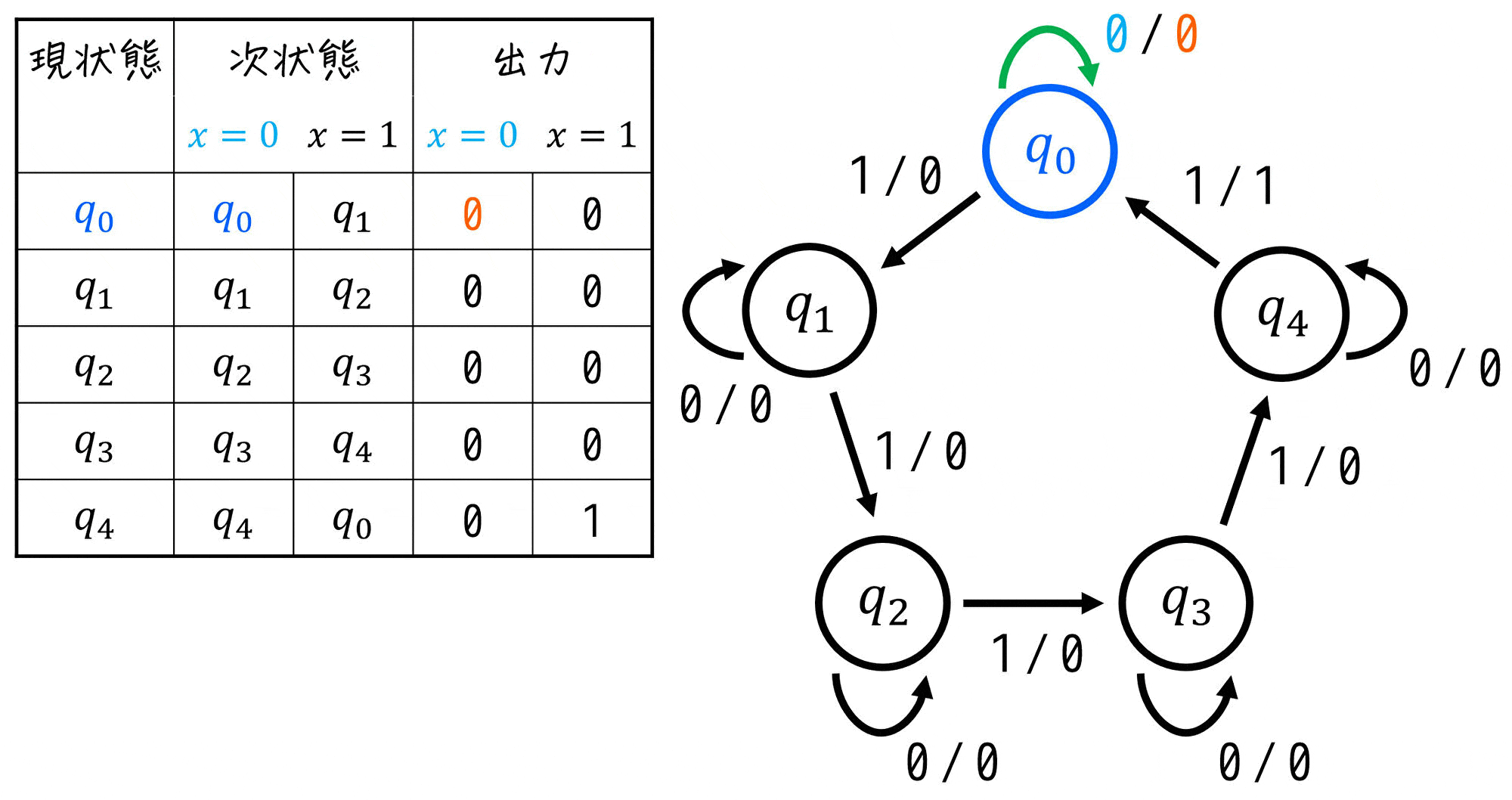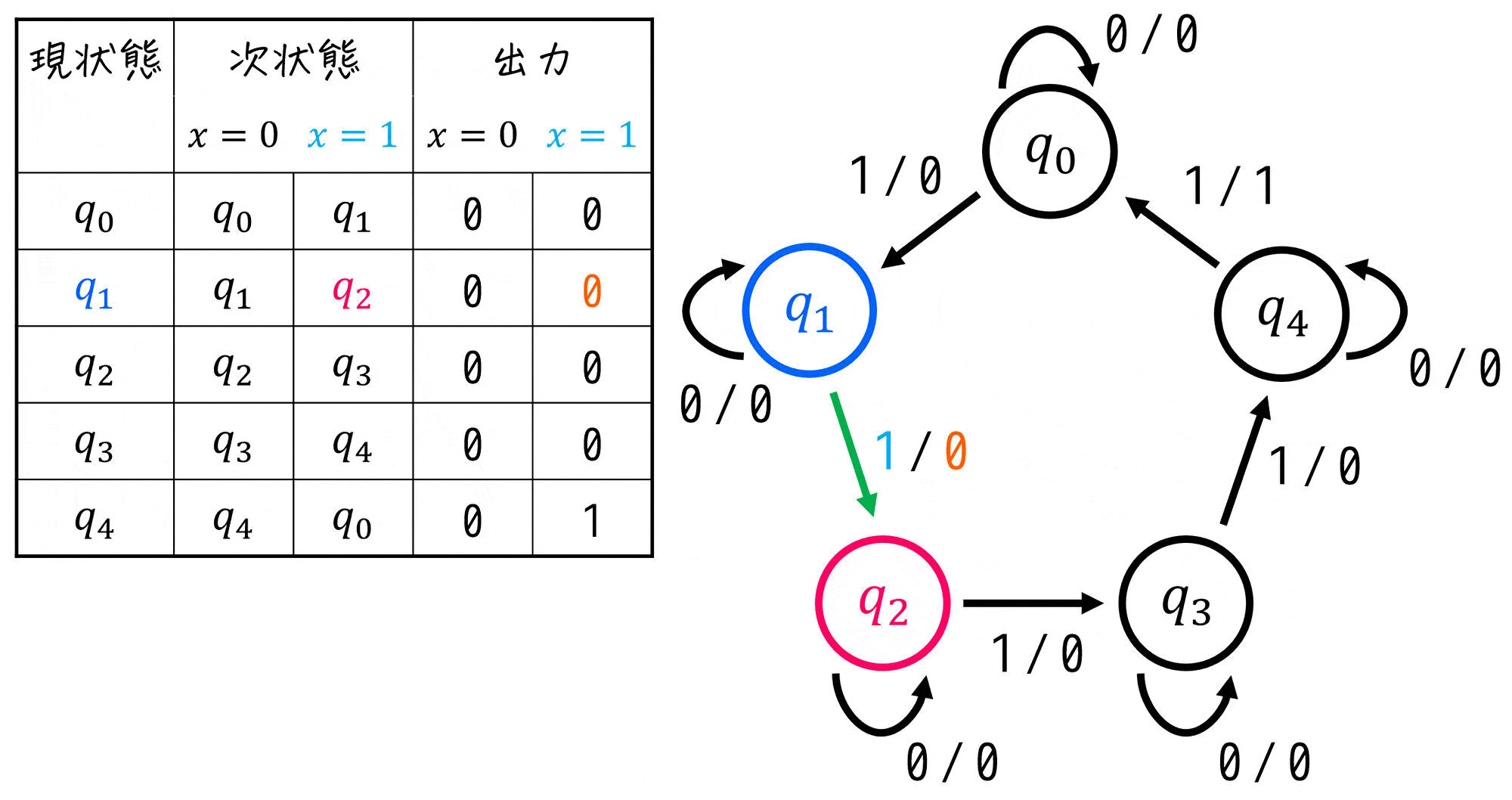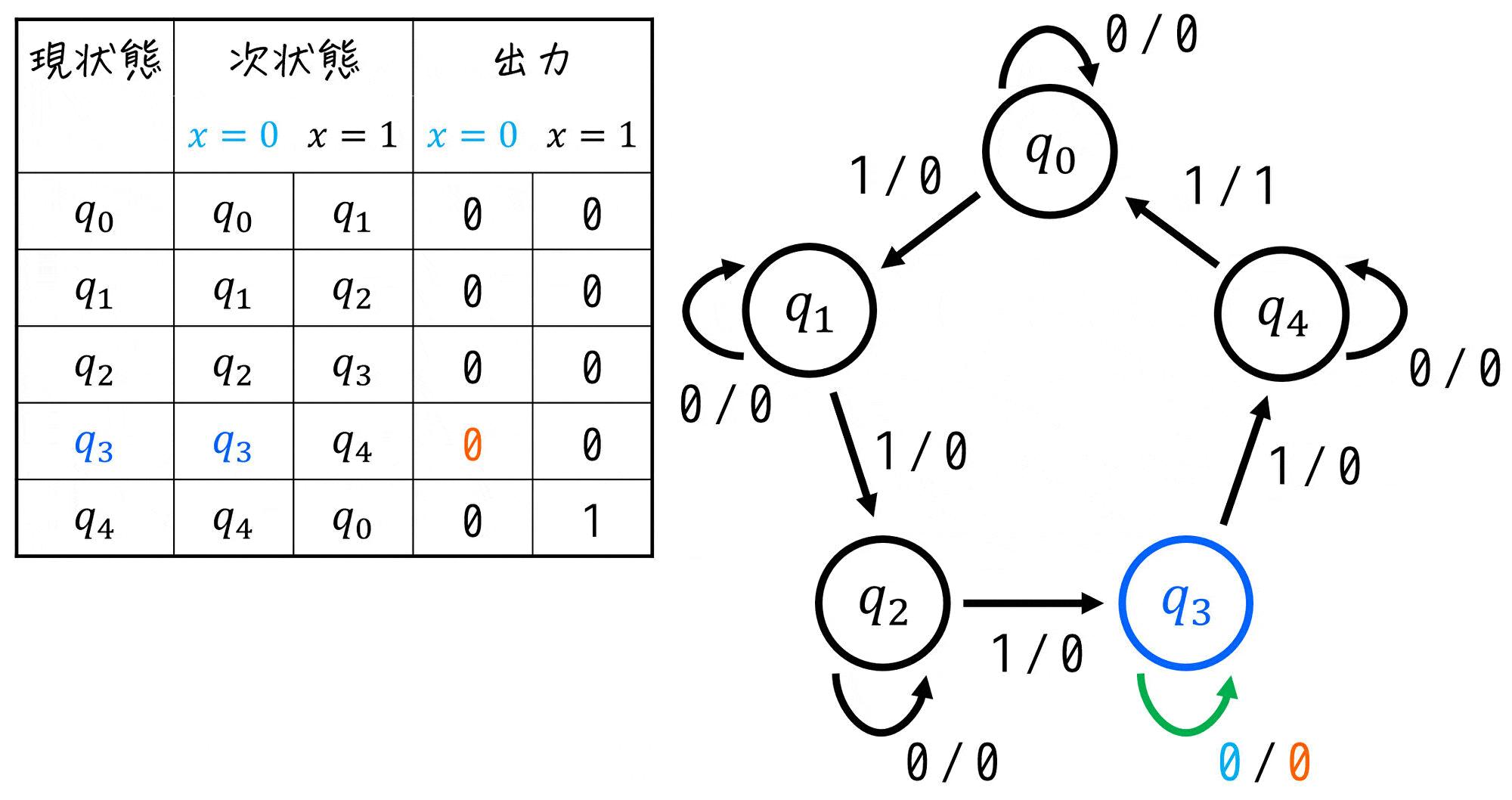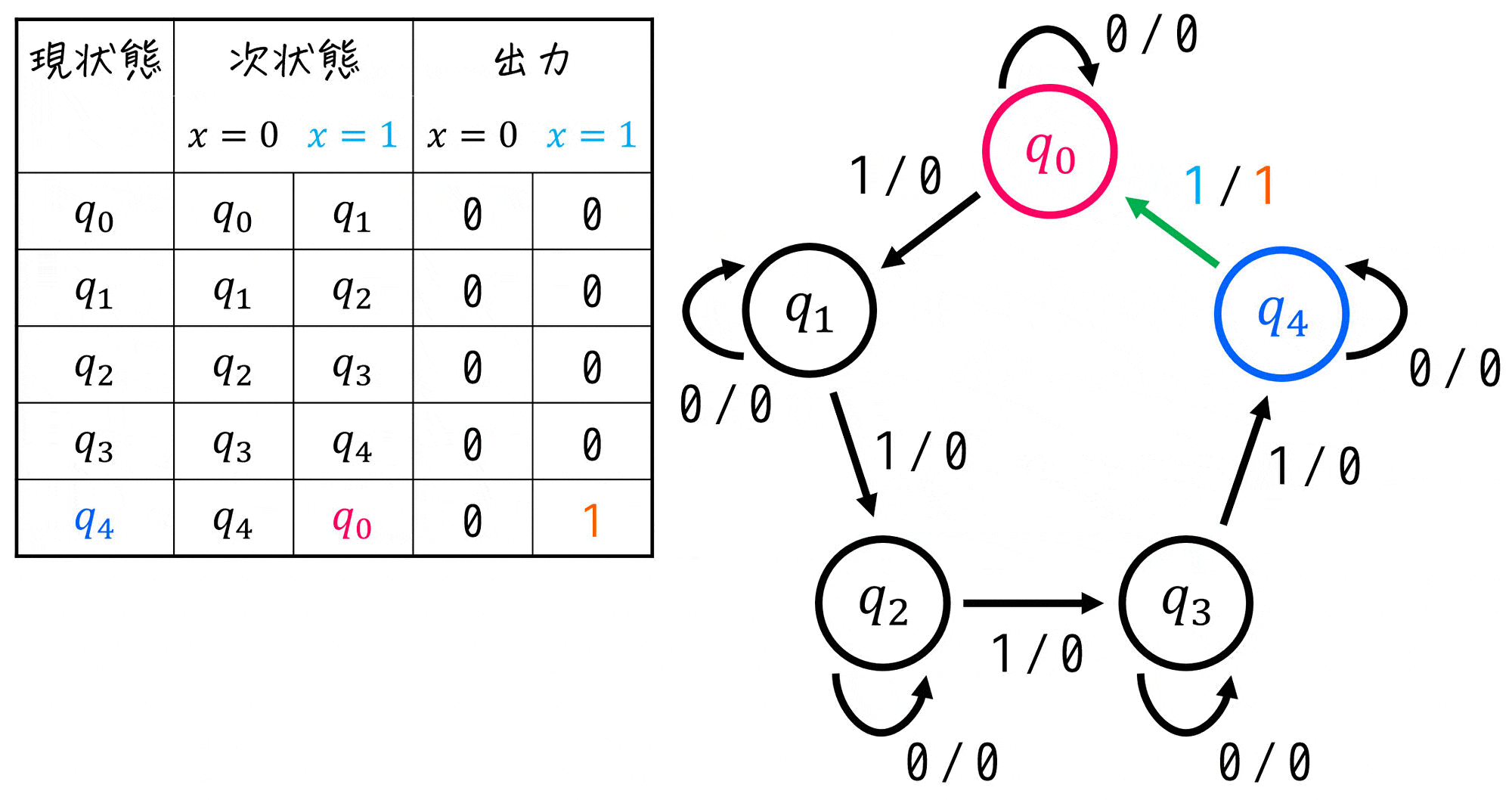
(4) 設計に必要なフリップフロップの数
今回は、全部で5つの状態を定義しました。
(=回路を表現するために5つの状態を記憶する必要があります)
そのため、2個のフリップフロップ(最大4状態を記憶可能)では5つの状態を記憶することができず回路を表現することができません。
一方、3個のフリップフロップ(最大8状態を記憶可能)を使えば、5つの状態を記憶できるため、回路を表現することができますね。
よって、この順序回路を設計するためには最低3個のフリップフロップが必要なことがわかりますね。
[練習問題2] 自動販売機の設計
最後に、自動販売機の設計に関する問題も練習しましょう。
(例題と仕様をちょっと変えています。)
つぎの[仕様]を満たす300円のおもちゃを販売するガチャガチャ(自動販売機)の回路を設計したい。
[仕様]- 100円硬貨と500円硬貨を受け付け、投入金額が合計300円になると商品が出てくる。
- 投入金額が300円を超えた場合は、おつりが返って来る。
- 商品が出たかどうか、おつりが返ってきたかどうかをこの回路で判定すること。
- 1度に2枚以上の硬貨が投入されることは考えなくてよい。
次の(1)~(4)の問いに答えなさい。
(1) 入力変数、出力変数は最低何個必要か答えなさい。
(2) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために最低何個の状態が必要?)
(3) 状態遷移図を書きなさい。
(4) 状態遷移表を書きなさい。
(1) 必要な入力変数・出力変数の定義
まずは、回路を設計する際に必要な入力変数と出力変数を考えましょう。
- 入力変数(2個)
- 100円硬貨が投入されたかを表す変数 \( x \)
(投入されていない → 0、投入された → 1) - 500円硬貨が投入されたかを表す変数 \( y \)
(投入されていない → 0、投入された → 1)
- 100円硬貨が投入されたかを表す変数 \( x \)
- 出力変数(2個)
- 商品が出たかを表す変数 \( z \)
(出なかった → 0、出た → 1) - おつりが出たかを表す変数 \( c \)
(出なかった → 0、出た → 1)
- 商品が出たかを表す変数 \( z \)
※ 0と1の割り当ては逆にしてもOKです。
(例: 100円硬貨が投入された状態を0、投入されていない状態を1)
よって、答えは
- 入力変数: 2個
- 出力変数: 2個
となります。
(2) 必要な内部状態を考えよう
つぎは、順序回路を設計するために必要な内部状態の数を考えましょう。
今回は「合計300円以上が投入されたら商品が出てくる(+必要であればおつりも出す)」回路を作りたいので、最後に商品が出てきてから投入された合計金額を100円単位で記憶する必要(=内部状態として定義する必要)があります。
よって、必要な内部状態は(最後に商品が出てきてから)
- 合計金額が0円
- 合計金額が100円
- 合計金額が200円
の3個となります。
※ 100円 or 500円硬貨が投入されて合計金額が300円以上になった場合は、商品を出して(\(z = 1 \) として)合計金額を0円にすればOKなので、300円以上の状態は記憶する必要はありません。
(3) 状態遷移図の設計
まずは、(2)で定義した3個の状態に名前を付けましょう。
- 合計金額が0円: \( q_0 \)
- 合計金額が100円: \( q_1 \)
- 合計金額が200円: \( q_2 \)
つぎに、この3つの状態を並べましょう。

あとは、各状態からの遷移先(次状態)と、そのときの入出力を矢印で表せばOKです。
今回の場合は、
- \( x = 0 \), \( y = 0 \) が入力された場合(硬貨が投入されなかった場合)
- 投入が入力されていないため、合計金額(状態)が変わらない。
→ 商品もおつりも出ないので出力は \( z = 0 \), \( c = 0 \)。(現状態と次状態が同じ)
- 投入が入力されていないため、合計金額(状態)が変わらない。
- \( x = 1 \), \( y = 0 \) が入力された場合(100円硬貨が投入された場合)
- \( q_0 \), \( q_1 \): 合計金額が100円アップ
→ \( q_0 \) の場合は \( q_1 \) に、\( q_1 \) の場合は \( q_2 \) に遷移 - \( q_2 \): 合計が300円になるので、商品が出てくる。投入金額も0円にリセットされる。
→ \( z = 1 \) を出力し、次状態は \( q_0 \) に遷移
- \( q_0 \), \( q_1 \): 合計金額が100円アップ
- \( x = 0 \), \( y = 1 \) が入力された場合(500円硬貨が投入された場合)
- 500円硬貨が投入されるため、現在の合計金額(状態)に関わらず必ず合計金額300円を超えるし、おつりも発生する。
→ どんな場合でも出力は \( z = 1 \), \( c = 1 \) となり、合計金額は0円にリセットされる(次状態は \( q_0 \) となる)。
- 500円硬貨が投入されるため、現在の合計金額(状態)に関わらず必ず合計金額300円を超えるし、おつりも発生する。
を満たすように矢印を追加すればOKです。
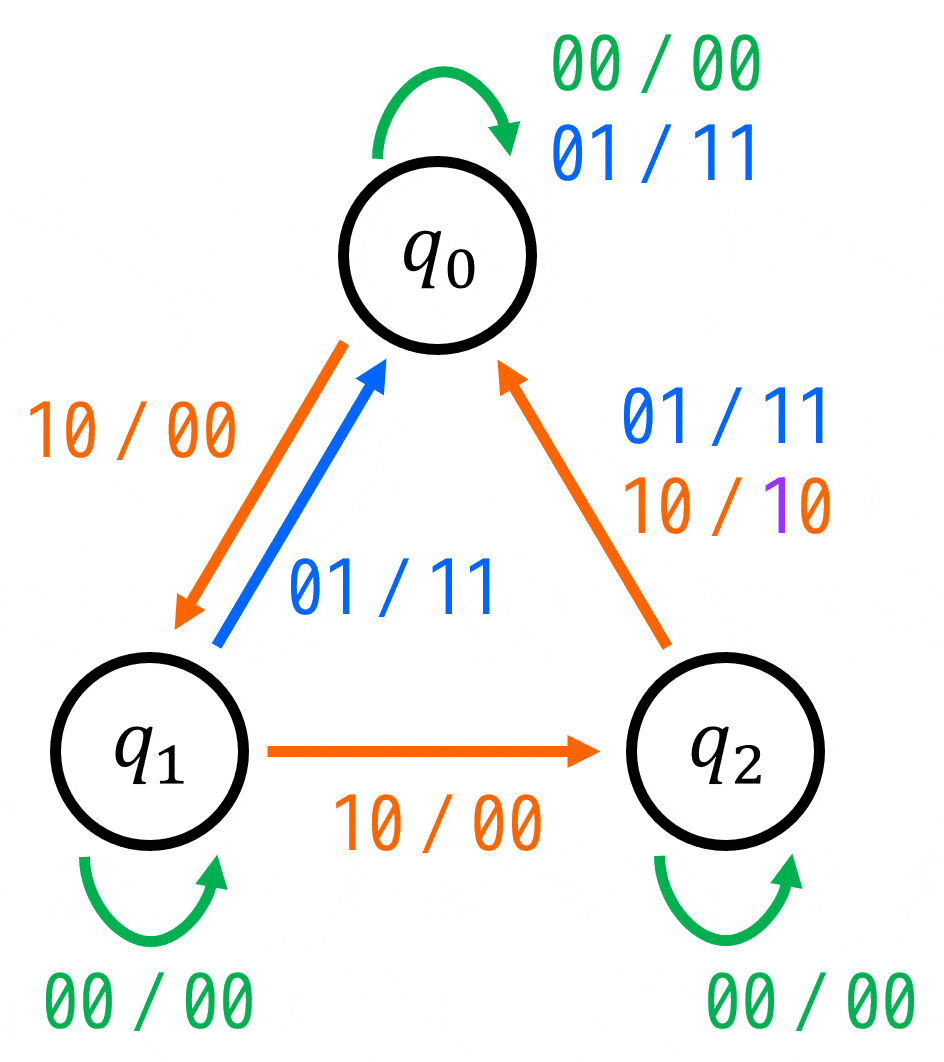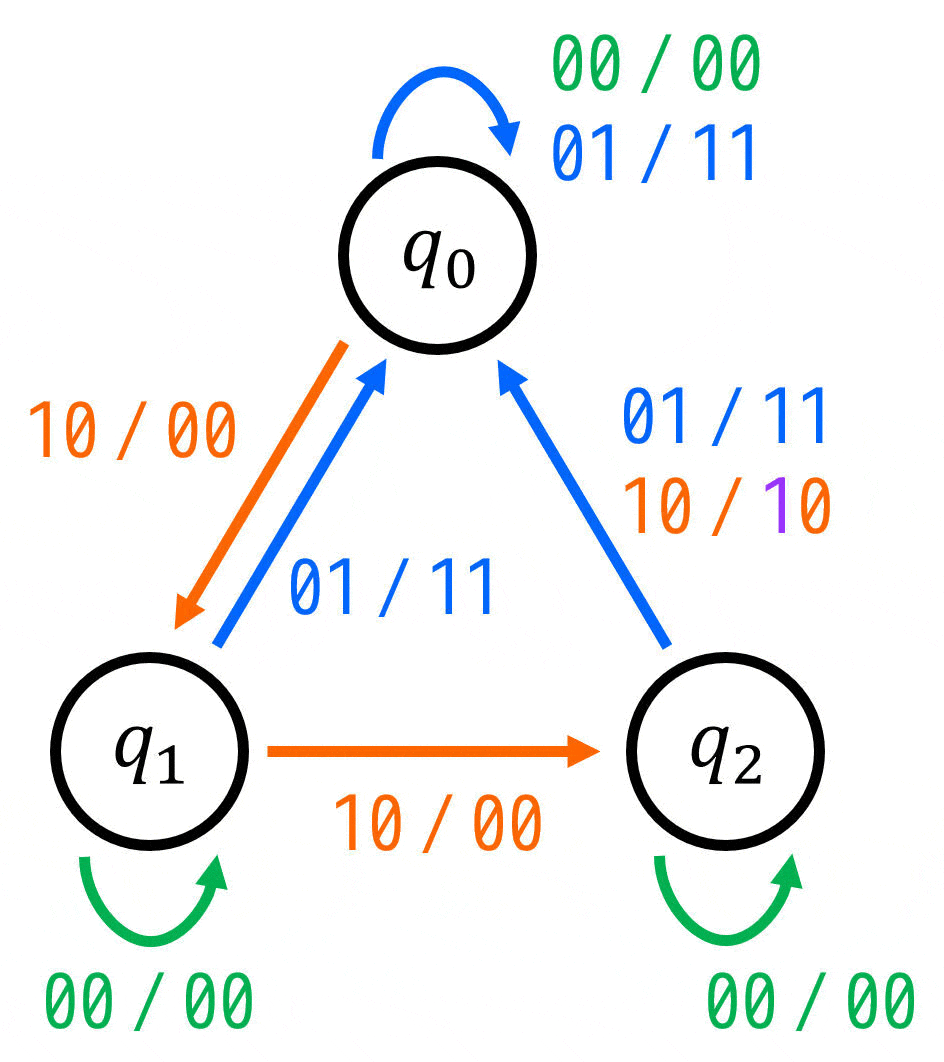
(入力 / 出力 = \( xy \) / \( zc \))
※ 入力・出力がともに複数あるので、変数をどの順番で書くかも明記しましょう。今回は「入力 / 出力 = \( xy \) / \( zc \)」で表すことにします。
(4) 状態遷移表の設計
(3)で設計したすべての状態(現状態とする)に対して、各入力 \( (x,y) = (0,0), (0,1), (1,0) \) ごとの「遷移先(次状態)」、および出力を表にすればOKです。
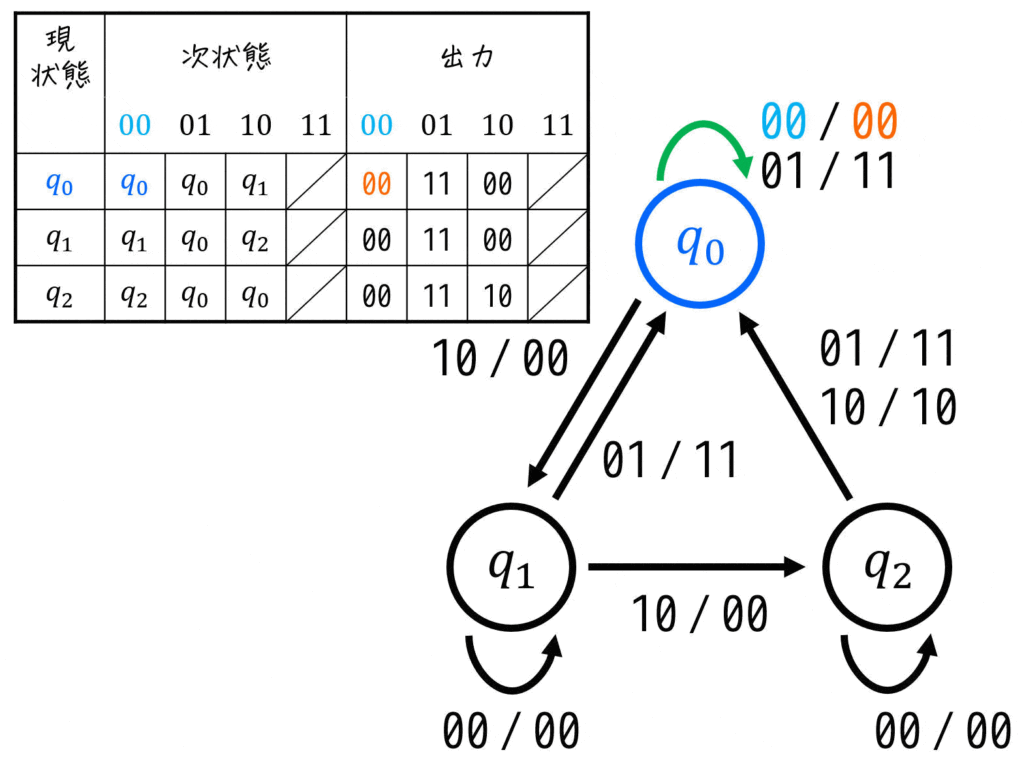
注釈
| ↑1 | 数学的にも考えてみましょう。「1が3回入力されるごとに1を出力する」というのは、「1が入力された回数を3で割った余りが0のときに1を出力する」と言い換えることができます。ここで、1が入力された回数を3で割った余りというのは、回数がどれだけ増えようが0, 1, 2のいずれかになりますよね。なので、必要な状態数は「1が入力された回数を3で割った余りが "0のとき"、" 1のとき"、"2のとき" 」の3個と考えることができます。 |
|---|---|
| ↑2 | オートマトンを習ったことがある人は、「この状態遷移図、オートマトンの状態遷移図に似てるじゃん」と思うかもしれません。その通りで、順序回路の状態遷移図はオートマトンの状態遷移図の書き方とほとんど同じです。ただし、下のように微妙な違いもあるのでオートマトンを習ったことはある人はちょっと気を付けましょう。
|
| ↑3 | 例えば、\( (x,y) = (1,1) \) の状態が定義されない場合は、\( (x,y) = (0,0), (0,1), (1,0) \) の3パターンを書けばOK。 |
| ↑4 | \( n \) 個のフリップフロップで与えられた回路が記憶できるとき、\( n -1 \) 個だとぎりぎり与えられた回路が記憶できませんよね。そのため、
の2つをはさみうちして、\( \textcolor{red}{ 2^{n-1} } < 3 \leqq \textcolor{blue}{ 2^n } \) を解くことで、フリップフロップの最低数 \( n \) が求まります。 |
| ↑5 | 100円硬貨以外の硬貨は入ってこないため、合計金額は必ず100円単位となる。 |
| ↑6 | 例えば入力が \( x = 0 \), \( y = 1 \) で、出力が \( z = 1 \), \( r = 0 \) であれば 01 / 10 と表記されます。 |
関連広告・スポンサードリンク