スポンサードリンク
こんにちは、ももやまです。
今回は前回の線形写像の続きとして合成写像・逆変換(逆写像)についてまとめていきたいと思います。
前回の線形写像の記事はこちら!
線形写像がまだよくわかっていない人はこちらで復習しましょう!
線形写像ではない合成写像、逆写像についてはこちらの記事をご覧ください。
スポンサードリンク
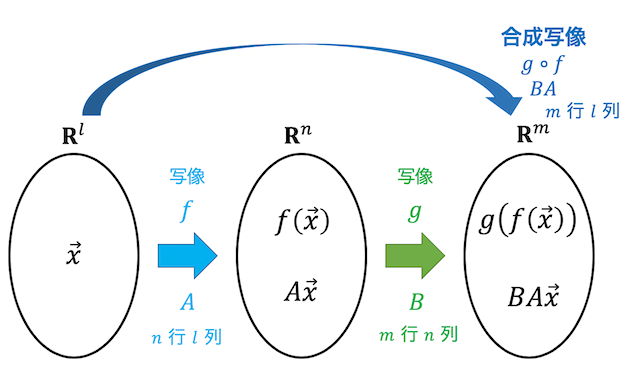
1.合成写像
合成写像とは、2つ連続した写像を1つの写像と見ることです。
例として表現行列 \( A \) で表される \( \mathbb{R}^l \) から \( \mathbb{R}^n \) への線形写像を \( f \) 、表現行列 \( B \) で表される \( \mathbb{R}^n \) から \( \mathbb{R}^m \) への線形写像を \( g \) とします。
(行列 \( A \) は \( n \) 行 \( l \) 列、行列 \( B \) は \( m \) 行 \( n \) 列)
まず、ベクトル \( \vec{x} \) に線形写像 \( f \) を適用し、ベクトル \( f ( \vec{x} ) \) とします。つぎに、先ほど線形写像を適応したベクトル \( f ( \vec{x} ) \) に線形写像 \( g \) を適用し、ベクトル \( g \left( \ f ( \vec{x} ) \right) \) とします。
このように、ベクトル \( \vec{x} \) に線形写像を \( f \), \( g \) の順に適応し、ベクトル \( g \left( \ f ( \vec{x} ) \right) \) とする変換を \( f \) と \( g \) の合成写像と呼び、\( g \circ f \) と書きます。
(注意:\( f \circ g \) ではないことに要注意! \( f \), \( g \) の順に適応する写像は \( g \left( \ f ( \vec{x} ) \right) \) となるので \( g \circ f \) と表す。)
合成写像 \( g \circ f \) の表現行列を考えてみましょう。
\( f(\vec{x}) = A \vec{x} \), \( g( \vec{x} ) = B \vec{x} \) ですね。なので、\[
\begin{align*}
g \left( \ f ( \vec{x} ) \right) & = g( A \vec{x} )
\\ & = B (A \vec{x})
\\ & = BA \vec{x}
\end{align*}
\]
と表わせますね。なので合成写像 \( g \circ f \) の表現行列は \( BA \) と表すことができます。
表現行列 \( A \) で表される \( \mathbb{R}^l \) から \( \mathbb{R}^n \) への線形写像を \( f \) 、表現行列 \( B \) で表される \( \mathbb{R}^n \) から \( \mathbb{R}^m \) への線形写像を \( g \) とする。
このとき、合成写像 \( g \circ f \) も線形写像となり、その表現行列は \( m \) 行 \( l \) 列となり、 \( BA \) となる。
線形代数を習いたてのころ、なぜ行列の掛け算は足し算に比べてこんなにめんどい操作をしなければならないのかと思ったと思います。
行列の掛け算は合成写像の表現行列になるようにするためにわざとめんどい操作にしているのです。
合成写像の表現行列となるように行列の掛け算を定義しているため、合成写像 \( g \circ f \) と \( f \circ g \) のように適応の順番を変えると異なる結果になりますね。なので、行列 \( BA \) と \( AB \) のように掛け算の順番を逆にすると計算結果も異なるものになることがおわかりいただけたかと思います。
スポンサードリンク
2.逆変換(逆写像)
逆変換とは、一度変換した写像を元にもどす操作です。
ですが、同じ次元同士の線形写像(線形変換)でしか逆変換は求められません。
なので、表現行列 \( A \) で表される \( \mathbb{R}^n \) から \( \mathbb{R}^n \) への線形写像を \( f \) とします。
ベクトル \( \vec{x} \) に線形写像 \( f \) を適用すると \( f( \vec{x}) \) となりますね。表現行列を用いると \( A \vec{x} \) と表せるので線形写像 \( f \) を適応するということは、ベクトル \( \vec{x} \) に左から \( A \) を掛けることと同じですね。
では、ベクトル \( f (\vec{x}) \) に逆変換 \( f^{-1} \) を適用し、もとのベクトル \( \vec{x} \) にする操作、つまり逆変換 \( f^{-1} \) の表現行列がどのようになるかを考えて見ましょう。
\( f ( \vec{x} ) \) の表現行列は \( A \vec{x} \) なので、\( A \vec{x} \) を \( \vec{x} \) に変えるような操作が逆変換の表現行列となります。
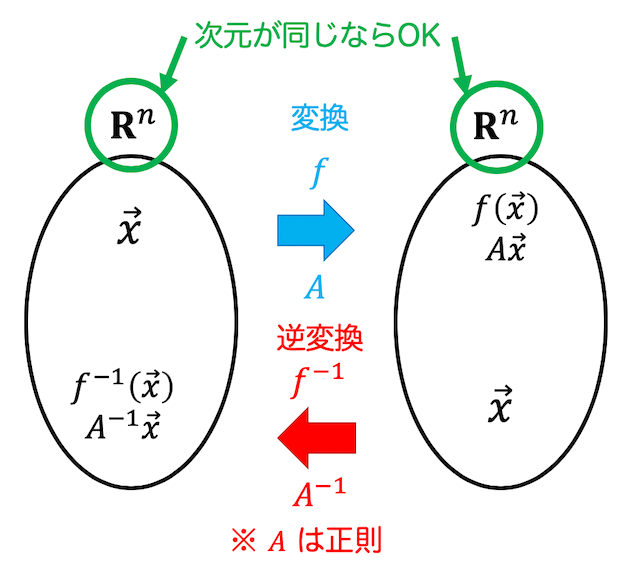
\( A \vec{x} \) を \( \vec{x} \) にするためには、左から \( A \) の逆行列である \( A^{-1} \) を掛けてあげればいいですね。つまり、\[
f^{-1} ( \vec{x} ) = A^{-1} \vec{x}
\]とします。
実際に計算してみると、\[
\begin{align*}
f^{-1} \left( f ( \vec{x} ) \right) & =
f^{-1} \left( A \vec{x} \right) \\ & =
A^{-1} (A \vec{x}) \\ & =
A^{-1} A \vec{x} \\ & =
E \vec{x} \\ & =
\vec{x}
\end{align*}
\]と元の \( \vec{x} \) に戻っていることがわかりますね。
なので逆変換 \( f^{-1} \) の表現行列は \( A^{-1} \) と表すことができます。
表現行列 \( A \) で表される \( \mathbb{R}^n \) から \( \mathbb{R}^n \) への線形写像(つまり \( \mathbb{R}^n \) の線形変換) を \( f \) とする。
このとき、逆写像 \( f^{-1} \) は、
- 逆行列 \( A^{-1} \) が存在すること。
(\( A \) が正則であれば逆行列は存在する) - \( \mathbb{R}^n \) から \( \mathbb{R}^n \) への線形写像(つまり線形変換)であること。
(逆行列は正方行列でないと定義できないため)
を満たすとき線形写像となり、その表現行列は \( A^{-1} \) で表される。
線形写像の逆の操作のことを逆写像ではなく逆変換と呼ぶことが多いのは、次元が同じベクトル空間同士でないと表現行列の逆行列が計算できず、逆写像も計算できないためです。
(次元が同じベクトル空間における線形写像のことは線形変換と呼ばれます。)
スポンサードリンク
3.合成写像の逆写像(逆変換)
合成写像と逆変換を同時に適用することを考えましょう。
表現行列 \( A \) で表される \( \mathbb{R}^n \) 同士の線形変換を \( f \) 、表現行列 \( B \) で表される \( \mathbb{R}^n \) 同士の線形変換を \( g \) とします*1。
このとき、\( f \), \( g \) の順に適用する合成写像 \( g \circ f \) の逆変換、つまり\( g \left( \ f ( \vec{x} ) \right) \) を \( \vec{x} \) に戻すような変換を2通りの方法で求め、さらに表現行列を求めてみましょう。
まずは、合成写像 \( g \circ f = h \) として、\( h \) の逆変換を求める方法で合成写像の逆変換を求めましょう。線形写像 \( h \) の表現行列を \( C = BA \) とすると、その逆変換は\[\begin{align*}
h^{-1} (\vec{x}) & =\left( g \circ f \right)^{-1} ( \vec{x} )
\\ & = C^{-1} \vec{x}
\\ & = (BA)^{-1} \vec{x}
\end{align*} \]となります。
なので合成写像の逆変換 \( \left( g \circ f \right)^{-1} \) の表現行列は \( (BA)^{-1} \) と表すことができます。
逆変換は、合成写像とは逆の順番、つまり\( g^{-1} \), \( f^{-1} \) の順に適用させる必要があります。なので、合成写像の逆変換は \( f^{-1} \circ g^{-1} \) となります。つまり、\[
\left( g \circ f \right)^{-1} = f^{-1} \circ g^{-1}
\]となります。
では、\( g^{-1} \), \( f^{-1} \) の順に適用させる方法で表現行列を求めてみましょう。
\( f^{-1} (\vec{x}) = A^{-1} \vec{x} \), \( g^{-1} ( \vec{x} ) = B^{-1} \vec{x} \) ですね。なので、\[
\begin{align*}
f^{-1} \left( \ g^{-1} ( \vec{x} ) \right) & = f( B^{-1} \vec{x} )
\\ & = A^{-1} (B^{-1} \vec{x})
\\ & = A^{-1} B^{-1} \vec{x}
\end{align*}
\]と表わせますね。なので合成写像の逆変換 \( f^{-1} \circ g^{-1} \) の表現行列は \( A^{-1} B^{-1} \) と表すことができます。
合成写像の逆変換を図に表すと下のようになります。
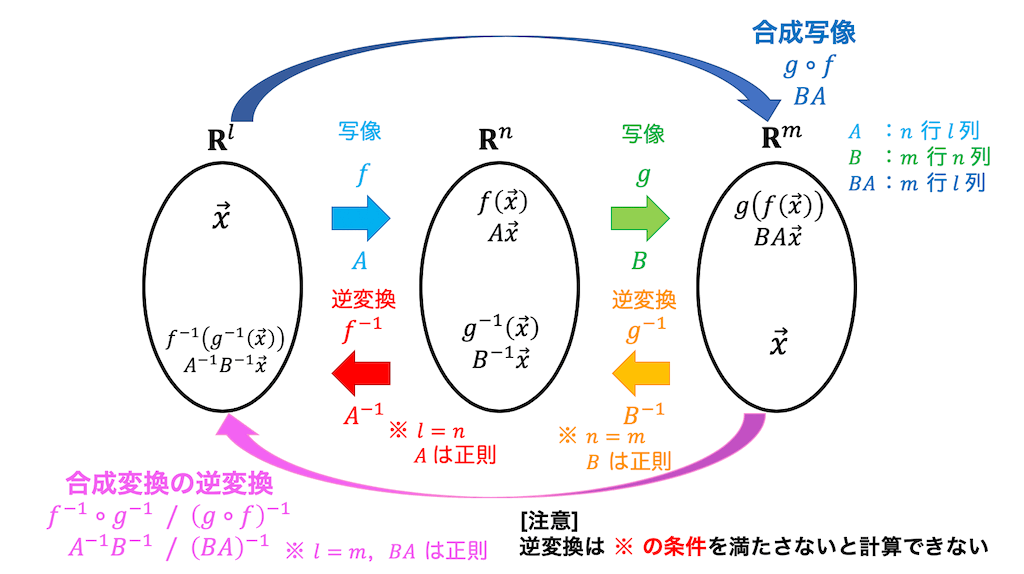
表現行列 \( A \) で表される \( \mathbb{R}^n \) の線形変換を \( f \) 、表現行列 \( B \) で表される \( \mathbb{R}^n \) の線形変換を \( g \) とする。
このとき、合成写像 \( g \circ f \) の逆変換 \( \left( g \circ f \right)^{-1} \) もしくは \( f^{-1} \circ g^{-1} \) の表現行列は \( (BA)^{-1} \) もしくは \( A^{-1} B^{-1} \) と表せる。
線形写像 \( f \), \( g \) の逆写像はともに次元が変わらない線形変換でないと求めることができませんが、合成写像 \( \left( g \circ f \right)^{-1} \) は \( f \), \( g \) がともに線形変換でなくても、つまり次元が変わる線形写像であっても計算ができることがあります。
合成写像の逆変換 \( \left( g \circ f \right)^{-1} \) の表現行列は \( (BA)^{-1} \) でしたね。つまり、\( BA \) が正方行列かつ正則であればたとえ行列 \( A \), \( B \) が正方行列でなくても \( BA \) の逆行列を求めることができますね。
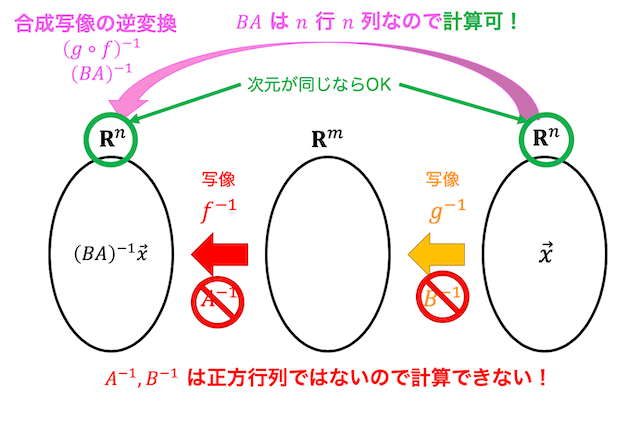
\( BA \) が正方行列となるための条件は、合成写像 \( g \circ f \) が線形変換(\( \mathbb{R}^n \) から \( \mathbb{R}^n \) への線形写像)であることといえますね。
なので、合成写像 \( g \circ f \) が線形変換となっていれば \( f \), \( g \) が線形変換でなくとも逆写像 \( \left( g \circ f \right)^{-1} \) を計算することができますね。
合成写像 \( g \circ f \) の逆変換 \( \left( g \circ f \right)^{-1} \) は \( f \), \( g \) がともに線形変換(つまり \( \mathbb{R}^n \) から \( \mathbb{R}^n \) への線形写像)でなくても計算が可能である。
具体的に言うと、線形写像 \( f \) が \( \mathbb{R}^n \) から \( \mathbb{R}^m \) 、線形写像 \( g \) が \( \mathbb{R}^m \) から \( \mathbb{R}^n \) のように合成写像 \( g \circ f \) が線形変換になっていれば合成写像の逆変換 \( \left( g \circ f \right)^{-1} \) を求めることができる。
では、実際に例題を見てみましょう。
例題
つぎの \( \mathbb{R}^2 \) から \( \mathbb{R}^2 \) への線形変換 \( f \), \( g \) がある。\[
f \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} 2x+y \\ 3x+2y \end{array} \right) \ \ \ g \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} x-2y \\ -x+3y \end{array} \right)
\](1)〜(4)の問いに答えなさい。
(1) \( f \) の表現行列 \( A \)、\( g \) の表現行列 \( B \) を求めなさい。
(2) 合成写像 \( g \circ f \) の表現行列 \( C \)、\( f \circ g \) の表現行列 \( D \) を求めなさい。
(3) 逆写像 \( f^{-1} \) の表現行列 \( F \)、\( g^{-1} \) の表現行列 \( G \) を求めなさい。
(4) 合成写像 \( g \circ f \) の逆変換 \( \left( g \circ f \right)^{-1} \) および合成写像 \( f^{-1} \circ g^{-1} \) が等しくなることを確認しなさい。
解説
(1) \[
\vec{e_1} = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) \ \ \
\vec{e_2} = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]とすると、\[
A = \left( f( \vec{e_1}), f( \vec{e_2} )) \right) = \left( \begin{array}{ccc} 2 & 1 \\ 3 & 2\end{array} \right) \\
B = \left( f( \vec{e_1}), f( \vec{e_2} )) \right) = \left( \begin{array}{ccc} 1 & -2 \\ -1 & 3 \end{array} \right)
\]となる。
(2)
\( g \circ f \) の計算\[
C = BA = \left( \begin{array}{ccc} 1 & -2 \\ -1 & 3 \end{array} \right) \left( \begin{array}{ccc} 2 & 1 \\ 3 & 2\end{array} \right) = \left( \begin{array}{ccc} -4 & -3 \\ 7 & 5 \end{array} \right) \]\( f \circ g \) の計算 \[
D = AB = \left( \begin{array}{ccc} 2 & 1 \\ 3 & 2 \end{array} \right) \left( \begin{array}{ccc} 1 & -2 \\ -1 & 3 \end{array} \right) = \left( \begin{array}{ccc} 1 & -1 \\ 1 & 0 \end{array} \right)
\]
(3)
\( f^{-1} \) の計算 \[
F = A^{-1} = \left( \begin{array}{ccc} 2 & -1 \\ -3 & 2 \end{array} \right) \]\( g^{-1} \) の計算 \[
G = B^{-1} = \left( \begin{array}{ccc} 3 & 2 \\ 1 & 1 \end{array} \right)
\]
(4)
\( \left( g \circ f \right)^{-1} \) の計算\[
H_1 = (BA)^{-1} = \left( \begin{array}{ccc} 5 & 3 \\ -7 & -4 \end{array} \right)
\]
\( f^{-1} \circ g^{-1} \) の計算\[ \begin{align*}
H_2 & = A^{-1} B^{-1} \\ & = \left( \begin{array}{ccc} 2 & -1 \\ -3 & 2 \end{array} \right) \left( \begin{array}{ccc} 3 & 2 \\ 1 & 1 \end{array} \right) \\ & = \left( \begin{array}{ccc} 5 & 3 \\ -7 & -4 \end{array} \right)
\end{align*} \]
確かに \( H_1 = H_2 \) となるので、\( \left( g \circ f \right)^{-1} \) と \( f^{-1} \circ g^{-1} \) は等しくなる。
4.練習問題
では、実際に練習してみましょう。
つぎの \( \mathbb{R}^2 \) から \( \mathbb{R}^3 \) への線形写像 \( f \) および \( \mathbb{R}^3 \) から \( \mathbb{R}^2 \) への線形写像 \( g \) がある。\[
f \left( \begin{array}{ccc} x \\ y \end{array} \right) = \left( \begin{array}{ccc} -x-3y \\ 3x - 4y \\ -4x \end{array} \right) \ \ \ g \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = \left( \begin{array}{ccc} -5x + 2y + 3z \\ x - y - z \end{array} \right)
\](1)〜(3)の問いに答えなさい。
(1) 線形写像 \( f \) の表現行列 \( A \) と線形写像 \( g \) の表現行列 \( B \) を求めなさい。行列 \( A \), \( B \) が何行何列の行列であるかも答えること。
(2) 合成写像 \( g \circ f \) の表現行列 \( C \) および \( f \circ g \) の表現行列 \( D \) を求めなさい。行列 \( C \), \( D \) が何行何列の行列であるかも答えること。
(3) 合成写像 \( g \circ f \) の逆変換 \( \left( g \circ f \right)^{-1} \) の表現行列 \( F \) を求めなさい。
5.練習問題の答え
(1)
線形写像 \( f \) の表現行列(3行2列)\[
A = \left( \begin{array}{ccc} -1 & -3 \\ 3 & -4 \\ -4 & 0 \end{array} \right) \]線形写像 \( g \) の表現行列(2行3列)\[
B = \left( \begin{array}{ccc} -5 & 2 & 3 \\ 1 & -1 & -1 \end{array} \right)
\]
(2)
合成写像 \( g \circ f \) の表現行列(2行2列)\[\begin{align*}
C & = BA \\ & = \left( \begin{array}{ccc} -5 & 2 & 3 \\ 1 & -1 & -1 \end{array} \right) \left( \begin{array}{ccc} -1 & -3 \\ 3 & -4 \\ -4 & 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 & 7 \\ 0 & 1 \end{array} \right)
\end{align*} \]
合成写像 \( f \circ g \) の表現行列(3行3列)\[\begin{align*}
D & = AB \\ & = \left( \begin{array}{ccc} -1 & -3 \\ 3 & -4 \\ -4 & 0 \end{array} \right) \left( \begin{array}{ccc} -5 & 2 & 3 \\ 1 & -1 & -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & 1 & 0 \\ -19 & 10 & 13 \\ 20 & -8 & -12 \end{array} \right)
\end{align*} \]
(3)
合成写像 \( g \circ f \) の逆変換 \( \left( g \circ f \right)^{-1} \) の表現行列\[
F = (BA)^{-1} = C^{-1} = \left( \begin{array}{ccc} -1 & 7 \\ 0 & 1 \end{array} \right)
\]
(実は元の行列 \( C \) と逆行列 \( C^{-1} \) は全く同じ)
5.さいごに
今回は線形写像の合成写像と逆写像についてのまとめを行いました。
行列の掛け算が足し算に比べてめんどくさくて複雑な計算になっている理由がこの記事をみてわかっていただけたかと思います。
次回は線形写像における核(カーネル)と像(イメージ)について説明していきたいと思います。
*1:逆行列が計算できるように両方の次元を \( \mathbb{R}^n \) としています。
関連広告・スポンサードリンク






![うさぎでもわかる計算機システム Part04 桁落ち・情報落ち・丸め誤差・打ち切り誤差について [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612150639-1-150x150.jpg)