スポンサードリンク
こんにちは、ももやまです。
「うさぎでもわかる線形代数」では、成分が実数のベクトル、行列を扱ってきました。\[
\left( \begin{array}{ccc} 3 \\ -3 \\ 4 \end{array} \right) , \ \ \ \left( \begin{array}{ccc} 1 & -2 \\ 5 & 0 \end{array} \right)
\]
応用編の第1羽では、ベクトルと行列の成分を複素数範囲に拡張したものを見ていきましょう。\[
\left( \begin{array}{ccc} 2+i \\ 3 \\ -1-i \end{array} \right) , \ \ \ \left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right)
\]
さらに、複素数範囲に拡張したときに出てくる線形代数の定義・用語についても確認していきましょう。
[注意]1.線形代数の本では、ベクトルは太字 \( \boldsymbol{a} \) で表されることが多いですが、この応用編でも \( \vec{a} \) と高校までの表記と同じ矢印表記でベクトルを表すことにします。
2.転置行列には \( {}^t \! A \)、\( A^T \)、\( A^{\top} \) など様々な表記法がありますが、この応用編では \( A^{\top} \) と表記することにします。
目次
スポンサードリンク
1. 基本的には実数のときと計算手順は変わらない!
ベクトルや行列の成分が複素数になったとしても、多くの場合は実数のときと同じように計算ができます。
頭の体操として、5つの例題を解いてみましょう。
(1) 行列・ベクトルの演算
次の行列・ベクトルの計算をしなさい。
(1) \[
\left( \begin{array}{ccc} 1+i \\ 2-i \end{array} \right) + \left( \begin{array}{ccc} 3-5i \\ 2 \end{array} \right)
\]
(2) \[
\left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right) \left( \begin{array}{ccc} i \\ -1 \end{array} \right)
\]
(1)\[
\left( \begin{array}{ccc} 1+i \\ 2-i \end{array} \right) + \left( \begin{array}{ccc} 3-5i \\ 2 \end{array} \right) = \left( \begin{array}{ccc} 4-4i \\ 4-i \end{array} \right)
\]
(2)\[\begin{align*}
\left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right) \left( \begin{array}{ccc} i \\ -1 \end{array} \right) & = \left( \begin{array}{ccc} 1 \cdot i + i \cdot (-1) \\ i \cdot i + 1 \cdot (-1) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 0 \\ -2 \end{array} \right)
\end{align*}\]
行列の計算方法があやふやな人はこちらの記事にて確認をしましょう。
(2) 行列式
行列式の求め方も実数範囲のときと同じです。サラスの公式も今まで通り使えます。
つぎの行列の行列式を求めなさい。\[
\left| \begin{array}{ccc} 1 & 1 & i \\ 1 & i & 1 \\ i & 1 & 1 \end{array} \right|
\]
そのままサラスの公式を使ってもOKです。\[\begin{align*}
\left| \begin{array}{ccc} 1 & 1 & i \\ 1 & i & 1 \\ i & 1 & 1 \end{array} \right| & = i + i + i - (i^3 + 1 + 1)
\\ & = 3i - (-i + 2)
\\ & = -2 + 4i
\end{align*}\]
もちろん行・列基本変形をして求めてもOKです[1]行列式を求めるときは、行基本変形・列基本変形を混合して使うことができます。。\[\begin{align*}
\left| \begin{array}{ccc} 1 & 1 & i \\ 1 & i & 1 \\ i & 1 & 1 \end{array} \right| & = \left| \begin{array}{ccc} 1 & 1 & i \\ 0 & i-1 & 1-i \\ 0 & 1-i & 1-i^2 \end{array} \right|
\\ & = \left| \begin{array}{ccc} 1 & 1 & i \\ 0 & i-1 & 1-i \\ 0 & 1-i & 2 \end{array} \right|
\\ & = \left| \begin{array}{ccc} i-1 & 1-i \\ 1-i & 2 \end{array} \right|
\\ & = 2(i-1) - (1-i)^2
\\ & = 2i - 2 - (1 -2i + i^2)
\\ & = 4i -3 - i^2
\\ & = -2 + 4i
\end{align*}\]
行列式の計算があやふやな人は、下の記事にて復習をしましょう。
(3) 逆行列
逆行列の公式も、実数のときと同じように使うことができます。
ここでは、2次の逆行列公式を確認しましょう[2]3次の逆行列公式は、余因子を用いた公式です。忘れてしまった人はこちらで確認しましょう。。
2次正方行列\[
A = \left( \begin{array}{ccc} a & b \\ c & d \end{array} \right)
\]の逆行列 \( A^{-1} \) は下のように求められる。\[
A^{-1} = \frac{1}{|A|}\left( \begin{array}{ccc} d & -b \\ -c & a \end{array} \right)
\]
※ 「対角成分 \( a \), \( d \) を入れ替え、それ以外の成分 \( b \), \( c \) の符号(+-) を入れ替えてから行列式で割る」と口に唱えて覚えておきましょう。
つぎの行列 \( A \) の逆行列を計算しなさい。\[
A = \left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right)
\]
行列式は、\[\begin{align*}
|A| & = 1 - i^2
\\ & = 2
\end{align*}\]なので、逆行列は\[\begin{align*}
A^{-1} & = \frac{1}{|A|} \left( \begin{array}{ccc} 1 & -i \\ -i & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 & -i \\ -i & 1 \end{array} \right)
\end{align*}\]と求められる。
複素数成分があった場合でも、掃き出し法を適用して逆行列を求めることができます。\[\begin{align*}
(A|E) & = \left( \begin{array}{cc|cc} 1 & i & 1 & 0 \\ i & 1 & 0 & 1 \end{array} \right)
\\ & = \left( \begin{array}{cc|cc} 1 & i & 1 & 0 \\ 0 & 1-i^2 & 0-i & 1-0 \end{array} \right)
\\ & = \left( \begin{array}{cc|cc} 1 & i & 1 & 0 \\ 0 & 2 & -i & 1 \end{array} \right)
\\ & = \left( \begin{array}{cc|cc} 2 & 2i & 2 & 0 \\ 0 & 2 & -i & 1 \end{array} \right)
\\ & = \left( \begin{array}{cc|cc} 2 & 0 & 2+i^2 & 0-i \\ 0 & 2 & -i & 1 \end{array} \right)
\\ & = \left( \begin{array}{cc|cc} 2 & 0 & 1 & -i \\ 0 & 2 & -i & 1 \end{array} \right)
\\ & = \left( \begin{array}{cc|cc} 1 & 0 & \frac{1}{2} & - \frac{1}{2} i \\ 0 & 1 & - \frac{1}{2} i & \frac{1}{2} \end{array} \right) \\ & = (E|A^{-1})
\end{align*}\]となるため、逆行列を\[
A^{-1} = \frac{1}{2} \left( \begin{array}{ccc} 1 & -i \\ -i & 1 \end{array} \right)
\]と求められる。
逆行列の計算があやふやな人は、下の記事にて復習をしましょう。
(4) 行列の階数
行列の階数も実数のときと同じように計算ができます。
つぎの行列 \( A \) の階数を求めなさい。\[
A = \left( \begin{array}{ccc} 1 & 1 & i \\ 2 & 1+i & 1+i \\ 3 & 2+i & 1+2i \end{array} \right)
\]
\[\begin{align*}
A & = \left( \begin{array}{ccc} 1 & 1 & i \\ 2 & 1+i & 1+i \\ 3 & 2+i & 1+2i \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & i \\ 0 & -1+i & 1-i \\ 0 & -1+i & 1-i \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & i \\ 0 & -1+i & 1-i \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]となるため、階数は2となる。
行列の階数計算があやふやな人は、下の記事にて復習をしましょう。
(5) 固有値・固有ベクトルと対角化
固有値・固有ベクトルの求め方や対角化の流れも実数のときと同じです。
つぎの行列 \( A \) がある。(1)~(3)の問いに答えなさい。\[
A = \left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right)
\]
(1) 固有値をすべて求めなさい。
(2) それぞれの固有値に対する固有ベクトルを求めなさい。
(3) 正則行列 \( P \) を用いて \( P^{-1} AP \) を対角化しなさい。
(1)
固有値を \( t \) とする。\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 1-t & i \\ i & 1-t \end{array} \right|
\\ & = (1-t)^2 - i^2
\\ & = (1 - 2t + t^2 ) + 1
\\ & = t^2 - 2t + 2
\\ & = 0
\end{align*}\]となる。よって固有値は \(
t = 1 \pm i
\) となる。
(2)
(i) 固有値が \( 1 + i \) のときの固有ベクトル \( \vec{p}_1 \)
連立方程式 \( (A - (1+i)E) \vec{p} = \vec{0} \) を満たす \( \vec{p} \) を求める。
\[\begin{align*}
\left( \begin{array}{ccc} -i & i \\ i & -i \end{array} \right) \to
\left( \begin{array}{ccc} -1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、連立方程式の解は任意定数 \( k \) を用いて\[
\vec{p} = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。
よって固有ベクトル \( \vec{p}_1 \) は、\( k = 1 \) を代入し、\[
\vec{p}_1 = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。
(ii) 固有値が \( 1 - i \) のときの固有ベクトル \( \vec{p}_2 \)
連立方程式 \( (A - (1-i)E) \vec{p}= \vec{0} \) を満たす \( \vec{p} \) を求める。
\[\begin{align*}
\left( \begin{array}{ccc} i & i \\ i & i \end{array} \right) \to
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、連立方程式の解は任意定数 \( k \) を用いて\[
\vec{p} = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。
よって固有ベクトル \( \vec{p}_2 \) は、\( k = 1 \) を代入し、\[
\vec{p}_2 = \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。
(3)
正則行列\[\begin{align*}
P & = ( \vec{p}_1 , \vec{p}_2 )
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right)
\end{align*}\]を用いて\[
P^{-1} AP = \left( \begin{array}{ccc} 1+i & 0 \\ 0 & 1-i \end{array} \right)
\]と対角化できる。
行列の対角化がまだあやふやな人は、下の記事にて復習をしましょう。
ここまでの計算で、ベクトルや行列の成分に複素数が含まれていたとしても、基本的に実数のときと同じように計算できることがわかりましたね。
しかし、中には実数のときとは違う計算をするものや、複素数範囲に拡張したときに出てくる独特な行列もあります。
スポンサードリンク
2. 複素内積
(1) 実数範囲の場合の内積
2つのベクトル \( \vec{a} \), \( \vec{b} \) の成分が実数の場合の内積 \( \vec{a} \cdot \vec{b} \) は、次のように計算できるのでしたね。
\[\begin{align*}
\left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right) \cdot
\left( \begin{array}{ccc} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right) & = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n
\\ & = \sum^{n}_{k = 1} a_k b_k
\\ & = \vec{a}^{\top} \vec{b}
\end{align*}\]
※1 \( a_1 \), \( a_2 \), …, \( a_k \) および \( b_1 \), \( b_2 \), …, \( b_k \) は実数
※2 \( \vec{a}^{\top} \) は \( \vec{a} \) の転置を表す。
内積計算の基本法則も確認しておきましょう。
成分が実数のベクトル \( \vec{a} \), \( \vec{b} \) には次の法則が成り立つ。
- \( \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} \)
(交換法則) - \( (k \vec{a}) \cdot \vec{b} = a \cdot (k \vec{b} ) = k ( \vec{a} \cdot \vec{b} ) \)
(定数倍の法則) - \( (\vec{a}+\vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \)
(分配法則)
※ \( k \) は実数の定数である。
また、ベクトル \( \vec{a} \) の大きさ(ノルム)\( | \vec{a} | \) は内積を用いて次のように書くことができます。
| \vec{a} |^2 & = \vec{a} \cdot \vec{a}
\\ | \vec{a} | & = \sqrt{ \vec{a} \cdot \vec{a} }
\end{align*}\] [定数倍分離]\[\begin{align*}
| k \vec{a} | & = k | \vec{a} |
\\ & = k \sqrt{ \vec{a} \cdot \vec{a} }
\end{align*}\]
※1 \( k \) は実数の定数
※2 \( | \vec{a} | = 0 \) であれば、必ず \( \vec{a} = \vec{0} \) となる。
(2) 複素内積の定義
ベクトルの成分が複素数のときの内積、複素内積は次のように定義、計算できます。
\[\begin{align*}
\left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right) \cdot
\left( \begin{array}{ccc} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right) & = a_1 \overline{b_1} + a_2 \overline{b_2} + \cdots + a_n \overline{b_n}
\\ & = \sum^{n}_{k = 1} a_k \overline{b_k}
\\ & = \vec{a}^{*} \vec{b}
\end{align*}\]
※1 \( a_1 \), \( a_2 \), …, \( a_k \) および \( b_1 \), \( b_2 \), …, \( b_k \) は複素数
※2 \( \overline{b_k} \) は \( b_k \) の共役複素数[3]元の複素数の実数部分をそのまま、虚数部分の正負を入れ替えたもの。を表す。
※3 \( \vec{a}^* \) は随伴[4]ベクトルや行列を転置した後に成分を共役複素数で置き換える処理を指す。を表す。詳しくは本記事の3章にて。
複素内積を計算する際に、ベクトル \( \vec{b} \) の成分は共役複素数として計算していますね。
このまま「\( \vec{b} \) の成分は共役複素数にする」と暗記してもいいですが、せっかくなので複素内積を共役複素数で定義しなければならない簡単な理由を説明しましょう。
(3) なぜ共役複素数で定義するのか
共役複素数を使って定義する理由は、ベクトルの大きさ計算にあります。
例えば、次のベクトル\[
\vec{a} = \left( \begin{array}{ccc} 1 \\ 2i \end{array} \right)
\]の大きさを実数Verの内積公式で求めてみましょう。
\[\begin{align*}
| \vec{a} | & = \sqrt{ \vec{a} \cdot \vec{a} }
\\ & = \sqrt{ 1 \cdot 1 + 2i \cdot 2i}
\\ & = \sqrt{ 1 - 4 }
\\ & = - \sqrt{3} i
\end{align*}\]となり、大きさが虚数という意味がわからない状態が起こります。
一方、共役複素数を使って定義すると、\[\begin{align*} | \vec{a} | & = \sqrt{ \vec{a} \cdot \vec{a} }
\\ & = \sqrt{ 1 \cdot \overline{1} + 2i \cdot \overline{2i}}
\\ & = \sqrt{ 1 \cdot 1 + 2i \cdot (-2i) }
\\ & = \sqrt{ 1 + 4 }
\\ & = \sqrt{5}
\end{align*}\]となり、大きさが実数となりました。
(3) 複素内積の計算法則
次に複素内積の計算法則を見ていきましょう。
実数Verと公式が少し変わるものがあるので、必ず確認しておきましょう。
成分が複素数のベクトル \( \vec{a} \), \( \vec{b} \) の複素内積の計算法則は次の通りである。
- \( \vec{a} \cdot \vec{b} = \overline{\vec{b} \cdot \vec{a}} \)
(★交換法則) - \( (k \vec{a}) \cdot \vec{b} = a \cdot (\overline{k} \vec{b} ) = k ( \vec{a} \cdot \vec{b} ) \)
(★定数倍1) - \( a \cdot (k \vec{b} )= (\overline{k} \vec{a}) \cdot \vec{b} = \overline{k} ( \vec{a} \cdot \vec{b} ) \)
(★定数倍2) - \( (\vec{a}+\vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \)
(分配法則1) - \( (\vec{a}+\vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \)
- (分配法則2)
★がついた公式は要注意!!
(実際に計算練習をして公式が成り立っていることを確認することをおすすめします!)
※ \( k \) は複素数の定数
(4) ベクトルの大きさと複素内積
また、成分に複素数が含まれるベクトル \( \vec{a} \) の大きさ(ノルム)\( | \vec{a} | \) は複素内積 \( \vec{a} \cdot \vec{a} \) を用いて次のように書くことができます。
| \vec{a} |^2 & = \vec{a} \cdot \vec{a}
\\ | \vec{a} | & = \sqrt{ \vec{a} \cdot \vec{a} }
\end{align*}\] [定数倍分離] \[\begin{align*} | k \vec{a} | & = |k| | \vec{a} |
\\ & = |k| \sqrt{ \vec{a} \cdot \vec{a} }
\end{align*}\]
※1 \( k \) は複素数
※2 \( k \) に絶対値を取る必要がある部分以外は実数のときと同じ
(5) 計算練習
それでは、実際に例題を用いて計算練習をしてみましょう!
つぎのベクトル\[
\vec{a} = 2 \left( \begin{array}{ccc} 1+2i \\ -2+i \\ 0 \end{array} \right) , \ \ \ \vec{b} = 3i \left( \begin{array}{ccc} 1 - 3i \\ 2-2i \\ -3i \end{array} \right)
\]について、(1)〜(3)の計算をしなさい。
(1) \( \vec{a} \cdot \vec{b} \)
(2) \( \vec{b} \cdot \vec{a} \)
(3) \( | \vec{b} | \)
[解説]
※内積の計算法則に慣れてもらうため、定数倍法則を使った解き方をここでは書きます。
ベクトル \( \vec{a}' \), \( \vec{b}' \) をそれぞれ\[\begin{align*}
\vec{a}' & = 2 \vec{a}
\\ & = \left( \begin{array}{ccc} 1+2i \\ -2+i \\ 0 \end{array} \right)
\end{align*}\]
\[\begin{align*}
\vec{b}' & = 3i \vec{b}
\\ & = \left( \begin{array}{ccc} 1 - 3i \\ 2-2i \\ -3i \end{array} \right)
\end{align*}\]と定義する。
(1)
\[\begin{align*}
\vec{a} \cdot \vec{b} & = (2 \vec{a}) \cdot (3i \vec{b})
\\ & = (2 \cdot \overline{3i}) \vec{a}' \cdot \vec{b}'
\\ & = -6i \left\{ (1+2i)\overline{(1-3i)} + (-2+i) \overline{(2-2i)} + 0 \overline{(-3i)} \right\}
\\ & = -6i \left\{ (1+2i)(1+3i) + (-2+i)(2+2i) \right\}
\\ & = -6i \left\{ (1+5i+6i^2) + (-4 -2i + 2i^2) \right\}
\\ & = -6i \left\{ (-5+5i) + (-6-2i) \right\}
\\ & = -6i \cdot (-11+3i)
\\ & = 66i - 18i^2
\\ & = 18 + 66i
\end{align*}\]
(2)
\[\begin{align*}
\vec{b} \cdot \vec{a} & = (3i \vec{b}) \cdot ( 2 \vec{a})
\\ & = (3i \cdot \overline{2}) \vec{b}' \cdot \vec{a}'
\\ & = 6i \left\{ (1-3i)\overline{(1+2i)} + (2-2i) \overline{(-2+i)} + (-3i) \overline{0} \right\}
\\ & = 6i \left\{ (1-3i)(1-2i) + (2-2i)(-2-i) \right\}
\\ & = 6i \left\{ (1-5i+6i^2) + (-4 +2i + 2i^2) \right\}
\\ & = 6i \left\{ (-5-5i) + (-6+2i) \right\}
\\ & = 6i \cdot (-11-3i)
\\ & = -66i - 18i^2
\\ & = 18 - 66i
\end{align*}\]
※ (1), (2) で \( \vec{a} \cdot \vec{b} \not = \vec{b} \cdot \vec{a} \) であること、および \( \vec{a} \cdot \vec{b} = \overline{\vec{b} \cdot \vec{a}} \) であることを確認できましたね。
(3) \[\begin{align*}
| \vec{b'} | & = \sqrt{ (1-3i)(1+3i) + (2-2i)(2+2i) + (-3i)(3i) }
\\ & = \sqrt{ (1+9) + (4+4) + 9 }
\\ & = \sqrt{27}
\\ & = 3 \sqrt{3}
\end{align*}\]となるため、\[\begin{align*}
| \vec{b} | & = |3i| \cdot | \vec{b}' |
\\ & = 3 \cdot 3 \sqrt{3}
\\ & = 9 \sqrt{3}
\end{align*}\]と計算できる。
ここからは、成分を複素数範囲に拡張したときに出てくる特殊な行列を見ていきましょう!
スポンサードリンク
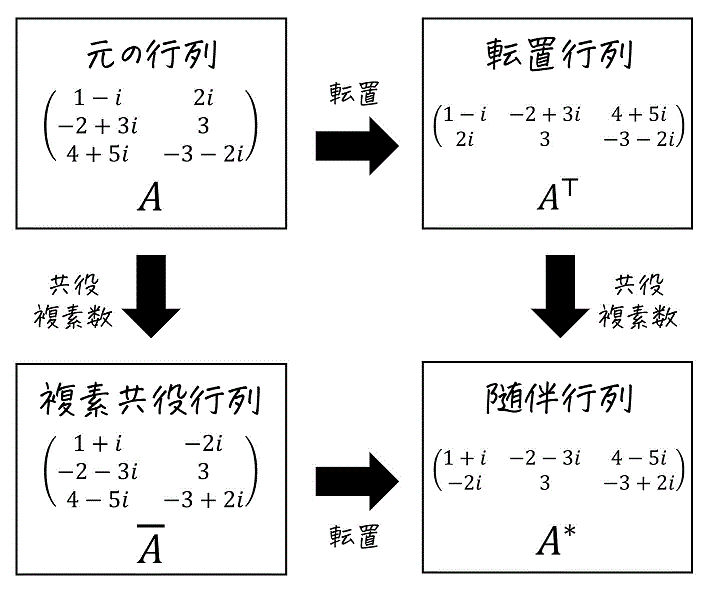
3. 随伴行列(転置行列+複素共役行列)
まずは転置行列を複素数Verに拡張した際に登場する随伴行列を見てみましょう。
(1) 転置行列 [復習]
元の行列 \( A \) の行にある成分を列に、列にある成分を行に入れ替えた行列のことを転置行列と呼び、\( {}^t \! A \) や \( A^{\top} \) などで表されます。
具体例を1つ見ておきましょう。\[
A = \left( \begin{array}{ccc} \textcolor{red}{1} & \textcolor{blue}{2} \\ \textcolor{red}{4} & \textcolor{blue}{-1} \\ \textcolor{red}{-3} & \textcolor{blue}{1} \end{array} \right) , \ \ \ \
A^{\top} =
\left( \begin{array}{ccc} \textcolor{red}{1} & \textcolor{red}{4} & \textcolor{red}{-3} \\ \textcolor{blue}{2} & \textcolor{blue}{-1} & \textcolor{blue}{1} \end{array} \right)
\]
※ 以後、行列 \( A \) を転置行列 \( A^{\top} \) にすることを「行列 \( A \) を転置する」と表現することがあります。
(2) 複素共役行列
ここからは成分を複素数範囲に拡張します。
元の行列 \( A \) の成分をすべて共役複素数にした行列を、複素共役行列と呼び、\( \bar{A} \) と表記されます。
\[
A = \left( \begin{array}{ccc} 1 \textcolor{blue}{+i} & 4 \\ \textcolor{blue}{-2i} & -1 \textcolor{blue}{+2i} \\ 3 \textcolor{blue}{-i} & \textcolor{blue}{i} \end{array} \right) , \ \ \
\bar{A} = \left( \begin{array}{ccc} 1 \textcolor{red}{-i} & 4 \\ \textcolor{red}{2i} & -1 \textcolor{red}{-2i} \\ 3 \textcolor{red}{+i} & \textcolor{red}{-i} \end{array} \right)
\]
(3) 随伴行列
元の行列 \( A \) を転置行列 \( A^{\top} \) にし、さらにすべての成分を共役複素数にした行列 \( \overline{A^{\top}} \) を随伴行列と呼び、\( A^{*} \) で表されます。
随伴行列を試しに1つ求めてみましょう。
次の行列 \( A \) の随伴行列 \( A^* \) を求めなさい。\[
A = \left( \begin{array}{ccc} 1-i & 2i \\ -2+3i & 3 \\ 4+5i & -3-2i \end{array} \right)
\]
[解説7]
行列 \( A \) を転置させ、さらに共役複素数を取ればOKです。(順不同)

よって、\[
A = \left( \begin{array}{ccc} 1+i & -2-3i & 4-5i \\ -2i & 3 & -3+2i \end{array} \right)
\]と求めることができます。
随伴行列の定義もあわせてみておきましょう。
行列 \( A \) に対し、次の1, 2を適用した行列を随伴行列と呼ぶ。
(※1, 2の順序は問わない。どちらから処理をしてもOK)
- 元の行列 \( A \) を転置
- すべての成分を共役複素数におきかえ
\[
A = \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & & \ddots & \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) , \ \ \ \ A^{*} = \left( \begin{array}{ccc} \overline{ a_{11} } & \overline{ a_{21} } & \cdots & \overline{ a_{m1} } \\ \overline{ a_{12} } & \overline{ a_{22} } & \cdots & \overline{ a_{2m} } \\ \vdots & & \ddots & \\ \overline{ a_{n1} } & \overline{ a_{n2} } & \cdots & \overline{ a_{nm} } \end{array} \right)
\] \( \overline{a} \)
4. エルミート行列(実対称行列の複素数Ver)
実対称行列の複素数Verに拡張した際に出てくるものがエルミート行列です。
(1) 実対称行列とは [復習]
(成分がすべて実数である)元の正方行列 \( A \) を転置させても全く同じ行列になる行列、つまり \( A = A^{\top} \) を満たす行列を実対称行列[5]単に対称行列と呼ぶこともあります。と呼びます。
具体例を1つ見ておきましょう。\[
A = \left( \begin{array}{ccc} \textcolor{red}{1} & \textcolor{blue}{2} & \textcolor{green}{-5} \\ \textcolor{red}{2} & \textcolor{blue}{0} & \textcolor{green}{1} \\ \textcolor{red}{-1} & \textcolor{blue}{-2} & \textcolor{green}{-4} \end{array} \right) , \ \ \ \
A^{\top} =
\left( \begin{array}{ccc} \textcolor{red}{1} & \textcolor{red}{2} & \textcolor{red}{-1} \\ \textcolor{blue}{2} & \textcolor{blue}{0} & \textcolor{blue}{-2} \\ \textcolor{green}{-5} & \textcolor{green}{1} & \textcolor{green}{-4} \end{array} \right)
\]
(2) エルミート行列とは
(成分に複素数が含まれる)正方行列 \( A \) を転置させ、さらに成分を複素共役数にしても元の行列 \( A \) と全く同じ行列になる行列のことをエルミート行列と呼びます。
つまり、元の行列と随伴行列 \( A^* \) が等しくなる行列のことをエルミート行列と呼びます。
1つ例を見てみましょう。
次の行列 \( A \) がエルミート行列であることを確認しなさい。\[
A = \left( \begin{array}{ccc} 3 & 2+3i & -4i \\ 2-3i & -3 & 7+i \\ 4i & 7-i & 4 \end{array} \right)
\]
この行列の随伴行列 \( A^* \) は、下のように求めることができますね。
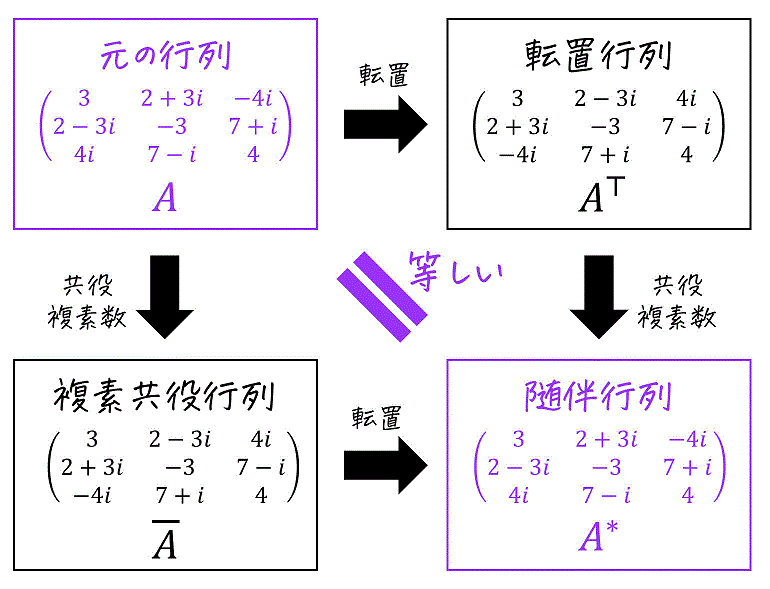
実際に求めてみると、\( A = A^* \) となるためエルミート行列となることが確認できます。
行列 \( A \) とその随伴行列 \( A^* \) が等しくなる(つまり \( A = A^* \) )行列のことをエルミート行列と呼ぶ。
(3) エルミート行列と対角成分
ある行列がエルミート行列の場合、その行列の対角成分は必ず実数となります。
その理由を簡潔に説明しましょう。
まず、随伴行列とは、元の行列を転置させてから全成分を共役複素数におきかえた行列でしたね。
ここで、正方行列を転置させても対角成分の値は変化しませんね。
そのため、元の行列と随伴行列を等しくさせるためには、対角成分は共役複素数に置き換えても値が同じでなければなりません。
言い換えると、虚部が0、つまり対角成分は実数でないといけませんね。
5. ユニタリ行列(直交行列の複素数Ver)
直交行列も複素数Verに拡張してみましょう。
(1) 直交行列とは [復習]
成分が実数のある行列 ( U ) とその転置 ( U^T ) に対して、\[
U U^{\top} = U^{\top} U = E
\]が成立する行列のことを直交行列と呼びます。
1つ例を用意しましょう。\[
U = \frac{1}{2} \left( \begin{array}{ccc} 1 & \sqrt{3} \\ - \sqrt{3} & 1 \end{array} \right), \ \ \ U^{\top} = \frac{1}{2} \left( \begin{array}{ccc} 1 & - \sqrt{3} \\ \sqrt{3} & 1 \end{array} \right)
\]
実際に計算すると、\[
U U^{\top} = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) = E
\]となり、確かに直交行列となりますね。
※ 直交行列かどうかを定義で確認する際には、\( U U^{\top} = E \) と \( U^{\top} U = E \) のうちどちらか一方でも確認できればOKです。
ある行列が直交行列 \( U \) のとき、(1)~(4)の法則が成り立つ。
(1) 直交行列とその転置の積は単位行列となる(積の順不同)\[
U U^{\top} = U^{\top} U = E
\]
(2) 直交行列を転置させたものは逆行列となる\[
U^{\top} = U^{-1}
\]
(3) 直交行列の行列式は1か-1のいずれかである\[
|U| = \pm 1
\]※行列式が1 or -1だからといって直交行列とはならないので要注意!
(4) ある直交行列 \( U \) を下のような縦ベクトルで分解する。\[
U = ( \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_n )
\]このとき、これらのベクトルを基底 \( \{ \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_n \} \)としたものは、正規直交基底となる。
(2) ユニタリ行列とは
直交行列を複素数Verに拡張した際に出てくるものがユニタリ行列です。
具体的には、成分が複素数の行列 \( U \) と、その行列の随伴行列 \( U^* \) において、\[
U U^{*} = U^{*} U = E
\]が成立する行列のことをユニタリ行列と呼びます。
1つ例を見てみましょう。
次の行列 \( U \) がユニタリ行列であることを確認しなさい。\[
U = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right)
\]
[解説9]
この行列の随伴行列は、下のようになりますね。\[
U^* = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -i \\ -i & 1 \end{array} \right), \ \ \
\]
さらに \( U U^* = E \) になるかを確認します。実際に計算すると、\[\begin{align*}
U U^* & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right) \cdot \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -i \\ -i & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 & i \\ i & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & -i \\ -i & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 2 & 0 \\ 0 & 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right)
\end{align*}\]となり、ユニタリ行列であることがわかりますね。
※ ユニタリ行列かどうかを定義で確認する際には、\( U U^{*} = E \) と \( U^{*} U = E \) のうちどちらか一方でも確認できればOKです。
ある行列がユニタリ行列 \( U \) のとき、(1)~(4)の法則が成り立つ。
(1) ユニタリ行列とその随伴行列の積は単位行列となる(積の順番はどちらからでもOK)\[
U U^{*} = U^{*} U = E
\]
(2) ユニタリ行列の随伴行列は逆行列となる\[
U^{*} = U^{-1}
\]
(3) ユニタリ行列の行列式の絶対値は1となる\[
| \det U | = 1
\]※行列式の絶対値が1だからといってユニタリ行列となるとは限らない
※ 絶対値と行列式の記号が紛らわしくなるので、行列式を \( \det \) 表記しています
(4) あるユニタリ行列 \( U \) を下のような縦ベクトルで分解する。\[
U = ( \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_n )
\]このとき、これらのベクトルを基底 \( \{ \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_n \} \)としたものは、正規直交基底となる。
6. 正規行列
(1) 正規行列とは
元の行列 \( A \) とその随伴行列 \( A^* \) の積 \( A A^* \) の計算順序を入れ替えても結果が変わらない行列、つまり \( A A^* = A^* A \) となる行列を正規行列と呼びます。
次の行列 \( A \) が正規行列であるかを確認しなさい。\[
A = \left( \begin{array}{ccc} -1+i & 2-2i \\ -2-2i & -1+2i \end{array} \right)
\]
[解説]
ここで、随伴行列 \( A^* \) は\[
A^* = \left( \begin{array}{ccc} -1-i & -2+2i \\ 2+2i & -1-2i \end{array} \right)
\]と計算できます。
さらに \( A A^* \) と \( A^* A \) を計算すると、\[\begin{align*}
A A^* & = \left( \begin{array}{ccc} -1+i & 2-2i \\ -2-2i & -1+2i \end{array} \right) \left( \begin{array}{ccc} -1-i & -2+2i \\ 2+2i & -1-2i \end{array} \right)
\\ & = \left( \begin{array}{ccc} 10 & -6-6i \\ -6+6i & 13 \end{array} \right)
\end{align*}\]
\[\begin{align*}
A^* A & = \left( \begin{array}{ccc} -1-i & -2+2i \\ 2+2i & -1-2i \end{array} \right) \left( \begin{array}{ccc} -1+i & 2-2i \\ -2-2i & -1+2i \end{array} \right)
\\ & = \left( \begin{array}{ccc} 10 & -6-6i \\ -6+6i & 13 \end{array} \right)
\end{align*}\]となり、\( A A^* = A^* A \) が確認できるため、 \( A \) が正規行列となることが確認できますね。
※ 一部途中計算を省略しています。ご了承ください。
ある行列 \( A \) の随伴行列を \( A^* \) とする。このとき、\( A A^* = A^* A \) を満たす行列のことを正規行列と呼ぶ。
※ 行列 \( A \) の成分がすべて実数のときは \( A A^{\top} = A^{\top} A \) を満たす行列が正規行列となる。(\( A^{\top} \) は行列 \( A \) の転置)
(2) 正規行列とエルミート行列
エルミート行列は、元の行列 \( A \) とその随伴行列 \( A^* \) が等しくなる、つまり \( A = A^* \) となる行列のことでしたね。
ここで、\( A = A^* \) ということは、\( A A^* = A^* A = A^2 \) が成立しますね。
よって、エルミート行列は必ず正規行列になることがわかりますね。
(3) 正規行列とユニタリ行列
ユニタリ行列は、元の行列 \( A \) とその随伴行列 \( A^* \) の積が単位行列となる、つまり \( A A^* = A^* A = E \) となる行列でしたね。
ここで、\( A A^* = A^* A = E \) なので、当然正規行列の条件である \( A A^* = A^* A \) をみたしていますね。
よって、ユニタリ行列は必ず正規行列になることがわかりますね。
エルミート行列は必ず正規行列である。
(正規行列だからといって必ずエルミート行列であるとは限らない)
ユニタリ行列は必ず正規行列である。
(正規行列だからといって必ずユニタリ行列であるとは限らない)
(4) 正規行列と対角化
正規行列は、必ずユニタリ行列を用いて対角化することが可能です。
ある行列 \( A \) が正規行列ならば、必ずユニタリ行列を用いて \( A \) を対角化することができる。
比較:実対称行列ならば、直交行列を用いて対角化が可能
(直交行列の複素数Verであるエルミート行列よりもさらに広い、正規行列でもユニタリ行列による対角化は可能だと頭に入れておけばOK)
※ 詳細な計算練習はまた別の記事にて行う予定なので、今は頭の片隅に入れておいてください。
7. 練習問題
では、随伴行列・エルミート行列・ユニタリ行列についてもう少し練習問題を解いてみましょう。
次の行列 \( A \) の随伴行列として正しいものはどれか。 \[
A = \left( \begin{array}{ccc} 3 & 1-i & 4+2i \\ 7-2i & 3+4i & -1-i \\ 2+i & -i & 2-3i \end{array} \right)
\]
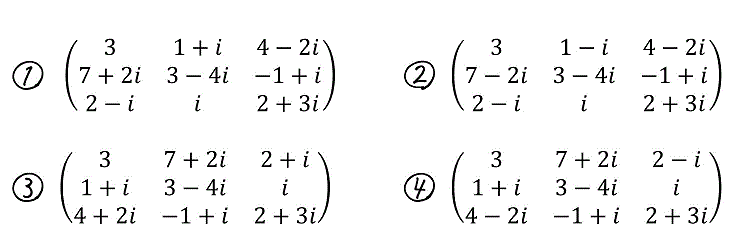
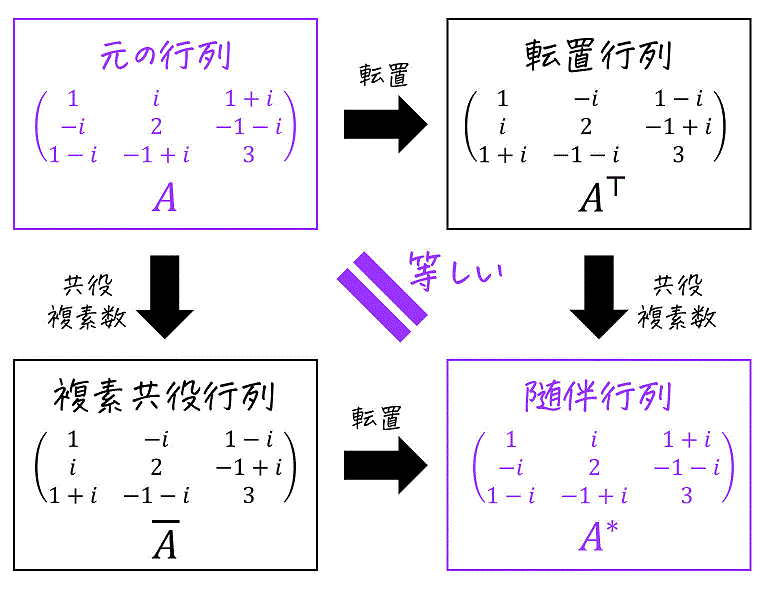
次の行列 \( A \) がエルミート行列であることを確認しなさい。\[
A = \left( \begin{array}{ccc} 1 & i & 1+i \\ -i & 2 & -1-i \\ 1-i & -1+i & 3 \end{array} \right)
\]
次の行列 \( A \) がユニタリ行列であることを確認しなさい。\[
A = \left( \begin{array}{ccc} 0 & 1 & 0 \\ -i & 0 & 0 \\ 0& 0 & -1 \end{array} \right)
\]
8. 練習問題の答え
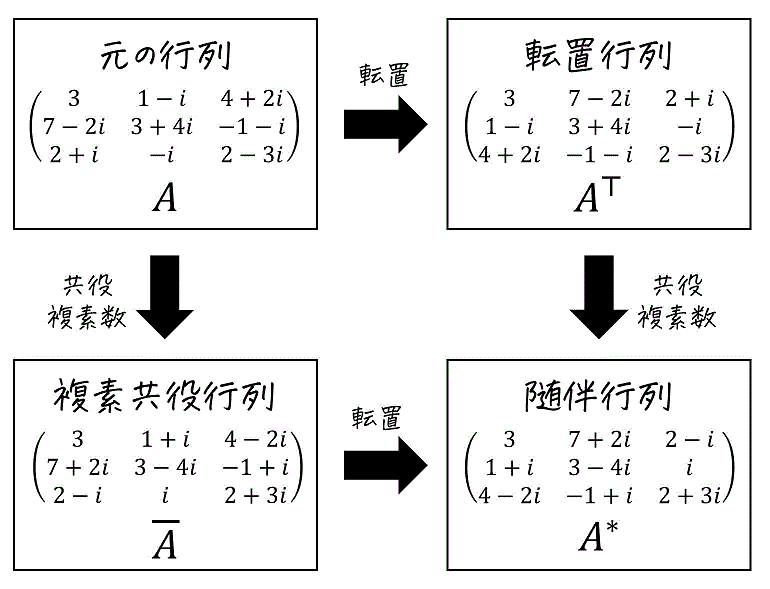
練習1
解答:④\[
\left( \begin{array}{ccc} 3 & 7+2i & 2-i \\ 1+i & 3-4i & i \\ 4-2i & -1+i & 2+3i \end{array} \right)
\]
計算過程は、下の通り。
練習2
下の画像の通り、\( A = A^* \) を確認すればOK。
練習3
随伴行列 \( A^* \) は\[
A^* = \left( \begin{array}{ccc} 0 & i & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{array} \right)
\]となる。
ここで、\[\begin{align*}
A A^* & = \left( \begin{array}{ccc} 0 & 1 & 0 \\ -i & 0 & 0 \\ 0& 0 & -1 \end{array} \right) \left( \begin{array}{ccc} 0 & i & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)
\end{align*}\]より、確かにユニタリ行列であることが確認できる。
※ \( A A^* = E \) と \( A^* A = E \) のうちのどちらか片方を計算し、確認すればOK。
9. さいごに
今回は、行列やベクトルの成分の範囲を複素数に拡張しました。
複素数に拡張した際に新たに出てくる概念(複素内積、随伴行列、エルミート行列、ユニタリ行列…)などを抑えておけば、実数のときとほとんど同じように計算ができることがわかりましたね。
次回からも、線形代数の中で発展的な内容を取り上げていこうと思います。
関連広告・スポンサードリンク