うさぎでもわかる離散数学（グラフ理論）　第11羽　木・根付き木

こんにちは、ももやまです。

今回はちょっと特殊なグラフである木についてまとめています。

１．木・森
２．根付き木
３．m分木（2分木）・完全m分木（完全2分木）
- (1) m分木（2分木）とは
- (2) 完全m分木（完全2分木）とは
４．練習問題
- 練習1
- 練習2
- 練習3
- 練習4
５．練習問題の答え
- 練習1
- 練習2
- 練習3
- 練習4
６．さいごに

前回の記事（第10羽）はこちら！

オイラーグラフ・ハミルトングラフについてです。

www.momoyama-usagi.com

１．木・森

(1) 木とは

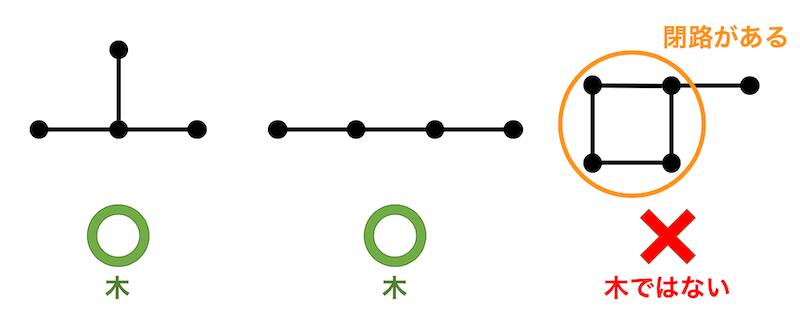
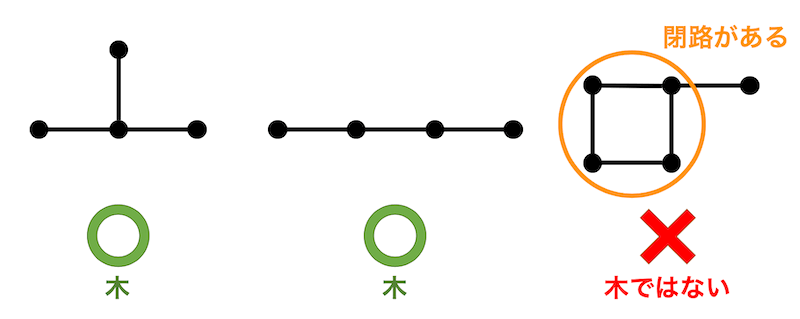
閉路を持たないような連結なグラフのことを木と呼びます。

下の図を例にすると、左と真ん中のグラフは閉路を持たないような連結なグラフなので木です。しかし、右のグラフは閉路があるので木と言うことができません。

f:id:momoyama1192:20191020184253g:plain

(2) 木の重要な5つの特徴

木構造には重要な5つの特徴があります。

木の大事な5つの特徴

つぎの1～5はすべてグラフが木というための条件であり、すべて同値関係にある（1～6のうちどれか1つでも示せたら他の5つもすべて成り立つ）。

グラフが閉路を持たず、連結である。
グラフの位数（点数）が $n$ のとき、辺数が $n-1$ となる。
（ (辺の数) = (点の数) - 1 で覚えましょう）
閉路を持たないグラフに隣接していない任意の2点を加えると閉路が1つだけできる。
グラフの辺を1本でも消すと連結ではなくなる。
グラフのどの2点間の道は1通りしかない（たどり方は必ず1通り）

特に点の数 $n$ と辺の数 $m$ の数の関係\[
m = n - 1
\]は非常に重要なので必ず頭に入れておきましょう。

(3) 森（林）とは

森とは、木の条件である「閉路を持たず、連結である」の「連結である」部分の縛りをなくしたものです*1。

つまり、閉路を持たないようなグラフが森となります。森のことを林と呼ぶ先生もいますが、本記事では森で統一したいと思います。

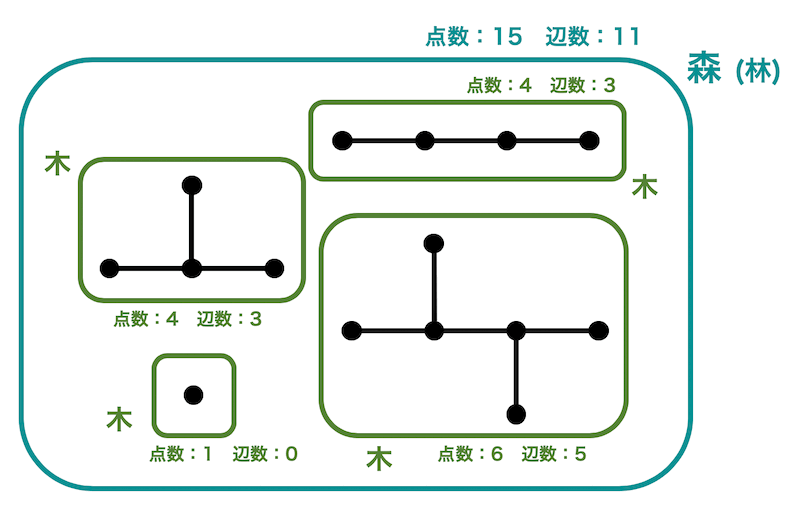
下のように木をいくつか集めたものが森と考えてもいいでしょう。

下の図を例にすると、4つの木が集まっていますね。練習にそれぞれの木の点数と辺数を数えてみましょう。

f:id:momoyama1192:20191022210618g:plain

あるグラフが森の場合の辺数 $m$ は、頂点数 $n$ 、連結数 $k$ を用いて\[
m = n - k
\]と表すことができます。

例えば上のグラフ（森）の場合、4つの木に分割することができるので連結数は4ですね。さらに頂点数は15なので、辺の数は\[
m = 15 - 4 = 11
\]と計算することができます。

（実際に手で数えても辺の数は11となるので公式が正しいことがわかりますね。

森の特徴

閉路を持たないようなグラフのことを森と呼ぶ。
（イメージ：木が何個か集まったもの）

また、あるグラフが森であるときの辺の数 $m$ は頂点の数 $n$ 、連結数 $k$ を用いて\[
m = n - k
\]と表される。

木単体も森と呼ぶので注意しましょう。（連結数 $k = 1$ の森）

では1問例題です。

例題1

つぎの(1)～(3)の問いに答えなさい。

(1) 位数（頂点数）が4のとき、5のときの辺の数、次数の総和を答えなさい。
(2) 位数（頂点数）が4の互いに同型ではない木をすべて書きなさい。
(3) 位数（頂点数）が5の互いに同型ではない木をすべて書きなさい。

解説1

(1)

(辺数) = (頂点数) - 1 、(次数の和) = 2 × (辺数) を使う（握手定理）

握手定理忘れた人はこちらで復習しましょう。

頂点数4：辺数は3、次数の和は6
頂点数5：辺数は4、次数の和は8

(2)

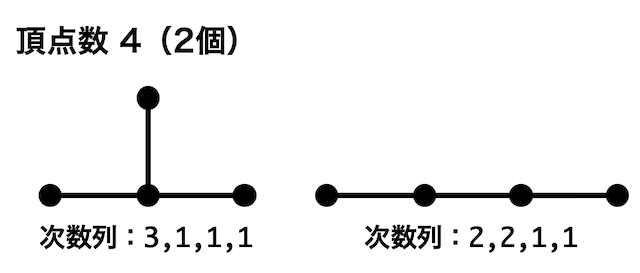
頂点数が4の木の次数の和は6であることに注目する。

次数列*2としては、「3,1,1,1」もしくは「2,2,1,1」の2つが考えられる。

※次数列が異なれば当然同型ではないので、次数列をすべて書き出すことで同型ではないグラフをすべて書き出しやすくなる。

（ただし次数列が同じ同型ではないグラフは1つとは限らないので注意）

よってそれぞれの次数列ごとの同型ではない頂点数4のグラフは下のようになる。

f:id:momoyama1192:20191020184327g:plain

(3)

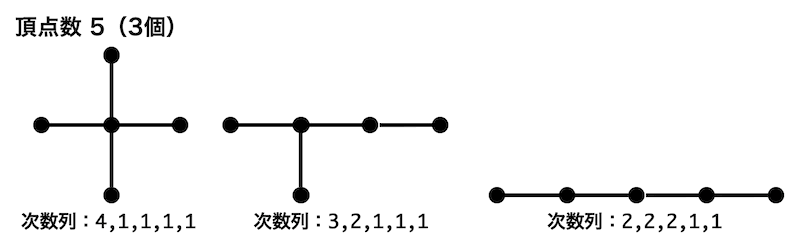
頂点数が5の木の次数の和は8となる。

次数列としては、「4,1,1,1,1」、「3,2,1,1,1」、「2,2,2,1,1」の3つが考えられる。

よってそれぞれの次数列ごとの同型ではない頂点数5のグラフは下の3つである。

f:id:momoyama1192:20191020184331g:plain

２．根付き木

木のとあるノード（点）を根とした木のことを根付き木と呼びます。

根付き木には木にはない特殊な用語がいくつかあるのでまとめて紹介をしたいと思います。

f:id:momoyama1192:20191022210623g:plain

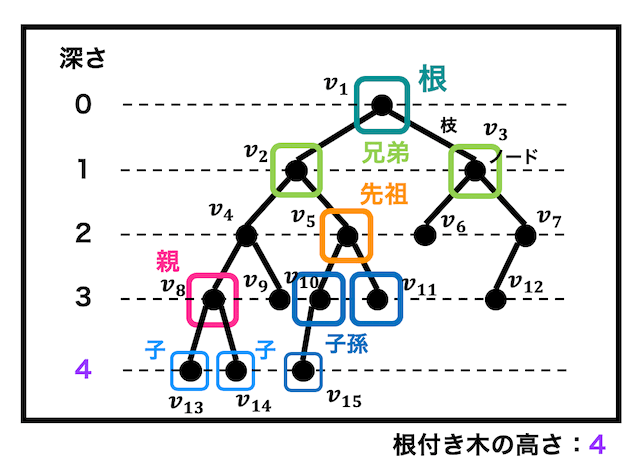
(1) 深さ

深さはある点から根からの長さ（たどる際に通った辺の本数）を表します。

上の図の例でいくと、 $v_2$ は根（ $v_1$ ）からの距離が1なので深さは1ですんね。同様に $v_{12}$ だと、根から3本の辺をたどる必要があるため深さは3となります。

(2) 高さ

あるノード（点）からより深い方向（根から遠ざかる方向）にたどっていった際にどれくらい深くたどれるかを表したものが高さとなります。

f:id:momoyama1192:20191020184314g:plain

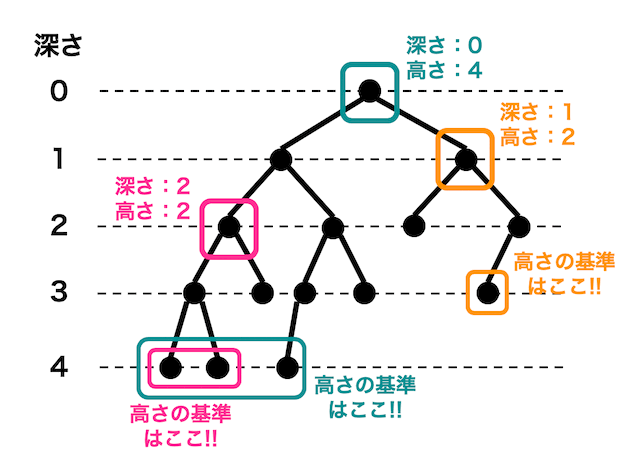
例えば深さが1であるオレンジで囲われたノードは深い方向にたどっていくと「深さ3」のノードまでたどることができますね。2つ分深いところまでたどれるので高さは2となります*3。

同様に深さが2であるピンクで囲われたノードは「深さ4」のノードまでたどれますね。2つ深いところまでたどれるので高さは2となります。

根（深さ0）の高さは根付き木の高さとなります。

根からは深さ4までのノードまでたどれ、4つ深いところまでたどれるので高さは4となります。

(3) 親・子

根付き木では頂点の関係を家系図のように例えます。

隣接してる2つの点に対して、より根に近い方を親、遠い方を子と呼びます。表記法としては、「xxxはyyyの親/子である」と表現します。

例えば $v_8$ と $v_{13}$ であれば「 $v_{8}$ は $v_{13}$ の親」、「 $v_{13}$ は $v_{8}$ の子」のように呼びます。

（ $v_{8}$ の子は $v{13}$ , $v_{14}$ の2つあります）

f:id:momoyama1192:20191022210623g:plain

(4) 先祖・子孫

あるノードを先祖としたとき、先祖のノードからより深い方向にたどっていったときにあるノードすべてを子孫と呼びます。

言い換えると、子孫のノードからより浅い方向にたどっていったときにあるノードすべてが先祖となります。

（親子関係と同じく、「xxxはyyyの先祖/子孫」であると表記します。）

例えば $v_{5}$ を基準に考えると $v_{10}$ , $v_{11}$ , $v_{15}$ の3つが $v_{5}$ の子孫となります。

逆に $v_{5}$ の先祖は $v_{2}$ , $v_{1}$ の2つがあてはまります。

(5) 兄弟

同じ深さにいるノード同士は兄弟となります。

例えば $v_{2}$ と $v_{3}$ は兄弟となります。

同様に $v_{4}$ , $v_{5}$ , $v_{6}$ , $v_{7}$ 同士も兄弟となります。

では、例題で用語の復習をしてみましょう。

例題2

$v_1$ を根とする根付き木がある。これについて、(1)～(5)の問いに答えなさい。

f:id:momoyama1192:20191022210630g:plain

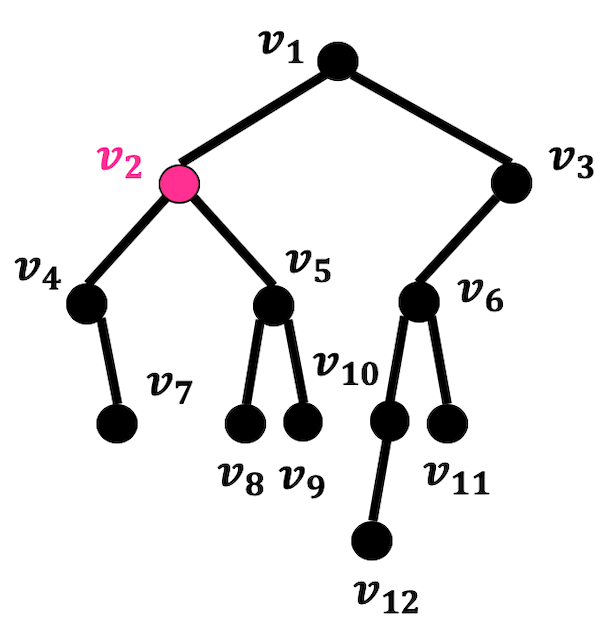
(1) $v_2$ の深さ、高さを求めなさい。
(2) この根付き木の高さを求めなさい。
(3) $v_2$ の親、子を求めなさい。
(4) $v_2$ の先祖、子孫を求めなさい。
(5) $v_2$ の兄弟を求めなさい。

（ (3)～(5)は複数ある場合はすべて求めること）

解説2

(1)

解答：深さ1　高さ2

$v_2$ と根 $v_1$ の距離は1なので深さは1、 $v_2$ から深くなる方向にたどった際に一番深くなるのは $v_7$ , $v_8$ , $v_9$ がある深さ3の部分である。よって高さは3 - 1 = 2となる。

(2)

解答：4

根（深さ0）から見たときにもっとも深いノードは $v_{12}$ となり、深さは4である。よって高さも4となる。

(3) 親： $v_1$ 　子： $v_4$ , $v_5$

(4) 先祖： $v_1$ 　子孫： $v_4$ , $v_5$ , $v_7$ , $v_8$ , $v_9$

(5) $v_3$

３．m分木（2分木）・完全m分木（完全2分木）

$m$ 分木の中でも $m = 2$ のとき、つまり2分木はデータ構造などでも頻繁に利用されます。

2分木は少なくとも頭にいれておきましょう。

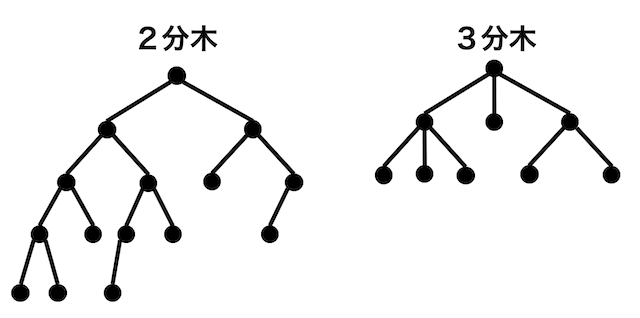
(1) m分木（2分木）とは

根付き木の中でもそれぞれの点における子の数が $m$ 個以下である根付き木のことを $m$ 分木と呼びます。

例えば $m = 2$ のとき（2分木）であればそれぞれの点が2個以下の子を持ちます。 $m = 3$ （3分木）であればそれぞれの点が3個以下の子を持ちます。

f:id:momoyama1192:20191020184318g:plain

(2) 完全m分木（完全2分木）とは

$m$ 分木の中でも葉以外のすべての点が $m$ 個ずつ子をもつ根付き木のことを完全 $m$ 分木と呼びます。

完全 $m$ 分木は中途半端に $m$ 個未満の子を持つような点はなく、すべての点が $m$ 個の子を持つか葉のどちらかになっています。

例えば $m = 2$ のとき（2分木）であれば葉以外のすべての点が2つの子をもち、 $m = 3$ （3分木）であれば葉以外のすべての点が3つの子を持ちます。

f:id:momoyama1192:20191022210626g:plain

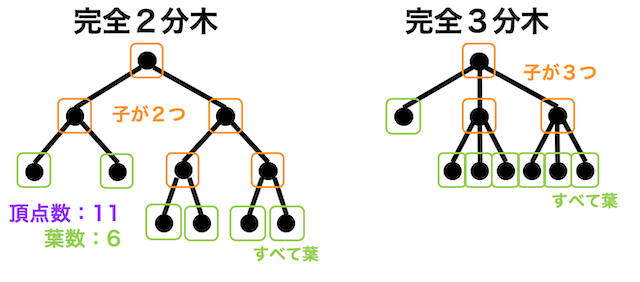
さらに完全2分木の頂点と葉数の数には下のような関係式が成り立ちます。

完全2分木の頂点数と葉数の関係

完全2分木の頂点の数を $n$ 、葉数を $l$ とすると、\[
n = 2l - 1
\]が成り立つ。

今回は練習問題に入れていませんが、与えられた葉の数から同型でない完全2分木をすべて答えるような問題の場合、上の公式から頂点数を求めると形を絞ることができます。

４．練習問題

では4問ほどですが練習してみましょう。

練習1

頂点数6の木について次の問いに答えなさい。

(1) 辺数と次数の合計を答えなさい。
(2) 頂点数6で互いに同型ではない木構造は全部で何個ありますか。

練習2

頂点数7の木で、葉の数が2～6個のグラフをそれぞれ1つずつ書きなさい。

練習3

任意の木は2部グラフであることを示しなさい。

練習4

点の数が $n$ 個、辺の数が $n-1$ 個のグラフは必ず木となることを数学的帰納法を用いて示しなさい。

５．練習問題の答え

練習1

(1)

頂点数 $n$ と辺数 $m$ には、\[
m = n - 1
\]の関係があるので、辺数は5となる。よって次数の和は10となる。

(2)

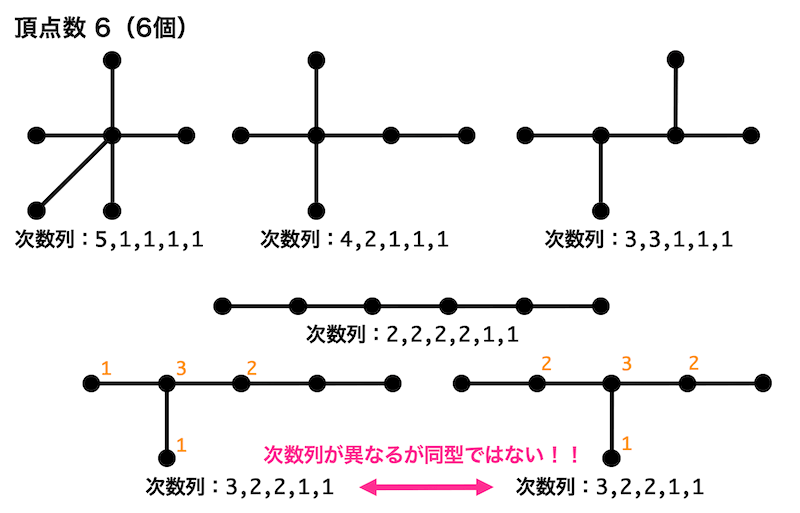
次数の和が10、点の数が6の場合の次数列の組み合わせを列挙すると、

5,1,1,1,1,1
4,2,1,1,1,1
3,3,1,1,1,1
3,2,2,1,1,1（2通り同型でないグラフが書ける）
2,2,2,2,2,2

の5つである。さらにそれぞれの次数列ごとに同型でない木を書いていくと、下のように6個書ける。

よって答えは6個となる。

f:id:momoyama1192:20191020184335g:plain

練習2

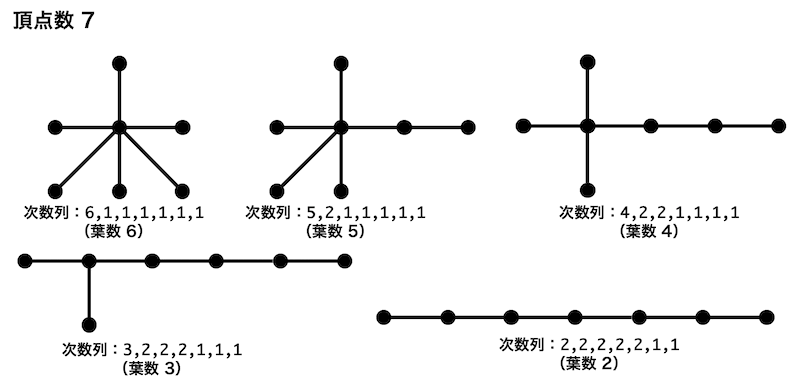
頂点数7なので、辺数は6、次数の和は12となる。

頂点数7、次数の和が12の場合の次数列の組み合わせを列挙すると、

葉が5つ：6,1,1,1,1,1
葉が4つ：5,2,1,1,1,1（4,3,1,1,1,1）
葉が3つ：4,2,2,1,1,1（3,3,2,1,1,1）
葉が2つ：3,2,2,2,1,1

となる。よってそれぞれの次数列ごとのグラフは下のようになる。

f:id:momoyama1192:20191020184339g:plain

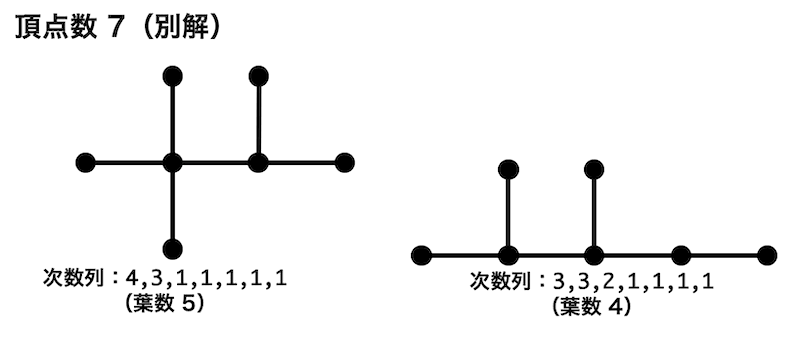
（別解）

葉が5つで次数列が「4,3,1,1,1,1,1」の場合、葉が4つで次数列が「3,3,2,1,1,1,1」の場合のグラフは下のようになる。

f:id:momoyama1192:20191020184344g:plain

練習3

2部グラフの条件を少し変形させるだけで簡単に証明ができます。

（証明）

2部グラフの条件はすべての閉路の長さが偶数となるである。

つまり、長さが奇数となるような閉路が存在しないようなグラフが2部グラフとなる。

どのような木であっても閉路は持たないため、当然長さが奇数となるような閉路も存在しない。

よって木は2部グラフであることが示された。

練習4

頂点数に関する数学的帰納法で示す。

（数学的帰納法が怪しい人はこちらの記事で復習しましょう。）

(1) 頂点数 $n = 1$ のとき

頂点は孤立点となるので辺の数は0本。よって(1)のとき成立。

(2) 頂点数が $n + 1$ のとき

頂点数が $n + 1$ のグラフを $T_1$ とする。

ここで $T_1$ の辺の数が $n$ になることを示す。

$T_1$ から次数が1である頂点、頂点に接続する辺を除去したグラフを $T_2$ とする。

ここで $T_2$ は $T_1$ から点を1本除去しているので頂点数は $n$ となる。さらに帰納法の仮定より $T_2$ の辺の数は $n-1$ となる。

$T_1$ から辺を1本除去したグラフが $T_2$ なので $T_2$ の辺の数は $n$ となり、(2)のときも成立。

(1), (2) より題意は満たされた。

６．さいごに

今回はグラフ理論における木・根付き木についてまとめました。

次回は探索アルゴリズムについて簡単にですがまとめていく予定です。

*1:離散数学の用語を使うと、「森は木の部分集合」である。と言えますね。

*2:グラフ内の点のそれぞれの次数を大きい順に羅列したもの。例えば「3,2,2,1」であれば次数3の点が1つ、次数2の点が2つ、次数1の点が1つあることを示す。

*3:言い方を変えると、深くなる方向にたどった際に見つかった一番深い点の深さから自分の点の深さを引いたものが高さとなる。

工業大学生ももやまのうさぎ塾

うさぎでもわかるをモットーに大学レベルの数学・情報科目をわかりやすく解説！　数式が読み込まれない場合は1回再読み込みしてみてください。