スポンサードリンク
こんにちは、ももやまです。
今回はグラフをコンピュータ上で探索する方法のうち、よく使われる幅優先探索と深さ優先探索について説明していきたいと思います。
前回の記事
目次
スポンサードリンク
1.探索とは
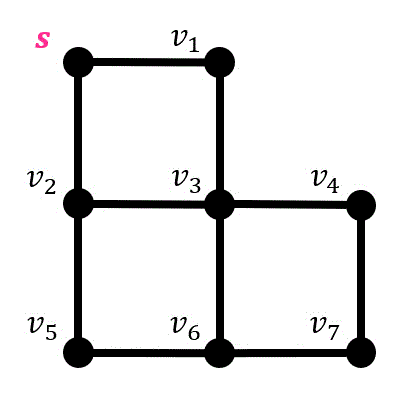
例えば、図の \( s \) から \( v_7 \) までの辺のたどる方法を考えてみましょう。
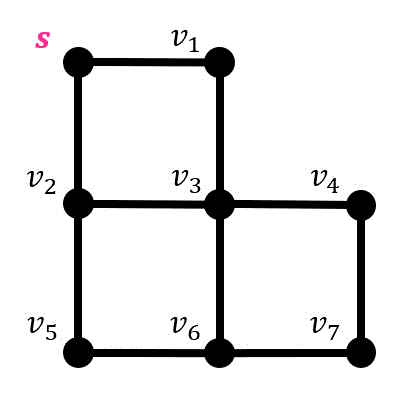
我々人間であれば、\[
s \to v_1 \to v_3 \to v_4 \to v_7 \\
s \to v_1 \to v_3 \to v_2 \to v_5 \to v_6 \to v_7
\]のように好き勝手にたどることができますね。
しかし機械(コンピュータ)は人間のようにやみくもにたどっていくことができません。なのである程度たどり方の方針を命令(プログラム)してあげなければなりません。
そこで今回はたどり方のの命令でよく使われる幅優先探索(横型探索)と深さ優先探索(縦型探索)について説明していきたいと想います。
スポンサードリンク
2.スタック・キュー
まずは幅優先探索・深さ優先探索で使うスタックとキューについて簡単にですが説明したいと思います。
スタック、キューは両方ともデータを出したり入れたりする構造なのですが、データの取り出し方が異なります。
(1) スタック
スタックは、新しく入れたデータ(最後に入れたデータ)から順番に取り出していきます。アルファベット4文字でLIFO (Last-In-First-Out) と表す人もいます。
(2) キュー
一方スタックは、古くからあったデータ(最初に入れたデータ)から順番に取り出していきます。スーパーのレジにできる列とかはまさにキューですよね*1。アルファベット4文字でFIFO (First-In-First-Out) と表す人もいます。
スタックとキューの違いをアニメーションで表してみました。
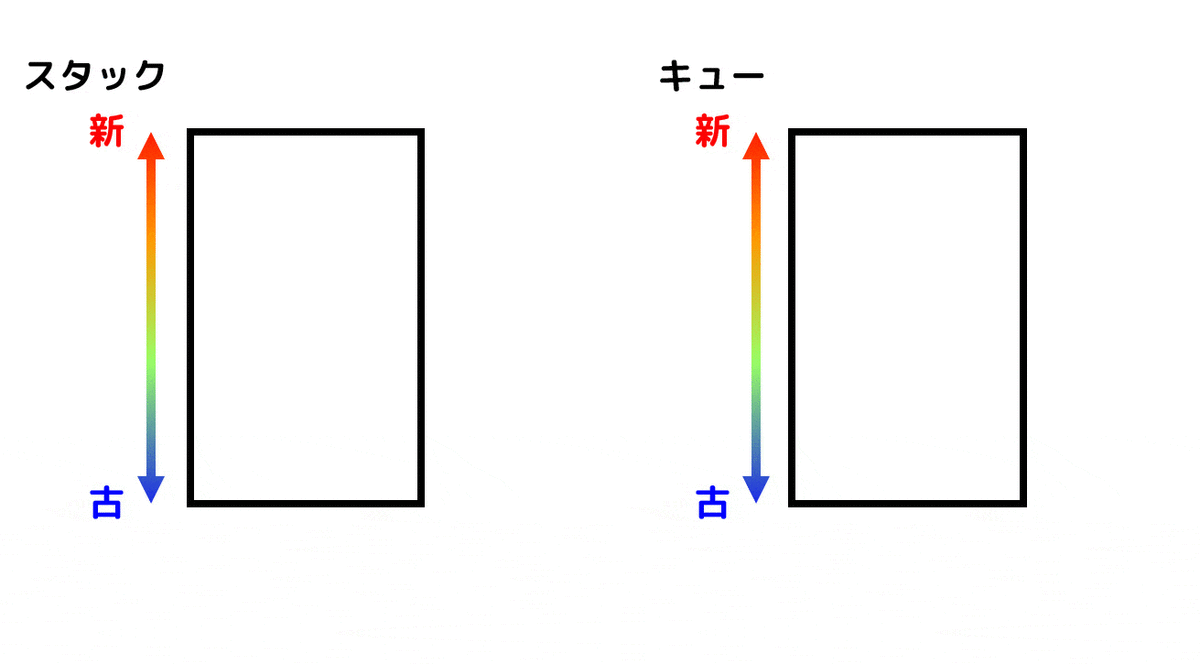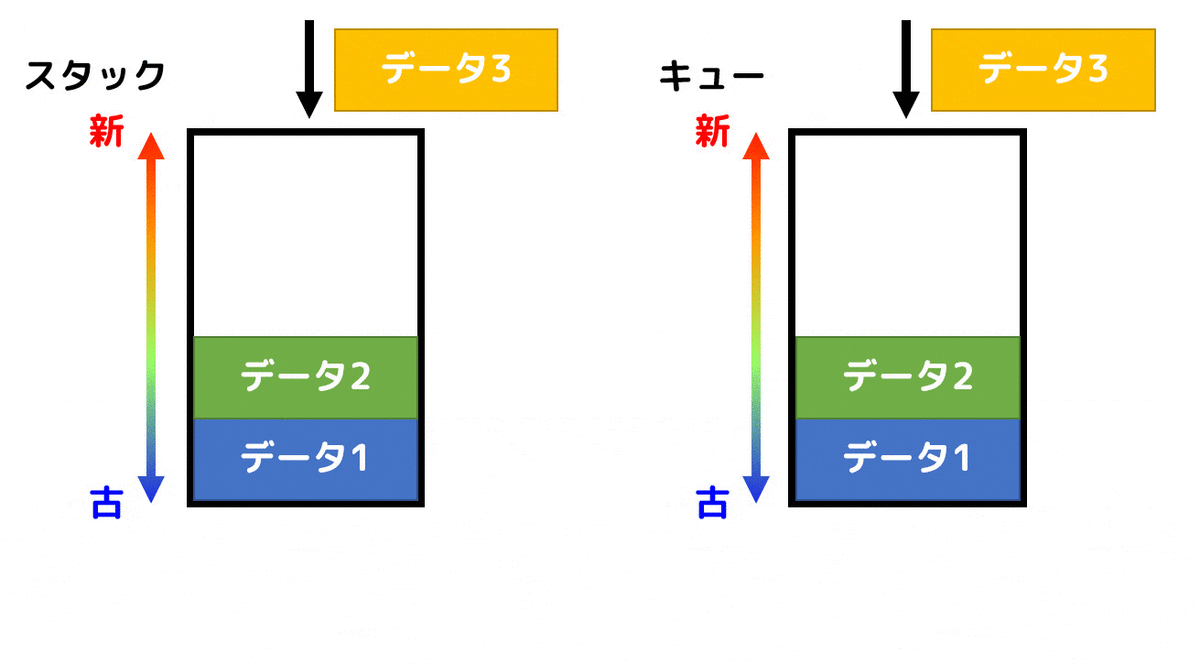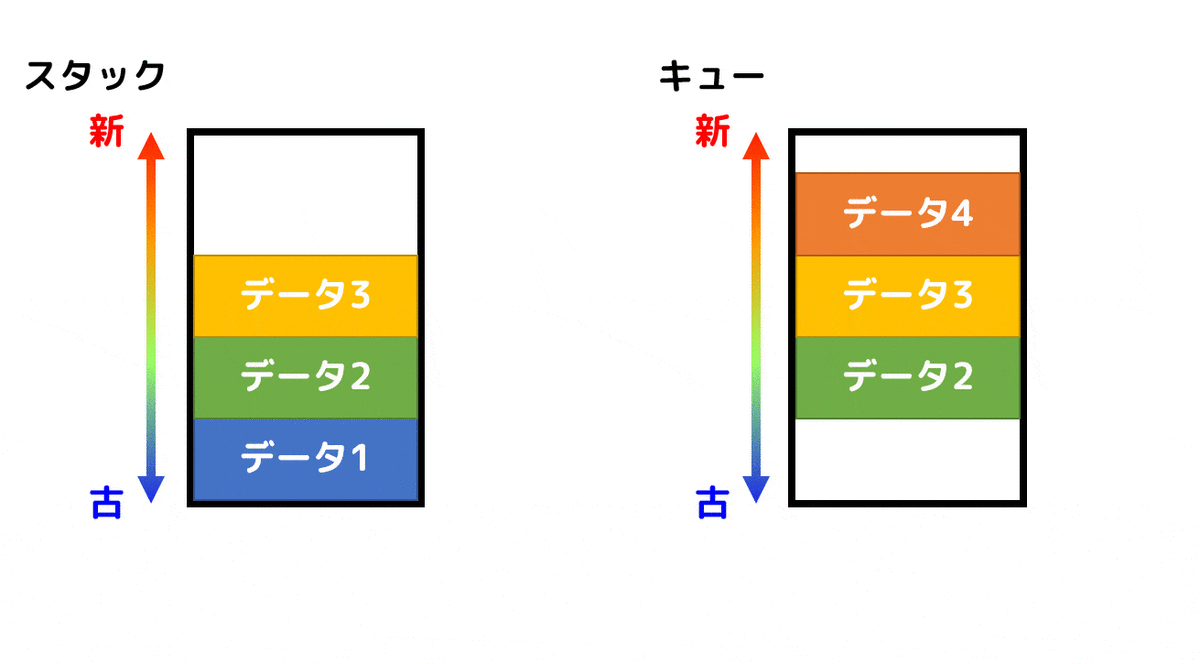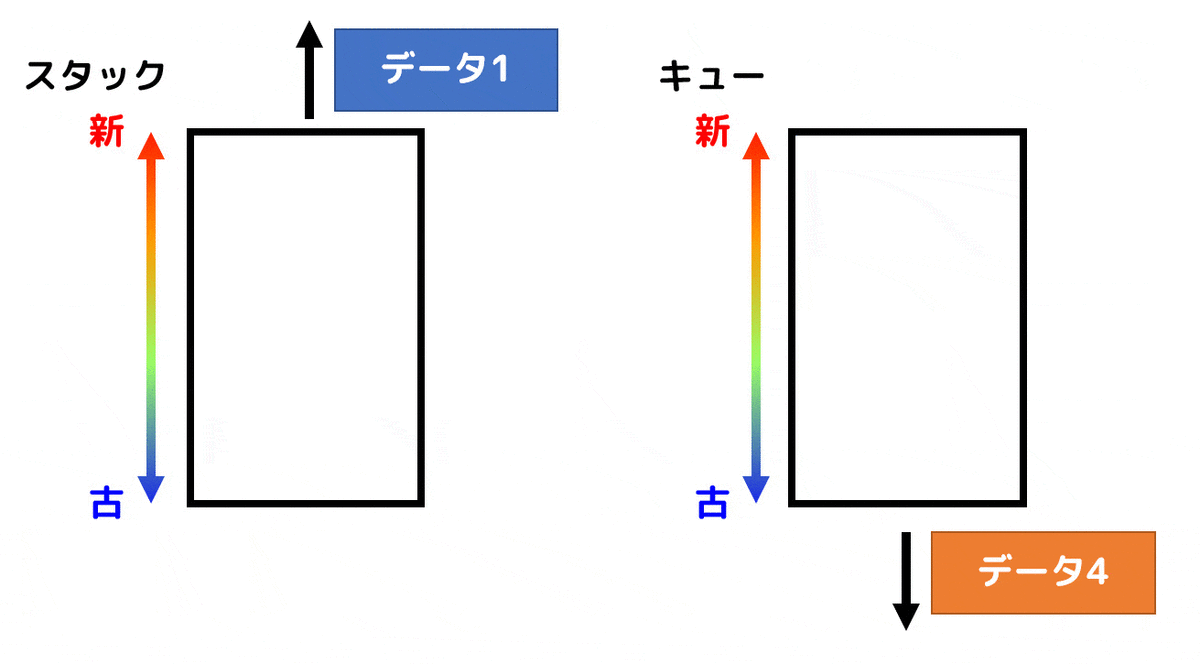
データを取り出すときにスタックとキューでは大きく異なる動きをしていることがわかるかと思います。
スポンサードリンク
3.幅優先探索(横型探索・BFS)
では本題の探索の説明をしていきましょう。
幅優先探索とは、探索開始地点に近い点からまんべんなく探索していく探索方法です。横型探索や、BFS(Breadth First Search) と呼ばれることもあります。
詳しく書くと下のようなアルゴリズムでグラフを探索していきます。
- スタート点を探索候補点とする
- 探索候補点の中から一番最初につくられた探索候補点を1つ取り出す。
このときの元の点と探索候補点をつないだものが経路(道)となる。 - 取り出した点から隣接している点を新たな探索候補点とする。
ただし、すでに探索候補点や探索が終了した点になっている場合は追加しない。 - すべての点が探索終了になるまで2に戻る(ループ)。
幅優先探索の探索方法
幅優先探索では、探索候補点を取り出す際に最初に入れられた点を取り出すため、データ構造としてキューが使われます。
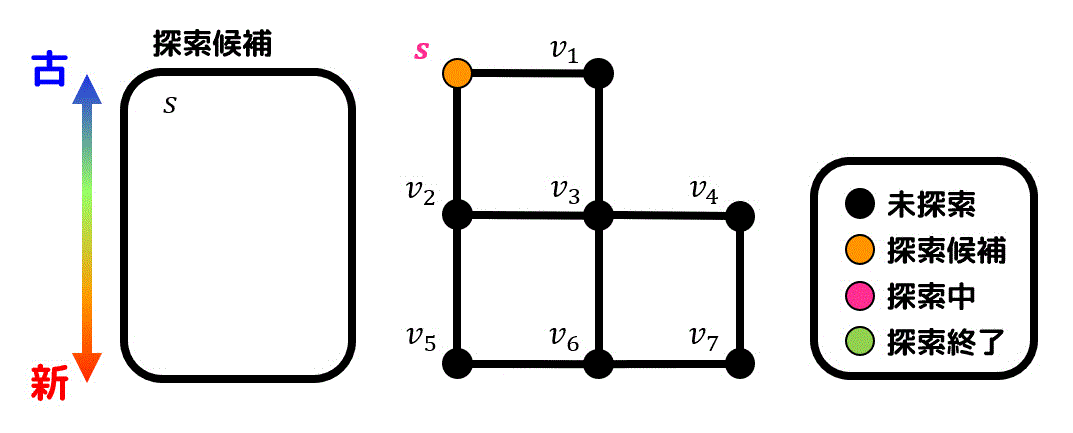
実際に幅優先探索の動きを下のグラフの例に見ていきましょう。始点は \( s \) です。

探索候補点をオレンジ色、探索中の点を赤色、 探索済の点を緑色にしています。また、探索経路を紫色で表示しています。
※同じタイミングで生成される探索候補点は、番号が小さい方を優先して先に探索しています。
まずはスタート点である \( s \) を探索候補点とします。
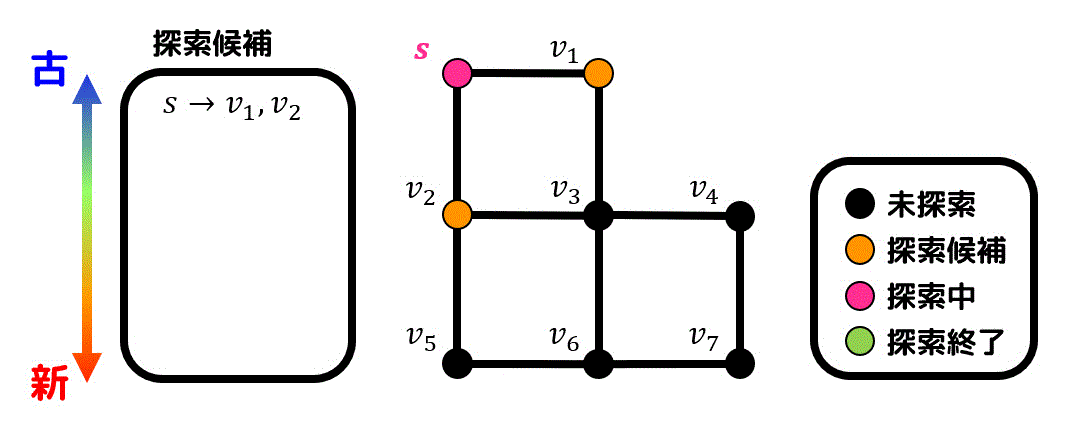
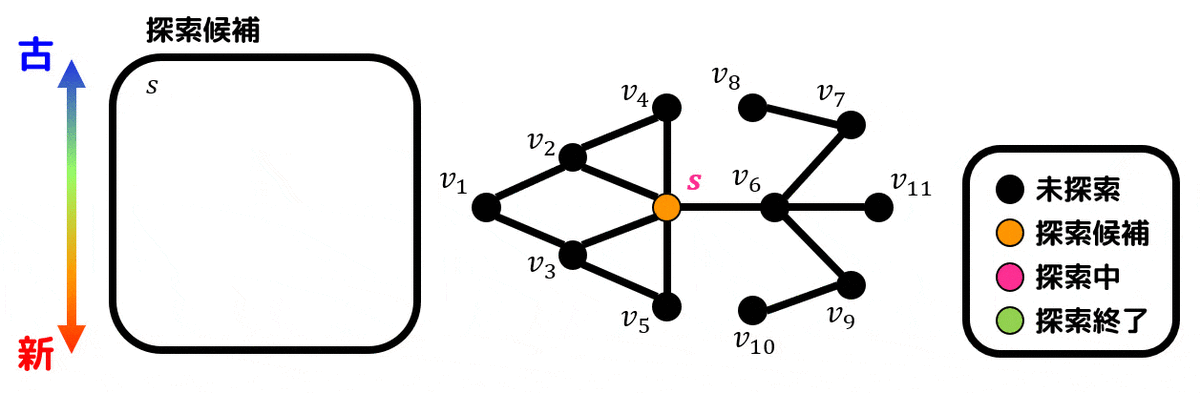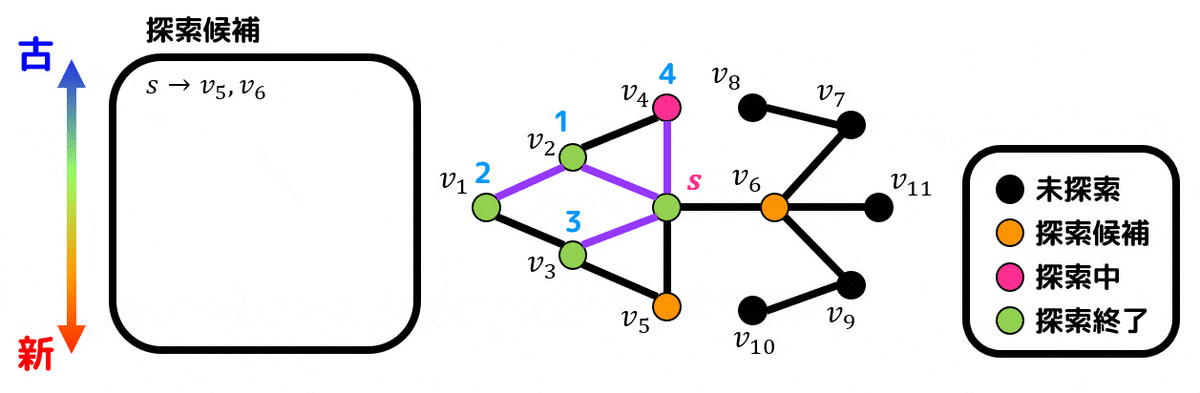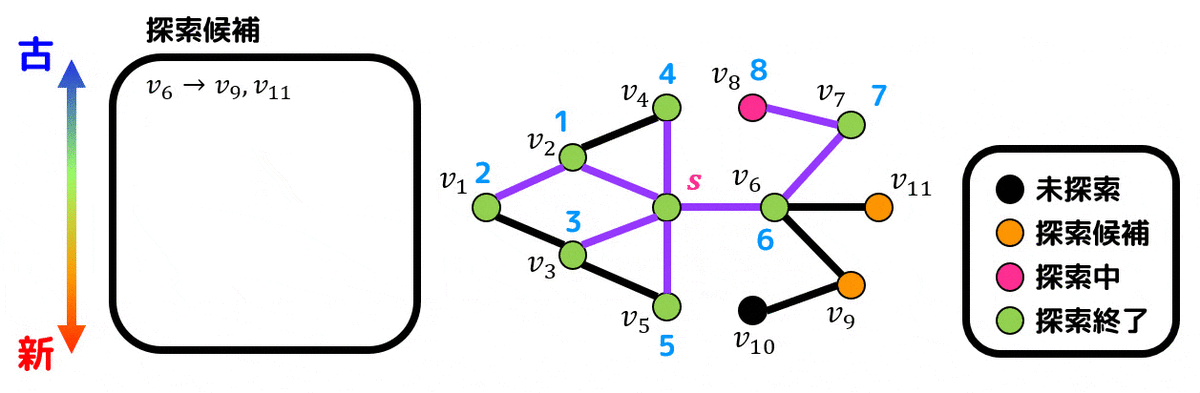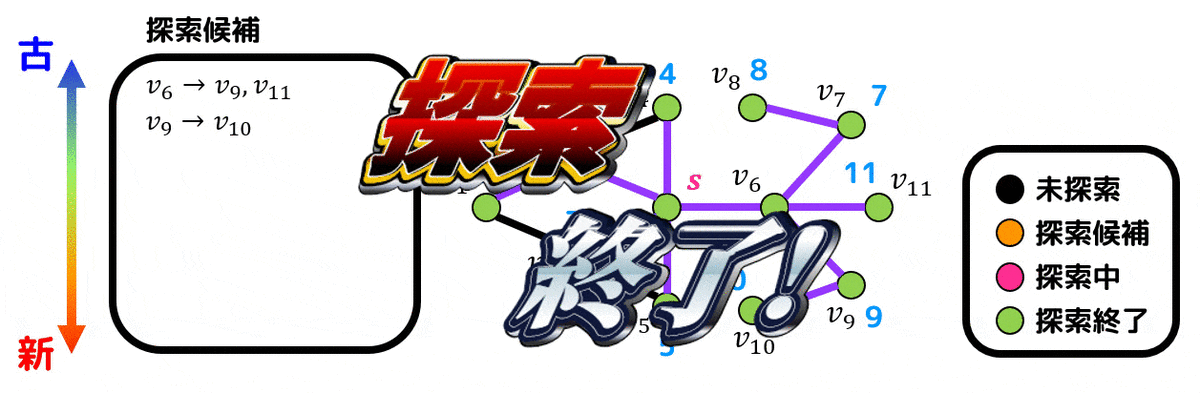
つぎに \( s \) と隣り合っている点(\( v_1 \), \( v_2 \))を探索候補点に追加します。
(探索候補にはどの点から生成されたかも書いておきましょう。今回の場合は \( s \) から \( v_1 \), \( v_2 \) が追加されたので \( s \to v_1, v_2 \) とします。
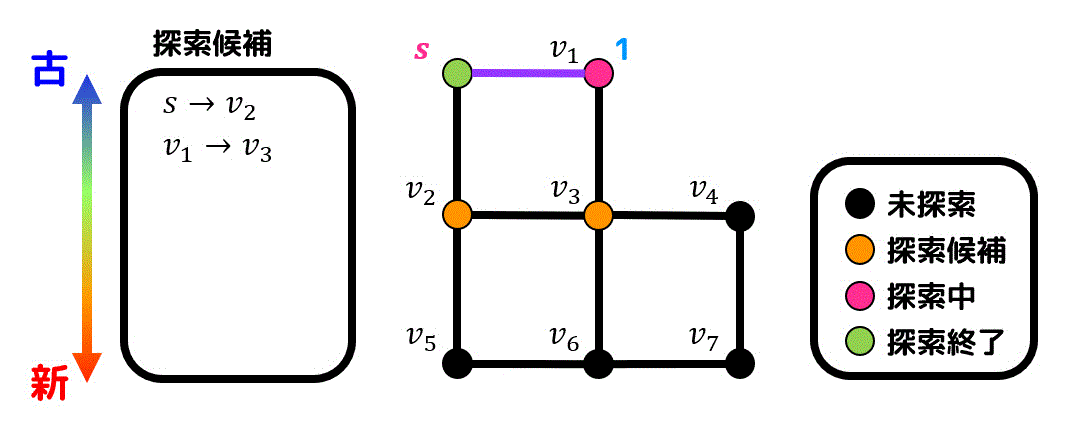
\( v_1 \), \( v_2 \) は同時に追加された点のため、先に番号が小さい \( v_1 \) から順番に探索していきます。
\( v_1 \) は \( s \) から追加された点なので、\( s \) と \( v_1 \) を結ぶ辺が経路となります。(経路は紫色で示しています)
\( v_2 \), \( v_3 \) の2つが候補点ですが、\( v_2 \) のほうが先に候補点になっているので \( v_2 \) から探索します。\( s \) から \( v_2 \) を結ぶ辺が経路に追加されます。
\( v_2 \) からは新たに \( v_5 \) にたどれるので \( v_5 \) が新たな候補点です。
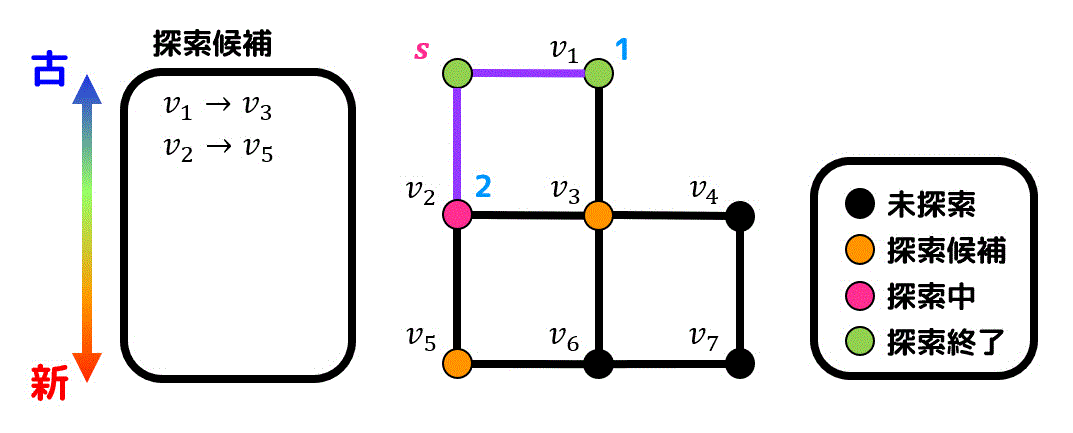
\( v_3 \), \( v_5 \) では \( v_3 \) のほうが古いので \( v_3 \) を探索します。新たに \( v_4 \), \( v_6 \) が候補点となります。
(\( v_3 \) は \( v_1 \) から生成されているので \( v_1 \) と \( v_3 \) を結ぶ辺が新たに経路に追加されます。)
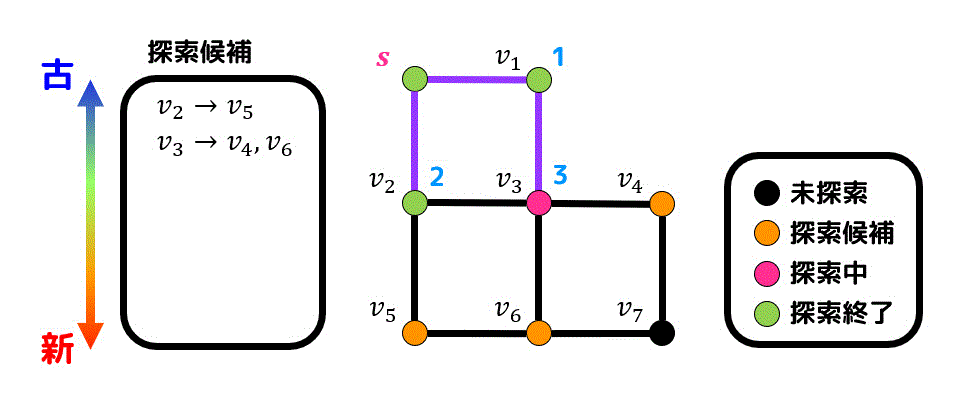
一番古く探索候補点になった \( v_5 \) を探索します。\( v_5 \) からたどれる新たな探索候補点はないので候補点は追加されません。
(\( v_5 \) は \( v_2 \) から生成されているので \( v_2 \) と \( v_5 \) を結ぶ辺が新たに経路に追加されます。)
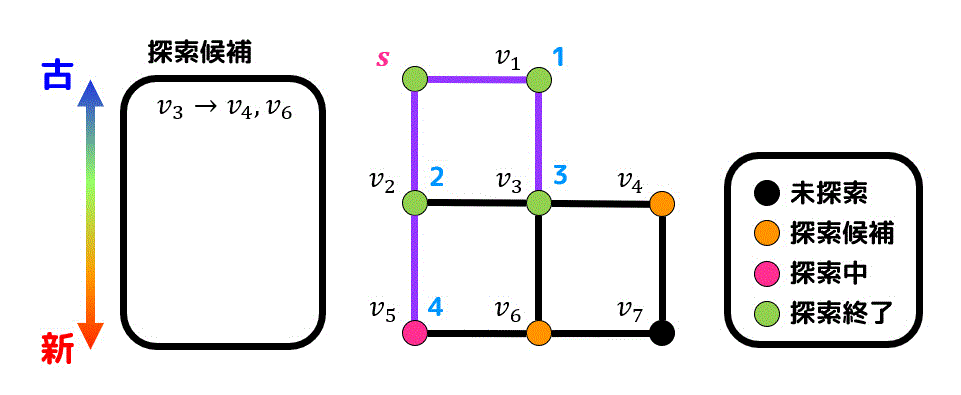
\( v_4 \), \( v_6 \) は同時に探索候補点になっているため、番号が若い \( v_4 \) から順番に探索します。新たに \( v_7 \) が探索候補点となります。
(\( v_4 \) は \( v_3 \) から生成されているので \( v_3 \) と \( v_4 \) を結ぶ辺が経路に追加されます。)
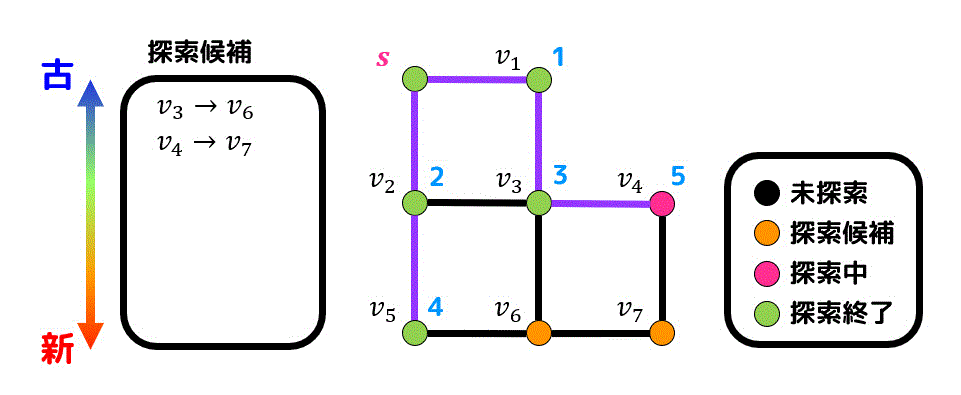
\( v_6 \) も探索していきましょう。\( v_6 \) は \( v_3 \) から生成されているので \( v_3 \) と \( v_6 \) を結ぶ辺が経路に追加されます。
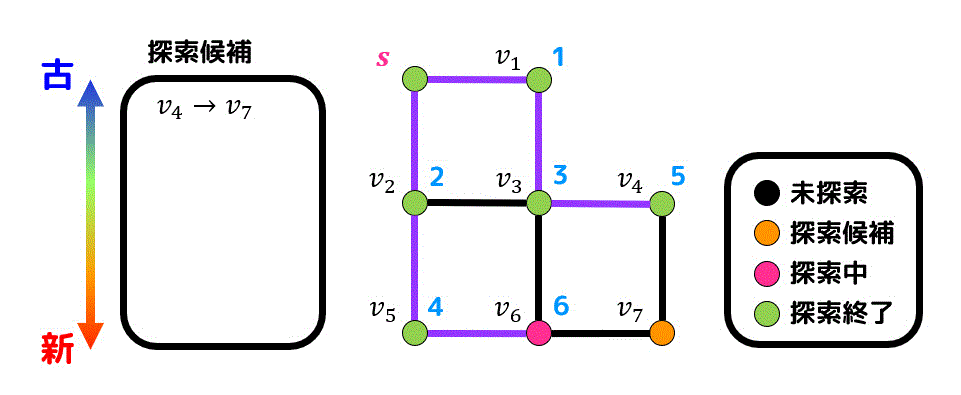
最後に \( v_7 \) を探索したら探索完了です!
\( v_4 \) から生成された候補点なので \( v_4 \) と \( v_7 \) を結ぶ辺を経路に追加しましょう。
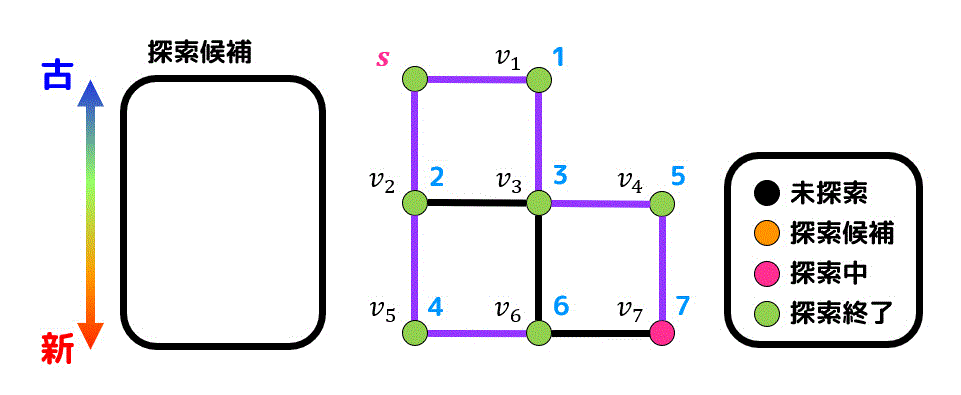
ここで、すべての点を探索した際に出てくる経路(紫色で表されている経路)は木となっていますね*2。この木のことを探索木と呼びます。
幅優先探索の探索木のことをBFS木と呼んだりもします。
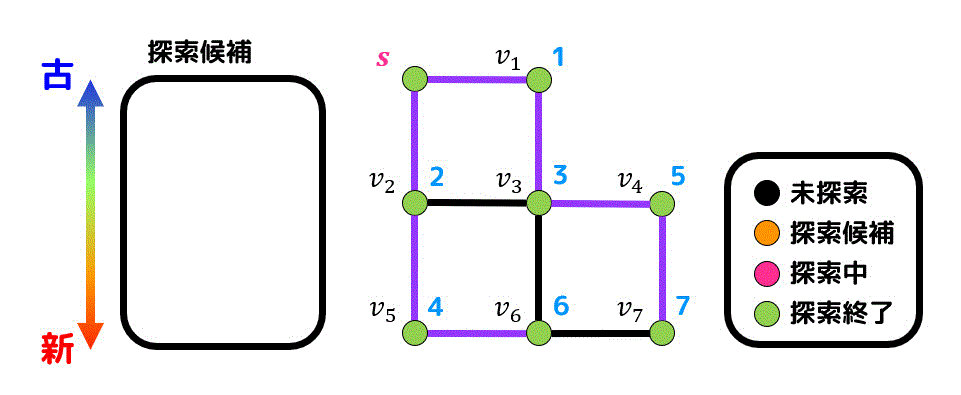
また、BFS木は始点からの最短経路を表しています。なので、BFS木をたどるだけで始点からの最短距離を求めることができます*3。
今回の問題の場合、\( s \) からの距離を下のように求めることができます。
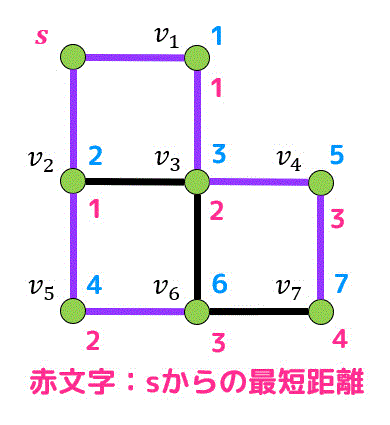
例えば \( s \) から \( v_4 \) への最短経路は探索木(紫色の辺)をたどると\[
s \to v_2 \to v_3 \to v_4
\]となり、距離が3であることがわかりますね。
4.深さ優先探索(縦型探索・DFS)
深さ優先探索とは、とにかく猪突猛進に進んでいくタイプの探索方法です。縦型探索や、DFS(Depth First Search) と呼ばれることもあります。
詳しく書くと下のようなアルゴリズムでグラフを探索していきます。
- スタート点を探索候補点とする
- 一番最後につくられた探索候補点を1つ取り出す。
このときの元の点と探索候補点をつないだものが経路(道)となる。 - 取り出した点から隣接している点を新たな探索候補点とする。
ただし、すでに探索候補点や探索が終了した点になっている場合は追加しない。 - すべての点が探索終了になるまで2に戻る(ループ)。
深さ優先探索の探索方法
幅優先探索では、探索候補点を取り出す際に最後に入れられた点を取り出すため、データ構造としてスタックが使われます。
幅優先探索の違いは、最初につくられた(一番新しい)探索候補点を優先的に取り出すか最後につくられた(一番新しい)探索候補点を優先的に取り出すかだけです。
幅優先のときと同じく実際に下のグラフを例に幅優先探索の動きを見ていきましょう。

※先程と同じように同じタイミングで生成される探索候補点は、番号が小さい方を優先して先に探索しています。
まずはスタート点である \( s \) を探索候補点とします。

つぎに \( s \) と隣り合っている点(\( v_1 \), \( v_2 \))を探索候補点に追加します。
(幅優先探索と同じように探索候補にはどの点から生成されたかも書いておきましょう。今回の場合は \( s \) から \( v_1 \), \( v_2 \) が追加されたので \( s \to v_1, v_2 \) とします。)

\( v_1 \), \( v_2 \) は同時に追加された点のため、先に番号が小さい \( v_1 \) から順番に探索していきます。
\( v_1 \) は \( s \) から追加された点なので、\( s \) と \( v_1 \) を結ぶ辺が経路となります。(経路は紫色で示しています)

ここからが幅優先探索と異なります。
\( v_2 \), \( v_3 \) の2つの点のうち、より新しく探索候補点となったのは \( v_3 \) なので、\( v_3 \) から探索をおこないます。
\( v_3 \) からは隣り合っている \( v_4 \), \( v_6 \) が新たに探索候補点となります。経路追加(\( v_1 \) から \( v_3 \) の辺)もお忘れなく。
(\( v_2 \) はすでに探索候補点なので無視)
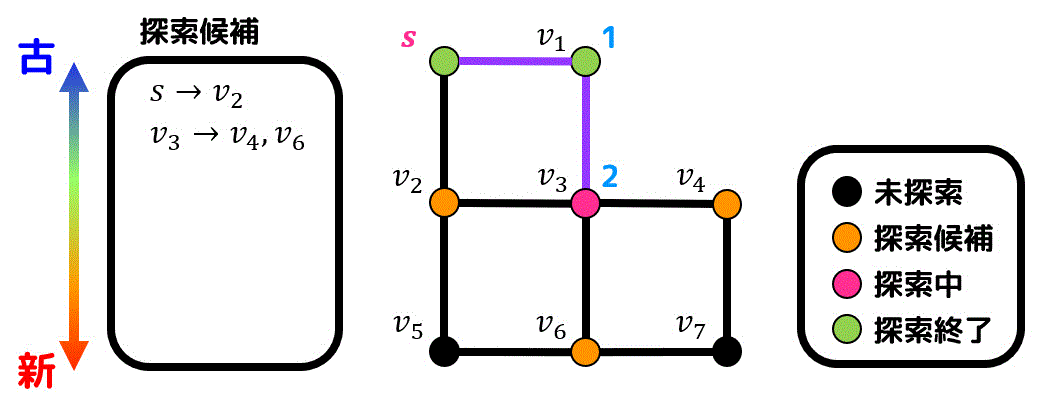
\( v_2 \), \( v_4 \), \( v_6 \) のうち、\( v_4 \), \( v_6 \) の2点がより新しい点なので、番号が若い \( v_4 \) から先に探索します。
\( v_4 \) からは新たに \( v_7 \) にたどれるため、\( v_7 \) が新たな候補点として追加されます。
\( v_4 \) は \( v_3 \) から生成された候補点なので \( v_3 \) と \( v_4 \) が経路として追加されます。
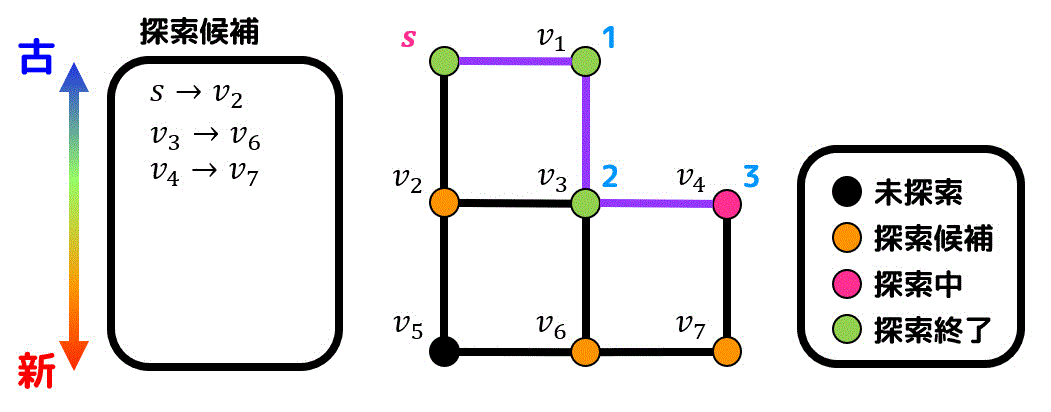
候補点である \( v_2 \), \( v_6 \), \( v_7 \) のうち、一番新しく生成されたのは \( v_7 \) なので \( v_7 \) を探索します。
\( v_7 \) から新たに探索できる点はないので候補点は追加無しです。
\( v_7 \) は \( v_4 \) から追加された点なので \( v_4 \) と \( v_7 \) を結ぶ辺が経路に追加されます。
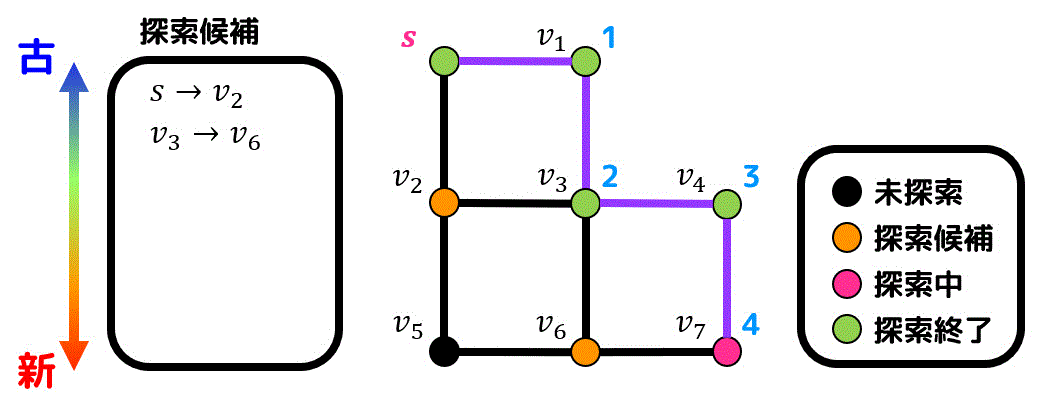
\( v_2 \) と \( v_6 \) の中では \( v_6 \) がより新しく追加された候補点なので \( v_6 \) を探索します。
\( v_6 \) からは新たに \( v_5 \) にたどることができるので \( v_5 \) が新たな候補点として追加されます。
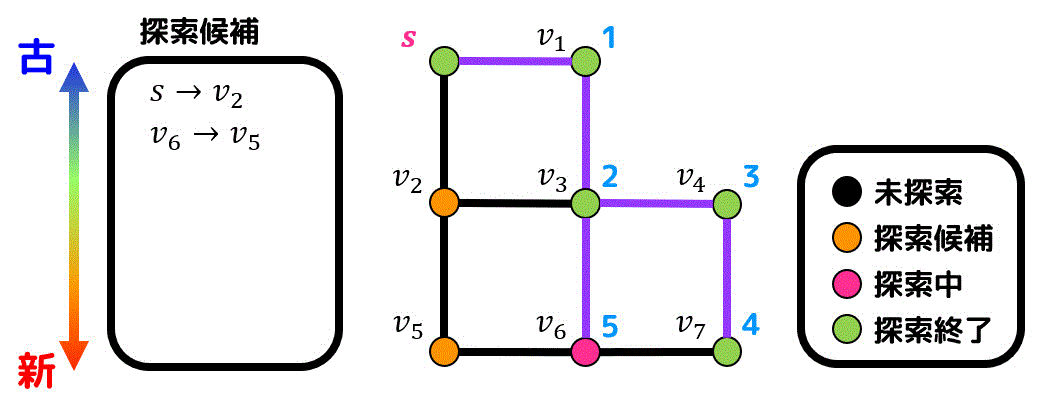
\( v_2 \), \( v_5 \) の2つでは \( v_5 \) のほうがより新しく追加された候補点なので \( v_5 \) を先に探索します。
新たな探索候補点はありません。\( v_6 \) は \( v_5 \) から生成された候補点なので \( v_5 \) から \( v_6 \) を結ぶ辺が経路に追加されます。
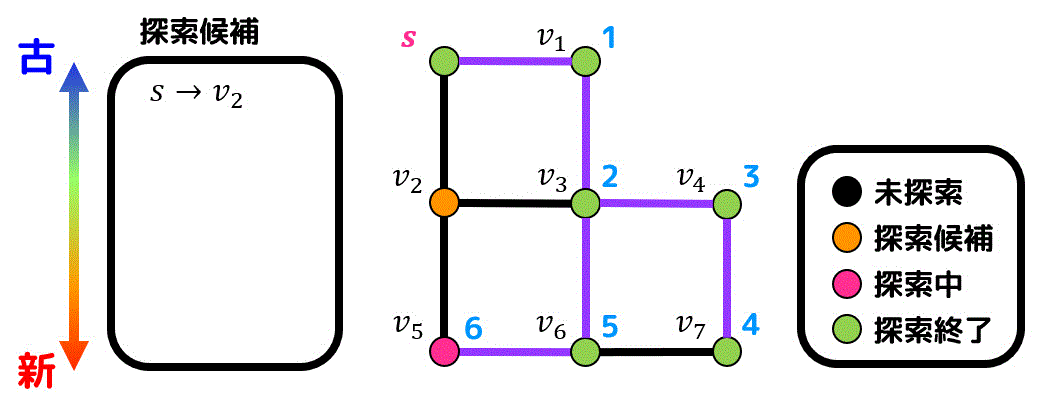
最後に残った \( v_2 \) を探索します。
\( s \) から生成されたので \( v_2 \) と \( s \) を結ぶ辺が経路として追加されます。
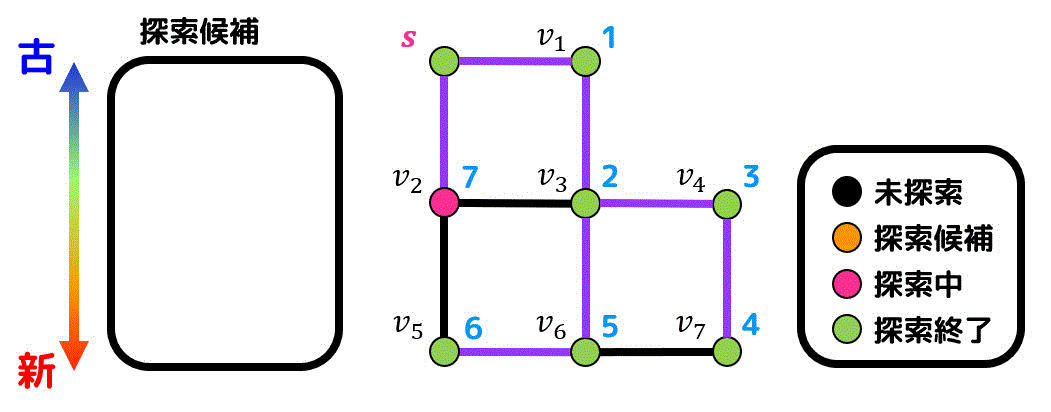
これで探索終了です!
探索順序と経路(探索木)は下のようになります! 深さ優先探索で生成される探索木のことをDFS木と呼びます。
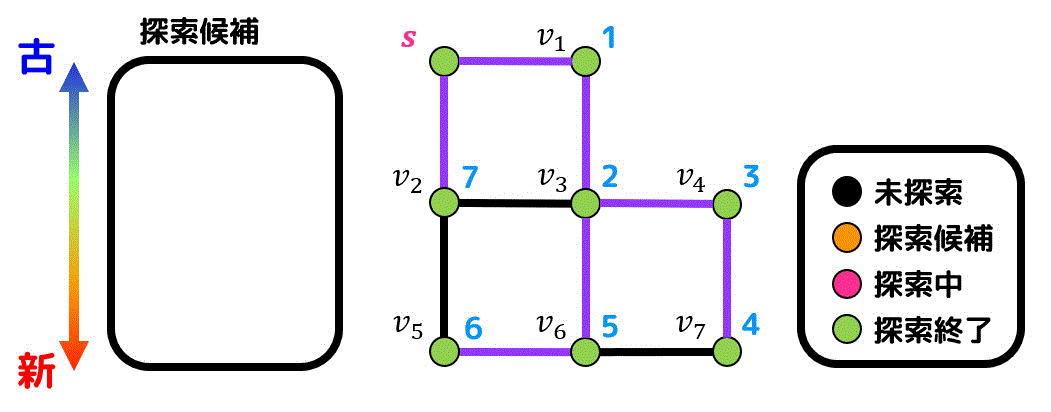
深さ優先探索の場合、とにかく1つのノードから行ける場所まで探索していき、探索できなくなったら別の点(探索できなくなった点から一番近い点)を探索していているのがわかりますね。
幅優先探索の場合の探索木(BFS木)と比べてみましょう。
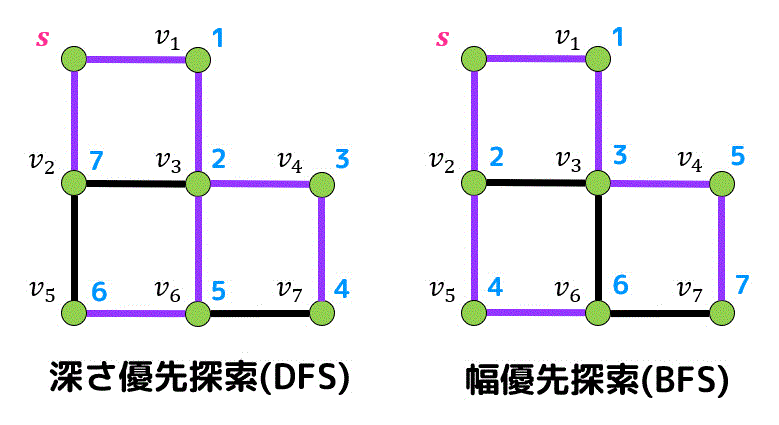
探索順序も探索木も幅優先探索とは全然違う結果になることがわかりますね!
5.練習問題
では3問ほど練習してみましょう!
練習1
次のグラフを \( s \) から幅優先探索し、探索木(BNS木)とそれぞれの点の探索順序を答えなさい。また、\( s \) からそれぞれの点の最短距離を探索木を用いて答えなさい。
ただし、同時に生成される点の場合はより番号が若いものから順番に探索すること。
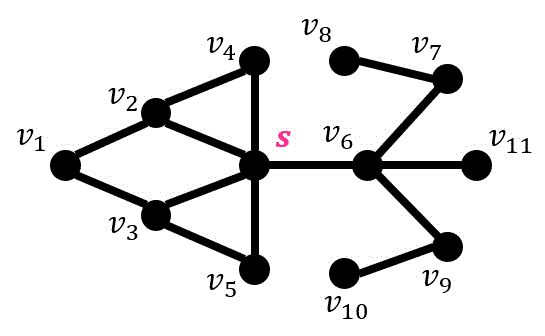
練習2
練習1と同じグラフを \( s \) から深さ優先探索し、探索木(DNS木)とそれぞれの点の探索順序を答えなさい。
ただし、同時に生成される点の場合はより番号が若いものから順番に探索すること。
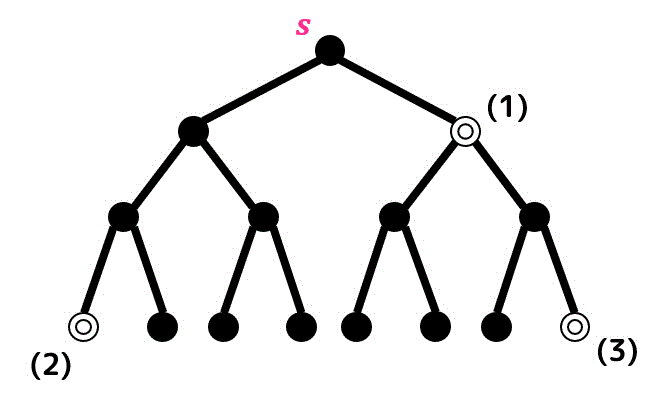
練習3
つぎのグラフ(木)がある。
このグラフを幅優先探索、深さ優先探索したとき、(1), (2), (3) それぞれの点の探索結果として正しいものを①~④の中から番号で答えなさい。
(ただし、同時に生成された候補点はより左側にあるノードを優先的に処理すること。)
- 幅優先探索のほうが早い
- 深さ優先探索のほうが早い
- どちらも同じ
- 上記の条件ではわからない
6.練習問題の答え
解答1
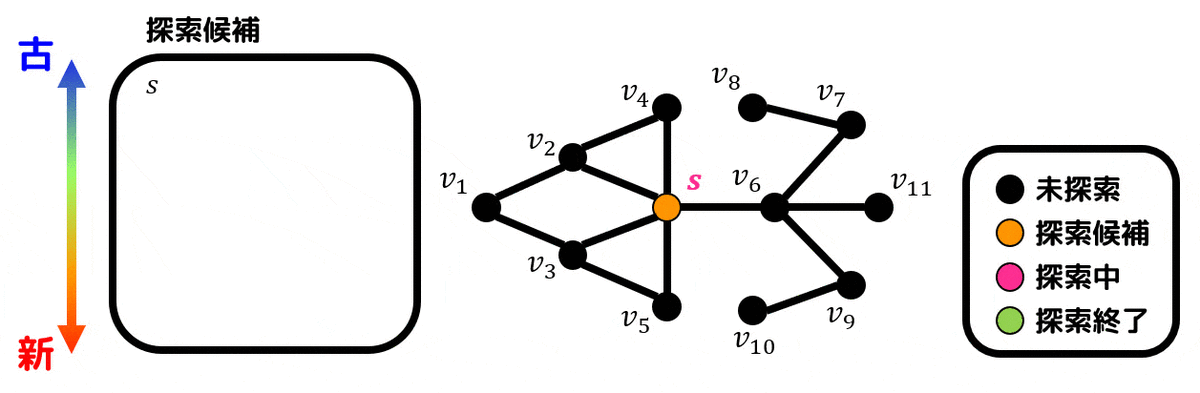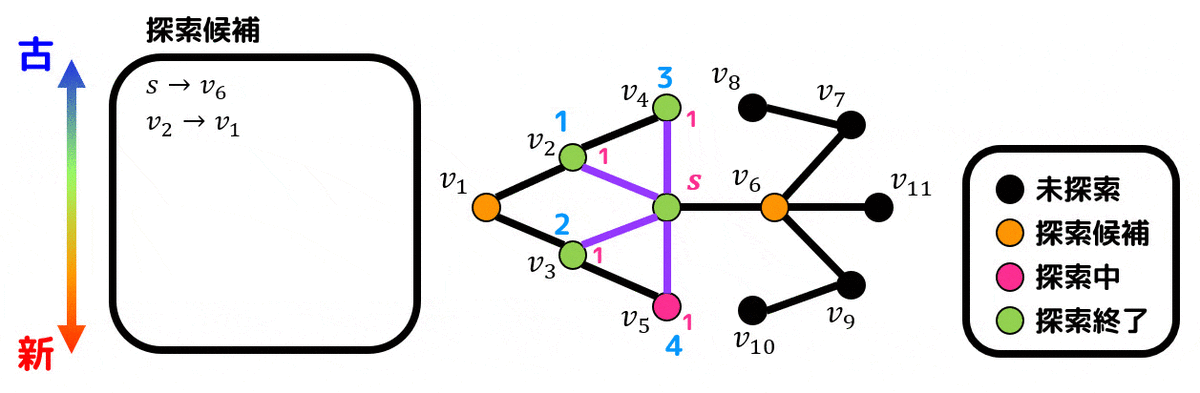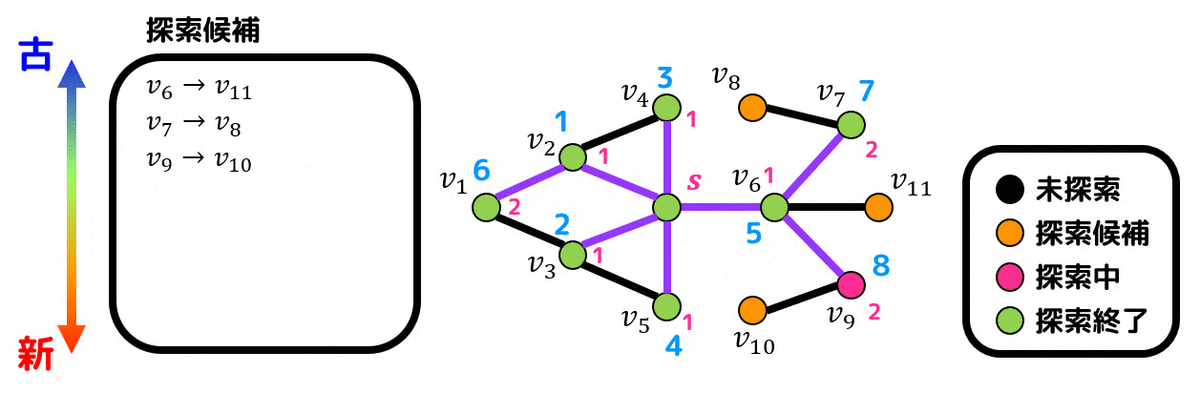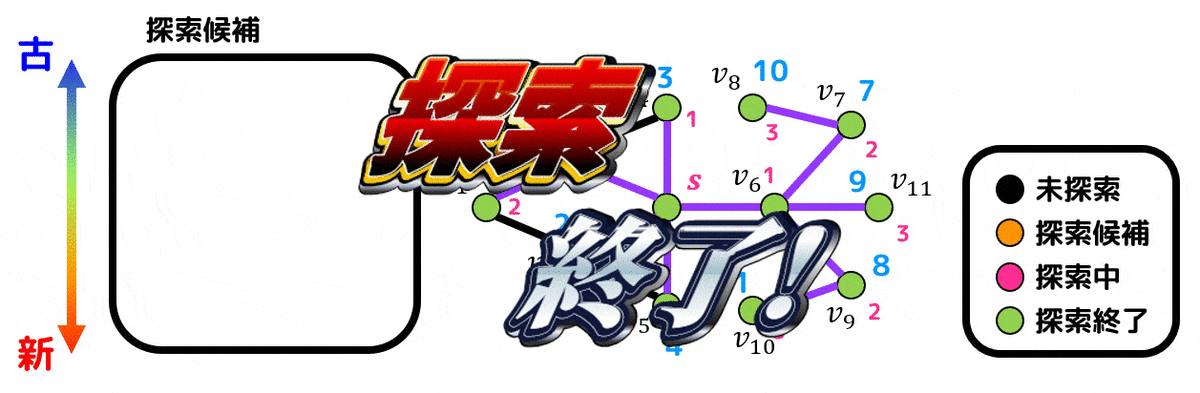
青色の数字は探索順序、赤色の数字はスタート点 \( s \) からの距離、紫色の辺が探索木(BFS木)を表しています。
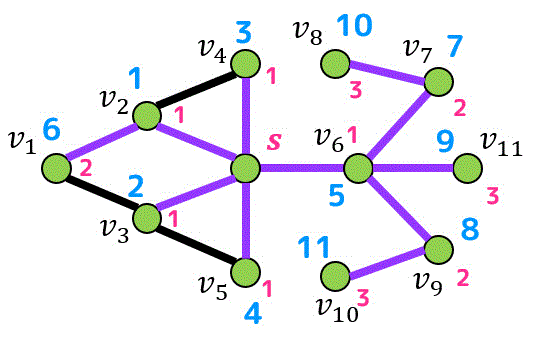
探索の途中過程はこちらのアニメーションをご覧ください。
解答2
青色の数字は探索順序、赤色の数字はスタート点 \( s \) からの距離、紫色の辺が探索木(BFS木)を表しています。
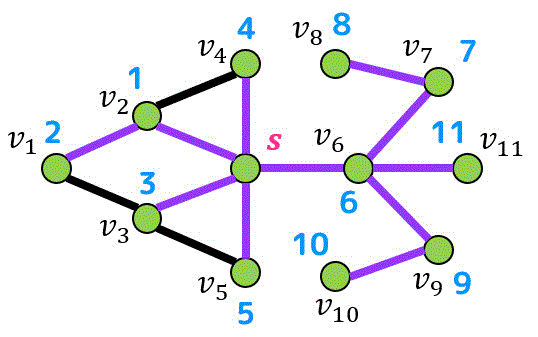
探索の途中過程はこちらのアニメーションをご覧ください。
解答3
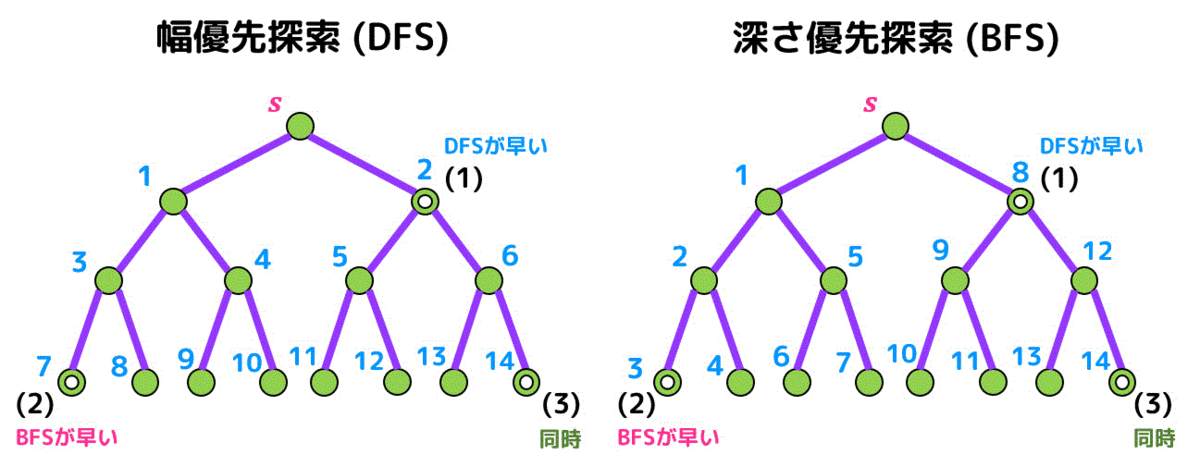
解答:(1) 1 (2) 2 (3) 3
幅優先探索、深さ優先探索の両方のそれぞれの点における探索順位を下に示しています。
幅優先探索・深さ優先探索の探索の動きを同時にアニメーションで表してみました。
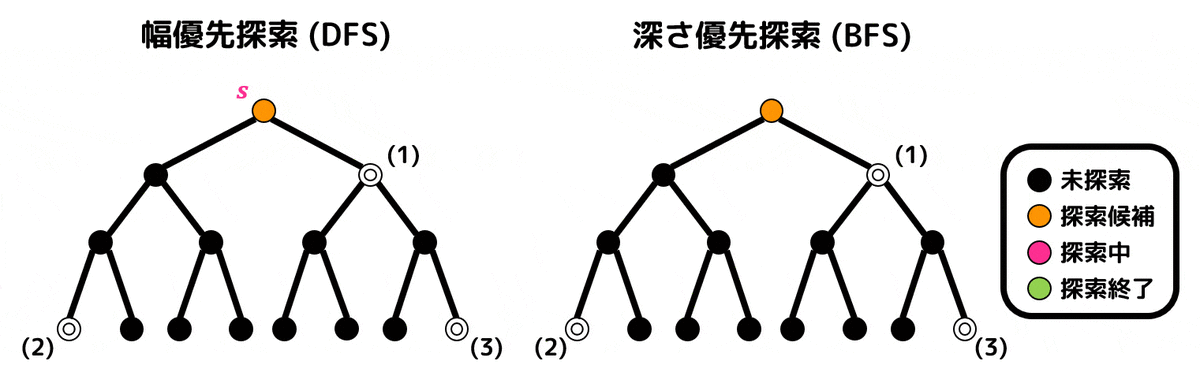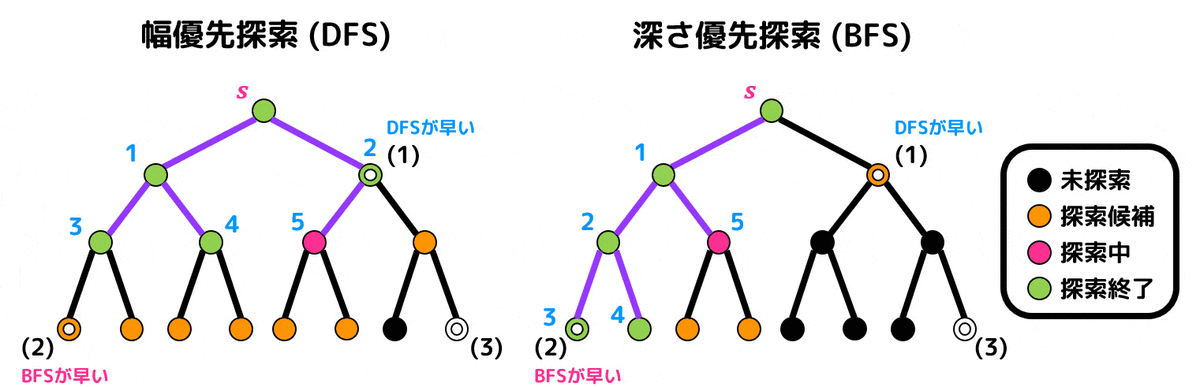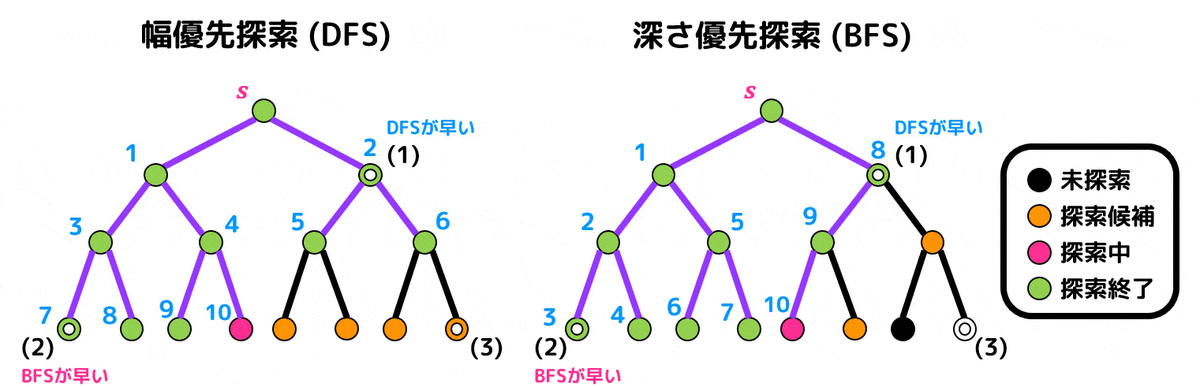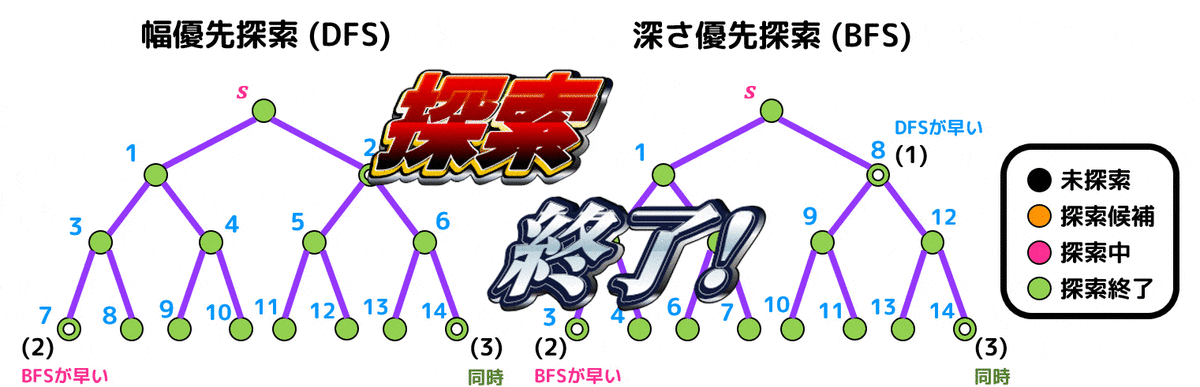
文章で理由を説明すると、下のようになります。
(1)
深さ優先探索はとにかく左の奥から探索するため右側のノードの探索優先順位が低い。一方幅優先探索は始点 \( s \) との距離が短い順に探索するため探索優先順位が高い。よって幅優先探索のほうが先に探索されるので答えは1。
(2)
(1)とは逆で幅優先探索では \( s \) から遠いノードの探索優先順位は低い。一方左側の奥のノードは深さ優先探索の場合の探索優先順位が高いので深さ優先探索のほうが先に探索され、答えは2。
(3)
右側の奥のノードは幅優先探索、深さ優先探索ともに最後に探索するのでタイミングは同時となり、答えは3。
7.さいごに
今回は幅優先探索・深さ優先探索の2つの探索の違いについて説明しました。
深さ優先探索は主に木構造のグラフを探索する際に頻繁に使われるので必ず頭にいれておきましょう。
次回は最小全域木を求める2つのアルゴリズムについて説明したいと思います。
関連広告・スポンサードリンク




![PROGテストについて [就活に活かせ!!]](https://www.momoyama-usagi.com/wp-content/themes/diver/images/noimage.gif)