うさぎでもわかる離散数学（グラフ理論）　第13羽　最小全域木の求め方（クラスカル法・プリム法）

こんにちは、ももやまです。

今回は最小全域木の求め方についてまとめていきたいと思います！

 

 

スポンサードリンク

１．全域木とは

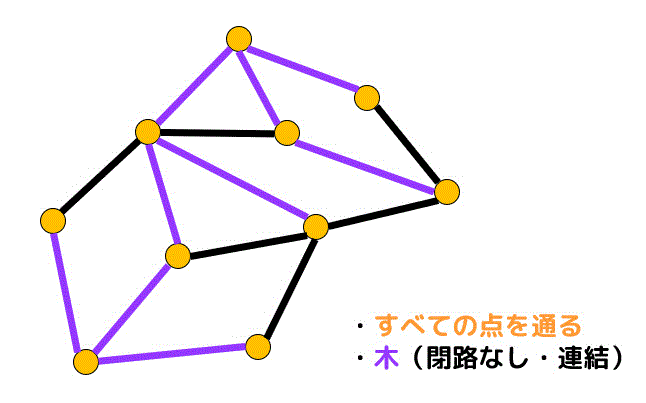
全域木とは、もとのグラフのすべての点を含み、さらに選んだ辺が木となっているようなグラフを表します。

（全域部分グラフが木となっているものを全域木と呼びます）

 

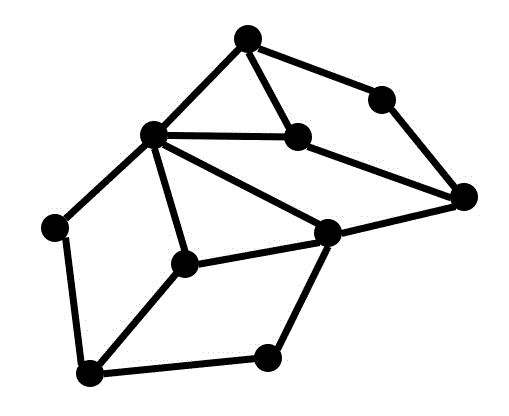
例えば、つぎのグラフの全域木を1つ考えてみましょう。

 

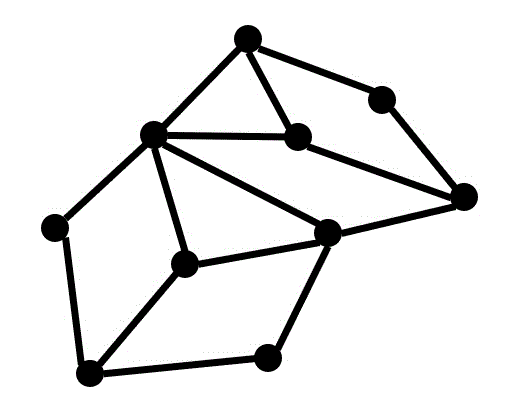
例えば、下の紫で表された辺を選ぶことですべての点を通るような木を作ることができます。

よって、紫色で示された辺は全域木のうちの1つであることがわかります。

 

スポンサードリンク

２．重み付きグラフ

今まで考えてきたグラフに重みという概念を追加したものを重み付きグラフと呼びます。

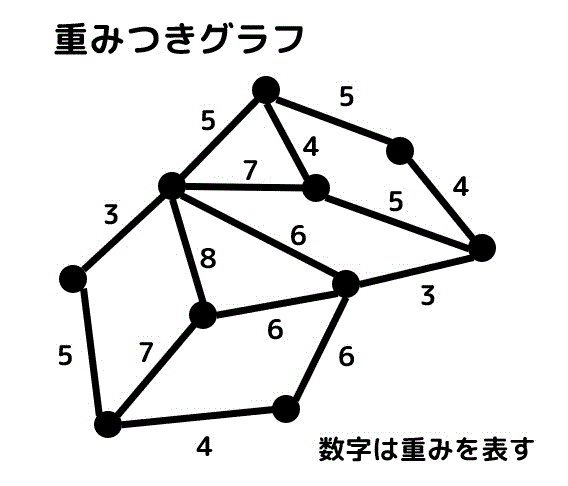
グラフにかかれている数字が重み、コストを表します。重みのことをコストと呼ぶこともあります。

（重みは距離や時間などを表します。）

 

重み付きグラフの場合も普通のグラフと同じく隣接行列やリストを用いてグラフを表現することができます。

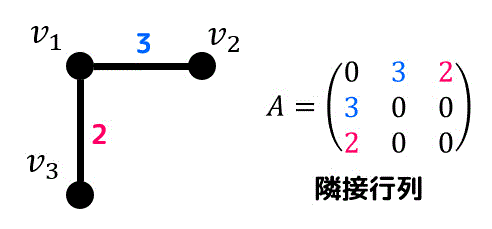
隣接行列の場合は、隣接していない辺は0、0以外の辺は隣接していて数字が重みを表しています。

 

スポンサードリンク

３．最小全域木とは

全域木の中でも、選んだ辺の重みの合計が一番小さい全域木のことを最小全域木と呼びます。

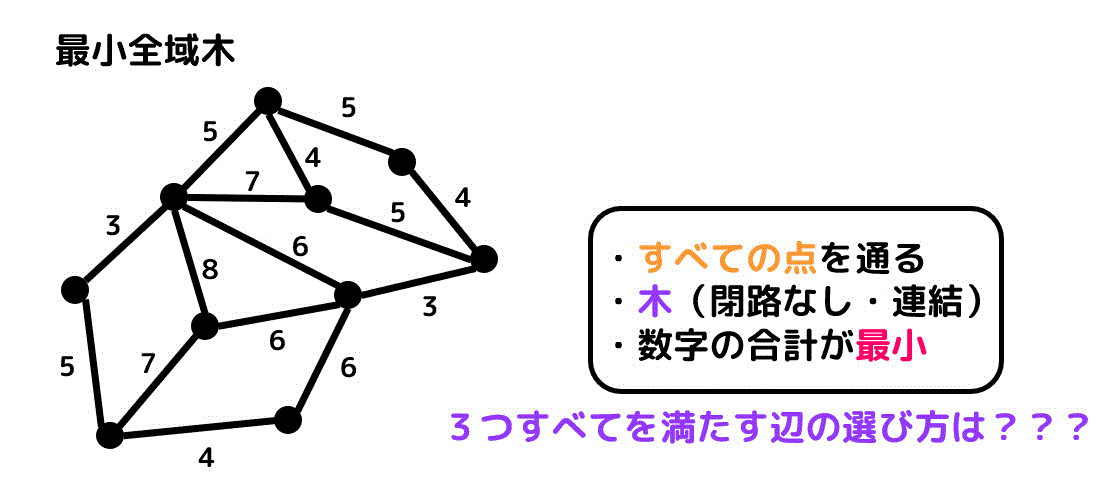
最小全域木を求めるためには、

• すべての点を通る
• 選んだ辺が木であること（閉路がなく、連結であること）
• 選んだ辺の重み（コスト）の合計が最小であること

の3つの条件を満たしている必要があります。

 

今回は最小全域木を求める方法として2つの方法（クラスカル法・プリム法）を紹介していきたいと思います。

 

４．クラスカル法

まずはクラスカル法について説明したいと思います。

クラスカル法の大まかな方針は閉路ができないように重みが小さい順番から辺を選び、追加していくです。

 

重みが小さい順に見る際に重みが同じ辺が複数ある場合はどの辺からチェックしてもOKです！（例えば重みが3,3,4,5,6だった場合、重みが3の辺の中から1つ好きな方をチェックしてもOK）

 

 

では、こちらのグラフを例にクラスカル法で最小全域木を求めていきましょう。

 

上のグラフの中で一番重みの小さい辺は3ですね。

なので、重み3の辺から好きな1辺を選びます。選んだ辺は赤色で示していきたいと思います。
（今回はより左側にある辺を優先的に選んでいきたいと思います。）

 

 

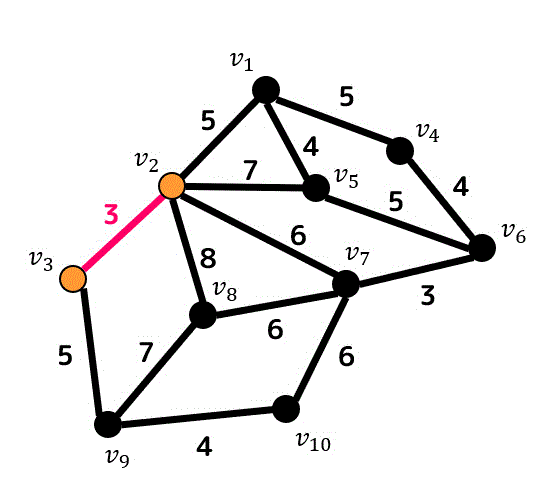
残りの重み3の辺も追加していきましょう。

 

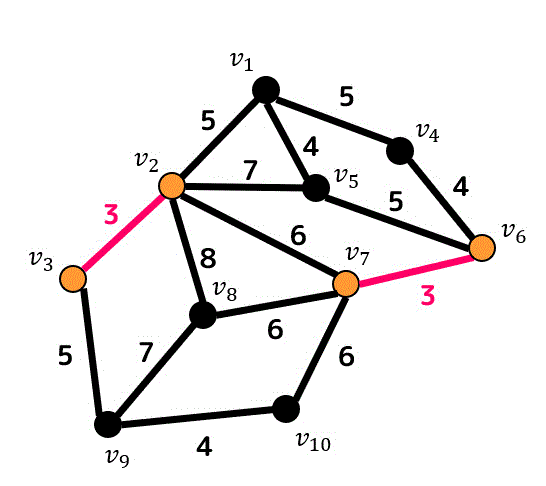
重み3の辺をすべて追加しましたね。

なので次に重みが小さい「重み4」の辺を追加していきます。

 

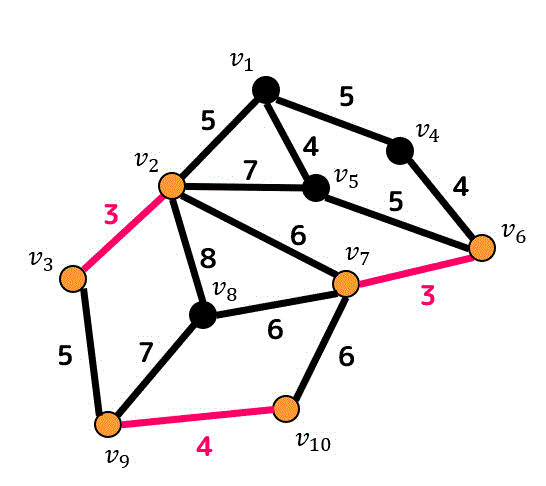
あと2つあるのでこちらも追加していきたいと思います。

 

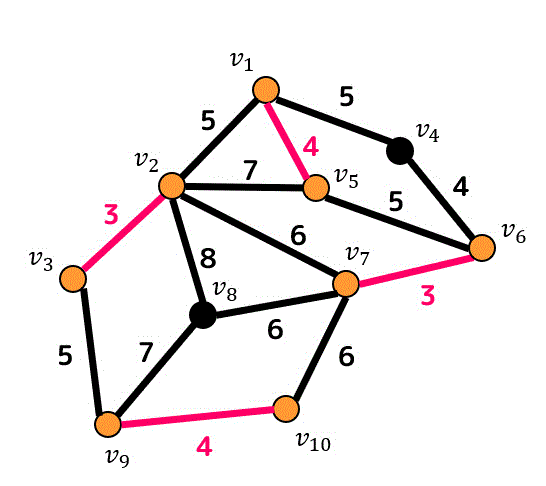
重み4の辺はあと1つですね。

 

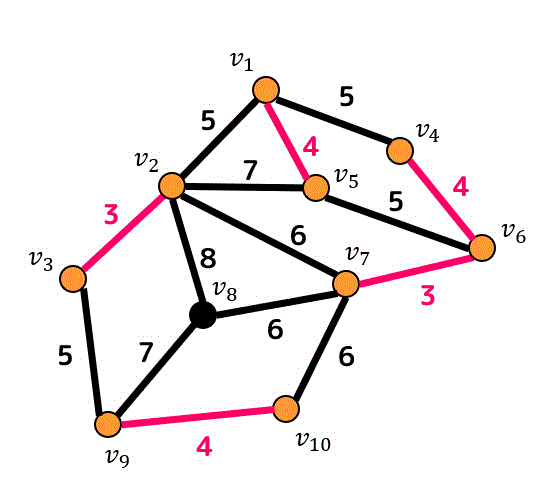
これで重み4の辺が追加し終わりました。つぎは重み5の辺です。

重み5の辺は4つあるのでどんどん追加しましょう。

 

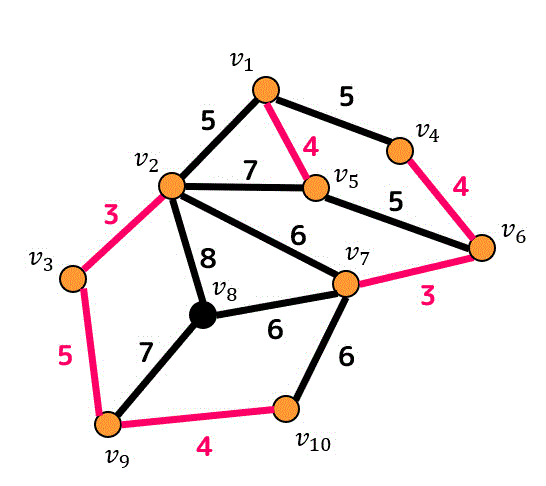
あと3つ。

ここで \( v_2 \) と \( v_5 \) をつなぐと閉路になってしまうので \( v_2 \) と \( v_5 \) をつなぐ辺は追加候補から外れますね*1。

候補から外れた辺は灰色で示しておきます。

 

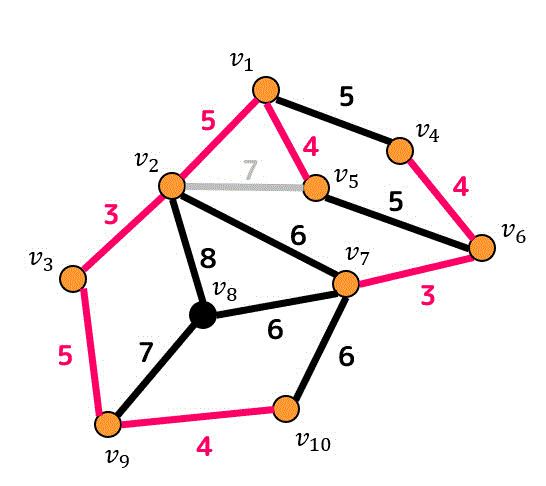
次に重み5の辺を追加すると「追加すると閉路となってしまうような辺」がたくさん出てきます。残り1つの重み5の辺も追加候補から外れてしまいましたね。

 

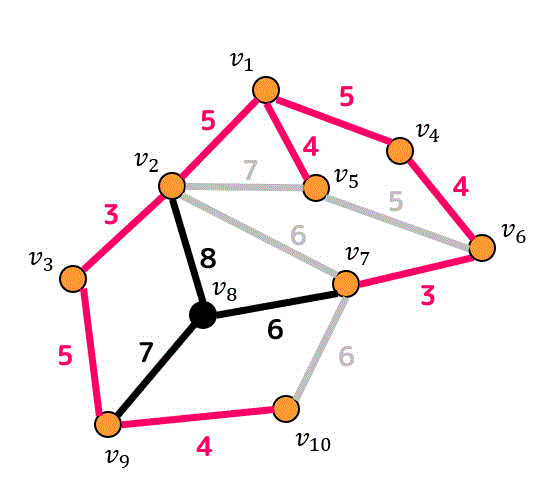
残された追加候補の辺は重みが6, 7, 8のうちのどれかですね。なので重み6の辺を追加します。

すると、どの辺をつないでも閉路となってしまうため、追加候補の辺がなくなります。

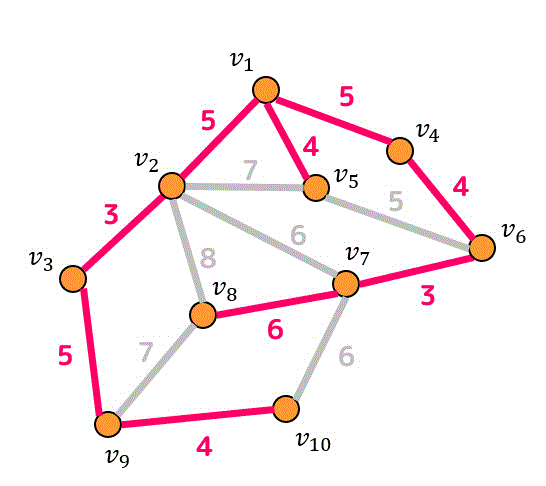
よって最小全域木は上の赤色で示された辺となります。

点の数が10個に対して、辺の数が9個なのでグラフが木になっていることがわかりますね！（求めたあとは必ず（辺の数）が（点の数 - 1）になっていることを必ず確かめましょう。）

 

また最小全域木の重みの合計は39となり、39が重みの最小であることがわかります。

 

ちなみに最小全域木の重みの最小は必ず1通りに決まりますが、辺の選び方は1つとは限りません。

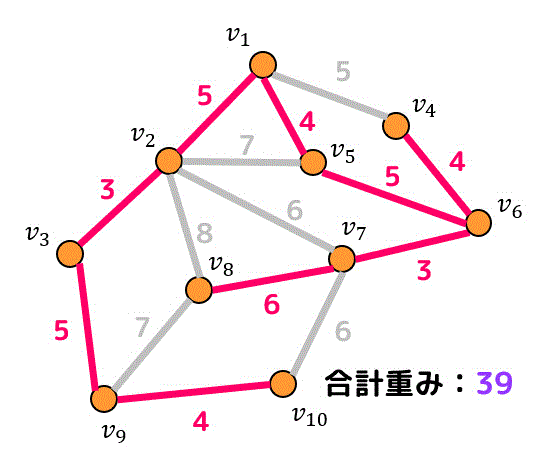
今回の例でいくと、下のようなグラフも最小全域木となります。（重みは同じく39）

 

 

５．プリム法

もう1つの方法はプリム法と呼ばれます。

クラスカル法に比べて少しだけ複雑です。

 

 では、先程と同じグラフを例にプリム法で最小全域木を求めていきましょう。

「頂点の数は10個なので9つの辺を追加する！」と最初から頭にいれておけばミスが減るのでぜひ試していきましょう。

 

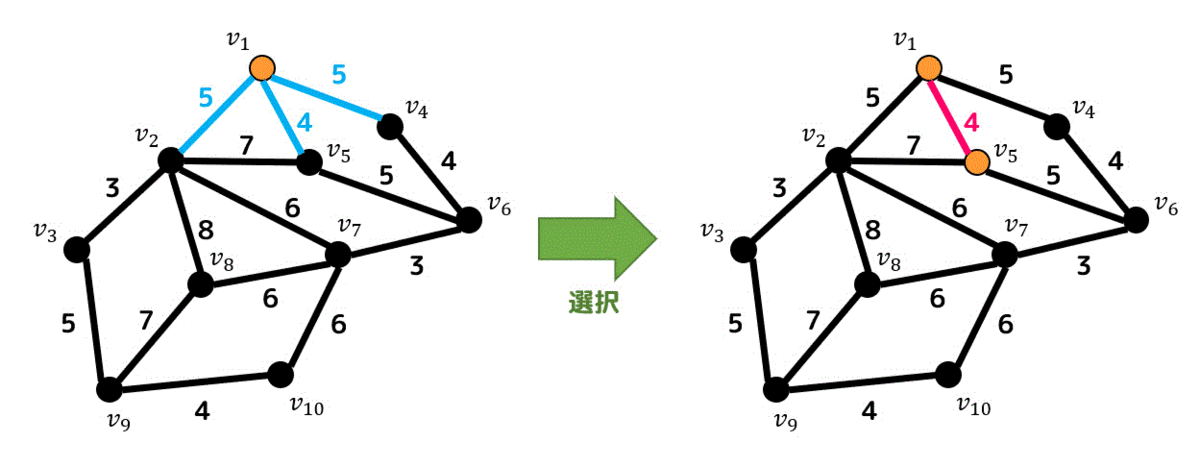
スタート点は \( v_1 \) としましょう。

なので \( v_1 \) からたどれる辺の中（水色で示しています）で一番重みが小さい辺を選びます。

1つだけ重み4の辺があるので重み4の辺を追加します。

 

追加した辺（赤色で示しています）からたどれる点は \( v_1 \), \( v_5 \) の2つですね。

なので \( v_1 \) と \( v_5 \) からたどれる辺が追加候補辺となります。

 

追加候補辺の中で一番重みが小さい5の辺が3つあるので、好きなものを1つ追加しましょう。今回は一番左側にある \( v_1 \), \( v_2 \) をつなぐ辺を追加します。

 

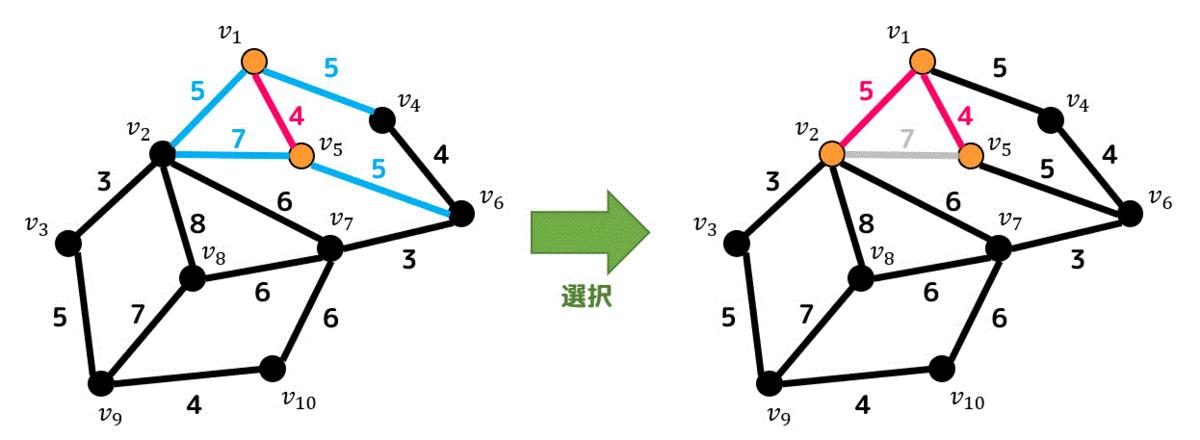
すると \( v_2 \), \( v_5 \) をつなぐと閉路となるので \( v_2 \), \( v_5 \) をつなぐ辺は追加候補辺から消えます。

 

追加した辺からたどれる点は \( v_1 \), \( v_2 \), \( v_5 \) の3つですね。

追加候補辺は \( v_1 \), \( v_2 \), \( v_5 \) からたどれるような辺となりますね。

 

追加候補辺の中から重みが一番小さいものに重み3の辺がありますね。なので重み3の辺を追加します。

 

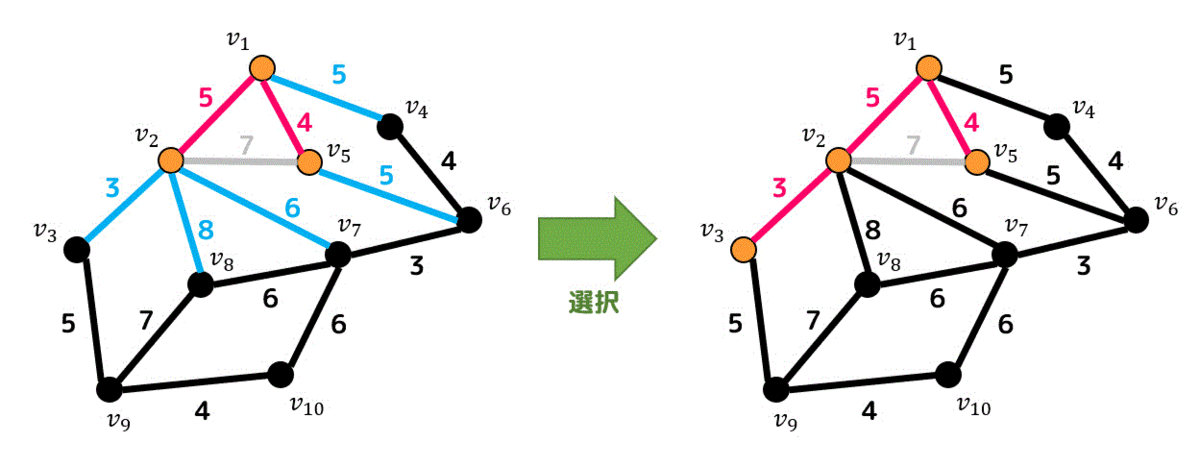
追加した辺からたどれる点が \( v_1 \), \( v_2 \), \( v_3 \), \( v_5 \) の4つになったので候補辺も4つの点からたどれるような辺となります。

候補辺の中で重みが一番小さいのは5の辺なので、3つの中から好きな辺を1つ選び、追加しましょう。

 

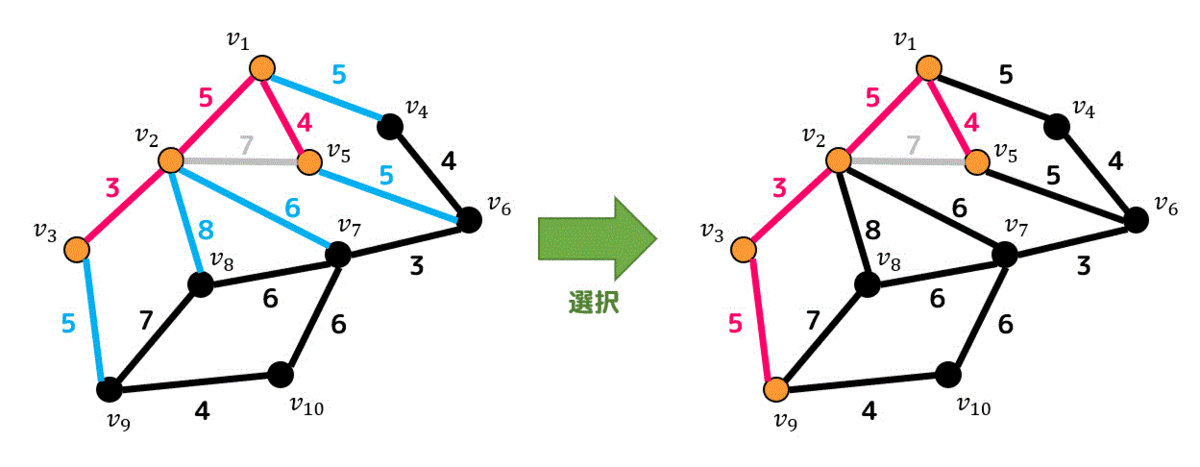
追加した辺からたどれる点は \( v_1 \), \( v_2 \), \( v_3 \), \( v_5 \), \( v_9 \) の5つなので5つの点からたどれるような辺が候補辺となります。

候補辺の中で一番小さい重みは4なので重み4の辺を1つ追加します。

 

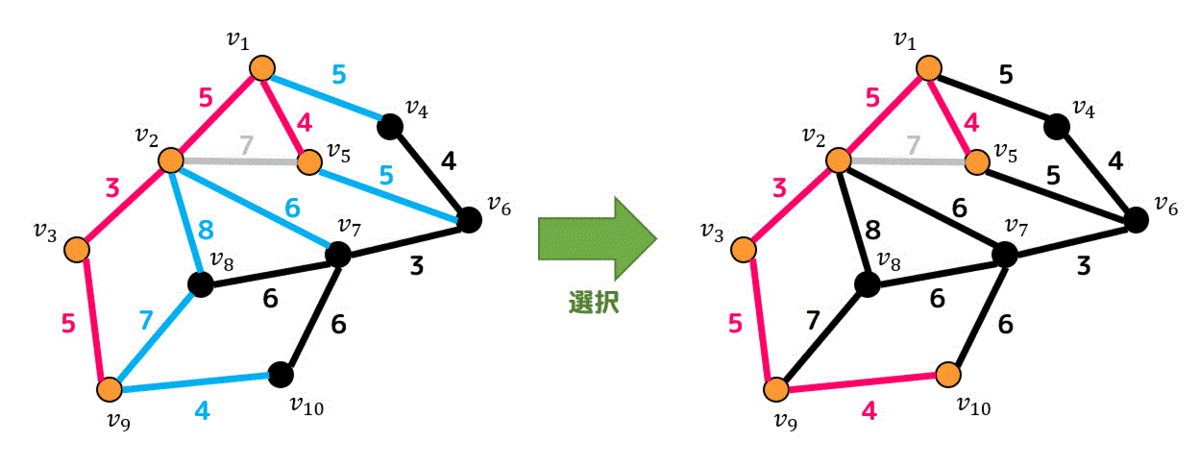
たどれる点が6つになりました。

6つの点からたどれる辺の中で重みが一番小さいのは5なので、重み5の辺の中から好きなの辺を追加します。

 

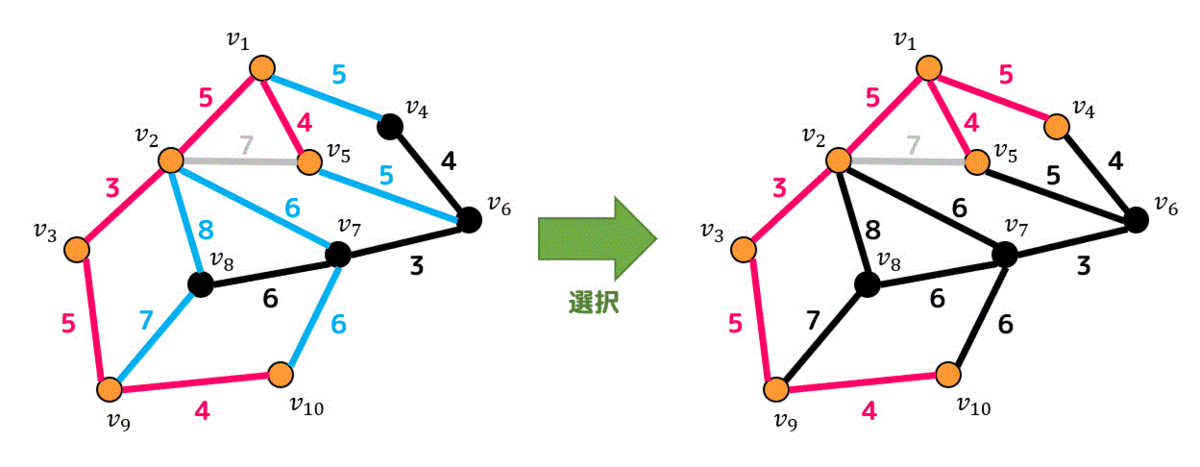
たどれる7つの点から重みが一番小さい辺をさがしましょう。

すると一番小さい重み4の辺があるので重み4の辺を追加しましょう。

 

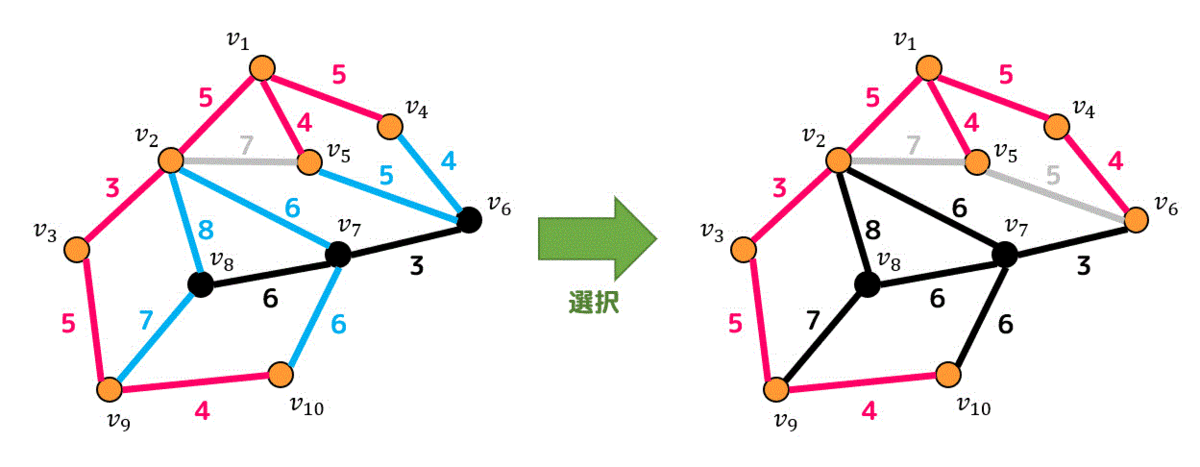
すると \( v_5 \) と \( v_6 \) を結ぶ辺は追加すると閉路となってしまうため、候補から外れます*2。

 

たどれる点は7点ですね。

7点の中からたどれる辺の中に重み3（一番小さい）の辺があるので追加しましょう。

 

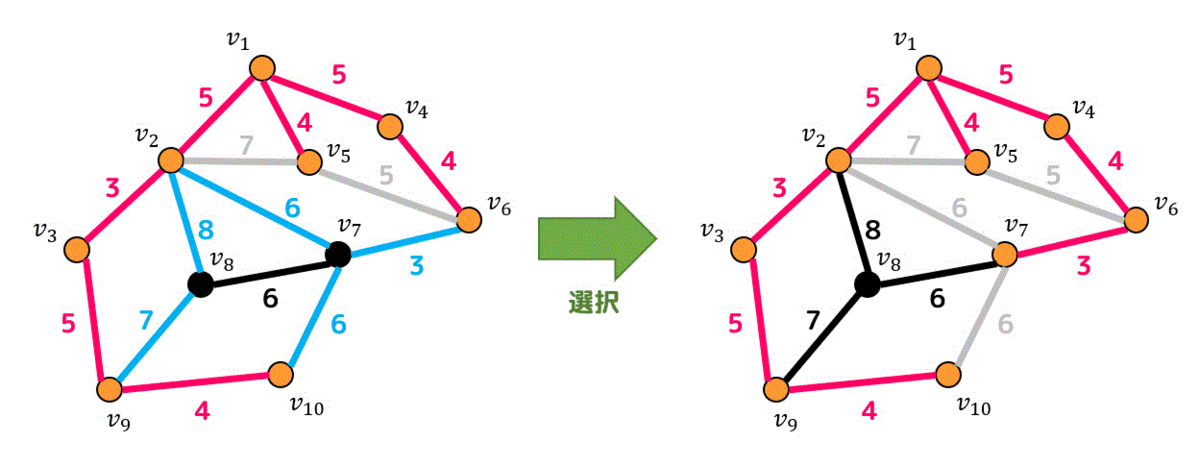
さらに2つの辺（\( v_2 \) と \( v_7 \) をつなぐ辺と \( v_7 \) と \( v_{10} \) をつなぐ辺）が追加すると閉路となってしまうため、追加候補辺から外れます。

 

再びたどれる辺の中から一番重みが小さい辺を1つ選び、追加します。今まで追加した辺の数が8なので、つぎに追加する辺が最後の辺です。

今回は3つの候補辺の中から一番重みが小さい6の辺を追加します。

 

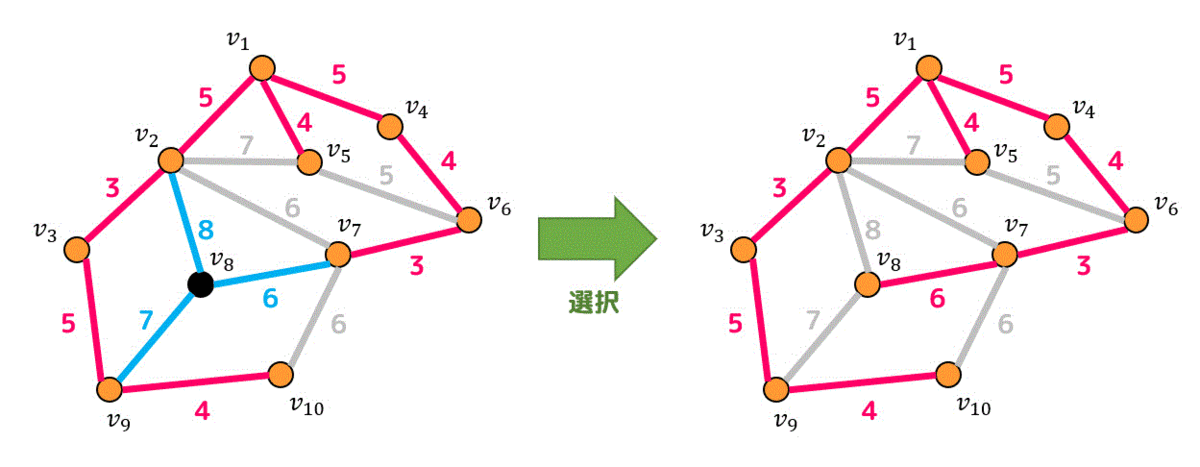
すると辺の数が9本となり、どの辺を追加しても閉路ができてしまいます。

なのでこれで追加は終了です。クラスカル法と同じ最小全域木が求まりましたね！　重みも39なので間違いありません！

 

６．練習問題

では1問だけですが実際に最小全域木を使った練習問題を解いてみましょう。

 

問題

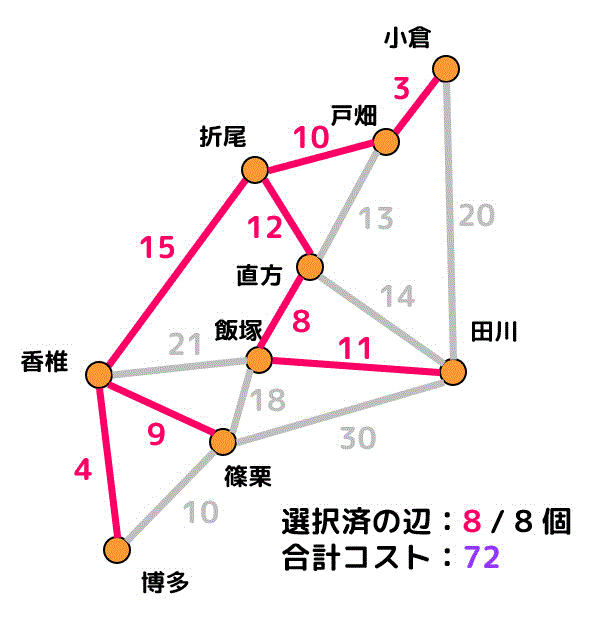
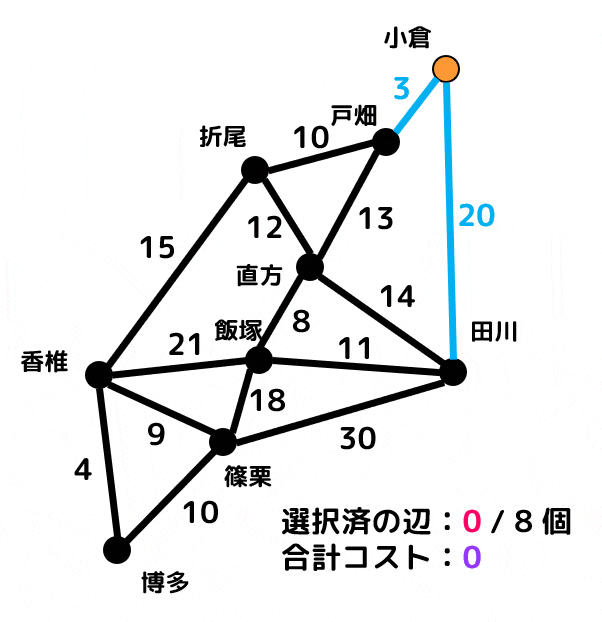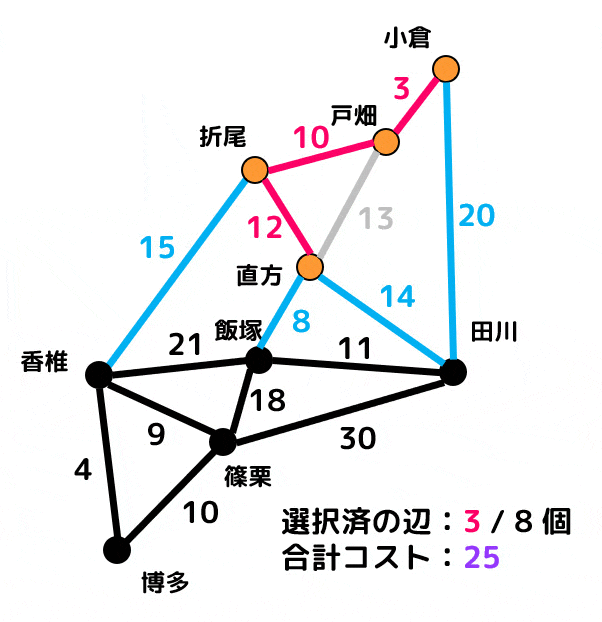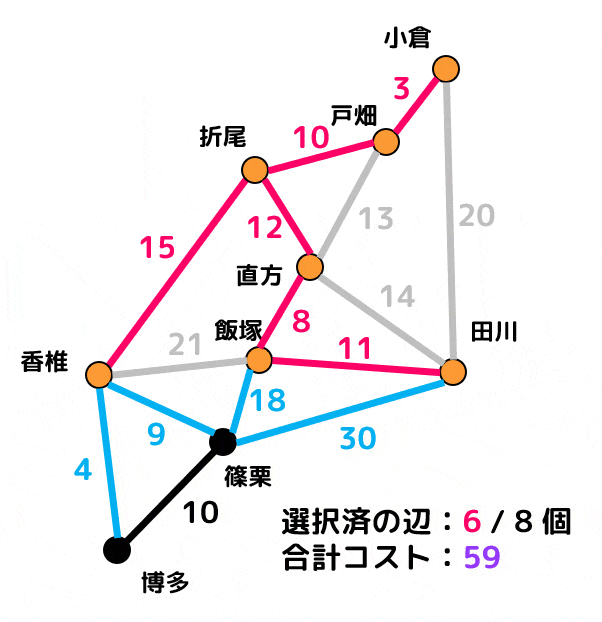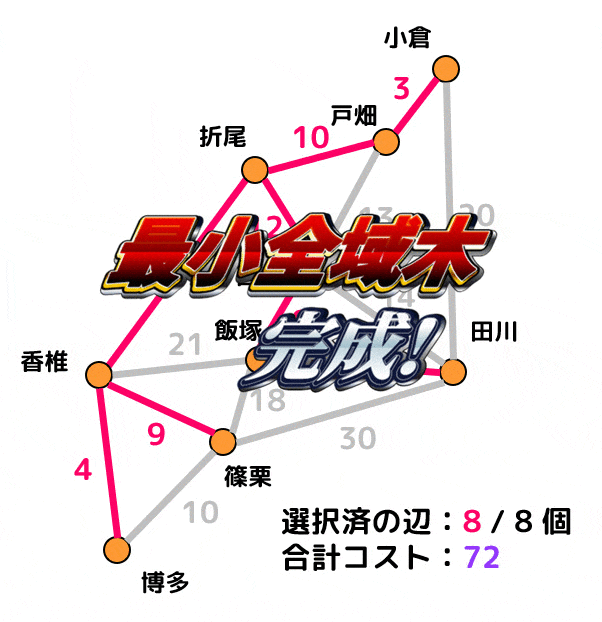
ある福岡の都市9個を結ぶような鉄道路線を作りたい。下のグラフに示されている数値は2つの都市間を結ぶ鉄道を建設するために必要なコストを示している。

例えば、小倉から戸畑までの鉄道路線を建設するためにはコスト3を支払う必要がある。

 

このとき、全駅間を行き来でき、かつコストが最小となる場合のコスト（建設費）と建設区間を最小全域木を求めることによって求めなさい。

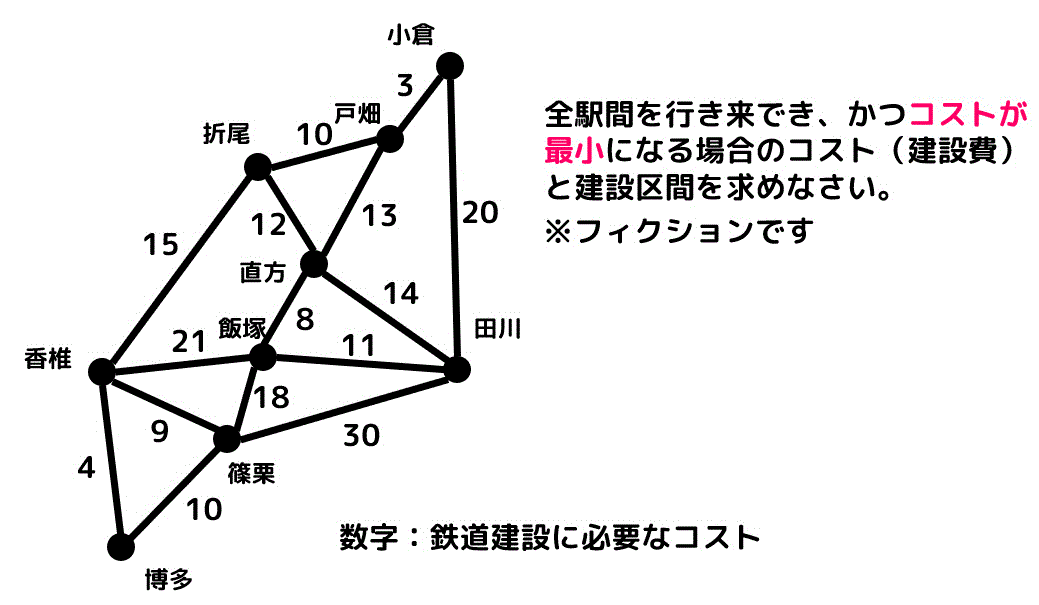
（クラスカル法・プリム法のどちらを使っても構いませんが、余裕があれば両方で求めてみましょう！）

 

７．練習問題の答え

解答

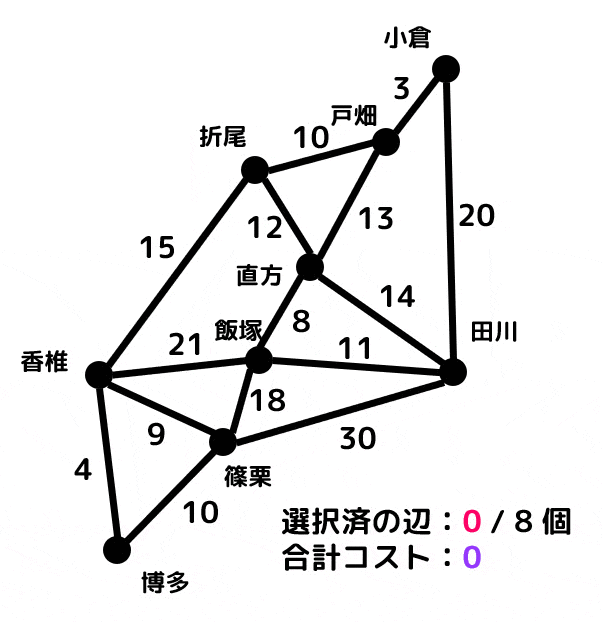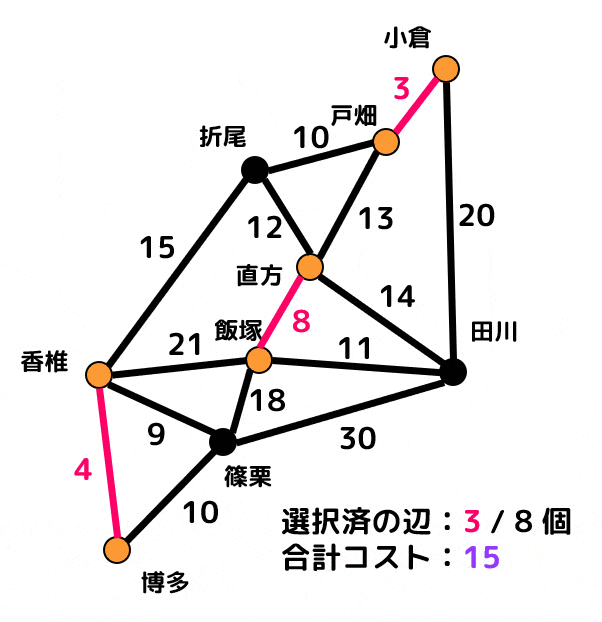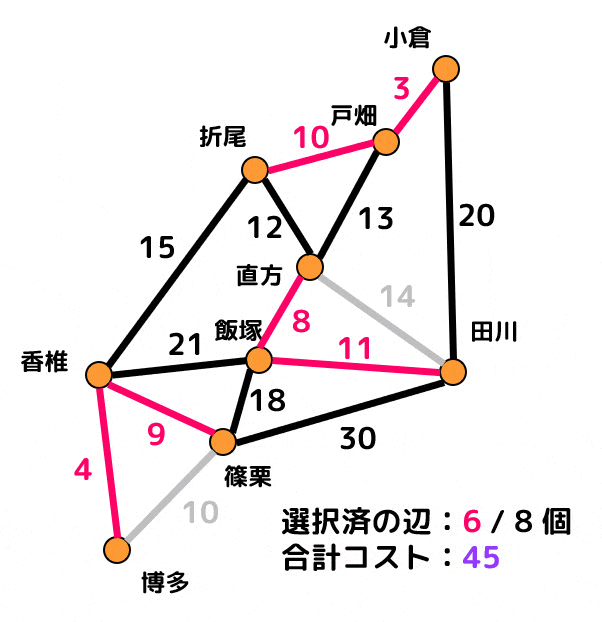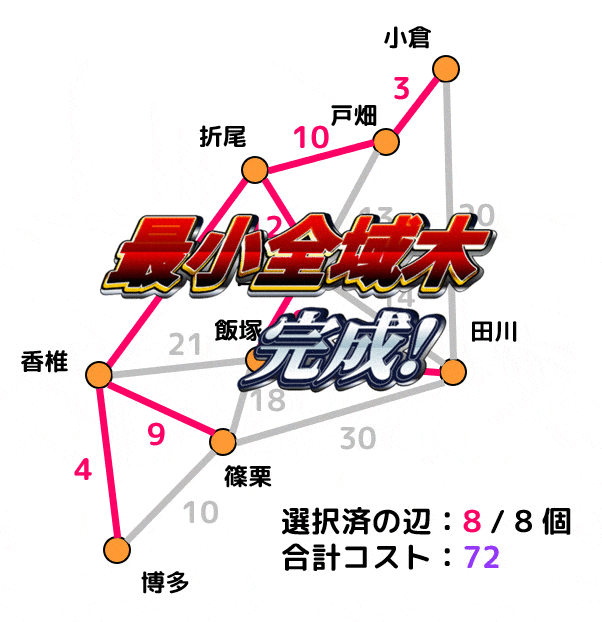
赤色で示された辺の部分の鉄道を建設することで、コスト72ですべての区間を行き来できるようになる。

 

2つの方法の辺の追加過程をアニメーションにしているので参考にしてください。

クラスカル法で解いた場合

ピンク色の辺が追加済の辺、灰色の辺は閉路ができるために追加できない辺を表します。

プリム法で解いた場合

赤色の辺が追加済の辺、青色の辺は追加候補辺（追加済の辺と隣り合っていてかつ閉路ができなければ追加候補）、灰色の辺は閉路ができるために追加できない辺を表します。

 

８．さいごに

今回は最小全域木を求める2つの方法としてクラスカル法、プリム法の説明をしました。

最小全域木はコストが最小となる問題を求めるときに頻繁に使うのでぜひ2つの方法ともマスターしましょう！

 

次回はある地点からある地点までの距離を求めるダイクストラ法について説明したいと思います。