スポンサードリンク
こんにちは、ももやまです。
線形代数を勉強していると、「また掃き出し法かぁ、行(列)基本変形かぁ」とうんざりするころではないでしょうか。
そこで、今回は掃き出し法や行(列)基本変形を一切使わずに、行列式(サラスの公式)だけで連立方程式を解く方法であるクラメルの公式を紹介します!
行列式をまだ勉強していない人・サラスの公式ってなんだっけという人は、ここから復習してください!! ↓↓
目次
スポンサードリンク
1. クラメルの公式の使い方
冒頭でも述べた通り、クラメルの公式は簡単に言うと、行列式だけで(掃き出し法や逆行列の算出などを全く行わずに)連立方程式の解を求めるテクニックです。
ただし、係数行列が正方行列となり、なおかつ解が1つに定まる連立方程式でのみ、クラメルの公式は適用できます。それ以外の連立方程式[1]\[\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) + \left( \begin{array}{ccc} -1 \\ 0 \end{array} … Continue readingでは使えません。
(言い換えると、逆行列を用いて連立方程式の解が出せるような連立方程式[2]つまり、係数行列が正則となる連立方程式でのみ使える。でしか使えません。)
まずは、クラメルの公式の使い方を見てみましょう。
(なぜこの方法で計算ができるか気になる人は、この記事の2章をご覧ください)
(1) 2元連立方程式(係数行列が2×2)の場合
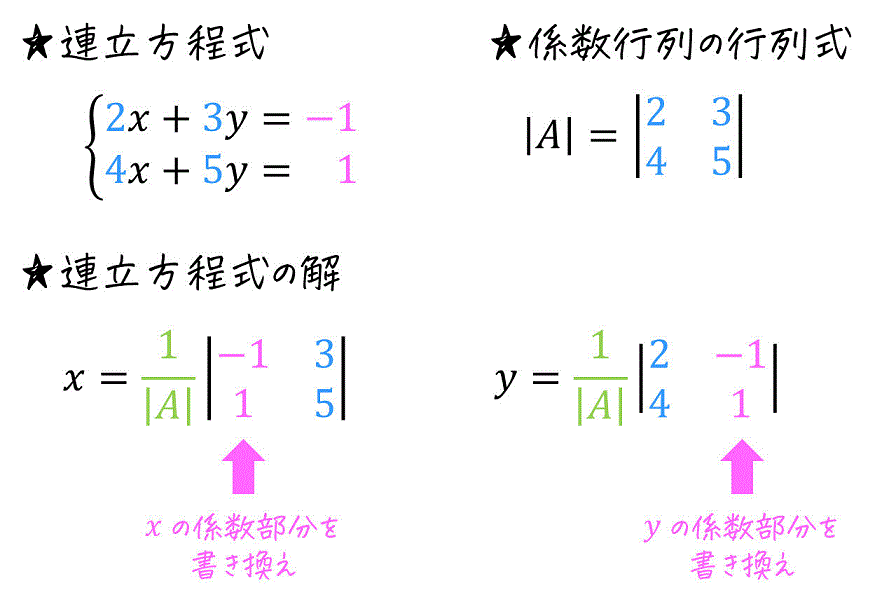
まずは、下のように2元連立方程式2次の係数行列で表せるような連立方程式をクラメルの公式で解いてみましょう。\[
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{2} x + \textcolor{deepskyblue}{3} y = \textcolor{magenta}{ -1 } \\ \textcolor{deepskyblue}{4} x + \textcolor{deepskyblue}{5} y = \ \ \ \textcolor{magenta}{1} \end{array} \right.
\]
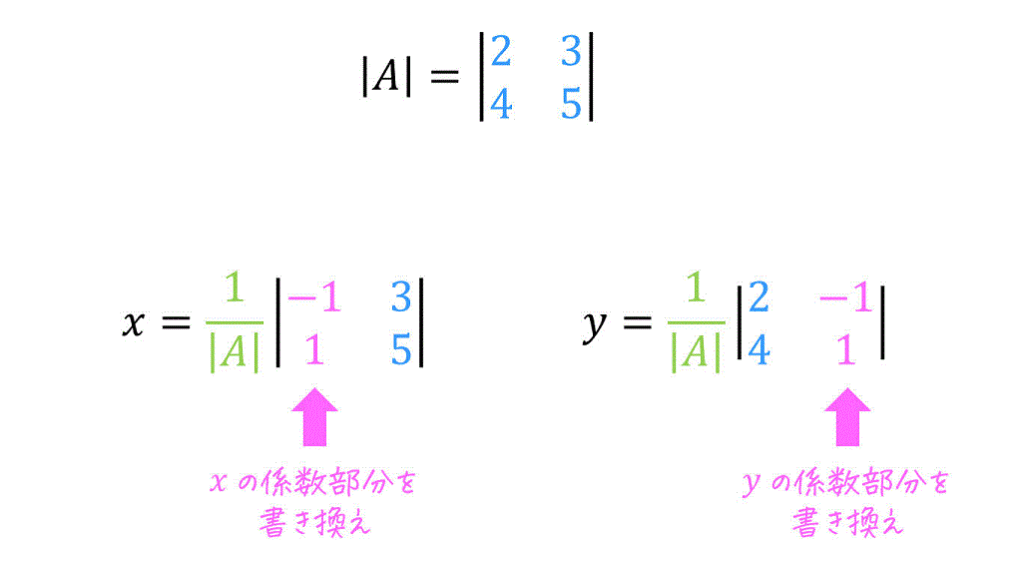
Step1. 係数行列の行列式を求める
まずは、係数行列の行列式を求めます。\[\begin{align*}
|A| & = \left| \begin{array}{ccc} \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{3} \\ \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{5} \end{array} \right|
\\ & = 10 - 12
\\ & = -2
\end{align*}\]
※1 万が一、係数行列の行列式 \( |A| \) が0になった場合は、クラメルの公式で解くことができない連立方程式[3]解を無数に持つ連立方程式、もしくは解を持たない連立方程式のこと。であることがわかります。
※2 係数行列の行列式 \( |A| \) を求めるので、 \( A \) が正方行列ではない場合にも、クラメルの公式が使えないことがわかります。
Step2. 解を求めていく
あとは、それぞれの解ごとに「解に対応する係数がある列の値を右辺の値に書き換えた係数行列の行列式」を求め、求まった行列式を \( |A| \) で割ることで解を求めることができます。
例えば、\( x \) の解は、係数行列の \( x \) の係数に対応する1列目を、右辺の値に書き換えた後に \( |A| \) で割ることで求められます。\[\begin{align*}
x & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{magenta}{-1} & \textcolor{deepskyblue}{3} \\ \textcolor{magenta}{1} & \textcolor{deepskyblue}{5} \end{array} \right|
\\ & = \frac{1}{-2} \left( -1 \cdot 5 - 3 \cdot 1 \right)
\\ & = - \frac{1}{2} \cdot (-8)
\\ & = 4
\end{align*}\]
同じように \( y \) の解は、係数行列の \( y \) の係数に対応する2列目を、右辺の値に書き換えた後に \( |A| \) で割ることで求められます。\[\begin{align*}
y & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{2} & \textcolor{magenta}{-1} \\ \textcolor{deepskyblue}{4} & \textcolor{magenta}{1} \end{array} \right|
\\ & = \frac{1}{-2} \left\{ 2 \cdot 1 - (-1) \cdot 4 \right\}
\\ & = - \frac{1}{2} \cdot 6
\\ & = -3
\end{align*}\]
よって、連立方程式の解を \( x = 4 \), \( y = -3 \) と求めることができましたね。
本当に求めた解が合っているかを確かめるために、与えられた連立方程式に入れてみましょう。\[
\left\{ \begin{array}{cc} 2 x + 3 y = 2 \cdot 4 + 3 \cdot (-3) = \textcolor{magenta}{ -1 } \\ 4x + 5y = 4 \cdot 4 + 5 \cdot (-3) = \ \ \ \textcolor{magenta}{1} \end{array} \right.
\]確かに求めた解が合っていることが確認できますね。
(2) 3元連立方程式(係数行列が3×3)の場合
1つ変数が増えて3元連立方程式になった場合でも、3次の係数行列が正則(逆行列を持つ)であれば、「(1) 2元連立方程式」のときと同じようにクラメルの公式から連立方程式の解を求めることができます。
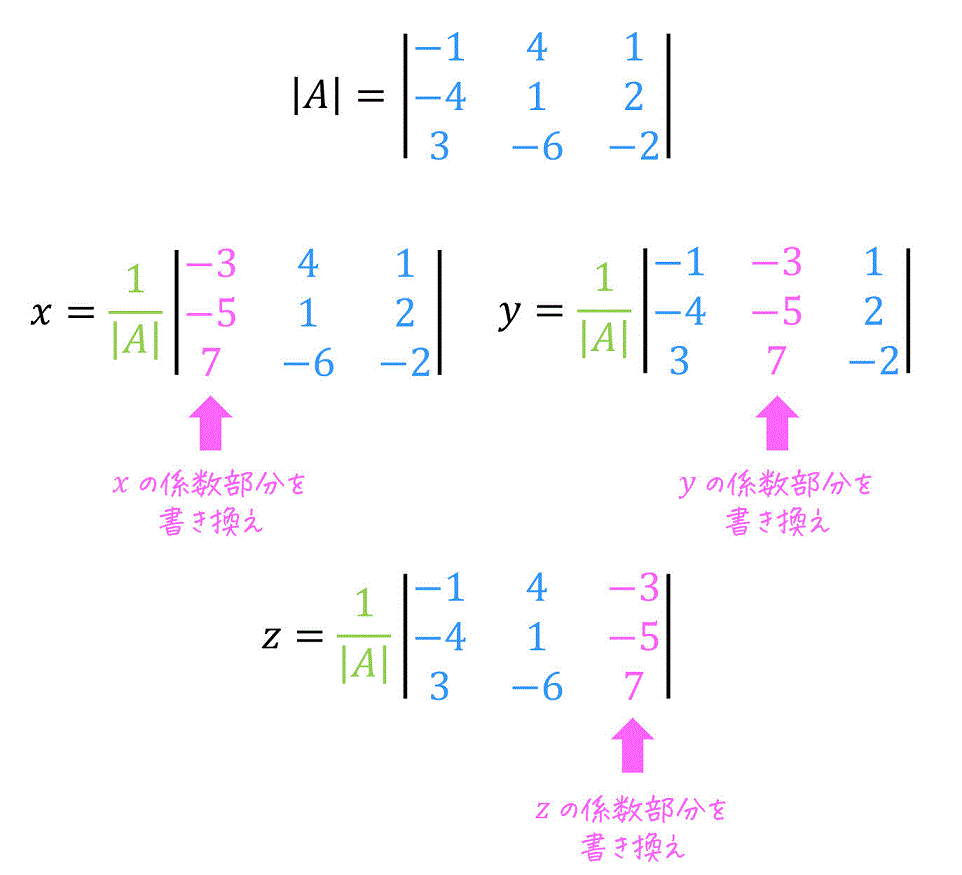
実際に、下の3元連立方程式の解をクラメルの公式で求めてみましょう。\[
\left\{ \begin{array}{cc} - \ \ x + 4y + \ \ z = -3 \\ -4x + \ \ y + 2z = -5 \\ \ \ \ 3x - 6y -2z = \ \ \ 7 \end{array} \right.
\]
ここで、少しわかりやすくするために、\( x \) や \( -x \) など、係数が1や-1のものを \( 1x \) や \( -1x \) と表したり、色を付けたりしましょう。すると、\[
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{- 1} x + \textcolor{deepskyblue}{4} y + \textcolor{deepskyblue}{1} z = \textcolor{magenta}{-3} \\ \textcolor{deepskyblue}{- 4} x + \textcolor{deepskyblue}{1} y + \textcolor{deepskyblue}{2} z = \textcolor{magenta}{- 5} \\ \ \ \ \textcolor{deepskyblue}{3} x \textcolor{deepskyblue}{- 6}y \textcolor{deepskyblue}{- 2} z = \ \ \ \textcolor{magenta}{7} \end{array} \right.
\]となります。
Step1. 係数行列の行列式を求める
下準備が終わったので、まずは連立方程式の係数行列の行列式を求めましょう。
\[\begin{align*}
|A| & = \left| \begin{array}{ccc} \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{1} \\ \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{1} & \textcolor{deepskyblue}{2} \\ \textcolor{deepskyblue}{3} & \textcolor{deepskyblue}{-6} & \textcolor{deepskyblue}{-2} \end{array} \right|
\\ & = 2 + 24 + 24 - (3 + 32+12)
\\ & = 50 - 47
\\ & = 3
\end{align*}\]
Step2. 解を求めていく
あとは2元連立方程式のときと同じく、「解に対応する係数がある列の値を右辺の値に書き換えた係数行列の行列式」を求め、求まった行列式を \( |A| \) で割ることで解を求めることができます。
ただし計算する行列式の数が1個増える点に注意です。
\[\begin{align*}
x & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{magenta}{-3} & \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{1} \\ \textcolor{magenta}{-5} & \textcolor{deepskyblue}{1} & \textcolor{deepskyblue}{2} \\ \textcolor{magenta}{7} & \textcolor{deepskyblue}{-6} & \textcolor{deepskyblue}{-2} \end{array} \right|
\\ & = \frac{1}{3} \left\{ 6 + 56 + 30 - (7 + 40 + 36) \right\}
\\ & = \frac{1}{3} (92 - 83)
\\ & = 3
\end{align*}\]
\[\begin{align*}
y & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{-1} & \textcolor{magenta}{-3} & \textcolor{deepskyblue}{1} \\ \textcolor{deepskyblue}{-4} & \textcolor{magenta}{-5} & \textcolor{deepskyblue}{2} \\ \textcolor{deepskyblue}{3} & \textcolor{magenta}{7} & \textcolor{deepskyblue}{-2} \end{array} \right|
\\ & = \frac{1}{3} \left\{ -10 - 18 - 28 - (-15 - 24 - 14) \right\}
\\ & = \frac{1}{3} (-56 + 53)
\\ & = -1
\end{align*}\]
\[\begin{align*}
z & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{4} & \textcolor{magenta}{-3} \\ \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{1} & \textcolor{magenta}{-5} \\ \textcolor{deepskyblue}{3} & \textcolor{deepskyblue}{-6} & \textcolor{magenta}{7}\end{array} \right|
\\ & = \frac{1}{3} \left\{ -7 - 60 - 72 - (-9 - 112 - 30) \right\}
\\ & = \frac{1}{3} (-139 + 151)
\\ & = 4
\end{align*}\]
よって、連立方程式の解を \( x = 3 \), \( y = -1 \), \( z = 4 \) と求めることができましたね。
本当に求めた解が合っているかを確かめるために、与えられた連立方程式に入れてみましょう。\[
\left\{ \begin{array}{ll} - x + 4y + z = -3 - 4 + 4 = -3 \\ -4x + y + 2z = -12 - 1 + 8 = -5 \\ \ \ \ 3x - 6y -2z = 9 + 6 - 8 = 7 \end{array} \right.
\]確かに求めた解が合っていることが確認できますね。
(3) 4元以上の連立方程式(係数行列が4×4以上の正方行列)の場合
連立方程式の変数の数がどれだけ増えたとしても、係数行列が正方行列で、なおかつ逆行列を持てば(正則であれば)クラメルの公式が適用できます。
例えば、\[
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{- 4} x \textcolor{deepskyblue}{-4} y \textcolor{deepskyblue}{-1} z + \textcolor{deepskyblue}{5} w = \textcolor{magenta}{-6} \\ \textcolor{deepskyblue}{- 3} x \textcolor{deepskyblue}{-6} y + \textcolor{deepskyblue}{4} z + \textcolor{deepskyblue}{2} w = \ \ \ \textcolor{magenta}{5} \\ \textcolor{deepskyblue}{-1} x + \textcolor{deepskyblue}{1}y \textcolor{deepskyblue}{- 2} z + \textcolor{deepskyblue}{3} w = \textcolor{magenta}{-7} \\ \ \ \ \textcolor{deepskyblue}{4} x + \textcolor{deepskyblue}{3} y + \textcolor{deepskyblue}{ 2} z \textcolor{deepskyblue}{-6} w = \ \ \ \textcolor{magenta}{9} \end{array} \right.
\]であれば、\[\begin{align*}
|A| = \left| \begin{array}{ccc} \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{5} \\ \textcolor{deepskyblue}{-3} & \textcolor{deepskyblue}{-6} & \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{2} \\ \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{1} & \textcolor{deepskyblue}{-2} & \textcolor{deepskyblue}{3} \\ \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{3} & \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{-6} \end{array} \right|
\end{align*}\]を計算した上で、4つの変数 \( x \), \( y \), \( z \), \( w \) それぞれに対して「解に対応する係数がある列の値を右辺の値に書き換えた係数行列の行列式」を求め、求まった行列式を \( |A| \) で割ることで解を求めることができます。
\[\begin{align*}
x & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{magenta}{-6} & \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{5} \\ \textcolor{magenta}{5} & \textcolor{deepskyblue}{-6} & \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{2} \\ \textcolor{magenta}{-7} & \textcolor{deepskyblue}{1} & \textcolor{deepskyblue}{-2} & \textcolor{deepskyblue}{3} \\\textcolor{magenta}{9} & \textcolor{deepskyblue}{3} & \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{-6} \end{array} \right| , \ \ \ \
y = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{-4} & \textcolor{magenta}{-6} & \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{5} \\ \textcolor{deepskyblue}{-3} & \textcolor{magenta}{5} & \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{2} \\ \textcolor{deepskyblue}{-1} & \textcolor{magenta}{-7} & \textcolor{deepskyblue}{-2} & \textcolor{deepskyblue}{3} \\ \textcolor{deepskyblue}{4} & \textcolor{magenta}{9} & \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{-6} \end{array} \right| \\
z & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{-4} & \textcolor{magenta}{-6} & \textcolor{deepskyblue}{5} \\ \textcolor{deepskyblue}{-3} & \textcolor{deepskyblue}{-6} & \textcolor{magenta}{5} & \textcolor{deepskyblue}{2} \\ \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{1} & \textcolor{magenta}{-7} & \textcolor{deepskyblue}{3} \\ \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{3} & \textcolor{magenta}{9} & \textcolor{deepskyblue}{-6} \end{array} \right| , \ \ \ \
w = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{-1} & \textcolor{magenta}{-6} \\ \textcolor{deepskyblue}{-3} & \textcolor{deepskyblue}{-6} & \textcolor{deepskyblue}{4} & \textcolor{magenta}{5} \\ \textcolor{deepskyblue}{-1} & \textcolor{deepskyblue}{1} & \textcolor{deepskyblue}{-2} & \textcolor{magenta}{-7} \\ \textcolor{deepskyblue}{4} & \textcolor{deepskyblue}{3} & \textcolor{deepskyblue}{2} & \textcolor{magenta}{9} \end{array} \right|
\end{align*}\]
しかし、4次以上の行列の行列式は、サラスの公式を使うために必ず行基本変形や余因子展開などを用いて3次以下の行列に変換する必要がありますね。そのため、クラメルの公式のメリットである掃き出し法を使わずに連立方程式の解を計算するというメリットが活かせません。
よって、4元以上の連立方程式に対しては、クラメルの公式の適用方法は知っておくべきですが、実際にクラメルの公式を使って連立方程式を計算することはおすすめしません。
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{a_{11}} x + \textcolor{deepskyblue}{a_{12}} y = \textcolor{magenta}{ b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } x + \textcolor{deepskyblue}{ a_{22} } y = \textcolor{magenta}{b_2} \end{array} \right.
\]の解は、次のように計算できる。\[
|A| = \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } \end{array} \right|
\]\[
x = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{12} } \\ \textcolor{magenta}{ b_{2} } & \textcolor{deepskyblue}{ a_{22} } \end{array} \right| , \ \ \ \
y = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{ b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{ b_{2} } \end{array} \right|
\]※ クラメルの公式は \( |A| \not = 0 \) となるときに適用可 [2]
3元連立方程式\[
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{a_{11}} x + \textcolor{deepskyblue}{a_{12}} y+ \textcolor{deepskyblue}{a_{13}} z = \textcolor{magenta}{ b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } x + \textcolor{deepskyblue}{ a_{22} } y + \textcolor{deepskyblue}{a_{23}} z = \textcolor{magenta}{b_2} \\ \textcolor{deepskyblue}{ a_{31} } x + \textcolor{deepskyblue}{ a_{32} } y + \textcolor{deepskyblue}{a_{33}} z = \textcolor{magenta}{b_3} \end{array} \right.
\]の解は、次のように計算できる。\[
|A| = \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right|
\]
\[
x = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right| , \ \ \
y = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right| , \ \ \
z = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{magenta}{b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{magenta}{b_{2} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{magenta}{b_{3} } \end{array} \right|
\]※ クラメルの公式は \( |A| \not = 0 \) となるときに適用可[4]重要なことなので、2回言いました。
スポンサードリンク
2. クラメルの公式の導出
ここでは2元連立方程式と、3元連立方程式の2つのパターンでクラメルの公式を導出(証明?)していきたいと思います。
(3元までの)連立方程式をクラメルの公式で解くだけであれば逆行列や余因子の知識は不要ですが、公式を導出するために「逆行列を用いて連立方程式を解く技」や「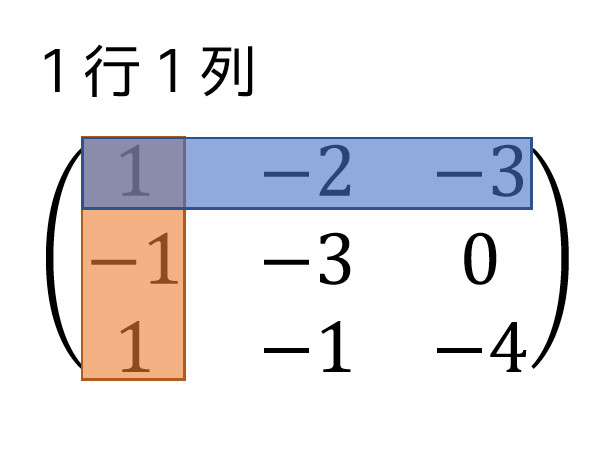
(1) 2元連立方程式(係数行列が2×2)の場合
2元連立方程式であれば、クラメルの公式を比較的簡単に導出することができます。
連立方程式\[
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{a_{11}} x + \textcolor{deepskyblue}{a_{12}} y = \textcolor{magenta}{ b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } x + \textcolor{deepskyblue}{ a_{22} } y = \textcolor{magenta}{b_2} \end{array} \right.
\]の解を、係数行列\[
A = \left( \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } \end{array} \right)
\]を用いて\[\begin{align*}
x & = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{12} } \\ \textcolor{magenta}{ b_{2} } & \textcolor{deepskyblue}{ a_{22} } \end{array} \right| \\
y & = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{ b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{ b_{2} } \end{array} \right|
\end{align*}\]で計算できることを導出します。
まず、連立方程式 \( A \vec{x} = \vec{b} \) の解は[5]ベクトル \( \vec{x} \), \( \vec{b} \) はそれぞれ\[\vec{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right) , \ \ \ \vec{b} = \left( \begin{array}{ccc} b_{1} \\ b_{2} \end{array} … Continue reading、係数行列が逆行列 \( A^{-1} \) を持つ(正則な)行列であれば、\( \vec{x} = A^{-1} \vec{b} \) と計算できるのでしたね。
逆行列を持つ行列かどうかについては、クラメルの公式が使える連立方程式は、係数行列が逆行列を持つという条件と同値なので気にしなくてOKです。なので、\( \vec{x} = A^{-1} \vec{b} \) から解 \( x \), \( y \) を求めることができますね。
つまり、\[\begin{align*}
\left( \begin{array}{ccc} x \\ y \end{array} \right) & = \left( \begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right)^{-1} \left( \begin{array}{ccc} b_{1} \\ b_{2} \end{array} \right)
\\ & = \frac{1}{|A|} \left( \begin{array}{ccc} a_{22} & - a_{12} \\ - a_{21} & a_{11} \end{array} \right) \left( \begin{array}{ccc} b_{1} \\ b_{2} \end{array} \right)
\\ & = \frac{1}{|A|} \left( \begin{array}{ccc} a_{22} b_{1} - a_{12} b_{2} \\ -a_{21} b_{1} + a_{11} b_{2} \end{array} \right)
\end{align*}\]の関係式が成立します。
あとは、バラバラにした関係式を行列式の形に書き直すことで、クラメルの公式を導出することができます。\[\begin{align*}
x & = \frac{1}{|A|} (a_{22} b_{1} - a_{12} b_{2} )
\\ & = \frac{1}{|A|} \left| \begin{array}{ccc} \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{12} } \\ \textcolor{magenta}{ b_{2} } & \textcolor{deepskyblue}{ a_{22} } \end{array} \right|
\end{align*}\]\[\begin{align*}
y & = \frac{1}{|A|} ( -a_{21} b_{1} + a_{11} b_{2} )
\\ & = \frac{1}{|A|} (a_{11} b_{2} -a_{21} b_{1})
\\ & = \frac{1}{|A|} \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{ b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{ b_{2} } \end{array} \right|
\end{align*}\]
(2) 3元連立方程式(係数行列が3×3)の場合
3元連立方程式に対して、クラメルの公式の導出をするためには余因子関連の知識が必要になってきます。
なので、余因子の理解があやふやな人は、導出を見る前にこちらの記事にて確認をすることをおすすめします。
準備ができたら、3元連立方程式\[
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{a_{11}} x + \textcolor{deepskyblue}{a_{12}} y+ \textcolor{deepskyblue}{a_{13}} z = \textcolor{magenta}{ b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } x + \textcolor{deepskyblue}{ a_{22} } y + \textcolor{deepskyblue}{a_{23}} z = \textcolor{magenta}{b_2} \\ \textcolor{deepskyblue}{ a_{31} } x + \textcolor{deepskyblue}{ a_{32} } y + \textcolor{deepskyblue}{a_{33}} z = \textcolor{magenta}{b_3} \end{array} \right.
\]のクラメルの公式\[\begin{align*}
x & = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right| \\
y & = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right| \\
z & = \frac{ 1 } { |A| } \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{magenta}{b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{magenta}{b_{2} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{magenta}{b_{3} } \end{array} \right|
\end{align*}\]を導出していきましょう。
まず、この連立方程式の係数行列\[
A = \left( \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right)
\]を用いて、連立方程式 \( A \vec{x} = \vec{b} \) から \( \vec{x} = A^{-1} \vec{b} \) と解いてみましょう[6]ベクトル \( \vec{x} \), \( \vec{b} \) はそれぞれ\[\vec{x} = \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) , \ \ \ \vec{b} = \left( \begin{array}{ccc} b_{1} \\ b_{2} \\ b_3 … Continue reading。
すると、\( i \) 行 \( j \) 列の余因子 \( \Delta_{ij} \) [7]元の行列から、\( i \) 行もしくは \( j \) 列となる成分を消すことで作成した行列となる。を用いて解 \( x \), \( y \), \( z \) を\[\begin{align*}
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) & = \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right)^{-1} \left( \begin{array}{ccc} b_{1} \\ b_{2} \\ b_{3} \end{array} \right)
\\ & = \frac{1}{|A|} \left( \begin{array}{ccc} \Delta_{11} & \Delta_{21} & \Delta_{31} \\ \Delta_{12} & \Delta_{22} & \Delta_{32} \\ \Delta_{13} & \Delta_{23} & \Delta_{33} \end{array} \right) \left( \begin{array}{ccc} b_{1} \\ b_{2} \\ b_{3} \end{array} \right)
\\ & = \frac{1}{|A|} \left( \begin{array}{ccc} \Delta_{11} b_{1} + \Delta_{21} b_{2} + \Delta_{31} b_{3} \\ \Delta_{12} b_{1} + \Delta_{22} b_{2} + \Delta_{32} b_{3} \\ \Delta_{13} b_{1} + \Delta_{23} b_{2} + \Delta_{33} b_{3} \end{array} \right)
\\ & = \frac{1}{|A|} \left( \begin{array}{ccc} x' \\ y' \\ z' \end{array} \right)
\end{align*}\]で計算することができます。
ここで、式がぐちゃぐちゃにならないように、余因子で表した計算結果をそれぞれ \( x' \), \( y' \), \( z' \) とおくことにします。
つぎに、余因子で表した計算結果を行列式の形に書き直すことで、\( x' \), \( y' \), \( z' \) の値を求めます。
※ \( \textcolor{orange}{ a_{11} } \) のようにオレンジ色の値で示している成分は、余因子展開の逆(2次正方行列から3次正方行列への変換)をする際に補っている成分を表します[8] … Continue reading。
\[\begin{align*}
x' & = \Delta_{11} b_{1} + \Delta_{21} b_{2} + \Delta_{31} b_{3}
\\ & = b_{1} \left| \begin{array}{ccc} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array} \right| - b_{2} \left| \begin{array}{ccc} a_{12} & a_{13} \\ a_{32} & a_{33} \end{array} \right| + b_{3} \left| \begin{array}{ccc} a_{12} & a_{13} \\ a_{22} & a_{23} \end{array} \right| \ \ \ (\mathrm{余因子のマイナス注意} )
\\ & = \left| \begin{array}{ccc} b_{1} & \textcolor{orange}{a_{12}} & \textcolor{orange}{a_{13}} \\ 0 & a_{22} & a_{23} \\ 0 & a_{32} & a_{33} \end{array} \right| + \left| \begin{array}{ccc} 0 & a_{12} & a_{13} \\ b_{2} & \textcolor{orange}{a_{22}} & \textcolor{orange}{a_{23}} \\ 0 & a_{32} & a_{33} \end{array} \right| + \left| \begin{array}{ccc} 0 & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ b_{3} & \textcolor{orange}{a_{32}} & \textcolor{orange}{a_{33}} \end{array} \right| \ \ \ ( \mathrm{余因子展開の逆} )
\\ & = \left| \begin{array}{ccc} \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right|
\end{align*}\]
\[\begin{align*}
y' & = \Delta_{12} b_{1} + \Delta_{22} b_{2} + \Delta_{32} b_{3}
\\ & = - b_{1} \left| \begin{array}{ccc} a_{21} & a_{23} \\ a_{31} & a_{33} \end{array} \right| + b_{2} \left| \begin{array}{ccc} a_{11} & a_{13} \\ a_{31} & a_{33} \end{array} \right| - b_{3} \left| \begin{array}{ccc} a_{11} & a_{13} \\ a_{21} & a_{23} \end{array} \right| \ \ \ (\mathrm{余因子のマイナス注意} )
\\ & = \left| \begin{array}{ccc}\textcolor{orange}{a_{11}} & b_{1} & \textcolor{orange}{a_{13}} \\ a_{21} & 0 & a_{23} \\ a_{31} & 0 & a_{33} \end{array} \right| + \left| \begin{array}{ccc} a_{11} & 0 & a_{13} \\ \textcolor{orange}{a_{21}} & b_{2} & \textcolor{orange}{a_{23}} \\ a_{31} & 0 & a_{33} \end{array} \right| + \left| \begin{array}{ccc} a_{11} & 0 & a_{13} \\ a_{21} & 0 & a_{23} \\ \textcolor{orange}{a_{31}} & b_{3} & \textcolor{orange}{a_{33}} \end{array} \right| \ \ \ ( \mathrm{余因子展開の逆} )
\\ & =\left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right|
\end{align*}\]
\[\begin{align*}
z' & = \Delta_{13} b_{1} + \Delta_{23} b_{2} + \Delta_{33} b_{3}
\\ & = b_{1} \left| \begin{array}{ccc} a_{21} & a_{22} \\ a_{31} & a_{32} \end{array} \right| + b_{2} \left| \begin{array}{ccc} a_{11} & a_{12} \\ a_{31} & a_{32} \end{array} \right| - b_{3} \left| \begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \ \ \ (\mathrm{余因子のマイナス注意} )
\\ & = \left| \begin{array}{ccc} \textcolor{orange}{a_{11}} & \textcolor{orange}{a_{12}} & b_{1} \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & 0 \end{array} \right| + \left| \begin{array}{ccc} a_{11} & a_{12} & 0 \\ \textcolor{orange}{a_{21}} & \textcolor{orange}{a_{22}} & b_{2} \\ a_{31} & a_{32} & 0 \end{array} \right| + \left| \begin{array}{ccc} a_{11} & a_{12} & 0 \\ a_{21} & a_{22} & 0 \\ \textcolor{orange}{a_{31}} & \textcolor{orange}{a_{32}} & b_{3} \end{array} \right| \ \ \ ( \mathrm{余因子展開の逆} )
\\ & = \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{magenta}{b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{magenta}{b_{2} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{magenta}{b_{3} } \end{array} \right|
\end{align*}\]
あとは、\( x' \), \( y' \), \( z' \) をもとの変数 \( x \), \( y \), \( z \) に戻してあげれば導出完了です。\[\begin{align*}
x & = \frac{1}{|A|} x'
\\ & = \frac{1}{|A|} \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right| \\
y & = \frac{1}{|A|} y'
\\ & = \frac{1}{|A|} \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{magenta}{b_{1} } & \textcolor{deepskyblue}{ a_{13} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{magenta}{b_{2} } & \textcolor{deepskyblue}{ a_{23} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{magenta}{b_{3} } & \textcolor{deepskyblue}{ a_{33} } \end{array} \right| \\
z & = \frac{1}{|A|} z'
\\ & = \frac{1}{|A|} \left| \begin{array}{ccc} \textcolor{deepskyblue}{a_{11} } & \textcolor{deepskyblue}{ a_{12} } & \textcolor{magenta}{b_{1} } \\ \textcolor{deepskyblue}{ a_{21} } & \textcolor{deepskyblue}{ a_{22} } & \textcolor{magenta}{b_{2} } \\ \textcolor{deepskyblue}{ a_{31} } & \textcolor{deepskyblue}{ a_{32} } & \textcolor{magenta}{b_{3} } \end{array} \right|
\end{align*}\]
スポンサードリンク
3. 練習問題
それでは、練習問題を2問用意してみたので実際に解いてみましょう。
練習1.2元連立方程式(係数行列が2×2)の場合
次の連立方程式\[
\left\{ \begin{array}{cc} ax + 3y = \ \ \ 1 \\ 2x + 4y = -2 \end{array} \right.
\]をクラメルの公式を使って解きたい。(1), (2)の問いに答えなさい。
(1) クラメルの公式が適用できるための \( a \) の条件を求めなさい。
(2) (1)の条件を満たすときの連立方程式の解を求めなさい。
練習2.3元連立方程式(係数行列が3×3)の場合
次の連立方程式\[
\left\{ \begin{array}{cc} \ \ \ 3x - 3y + 2z = -1 \\ -2x + 2y - \ \ z = \ \ \ 0 \\ -4x + 5y - 2z = \ \ \ 4 \end{array} \right.
\]をクラメルの公式を使って解きなさい。
4. 練習問題の答え
解答1.2元連立方程式(係数行列が2×2)の場合
(1)
答え: \( a = 3/2 \)
クラメルの公式を使うための条件は2つありましたね。
- 連立方程式の係数行列 \( A \) が正方行列となること
- \( A \) が正則であること → \( |A| \not = 0 \) であること
今回は、連立方程式が\[
\left\{ \begin{array}{cc} \textcolor{deepskyblue}{a} x + \textcolor{deepskyblue}{3} y = \ \ \ \textcolor{magenta}{1} \\ \textcolor{deepskyblue}{2} x + \textcolor{deepskyblue}{4} y = \textcolor{magenta}{-2} \end{array} \right.
\]となるので、係数行列 \( A \) は\[
A = \left( \begin{array}{ccc} \textcolor{deepskyblue}{a} & \textcolor{deepskyblue}{3} \\ \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{4} \end{array} \right)
\]となりますね。
この係数行列 \( A \) の行列式 \( |A| \) が \( |A| \not = 0 \) となればよいので、\[\begin{align*}
|A| & = \left| \begin{array}{ccc} \textcolor{deepskyblue}{a} & \textcolor{deepskyblue}{3} \\ \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{4} \end{array} \right|
\\ & = 4a - 6 \not = 0
\end{align*}\]となり、クラメルの公式が適用できるための条件が \( a \not = \frac{3}{2} \) と導出できますね。
(2)
\( x \), \( y \) それぞれに対して「解に対応する係数がある列の値を右辺の値に書き換えた係数行列の行列式」を求め、求まった行列式を \( |A| \) で割ればOK。
\[\begin{align*}
x & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{magenta}{1} & \textcolor{deepskyblue}{3} \\ \textcolor{magenta}{-2} & \textcolor{deepskyblue}{4} \end{array} \right|
\\ & = \frac{1}{4a-6} \left\{ 4 - (-6) \right\}
\\ & = \frac{1}{2(2a-3)} \cdot 10
\\ & = \frac{5}{2a-3}
\end{align*}\]
\[\begin{align*}
y & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{a} & \textcolor{magenta}{1} \\ \textcolor{deepskyblue}{2} & \textcolor{magenta}{-2} \end{array} \right|
\\ & = \frac{1}{4a-6} \left( -2a - 2 \right)
\\ & = \frac{1}{2(2a-3)} \cdot \left\{ -2 (a+1) \right\}
\\ & = - \frac{a+1}{2a-3}
\end{align*}\]
よって、連立方程式の解は\[
x = \frac{5}{2a-3} , \ \ \ y = - \frac{a+1}{2a-3}
\]となる。
解答2.3元連立方程式(係数行列が3×3)の場合
まずは、連立方程式\[
\left\{ \begin{array}{cc} \ \ \ \textcolor{deepskyblue}{3} x \textcolor{deepskyblue}{-3} y + \textcolor{deepskyblue}{2} z = \textcolor{magenta}{-1} \\ \textcolor{deepskyblue}{-2} x + \textcolor{deepskyblue}{2} y \textcolor{deepskyblue}{-1} z = \ \ \ \textcolor{magenta}{0} \\ \textcolor{deepskyblue}{-4} x + \textcolor{deepskyblue}{5} y \textcolor{deepskyblue}{-2} z = \ \ \ \textcolor{magenta}{4} \end{array} \right.
\]に対する係数行列の行列式 \( |A| \) を求める。
\[\begin{align*}
|A| & = \left| \begin{array}{ccc} \textcolor{deepskyblue}{3} & \textcolor{deepskyblue}{-3} & \textcolor{deepskyblue}{2} \\ \textcolor{deepskyblue}{-2} & \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{-1} \\ \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{5} & \textcolor{deepskyblue}{-2} \end{array} \right|
\\ & = -12 -12 -20 - (-16 -12 -15)
\\ & = -44 + 43
\\ & = -1
\end{align*}\]
あとは \( x \), \( y \), \( z \) それぞれに対して、「解に対応する係数がある列の値を右辺の値に書き換えた係数行列の行列式」を求め、求まった行列式を \( |A| \) で割ればOK。
\[\begin{align*}
x & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{magenta}{-1} & \textcolor{deepskyblue}{-3} & \textcolor{deepskyblue}{2} \\ \textcolor{magenta}{0} & \textcolor{deepskyblue}{2} & \textcolor{deepskyblue}{-1} \\ \textcolor{magenta}{4} & \textcolor{deepskyblue}{5} & \textcolor{deepskyblue}{-2} \end{array} \right|
\\ & = \frac{1}{-1} \left\{ 4 + 12 + 0 - (16 + 0 + 5) \right\}
\\ & = -1 \cdot (16 - 21)
\\ & = 5
\end{align*}\]
\[\begin{align*}
y & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{3} & \textcolor{magenta}{-1} & \textcolor{deepskyblue}{2} \\ \textcolor{deepskyblue}{-2} & \textcolor{magenta}{0} & \textcolor{deepskyblue}{-1} \\ \textcolor{deepskyblue}{-4} & \textcolor{magenta}{4} & \textcolor{deepskyblue}{-2} \end{array} \right|
\\ & = \frac{1}{-1} \left\{ 0- 4 - 16 - (0-4-12) \right\}
\\ & = -1 \cdot (-20 + 16)
\\ & = 4
\end{align*}\]
\[\begin{align*}
z & = \textcolor{limegreen}{ \frac{1}{ |A| } } \left| \begin{array}{ccc} \textcolor{deepskyblue}{3} & \textcolor{deepskyblue}{-3} & \textcolor{magenta}{-1} \\ \textcolor{deepskyblue}{-2} & \textcolor{deepskyblue}{2} & \textcolor{magenta}{0} \\ \textcolor{deepskyblue}{-4} & \textcolor{deepskyblue}{5} & \textcolor{magenta}{4} \end{array} \right|
\\ & = \frac{1}{-1} \left\{ 24 + 10 - (8 + 24 + 0) \right\}
\\ & = -1 \cdot (34 - 32)
\\ & = -2
\end{align*}\]
よって、連立方程式の解は\[
x = 5 , \ \ \ y = 4 , \ \ \ z = -2
\]となる。
注釈
| ↑1 | \[ \left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) + \left( \begin{array}{ccc} -1 \\ 0 \end{array} \right) \]のように解を無数に持つ(すべての解を表現するために任意定数が必要な)連立方程式や、\[ \left\{ \begin{array}{cc} 2x + 3y - 5z = 7 \\ 3 x - 4x + 2z = 3 \end{array} \right. \]のように係数行列が正方行列とはならない連立方程式では使えません。もちろん解を持たない連立方程式であってもクラメルの公式は使えません。 |
|---|---|
| ↑2 | つまり、係数行列が正則となる連立方程式でのみ使える。 |
| ↑3 | 解を無数に持つ連立方程式、もしくは解を持たない連立方程式のこと。 |
| ↑4 | 重要なことなので、2回言いました。 |
| ↑5 | ベクトル \( \vec{x} \), \( \vec{b} \) はそれぞれ\[ \vec{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right) , \ \ \ \vec{b} = \left( \begin{array}{ccc} b_{1} \\ b_{2} \end{array} \right) \]を指します。 |
| ↑6 | ベクトル \( \vec{x} \), \( \vec{b} \) はそれぞれ\[ \vec{x} = \left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) , \ \ \ \vec{b} = \left( \begin{array}{ccc} b_{1} \\ b_{2} \\ b_3 \end{array} \right) \]を指します。 |
| ↑7 | 元の行列から、\( i \) 行もしくは \( j \) 列となる成分を消すことで作成した行列となる。 |
| ↑8 | このオレンジ色の成分は、3次正方行列から2次正方行列へ変換する際に消える成分なので、どんな値を入れてもOK。今回はクラメルの公式を導出するために、元々の係数行列の \( i \) 行 \( j \) 列の成分 \( a_{ij} \) を入れている。 |