スポンサードリンク
こんにちは、ももやまです。
今回は再帰関数の基本についてわかりやすく説明していきたいと思います。
なお、今回はC言語で説明していますが、仕組みは他の言語の場合でも同じなのでC言語以外でプログラミングしている人もぜひご覧ください。
目次
スポンサードリンク
1.再帰関数とは
突然ですが階乗を求める下の関数 fact をご覧ください。
int fact(int n) {
if(n == 0) {
return 1; // 0! = 1
}
else {
return n * fact(n-1); // ここで fact 自身を呼び出す
}
}
関数 fact の中で fact 自身を呼び出していますよね。
このように自分自身を呼び出す関数のことを再帰関数と呼びます。
スポンサードリンク
2.再帰関数の基本
再帰関数の基本的なルールは下の2つです。
- 自分自身の関数を用いて、問題を少し簡単にするための計算式をたてる
- すごく簡単なパターンのときの答えを用意する
この2つのルールについて、先程紹介した階乗を求める関数 fact を用いて詳しく説明していきましょう。
ルール1 自分自身の関数を用いて、問題を少し簡単にする
再帰関数の基本は、自分自身を呼び出して問題を少し簡単にするための式をたてることです。
少し簡単にするところがポイントです*1。
例えば、階乗 \( n! \) は、\[
n \times (n-1)!
\]とすることで、階乗部分 \( n! \) が \( (n-1)! \) となり、少し簡単になりますね。
実際に数値を入れてみても 5! よりも 5 × 4! のほうが少し簡単に見えますよね。
先程のプログラムの
else {
return n * fact(n-1); // ここで fact 自身を呼び出す
}
の部分に相当します。
ルール2 すごく簡単なパターンの答えを用意する
ルール1の再帰呼び出しの部分だけだと、再帰呼び出しが無限に行われ、無限ループします。最悪の場合、兵庫県警にお世話になるかもしれません。
そのため、ループを止めるためのすごく簡単な場合の答えを用意する必要があります。
先程のプログラムの場合だと
if(n == 0) {
return 1; // 0! = 1
}
の部分に相当します。
※ \( 0! = 1 \) は当たり前ですよね。
基本的には1つ用意すればOKなのですが、例えば
int fib(int n) {
if(n == 0) {
return 0;
}
else if(n == 1) {
return 1;
}
else {
return fib(n-1) + fib(n-2); // fib(0), fib(1) の2つがないと止められない
}
}
の else 部分では
return f(n-1) + f(n-2) // 2つ呼び出すので初期値も2つ必要
と2つ再帰を使っていますね。
そのため、fib(0) = 0, fib(1) = 1 と2つの簡単なパターンがないと再帰呼び出しを止められず兵庫県警に捕まってしまいます。
ところで皆さんは高校のときに習った漸化式*2は覚えていますか?
実は再帰関数と漸化式はほぼ全く同じものなので、
再帰関数を組む ≒ 漸化式を組む
ものだと思ってOKです!
スポンサードリンク
3.再帰関数の動き
では、再帰関数を実行したときにどのような動きをするかを階乗を計算するプログラム fact で確認していきましょう。
f(4) = 4*f(3) // f(4) = 4*f(3)
= 4*3*f(2) // f(3) = 3*f(2)
= 4*3*2*f(1) // f(2) = 2*f(1)
= 4*3*2*1*f(0) // f(1) = 1*f(0)
= 4*3*2*1*1 // f(0) = 1
= 24
例えば fact(4) (以下 f(4))を実行すると、
と計算できます。
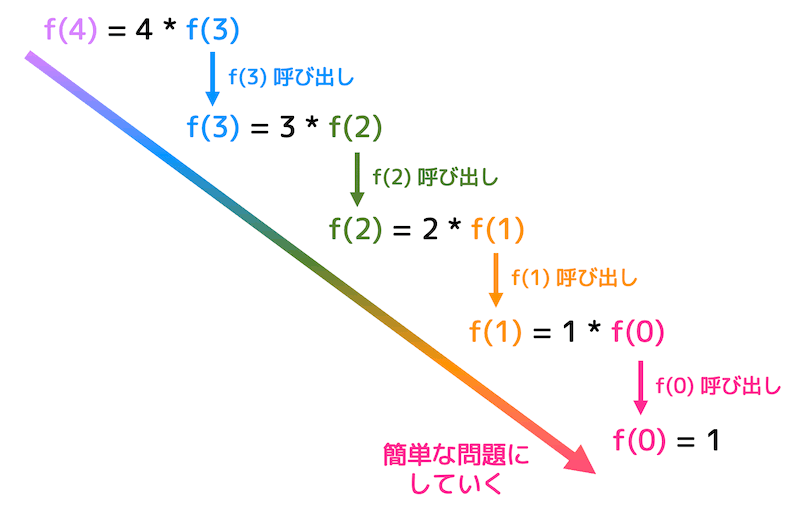
図でわかりやすく説明すると、まず与えられた f(4) を少しずつ簡単にしていき、一番簡単なパターンである f(0) まで変形します。
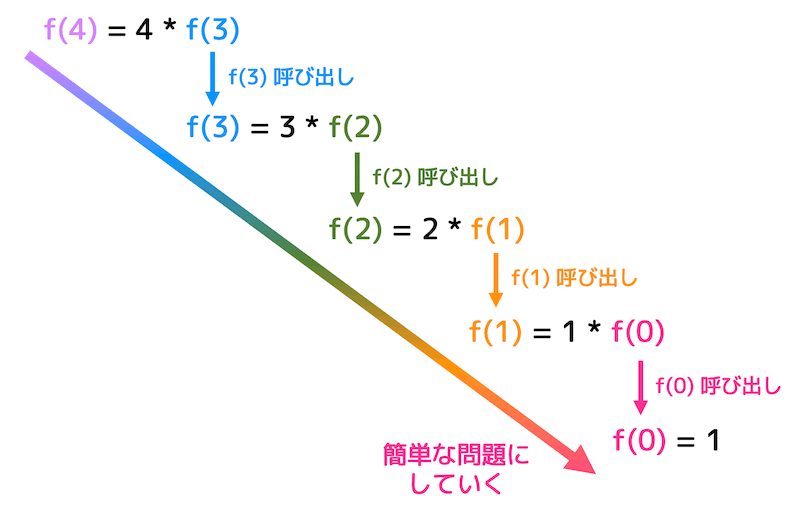
一番簡単なパターンである f(0) であれば、f(0) = 1 がわかるので、f(1), f(2), f(3), f(4) の値をドミノ倒しに求めることができますね。
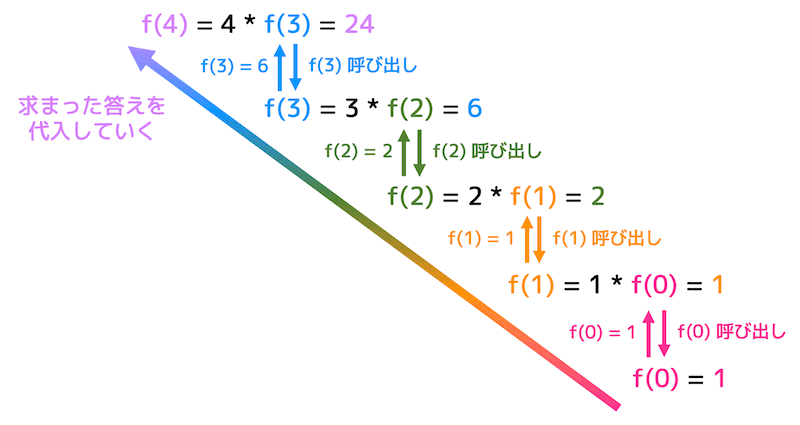
下のように2つ同時に再帰させる場合の動きも図で確認していきましょう。
// フィボナッチ数列を求める関数
int fib(int n) {
if(n == 0) {
return 0;
}
else if(n == 1) {
return 1;
}
else {
return fib(n-1) + fib(n-2);
}
}
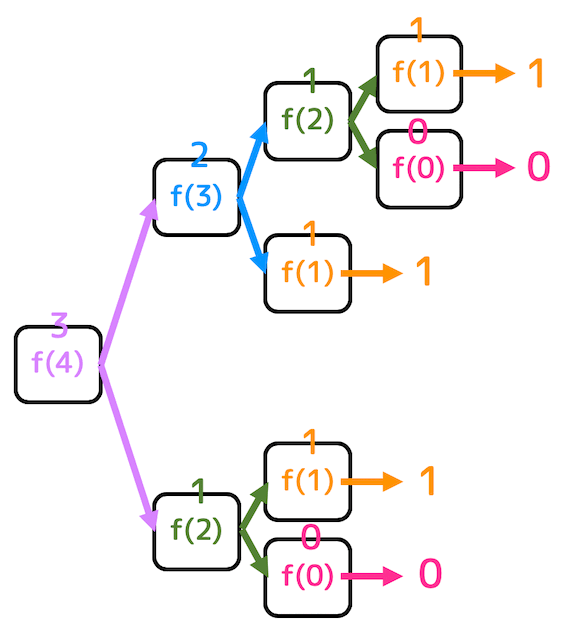
このようにそのまま解くと難しいような問題を徐々に簡単にしていき、最後に計算結果をあわせて求められていることが図からわかりますね*3。
3.再帰を用いるメリットとデメリット
メリット 見栄え
再帰の大きなメリットは複雑に行われる処理を簡単に書くことができ、プログラムの見栄えもよくなります。
例えば、再帰を用いずに最大公約数を求めるプログラムは、下のように書くことができます。
int find_gcd1(int a,int b) {
int r;
while(b != 0) {
r = a % b;
a = b;
b = r;
}
return a;
}
これを再帰で書くと、
int find_gcd2(int a,int b) {
if(b == 0) {
return a;
}
else {
return find_gcd2(b, a % b);
}
}
このように見栄えがよくなります!
デメリット1 スタック領域の不足
再帰呼び出しを行うと、スタック領域に再帰するために必要な情報が記録されていきます。
しかし、メモリの量は無限ではないので、再帰を使いすぎるとスタック領域がなくなり、プログラムがクラッシュします。
(スタックオーバーフローと呼ばれます。)
デメリット2 計算時間がかかる
2つ目のデメリットは計算時間がかかることです。
特に先程紹介したフィボナッチ数列を求めるプログラムの、
return fib(n-1) + fib(n-2)
のように1つの命令で2つ以上の再帰をするプログラムの場合の多くは n の値を少し大きくしただけで計算に非常に時間がかかります*4。
その理由として、下の図の紫色部分のように全く同じ計算を何度も何度も繰り返していることが挙げられます。
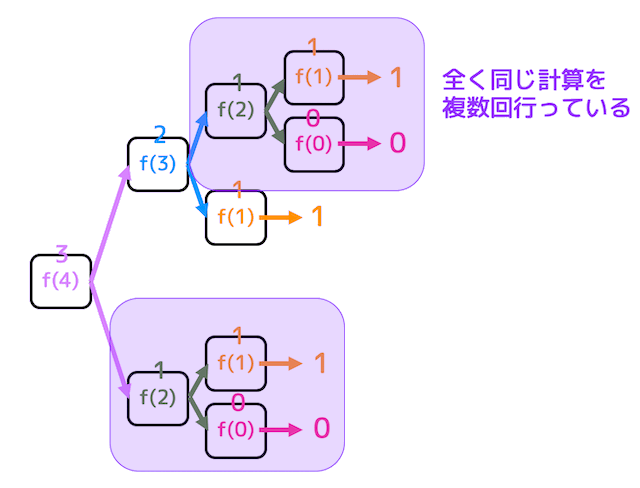
そのため、実際に再帰を行う場合には
- 初めて計算するときに計算結果を変数にメモ
- 1回求めた値をメモから参照
することで計算時間を抑えるテクニックを使います。
(メモ化再帰・動的計画法と呼ばれます。)
4.再帰関数の応用例
今までは、再帰関数で何かしらの値を求めるようなプログラムばかりでした。
少し応用して数字以外(文字とか)を処理するようなプログラムを紹介していきたいと思います。
※ 少しずつ追記していきたいと思います。
その1 2つの文字列を比較する関数 stringCompare
文字列 s1 と s2 の大小を比べる関数 stringCopareは、下のように再帰を用いて表現することができます。
(仕様はデフォルトで入っている strcmp 関数と全く同じです*5。)
int stringCompare(char *s1, char *s2) {
if(*s1 != *s2) {
return *s2 - *s1; // 文字列が異なるとき
}
else if (*s1 == '\0' && *s2 == '\0' ) {
return 0; // 文字列が全く等しいとき
}
else {
return stringCompare(s1+1,s2+1); // 次の文字へ
}
}
その2 再帰を用いた二分探索 binarySearch
二分探索も再帰を用いて書くことができます。
int binarySearch(int a[],int x,int left, int right) {
int mid = (left + right) / 2; // 基準点
if(a[mid] == x) {
return mid; // 探索成功(最も簡単な場合の答えの1つ)
}
else if(left > right) {
return -1; // 探索失敗(最も簡単な場合の答えの1つ
}
else if(a[mid] < x) {
return binarySearch(a,x,mid + 1,right); // 右半分に絞り込む
}
else {
return binarySearch(a,x,left,mid - 1); // 左半分に絞り込む
}
}
二分探索について詳しい内容はこちらの記事に書いてあるので、興味がある方はぜひお読みください。
5.練習問題
では、実際に練習してみましょう!
前半は再帰で書かれたプログラムの実行結果を求める問題で、後半は再帰を用いたプログラム作成を行う問題となっています。
練習1
自然数nに対して、次のように再帰的に定義される関数f(n)を考える。
f(5) の値はどれか。
int f(int n) {
if(n <= 1) {
return 1;
}
else {
return n + f(n-1);
}
}
ア:6
イ:9
ウ:15
エ:25
練習2
関数 f(x,y) が次のように定義されているとき、f(775, 527) の値は幾らか。ここで,x % y はxをyで割った余りを返す。
int f(int x, int y) {
if(y == 0) {
return x;
}
else {
return f(y, x % y);
}
}
ア:0
イ:31
ウ:248
エ:527
練習3
次の関数 f(n,k) がある。f(4,2) の値はいくらか。
int f(int n,int k) {
if(k == 0) {
return 1;
}
else if(0 < k && k < n){
return f(n - 1, k - 1) + f(n - 1, k);
}
else if(k == n) {
return 1;
}
}
練習4
再帰的に定義された手続き proc で、proc(5) を実行したとき,印字される数字を順番に並べたものはどれか。
void proc(int n) {
if(n == 0) {
return;
}
else {
printf("%d",n);
proc(n-1);
printf("%d",n);
return;
}
}
ア:543212345
イ:5432112345
ウ:54321012345
エ:543210012345
練習5
[2019/3/11 問題文をわかりやすくするために、例を加えるなどして修正しております。]某寿司屋チェーンで働いているかっぱくんの報酬は、時給となっており、次のように決まる。
- 最初の1時間働いたときの時給はきゅうり10本である
- 次の1時間からは時給がアップし、時給は「前の1時間でもらった褒美 × 2 - 5」本のきゅうりとなる
例えば、2時間働いたときの時給は 10×2-5 = 15本、3時間働いたときの時給は 15×2-5 = 25 本となる。
ここで、かっぱが n 時間働いた時の時給を計算する関数 kappa_salary(n) を再帰を用いて作成しなさい。
練習6
\( \sin x \) のべき乗の定積分を下のようにおく\[
I_{n} = \int^{ \frac{ \pi}{ 2 } }_{0} \sin^{n} x \ dx
\]すると、\[
I_{n} = \frac{ n-1 }{n} I_{n-2}
\]が成立する。ここで、\( I_{n} \) を求める再帰関数 sinexp(n) を作成しなさい。
ただし、必要であれば \( I_{0} = \pi / 2 \), \( I_{1} = 1 \) を用いてよい。また、\( \pi \) は M_PI で表記すること。
6.練習問題の答え
解答1
解答:ウ
実行結果をたどっていくと下のように計算することができる。
f(5) = 5+f(4) // f(5) = 5+f(4)
= 5+4+f(3) // f(4) = 4+f(3)
= 5+4+3+f(2) // f(3) = 3+f(2)
= 5+4+3+2+f(1) // f(2) = 2+f(1)
= 5+4+3+2+1 // f(1) = 1
= 15
よって、f(5)=15 となり、答えはウ。
解答2
解答:イ。
実行結果をたどっていくと下のように計算することができる。
f(775, 527) = f(527, 248) // 775 % 527 = 248
= f(248, 31) // 527 % 248 = 31
= f(31, 0) // 248 % 31 = 0
= 31
となるので、f(775,527) = 31 となり、答えはイ。
解答3
解答:エ
実行結果をたどっていくと下のように計算することができる。
f(4, 2) = f(3,1) + f(3,2);
f(4, 2) = f(3,1) + f(3,2)
= f(2,0) + f(2,1) + f(2,1) + f(2,2)
= 1 + f(1,0) + f(1,1) + f(1,0) + f(1,1) + 1
= 1 + 1 + 1 + 1 + 1 + 1
= 6
となるので、f(4,2) = 6 となり、答えはエ。
※ 実はこの関数は nCr を再帰で求める関数でした。
解答4
解答:イ
proc(5):5を出力しproc(4)を呼び出す(文字列:5) proc(4):4を出力しproc(3)を呼び出す(文字列:54) proc(3):3を出力しproc(2)を呼び出す(文字列:543) proc(2):2を出力しproc(1)を呼び出す(文字列:5432) proc(1):1を出力しproc(0)を呼び出す(文字列:54321) proc(0):return し、proc(1)に戻る
これ以上は再帰呼び出しが行われないので、呼び出す前の関数に戻っていきます。
1を出力し、returnされ proc(2)に戻る (文字列:543211) 2を出力し、returnされ proc(3)に戻る (文字列:5432112) 3を出力し、returnされ proc(4)に戻る (文字列:54321123) 4を出力し、returnされ proc(5)に戻る (文字列:543211234) 5を出力し、returnされて実行終了(文字列:5432112345)
となるので実行結果は 5432112345 となり、答えはイ。
解答5
解答例
int kappa_salary(int n) {
if(n == 1) {
return 10; // 1時間働いたら10本
}
else {
return 2 * kappa_salary(n-1) - 5; // 2時間目以降は前の時間でもらったキュウリ×2-5本
}
}
解答6
答えに M_PI を含んだ数式が含まれるので、int 型ではなく double 型となります。
また、意外と再帰部分のキャスト忘れやすいので注意しましょう。
double sinexp(int n) {
if(n == 0) {
return M_PI / 2; // 偶数のときの最も簡単な答え
}
else if(n == 1) {
return 1; // 奇数のときの最も簡単な答え
}
else {
return (n-1) * 1.0 / n * sinexp(n-2); // 再帰部分・キャスト忘れ注意
}
}
7.さいごに
今回は再帰関数の基礎部分についてまとめていきました。
基本情報では再帰関数の実行結果を答えさせる問題がたまに出るので動きが理解できているかを確認しましょう。
また、再帰関数は単に漸化式を計算させるだけでなく、マージソートやクイックソートなどの様々なアルゴリズムに利用されている非常に重要なテクニックの1つなのでぜひ理解しておきましょう。
*1: 簡単にしないと(引数を減らさないと)永久に問題が解けません()
*2:余談ですが大学の教授によっては漸化式のことを差分方程式と呼ぶこともあります。
*3:このように「普通に解くと難しいような問題」を「簡単な問題」に分割していき、「簡単な問題」の答えをあわせていくことで「元の難しい問題」の答えを求める方法を分割統治法といいます。分割統治法をうまく使っているアルゴリズムの1つにマージソートがあります。
*4:実際に\[
a_{n} = a_{n-1} + a_{n-2}, \ \ a_{0} = 0, \ \ a_{1} = 1
\]の漸化式(差分方程式)を解くと、\[
n = \frac{1}{ \sqrt{5} } \left( \left( \frac{1 + \sqrt{5} }{ 2 } \right)^{n} - \left( \frac{1 - \sqrt{5} }{ 2 } \right)^{n} \right)
\]となるのでオーダーは \( O \left( \frac{1 + \sqrt{5} }{ 2 } \right)^{n} \) となり、指数関数的に計算量が増えていくことがわかります。
もし差分方程式の解き方に興味がある人はこちらの記事を御覧ください。
*5:具体的には s1 と s2 のどちらが辞書式順序で前・後・一致しているかを調べ、 s1 が前なら -1(負の値)、s2が後なら1(正の値)、全く同じ文字列なら0を返します。
関連広告・スポンサードリンク