スポンサードリンク
こんにちは、ももやまです。
今回は基本情報にもよく出てくる探索アルゴリズム(線形探索・2分探索・ハッシュ探索)について説明していきたいと思います。
目次
スポンサードリンク
1.探索とは
配列やリストなどのデータ構造の中から目的のデータを探した出すことを探索といいます。
「データなんて最初から順番に探し出していけばいいじゃん!」
と思うかもしれません。
しかし、もしデータ数が100億あったらどうでしょう。
地道に計算すると日がくれそうです。もっといいアルゴリズムがないかなぁと思いたくなりますよね。
そこで今回はコンピュータ上でよく使う探索アルゴリズム、具体的には
- 線形探索
- 二分探索
- ハッシュ探索
の3つを紹介していきたいと思います。
スポンサードリンク
2.線形探索
(1) 線形探索とは
配列の先頭から順番に目的のデータかどうかを調べていく方法を線形探索と呼びます。
しらみつぶしに探していく最も単純な探索アルゴリズムです。
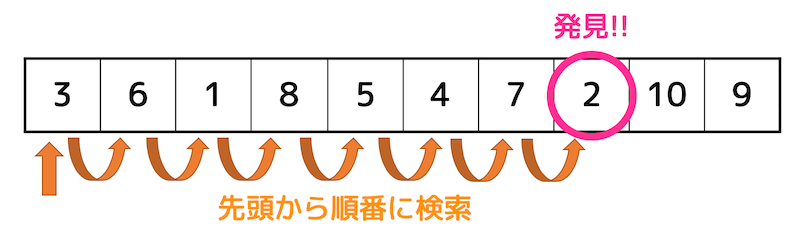
アルゴリズムとしては、先頭(0番目)の配列から順番にチェックしていき、目的のデータを見つけられたら探索成功、最後まで目的のデータが見つからなければ探索失敗となります。
(2) 線形探索のプログラム
要素数 n の配列 data から線形探索法でデータ x を探すプログラムは、下のようになります。
// 線形探索法 配列の先頭からしらみつぶしに調べていく
int linearSearch(int data[], int n, int x) {
for(int i = 0; i < n; i += 1) {
if(data[i] == x) {
return i; // 見つかれば場所を返す
}
}
return -1; // 見つからなければ-1を返す
}
データが見つかれば見つけた場所(配列番号)を、見つからなければ-1を返しています。
(3) 線形探索の探索回数・計算量
n個のデータがある配列から線形探索で目的データを探す場合の効率性(計算量)を探索回数で考えていきましょう。
最も早い場合は先頭に目的のデータがあるときで1回、最も遅い場合は最後尾に目的のデータがある場合でn回となります。
そのため、平均で (1+n)÷2 回、最悪の場合で n 回かかります。
計算量をオーダー表記で表すと、平均の場合、最悪の場合(最も計算時間がかかる場合)ともに \( O(n) \) となります*1。
※ 最悪の場合の探索回数、計算量の求め方がわかればOKです。以後紹介するアルゴリズムでは最悪の場合の探索回数、計算量についてのみ説明します。
(4) 線形探索における番兵
上のプログラムの場合、データを探していくforループの中で「目的のデータかどうか」と「配列の最後尾までチェックしたかどうか」を毎回判定しているので少しかっこわるいですよね。
そこで、下の図のようにあらかじめ目的のデータを配列の末尾につけたします。この付け足したデータのことを番兵と呼びます。
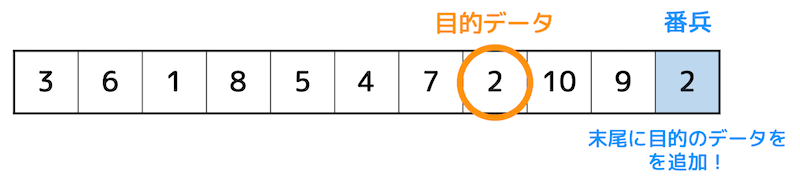
なんでそんなことするんだ?? と思ったかもしれません。
番兵を付け加えると、配列の中に探したい目標データが少なくとも1つは存在しますよね。
そのため、「配列の最後尾までチェックしたかどうか」を毎回チェックする必要がなくなり、「目的のデータかどうか」だけをループ内で判定するだけで済み、判定が少しスマートになります。
番兵を用いた線形探索のアルゴリズムでは、見つかったデータが番兵かもともとあったデータかどうかで判定します。
番兵より前で目的のデータが見つかれば目的データがあることがわかります。
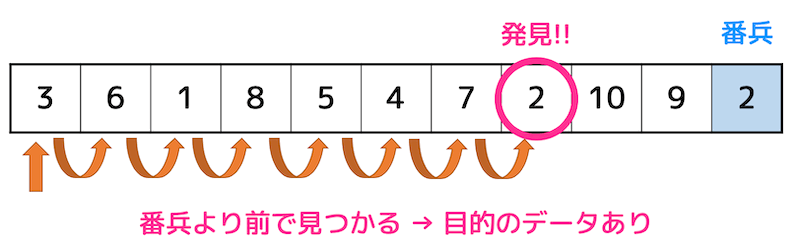
一方目的のデータがない場合、番兵しか見つかりません。
そのため、番兵が見つかった場合は目的のデータがないことがわかります。
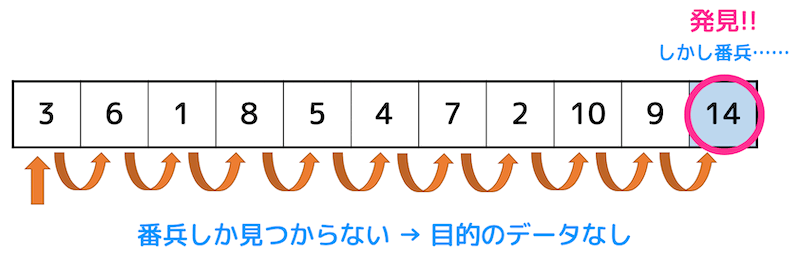
なお、番兵があった場合でも最大で n+1 回の探索が必要なのでオーダーは \( O(n) \) のままです。
(5) 番兵あり線形探索のプログラム
番兵ありバージョンの線形探索のプログラムも紹介したいと思います。
要素数 n の配列 data から番兵を入れた線形探索でデータ x を探すプログラムは、下のようになります。
// 番兵あり線形探索
int linearSearch2(int a[],int x) {
a[N] = x; // 番兵追加
int i = 0;
// この部分を forとifから while1個 に減らせるので効率UP
while(a[i] != x) {
i += 1; // データが見つかるまでwhileループ
}
if(i != N) {
return i; // 見つかった場合(添字を返す)
}
return -1; // 番兵までデータがない -> 探索失敗
}
先程と同じくデータが見つかれば見つけた場所(配列番号)を、見つからなければ-1を返しています。
スポンサードリンク
3.2分探索
(1) 2分探索とは
突然ですが下の会話をご覧ください。
友1「ねぇねぇ、今日のテスト何点だった?」
友2「教えないよ。」
友1「ちぇっ。なら今日のテスト50点以上とれた?」
友2「うん。」(点数の範囲:50点〜100点)
友1「なら75点以上は?」
友2「取れてるよ。」(範囲:75点〜100点)
友1「なら88点以上は?」
友2「取れてないよ。」(範囲:75点〜88点)
友1「じゃあ82点以上?」
友2「うん。さっきからしつこいなぁ。」(範囲:82点〜88点)
友1「あ、もしかして85点??」
友2「なんでわかったの!? 怖!」
まさに、友達1が上の会話のように点数を特定していく方法が2分探索(法)です。
もう少し丁寧に書くと、目的のデータとの大小を比べることでデータを探し出すアルゴリズムが2分探索です。
データの大小を利用して探すので、あらかじめデータが小さい順(昇順)もしくは大きい順(降順)にソートしておく必要があります。
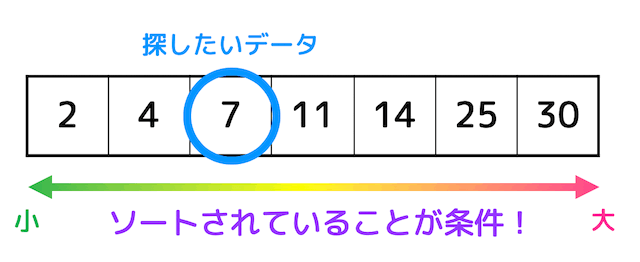
2分探索法のアルゴリズムを上のデータを例にして説明しましょう。
まず、基準となる真ん中のデータと探したいデータの大小を比べます。
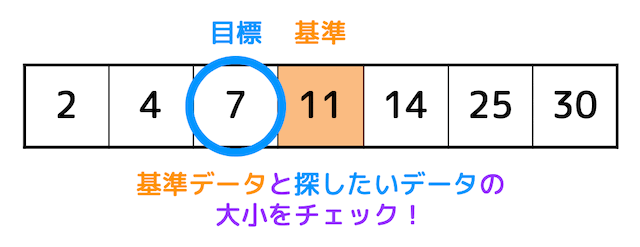
目標データは7に対し基準データは11なので、目標データのほうが基準データよりも小さいですね。
すると、11以上のデータは目標データではないことがわかり、目標データがある場所を左半分にしぼりこむことができます。

再び基準となる真ん中の点を決め、目標データとの大小を比べます。

今度は目標データが7に対し基準データが4なので目標データのほうが基準データよりも大きいですね。
すると、4以上のデータは目標データではないことがわかり、目標データがある場所を左半分にしぼりこむことができます。

再び基準となる真ん中の点を決めると、目標データと基準データが一致しましたね。
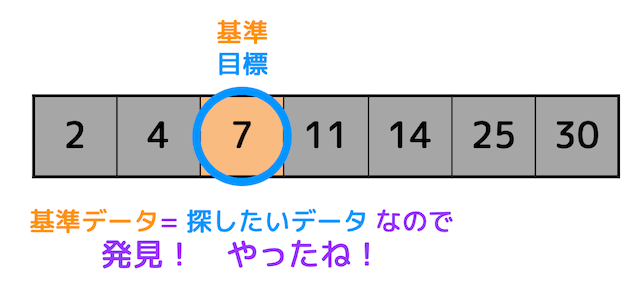
目標データと基準データが一致すれば探索成功です。
逆に探索データが1つのときに「目標データ=基準データ」とならなければ探索失敗です。
このように2分探索は、データを半分ずつにしぼりこんでいくので線形探索よりも効率よく目的データの場所(有無)を調べることができます。
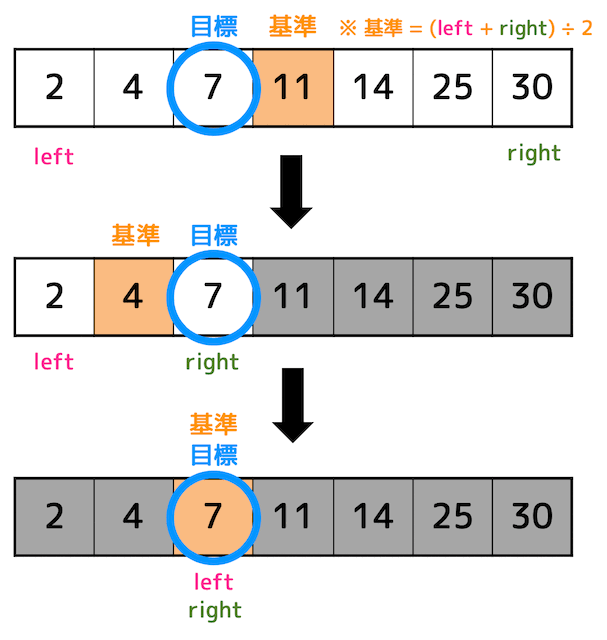
なお、プログラムでは探索範囲(データがありそうな場所)の先頭を left、最後尾を right と表現します。
(2) 2分探索のプログラム
要素数 n の配列 data から2分探索法でデータ x を探すプログラムは、下のようになります。
// 二分探索 データを半分ずつにしぼりこんで特定
// 二分探索
int binarySearch(int a[],int x) {
int left = 0, right = N - 1; // 探索範囲 left 〜 right
int mid; // 基準点
while(left <= right) {
mid = (left + right) / 2; // 基準データ
if(a[mid] == x) {
return mid;
}
else if(a[mid] < x) {
left = mid + 1; // データを右半分にしぼり込む
}
else {
right = mid - 1; // データを左半分にしぼり込む
}
}
return -1; // 見つからなければ-1を返す
}
線形探索のときと同じくデータが見つかれば見つけた場所(配列番号)を、見つからなければ-1を返しています。
(3) 2分探索法の探索回数・計算量
n個のデータがある配列から2分探索で目的データを探す場合の効率性(計算量)を探索回数で考えていきましょう。
2分探索の場合、データを半分ずつしぼりこみながら探索します。そのため、データ数が2倍になってはじめて探索回数が1回増えますね。
データ数が1個の場合、必ず1回で見つけ出せるので n回の探索で \( 2^{n} \) 個のデータを探索することができます。
そのため、\( n \) 個のデータを探索するために約 \( \log_{2} n \) 回かかりますね。
計算量をオーダー表記で表すと、 \( O(\log n) \) となります*2。
2分探索は線形探索に比べてとても早いことがわかりましたね!
実はデータ数が100億あっても、たったの34回で必ずデータを発見できちゃいます!
(線形探索なら最大で100億回かかります。日が暮れますね。)
4.ハッシュ探索
(1) ハッシュ探索とは
ハッシュ探索法は、何かしらの計算式を用いて格納先を決めて格納する探索方法です。
この「何かしらの計算式」を計算する関数のことをハッシュ関数と呼びます。
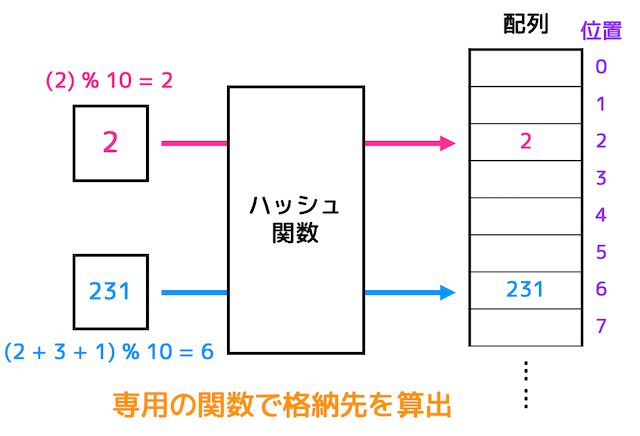
上の図の例では、「それぞれの桁ごとの数字を足した合計を10で割ったあまり」で求めています。
(ハッシュ関数で使われる計算式ではあまりを使うことが多いです。)
(2) ハッシュ探索の長所・短所
ハッシュ関数は専用の計算式からデータの格納先がわかるため、原則探索回数1回でデータを見つけ出すことができます。
計算量をオーダーで表すとなんと \( O(1) \) です。
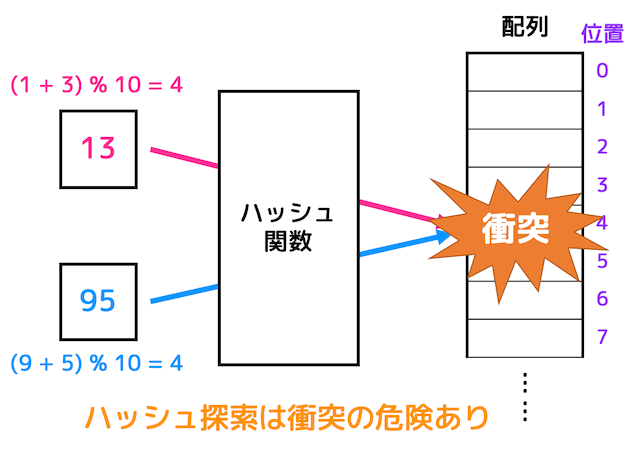
しかしいつもうまくいくとは限らず、ハッシュ関数格納しようとした場所にすでにデータが存在し、衝突してしまうことがあります。
例えば、先程のハッシュ関数だと、13の格納位置は4、95の格納位置も同じく4となり、衝突してしまいます。
衝突してしまった場合の対策として、
- あきらめて別の計算で新しい格納先を決める
- 配列をもっと広く取って衝突の可能性を下げる
- 重複したデータをリストでつなげていく(チェイン法)
の3つがあります。
よく使われるのが、3番目の重複したデータを下のようにリストでつなげていく方法です。
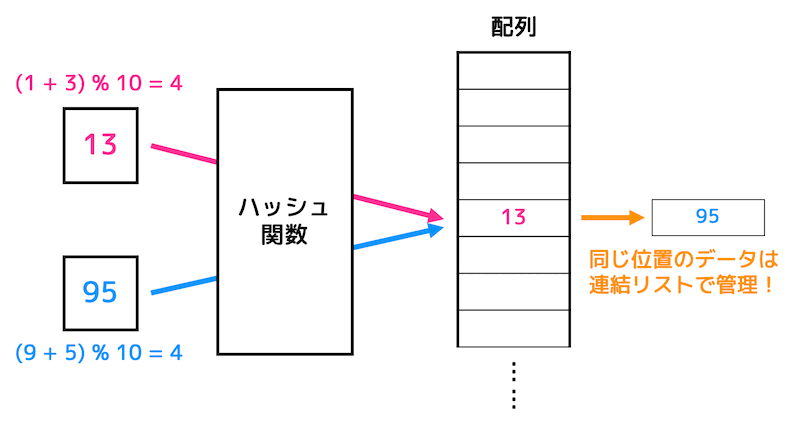
5.3つの探索法の比較
では、今回紹介した3つの探索法を簡単にまとめていきましょう。
| 探索法 | 計算量 | |
|---|---|---|
| 線形探索 | \( O(n) \) | 特になし。 |
| 2分探索 | \( O(\log n) \) | ソートの必要あり。 |
| ハッシュ探索 | \( O(1) \) | 衝突しないことが条件。 |
- 線形探索法( オーダー:\( O(n) \) )
→ 先頭から順番に地道にデータを探すアルゴリズム - 2分探索法( オーダー:\( O(\log n) \) )
→ データの大小から半分ずつしぼりこみ、データを探すアルゴリズム
※ データがソートされている必要あり - ハッシュ探索法( オーダー:衝突しなければ \( O(1) \) )
→ ハッシュ関数と呼ばれる計算式からデータの格納先を探すアルゴリズム
6.練習問題
では、いつものように基本情報などの問題で練習(復習)していきましょう。
練習1
2分探索に関する記述のうち,適切なものはどれか。
[基本情報技術者平成26年秋期 午前問6]ア:2分探索するデータ列は整列されている必要がある。
イ:2分探索は線形探索より常に速く探索できる。
ウ:2分探索は探索をデータ列の先頭から開始する。
エ:n 個のデータの探索に要する比較回数は,\( n \log_{2} n \) に比例する。
練習2
つぎの探索方法のうちで番兵が有効なものはどれか。
[基本情報技術者平成11年秋期 午前問26]ア:2分探索
イ:線形探索
ウ:ハッシュ探索
エ:幅優先探索
練習3
2分探索において、データの個数が4倍になると最大探索回数はどうなるか。
[基本情報技術者平成17年春期 午前問15]ア:1回増える
イ:2回増える
ウ:約2倍になる
エ:約4倍になる
練習4
探索方法とその実行時間のオーダの正しい組合せはどれか。ここで、探索するデータ数をnとし、ハッシュ値が衝突する(同じ値になる)確率は無視できるほど小さいものとする。また,実行時間のオーダが \( n^{2} \) であるとは,n 個のデータを処理する時間が \( c n^{2} \) (cは定数) で抑えられることをいう。
[基本情報技術者平成16年春期 午前問11]| 2分探索 | 線形探索 | ハッシュ探索 | |
|---|---|---|---|
| ア | \( \log_{2} n \) | \( n \) | \( 1 \) |
| イ | \( n \log_{2} n \) | \( n \) | \( \log_{2} n \) |
| ウ | \( n \log_{2} n \) | \( n^{2} \) | \( 1 \) |
| エ | \( n^{2} \) | \( 1 \) | \( n \) |
練習5
表探索におけるハッシュ法の特徴はどれか。
[基本情報技術者平成19年春期 午前問15]ア:2分木を用いる方法の一種である。
イ:格納場所の衝突が発生しない方法である。
ウ:キーの関数値によって格納場所を決める。
エ:探索に要する時間は表全体の大きさにほぼ比例する。
練習6(応用)
キー値が1~1,000,000の範囲で一様にランダムであるレコード3件を、大きさ10のハッシュ表に登録する場合、衝突が起こらない確率は幾らか。ここで、ハッシュ値にはキー値をハッシュ表の大きさ10で割った余りを用いる。
[ソフトウェア開発技術者平成18年春期 午前問13]ア:0.28
イ:0.7
ウ:0.72
エ:0.8
7.練習問題の答え
解答1
解答:ア
それぞれの選択肢ごとにの解説
ア:正しい。ソートされているデータでないと2分探索はできない。
イ:誤り。先頭にあるデータは線形探索では1ステップで求められるが、2分探索の場合は中央のデータを最初に探すので先頭にあるデータが1ステップで求められるとは限らない(というか低い)。
ウ:誤り。先頭から探索を始めるのは線形探索。2分探索は中央のデータから探索を始める。
エ:誤り。n 個のデータの探索に要する比較回数は \( \log_{2} n \) に比例する。
解答2
解答:イ
番兵は線形探索のときに使われます。
「末尾に探したいデータと同じデータ(番兵)」を追加することで、判定条件の1つである「目的のデータかどうか」を省略し、効率よく探索を行うことができます。
解答3
解答:イ
2分探索では、データの個数が2倍になって初めて最大探索回数が1回増えます。
そのため、データの個数が4倍になると最大探索回数は2回となり、答えはイとなります。
解答4
解答:ア
2分探索:データを半分ずつに絞り込めるのでオーダーは \( \log_{2} n \)
線形探索:データを先頭から順番に探すので最大で n 回調べる必要がある。よってコーダーは \( n \)
ハッシュ探索:専用の関数(ハッシュ関数)で求めるので1回で済む。ハッシュの衝突は無視できるのでオーダーは 1 となる。
よって答えはア。
解答5
解答:ウ
選択肢ごとの解説
ア:2分木を用いるのは2分探索。NG。
イ:衝突が発生するのがハッシュ探索法の欠点。NG。
ウ:大正解。関数値によって格納先を決定。
エ:ハッシュ探索は衝突が起こらない限り1回の探索で場所がわかる。よってこれもNG。
解答6
解答:ウ
大きさ10のハッシュ表 → 10箇所入れるところがある
まず、1件目、2件目、3件目のデータを入れたときに衝突する確率を求める
1件目のデータ:10箇所どこに入れても衝突は起こらない。確率は1
2件目のデータ:1件目に入れた1箇所以外なら衝突が起こらないので確率は 9/10 = 0.9
3件目のデータ:1,2 件目に入れた2箇所以外なら衝突が起こらないので確率は 8/10 = 0.8
よって3件データを入れたときに衝突する確率は上の3つの積で求められるので、\[
1 \times 0.9 \times 0.8 = 0.72
\]と求められる。
余談
この問題、メタ読みできる人は
「選択肢ア(0.28)だけやけに小さい確率だな…… もしかして、これ逆の確率(衝突する確率)なのかな…… ってことは答えはウの0.72……??」
と思うのかもしれません……。私は少し疑いました。
8.さいごに
今回は、基本情報にもよく出てくる3つのアルゴリズム(線形探索・2分探索・ハッシュ探索)についてのまとめでした。
探索アルゴリズムの仕組み、使える条件、計算速度の3つが重要なので必ず抑えておきましょう。
関連広告・スポンサードリンク