スポンサードリンク
こんにちは、ももやまです。
今回は「うさぎでもわかるデータ構造とアルゴリズム」の総復習として、C言語における構造体・ポインタ・および各種データ構造の復習問題を作成してみました!
具体的には、
- 基礎的なプログラミング力
- 構造体
- 再帰関数
- ポインタ
- 配列・連結リスト
- 線形探索・2分探索
- スタック・キュー
- 2分探索木
- ソーティング
の復習問題となっております。
試験時間は90分で100点満点で、60点以上が合格です。
試験前や腕試しに是非チャレンジしてみてください!
目次
スポンサードリンク
1.小問集合
(1) 値渡し・参照渡し
つぎのCプログラムの実行結果として正しいものを①〜⑧の中から選びなさい。
マーク番号 :[ 1 ]
int f1(int a, int *b){
a += 10;
*b += 10;
return a;
}
int main(void) {
int a = 10, b = 10, c = 10;
c = f1(a,&b);
printf("%d,%d,%d\n",a,b,c);
return 0;
}
- 10,10,10
- 10,10,20
- 10,20,10
- 10,20,20
- 20,10,10
- 20,10,20
- 20,20,10
- 20,20,20
解答:4
関数 f1 の引数 a は値渡しなので、関数を実行しても値が一切変化しない。(なので10のまま)
一方引数 b はポインタなので参照渡しとなり、関数実行により値が変化する(なので20に変化)
c には戻り値である20が入るので、出力結果として正しいものは4となる。
★コメント★
値渡し、参照渡しの復習でした。
忘れてしまった人や覚えていない人はこちらから復習しましょう。
(2) 再帰関数
関数f2が下のように定義されている。
int f2(int a, int b) {
if(b == 0) {
return a;
}
else {
return f2(b,a % b);
}
}
このとき、f2(180,54) の返り値として正しいものを選びなさい。
マーク番号:[ 2 ]
[選択肢]
- 1
- 2
- 3
- 9
- 18
- 36
- 54
- 180
解答:5
地道に実行結果をたどればよい。
f2(180,54) = f2(54,18) // 180 % 54 = 18
= f2(18,0) // 54 % 18 = 0
= 18
となるので、18が返ってくるのでマーク番号 5 が答え。
★コメント★
再帰関数の復習でした。
忘れてしまった人や覚えていない人はこちらから復習しましょう。
(3) 探索(線形探索・2分探索)
うさぎ塾の生徒1,000人の模試成績が学生番号順に格納されているデータから、データを探し出したい。
[i] 線形探索、2分探索それぞれでデータを探索する際の最大探索回数(目的のデータかどうかをチェックするために必要な最大の回数)として正しいものをそれぞれ下から選びなさい。線形探索:[ 3 ] 2分探索:[ 4 ] [マーク番号3, 4の選択肢]
- 1
- 2
- 8
- 9
- 10
- 100
- 250
- 1000
- 変わらない
- 2倍になる
- 4倍になる
- 16倍になる
- 1回増える
- 2回増える
- 3回増える
- 4回増える
★解答★
[ 3 ]:8(1,000回)[ 4 ]:5(10回)
[ 5 ]:3(4倍になる)
[ 6 ]:6(2回増える)
★解説★
[i]線形探索は、前から順番にデータを探す必要があるので、一番うしろにデータがある場合、1,000回の探索が必要である。そのため、[ 3 ] の答えは8となる。
一方2分探索の場合、データを半分ずつに絞り混むので、n 回の探索で \( 2^{n} \) 個のデータを探すことができる。今回は、1,000個のデータなので、\[
2^{n} \geqq 1000
\]を満たす最小の n が最大探索数となる。n = 10 のときが最小なので[ 4 ]の答えは5となる。
線形探索の場合は前からデータを探すため、データ数が増えると、増えた分だけそのまま時間がかかる。今回は4倍なので、最大探索時間も4倍となる。よって[ 5 ]の答えは3。
2分探索の場合、データ数が2倍になって初めて探索回数が1回増える。そのため、4倍になってもたった2回しか探索時間が増えない。よって[ 6 ]の答えは6。
★コメント★
線形探索、2分探索の復習でした。
できれば「2分探索はデータ量が2倍になると1回増える…」のように丸暗記するのではなく、原理を理解しておくことをおすすめします。
復習はこちらから。
(4) オーダーの基礎
関数 matMul は n 次行列の積を計算する関数である。
void matMul(int a[n][n],int b[n][n], int c[n][n]) {
for(int i = 0; i < n; i += 1) {
for(int j = 0; j < n; j += 1) {
for(int k = 0; k < n; k += 1) {
c[i][j] += a[i][k] * b[k][j];
}
}
}
}
この関数の n に対する計算量(オーダー)として適切なものを選びなさい。
マーク番号:[ 7 ]
[選択肢]
- \( O(1) \)
- \( O(n) \)
- \( O(n^{2}) \)
- \( O(n^{3}) \)
- \( O(2^{n}) \)
- \( O(3^{n}) \)
解答:4
関数 matMul には n 回ループするfor文が3重になっている。そのため、合計で\[
n \times n \times n = n^{3}
\]回ループすることになる。これをオーダー表記にすると \( O(n^{3} ) \) となるので答えは4。
★コメント★
オーダーに関する問題でした。
基本的には最悪計算量(最も時間がかかる場合の計算量の見積もり)の見積もり方を理解していればOKです。
復習はこちらから。
(5) 単純ソート(バブルソート)
関数 bubble_sort は昇順のバブルソートを行うプログラムである。
void bubble_sort(int data[],int n) {
int tmp;
for(int i = 0; i < n - 1; i += 1) {
for(int j = n - 1; j >= i + 1; j -= 1) {
if(data[j-1] > data[j]) {
// 入れ替え始まり(ここが実行される回数は?)
tmp = data[j-1];
data[j-1] = data[j];
data[j] = tmp;
// 入れ替え終わり
}
}
}
}
main関数が下のように与えられているとき、配列aのデータが入れ替わる関数は何回になるか。その回数をマーク番号 [ 8 ] にマークしなさい。
int main(void) {
int a[4] = {2,4,3,1};
bubble_sort(a,4); // [2,4,3,1] を [1,2,3,4] になるようにバブルソート
return 0;
}
解答:4
与えられたバブルソートは「隣り合った要素を後ろから前の順に比較し、隣り合ってなければ入れ替えることで先頭から順に要素を確定させていく」アルゴリズムです。
配列の動きを確認すると、
[2,4,3,1]:スタート [2,4,1,3]:3,1の順番が逆なので交換 [2,1,4,3]:1,4の順番が逆なので交換 [1,2,4,3]:1,2の順番が逆なので交換(1が確定) [1,2,3,4]:4,3の順番が逆なので交換(昇順になったのでこれ以上入れ替わらない)
となるので、4回要素を入れ替わります。
答えは4回なのでマークの答えも4です。
★コメント★
基本的なソートアルゴリズム(バブルソート)の動きを確認する問題でした。
できれば仕組みだけではなく、プログラムまで書けるようになりましょう。
基本的なソートアルゴリズムの復習はこちらから。
(6) 応用ソート(クイックソート)
関数findpivot1, findpivot2はクイックソートのピボット(基準値)を決める関数である。
int find_pivot1(int data[], int left, int right) {
int mid = (left + right) / 2;
return pivot_kouho[mid];
}
int find_pivot2(int data[], int left, int right) {
int mid = (left + right) / 2;
int pivot_kouho[3] = {data[left], data[mid],data[right]};
bubble_sort(pivot_kouho,3); // 昇順ソート
return pivot_kouho[1];
}
ここで、配列を
data[10] = {6, 3, 1, 4, 0, 8, 2, 7, 5, 9}
とするとき、find_pivot1(data,0,9) および find_pivot2(data,0,9) の返り値として正しいものをマークしなさい。
(例:3が返り値だと思ったら3にマーク)
find_pivot1:[ 9 ] find_pivot2:[ 10 ]
★解答★
No.09:0
No.10:6
2つの関数を実行したときの変数の変化をメモしていくと、
int find_pivot1(int data[], int left, int right) {
int mid = (left + right) / 2; // mid = 4
return data[mid]; // data[4] = 0
}
int find_pivot2(int data[], int left, int right) {
int mid = (left + right) / 2; // mid = 4
int pivot_kouho[3] = {data[left], data[mid],data[right]};
// pivot_kouho = [6,0,9]
bubble_sort(pivot_kouho,3); // 昇順ソート // pivot_kouho = [0,6,9]
return pivot_kouho[1]; // pivot_kouho[1] = 6
}
となる。なので、find_pivot1 では0が返され、find_pivot2 では6が返される。
よってマークNo.09の答えは0、マークNo.10の答えは6となる。
ちなみに
find_pivot1:中央にあるデータを返す関数
find_pivot2:配列の先頭、中央、最後尾の中から中央値を選び、返す関数
でした。
応用ソートの1つであるクイックソートのピボットを決める問題でした。
ちなみにクイックソートは、ピボットの決め方によって計算時間が結構変化します。
クイックソートなどの応用ソートの復習はこちらから。
(7) 番兵とは
つぎの探索アルゴリズムの中で、番兵が有効なものはどれか。
マーク番号:[ 11 ]
[選択肢]
- 深さ優先探索
- 線形探索
- 2分探索
- 幅優先探索
- ハッシュ探索
解答:2
番兵は、線形探索
においてあらかじめ目的のデータを配列の末尾につけておくことで探索の効率を上げるテクニックの1つです。
★コメント★
番兵とはなにかを聞く問題でした。
それぞれのテクニックがどのアルゴリズムに使われているかはセットで頭に入れておきましょう。
(8) データ構造の総まとめ
データ構造に関する記述のうち、適切なものはどれか。
マークNo.12
- 2分木は、データ間の関係を階層的に表現する木構造の一種であり、すべての節が二つの子をもつデータ構造である。
- スタックは、最初に格納したデータを最初に取り出す先入れ先出しのデータ構造である。
- 線形リストは、データ部と次のデータの格納先を指すポインタ部から構成されるデータ構造である。
- 配列は、ポインタの付替えだけでデータの挿入・削除ができるデータ構造である。
解答:3
一つずつ選択肢を見ていきましょう。飛びついて1番を選ばないように注意してください。
- 一見正しそうに見えるが、2分木はすべての節が2つ以下の子を持つデータ構造です。なので誤り。
- スタックは最後に格納したデータを最初に取り出すデータ構造です。(選択肢の説明はキューの説明)
- 大正解!
- 連結リストの説明。
★コメント★
データ構造の総復習問題でした。
一見正しそうに見えるひっかけ選択肢を選ばないように選択肢をよく読んでから答えを選びましょう。
スポンサードリンク
2.スタック・キュー
次の(1)〜(3)の問いに答えなさい。
ただし、それぞれの問いにある図のスタック・キューは下から順番にデータが入る。
(1) スタック・キューの基礎
(1) 空の状態のスタックとキューから、次の手続を順に実行していく。このとき、図の
[ 13 ] ~ [ 19 ] に入っているデータの値を解答欄にマークしなさい。ただし、空欄の(何も入っていない)場合は0をマークすること。
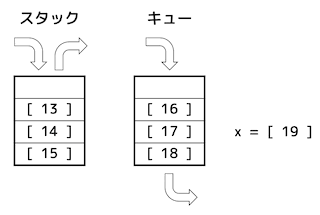
ここで、手続きに引用している関数は、次のとおりとする。
★関数★ ※(2)以降も用いる
push(x):データxをスタックに積む。 pop():データをスタックから取り出して,その値を返す。 enqueue(x):データxをキューに挿入する。 dequeue():データをキューから取り出して,その値を返す。
★手続き★
enqueue(1) push(2) enqueue(3) push(dequeue()) enqueue(4) enqueue(pop()) push(5) enqueue(dequeue()) enqueue(pop()) push(6) x = dequeue()
★解答★
[1点 × 7 = 7点]No.13:0
No.14:6
No.15:2
No.16:5
No.17:3
No.18:1
No.19:4
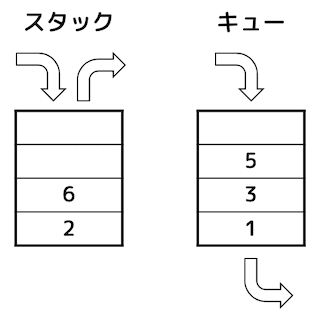
それぞれの手続きごとのスタック、キューの変化を書くと、下の表のようになる。
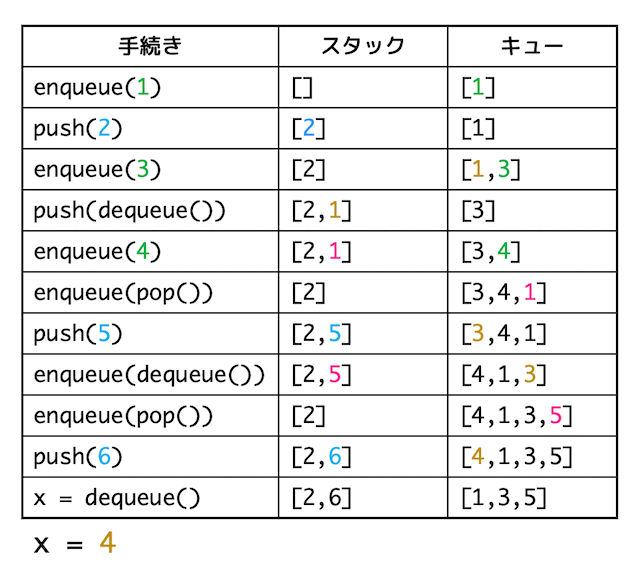
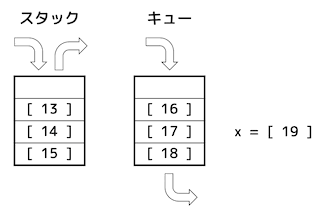
よって、最後の x = dequeue() を実行し終わったときのスタック、キューの中身は下の図のようになり、X の値は4となる。
★コメント★
スタック、キューの操作の過程を答える問題でした。基本情報にも出てくるタイプの問題です。
頭でやるのではなく、落ち着いて1ステップずつ書き出していくことを強くおすすめします。
スタック、キューの復習はこちらから。
(2) スタック・キューの応用
(2) ある状態(空ではない)から次の手続きを順に実行すると、スタック・キューの中身は下の図のようになった。
このとき、X, Y に当てはまるデータの値をマークしなさい。ただし、データの値が確定しないときは0をマークすること。
ただし、*, X, Y には1〜9の値が入り、それぞれの * は違う数字となる。
★手続き★
push(X) enqueue(*) push(*) enqueue(pop()) enqueue(Y) push(dequeue()) a = pop() a = pop() a = dequeue()
★解答★
[3点 × 2 = 6点]No.20:2
No.21:7
(1)と同じように手続きによるスタック、キューの変化を書いていく。
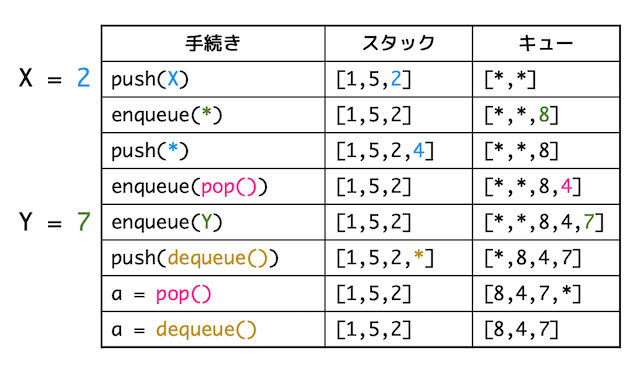
ただし、逆順なので(1)よりも慎重に変化の流れを書いていこう。
すると、X = 2, Y = 7 となることがわかる。
★コメント★
(1)とは異なり、逆順にさかのぼっていく必要があるため、より慎重に1ステップずつ書き出していきましょう。(大切なことなので2回いいました)
(3) スタックを用いたデータ出力
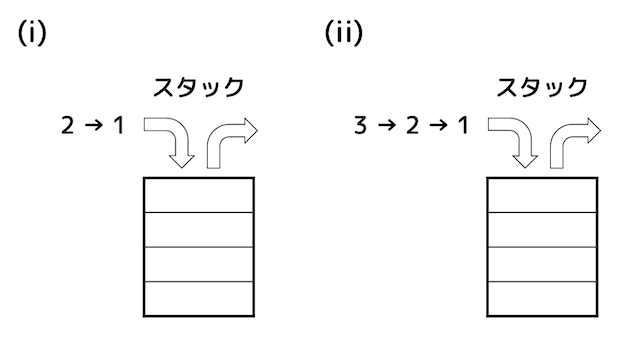
つぎの図で表される2つの順序(i), (ii)で入力されるデータがある。各データについて1回ずつスタックの挿入(push)と取り出し(pop)を行うことができる場合、データの出力順序は何通りあるかをそれぞれマークしなさい。
(i) 1 → 2 [ 22 ]
(ii) 1 → 2 → 3 [ 23 ]
★解答★
No.23:2 [3点]
No.24:5 [4点]
(i)
1→2:スタック、キューを使わずそのまま 2→1:push(1) → push(2) → pop(2) → pop(1)
の2通り。
(ii)
1→2→3:スタック、キューを使わずそのまま 1→3→2:1 →push(2) → push(3) → pop(3) → pop(2) 2→1→3:push(1) → push(2) → pop(2) → pop(1) → 3 2→3→1:push(1) → push(2) → pop(2) → 3 → pop(1) 3→2→1:push(1) → push(2) → push(3) → pop(3) → pop(2) → pop(1)
の5通り。
なお、「3→1→2」を入れて6通りでは? と思った人もいるかもしれません。
しかし、最初に3を出力するためには1, 2, 3を順番に一旦スタックに入れる必要があります。
1 → 2 → 3の順にスタックに入れてしまうと、どうがんばっても2よりも先に1を出力することができません。
そのため、3→1→2 の順に出力することはできません。
★コメント★
スタック、キューの応用問題でした。
この問題が初見で解ければスタック、キューは理解したと思っていただいてOKです。
スポンサードリンク
3.2分探索木
次の(1)〜(2)の問いに答えなさい。ただし、(1), (2)ともに同じデータ値のノードは考えないものとする。
(1) ノードの走査
下図のような2分木の走査順を考える。
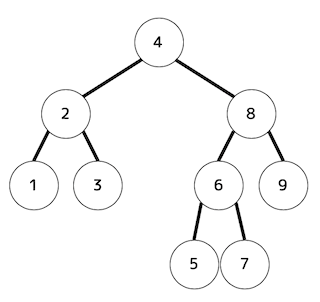
このとき、つぎの[i]〜[iv]の走査方法で、4番目と7番目に走査されるデータの値をそれぞれマークしなさい。
[i] 幅優先探索→ 4番目:[ 24 ] 7番目:[ 25 ][ii] 行きがけ順(先行順)→ 4番目:[ 26 ] 7番目:[ 27 ]
[iii] 通りがけ順(中間順)→ 4番目:[ 28 ] 7番目:[ 29 ]
[iv] 帰りがけ順(後行順)→ 4番目:[ 30 ] 7番目:[ 31 ]
★解答★
[1点 × 8 = 8点]No.24:1
No.25:9
No.26:3
No.27:5
No.28:4
No.29:7
No.30:5
No.31:9
幅優先探索
深さ順に見ていく。(同じ深さは左側優先)
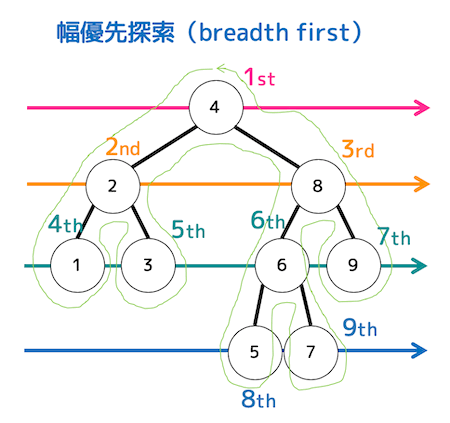
「4, 2, 8, 1, 3, 6, 9, 5, 7」の順に走査するため、4番目は1、7番目は9となる。
行きがけ順(先行順)
ノード→左側→右側の順に見ていく。
ノードを反時計回りに一筆書きしたとき(緑色の線)のノードの左側を通る順番がそのまま行きがけ順となる。
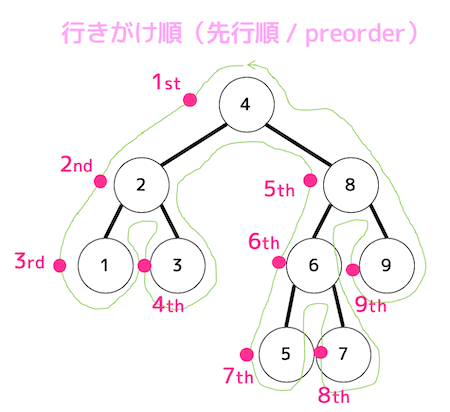
「4, 2, 1, 3, 8, 6, 5, 7, 9」の順に走査するため、4番目は3、7番目は5となる。
通りがけ順(中間順)
左側→ノード→右側の順に見ていく。
ノードを反時計回りに一筆書きしたとき(緑色の線)のノードの下側を通る順番がそのまま通りがけ順となる。
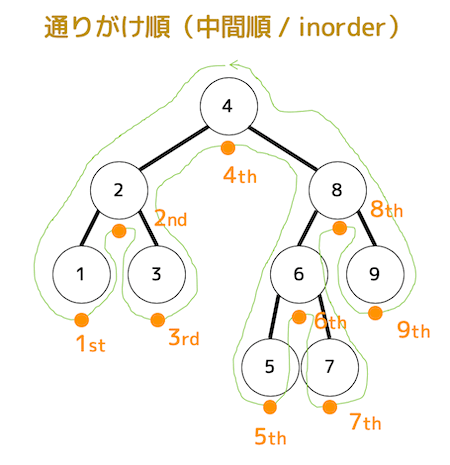
「1, 2, 3, 4, 5, 6, 7, 8, 9」の順に走査するため、4番目は4、7番目は7となる。
(なお、通りがけ順による2分探索木の走査順は、ノードの値を昇順に並べたものと必ず一致します。)
帰りがけ順(後行順)
左側→右側→ノードの順に見ていく。
ノードを反時計回りに一筆書きしたとき(緑色の線)のノードの右側を通る順番がそのまま帰りがけ順となる。
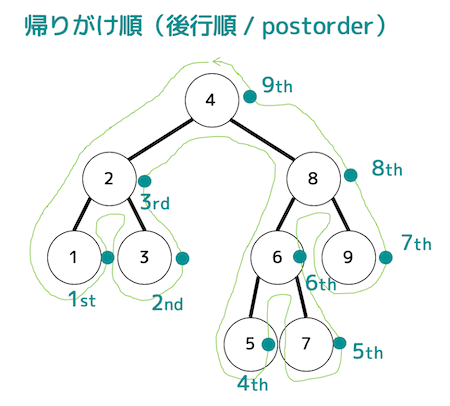
「1, 3, 2, 5, 7, 6, 9, 8, 4」の順に走査するため、4番目は5、7番目は9となる。
★コメント★
2分探索の走査に関する問題でした。
行きがけ順、通りがけ順、帰りがけ順は、解答例のように反時計周りにノードを囲うように一筆書きしてから解いていくことをおすすめします。
2分探索の走査の復習はこちらから!
(一筆書きから行きがけ順・通りがけ順・帰りがけ順を求めるも書いています)
(2) 2分探索木の追加・削除
(2) (1)とは別の下図のような2分探索木(順序木となる2分木)を考える。
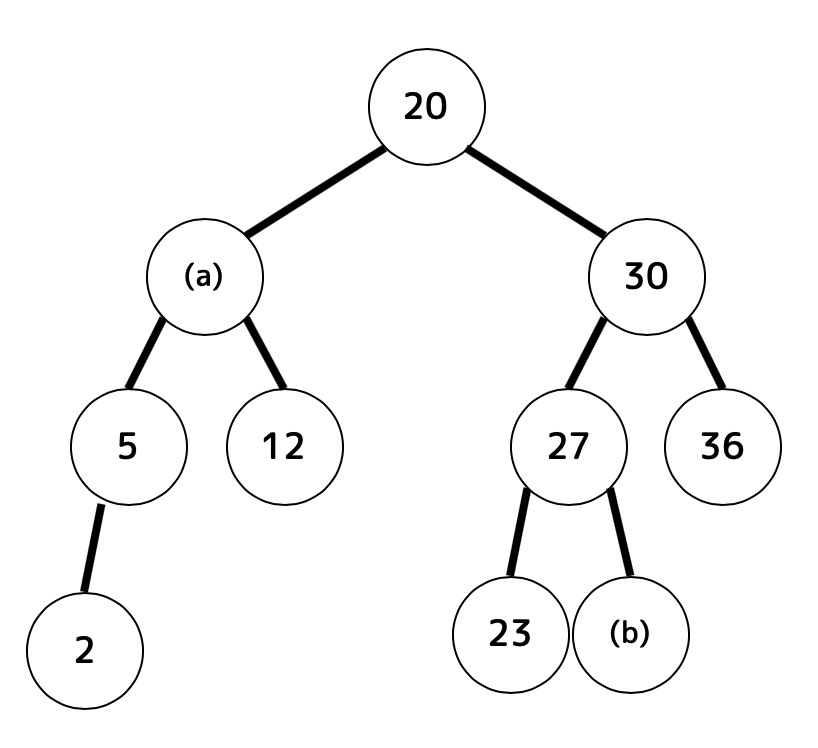
このとき、[i], [ii] の問いに答えなさい。
[i] (a)と(b)に入れられる自然数(1以上の整数)は全部で何通りあるかをマークしなさい。ただし、無限に存在する場合は0をマークすること。(0通りでも0をマーク) [注意:2分探索木内に同じ値のノードは2つ以上含まれない]
(a):[ 32 ] 通り
(b):[ 33 ] 通り
★解答★
[3点 × 2 = 6点]No.24:6
No.25:2
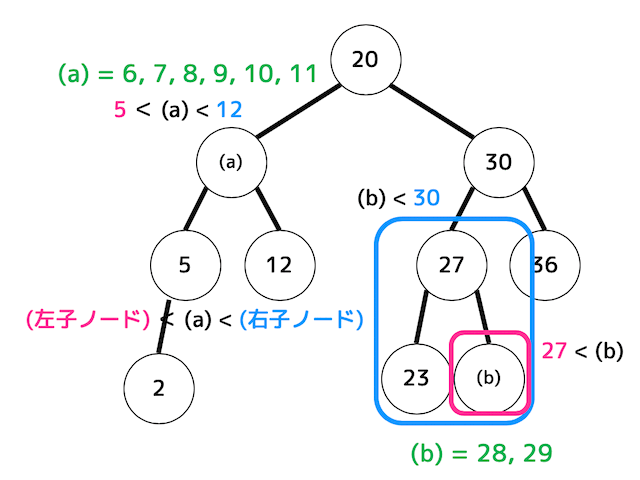
(a)には、左子ノードと右子ノードの2つがある。そのため、必ず(a)の値は「(左子ノード)< (a) <(右子ノード)」となる必要がある。
左子ノードは5、右子ノードは12なので、(a)に入れられる値は 6, 7, 8, 9, 10, 11 の合計6通りである。
(b)は子ノードはないが、30のノードの左部分木なので、「(b) < 30」を満たす必要がある。また、27のノードの右部分木なので、「27 < (b)」を満たす必要である。
よって(b)に入れられる値は 28, 29 の合計2通りとなる。
[ii] 子ノードを持つ親ノードを削除することを考える。このとき、自身以下の部分木から新しく親となるノードを移動させることで順序木を崩さずに2分探索木を構成することができる。
ここで、次の(a), (b)で表されるノードを削除するとき、それぞれどのノードを新しく親にすれば(削除した場所にノードを移動させれば)順序木を崩さずに2分探索木を構成することができるかを下の選択肢の中からすべて選び、該当する番号をマークしなさい。
(a) 5を削除したとき [ 34 ]
(b) 20を削除したとき [ 35 ]
[No.34, No.35の選択肢]
- 2
- 5
- 12
- 23
- 27
- 30
- 36
- [i]の(a)
- [i]の(b)
★解答★
[3点 × 2 = 6点]No.34:1
No.35:3, 4
5のノードには、子が1つなので移動できる候補は1つしか存在しない。
さらに、5のノードの部分木には「2のノード」しかないため、2を移動させるしか方法がない。
よって、[ 34 ] の答えは1だけとなる。
一方20のノードには子が2つあるため、移動できる候補が2つ存在する。
左部分木で一番大きいノードは12、右部分木で一番小さいノードは23なのでこの2つのノードを移動させればよい。
よって、[ 35 ] の答えは3, 4となる。
★コメント★
2分探索木の追加、削除に関する問題でした。
2つ子ノードがあるノードを削除するときが少しややこしいのであやふやな人は復習しましょう。
復習はこちらから。
4.総合問題
某Y音楽能力検定の指導グレードの成績を処理するプログラムを作りたい。
(1)〜(3)の問いに答えなさい。
ここで、指導グレードの成績はソルフェージュ(solf)・鍵盤実技(key)・調音(choon)・楽典(gakuten)・コード(chord)の5つで評価される(成績は0点〜100点の1点刻み)。下の表は、指導グレードの成績の例である。
(1) 構造体
(1) 受験番号をid、名前をname、ソルフェージュの成績をsolf、鍵盤実技の成績をkey、調音の成績をchoon、楽典の成績をgakuten、コードの成績をchordを管理する構造体RESULTを解答欄に記入しなさい。ただし、次の条件に注意しながらデータの型を決めること。
★条件★ ・名前は20桁以内の英数字で管理される。 ・受験番号は必ず数字となり、小数、英字は入らない。 ・各5科目はそれぞれ100点満点で、0〜100点の1点刻みで採点される。
解答
struct RESULT {
int id; // 受験番号
char name[21]; // 名前(20桁 + NULL文字分の配列の領域を取ればOK)
int solf, key, choon, gakuten, chord; // それぞれの成績
}; // セミコロン忘れ要注意
name は、半角20文字だけでなく、NULL文字分1文字を入れて合計21文字分の領域が必要なので注意。
最後のセミコロン ; を忘れる人が多いので要注意!
もしくは、typedef を用いて、
typedef struct result {
int id; // 受験番号
char name[21]; // 名前
int solf,key,choon,gakuten,chord;
// それぞれソルフェージュ・鍵盤実技・調音・楽典・コード進行のスコア
} RESULT;
と書いてもOK*1。
★基準★
最後のセミコロン忘れ:-3
ケアレスミス:-1(変数不足)
型・配列宣言のミス:-2
★コメント★
構造体を作成する基本問題でした。
何度も言いますが、最後のセミコロンを忘れないようにしましょう。
(2) 構造体とプログラミング
(2) 次の[i], [ii]の処理を行う関数を作りなさい。
[i]
構造体 RESULT の変数である r を引数としてとり、rに格納されている5科目の合計点数を出力する関数sum_score。
(ある受験者rの5科目の合計点を出す関数を作ればよい。)
★解答★
[5点]
int sum_score(struct RESULT r) {
return r.solf + r.key + r.choon + r.gakuten + r.chord;
}
構造体の中身を参照するときにはドット . を使います。
例えば、 r.solf とすると、構造体 r の中身 solf (ソルフェージュの点数)の値を取得できます。
[ii] 構造体
RESULT の変数である r を引数としてとり、受験者 r が合格なら1、不合格なら0を返す関数関数 isPass 。(必要ならば関数 sum_score を用いてよい)ただし、合格条件は下の2つの条件を両方満たした場合である。
(ある受験者rの合否を判定する関数を作ればよい。)
★合格条件★ ・それぞれの項目の平均点が75点以上 ・5つの項目のうち、60点未満の項目が1つも存在しないこと 前のページにある表の受験者のうち、合格しているのは受験番号が1番、2番、5番、3番の人である。 (4番は60点未満の科目あり、6番は平均点が75点未満のため不合格)
★解答★
[8点]
int isPass(struct RESULT r) {
if(r.solf < 60 || r.key < 60 || r.choon < 60 || r.gakuten < 60 || r.chord < 60) {
return 0; // どれか1つでも基準点(60点)に満たなければ不合格
}
if(sum_score(r) >= 75 * 5) {
return 1; // 平均75点(合計75*5点)以上あれば合格
}
return 0; // それ以外は平均75点未満なので不合格
}
★採点基準★
おかしい箇所1箇所ごとに:-2
条件分岐に注意しましょう。
- まず、基準点以下であれば不合格
- あとは平均75点(合計375点)以上あるかの判定
と書くのがおすすめです。
★コメント★
ほぼプログラミングができるかどうかの問題でした。
「平均点75点以上=合計点375点以上」と置き換えると、キャストを考えなくていいので楽です。
(3) 探索アルゴリズムの応用
指導グレードの成績が構造体 RESULT の配列で格納されている。ただし、データは全くのランダムな順に並んでいる。(受験番号順でもなく、成績順でもない。)
ここで、ある受験番号 myid が与えられたときに、与えられた myid の受験者が合格しているかどうかを調べたい。
[i] 構造体
RESULT の配列から受験番号 id を探索したい場合、線形探索・2分探索のどちらで行うのが効率的か。理由とともに答えなさい。
解答:線形探索 [2点]
理由:受験番号順の昇順に並んでいないため、2分探索は行えない。また、2分探索ができるようにソートするにも時間がかかるため、最初から線形探索を行ったほうが早くデータの探索ができるから。[3点]
★基準★
- 昇順じゃないから2分探索はできない [2点]
- ソートに時間がかかるから線形探索でやったほうが早い [1点]
線形探索(オーダー:\( O( n ) \))と2分探索(オーダー:\( O( \log n) \))なら、当然2分探索のほうが早いですが、2分探索には探索するデータ(今回は受験番号)が昇順 or 降順に並んでいる必要があります。
今回探索する受験番号は、順番には並んでいないため、ソートを行う必要があります。
しかし、ソートには時間がかかる(最低でも \( O( n \log n ) \) 程度)ので、「ソート」と「2分探索」の両方をする時間よりも「線形探索」だけをする時間のほうが短くなりますよね。
なので、線形探索のほうが効率がよいといえます。
[ii] 構造体RESULTの配列である
r 、r の要素数 n(受験人数)、受験番号 myid を引数としてとり、受験番号 myid の人が合格していれば 1、不合格なら 0、該当する受験番号の人がいなければ -1 を返す関数 check_res を作りなさい。ただし、必要ならば関数 sum_score、関数 isPass を用いても構わない。
(※ [i]で答えた探索アルゴリズム以外を用いても構わない。)
★解答★
[7点]
int check_res(struct RESULT r[],int n, int myid) {
for(int i = 0; i < n; i += 1) {
if(r[i].id == myid) {
return isPass(r[i]); // isPass(r[myid]) をreturnしてもOK
}
}
return -1; // データが見つからない場合
}
採点基準:1ミスにつき-2
ただし、2分探索で書いている場合は5点からスタート。
★コメント★
データ構造で習うアルゴリズムの1つ「線形探索」を実装する少し応用的な問題でした。
この問題が解ければデータ構造とアルゴリズムを理解したと思っていいでしょう!
さいごに
今回はデータ構造とアルゴリズムのスキルチェック問題とその解説を作成してみました。
採点基準が少し雑ですがご了承ください。
60点未満だった人はもう1度復習してからチャレンジしてみましょう!
*1:typedefを用いると宣言のときの struct RESULT の struct を省略することができます。
関連広告・スポンサードリンク