スポンサードリンク
こんにちは、ももやまです。
今回は期末試験や基本情報に頻出する2分探索木について説明していきたいと思います。
目次
スポンサードリンク
1.2分木
2分探索木について説明する前にデータ構造の1つである2分木(木構造)について簡単にですが説明したいと思います。
より詳しい記事はこちらに用意してあるので興味がある人はご覧ください。
(1) 用語復習
まず、2分木で頻繁に出てくる用語の復習をしておきましょう。
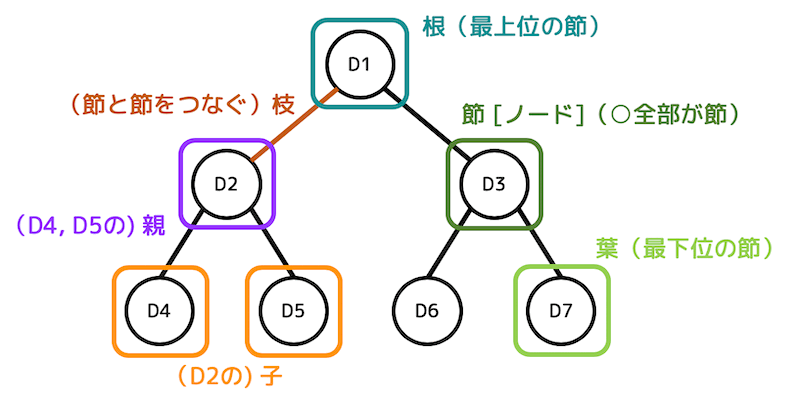
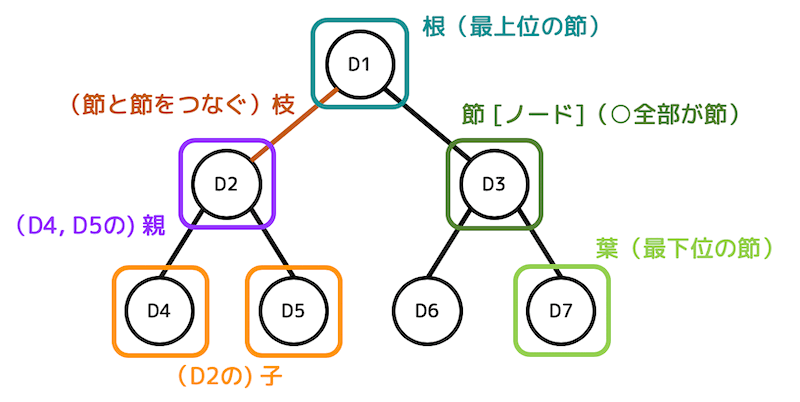
節 [ノード]
○の部分を節もしくはノードと呼びます。上の図の場合、D1〜D7までの節があります。
節には、各種データが入っています。
枝
○と○(節と節)を結ぶ線のことを枝と呼びます。
親・子
あるノード(節)から見て1つ上のノードのことを親、1つ下のノードのことを子と呼びます。
例えば、D2はD4, D5の親、D4(とD5)はD2の子です。
根
最上位のノード(節)を根と呼びます。
親子で表現すると、親を持たないノードが根となります。
葉
最下位のノード(節)を葉と呼びます。
親子で表現すると、子を持たないノードが葉となります。
(2) 部分木
ある節からぶら下がる部分を部分木と呼びます。
節の左側にぶら下がっている部分を左部分木、右側にぶら下がっている部分を右部分木と呼びます。
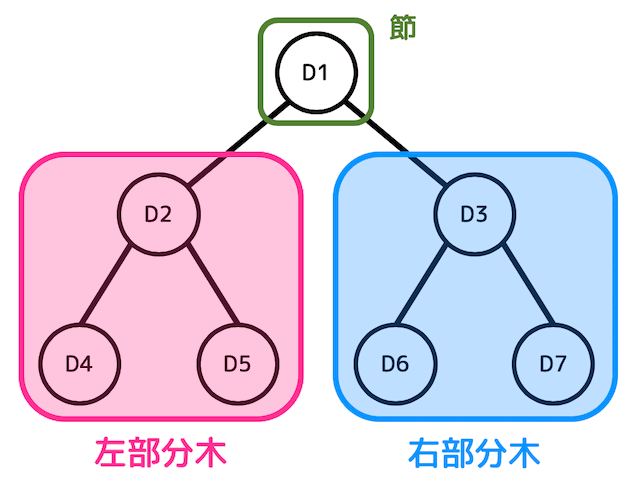
(3) 二分木の表現方法
2分木は、要素 data、あるノードの左の子を指すポインタ left、あるノードの右の子をさすポインタ right の3つで表現することができます。
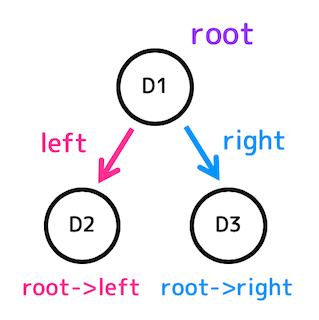
C言語で2分木を表現する場合、下のように定義することで構造体 TREE を用いることができます。
struct TREE {
int data; // 要素
struct TREE *left; // 左の子の場所(ポインタ)
struct TREE *right; // 右の子の場所(ポインタ)
};
スポンサードリンク
2.2分探索木とは
親の左側のノードの値が必ず親よりも小さく、右側のノードの値が必ず親よりも大きくなっている2分木のことを2分探索木と呼びます。
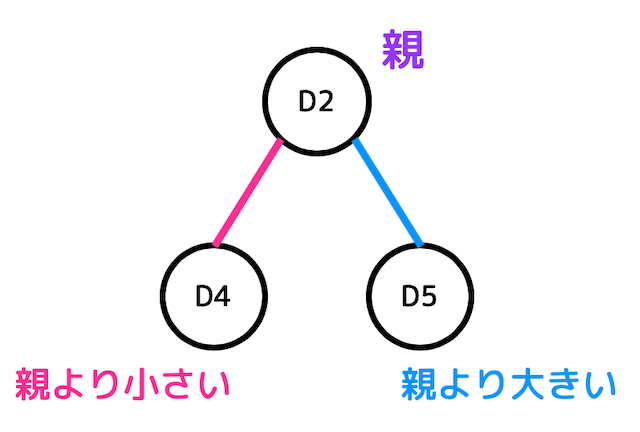
2分探索木では、下の図のようにどの親に対しても値が必ず左の子<親<右の子となっています。
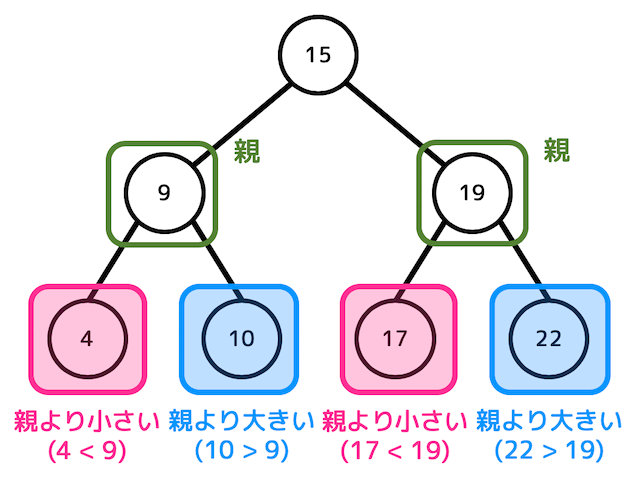
さらに左の子だけでなく、左部分木のすべてのノードの値が親よりも小さくなる特性があります。
右部分木のすべてのノードの値も同様に親よりも大きくなる特性があります。
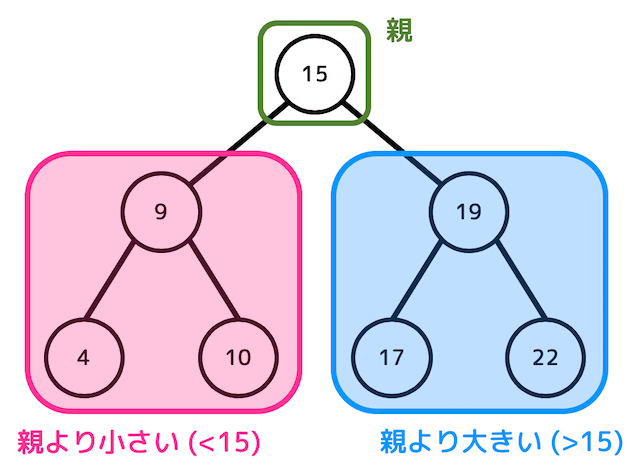
つまり左部分木のそれぞれのノード<親<右部分木のそれぞれのノードの関係も成立します。
よって、上の図にある2分探索木のそれぞれのノードに入る値の範囲は下のようになります。
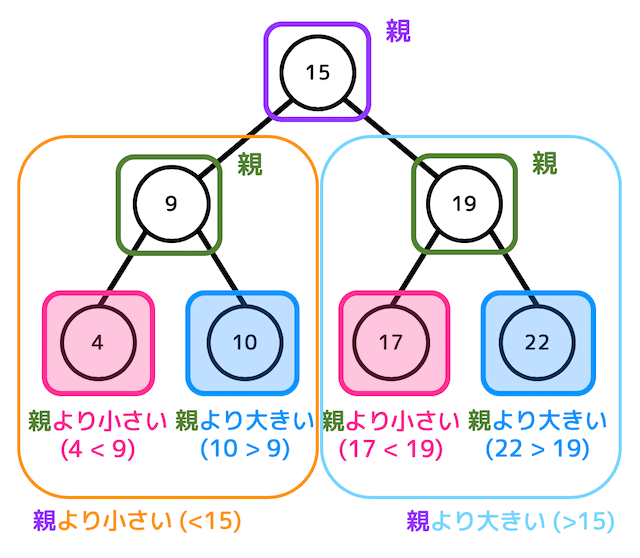
スポンサードリンク
3.2分探索木を用いた探索
2分探索木では、それぞれのノードに対し、「左部分木のそれぞれのノード<基準ノード<右部分木のそれぞれのノード」が成り立つので、データの探索を簡単に行うことができます。
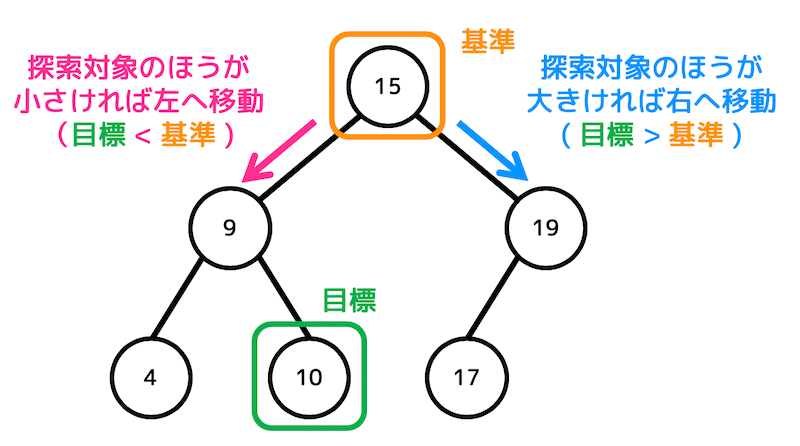
実際に上の木構造から「10が入ったノード」を探してみましょう。
2分探索木による探索は、根からスタートします。なので、最初は根が基準となります。
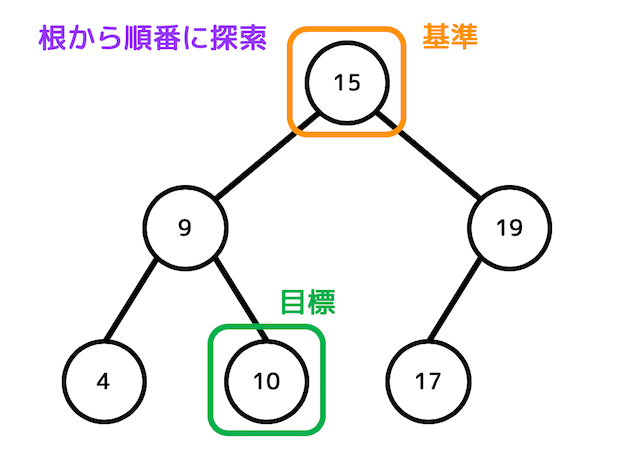
まず、目標データと基準の大小を比べます。
今回は、(目標データ)<(基準)なので、目標データは左部分木にあることがわかります。なので、基準を左に動かします。
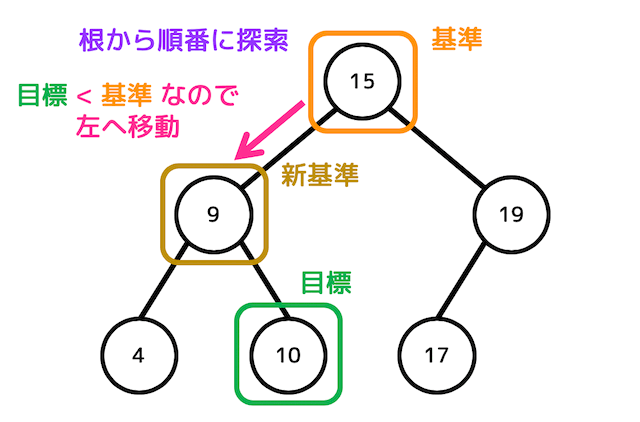
再び、目標データと基準の大小を比べます。
すると、(目標データ)>(基準)なので、目標データは右部分木にあることがわかります。なので今度は基準を右に動かします。
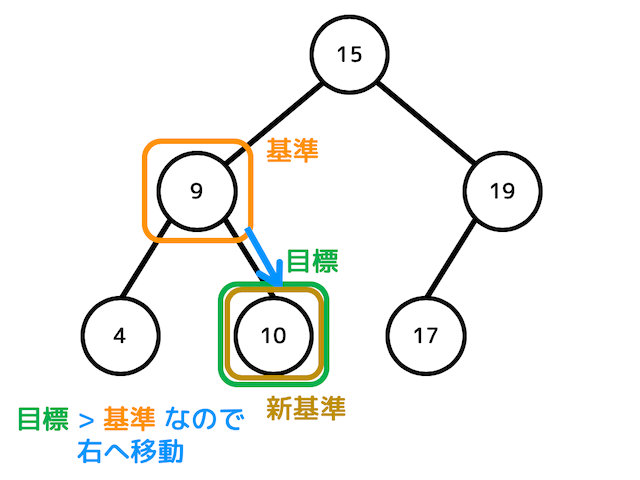
すると、(目標)=(新基準)となるので探索が成功し、探索終了です。
逆に目標データと基準の大小を比べて基準を動かす際に移動するノードが見つからなければ探索失敗となります。
2分探索を行うプログラム
データ x を持つノードを木構造の先頭を持つポインタ *p から探すプログラムは、下のように書くことができます。
// データxをもつノード検索、ポインタを返すので search ではなく *search
struct TREE *search(struct TREE *p, int x) {
while(p != NULL) {
if(x == p->data) {
return p; // データ発見
}
else if(x < p->data) {
return search(p->left,x); // データは左部分木にあり
}
else {
return search(p->right,x); // データは右部分木にあり
}
}
return NULL; // データがなければNULL
}
2分探索木を用いるプログラムでは、再帰処理を行うことがほとんどです。もし、再帰を理解できていない人はこちらの記事で復習しておきましょう。
4.2分探索木のノード追加
つぎは元々の木構造を崩さずに2分探索木にデータを追加する方法について説明したいと思います*1。
下の木構造に「20が入ったノード」を追加してみましょう。
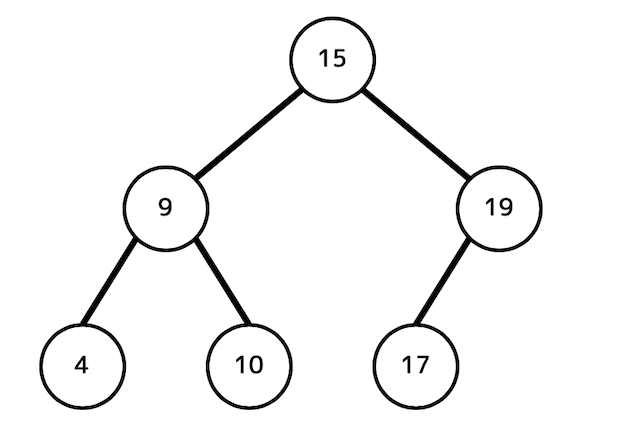
2分探索木に追加する場合も、探索するときと同様に根のノードから順番にチェックしていきます*2。
今回は追加データのほうが大きいので、基準を右に移動します。
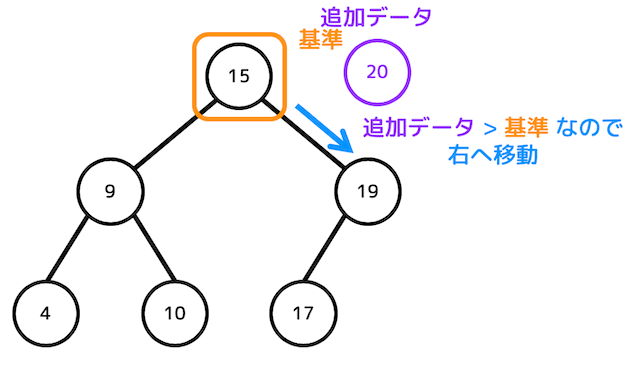
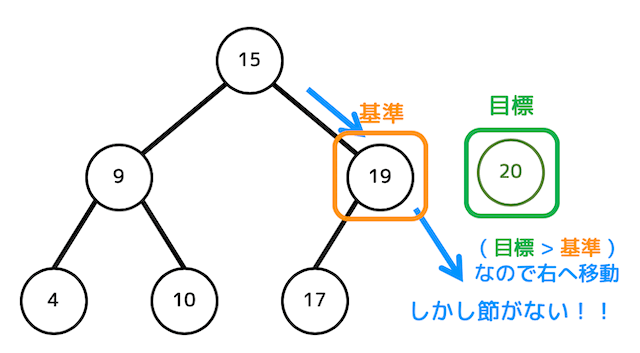
再び追加データと基準データの大小をチェックすると、追加データのほうが大きいので基準を右に移動しようとします。
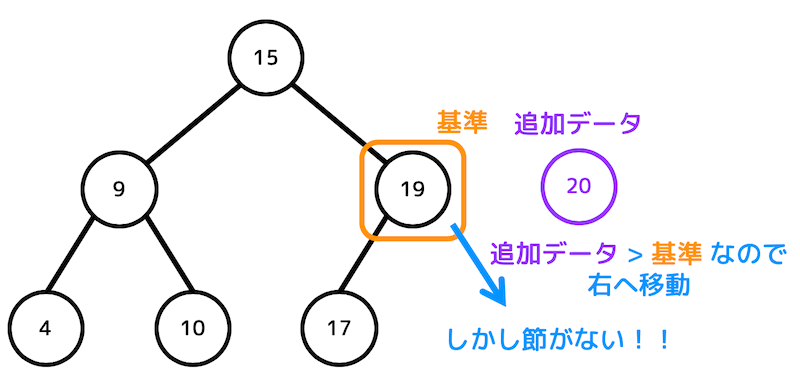
しかし、右側には節がありませんね。
なのでここに20を追加します。
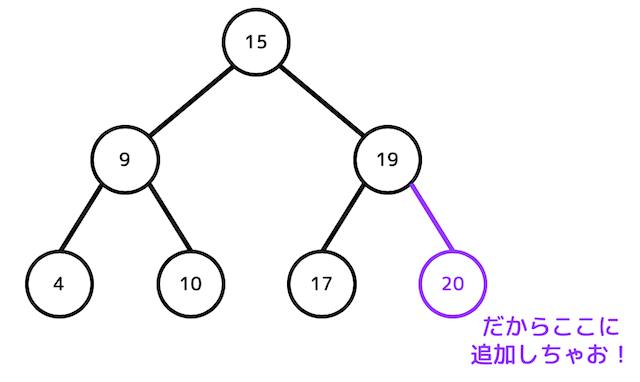
すると、元の形を崩さずにデータを簡単に入れることができますね!
5.2分探索木のノード削除
2分探索木にあるノードをなるべく木構造を崩さずに削除する方法についても説明しておきましょう。
しかし追加のときとは異なり、削除するノードについている子の数によって削除手順が変わります。
(1) 削除するノードに子がないとき(葉の場合)
削除するノードに子がない場合は簡単です。
ノードを削除して終わりです。
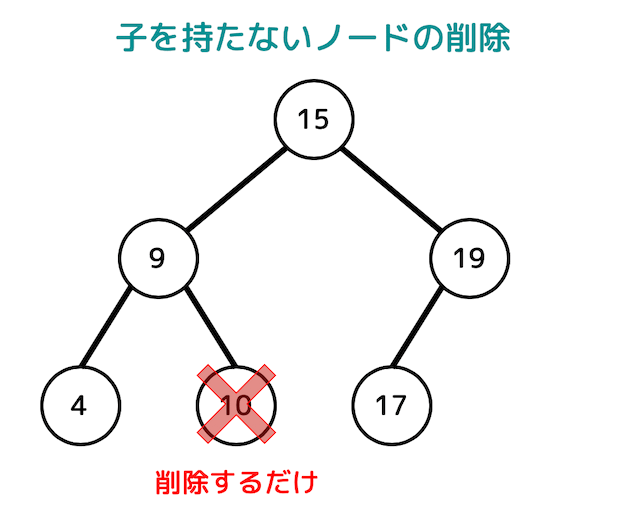
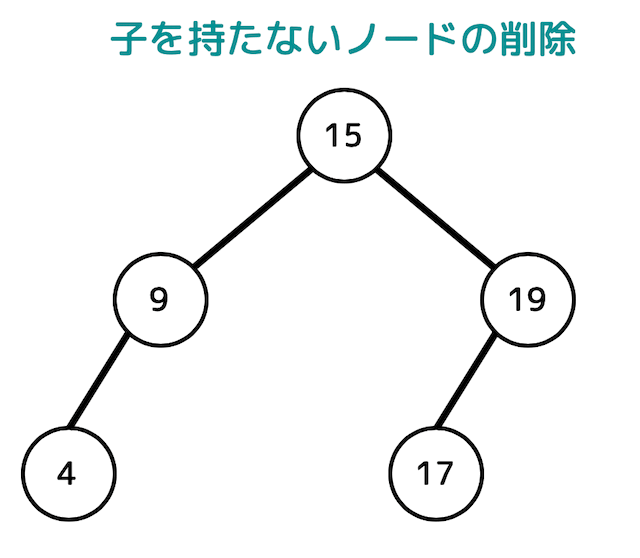
例えば10が入ったノードを削除すると、木構造は下の図のようになります。
(2) 削除するノードの子が1つのとき
削除するノードの子が1つのときは、子がないときに比べて少し処理が複雑になります。
ノードの削除に加え、「削除したノード」の部分木をまるごと元々ノードがあった部分に移動させる必要があります。
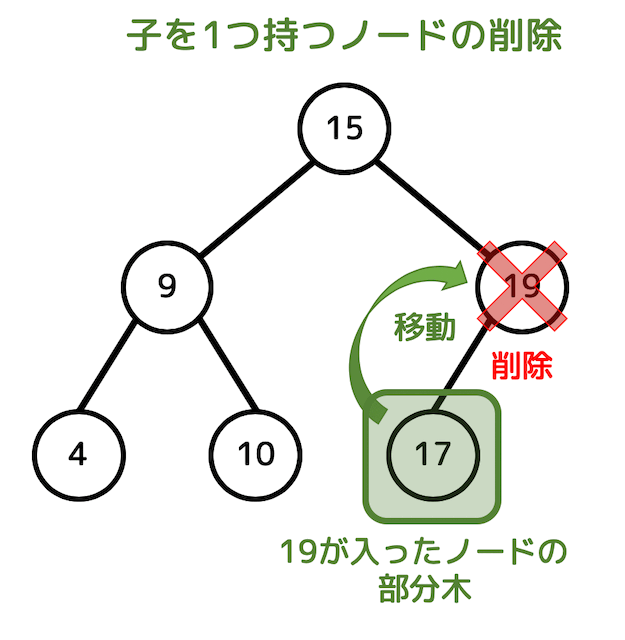
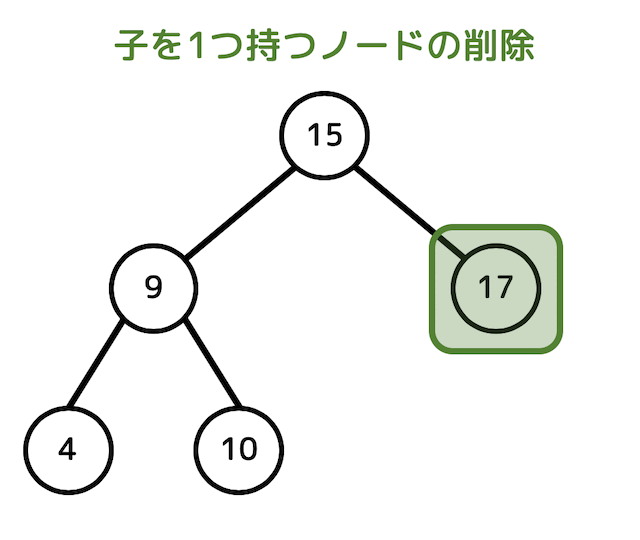
例えば19が入ったノードを削除すると、木構造は下の図のようになります。
(3) 削除するノードの子が2つのとき
削除するノードの子が2つになると、子がないときに比べてさらに処理が複雑になります。
ノードの削除に加え、元々ノードがあった部分に
- 削除したノードの左部分木の最大値(削除したノードの値より1つ小さい値のノード
- 削除したノードの右部分木の最小値(削除したノードの値より1つ大きい値のノード)
のどちらかを移動させる必要があります。
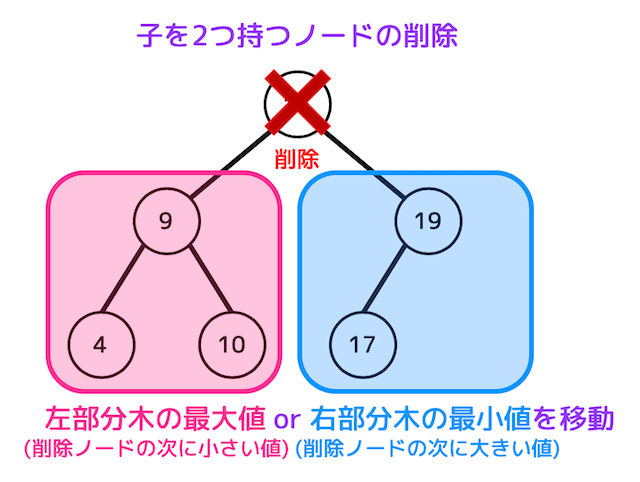
今回は、15が入ったノードを削除する際に右部分木の最小値を交換することにします。
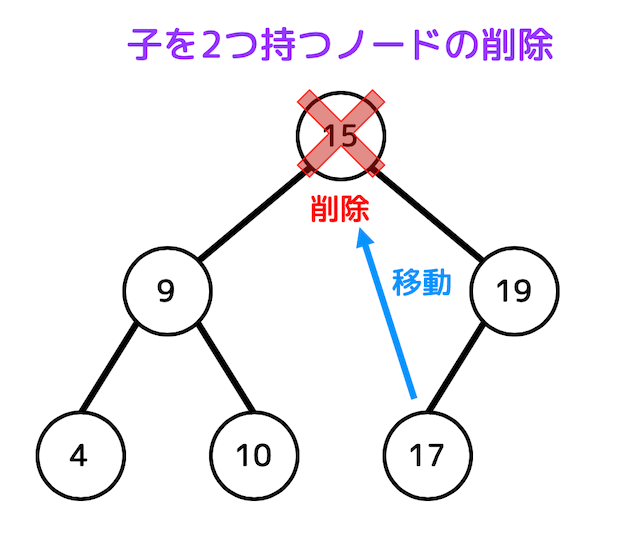
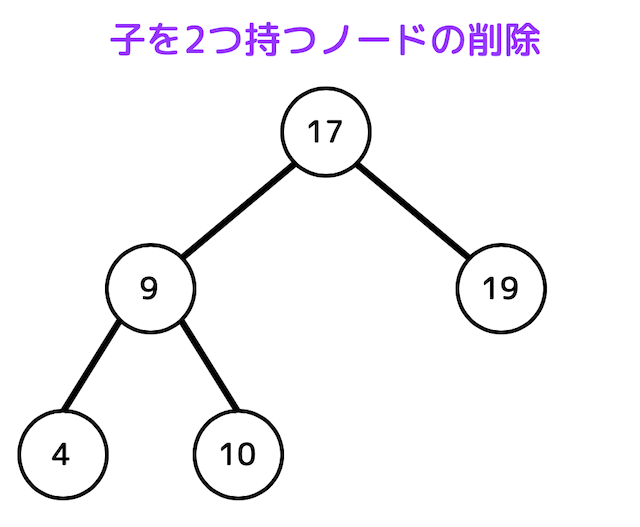
すると、木構造は下のようになります。
6.2分探索木の走査
木構造のすべてのノードを1回だけチェック(訪問)することを走査と呼びます。
走査については下の記事で別に説明しているのでぜひご覧ください。
7.練習問題
では、6問ほど練習しましょう。
後ろの4問は基本情報などの過去問となっています。
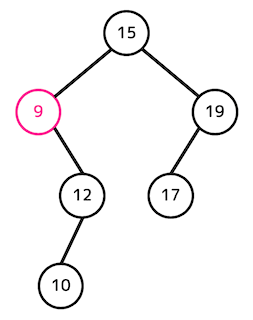
練習1
下の2分探索木から「9が入ったノード」を削除したとき、2分探索木はどうなるかを図示しなさい。
練習2
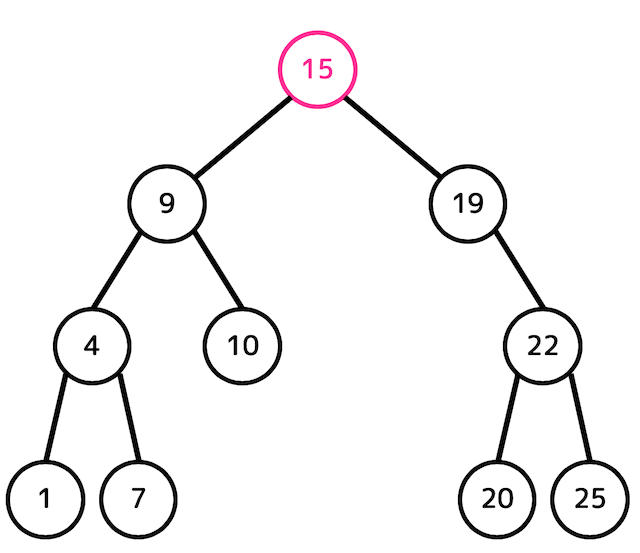
下の2分探索木から「15が入ったノード」を削除したとき、2分探索木はどうなるかを図示しなさい。
ただし、子が2つあるノードを削除したあとは右部分木の最小値を用いること。
練習3
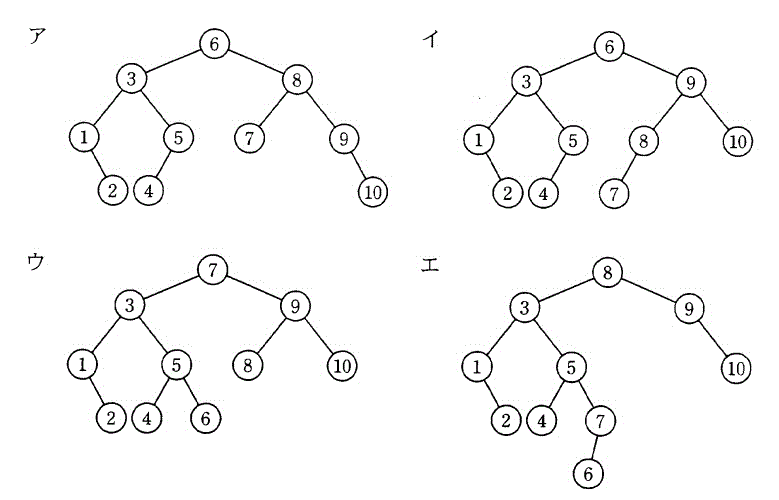
2分探索木になっている2分木はどれか。
[基本情報技術者平成28年秋期 午前問6]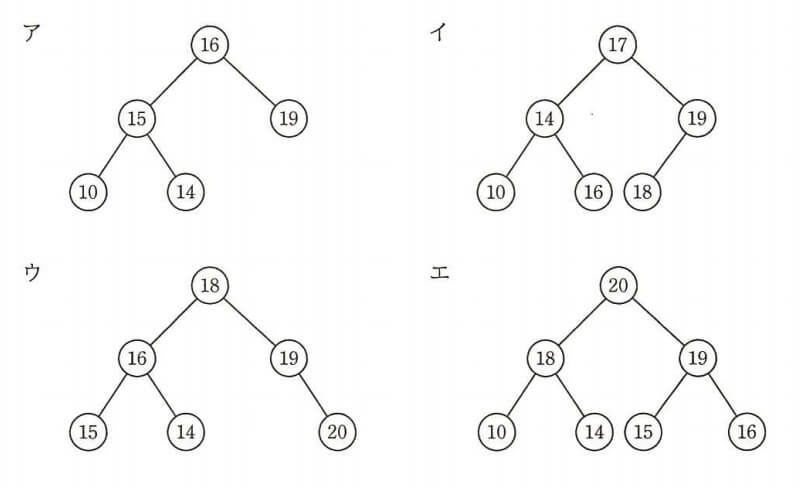
練習4
次の2分探索木から要素12を削除したとき、その位置に別の要素を移動するだけで2分探索木を再構成するには、削除された要素の位置にどの要素を移動すればよいか。
[基本情報技術者平成25年春期 午前問5]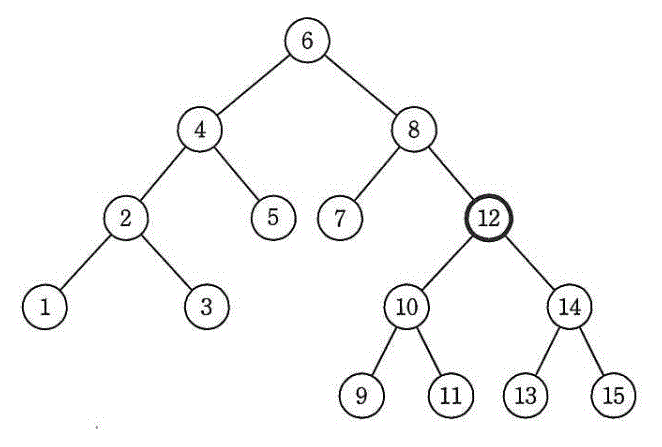
ア:9
イ:10
ウ:13
エ:14
練習5
空の2分探索木に、8, 12, 5, 3, 10, 7, 6の順にデータを与えたときにできる2分探索木はどれか。
[基本情報技術者平成23年特別 午前問5]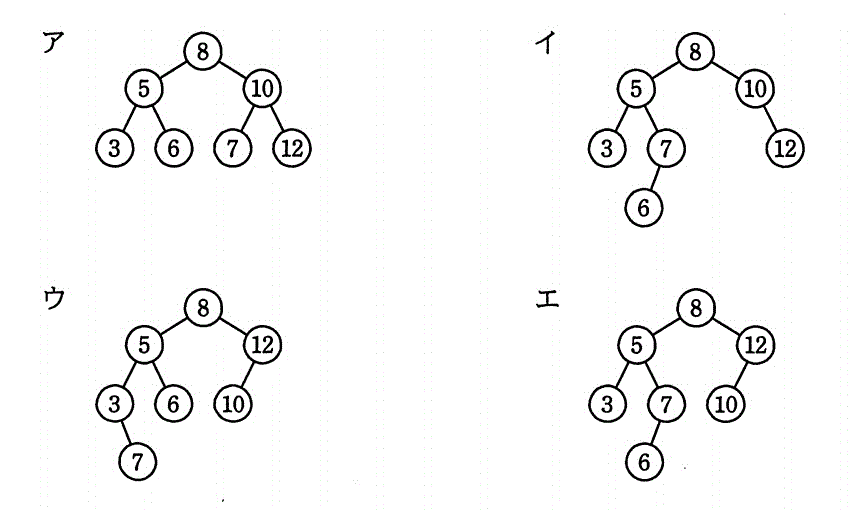
練習6
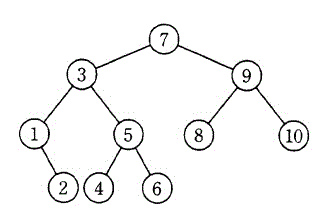
次の2分探索木からルートノード7を削除し、再び7を追加した2分探索木はどれか。
8.練習問題の答え
解答1
まず、9が入ったノードを削除します。
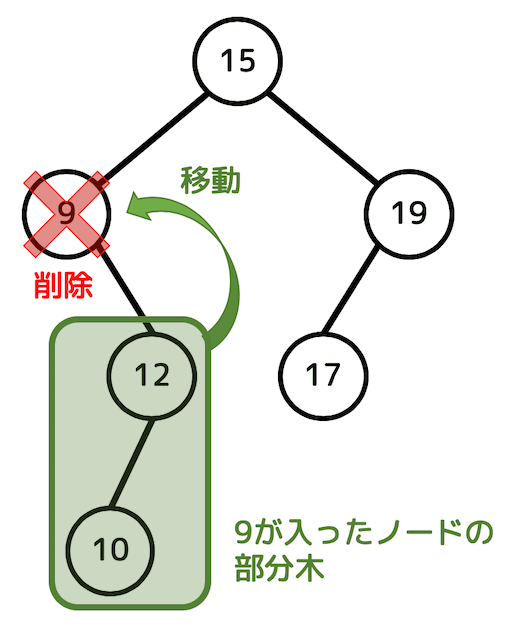
つぎに、9が入ったノードの部分木を丸ごと移動させます。
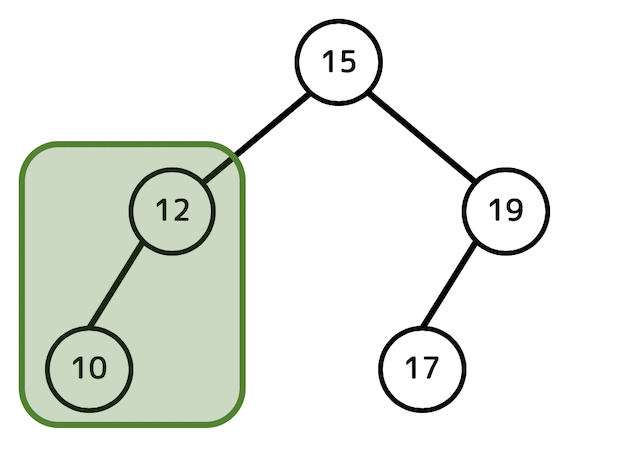
これで削除完了です。
解答2
「15が入ったノード」は子が2つなので、削除したノードの部分に「右部分木の最小値」が移動します。
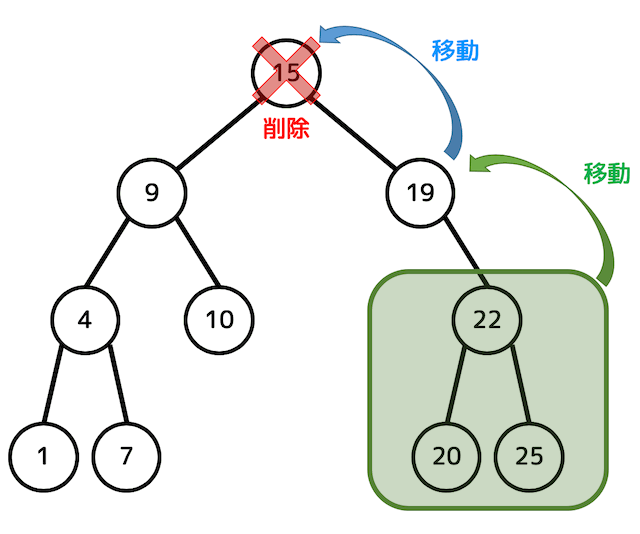
移動するときに19の部分木が崩れないように注意しましょう。
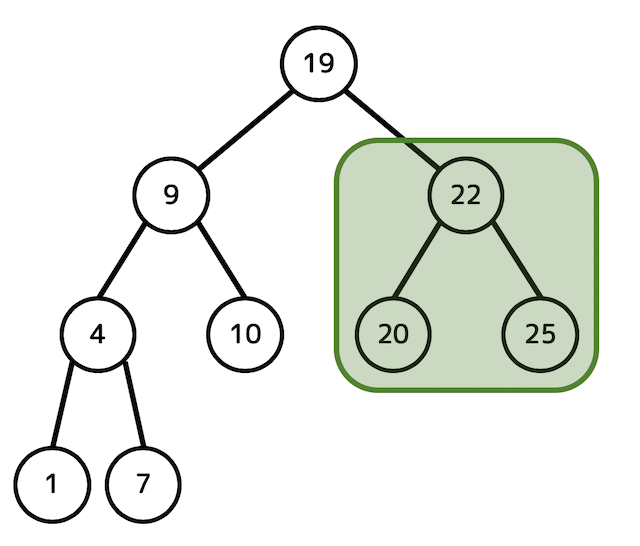
よって「19のノード」を削除したときの2分探索木は上の図となります。
解答3
解答:イ
それぞれのノードを親としたときに、「左部分木のそれぞれのノード<親<右部分木のそれぞれのノード」が必ず成立しているのが2分探索木の特徴です。
イ以外の2分探索木には、値の制約がおかしいノードがあるため誤りです。
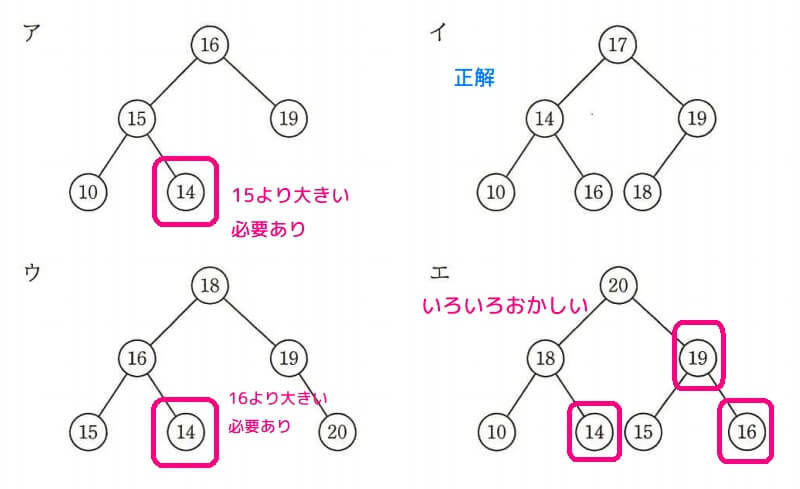
解答4
解答:ウ
12を削除したときに別の要素を移動させるだけで2分探索木を再構築するためには、12より1つ小さい値 or 1つ大きい値を持ってくる必要があります。
1つ小さい値であれば11、1つ大きい値であれば13となるので、選択肢がある13を移動させればよい。
よってウが答え。
解答5
解答:エ
下のような順番で2分木が挿入される。
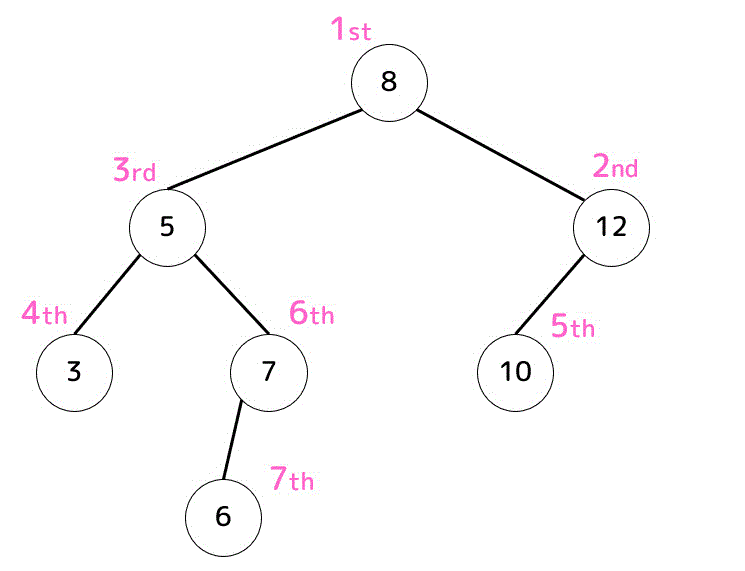
よって、答えはエとなる。
[消去法で解くのもあり]ア・イ:10と12の位置関係がおかしいからダメ
(10を先に挿入しないとこのような形にならない)
ウ:5の左部分木に7が入っているためダメ
(5の左部分木のデータは必ず5未満となるため)
解答6
7が入ったノードは子を2つ持つので削除したときに1つ大きい or 小さい値を削除した位置に持ってくる必要がある。
(この時点でウの選択肢が論外なことがわかる)
6を持ってきた場合
6を持ってくる場合、もともと7があった位置に6を移動させる
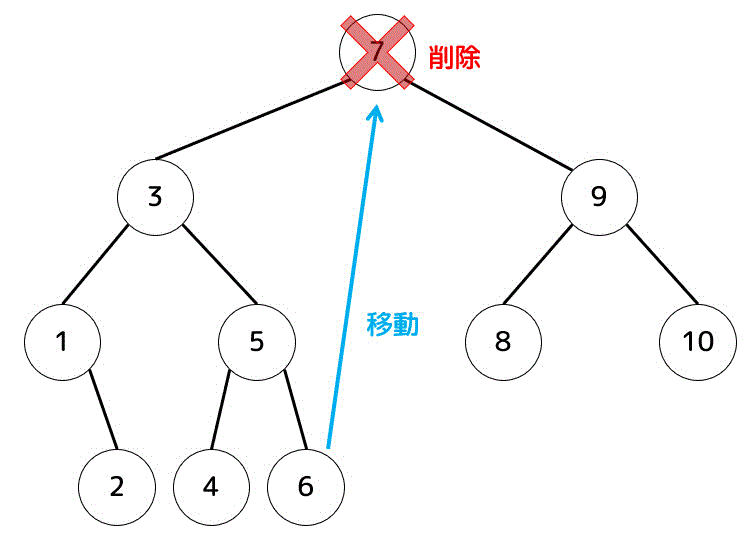
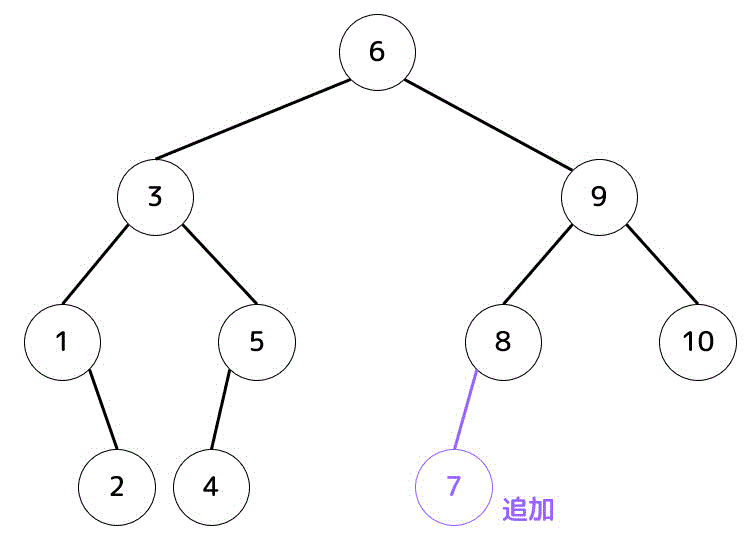
つぎに、消した7を木構造が崩れないように追加する。
8を持ってきた場合
8を持ってくる場合、もともと7があった位置に8を移動させる
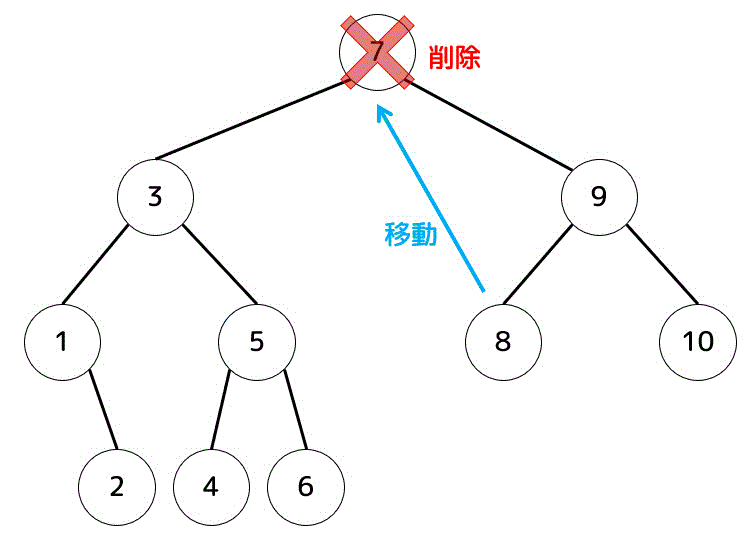
つぎに、消した7を木構造が崩れないように追加する。
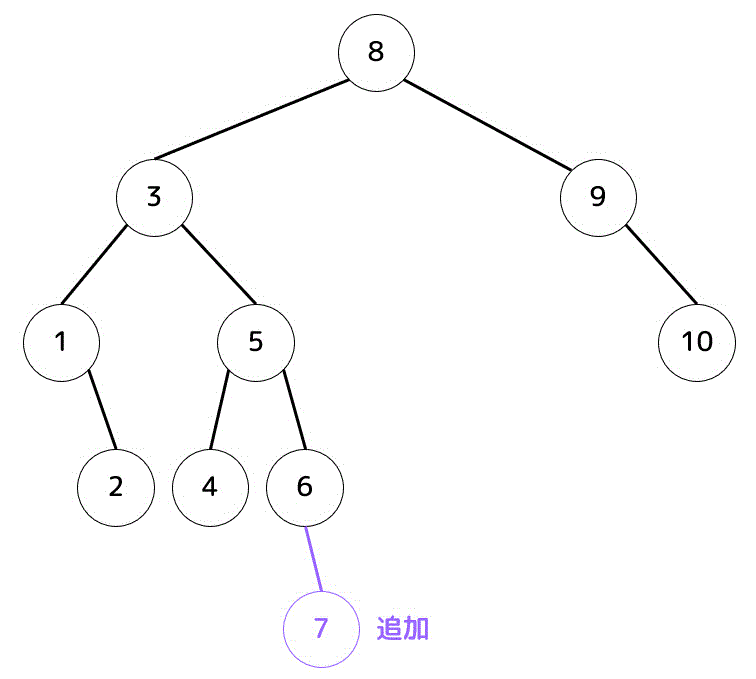
この2つのどちらかが答えとなる。
選択肢イは、6を持ってきた場合の木構造と一致する。よって答えはイ。
9.さいごに
今回は、データ構造の1つである2分木を用いている2分探索木についてまとめました。
2分探索木になっているか判定するだけでなく、要素の追加 or 削除も基本情報ではよく出てくるので確認していきましょう。
2分探索木の走査(列挙)について説明していきたいと思います。
関連広告・スポンサードリンク