スポンサードリンク
こんにちは、ももやまです。
今回もグラフ理論における基本用語をまとめていきたいと思います。
前回の離散数学(グラフ理論)第8羽はこちら!
グラフの基礎1はこちらから!
スポンサードリンク
1.グラフの連結性・連結グラフ
まずは連結グラフと非連結グラフの2つについて説明していきます。
連結グラフ
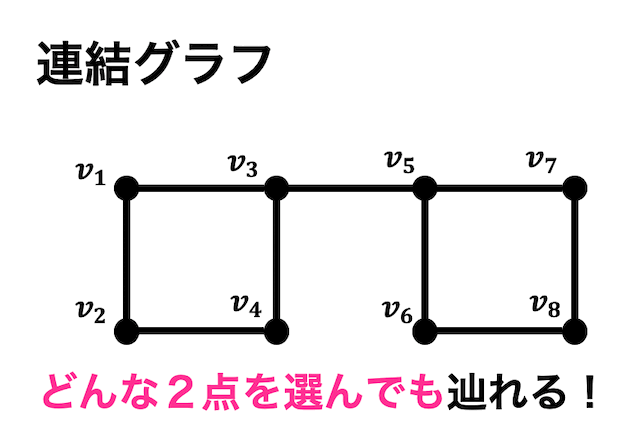
連結グラフは、グラフの中のどのような2点を選んでもたどることができるようなグラフのことをいいます。
厳密にいうと、任意の2点の間に道が存在するようなグラフのことを表します。
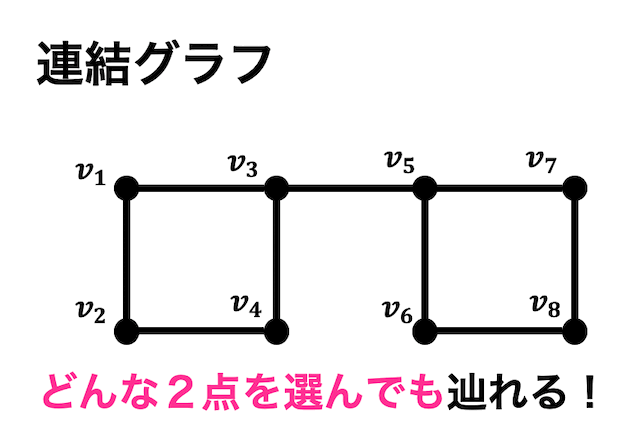
例えば上のグラフの場合、\( v_1 \) から \( v_7 \) のどの2点を選んでも道が存在しますよね(たどることができますよね)。なので連結グラフです。
非連結グラフ
連結グラフではないようなグラフのこと、つまりある2点を選ぶとたどることができないような(ある2点間に道がないような)グラフのことを非連結グラフと呼びます。
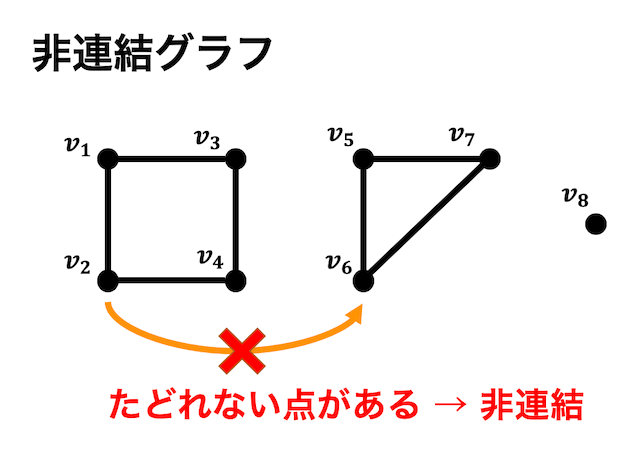
例えば上のグラフの場合、\( v_2 \) から \( v_6 \) までたどろうと思ってもたどることができませんよね*1。なので連結グラフとはいえず非連結グラフとなります。
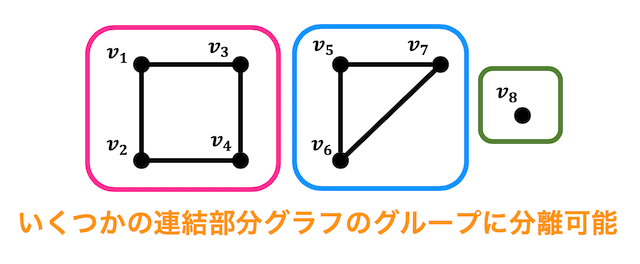
非連結グラフを連結成分からなるグループで分離
非連結グラフはいくつかの連結部分グラフのグループに分割することができます。この連結部分グラフのことを連結成分と呼びます。
先ほどの例でいうと、下のように3つの連結成分に分けることができますね。
関節点
あるグラフにある点の中で、削除すると連結部分グラフのグループが増える点のことを関節点(カット点)と呼びます。
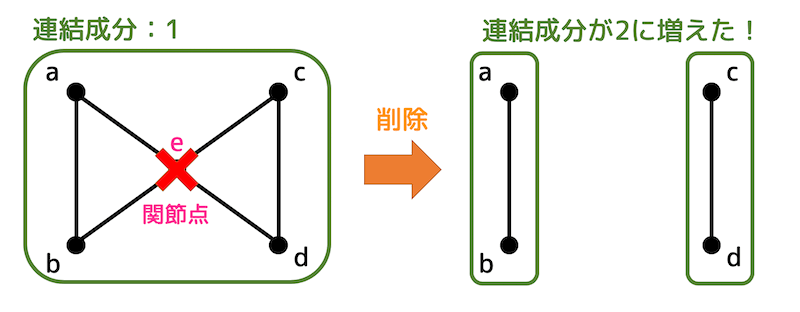
上のグラフの場合、点 \( e \) を削除するとグループ(連結成分)が1つ増えますね。
なので点 \( e \) は関節点と言えます。
橋
関節点の辺バージョンも存在し、削除すると連結部分グラフのグループが増える辺のことを橋(橋辺)と呼びます。
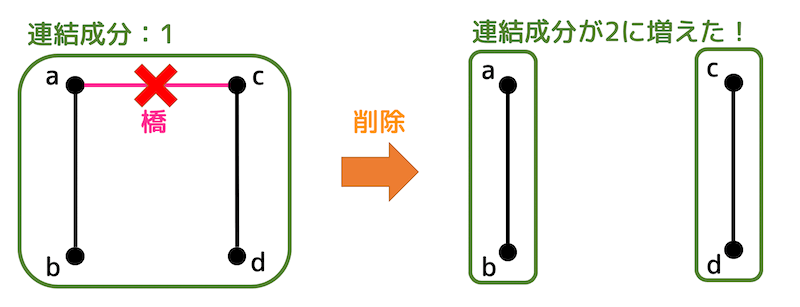
上のグラフの場合、\( a \) と \( c \) を結んでいる辺を削除するとグループ(連結成分)が1つ増えますね。
なので、\( a \), \( c \) を結んでいる辺は橋と言えます。
グラフの連結性やどれくらい強く連結しているか(連結度)については、こちらで詳しく説明しているので、もし興味があればこちらの記事もご覧ください。
スポンサードリンク
2.完全グラフ
(1) 完全グラフとは
どの2点の間にも辺があるような単純グラフのことを完全グラフと呼びます。
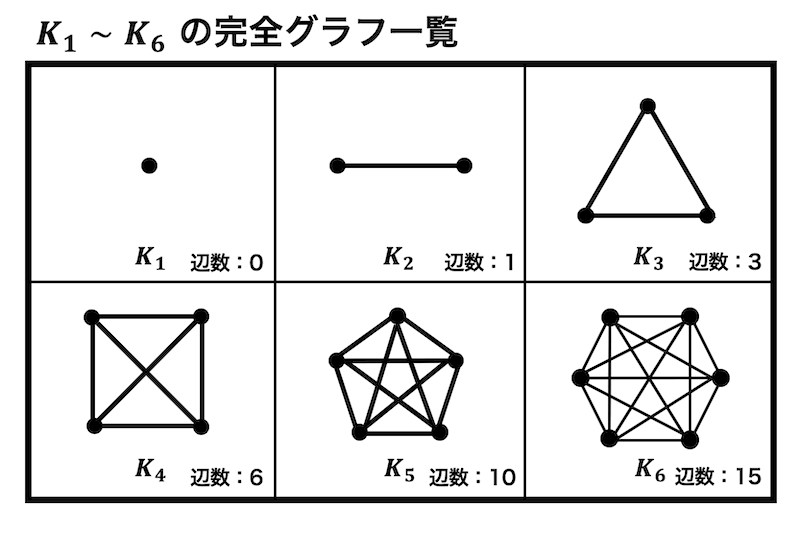
\( n \) 個の点からなる完全グラフのことを記号で \( K_n \) と表します。例えば、3点からなる完全グラフの場合、\( K_3 \) と表します。
\( K_1 \) から \( K_6 \) の完全グラフを下にまとめてみました。
(2) 完全グラフの辺の数
完全グラフの辺の数は簡単に計算をすることができます。
\( n \) 個の点からなる完全グラフの辺の数はどう表されるかを考えてみましょう。
どの2点の間にも辺があるような単純グラフということは、自分以外の点 \( n-1 \) 個すべてに辺があるということですね。
\( n-1 \) 個ずつの辺がそれぞれの点( \( n \) 個)にあるので、合計で \( n(n-1) \) 個の辺が存在しますね。
しかし、無向グラフは向きがないグラフなので、\( a \) から \( b \) という辺と \( b \) から \( a \) という辺で2重にカウントしてしまいます。なので合計の個数から2で割ってあげる必要がありますね。
なので \( n \) 個の点からなる完全グラフ \( K_n \) の辺の個数は\[
\frac{1}{2} n(n-1) = {}_n \mathrm{C} _2
\]個となります。*2。
スポンサードリンク
3.2部グラフ
(1) 2部グラフとは
グラフ \( G \) の点を2つのグループ \( X \), \( Y \) に分けた際に \( X \) 同士の点、\( Y \) 同士の点それぞれに辺がないようなグラフのことを2部グラフと呼びます。
グラフ \( G = (V,E) \) の点集合 \( V \) を2つの部分集合 \( X \), \( Y \) に分割したときにどの辺も \( X \), \( Y \) を結ぶようにできるようなグラフを2部グラフといい、\[
G = (X \cup Y, E)
\]と書く。
(言い換えると \( X \) 同士、\( Y \) 同士で辺を結んでいないようなグラフが2部グラフとなる。)
\( X \), \( Y \) のグループ分けが済んでいる下の2つのグラフを例に説明してみましょう。
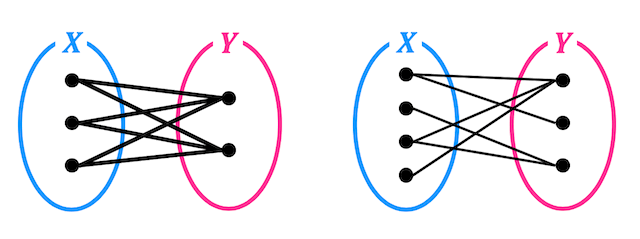
グラフを見ると、\( X \) にある点はすべて \( Y \) にある点とつながっていて(接続していて)、\( Y \) にある点はすべて \( X \) にある点とつながっていますね。
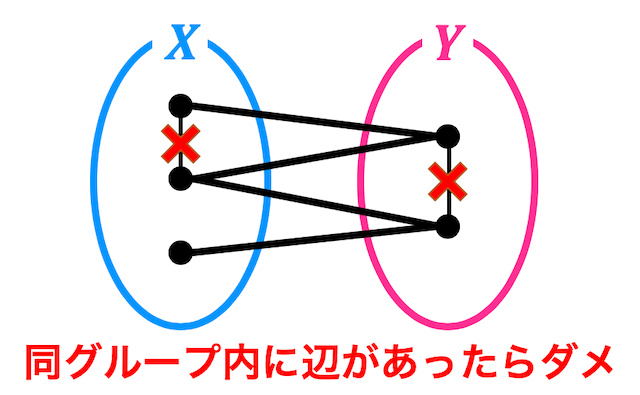
下のように \( X \) 同士の点と接続していたり、\( Y \) 同士の点と接続しているようなグラフは2部グラフと呼べません。
(2) 2部グラフの判定方法
与えられたグラフが2部グラフかどうか判定する方法は簡単です。
下の2つのグラフで試してみましょう。
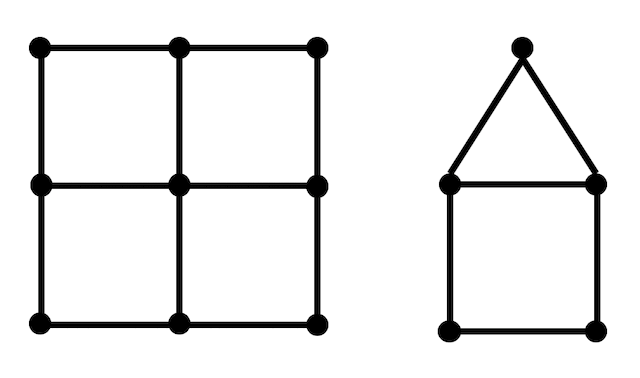
2部グラフは、2つのグループ \( X \), \( Y \) に分けた際に \( X \) グループ同士、\( Y \) グループ同士で辺がないようなグラフでしたね。
つまりそれぞれの点を2つのグループ(0,1と分けるのをおすすめします)にわけて、すべての点が同じグループ同士の点と隣接しなければ2部グラフということができるのです!
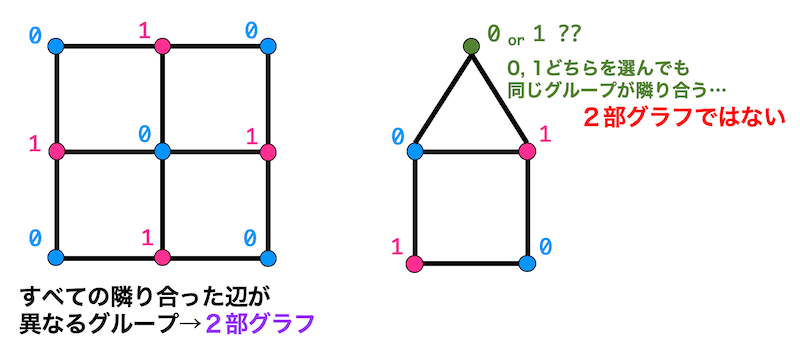
左上のグラフの場合、隣り合ってるすべての点同士が異なるグループになっていますよね。なので2部グラフということができます。
しかし、右上の場合、緑色の部分の点をどちらのグループに分けたとしても同じグループ同士で隣接してしまう点が出てしまいますね。なので2部グラフということができません。
(3) 2部グラフと閉路の長さ
実は2部グラフであるための条件は前回紹介した閉路の長さと関係しているのです。
グラフ \( G \) のすべての閉路の長さが偶数であれば、\( G \) は2部グラフである。
言い換えると、グラフ \( G \) に長さが奇数である閉路が1つでもあれば \( G \) は2部グラフではない。
先ほどの2つのグラフをみてみましょう。

左側のグラフには閉路の長さが奇数である閉路がありませんね。なので2部グラフと言えます。
一方、右側のグラフには長さが3の閉路(三角部分)がありますね。なので2部グラフとは言えません。
(4) 2部グラフと彩色数
あるグラフの頂点を隣に同じ色が来ないように色分けするために必要な色の最低数のことを彩色数といいます。
実は2部グラフであれば、必ず2色で頂点を色分けすることができるのです!
(2部グラフの判定方法で0, 1を書く代わりに青・赤で塗り分けることを考えればOK)
グラフの彩色について詳しく知りたい人はこちらの記事をご覧ください!
(頂点の彩色・辺の彩色両方載せています!)
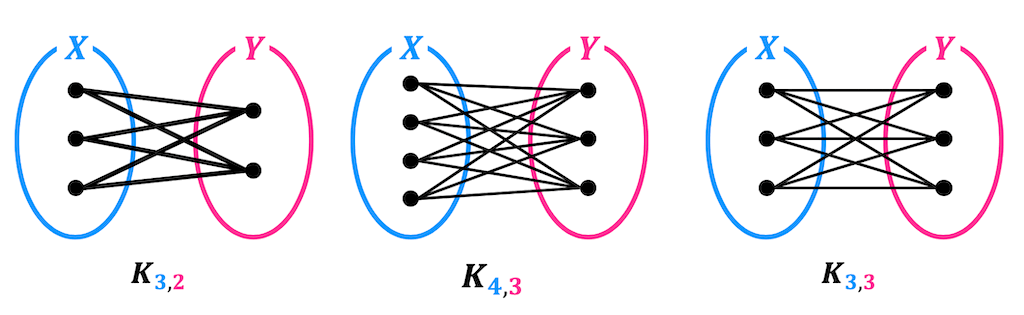
4.完全2部グラフ
(1) 完全2部グラフとは
2部グラフの中でも \( X \) のすべての点と \( Y \) のすべての点を結ぶような辺が全部あるようなグラフのことを完全2部グラフと呼びます。
\( X \) の点の数が \( m \)、\( Y \) の点の数が \( n \) のときの完全2部グラフを記号で \( K_{m,n} \) と表します。
下に完全2部グラフの例を3つ示しておきます。
(2) 完全2部グラフの辺の個数
完全2部グラフの辺の数も簡単に計算をすることができます。
\( X \) の点 \( m \) 個、\( Y \) の点 \( n \) 個からなる完全グラフの辺の数はどう表されるかを考えてみましょう。
完全2部グラフは、\( m \) 個ある \( X \) のすべての点と \( n \) 個ある \( Y \) のすべての点を結ぶような辺が全部あるようなグラフでしたね。
\( X \) を基準に考えましょう。それぞれの \( X \) 上の点 \( m \) 個に対し、\( Y \) のすべての点 \( n \) 個に辺を接続していますね。なので、\( m \) 個に対して \( n \) 通りの辺がありますね。
よって、\( X \) の点 \( m \) 個、\( Y \) の点 \( n \) 個からなる完全グラフの辺の数は \( mn \) 個となります。
5.同型グラフ
(1) 同型とは
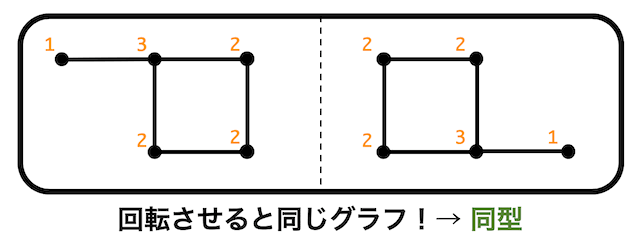
グラフの見た目が違っていても、回転、変形などを駆使することでもとのグラフと同じ形になるようなグラフのことを同型グラフ(同形グラフ)と呼びます。
例えば、下の2つのグラフは180°回転させると同じグラフになりますよね。なので同型です*3。
しかし、この2つのグラフだとどうでしょうか。
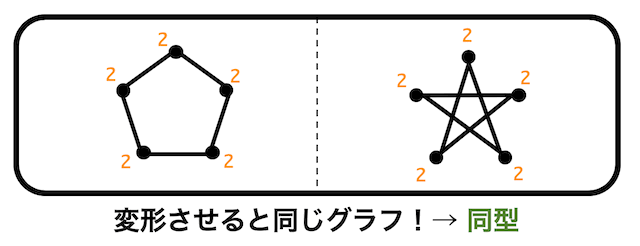
見た目が全然違うので同型には見えませんね。しかし、
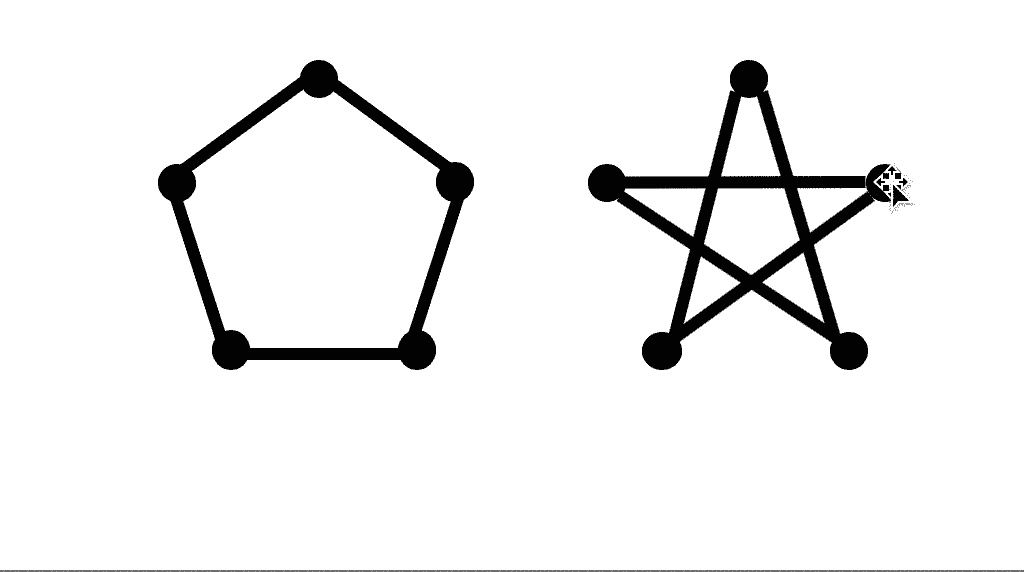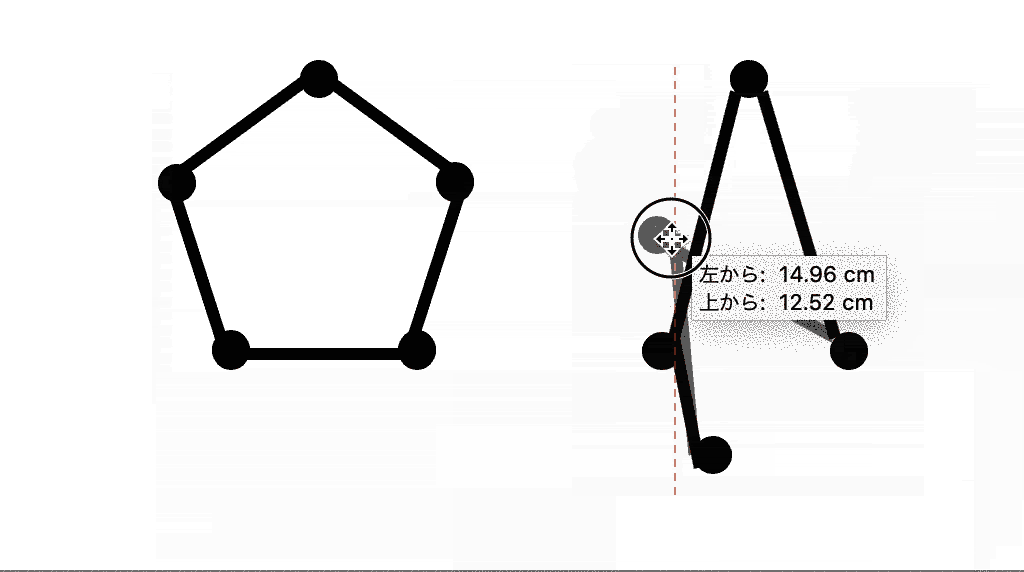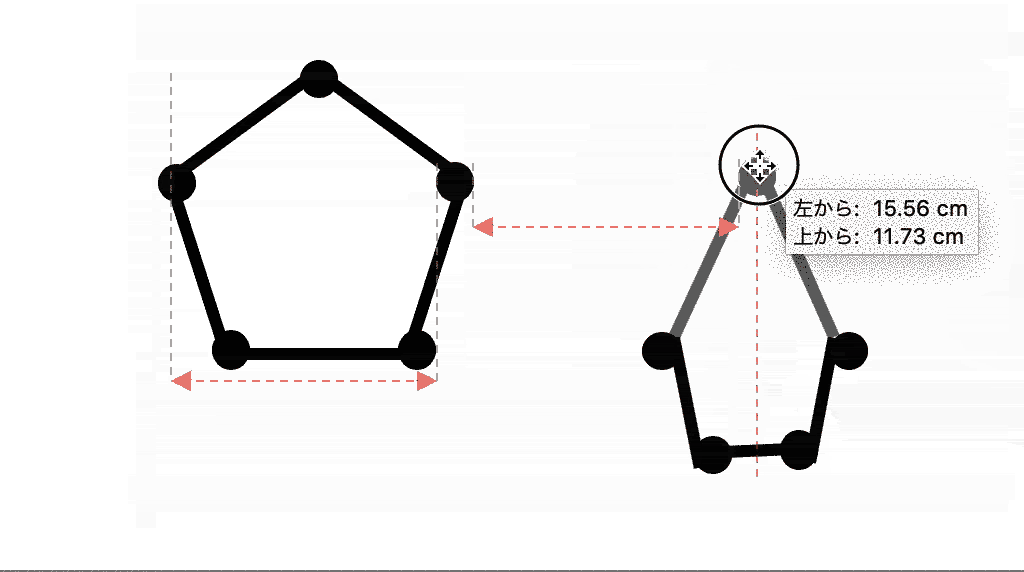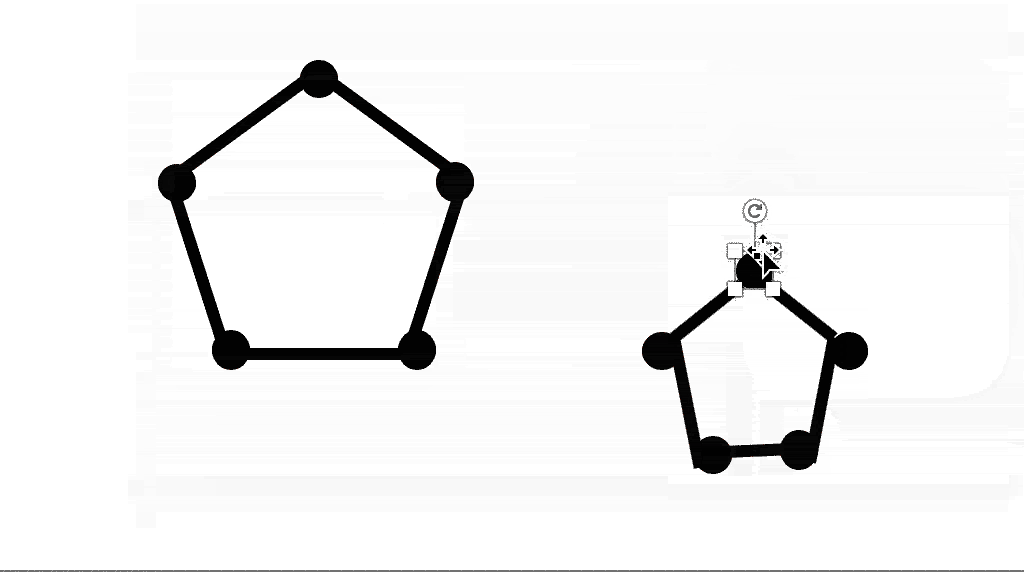
このように変形をさせると左側のグラフと一致させられますね。
なので同型です。
一応同型の厳密な定義もみてみましょう。
グラフ \( G_1 = (V_1,E_1) \)、グラフ \( G_2 = (V_2,E_2) \) に対し、任意の2つの頂点 \( u,v \in V_1 \) に対し、隣接関係\[
(u,v) \in E_1 \Leftrightarrow ( f(u),f(v) ) \in E_2
\]となるとき*4、\( G_1 \) と \( G_2 \) は同型であるという。さらに写像(関数) \( f \) を同型写像と呼ぶ。
さらに、同型であるグラフには下のような関係も成り立ちます。
同型であるグラフは必ず辺の数、点の数が等しい。
ただし、辺の数、点の数がともに等しくても同型であるとはかぎらない。
必要十分条件を用いて表すと、2つのグラフの辺の数、点の数が等しいことは同型であることの必要条件である(十分条件とはならない)。となります。
(2) 同型の判定法のコツ
見た目からあるグラフが同型かどうかわからないようなグラフについては同型かどうか判定するのに少しテクニックがいります。
例えば次の2つの図形が同型かどうかを調べてみましょう。
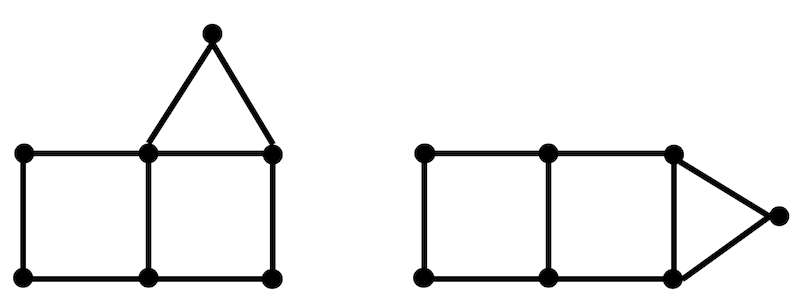
Step1:辺の数、点の数を確認
まず辺の数、点の数を確認します。2つのグラフでどちらか一方でも異なった場合は同型ではありません。
今回の場合、左のグラフ、右のグラフともに点が7個、辺が9個なので同型の可能性が残っています。
Step2:それぞれの次数が何個ずつあるのかを確認(次数列の確認)
つぎにそれぞれのグラフにおいて、各点における次数が何個ずつあるのかを確認します。
確認する際には次数列*5を列挙するのがおすすめです。
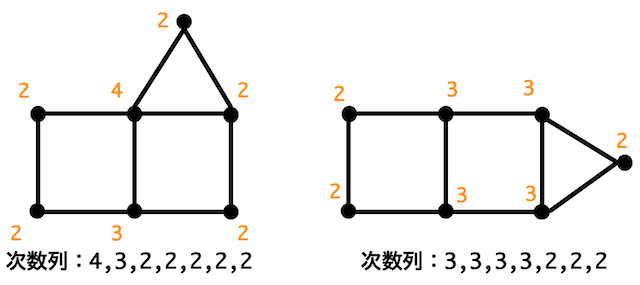
今回のグラフの場合は、次数列が
左:4,3,2,2,2,2,2
右:3,3,3,3,2,2,2
となり、次数列が異なるので2つのグラフは同型ではないことがわかります。
もう1つ別のグラフで試してみましょう。
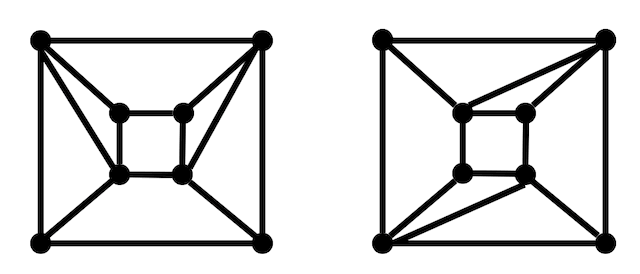
この2つが同型かどうかを調べてみましょう。
Step1:辺の数、点の数を確認
ともに点が8個、辺が12個なのでOK。
Step2:次数列を確認
次数列もともに 4,4,4,4,3,3,3,3 になるのでOK。
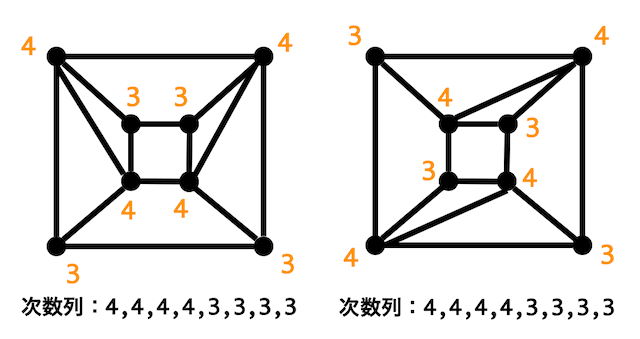
しかし、ここまで調べても同型かどうかはわかりません。
Step3:同じ次数の点の隣接する点の次数の組み合わせをチェック
2つのグラフはともに次数4の点が4つ、次数3の点も4つありましたね。
なので次数ごとに隣接する点の次数の組み合わせをチェックします。
今回の場合、左側のグラフの次数4の点に注目すると、4つとも次数4の点2つと次数3の点2つと隣接しています。しかし、右側のグラフの次数4の点に注目すると、4つとも次数4の点1つと次数3の点3つと隣接していますね。
なので同型ではないことが示せましたね。
このように同型かの判断は3ステップで行うことができるのです。
今の3ステップをまとめてみましょう。
つぎの手順で同型かどうかを判定すると、比較的早く同型かどうかを見つけられる。
(順番にチェックしていって、該当しないものがあった時点で同型ではないことがわかる)
- それぞれのグラフの点の数、辺の数が同じかを確認。
- それぞれのグラフの次数列が同じになるかを確認。
(次数列ではなくても、それぞれの次数が何個あるかを確認して2つの次数で完全一致するかどうかを確認すればいい。) - 同じ次数の点に対して、それぞれの点に隣接する点の次数を比べて一致するかを確認
(基本的に同型ではないグラフのほとんどは2までで判明するはずです)
同型の判定
6.正則グラフ
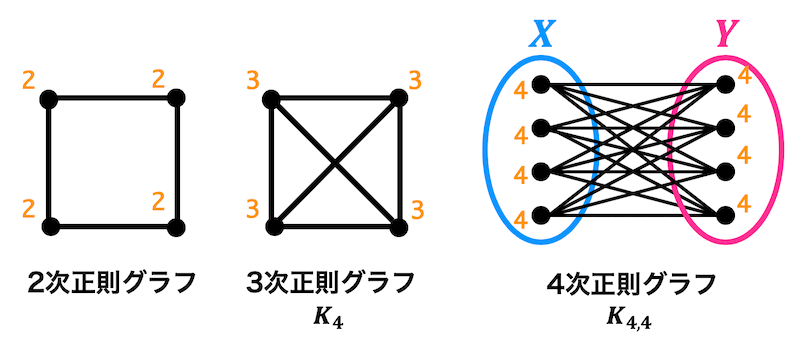
(1) 正則グラフとは
あるグラフのすべての点における次数が同じようなグラフのことを正則グラフと呼びます。それぞれの次数がすべて \( n \) であるとき、\( n \) 次正則グラフ (n-正則グラフ)と呼びます。
あるグラフ \( G \) における次数がすべて同じ \( n \) であるとき、\( G \) を\( n \) 次正則グラフと呼ぶ。
正則グラフの例を3つほど下に載せておきます。
(オレンジ色の数字は次数を表しています)
(2) 完全グラフ・完全2部グラフと正則グラフの関係
完全グラフと正則グラフ
\( n \) 個の点からなる完全グラフ \( K_n \) は実は必ず正則グラフとなります。
\( K_n \) は自分以外の点 \( n-1 \) 個すべてに辺が接続されていますね。なので、どの点においても \( n-1 \) 個の辺が接続されています。つまり、すべての点において次数が \( n-1 \) となります。
なので、完全グラフ \( K_n \) は \( n-1 \) 次の正則グラフとなるのです!
例えば、\( K_4 \) であれば3次正則グラフとなります。
完全2部グラフと正則グラフ
\( X \) の点と \( Y \) の点がともに同じ \( n \) 個の場合の完全2部グラフを考えてみましょう。
このとき、それぞれの \( X \) 上の点 \( n \) 個に対し、\( Y \) のすべての点 \( n \) 個に辺を接続していますね。
なので、\( X \) 上のすべての点、\( Y \) 上のすべての点ともに次数が \( n \) になりますね。
なので、完全2部グラフ \( K_{n,n} \) は \( n \) 次の正則グラフとなりますね。
完全グラフ \( K_n \) は必ず \( n-1 \) 次正則グラフとなる。
また、完全グラフ \( K_{m,n} \) は \( m = n \) のとき、必ず \( n \) 次正則グラフとなる。
7.補グラフ
あるグラフにおいて、もともと辺があった場所の辺をなくし、もともと辺がなかった場所の辺をつけた(辺の有無を反対にしたような)グラフのことを補グラフと呼びます。
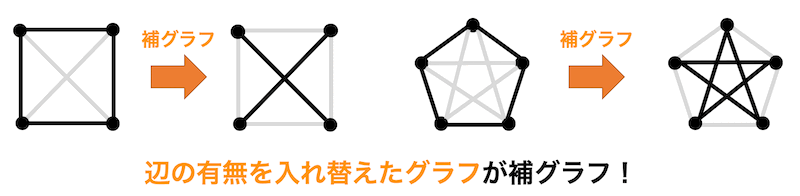
定義でも書いてみましょう。
グラフ \( G = (V,E) \) に対し、辺集合を\[
\overline{E} = \{ (u,v) \ \mid \ u,v \in V, \ (u,v) \notin E \}
\]としたグラフ \( G' = (V,\overline{E}) \) を \( G \) の補グラフと呼ぶ。
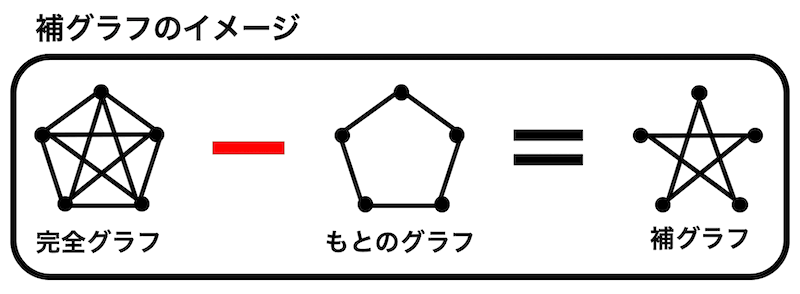
補グラフのイメージは、完全グラフからもとのグラフを引いたものと覚えておくとわかりやすいと思います。
補グラフには、以下のような連結性の定理も成り立ちます。
グラフ \( G = (V,E) \) に対し、もとのグラフ \( G \) と補グラフ \( \overline{G} \) のどちらかが必ず連結である。
簡単に理由を説明したいと思います。
もとのグラフ \( G \) が連結でなければ、補グラフが連結になることを示します。
下の図のように非連結グラフは、2つ以上の連結成分に分けることができます。これを \( C_1 \), \( C_2 \), … ,\( C_n \) としましょう。
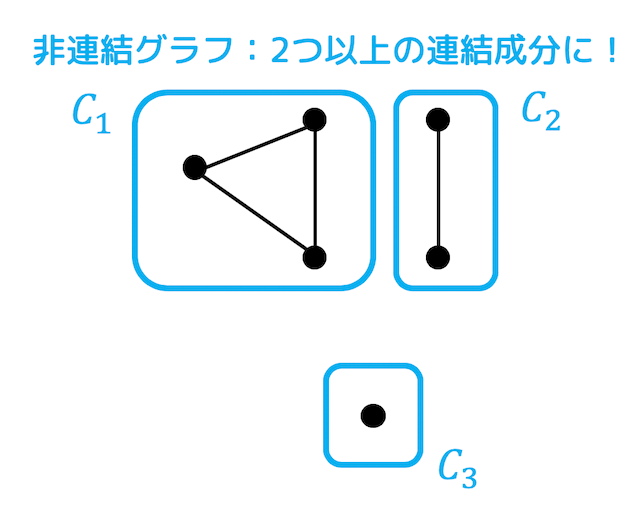
非連結グラフの補グラフを取ると、任意のグループ同士の2点を他のグループの点を経由して戻ってくることができますね。
(任意のグループ同士の2点 \( x \) ,\( y \) は、ある他のグループの1点 \( t \) を通り、\[
x \to t \to y
\]の長さ2の道で結ばれる。)
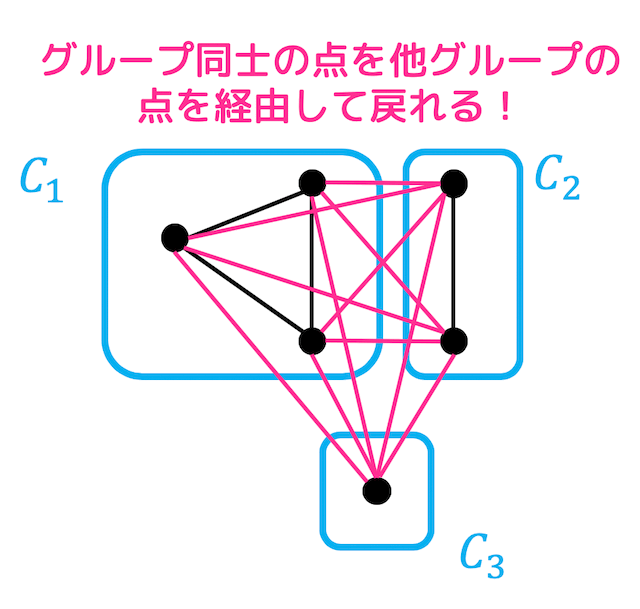
上の図の場合、例えば \( C_1 \) 同士のどの2点も他のグループ \( C_2 \), \( C_3 \) のどの点を経由しても2辺だけたどって戻ることができますね。
(\( C_1 \) の任意の2点 \( x \), \( y \) は他のグループ \( C_2 \), \( C_3 \) の中の1点を通る長さ2の道で結ばれる)
そのため、もとのグラフ \( G \) が非連結であった場合は必ず補グラフ \( \overline{G} \) が連結となるので、\( G \) か \( \overline{G} \) のどちらかが必ず連結となるのです!
8.練習問題
では、6問ほど練習しましょう。
少し多めですが、がんばりましょう。
練習1
次の①〜④のグラフがある。これについて、次の問いに答えなさい。
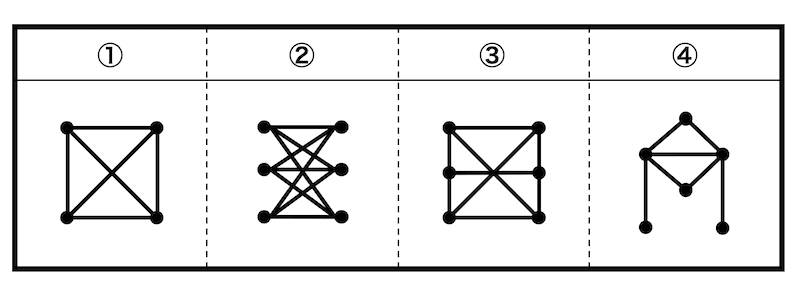
(1) 完全グラフを1つ選びなさい。
(2) 2部グラフをすべて選びなさい。
(3) 正則グラフになるものをすべて選び、何次の正則グラフになるかを答えなさい。
(4) 互いに同型となるペアを1つ見つけなさい。
練習2
つぎの問いに答えなさい。
(1) 完全グラフ \( K_{10} \) の辺の数を答えなさい。
(2) 完全2部グラフ \( K_{8,6} \) の辺の数を答えなさい。
練習3
5つの点からなる3次の正則グラフがあれば求め、なければその理由を書きなさい。
練習4
同型でない4点からなる連結グラフをすべて求め、さらにそれぞれのグラフに対して補グラフを書きなさい。
練習5
2つのグラフの点の数と辺の数が等しいからといって同型とは限らないことを示したい。点の数と辺の数は等しいが同型ではないグラフのペアを1つ書きなさい。
練習6
点数が6のグラフの中で、同型でない正則グラフは何個あるか答えなさい。
ヒント:補グラフをうまく使いましょう。
9.練習問題の答え
解答1
(1)
解答:①
1は \( K_4 \) の完全グラフである。
(2)
解答:②・③
(実は両方とも完全2部グラフ \( K_{3,3} \) になります。)
それぞれの点に0, 1を書いていくと、②以外は緑色の点に0,1どちらを入れても0同士、1同士が接続してしまい、2部グラフにならないため。
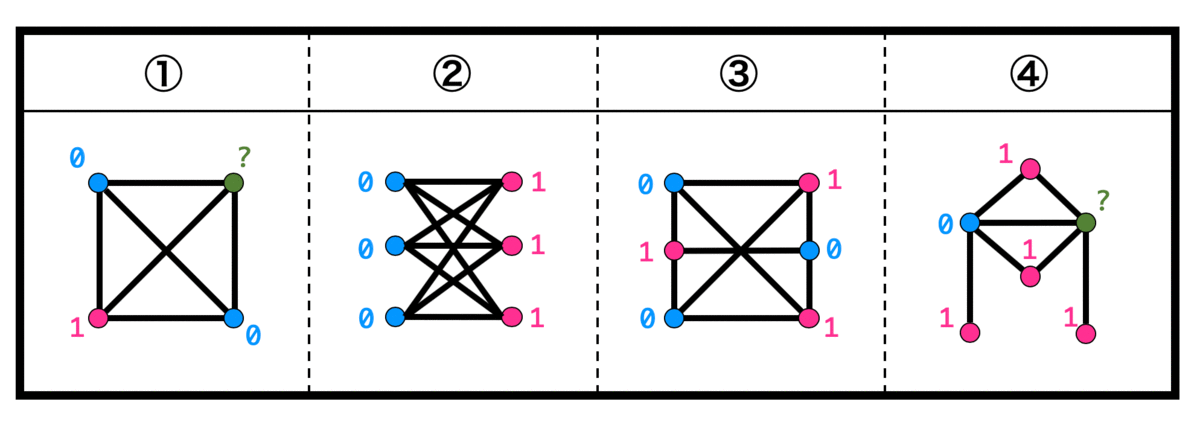
①、③、④にはそれぞれ長さ3の閉路をもつため、2部グラフではない。なので答えは②。
(3)
解答:①・②・③(すべて3次の正則グラフ)
それぞれの点における次数は下の通りとなる。
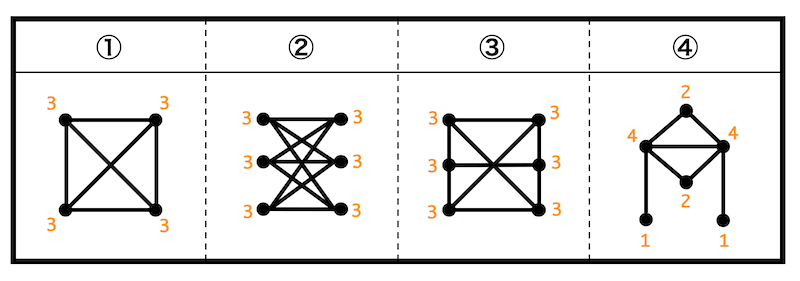
よってすべての点における次数が3である①、②、③が3次の正則グラフとなる。
(4)
解答:②と③
①は点の数が異なるので同型ではない。また、④も次数列(それぞれの次数における点の数)が異なるので同型ではない。よって残った②と③が同型。
解答2
つぎの問いに答えなさい。
(1)
解答:45個
\( K_{10} \) にはそれぞれの点10個が、自分以外の点9個と辺を接続している。しかし、無向グラフなのでそれぞれの辺をダブルカウントしないように2で割る必要がある。よって、\[
\frac{1}{2} \cdot 10 \cdot 9 = 45
\]となる*6。
(2)
解答:48個
\( K_{8,6} \) は8個の点が6方向に対して辺を接続している。なので、\[
8 \times 6 = 48
\]となる。
解答3
解答:存在しない
理由:5つの点からなる3次の正則グラフということは次数の和が15となる。しかし、どのようなグラフであっても次数の和は偶数となる必要がある(握手定理)ため、次数の和が15となるようなグラフは書けないから。
解答4
4点からなる連結グラフを上に、それぞれの補グラフを下にすべて記した。
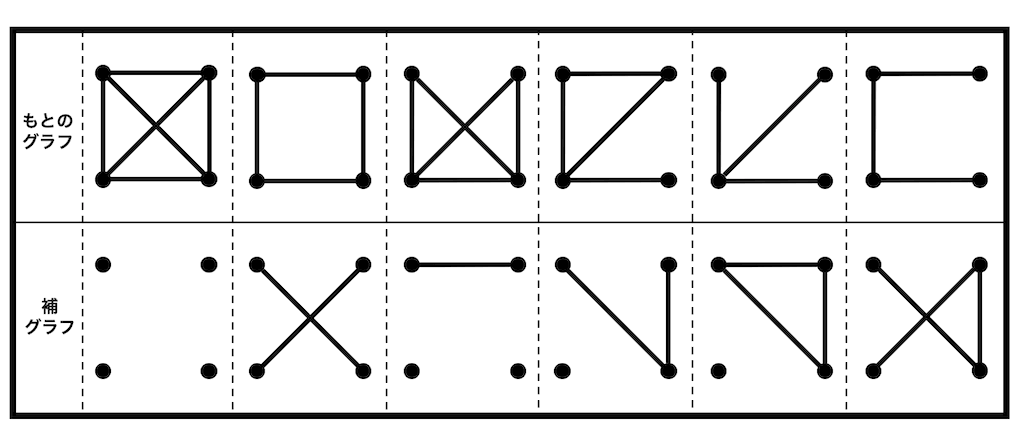
解答5
例えば、下の2つのグラフなどがある。
(オレンジ色の数字は各点における次数を表す。)
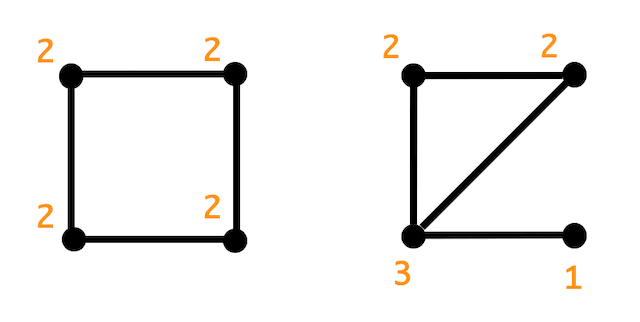
2つのグラフは辺の数が4、点の数も4のグラフである。
しかし、左のグラフはすべて次数が2に対し、右のグラフは次数が2でない点がある、なので同型ではない*7。
解答6
0-正則グラフ〜 2-正則グラフまでは下のように書くことができます。
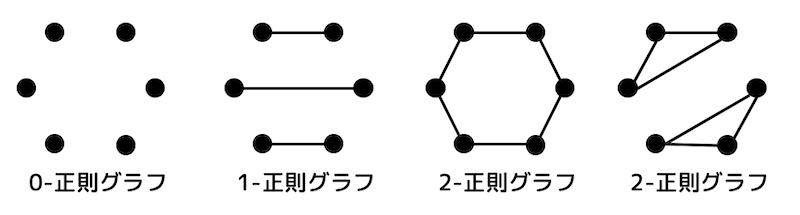
しかし、3-正則グラフ、4-正則グラフのような次数が大きいグラフとなると同型かどうかの判断が難しくなってしまいます。
そこで、元のグラフの補グラフを取ることを考えてみましょう。
点数が6の完全グラフ \( K_6 \) のそれぞれの次数は5ですね。
(わからなければ実際に書いてみましょう)
補グラフは、完全グラフから元のグラフを引いたものなので、次数も完全グラフから元のグラフを引いたものになります。
つまり、3-正則グラフ〜5-正則グラフは、0-正則グラフ〜2-正則グラフの補グラフを取ることで求めることができます。
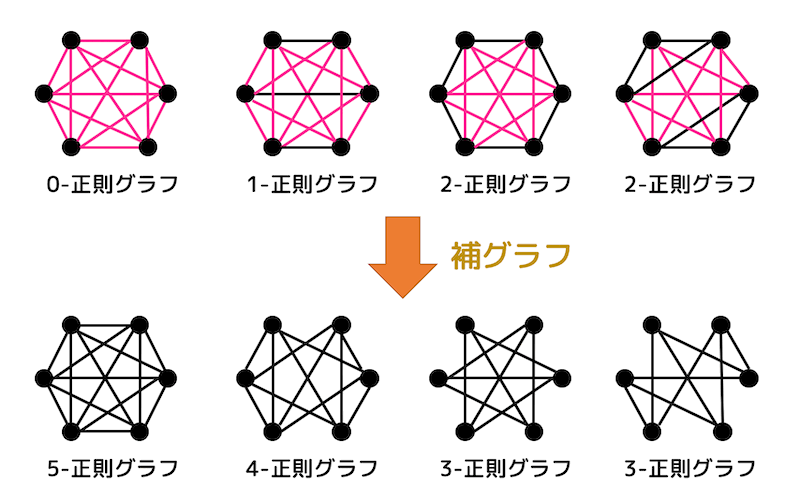
よって点数が6の正則グラフは全部で8個あることがわかります。
10.さいごに
今回も離散数学(グラフ理論)におけるグラフの基本用語についてまとめていきました。
今回で基本用語に関する説明はおしまいです!
次回は一筆書きができるようなグラフの判定法などをまとめていきたいと思います。
ではまた次回、さらば。
*1:たどるためには \( v_3 \) と \( v_5 \) の間、もしくは \( v_4 \) と\( v_6 \) を結ぶような辺が必要。
*2:普通に \( n \) 個の中から順番を考えずに2つ取り出すから \( {}_n \mathrm{C} _2 \) でもいいが今回はあえて詳しく説明しています。
*3:有機化学の構造式を書くときのルールに似てますね。
*4:述語論理を使って書くと、\[
\forall u,v \in E_1 \ \ \mathrm{s.t} \ \ (u,v) \in E_1 \Leftrightarrow ( f(u),f(v) ) \in E_2
\]となる。
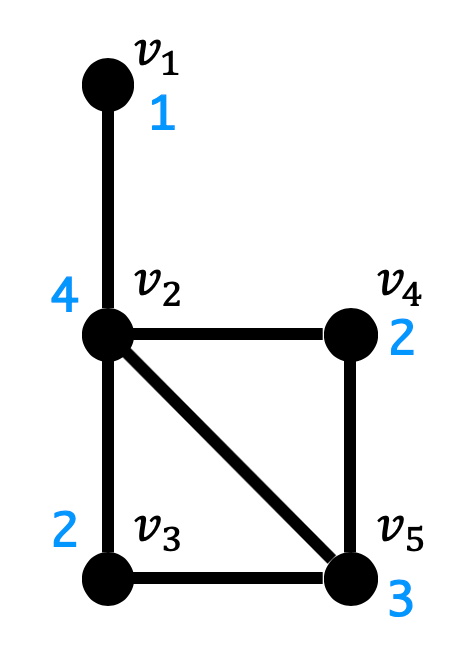
*5:グラフの各点におけるそれぞれの次数を大きい順に並べたもの。例えば、下のような図の場合、各点における次数は1, 4, 2, 2, 3なので次数列はそれぞれの次数を大きい順に並び替えた4,3,2,2,1となる。
*6:普通に \( {}_{10} \mathrm{C} _2 = 45 \) でもOK
*7:それぞれの次数列は、2,2,2,2と3,2,2,1と異なるため同型ではない、などでもOK
関連広告・スポンサードリンク