スポンサードリンク
こんにちは、ももやまです。
今回からはしばらくアセンブラ(アセンブリ言語)についてまとめていきたいと思います。
※正式にはアセンブラは「アセンブリ言語で書かれたものを実行できる形(機械語)に変換するソフトウェア」のことですが、アセンブリ言語のことをアセンブラと呼ぶことが多いため、今回の記事ではアセンブリ言語のことをアセンブラと呼びたいと思います*1。
この記事を見ている人で、将来アセンブラで食っていくような人は少ないかもしれません。
しかし、アセンブラを学ぶことでCPU(プロセッサ)、レジスタなどのハードウェアがどのように動作しているかを体感することができます。
つまり、アセンブラを学ぶことでコンピュータの気持ち(姿?)を少し理解することができるのです!
ということで、まずはアセンブラを学ぶ前に知っておくべき9つの知識を今回は説明していきたいと思います。
目次
スポンサードリンク
0.アセンブラとは
CPUが直接実行できる言語は機械語のみです。
(皆さんがおそらく書いたことであるだろうC言語、Java、Python、Rubyは、そのまま実行することはできず、コンパイラやインタプリタを使って機械語に直してあげなければなりません*2。)
しかし、機械語は2進数、つまり0,1だけで書かれているので普通の人間には理解することができません。
人間が機械語を書くなんてもってのほかです。
そこで機械語で記された命令を人間でもわかるように名前をつけたものをアセンブラと呼びます。
ただ機械語に名前をつけているだけなので、アセンブラは機械語と1対1対応します。
機械語と1対1対応しているアセンブラを学ぶことは、CPU依存の機械語も学ぶことと同様です。
なので、機械語ではなく、アセンブラを学ぶことでもコンピュータのハードウェアについて学ぶことができます。
今回はアセンブラを学ぶ前に必ず知っておくべき9つの知識、具体的には
- CPU内の部品
- 命令実行時のCPUの動き
- 2進数から10進数への相互変換
- 2進数から16進数への相互変換
- 2進数での足し算・掛け算
- 2の補数を用いた負の数の表現
- ビット演算(AND・OR・XOR)
- 論理シフト・算術シフトの違い
- 符号拡張・ゼロ拡張の違い
を簡単にですが説明していきたいと思います。
なお、機械語はCPU依存なので、1対1対応しているアセンブラもCPU依存となります。
つまり、CPUによってアセンブラの書き方(文法)が変わってきます。
代表的なアセンブラの例として「X86」、「MIPSアーキテクチャ」や基本情報でも使われる「CASL II*3」などがあります。
スポンサードリンク
1.CPU内のよく出てくる6つ部品
部品1:プログラムカウンタ(プログラムレジスタ)
次に実行される命令のアドレスを保持するレジスタです。
命令フェッチ*4をするたびに一定数増加します。
プログラムカウンタの1回あたりの増加量は命令の長さに比例します。
例えば命令の長さが2バイト(16ビット)であれば2ずつ増加し、4バイト(32ビット)であれば4ずつ増加します。
部品2:命令レジスタ
現在実行している命令の内容(コード)を一時的に格納する部品です。
部品3:フラグレジスタ(ステータスレジスタ)
各種フラグが立っているかどうかを格納するレジスタです。
なお、プロセッサによってはフラグレジスタがないこともあります。
(例:MIPSアーキテクチャ)
代表的なフラグにSF(Sign Flag)、ZF(Zero Flag)、OF(Overflow Flag)の3つがあるので簡単に紹介したいと思います。
SF:サインフラグ
ACC(アキュームレータ)の値、つまり演算結果が負であれば「1」、そうでなければ「0」が立つフラグです
ZF:ゼロフラグ
ACC(アキュームレータ)の値(演算結果)が0であれば「1」、0以外なら「0」がたつフラグです。
OF:オーバーフローフラグ
ACC(アキュームレータ)の値(計算結果)がオーバーフローしたときに「1」となるフラグです。
部品4:汎用レジスタ
特別な用途を持たないただのレジスタです。
例えば演算の結果や読みだしたデータを一時的に格納するときに使われます。
部品5:デコーダ
命令レジスタに保存した命令を解読します。
部品6:ALU (Arithmetic Logic Unit)
算術演算・論理演算を行います。
では練習問題で確認してみましょう。
練習1
つぎの(1), (2)の処理をする部品の名称として正しいものを選びなさい。
(1) つぎに実行される命令のアドレスを保持するレジスタ
(2) 算術演算・論理演算を行う
★選択肢★
- 命令レジスタ
- プログラムカウンタ(プログラムレジスタ)
- ALU
- 汎用レジスタ
- ACC
解答1
(1) 2 (2) 3
(プログラムカウンタと命令レジスタは間違えやすいので注意!!)
スポンサードリンク
2.命令実行時のCPUの動き
プロセッサの命令実行の4ステップも確認しておきましょう。
命令実行時、CPUは
- 命令フェッチ(メモリ→CPUへ命令読み込み)
- 命令解読(読み込んだ命令をデコーダで解読)
- 命令実行(解読された命令の実行、ALUで演算)
- 結果の格納(演算結果をメモリ・レジスタに格納)
の4ステップをひたすら繰り返します。
DMA(転送)
CPUを経由せずにメインメモリと入出力装置間のデータ転送を制御することをDMA(転送)と呼びます。
DMAを用いることで、データ転送中にも(CPUを使う)別の処理を行うことができます。
練習2
つぎの(1), (2)の問いに答えなさい。
(1)
命令が実行されるときのCPUの動きになるように1〜4を並び替えなさい
- 命令を解読する
- メインメモリからCPUに命令を読み込む
- 結果をレジスタに格納する
- 命令を実行する
(2)
DMAの説明として、適切なものを1つ選びなさい。
[応用情報技術者平成23年秋期 午前問13]ア;CPUが磁気ディスクと主記憶とのデータの受渡しを行う転送方式である。
イ:主記憶の入出力専用アドレス空間に入出力装置のレジスタを割り当てる方式である。
ウ:専用の制御回路が入出力装置や主記憶などの間のデータ転送を行う方式である。
エ:複数の命令の実行ステージを部分的にオーバラップさせて同時に処理し,全体としての処理時間を短くする方式である。
解答2
(1) 2→1→4→3
(2) ウ
(アはDMAを使わない通常の処理形式の説明)
ここまでの記事を見てもう少し復習しておきたいなと思う人はこちらの記事をご覧ください。
3.2進数と10進数への相互変換
アセンブラでは2進数についての知識を頻繁に使用します。
なので、ここからは2進数の知識について簡単にですが復習していきたいと思います。
まずは2進数と10進数の相互変換ができるかを確認しましょう。
練習3
(1), (2)の2進数を10進数に直し、(3), (4)の10進数を2進数に直しなさい。
(1) 100 1000(2進数→10進数)
(2) 1110 1101(2進数→10進数)
(3) 37(10進数→2進数)
(4) 2020(10進数→2進数)
解答3
(1) 72
(2) 237
(3) 10 0101(2進数)
(4) 111 1110 0100(2進数)
なお、2進数であることを表すために 10 0101b のように値の最後にbを付けたり、0b100101 のように最初に0bをつけることが多いです。
4.2進数と16進数への相互変換
「1010110101101000101010」のように0, 1の数が多くなると見にくいですよね。
そこで、下のように4桁を1区切りで表記できる16進数を使うことで2進数で桁数が多くなっても、少ない桁数で見やすくなります。
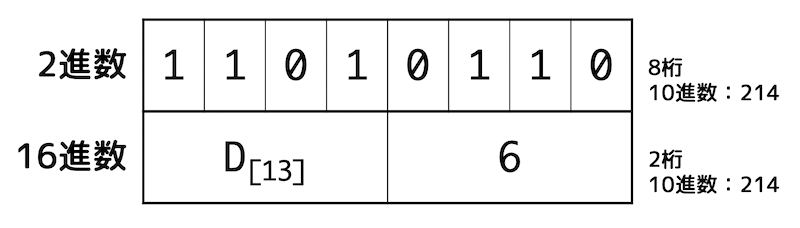
16進数では10〜15を1文字で表現できるようにするために、それぞれの数字をアルファベットで表現します。
具体的には10をA、11をB、12をC、13をD、14をE、15をFとしています。
練習4
(1)の2進数を16進数に、(2)の16進数を2進数に直しなさい。
(1) 1101011010011111(2進数)
(2) ACE2(16進数)
解答4
(1) D69F(16進数)
(2) 1010 1100 1110 0010(2進数)
なお、16進数であることを表すために、D69Fh のように最後にhをつけるか、0xD69Fのように最初に0xをつけることが多いです。
5.2進数の足し算・掛け算
2進数の足し算(引き算)、掛け算も10進数と同じようにできちゃいます。
早速練習問題で確認しましょう。
練習5
つぎの2進数同士の計算をしなさい。
(1) 0x1110111 + 0x100110
(2) 0x1110 × 0x101
おまけ 16進数同士の計算もやってみよう
(3) 0x77 + 0x49
解答5
(1)
下の図のように筆算でやることを強くおすすめします。
2進数は2で繰り上がりが発生するので注意しましょう。
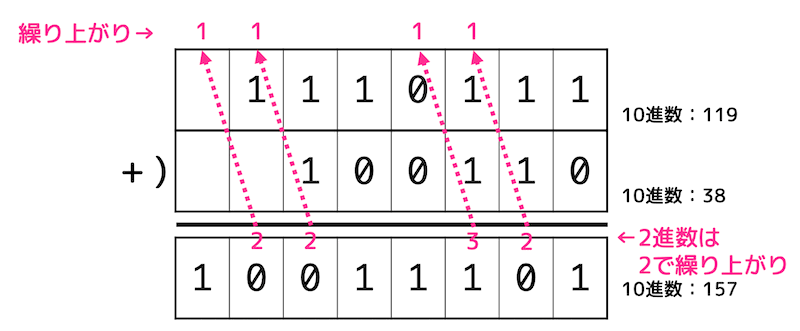
(2)
掛け算も10進数と同じように計算できます。
ただし、足す回数が増えるので計算ミスなどに気をつけましょう。
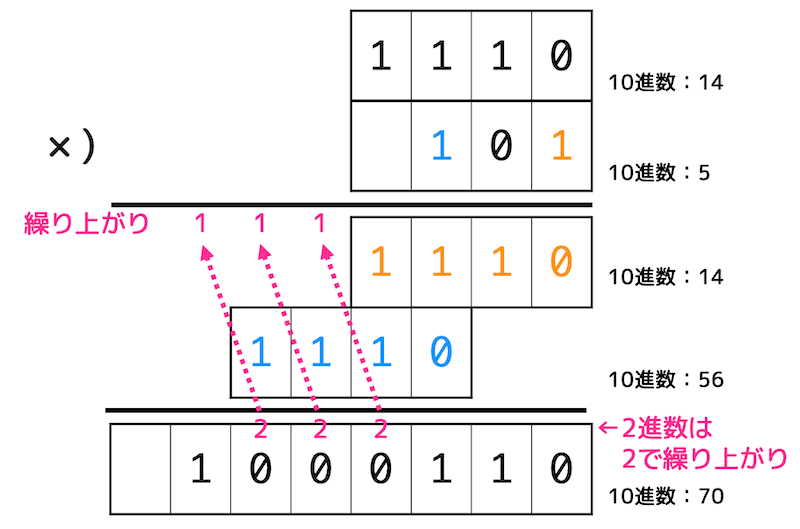
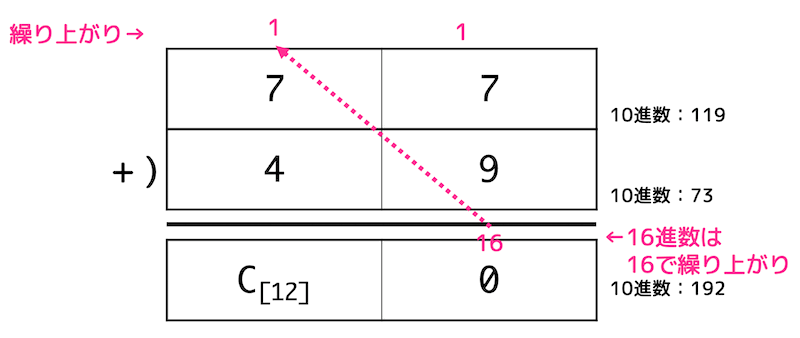
(3)
16進数の場合は16で繰り上がりで発生します。
2進数よりも桁数が少ないので計算はしやすいかと思います。
6.2の補数を用いた負の数の表現
引き算を足し算と同じように処理できるように作られたのが2の補数です。
アセンブラでも2の補数の知識が必要なので、2の補数を使って負の数を作り出す方法を確認しておきましょう。
練習6
「-100」を8ビットの2の補数を用いて表現しなさい。
また、8ビットの2の補数表現で表せる数の範囲を10進数で答えなさい。
解答6
まず、作りたい数の絶対値(今回は-100の絶対値である100)を2進数で表現します。
100を2進数で表現すると、01100100(2進数)となりますね。
ここから2の補数を作るのですが作り方は2パターンあるので両方のパターンを紹介します。
パターン1:ビットを反転させて1を加算
2の補数は、最初に作った絶対値のビット(0,1)を反転し、1を加算することで求めることができます。
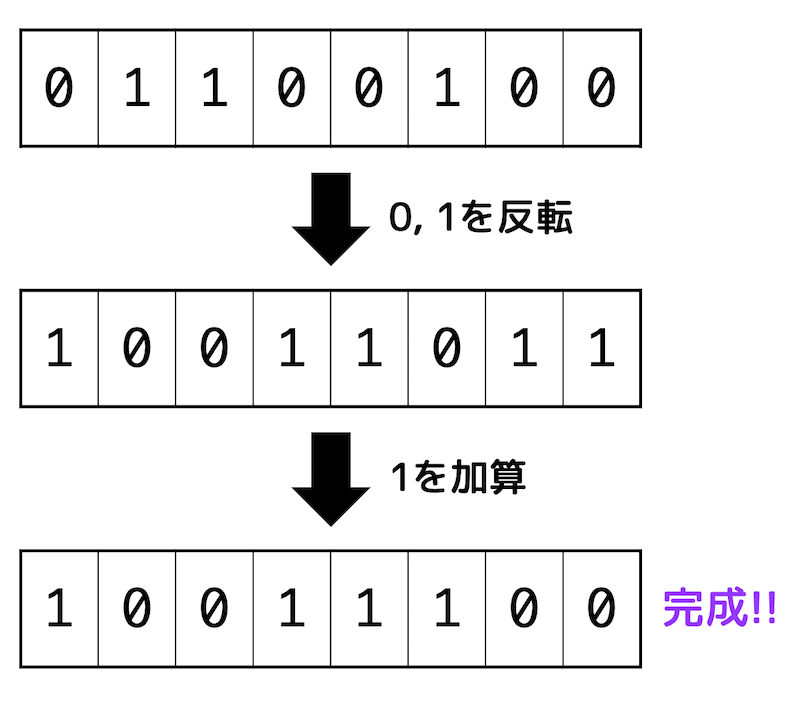
よって「-100」を8ビットの2の補数で表すと「0b10011100」となります。
パターン2:100……0 から減算して求める
ビット数+1の位が1、残りが0の2進数(100……00)から絶対値(今回の場合は100を2進数にしたもの)を引くことで求めることもできます。
今回の場合、0b1 0000 0000から絶対値(0b01100100)を引いて求めます。
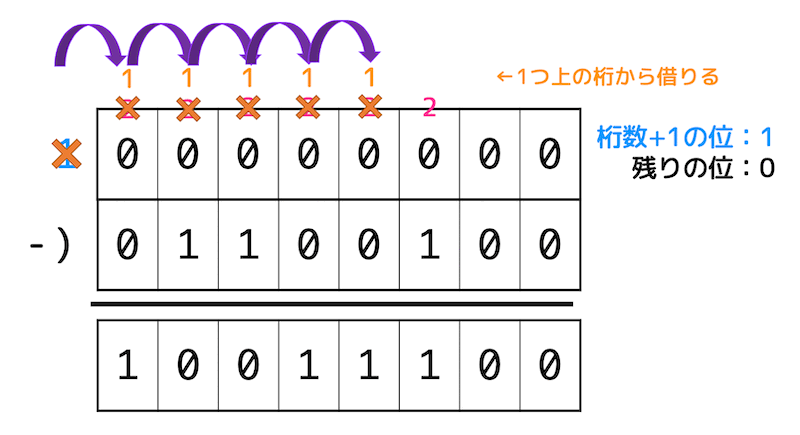
2進数の引き算では「1つ上の桁から借りる」動作が多くなるので計算ミスに気をつけましょう。
8ビットの2の補数表現で表せる数の範囲
8ビットなので全部で \( 2^8 = 256 \) 個の数を表すことができます。
256個を正の数と負の数で表現するため、正の数(と0)で128個、負の数で128個の数を表せます。
なので負の数は -128 〜 -1 の128個、正の数は0と 1〜127 の128個を表すことができます。
よって8ビットの2の補数表現では -128〜127以下が表せます。
\( n \) ビットの2の補数表現で表せる範囲が \( - 2^{n-1} \) 〜 \( 2^{n-1} - 1 \) となることは必ず覚えておきましょう。
7.ビットごとの論理演算(OR・AND・XOR)
2進数のそれぞれのビットごとに対し、OR、AND、XOR演算を行うことができます。
練習問題で確認していきましょう。
練習7
2つの自然数「230」、「119」を8ビットの2進数(補数表現ではない)で考え、ビットごとにOR、AND、XOR演算を行った結果を10進数で答えなさい。
解答7
「230」を2進数に直すと「0b11100110」、「119」を2進数に直すと「01110111b」となる。
(1) OR演算
それぞれのビットごとにOR演算(片方でも1なら結果が1)を行う。
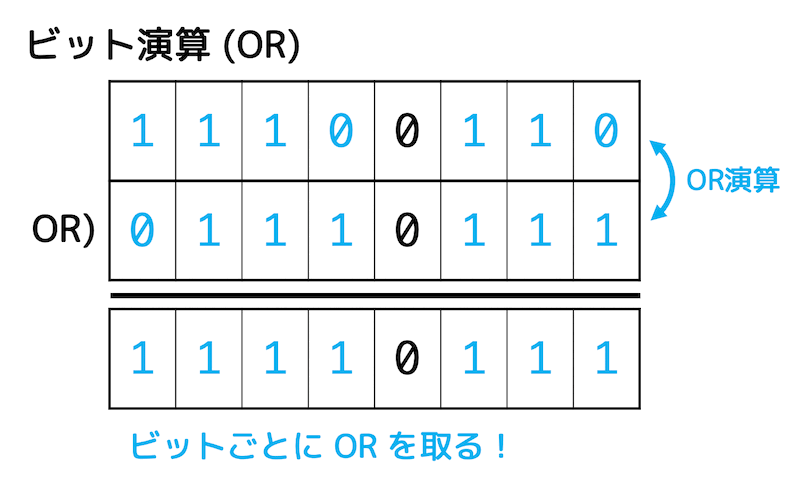
すると、「0b11110111」となり、10進数に直すと247になります。
(2) AND演算
それぞれのビットごとにAND演算(両方が1のときだけ1)を行います。
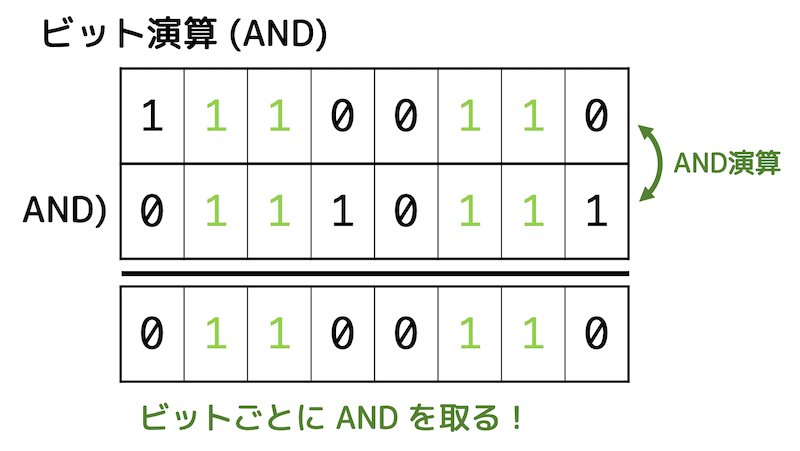
すると、「0b01100110」となり、10進数に直すと102になります。
(3) XOR演算
それぞれのビットごとにXOR演算(2つのビットが異なるときに1)を行います。
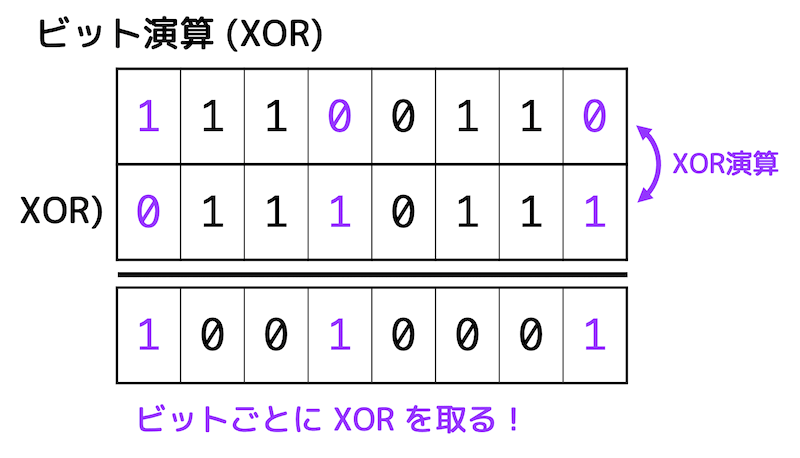
すると、「0b10010001」となり、10進数に直すと145になります。
排他的論理和(XOR)は、特定のビットを反転させるときに使われます。
元の数と反転させたいビットを1とした数の排他的論理和を取ることで特定のビットを反転させることができます。
例えば、1001の偶数番目の桁のビットを反転させたいときは、元の数1001と反転させたいビットを1とした0101の排他的論理和を取ります(答え:1100)。
アセンブラでは、算術演算(足し算・引き算)、論理演算を用いた処理がよく出てきます。
下の練習問題で少し確認してみましょう。
練習8
つぎの(1), (2)の処理を「2進数の加算」・「2進数の論理演算」だけで行うためにはどのような処理をすればいいかを考えてみましょう。
(1) 計算結果が偶数であれば0、奇数であれば1とする処理
(2) 計算結果の2の補数を取る処理
解答8
(1)
偶数であれば、2進数において1の位は必ず0、奇数であれば1の位は必ず1となります。
(どんな偶数でも2進数に直すと1の位は0、どんな奇数でも2進数に直すと1の位は1となります。疑う人は何個か実際に試してみましょう。)
なので、1の位以外をすべて消し、1の位だけを残すことで偶数か奇数かを判定できます。
そのため、「元の数」と「1」の論理積を取ることで1の位を残すことができます。
(2進数の1は、1の位以外はすべて0なので「元の数」と論理積を取ると1の位以外がきれいに消滅する)
処理例:24は偶数か判定する
→24の2進数は11000、11000と1の論理積は0。よって偶数。
(2)
ある数の2の補数を取るためには、元の数のビットを反転し、1を加算することで求めることができます。
なので、元の数のビットをすべてを反転させる動作、つまり「元の数」と「元の数と同じ桁数だけ1になっている数」の排他的論理和をとり、最後に1を足すことで2の補数を取ることができます。
処理例:0101の2の補数を求める
→ 0101と1111の排他的論理和は1010、1を足して1011。
よって2の補数を取ると1011となる。
8.論理シフトと算術シフトの違い
シフト演算とは
2進数の桁を左にずらすと値を2倍、4倍、8倍、……、\( 2^n \) 倍にすることができ、右にずらすと1/2倍、1/4倍、1/8倍、……、\( 1/2^n \) 倍にすることができます。
このように桁をシフトさせて値を変えることをシフト演算と呼びます。
論理シフト演算
左シフト(2倍、4倍……)
\( n \) ビット左にシフトさせることで値を \( 2^n \) 倍することができます。
シフトにより空いた桁には0を挿入します。
例えば2ビット左シフトさせると、値は4倍になります。
なお、左側の溢れた桁は消滅するので注意してください。
(消えた桁によってはオーバーフローになる可能性あり)
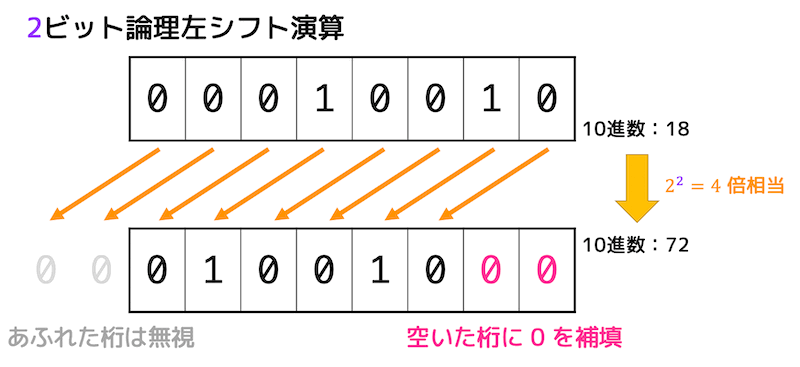
右シフト(2倍、4倍……)
\( n \) ビット右にシフトさせることで値を \( 1/2^n \) 倍することができます。
シフトにより空いた桁には0を挿入します。
例えば2ビット右シフトさせると、値は1/4倍になります。
(小数点以下は切り捨てられます)
なお、右側の溢れた桁は消滅するので注意してください。
(左側だけでなく、右側の桁が消えた場合でもオーバーフローとなるので注意してください。)
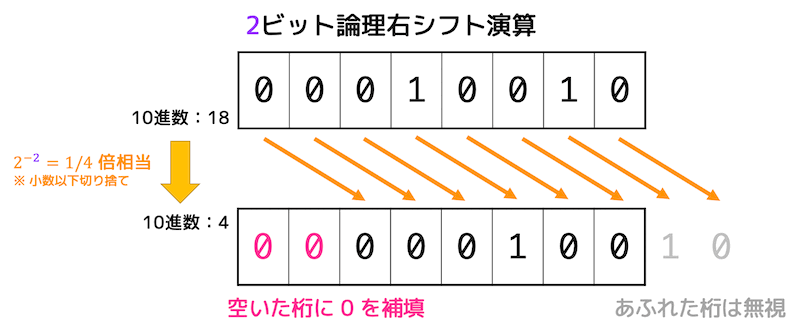
算術シフト演算
2の補数の場合、そのままシフト演算を行うと符号が変わってしまい、思った結果が得られません。
そのため、普通の2進数と正負を考える2進数(補数表現)ではシフトの方法が少し変える必要があります。
算術シフト演算は、(2の補数表現で)正負を考えた2進数のシフト演算で使います。
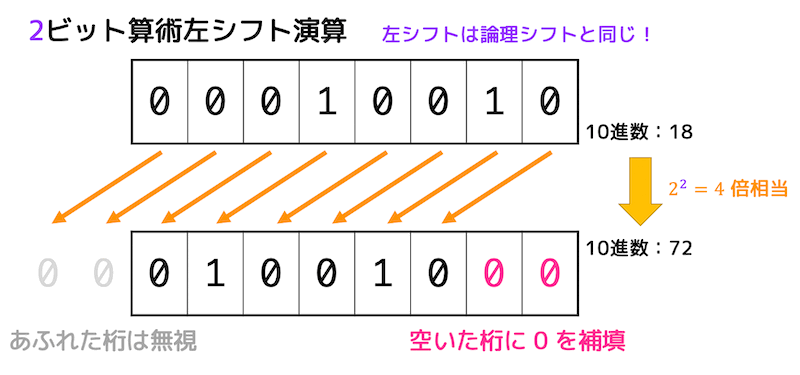
左シフト(2倍、4倍……)
\( n \) ビット左にシフトさせることで値を \( 2^n \) 倍することができます。
シフトにより空いた桁には0を挿入します。
例えば2ビット左シフトさせると、値は4倍になります。
論理シフトと同じように左側の溢れた桁は消滅するので注意してください。
(消えた桁によってはオーバーフローになる可能性あり)
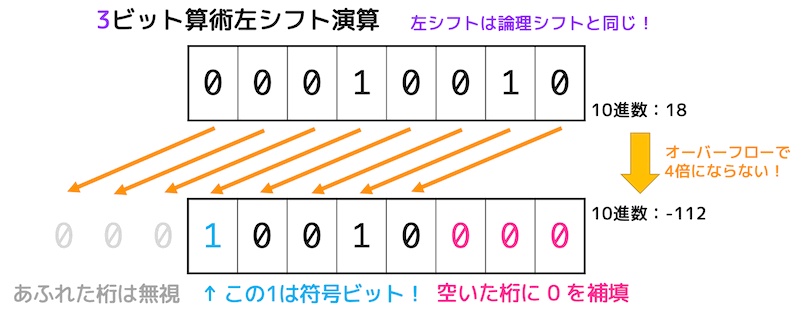
ここで、最上位ビットは符号ビットであるところに注意が必要です。
下のように見た目ではオーバーフローが起こっていないような場合でも、最上位ビットが変わることによりオーバーフローが発生することがあります。
(2の補数で計算できる範囲を確認しましょう。)
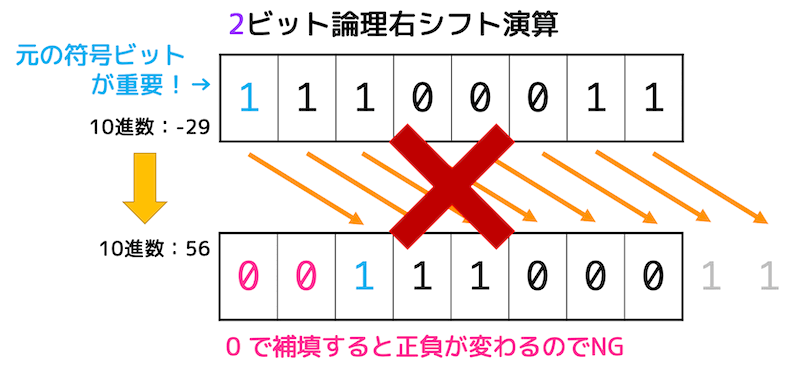
右シフト(1/2倍、1/4倍……)
\( n \) ビット右にシフトさせることで値を \( 1/2^n \) 倍することができます。
しかし、論理ビットと同じように右シフトを行うと、正負が変わってしまい正しく結果を求めることができません。
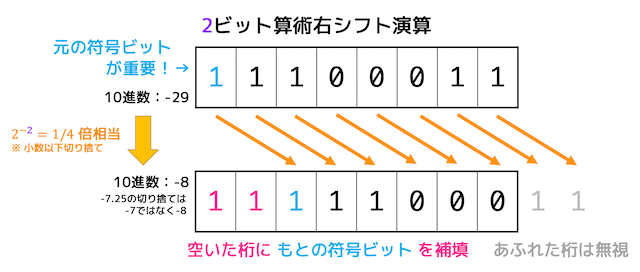
そこで元の2進数の符号ビットによって空いた桁に挿入する数を変えることで正しく算術右シフトを行うことができます。
例えば2ビット右シフトさせると、値は1/4倍になります。
(小数点以下は切り捨てられます。ただし、負の数の切り捨てに注意してください*5。)
もちろん下のような元の符号ビットが0の2進数であれば、空いた位には0が挿入されます。
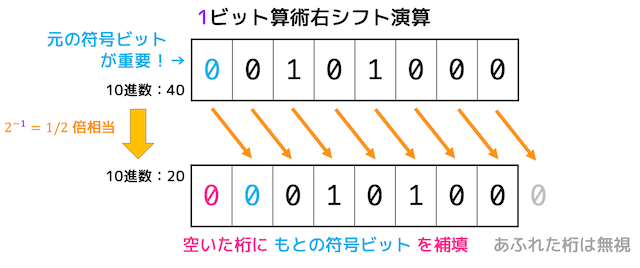
右側の溢れた桁は消滅するので注意してください。
(論理シフトと同じく消えた桁によってはオーバーフローになる可能性あり)
9.符号拡張・ゼロ拡張の違い
符号拡張、ゼロ拡張の違いについても簡単に確認しておきましょう。
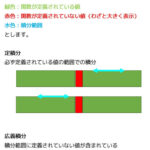
(1) 符号拡張
符号拡張は2の補数表現を用いた計算をする場合に必要です。
例えば、下のようなビット数が異なる2進数の計算をすると、計算結果が思った通りにならないことがあります。
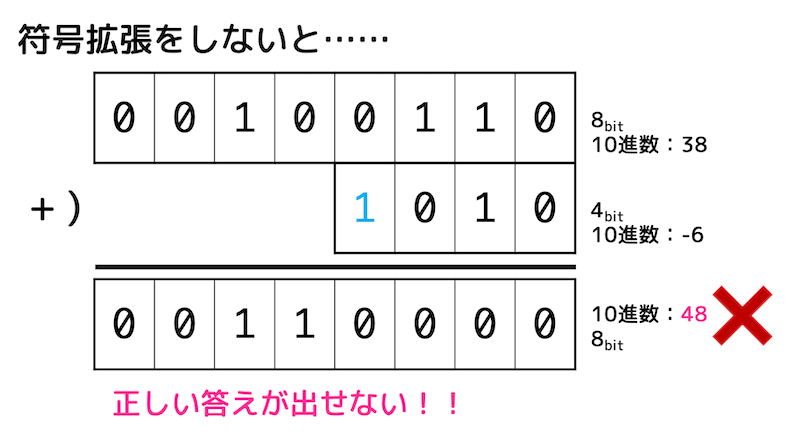
そのため、2の補数表現を用いた2進数の計算をする際には必ず2つのビット数をあわせてから計算を行う必要があります。
このビット数をあわせるために符号拡張を使います。
符号拡張では、左側に追加したビットに元の桁の符号ビットと同じ数字を追加します。
例えば、4ビットの2進数0b1001を8ビットに符号拡張することを考えましょう。
符号ビットは1(つまり負)なので、追加する4ビットにすべて1を追加すると、0b11111001となります。
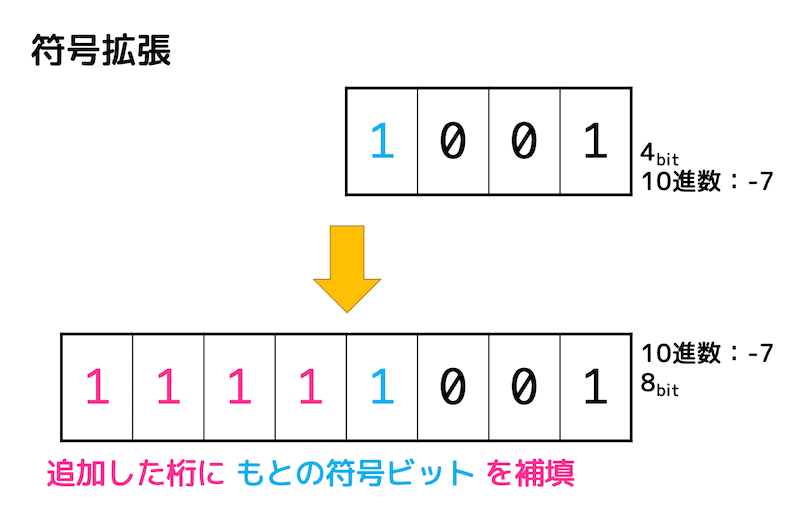
先程紹介した計算も、符号拡張をすることで正しく計算を行うことができます。
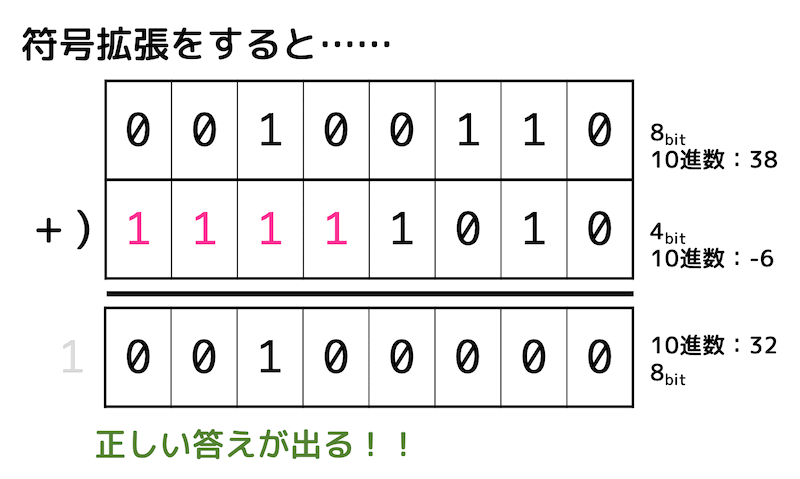
(2) ゼロ拡張
ゼロ拡張は2の補数表現を用いない(つまり自然数の)2進数計算をする場合に使います。
追加する桁数分だけ左側に0をつけるだけでゼロ拡張の完了です。
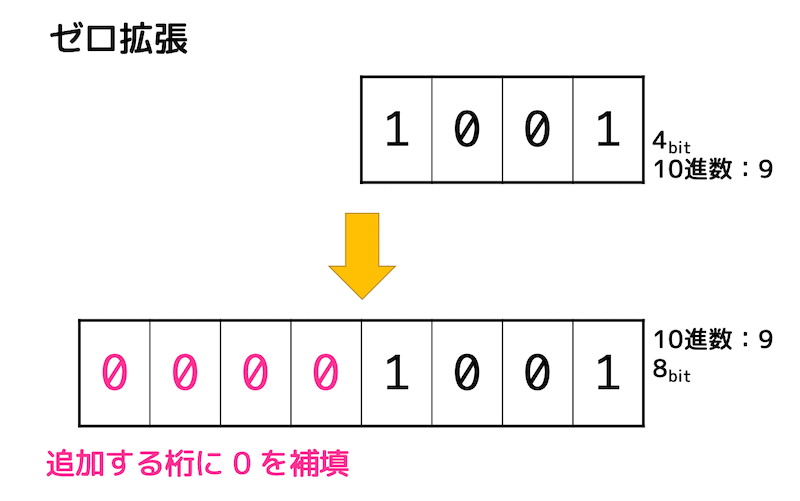
ほら、簡単でしょ??
10.さいごに
今回はアセンブラを学ぶ前に確認すべき9つの知識について簡単にですが説明しました。
今回紹介した9個の知識(特に2進数関連)はアセンブラを学ぶ上で非常に大切なので必ず覚えておきましょう。
まだ2進数関連の処理が不安な人向けに、関連の記事を2つほど用意しているのでもう少し復習したい人はぜひご覧ください。
2進数の基礎1(絶対値表現、負の数が出てこない処理)
2進数の基礎2(2の補数表現、負の数も出てくる処理)
次回からはいよいよアセンブラの命令(mipsアーキテクチャを使いたいとおもいます)について2回にわけて説明していきたいと思います。
では、また次回。
関連広告・スポンサードリンク




![うさぎでもわかる計算機システム Part04 桁落ち・情報落ち・丸め誤差・打ち切り誤差について [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612150639-1-150x150.jpg)