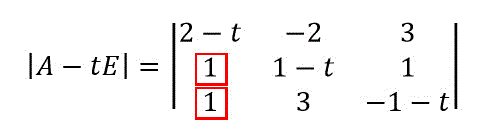
スポンサードリンク
こんにちは、ももやまです。
線形代数の試験では固有値を求める問題がかなり頻出します。
固有値を求める問題は、大学の期末試験・数検1級・院試・編入試験・微分方程式を求める際など、様々な場面で固有値を求める場面がやってきます。
ということで、今回は固有値や固有ベクトルを素早く求める方法をまとめてみました。
この記事では固有値の計算方法についてのみをまとめています。
固有値、固有ベクトルが何を表しているかについてはこちらの記事に載せているのでわからなければこちらを御覧ください。
スポンサードリンク
１．固有値の算出公式
念の為固有値を求める方法を説明します。
固有値を求める行列を \( A \) とし、その固有値を \( t \) とします。
そのとき、\( |A - tE| = 0 \) もしくは \( |tE- A| = 0 \) となるような \( t \) を求める問題です。
人によって前者と後者のどちらで固有値を求めるかはわかれますが、僕は前者、つまり \( |A - tE| = 0 \) で求めることをおすすめします。
理由は、後者だと、元の行列の正負を入れ替える際に入れ替え忘れてしまうミスが頻発する*1からです。
この固有値を求める際に文字列の入った行列式を解く必要があるので、文字列の入った行列式がうまく解けないと固有値を含め、固有値を用いたそれ以降の問題が解けなくなり、大量失点の原因となってしまいます。
多くの期末試験では大学院入試では、3次正方行列の固有値を算出する問題が多いので、今回は3次正方行列で説明したいと思います。
※注意
普通固有値は \( \lambda \) で表されますが、僕は \( \lambda \) があまり好きではないので、今回は固有値は \( t \) で説明します。
スポンサードリンク
２．固有値の裏技
例えば、\[ A = \left( \begin{array}{ccc} 2 & -2 & 3 \\ 1 & 1 & 1 \\ 1 & 3 & -1 \end{array} \right) \]の固有値をすばやく求めてみましょう。
まずは、\( |A - tE| = 0 \) を求めてみましょう。すると、\[ |A - tE| = \left| \begin{array}{ccc} 2-t & -2 & 3 \\ 1 & 1-t & 1 \\ 1 & 3 & -1-t \end{array} \right| = 0 \]を求めればいいことになりますね。
固有値をすばやくしかも正確に求めるためには、行・列基本変形の性質を利用します。
その1 同じ行 or 列の絶対値が同じ成分を使う
多くの3次正方行列 \( A \) の固有値算出問題の場合、行列 \( A- tE \) の同じ行もしくは列の絶対値が同じ成分が存在します。その2箇所を行基本変形で使うことで多くの場合、簡単に文字 \( t \) が入った行列式を外に出してあげることができます。
まず、\( A- tE \) の同じ行・列内に絶対値が等しい成分がないか探します。
今回の場合だと、1行目のこの2つの絶対値は等しいですね。
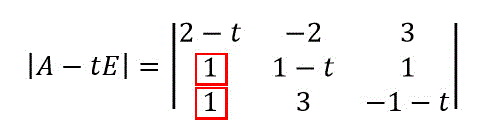
つぎに、片方の絶対値が等しい成分が0になるような変形をします。
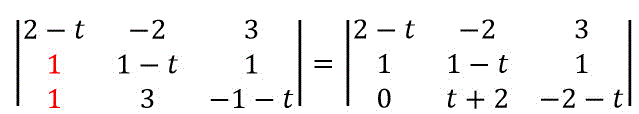
すると、3行目は \( -t-2 \) （もしくは \( t+2 \)）を行列式の外に出すことができますね。
このときにうまく文字の成分を行列式の外に出せないときは他の絶対値が等しい同じ行・列の２つの成分を見つけましょう。
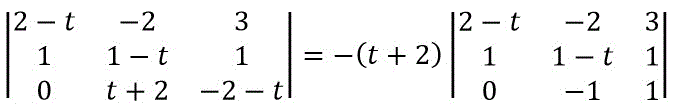
すると、3列目の行列の成分から \( t \) が消滅しましたね。
なので、1つの成分以外を0にするような変形をしてあげましょう。
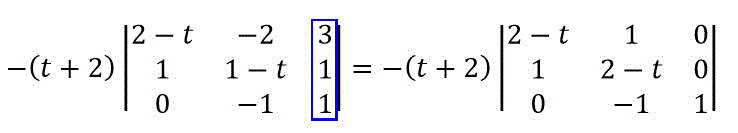
この形になったら余因子展開を使います。
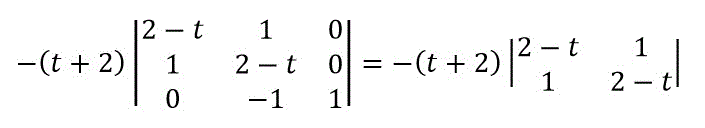
すると、2×2の行列になりましたね。
2×2の公式ならサラスの公式も楽勝なのでここからはサラスの公式で倒してあげましょう。
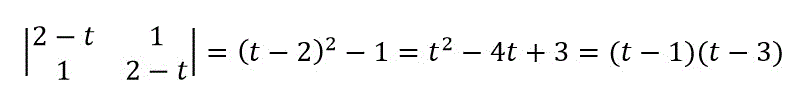
別解ですが、サラスの公式を使いたくなければ、1行目に2行目を足し込むことで \( 3-t \) を行列の外に出すことができるのでそちらでやってもOKです。
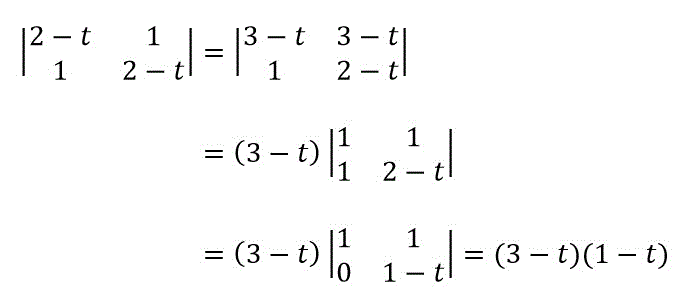
よって、
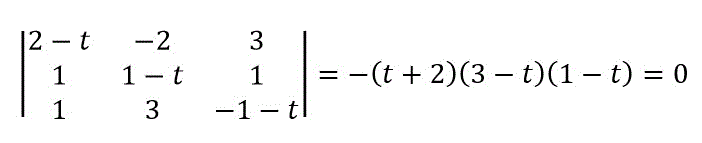
が計算でき、固有値 \( t \) は、-2,1,3 となります。
一応列の場合でもやってみましょう。
\[ A = \left( \begin{array}{ccc} -8 & 6 & -6 \\ -4 & 4 & -3 \\ 8 & -5 & 6 \end{array} \right) \]の固有値をすばやく求めてみましょう。
まずは、\( |A - tE| = 0 \) を求めてみましょう。すると、\[ |A - tE| = \left| \begin{array}{ccc} -8-t & 6 & -6 \\ -4 & 4-t & -3 \\ 8 & -5 & 6-t \end{array} \right| = 0 \]を求めればいいことになりますね。
この行列を基本変形を使ってすばやくかつ正確に求めてみましょう。
今回は1列目のこの2つが絶対値が等しい成分ですね。
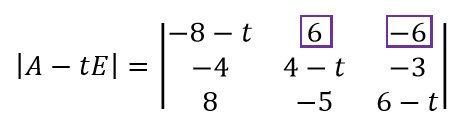
なので、この2つを使って変形しましょう。
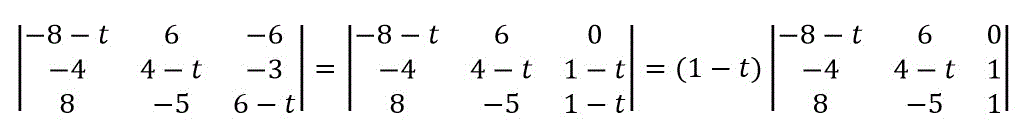
変形すると、\( 1-t \) を出すことができます（固有値1があることが確定）。
次に、3列目の成分から \( t \) が消滅してあげたので、1つの成分以外を0にし、さらに余因子展開をします。
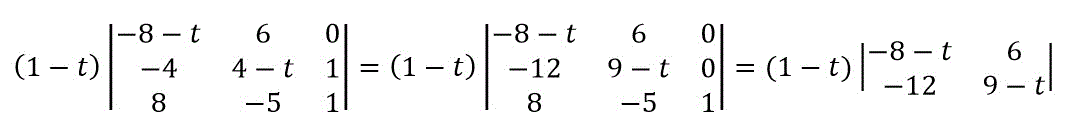
余因子展開をすると2×2の行列となりますね。
あとはサラスの公式で求めるだけです。
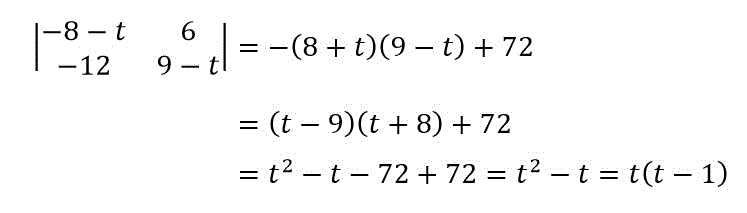
よって、
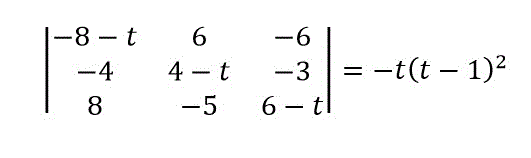
と変形できるので固有値は0と1 (2重解) となります。
その2 1つの行に他の行すべてを足し込む
万が一、その1が使えないときはこの手法を試してみましょう。
かなりの確率で使えます。
4次以上の正方行列場合はその1の解法が使えないことが多いので、こちらの手法を先に試したほうがいいかもしれません。
\[ A = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 4 \\ 5 & 3 & 1 \end{array} \right) \]の固有値を求めてみましょう。
まずは、\( |A - tE| = 0 \) を求めてみましょう。すると、\[ |A - tE| = \left| \begin{array}{ccc} 1-t & 2 & 3 \\ 2 & 3-t & 4 \\ 5 & 3 & 1-t \end{array} \right| = 0 \]を求めればいいことになりますね。
今回は同じ行や列に絶対値が等しい成分がありませんね。
なので、全行足す技を試してみましょう。
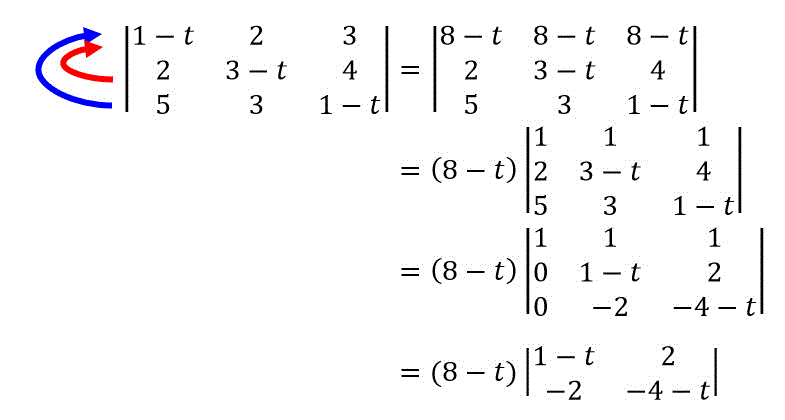
このように、全行足すと \( 8-t \) が出てきます。
なので、\( 8-t \) を行列の外に出します。
あとはその1と同じように \( t \) が消滅した成分に0の成分を集め、2×2の行列にしてあげます。
2×2になったらサラスの公式で求めましょう。
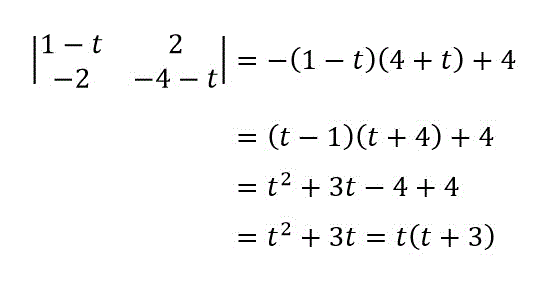
よって、
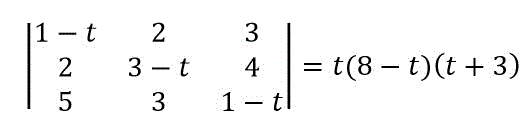
と求めることができ、固有値 \( t \) は -3, 0, 8 となります。
この2つのパターンに当てはまりそうになく、かつ簡単な行基本変形で固有値が求まりそうにないときだけサラスの公式を使ってください。
スポンサードリンク
３．素早くできる固有値の検算
固有値を算出した後でも正しく固有値が求まっているか不安ですよね。
なので、素早くできる固有値の検算テクニックを紹介します。
先程固有値を求めた、\[ A = \left( \begin{array}{ccc} 2 & -2 & 3 \\ 1 & 1 & 1 \\ 1 & 3 & -1 \end{array} \right) \]の固有値が本当に正しいかどうか検算してみましょう。
（固有値は-2,1,3）
行列の固有値の和は、行列の対角成分の和に等しい。
なので、行列の固有値の和が対角成分の和に等しいかどうか確認するだけで検算となる。。
今回の場合は対角成分は2, 1, -1なので、この3つの和（2）が固有値の和に等しいかどうか確認するだけです。
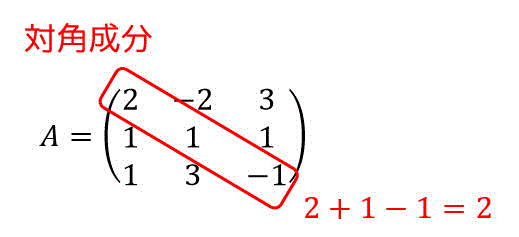
-2 + 1 + 3 = 2 となるので、対角成分の和と等しくなりますね。
なので固有値が正しいことが検算できましたね。
同様に先程求めた残り2つの行列の検算をしてみましょう。
1つ目
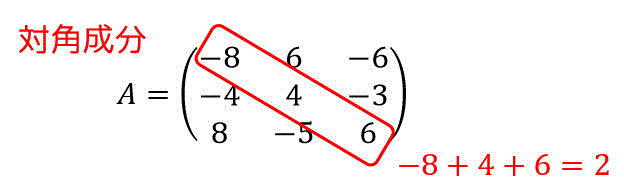
この行列の固有値は0と1（2重解）でしたね。なので、0 + 1 + 1 = 2 となり対角成分と等しくなります。
2重解の場合は2回カウントするのを忘れないようにしてください。
（3重解なら3回カウント、とにかく重解の数だけカウント）
2つ目
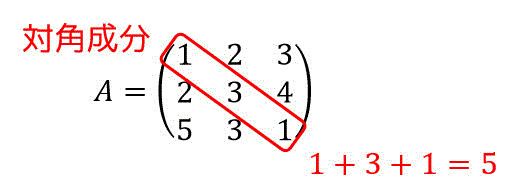
もう一方の行列の固有値は、-3, 0, 8 となり、和は5ですね。対角成分と等しくなりました。
４．練習問題
では、1問練習してみましょう。
4次正方行列の固有値ですが、先程紹介した2つのテクニックを使えばかなり簡単に解くことができます。
５．練習問題の解答
まずは、\( |A-tE| \) を作りましょう。
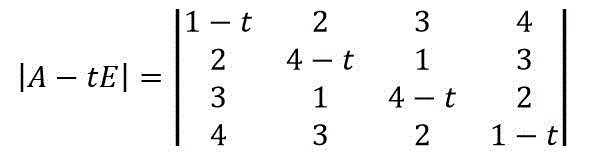
まずは、4×4の行列式を3×3の行列式にしましょう。
4次以上の固有値の場合、絶対値の等しい成分を見つけるのが難しくなるため、このように1つの行に残りの行をすべて足し込む技が有効です。
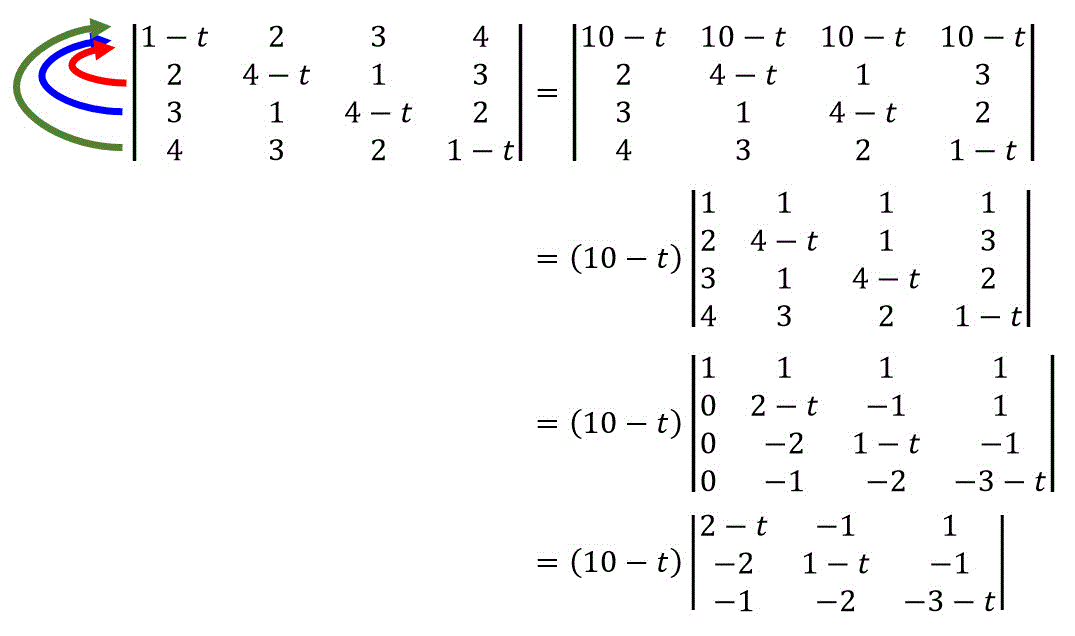
これで3×3の形にできましたね（ついでに固有値10も求めた）。
次に3×3の行列式を2×2の行列式にしていきましょう。
この変形では、絶対値が等しい2つの成分を利用します。
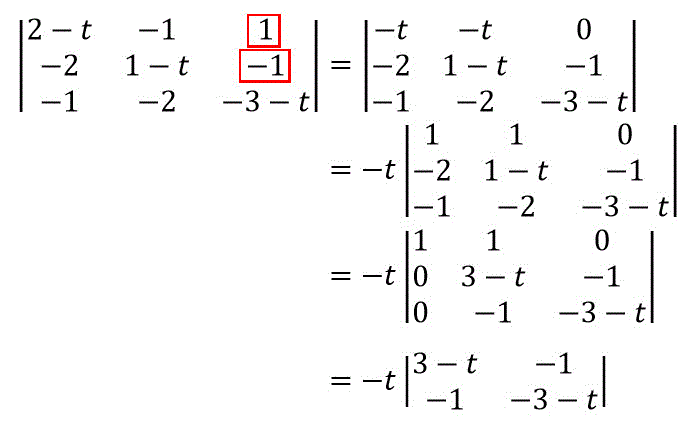
無事2×2の行列に変形できましたね（固有値0も求まった）。
あとはサラスの公式を使って残りの固有値も出してあげましょう！
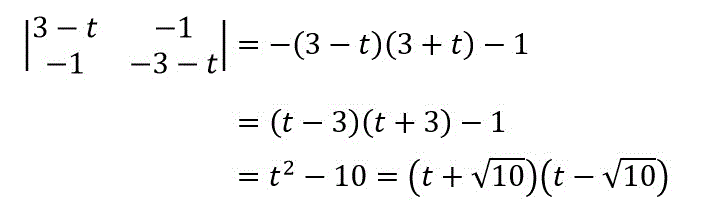
よって、
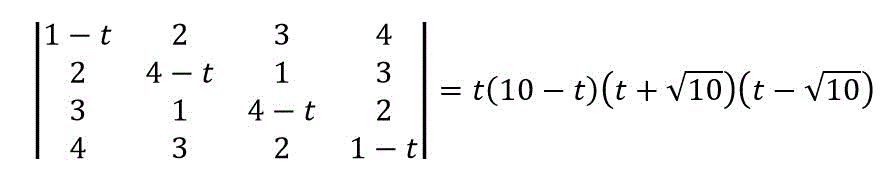
と変形でき、固有値は、\( 0 \), \( 10 \), \( \sqrt{10} \), \( -\sqrt{10} \) の4つとなりますね。
最後に検算をきちんとしておきましょう。
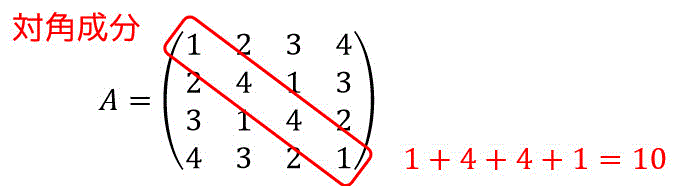
固有値のすべての和は10になり、対角成分の和と一致しますね。
６．さいごに
今回は固有値を素早くかつ正確に求めるテクニックを紹介しました。
固有値は線形代数の期末試験でほぼ確実に出る問題なので、確実に求められるようにしておきましょう。
固有値を間違えてしまうと、固有ベクトル（もしくは固有空間）の結果も誤った結果となり、連鎖的に間違えてしまうので固有値は正確かつ素早く求められるようにしましょう！ 検算も忘れずに！
*1:ミスの仕方には個人差があります。
関連広告・スポンサードリンク
