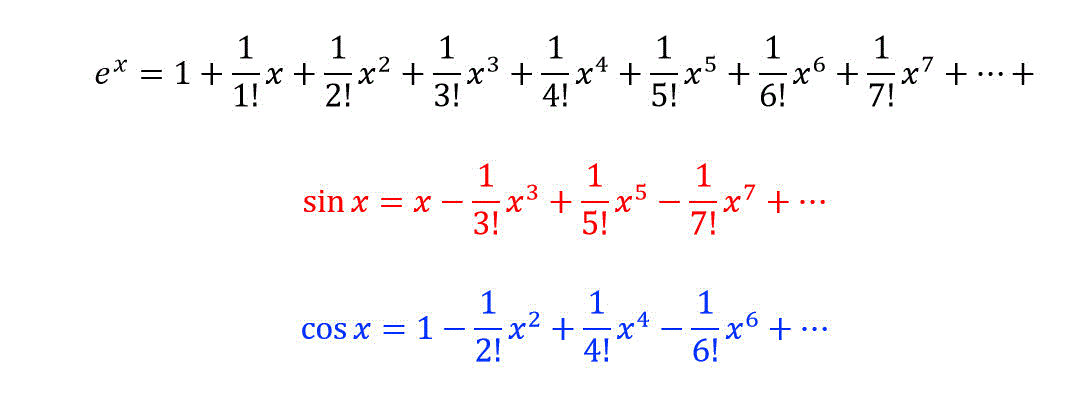
スポンサードリンク
こんにちは、ももやまです。
今回は解析学の最初ほうで習うマクローリン展開、テイラー展開についてまとめてみます。
注意:今回は特に何も書かれていない限り、関数は無限回微分することができる関数とします。
目次
スポンサードリンク
1.マクローリン展開
マクローリン展開を用いると、(無限に微分できる関数であれば)関数 \( f(x) \) を多項式のみで表してあげることができます。
マクローリン展開のことを、\( x = 0 \) のまわり(近傍)の展開と呼ぶことも多いです。名前の通り、マクローリン展開の精度は、 \( x \) が0に近づけば近づくほど精度が上がっていきます。
展開の公式は次のような公式で表されます。
関数 \( f(x) \) マクローリン展開すると、\[ \begin{align*}
f(x) & = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n
\\ & = f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3 + \cdots + \frac{f^{(n)}(0)}{n!} x^n + \cdots
\end{align*} \]
となる。
試しに1問マクローリン展開してみましょう。
例題1
(1) \( \sin x \) を5次の項までマクローリン展開しなさい。
(2) \( e^x \) を \( n \) 次の項までマクローリン展開しなさい。
解答1
(1)
まずは5次の項まで求めてみます。\[\begin{align}
f(x) = \sin x, \ \ \ f(0) = \sin 0 = 0 \\
f'(x) = \cos x, \ \ \ f'(0) = \cos 0 = 1 \\
f''(x) = - \sin x, \ \ \ f''(0) = - \sin 0 = 0 \\
f'''(x) = - \cos x, \ \ \ f'''(0) = - \cos 0 = -1 \\
f''''(x) = \sin x, \ \ \ f''''(0) = \sin 0 = 0 \\
f'''''(x) = \cos x, \ \ \ f'''''(0) = \cos 0 = 1 \\
\end{align}\]となります。あとは公式に代入します。\[ \begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3 + \frac{f''''(0)}{4!} x^4 + \frac{f'''''(0)}{5!} x^5
\\ & = x - \frac{1}{6} x^3 + \frac{1}{120} x^5
\end{align*} \]となる。
(2)
\( n \) 次の項までに求めるためには、\( n \) 次導関数を求める必要がある。
\( e^x \) の \( n \) 次導関数は \( e^x \) なので、\( n \) 次導関数は、\[\begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \cdots +\frac{f^{(n)}(0)}{n!} x^n \\ & = 1 + x + \frac{1}{2} x^2 + \cdots + \frac{1}{n!} x^n
\\ & = \sum_{k=0}^{n} \frac{1}{k!} x^k
\end{align*} \]となる。
ここで主要な関数のマクローリン展開を紹介します。
\[\begin{align} e^x = 1 + x + \frac{1}{2} x^2 + \frac{1}{6} x^3 + \frac{1}{24} x^4 + \frac{1}{120} x^5 + \cdots \\ \sin x = x - \frac{1}{6} x^3 + \frac{1}{120} x^5 + \cdots \\ \cos x = 1 - \frac{1}{2} x^2 + \frac{1}{24} x^4 - \frac{1}{720} x^6 + \cdots \\ \frac{1}{1-x} = 1 + x + x^2 + x^3 + x^4 + x^5 + \cdots
\\ \frac{1}{1+x} = 1 - x + x^2 - x^3 + x^4 - x^5 + \cdots
\\ \tan^{-1} x = x - \frac{1}{3} x^3 + \frac{1}{5} x^5 - \frac{1}{7} x^7 + \cdots
\\ \log (1 + x) = x - \frac{1}{2} x^2 + \frac{1}{3} x^3 - \frac{1}{4} x^4 + \frac{1}{5} x^5 + \cdots
\end{align}\]
これらのマクローリン展開を覚えておくと、色んな場面で便利かもしれません。
スポンサードリンク
2.テイラー展開
1のマクローリン展開の拡張バージョンがテイラー展開となります。
テイラー展開をすると、、関数 \( f(x) \) の\( x \fallingdotseq 0 \) だけでなく、様々な \( x \) のときの近似を考えることができるようになります(様々な \( x \) のまわりでの展開ができるようになります)。
関数 \( f(x) \) の \( x = a \) のまわりでのテイラー展開は、\[ \begin{align*}
f(x) & = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^n
\\ & = f(a) + \frac{f'(a)}{1!} (x-a) + \frac{f''(a)}{2!} (x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!} (x-a)^n + \cdots
\end{align*} \]
となる。
※マクローリン展開は \( a = 0 \) のときの展開
テイラー展開の \( x - a \) の部分は、\( x \) が \( a \) に近づけば近づくほど \( x - a \) は0に近づきますね。\( x - a \) の部分が0に近ければ近いほど、マクローリン展開と同じように誤差を小さくなります。
では、テイラー展開についても、1問練習してみましょう。
例題2
\( \log x \) を \( x = 1 \) のまわりで4次の項までテイラー展開しなさい。
解答2
関数を4回微分して、\( x = 1 \) を代入します。\[\begin{align}
f(1) = \log 1 = 0
f'(x) = \frac{1}{x} \ \ \ f'(x) = 1 \\
f''(x) = - \frac{1}{x^2} \ \ \ f'(x) = -1 \\
f'''(x) = \frac{2}{x^3} \ \ \ f'(x) = 2 \\
f''''(x) = - \frac{6}{x^4} \ \ \ f'(x) = -6 \\
\end{align}\]となります。あとは公式に代入。\[ \begin{align*}
f(x) & \fallingdotseq f(1) + \frac{f'(1)}{1!} (x-1) + \frac{f''(1)}{2!} (x-1)^2 + \frac{f'''(1)}{3!} (x-1)^3 + \frac{f''''(1)}{4!} (x-1)^4
\\ & = (x-1) -\frac{1}{2} (x-1)^2 + \frac{1}{3} (x-1)^3 - \frac{1}{4} (x-1)^4
\end{align*} \]となる。
スポンサードリンク
3.オイラーの公式
マクローリン展開を使うことでオイラーの公式を導くことができます。
\( e^x \), \( \sin x \), \( \cos x \) のマクローリン展開は、つぎのような式で現れます。
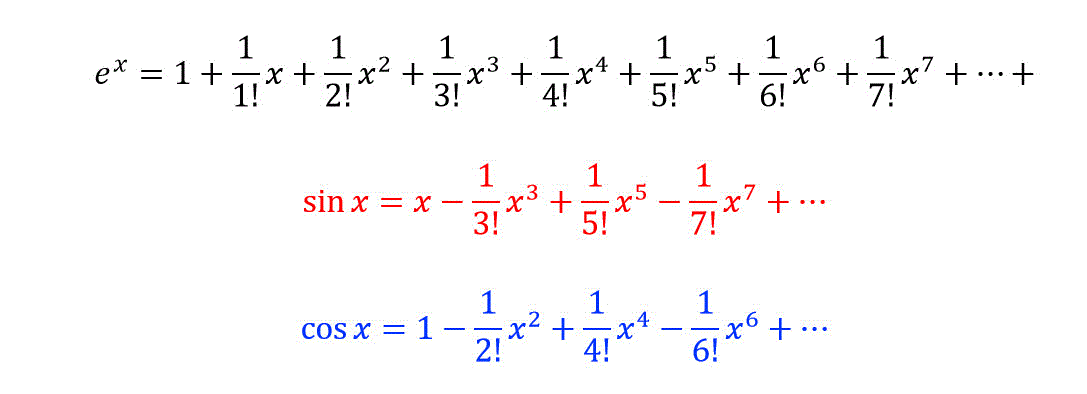
この3つの公式を使うことで、超有名公式であるオイラーの公式を導き出すことができます。
マクローリン展開の \( e^x \) を \( e^{ix} \) にチェンジしましょう。
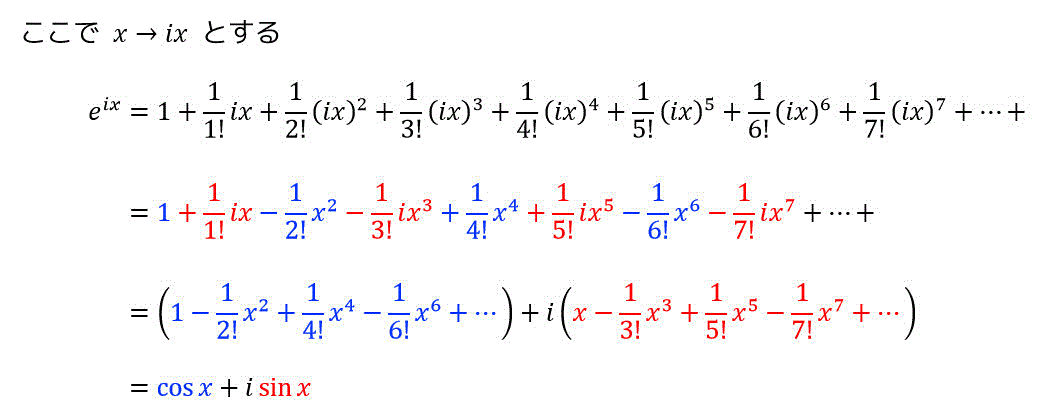
さらに、この公式に \( x = \pi \) を代入すると、オイラーの定理\[ e^{i \pi} = -1 \]を示すことができます。
4.マクローリン展開を用いた近似計算
マクローリン展開を使って関数の近似計算を行うことができます。
例題3
\( \log 1.1 \) の近似値を求めなさい。
解説3
\( \log (1+x) \) の3次までのマクローリン展開は、\[\log (1+x) \fallingdotseq x - \frac{1}{2} x^2 + \frac{1}{3} x^3\]となります。
あとは、\( x = 0.1 \) を代入してみましょう。 \[\begin{align*} & x - \frac{1}{2} x^2 + \frac{1}{3} x^3 \\ \fallingdotseq & \frac{1}{10} - \frac{1}{2} \cdot \frac{1}{100} + \frac{1}{3} \cdot \frac{1}{1000} \\ = & 0.1 - 0.005 + 0.0003 = 0.0953
\end{align*} \] となり、0.0953と求めることができます。
実際に \( \log 1.1 \) の計算をExcelや関数電卓ですると、0.0953102…となり、マクローリン展開を用いてうまく近似計算することができます*1。
5.マクローリン展開を用いた極限計算
マクローリン展開は極限計算に応用することができます。
\( \sin x \), \( e^x \), \( \cos x \), \( \tan x \) などのマクローリン展開を3次の項まで覚えておくと、ロピタルの定理を使ってもどうにもならない極限を求めることができます(ただし、正当法ではないので指示されたとき以外は記述答案では書かないことをおすすめします)。
例題4
次の極限計算を \( e^x \) のマクローリン展開を用いてしなさい。\[ \lim_{x \to 0} x \log x = \lim_{x \to 0} \frac{e^x - 1 - x}{x^2} \]
解説4
形を見ると、分母に \( x^2 \) の項があるので、不定形を解消するためには \( x^2 \) の項までのマクローリン展開が必要なことがわかります(3次以上の項を適用しないように注意)。2次の項まで求めると、\[ e^x = 1+ x + \frac{1}{2} x^2 \]となります。
上の極限式に代入すると、\[ \lim_{x \to 0} \frac{1 + x + \frac{1}{2} x^2 - 1 - x}{x^2} = \frac{1}{2} \]と求めることができます。
6.マクローリン展開の誤差見積もり
マクローリン展開を有限の項まで求めた場合は、誤差が発生します。
\( n \) 次のマクローリン展開をした場合でも、\( n + 1 \) 次以降の項は計算されないため、その分の誤差が発生しますね。関数 \( f(x) \) を \( n \) 次マクローリン展開したときの誤差は \( R_{n+1} (x) \) で表されます。この \( n + 1 \) の添字は、\( n + 1 \) 次以降の誤差という意味だと思ってください。
例えば、3次のマクローリン展開をした場合は、4次以降の項が考慮されませんね。
なので誤差は \( R_4 (x) \) で表されます。
また、関数を \( f(x) \) (無限の項までマクローリン展開した結果と等しい)と、関数 \( f(x) \) を \( n \) 次マクローリン展開したときの誤差 \( R_{n+1} (x) \) は、
\[ R_{n+1} (x) = f(x) - \left(
f(0) + \frac{f'(0)}{1} x + \frac{f''(0)}{2} x^2 + \cdots + \frac{f^{(n)}(0)}{n!} x^n
\right)\]と表されます。これを剰余項といい、この誤差は \[ R_{n+1} (x) = \frac{f^{(n+1)} (\theta x)}{(n+1) !} x^{n+1} \] であらされます。この \( \theta \) は角度ではなく、\( 0 \lt \theta \lt 1 \) の範囲にある変数だと思ってください。
\( \theta x \) のことをまとめて \( c \) などの変数とし、 \[ R_{n+1} (x) = \frac{f^{(n+1)} (c)}{(n+1) !} x^{n+1} \]として表す表記もあります。このときの \( c \) の範囲は、\( 0 \lt c \lt x \) だと思ってください(最大 \( x \) の誤差が発生する的な意味と考えてください)。
無限に微分できる関数 \( f(x) \) を \( n \) 回マクローリン展開したときの元の関数との誤差(剰余項) \( R_{n+1} \) は、\[ R_{n+1} (x) = \frac{f^{(n+1)} (\theta x)}{(n+1) !} x^{n+1} \]もしくは\[ R_{n+1} (x) = \frac{f^{(n+1)} (c)}{(n+1) !} x^{n+1} \]で表される。
ただし、\( 0 \lt \theta \lt 1 \)、\( 0 \lt c \lt x \) である。
(ラグランジュの剰余項と呼ばれます。)
1問例題を解いてみましょう。
例題5
\( e \) の値を求めたい。
(1) \( e^x \) を5次の項までマクローリン展開しなさい。
(2) \( x = 1 \) を代入し、\( e^x \) の値を小数第3位まで見積もりなさい。
(3) (2)の誤差が0.01未満であることを示しなさい。必要であれば \( e \lt 3 \) を使ってもよい。
解説5
(1)
\( e^x \) の5次までのマクローリン展開は、\[ e^x = 1 + x + \frac{1}{2} x^2 + \frac{1}{6} x^3 + \frac{1}{24} x^4 + \frac{1}{120} x^5 \] と表される。
(2)
\( x = 1 \) を代入すると、\[ \begin{align*} & 1 + 1 + \frac{1}{2} + \frac{1}{6}+ \frac{1}{24} + \frac{1}{120} \\ = & 2.5 + \frac{1}{6} + \frac{1}{24} + \frac{1}{120} \\ = & 2.5 + \frac{26}{120} \\ = & 2.5 + 0.217 = 2.717
\end{align*}\]となる。
(3)
今回は5次の項までの求めたので誤差は6次の項以降になる。よって \( R_6 (1) \) をもとめればよい。\[ R_{6} (1) = \frac{f^{(6)} (c)}{6 !} = \frac{e^{c}}{720}\]となる。ここで、\( x = 1 \) なので、\( 0 \lt c \lt 1 \) であることがわかる。
また、\( e \lt 3 \) なので、最大の誤差は、\[\frac{e^{c}}{720} \to \frac{e}{720} \to \frac{1}{240} < \frac{1}{100}\]となり、どんなに誤差が起こっても0.01未満で収まることが示せた。
マクローリン展開だけでなく、\( x = 0 \) 以外の展開(マクローリン展開以外の展開、)の、誤差の見積もりをすることができます。
無限に微分できる関数 \( f(x) \) を \( n \) 回 \( x = a \) の近くでテイラー展開したときの元の関数との誤差(剰余項) \( R_{n+1} \) は、\[ R_{n+1} (x) = \frac{f^{(n+1)} \left(\theta (x-a) \right)}{(n+1) !} (x-a)^{n+1} \]
ただし、\( 0 \lt \theta \lt 1 \) である。
7.練習問題
では何問か練習してみましょう。
練習1
\( \sin 4x \) を \( x^3 \) の項までマクローリン展開しなさい。
練習2
\( e^{2x} \cos x \) を \( x^3 \) の項までマクローリン展開しなさい。
練習3
\( \cos^2 x \) を \( x^4 \) の項までマクローリン展開しなさい。
練習4
\( |x| \lt 1 \) のとき、\[ \frac{1}{(1-x)(2-x)} \]のマクローリン展開を \( x^3 \) の項まで計算しなさい。
練習5
\( x^3 \) の \( x = 1 \) におけるテイラー展開を求めなさい。
練習6
\( \sqrt{1+x} \) について、つぎの問いに答えなさい。
(1) \( \sqrt{1+x} \) を \( x^3 \) の項までマクローリン展開しなさい。
(2) (1)の結果を用いて \( \sqrt{1.01} \) の値を小数第3位まで(第4位以降四捨五入)求めなさい。
練習7
つぎの2つの関数 \[ f(x) = \frac{1}{1-x} , \ \ g(x) = \cos x \] についてつぎの問いに答えなさい。ただし、\( |x| \lt 1 \) とする。
(1) 関数 \( f(x), g(x) \) の \( x^3 \) までの項のマクローリン展開を求めなさい。
(2) (1)を用いて関数 \[ h(x) = \frac{\cos x}{1-x} \] のマクローリン展開を \( x^3 \) の項まで求めなさい。
練習8
関数 \( \sin x \) について、つぎの問いに答えなさい。
(1) \( \sin x \) を \( x^6 \) の項までマクローリン展開しなさい。
(2) \( \sin 1 \) の値を(1)を用いて小数第3位まで表しなさい。
(3) (2)の誤差が0.001未満であることを示しなさい。
練習9
関数 \( f(x) = \tan x \) について、つぎの問いに答えなさい。
(\( \tan x \) のマクローリン展開は数検でよく出ます!)
(1) \( \tan x \) の導関数を求めなさい。
(2) \( \tan x \) の第2次~第5次の導関数を求めなさい。
(3) \( \tan x \) のマクローリン展開を \( x^5 \) の項まで求めなさい。
(4) (3)を用いて \( \tan 0.5 \) の値を小数第2位まで答えなさい。
(5) (3)を用いてつぎの極限を求めなさい。\[ \lim_{x \to 0} \frac{\tan x - \sin x}{x^3}\]
8.練習問題の答え
解答1
ひたすら微分しましょう。\[\begin{align}
f(x) = \sin 4x \ \ \ f(0) = \sin 0 = 0 \\
f'(x) = 4 \cos 4x \ \ \ f'(0) = \cos 0 = 4 \\
f''(x) = - 16 \sin 4x \ \ \ f''(0) = - \sin 0 = 0 \\
f'''(x) = - 64 \cos 4x \ \ \ f'''(0) = - \cos 0 = -64 \\
\end{align}\]となります。あとは公式に代入します。\[ \begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3
\\ & = 4x - \frac{32}{3} x^3
\end{align*} \]となる。
☆別解☆
\[ \sin x \fallingdotseq x - \frac{1}{6} x^3\]なので、\( x \to 4x \) として、\[ \sin x \fallingdotseq 4x - \frac{1}{6} (4x)^3 = 4x - \frac{32}{3} x^3\]となる。
解答2
ひたすら微分をしていく。\[
f(x) = e^{2x} \cos x \ \ \ f(0) = 1 \\
\begin{align*}
f'(x) & = 2 e^{2x} \cos x - e^{2x} \sin x \\ & = e^{2x} (2 \cos x - \sin x)
\end{align*}
\ \ \ f'(0) = 2 \]\[
\begin{align*}
f''(x) & = 2 e^{2x} (2 \cos x - \sin x) + e^{2x} (- 2 \sin x - \cos x) \\ & = e^{2x} (3 \cos x - 4 \sin x)
\end{align*}
\\ f''(0) = 3 \] \[
\begin{align*}
f'''(x) & = 2 e^{2x} (3 \cos x - 4 \sin x) + e^{2x} (- 3 \sin x - 4 \cos x) \\ & = e^{2x} (2 \cos x - 11 \sin x)
\end{align*}
\\ f'''(0) = 2
\]となります。あとは公式に代入します。\[ \begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!}
\\ & = 1 + 2x + \frac{3}{2} x^2 + \frac{1}{3} x^3
\end{align*} \]となる。
☆別解☆
\( e^{2x} \), \( \cos x \) のマクローリン展開を3次まで別々に計算する。\[ e^{2x} \fallingdotseq 1 + 2x + 2x^2 + \frac{4}{3} x^3 \]\[ \cos x \fallingdotseq 1 - \frac{1}{2} x^2\]あとは2つを掛け合わせるだけ。\[ \begin{align*}
e^{2x} \cos x & = \left( 1 + 2x + 2x^2 + \frac{4}{3} x^3 \right) \left( 1 - \frac{1}{2} x^2 \right)
\\ & = 1 + 2x + \left(2 - \frac{1}{2} \right) x^2 + \left( \frac{4}{3} - 1 \right) x^3 \\ & =
1 + 2x + \frac{3}{2} x^2 + \frac{1}{3} x^3
\end{align*}\]と計算できます。
解答3
まずは、半角の定理(知らなければ倍角や加法定理から導きましょう)で2乗をはずします。
\[ \cos^2 x = \frac{1 + \cos x}{2} \]となります。
あとはゴリ押し。\[\begin{align}
f(x) = \frac{1 + \cos 2x}{2} \ \ \ f(0) = 1 \\
f'(x) = - \sin 2x \ \ \ f'(0) = 0 \\
f''(x) = - 2 \cos 2x \ \ \ f''(0) = -2 \\
f'''(x) = 4 \sin 2x \ \ \ f'''(0) = 0 \\
f''''(x) = 8 \cos 2x \ \ \ f''''(0) = 8
\end{align}\]あとはいつものように公式。\[ \begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3 + \frac{f''''(0)}{4!} x^4
\\ & = 1 - x^2 + \frac{1}{3} x^4
\end{align*} \]となる。
☆別解☆
\( \cos x \) の4回微分まで求める。
\[ \cos x \fallingdotseq 1 - \frac{1}{2} x^2 + \frac{1}{24} x^4\]なので、\( \cos 2x \) の4回微分は、\( x \to 2x \) にして、\[ \cos 2x \fallingdotseq 1 - \frac{1}{2} (2x)^2 + \frac{1}{24} (2x)^4 = 1 - 2x^2 + \frac{2}{3} x^4\]となる。
あとは\[ \cos^2 x = \frac{1 + \cos x}{2} \]に \( \cos 2x \) のマクローリン展開の結果を突っ込む。\[\begin{align*} \cos^2 x & \fallingdotseq \frac{1}{2} + \frac{1}{2} \left( 1 - 2x^2 + \frac{2}{3} x^4 \right) \\ & = 1 - x^2 + \frac{1}{3} x^4
\end {align*} \]となる。
解答4
\[ \frac{1}{(1-x)(2-x)} = \frac{1}{1-x} - \frac{1}{2-x} \]となる(部分分数分解)。
あとは2つのマクローリン展開をそれぞれ求めればよい。
\[\begin{align}
f(x) = (2-x)^{-1} \ \ \ f(0) = \frac{1}{2} \\
f'(x) = (2-x)^{-2} \ \ \ f'(0) = \frac{1}{4} \\
f''(x) = 2 (2-x)^{-3} \ \ \ f''(0) = \frac{1}{4} \\
f'''(x) = 6 (2-x)^{-4} \ \ \ f'''(0) = \frac{3}{8} \\
\end{align}\]となり、\[ \begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3
\\ & = \frac{1}{2} + \frac{1}{4} x + \frac{1}{8} x^2 + \frac{1}{16} x^3
\end{align*} \]となる。また、\[ \frac{1}{1-x} = 1 + x + x^2 + x^3 \] なので、\[
\begin{align*}
\frac{1}{(1-x)(2-x)} & \fallingdotseq \left( 1 + x + x^2 + x^3 \right) - \left( \frac{1}{2} + \frac{1}{4} x + \frac{1}{8} x^2 + \frac{1}{16} x^3 \right) \\ & = \frac{1}{2} + \frac{3}{4} x^2 + \frac{7}{8} x^2 + \frac{15}{16} x^3
\end{align*} \]となる。
解答5
\[\begin{align}
f(x) = x^3 \ \ \ f(1) = 1 \\
f'(x) = 3x^2 \ \ \ f'(1) = 3 \\
f''(x) = 6x \ \ \ f''(1) = 6 \\
f'''(x) = 6 \ \ \ f'''(1) = 6 \\
\end{align}\]となる。4回微分以降は0になるまで、3次までの \( x = 1 \) におけるテイラー展開を考えればよい。よって、\[ \begin{align*}
f(x) & \fallingdotseq f(1) + \frac{f'(1)}{1!} (x-1) + \frac{f''(1)}{2!} (x-1)^2 + \frac{f'''(1)}{3!} (x-1)^3
\\ & = 1 + 3 (x-1) + 3 (x-1)^2 + (x-1)^3
\end{align*} \]と計算できる。
解答6
(1)
\( \sqrt{1+x} = (1+x)^{\frac{1}{2}} \) とする。\[\begin{align}
f(x) = (1+x)^{\frac{1}{2}} \ \ \ f(0) = 1 \\
f'(x) = \frac{1}{2} (1+x)^{- \frac{1}{2}} \ \ \ f'(0) = \frac{1}{2} \\
f''(x) = - \frac{1}{4} (1+x)^{- \frac{3}{2}} \ \ \ f''(0) = - \frac{1}{4} \\
f'''(x) = \frac{3}{8} (1+x)^{- \frac{5}{2}} \ \ \ f'''(0) = \frac{3}{8} \\
\end{align}\]となります。あとは公式に代入します。\[ \begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3
\\ & = 1 + \frac{1}{2} x - \frac{1}{8} x^2 + \frac{1}{16} x^3
\end{align*} \]となる。
(2)
\( x = 0.01 = 1/100 \) を代入する。
計算をしていくと、\( x^2 \) の項以降は非常に小さいので無視することができることがわかります。
\[ \begin{align*} &
1 + \frac{1}{2} x - \frac{1}{8} x^2
\\ = & 1 + \frac{1}{2} \cdot \frac{1}{100} - \frac{1}{8} \cdot \frac {1}{10000} \\ = & 1 + \frac{1}{200} \\ \fallingdotseq & 1 + 0.005 = 1.005
\end{align*} \]
となり、1.005となることがわかります。
解答7
(1) \[ \frac{1}{1-x} \fallingdotseq 1 + x + x^2 + x^3 \\ \cos x \fallingdotseq 1 - \frac{1}{2} x^2 \]となる。
(2) (1)より、\[\begin{align*} \frac{\cos x}{1-x} = \frac{1}{1-x} \cdot \cos x & =
\left(1 + x + x^2 + x^3 \right) \left(1 - \frac{1}{2} x^2 \right) \\ & =
1 + x + \left(1 - \frac{1}{2} \right) x^2 + \left(1 - \frac{1}{2} \right) x^3 \\ & = 1 + x + \frac{1}{2} x^2 + \frac{1}{2} x^3
\end{align*} \]となる。
解答8
(1)
\[ \sin x \fallingdotseq x - \frac{1}{6} x^3 + \frac{1}{120} x^5 \]
(2)
\( x = 1 \) を代入すると、\[ 1 - \frac{1}{6} + \frac{1}{120} = \frac{101}{120} \fallingdotseq 0.842 \]となる。
(3)
6次の項までの求めたので誤差は7次の項以降になる。
よって \( R_7 (1) \) をもとめればよい。\[ R_{7} (1) = \frac{f^{(7)} (c)}{7 !} = \frac{- \cos c}{5040}\]となる。ここで、\( x = 1 \) なので、\( 0 \lt c \lt 1 \) であることがわかる。
また、\( |- \cos x| \leqq 1 \) なので、最大の誤差は、\[\frac{- \cos c}{5040} \to \frac{1}{5040} \lt \frac{1}{1000}\]となり、どんなに誤差が起こっても0.001未満で収まることが示せた。
解答9
(1)
公式を忘れてしまった人は、\[ \tan x = \frac{\sin x}{ \cos x}\] と分数の微分公式から導出しましょう。導関数は\[ f'(x)= \frac{1}{\cos^2 x} \] となります。
(2)
(1)の形式のまま2次以降の導関数を計算すると溝にはまって詰みます。
なので、導関数の形を変えて挙げましょう。\[ f'(x)= \frac{1}{\cos^2 x} = 1 + \tan^2 x\] と変形ができます。
さらに合成関数の微分公式を使います。\( t = \tan x \) とすると、関数は \( f(t) = 1 + t^2 \) と変えることができます。
2次の導関数は、\[ \frac{df}{dt} = 2t = 2 \tan x , \ \ \ \frac{dt}{dx} = \frac{1}{\cos^2 x} = 1 + \tan^2 x \]なので、\[\begin{align*} \frac{df}{dx} & = \frac{df}{dt} \cdot \frac{dt}{dx} \\ & = 2 \tan x (1 + \tan^2 x) \\ & = 2 \tan x + 2 \tan^3 x
\end{align*} \]と求められます。
同様に \( t = \tan x \) として3次〜5次まで求めると、
3次のとき
\( f(t) = 2t^3 + 2t \) となる。
\[ \frac{df}{dt} = 6t^2 + 2 = 6 \tan^2 x + 2, \ \ \ \frac{dt}{dx} = \frac{1}{\cos^2 x} = 1 + \tan^2 x \]なので、\[\begin{align*} \frac{df}{dx} & = \frac{df}{dt} \cdot \frac{dt}{dx} \\ & = (6 \tan^2 x + 2)(1 + \tan^2 x) \\ & = 2 + (2 + 6) \tan^2 x+ 6 \tan^4 x \\ & = 2 + 8 \tan^2 x + 6 \tan^4 x
\end{align*} \]
4次のとき、
\( f(t) = 6t^4 + 8t^2 + 2 \) となる。
\[ \frac{df}{dt} = 24t^3 + 16t = 24 \tan^3 x + 16 \tan x, \ \ \ \frac{dt}{dx} = \frac{1}{\cos^2 x} = 1 + \tan^2 x \]なので、\[\begin{align*} \frac{df}{dx} & = \frac{df}{dt} \cdot \frac{dt}{dx} \\ & = (24 \tan^3 x + 16 \tan x)(1 + \tan^2 x) \\ & = 16 \tan x + (16 + 24) \tan^3 x+ 24 \tan^5 x \\ & = 16 + 40 \tan^3 x + 24 \tan^5 x
\end{align*} \]
5次のとき、
\( f(t) = 24t^5 + 40t^3 + 16t \) となる。
\[ \frac{df}{dt} = 120t^4 + 120 t^2 + 16 = 120 \tan^4 x + 120 \tan^2 x + 16 , \ \ \ \frac{dt}{dx} = \frac{1}{\cos^2 x} = 1 + \tan^2 x \]なので、\[\begin{align*} \frac{df}{dx} & = \frac{df}{dt} \cdot \frac{dt}{dx} \\ & = (120 \tan^4 x + 120 \tan^2 x + 16)(1 + \tan^2 x) \\ & = 16 + (120+16)\tan^2 x + (120 + 120) \tan^4 x + 120 \tan^6 x \\ & = 16 + 136 \tan^2 x + 240 \tan^4 x + 120 \tan^6 x
\end{align*} \]
とそれぞれ求めることができます。
(3)
(2)で求めた導関数に \( x = 0 \) を代入します。\[ f(0) = 0 \\ f'(0) = 1 \\ f''(0) = 0 \\ f'''(0) = 2 \\ f''''(0) = 0 \\ f'''''(0) = 16 \]となるので、マクローリン展開は、\[ \begin{align*}
f(x) & \fallingdotseq f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3 + \frac{f''''(0)}{4!} x^4 + \frac{f'''''(0)}{5!} x^5
\\ & = x + \frac{1}{3} x^3 + \frac{2}{15} x^5
\end{align*} \]と求めることができます。
(4)
(3)の答えに \( x = 0.5 = 1/2 \) を代入する。\[ \frac{1}{2} + \frac{1}{3} \cdot \frac{1}{4} + \frac{2}{15} \cdot \frac{1}{32} = 0.5 + \frac{11}{240} \fallingdotseq 0.55 \]と求めることができます。
(5)
分母が \( x^3 \) なので、\( \tan x \), \( \sin x \) ともに \( x^3 \) までのマクローリン展開を使えばよい。\[ \tan x = x + \frac{1}{3} x^3, \ \ \sin x = x - \frac{1}{6} x^3 \]として、\[ \lim_{x \to 0} \frac{\left( x + \frac{1}{3} x^3 \right) -\left( x - \frac{1}{6} x^3 \right)}{x^3} = \lim_{x \to 0} \frac{\frac{1}{2} x^3 }{x^3} = \frac{1}{2} \]と求めることができる。
9.さいごに
今回は、マクローリン展開・テイラー展開についてまとめをしました。
大学の解析学の期末試験・数検などに頻出する分野なのでぜひ理解しましょう!
主要な関数のマクローリン展開を覚えておくと、極限などをどうしても求めることができないときに使うと答えが出せるので最後の悪あがきに試してみましょう。
*1:もっと正確な値がほしいときは更に高次のマクローリン展開をすると正確な値を出すことができます。
関連広告・スポンサードリンク