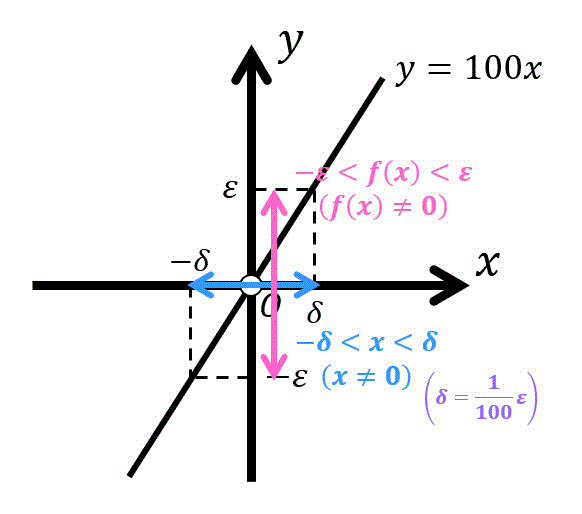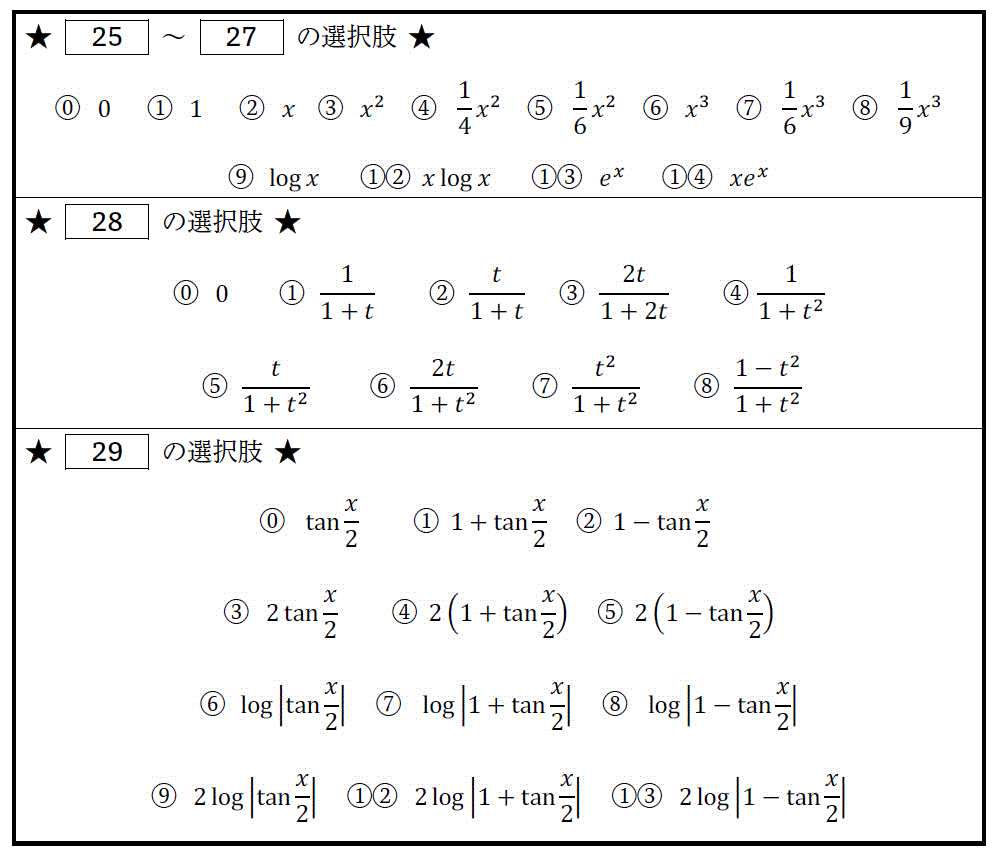スポンサードリンク
こんにちは、ももやまです。
「1年前期の解析学の試験まであと1日しかない、あきらめよう。」って思ってる人、諦めないでください!!
そこで、試験前日でも数3レベルの知識があれば3時間で総復習ができるように10題の練習問題を作成しました!
なお、εーδ(イプシロンデルタ)論法についての問題はここにはまとめていないため、もし必要な方はこちらの記事にて復習をお願いします。
こちらは微分編の解説記事です!
- 90分間で問題を解く。答えを回答フォームに入力する。
- 答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 時間があれば、合っている箇所も確認する。(青色と赤色の枠部分)
- 寝る。
時間がある人はじっくり、時間がない人は素早くこの記事にて1年前期の解析学の復習をしましょう!
それぞれの練習問題の解説では、
- 試験で必要な知識:青色の枠
- 試験で必要な解き方:赤色の枠
- 覚えておくと便利な公式: 緑色の枠
で要点をまとめています。
※ 高校レベルの極限計算、微分計算に不安がある人は、下の記事にて復習することを強くおすすめします。
スポンサードリンク
問題1. 極限計算
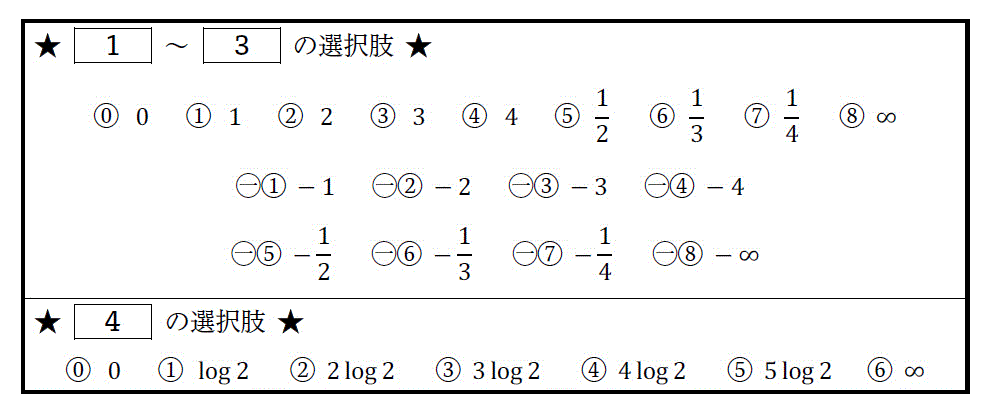
次の(1)〜(4)の極限を計算し、計算結果として正しいものを対応する選択肢の中から1つ選びなさい。(配点 10)
(1)\[
\lim_{x \to 1} \frac{ \sqrt{x+3} - 2 }{ x - 1} = \left[ \ \ \ 1 \ \ \ \right]
\]
(2) \[
\lim_{ x \to \infty } x \left\{ \log (x+2) - \log x \right\} = \left[ \ \ \ 2 \ \ \ \right]
\]
(3) \[
\lim_{ x \to 0 } \frac{ \sin x - \tan x }{ x^3 } = \left[ \ \ \ 3 \ \ \ \right]
\]
(4) \[
\lim_{ x \to \infty} \frac{1}{x} \log \left( 2^x + 4^x \right) = \left[ \ \ \ 4 \ \ \ \right]
\]
極限の問題の場合、解く方法は大きく分けて3通りあります。
- 高校数学までの方法で解く
- ロピタルの定理を使う
- (0に収束する問題の場合は)マクローリン展開を使う
今回は、2パターン(3パターン)両者の方法を説明していきたいと思います。
(1) 有理化して消すパターン
そのまま極限 \( x \to 1 \) を適用すると、\( 0 / 0 \) の不定形になってしまいますね。今回は(i), (ii)の2つの方法を用いて不定形を解消したいと思います。
(i) 高校数学までの方法で解く
シンプルにルート部分が邪魔なので、有理化してルートを消しましょう。すると、不定形が解消されます。
\[\begin{align*}
\lim_{x \to 1} \frac{ \sqrt{x+3} - 2 }{ x - 1} & =
\lim_{x \to 1} \frac{ ( \sqrt{x+3} - 2 )( \sqrt{x+3} + 2 ) }{ (x - 1)( \sqrt{x+3} + 2 )}
\\ & = \lim_{x \to 1} \frac{ \left( \sqrt{x+3} \right)^2 - 2^2 }{ (x - 1)( \sqrt{x+3} + 2 )}
\\ & = \lim_{x \to 1} \frac{ x + 3 - 4 }{ (x - 1)( \sqrt{x+3} + 2 )}
\\ & = \lim_{x \to 1} \frac{ x - 1 }{ (x - 1)( \sqrt{x+3} + 2 )}
\\ & = \lim_{x \to 1} \frac{ 1}{\sqrt{x+3} + 2 }
\\ & = \frac{1}{4}
\end{align*}\]
(ii) ロピタルの定理を使う
ロピタルの定理を使って解くこともできます。
(このレベルの程度の極限はロピタルを使ってほしくはないのですが…)
\[\begin{align*}
\lim_{x \to 1} \frac{ \sqrt{x+3} - 2 }{ x - 1} & = \lim_{x \to 1} \frac{ (\sqrt{x+3} - 2)' }{ (x - 1)' }
\\ & = \lim_{x \to 1} \frac{ \frac{1}{2 \sqrt{x+3} } }{ 1}
\\ & = \lim_{x \to 1} \frac{1}{2 \sqrt{x+3} }
\\ & = \frac{1}{4}
\end{align*}\]
(2) eの定義に関する問題
(i) 高校数学までの方法で解く
\( \log \) がついているので少しわかりにくいかもしれませんが、変形をすると自然対数 \( e \) の定義式\[
\lim_{x \to \infty} \left( 1 + \frac{1}{x} \right)^x = e
\]の形に変形することができます。
\[\begin{align*}
\lim_{ x \to \infty } x \left\{ \log (x+2) - \log x \right\} & = \lim_{ x \to \infty } x \left\{ \log \left( \frac{x+2}{x} \right) \right\}
\\ & = \lim_{ x \to \infty } x \log \left( 1 + \frac{2}{x} \right)
\\ & = \lim_{ x \to \infty } \log \left( 1 + \frac{2}{x} \right)^x
\\ & = \lim_{ t \to \infty } \log \left( 1 + \frac{2}{2t} \right)^{2t} \ \ \left( ここで \ x \to 2t \right)
\\ & = \lim_{ t \to \infty } \log \left\{ \left( 1 + \frac{1}{t} \right)^{t} \right\}^2
\\ & = \log e^2
\\ & = 2
\end{align*}\]途中で、\( x \to 2t \) とおいています。
(ii) ロピタルの公式を使う
一見分数の式がなくても、変形して分数の式を作ることでロピタルの形に持ち込むことができます。ただし、変形後の式がロピタルの公式の適用条件に満たしているかを確認すること。
\[\begin{align*}
\lim_{ x \to \infty } x \left\{ \log (x+2) - \log x \right\} & = \lim_{ x \to \infty } \frac{\log (x+2) - \log x}{ \frac{1}{x} }
\\ & = \lim_{ x \to \infty } \frac{ \left( \log (x+2) - \log x \right)'}{ \left( \frac{1}{x} \right)' }
\\ & = \lim_{ x \to \infty }\frac{ \frac{1}{x+2} - \frac{1}{x} }{ - \frac{1}{x^2} }
\\ & = \lim_{ x \to \infty } \frac{ \left( \frac{1}{x+2} - \frac{1}{x} \right) (-x^2) }{ - \frac{1}{x^2} \cdot (-x^2) }
\\ & = \lim_{ x \to \infty } \left( \frac{x - (x+2)}{x(x+2)} \right) (-x^2)
\\ & = \lim_{ x \to \infty } \left( \frac{-2}{x^2+2x} \right) (-x^2)
\\ & = \lim_{ x \to \infty } \frac{2x^2}{x^2 + 2x}
\\ & = \lim_{ x \to \infty } \frac{2}{1 + \frac{2}{x}}
\\ & = 2
\end{align*}\]
(3) 三角関数の極限
(i) 高校数学までの方法で解く
三角関数が出てくる極限は、\[
\lim_{x \to 0} \frac{\sin x}{x} = 1
\]の形が出てくるように変形を行います。\[\begin{align*}
\lim_{ x \to 0 } \frac{ \sin x - \tan x }{ x^3 } & = \lim_{ x \to 0 } \frac{ \sin x - \frac{ \sin x }{ \cos x } }{ x^3 }
\\ & = \lim_{ x \to 0 } \frac{ \sin x \cos x - \sin x }{ x^3 \cos x }
\\ & = \lim_{ x \to 0 } \frac{ \sin x (\cos x - 1) }{ x^3 \cos x }
\\ & = \lim_{ x \to 0 } \frac{ \sin x (\cos x - 1)(\cos x + 1) }{ x^3 \cos x (\cos x + 1) }
\\ & = \lim_{ x \to 0 } \frac{ \sin x (\cos^2 x - 1) }{ x^3 \cos x (\cos x + 1) }
\\ & = \lim_{ x \to 0 } \frac{ \sin x (- \sin^2 x) }{ x^3 \cos x (\cos x + 1) }
\\ & = \lim_{ x \to 0 } \frac{ - \sin^3 x }{ x^3 \cos x (\cos x + 1) }
\\ & = \lim_{ x \to 0 } (-1) \cdot \underbrace{ \frac{ \sin^3 x }{ x^3 } }_{1} \cdot \underbrace{\frac{1}{\cos x (\cos x + 1)}}_{ \frac{1}{2} }
\\ & = - \frac{1}{2}
\end{align*}\]
(ii) ロピタルの定理を使う
ロピタルの定理を使って
\[\begin{align*}
\lim_{ x \to 0 } \frac{ \sin x - \tan x }{ x^3 } & = \lim_{ x \to 0 } \frac{ (\sin x - \tan x)' }{ (x^3)' }
\\ & = \lim_{ x \to 0 } \frac{ \cos x - \frac{1}{ \cos^2 x } }{ 3x^2 }
\\ & = \lim_{ x \to 0 } \frac{ \cos^3 x - 1 }{ 3x^2 \cos^2 x}
\\ & = \lim_{ x \to 0 } \frac{ \cos^3 x - 1 }{ 3x^2} \times \lim_{ x \to 0 } \frac{1}{ \cos^2 x }
\\ & = \lim_{ x \to 0 } \frac{ ( \cos^3 x - 1 )' }{ (3x^2)'} \times 1
\\ & = \lim_{ x \to 0 } \frac{ 3 \cos^2 x ( - \sin x ) }{6x}
\\ & = \lim_{ x \to 0 } \underbrace{ \frac{ \sin x }{x} }_{ 1 } \cdot \underbrace{ \cos^2 x }_{ 1 } \cdot \frac{-3}{6}
\\ & = - \frac{1}{2}
\end{align*}\]
途中の極限分配は、分配した2つの極限がともに収束するときだけ可能です。
(iii) マクローリン展開を使う
0に収束させるタイプの極限は、三角関数やルートなどに対してマクローリン展開を行うことでかなり簡単に極限を求めることができます。
\( x \to 0 \) に収束させるタイプの極限では、以下のマクローリン展開を使うことで早く計算ができることもある。\[
\sin x = x - \frac{1}{6} x^3 + \frac{1}{120} x^5 + \cdots
\]\[
\cos x = 1 - \frac{1}{6} x^2 + \frac{1}{24} x^4 + \cdots
\]\[
\tan x = x + \frac{1}{3} x^3 + \frac{2}{15} x^5 + \cdots
\]\[
e^x = 1 + x + \frac{1}{2} x^2 + \frac{1}{6} x^3 + \frac{1}{24} x^4 + \cdots
\]
※ マクローリン展開を用いて極限を求める方法のより詳しい解説記事はこちら!
今回の場合、分母が \( x^3 \) なので、\( \sin x \), \( \tan x \) も以下のように3次の項までのマクローリン展開を考慮すればOKです。
(4次の項以降はすべて \( x \to 0 \) により、0になる)
\[
\sin x = x - \frac{1}{6} x^3 + o_1( x^4 )
\]\[
\tan x = x + \frac{1}{3} x^3 + o_2( x^4 )
\]
\[\begin{align*}
\lim_{ x \to 0 } \frac{ \sin x - \tan x }{ x^3 } & = \lim_{ x \to 0 } \frac{ x - \frac{1}{6} x^3 + o( x^4 ) - \left( x + \frac{1}{3} x^3 + o( x^4 ) \right) }{ x^3 }
\\ & = \lim_{ x \to 0 } \frac{ - \frac{1}{2} x^3 + o_1(x^4) - o_2(x^4) }{ x^3 }
\\ & = \lim_{ x \to 0 } \left( - \frac{1}{2} + \frac{ o_1(x^4) - o_2(x^4) }{ x^3 } \right)
\\ & = - \frac{1}{2}
\end{align*}\]
※ 途中過程が不要な場合、かなりの力を発揮するはずです!
(4) はさみうちの原理
(i) 高校数学までの方法で解く
(1)~(3)のように、有理化、\( e \) の定義、基本公式の形への持ち込みができません。そこで、今回ははさみうちの原理を使って解いてみましょう。
十分大きい \( x \) において、\[
g(x) \leqq f(x) \leqq h(x)
\]となっており、さらに\[
\lim_{x \to \infty} g(x) = \lim_{x \to \infty} h(x) = \alpha
\]が成立するとき、\[
\lim_{x \to \infty} f(x) = \alpha
\]となる。
ここで、\( 2^x < 4^x \) なので、\[
4^x < 2^x + 4^x < 2 \cdot 4^x
\]\[
\frac{1}{x} \log 4^x < \frac{1}{x} \log ( 2^x + 4^x ) < \frac{1}{x} \log (2 \cdot 4^x)
\]が成立します。
ここで、\[\begin{align*}
\lim_{ x \to \infty} \frac{1}{x} \log 4^x & = \lim_{ x \to \infty} \frac{\log 4^x}{x}
\\ & = \lim_{ x \to \infty} \frac{x \log 4}{x}
\\ & = \lim_{ x \to \infty} \frac{\log 4}{1}
\\ & = \log 4
\end{align*}\]\[\begin{align*}
\lim_{ x \to \infty} \frac{1}{x} \log ( 2\cdot 4^x ) & = \lim_{ x \to \infty} \frac{\log (2 \cdot 4^x)}{x}
\\ & = \lim_{ x \to \infty} \left( \frac{\log 2}{x} + \frac{\log 4^x}{x} \right)
\\ & = \lim_{ x \to \infty} \left( \frac{\log 2}{x} + \frac{x \log 4}{x} \right)
\\ & = \lim_{ x \to \infty} \left( \underbrace{ \frac{\log 2}{x} }_{ 0 } + \log 4 \right)
\\ & = \log 4
\end{align*}\]となるので、はさみうちの原理により、\[\begin{align*}
\lim_{ x \to \infty} \frac{1}{x} \log ( 2^x + 4^x ) & = \log 4
\\ & = 2 \log 2
\end{align*}\]となります。
(ii) ロピタルの定理を使う
ロピタルの定理を使うと、はさみうちを使わずに極限計算が可能です。\[\begin{align*}
\lim_{ x \to \infty} \frac{1}{x} \log \left( 2^x + 4^x \right) & = \lim_{ x \to \infty} \frac{ \log ( 2^x + 4^x ) }{x}
\\ & = \lim_{ x \to \infty} \frac{( \log(2^x + 4^x) )'}{(x)'}
\\ & = \lim_{ x \to \infty} \frac{ \frac{\log 2 \cdot 2^x + \log 4 \cdot 4^x}{2^x + 4^x} }{1}
\\ & = \lim_{ x \to \infty} \frac{\log 2 \cdot 2^x + \log 4 \cdot 4^x}{2^x + 4^x}
\\ & = \lim_{ x \to \infty} \frac{\log 2 \cdot \left( \frac{2}{4} \right)^x + \log 4}{\left( \frac{2}{4} \right)^x + 1}
\\ & = \log 4
\\ & = 2 \log 2
\end{align*}\]
★ マーク解答 ★
No.01: 7 [2点]
No.02: 2 [2点]
No.03: -5 [3点]
No.04: 2 [2点]
ロピタルの定理について、ここでまとめておきましょう。
極限\[
\lim_{x \to a} \frac{f(x)}{g(x)}
\]が \( \frac{0}{0} \) もしくは \( \frac{\infty}{\infty} \) の不定形で、かつ\[
\lim_{x \to a} \frac{f'(x)}{g'(x)}
\]が収束 or 無限大 \( \pm \infty \) になるとき、\[
\lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)}
\]が成立する。
ロピタルの定理がよくわからない、使える条件があやふやだという人は、こちらの記事にて復習をしましょう!
スポンサードリンク
問題2. 逆三角関数
次の(1)〜(3)の問いに答えなさい。(配点 10)
(1) 次の関数 \( f(x) = 2 \cos^{-1} (2x-1) \) について、(i), (ii)にある空欄を埋めなさい。
(i) \( f(x) \) の定義域は [ 5 ] となる。
(ii) \( f(x) \) の値域は [ 6 ] となる。

(2) 次の計算をしなさい。\[
\sin^{-1} \left( - \frac{ \sqrt{3} }{2} \right) + \cos^{-1} \frac{ \sqrt{2} }{2} + \tan^{-1} \frac{ \sqrt{3} }{3} = \left[ \ \ \ 7 \ \ \ \right]
\]
(3) 次の計算をしなさい。\[
\tan^{-1} \frac{1}{2} + \tan^{-1} \frac{1}{3} = \left[ \ \ \ 8 \ \ \ \right]
\]
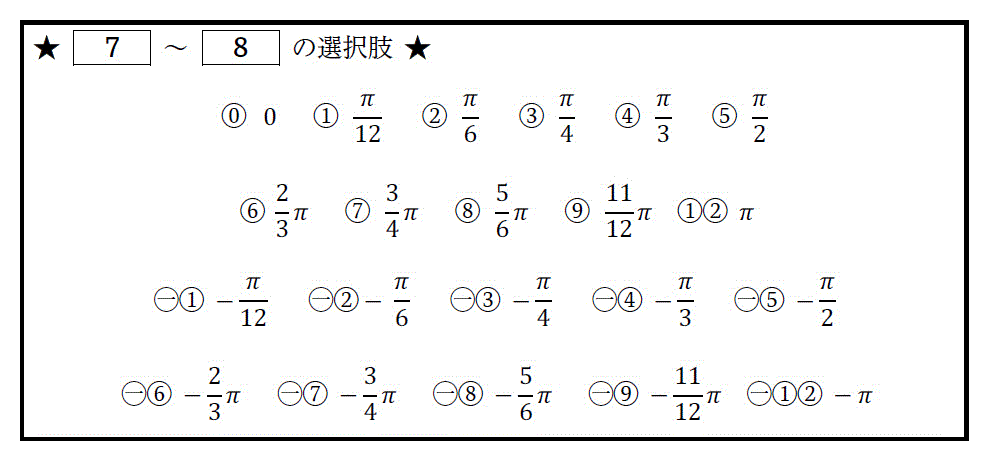
(1) 逆三角関数の定義域と値域
まずは逆三角関数の定義域と値域を復習しましょう。
※ 不等号に = が含まれるかどうかも非常に重要です。
| 関数 | 定義域 | 値域 |
|---|---|---|
| \( y = \sin^{-1} x \) | \( -1 \leqq x < 1 \) | \( - \frac{\pi}{2} \leqq y \leqq \frac{\pi}{2} \) |
| \( y = \cos^{-1} x \) | \( -1 \leqq x < 1 \) | \( 0 \leqq y \leqq \pi \) |
| \( y = \tan^{-1} x \) | 実数全体 | \( - \frac{\pi}{2} < y <\frac{\pi}{2} \) |
ちょっと難しいと思った人は、\( x = \sin y \), \( x = \cos y \), \( x = \tan y \) の取りうる \( x \), \( y \) の範囲を考えるのがおすすめです。
今回の場合は、\( f(x) = \cos^{-1} (2x + 1) \) ですね。
(i) 定義域
\( \cos^{-1} t \) の \( t \) が取りうる値の範囲は \( -1 \leqq t \leqq 1 \) である。
この \( t \) を \( 2x-1 \) に変えると \( -1 \leqq 2x-1 \leqq 1 \) となる。よって、\[
-1 \leqq 2x + 1 \leqq 1
\]\[
0 \leqq 2x \leqq 2
\]\[
0 \leqq x \leqq 1
\]となるため、定義域は \( 0 \leqq x \leqq 1 \) となる。(マーク番号: 1)
(ii) 値域
\( \cos^{-1} t \) が取りうる値の範囲は \( 0 \leqq \cos^{-1} t \leqq \pi \) である。
今回は \( 2 \cos^{-1} t \) なので、取りうる値の範囲は \( 0 \leqq 2 \cos^{-1} t \leqq 2 \pi \) となる。
よって、\( f(x) = 2 \cos^{-1} (2x-1) \) が取りうる値の範囲は \( 0 \leqq f(x) \leqq 2 \pi \) となる。(マーク番号: 7)
★ マーク解答 ★
No.05: 1 [2点]
No.06: 8 [2点]
(2) 逆三角関数の定義域と値域
1つ1つ順番に処理をしましょう。
(i) [意味] \( \sin y = - \frac{ \sqrt{3} }{2} \) となるような \( y \) の値は?\[
\sin^{-1} \left( - \frac{ \sqrt{3} }{2} \right) = - \frac{\pi}{3}
\]
(ii) [意味] \( \cos y = \frac{ \sqrt{2} }{2} \) となるような \( y \) の値は?\[ \cos^{-1} \frac{ \sqrt{2} }{2} = \frac{\pi}{4}
\]
(iii) [意味] \( \tan y = \frac{ \sqrt{3} }{3} \) となるような \( y \) の値は?\[ \tan^{-1} \frac{ \sqrt{3} }{3} = \frac{\pi}{6}
\]
これら3つを全部足すと、\[\begin{align*}
& \sin^{-1} \left( - \frac{ \sqrt{3} }{2} \right) + \cos^{-1} \frac{ \sqrt{2} }{2} + \tan^{-1} \frac{ \sqrt{3} }{3}
\\ = \ & - \frac{\pi}{3} + \frac{\pi}{4} + \frac{\pi}{6}
\\ = \ & \frac{ -4 \pi + 3 \pi + 2 \pi }{12}
\\ = \ & \frac{ \pi }{12}
\end{align*}\]となる。
(3) tanの加法定理
\[
\tan a = \frac{1}{2} , \ \ \ \tan b = \frac{1}{3}
\]となるような \( a \), \( b\) なんて普通の人はわかりませんよね。
このように、知らない三角関数の値が出てきたときは、加法定理などを使って知っている三角関数の値に持ち込むのがセオリーです。
ここで、\[
\tan^{-1} \frac{1}{2} = a , \ \ \ \tan^{-1} \frac{1}{3} = b
\]とおきます。すると、\[
\tan a = \frac{1}{2} , \ \ \ , \tan b = \frac{1}{3}
\]となりますね。
tanの加法定理を使うと、\[\begin{align*}
\tan (a+b) & = \frac{\tan a + \tan b}{1 - \tan a \tan b}
\\ & = \frac{ \frac{1}{2} + \frac{1}{3} }{ 1 - \frac{1}{2} \cdot \frac{1}{3} }
\\ & = \frac{ \frac{5}{6} }{ \frac{5}{6} }
\\ & = 1
\end{align*}\]となりますね。
よって、\[
\tan (a+b) = 1
\]\[
\tan^{-1} ( \tan (a+b) ) = \tan^{-1} 1
\]\[
a + b = \tan^{-1} \frac{1}{2} + \tan^{-1} \frac{1}{3} = \frac{\pi}{4}
\]と計算することができます。
※ 全然解き方がわからなかったとしても、\[
\tan^{-1} \frac{1}{3} < \tan^{-1} \frac{1}{2} < \tan^{-1} \frac{ \sqrt{3} }{3}
\]だから、少なくとも\[
2 \tan^{-1} \frac{ \sqrt{3} }{3} = \frac{ \pi }{ 3 }
\]よりは小さい答えだな…。と思って3択くらいまでは絞りましょう。
★ マーク解答 ★
No.07: 1 [3点]
No.08: 3 [3点]
逆三角関数の復習をしたい人はこちらから!
また、念の為に tan の加法定理公式を確認しておきましょう。
\[
\tan (a \textcolor{blue}{+} b) = \frac{ \tan a \textcolor{blue}{+} \tan b }{1 \textcolor{red}{-} \tan a \tan b}
\]\[
\tan (a \textcolor{red}{-} b) = \frac{ \tan a \textcolor{red}{-} \tan b }{1 \textcolor{blue}{+} \tan a \tan b}
\]※ 符号に要注意!!
スポンサードリンク
問題3. 微分可能性
次の(1), (2)の問いに答えなさい。
(1) 次の(i), (ii) の関数の連続性、微分可能性について述べた文章として正しいものを選びなさい。
(i) 回答番号 [ 9 ]\[
f(x) = x |x|
\]
(ii) 回答番号 [ 10 ]\[
f(x) = \left\{ \begin{array}{l} x \sin \frac{1}{x} \ \ ( x \not = 0 ) \\
0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ( x = 0 )
\end{array} \right.
\]

(2) 次の関数\[
f(x) = \left\{ \begin{array}{l} 2x^2 - 6x + a \ \ ( x \geqq 1 ) \\
bx^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ( x < 1 ) \end{array} \right.
\]が \( x = 1 \) で微分可能となるような定数 \( a \), \( b \) の値を求め、その値を入力しなさい。
回答番号 \( a = \left[ \ \ 11 \ \ \right] \), \( b = \left[ \ \ 12 \ \ \right] \)
(1) 連続性、微分可能性の判定
まずは、連続性と微分可能性の判定方法を確認しましょう。
\[
\lim_{ x \to a } f(x) = f(a)
\]つまり\[
\lim_{ x \to a + 0 } f(x) = \lim_{ x \to a - 0 } f(x) = f(a)
\]が成立するとき、関数 \( f(x) \) は \( x = a \)で連続であるといえる。
\[
\lim_{ x \to a } \frac{ f(a+h) - f(a) }{h}
\]が存在するとき、言い換えると、それぞれの方向からの極限\[
\lim_{ h \to + 0 } \frac{ f(a+h) - f(a) }{h} = \lim_{ h \to - 0 } \frac{ f(a+h) - f(a) }{h}
\]が成立するとき、関数 \( f(x) \) は \( x = a \)で微分可能であるといえる。
なお、ある関数が \( x = a \) で微分可能である場合、必ず \( x = a \) で連続である。
※ 逆に連続であるからといって微分可能であるとは限らないので注意!!
(i) [連続性の判定]
\[\begin{align*}
\lim_{ x \to +0 } x |x| & = \lim_{x \to +0} x^2
\\ & = 0
\end{align*}\]
\[\begin{align*} \lim_{ x \to -0 } x |x| & = \lim_{x \to +0} -x^2
\\ & = 0
\end{align*}\]
より、\[
\lim_{ x \to +0 } x |x| = \lim_{ x \to -0 } x |x| = 0
\]を満たすので連続であるといえる。
(i) [微分可能性の判定]
\[ \begin{align*}
\lim_{ h \to +0 } \frac{ f(0+h) - f(0) }{h} & = \lim_{ h \to +0 } \frac{ h^2 - 0 }{h}
\\ & = \lim_{ h \to +0 } h
\\ & = 0
\end{align*}\] \[ \begin{align*}
\lim_{ h \to -0 } \frac{ f(0+h) - f(0) }{h} & = \lim_{ h \to -0 } \frac{ -h^2 - 0 }{h}
\\ & = \lim_{ h \to -0 } -h
\\ & = 0
\end{align*}\]
(ii) 連続性の判定
\[
\lim_{x \to a } f(x) = f(a)
\]が成立するかを確認する。
ここで、\[
0 \leqq \left| \sin \frac{1}{x} \right| \leqq 1
\]なので[1]意味的には、\[ -1 \leqq \sin \frac{1}{x} \leqq 1 \]と同じ。 、\[
0 \leqq \left| x \sin \frac{1}{x} \right| \leqq |x|
\]も成立する。
ここで、\[
\lim_{x \to 0} 0 = 0 , \ \ \ \lim_{x \to 0 } |x| = 0
\]なので、はさみうちの原理により、\[
\lim_{x \to 0 } \left| x \sin \frac{1}{x} \right| = 0
\]となる。よって、\[
\lim_{x \to 0} f(x) = f(0)
\]となり、連続であることがわかる。
(ii) 微分可能性の判定
\[\begin{align*}
\lim_{h \to 0} \frac{ f(0 + h) - f(0) }{h} & = \lim_{h \to 0} \frac{ h \sin \frac{1}{h} - 0 }{ h }
\\ & = \lim_{h \to 0} \sin \frac{1}{h}
\end{align*}\]
ここで、極限\[
\lim_{h \to 0} \sin \frac{1}{h}
\]は、-1から1の範囲で振動してしまうため極限値をもたない(収束しない)。
よって、微分可能ではない。
★ マーク解答 ★
No.09: 0 [3点]
No.10: 1 [3点]
(2) 微分可能性のちょっと応用
\( x = 1 \) で微分可能であるこということは、\( x = 1 \) で連続であるということである。
そのため、\[
\lim_{x \to 1+0} (2x^2 - 6x +a) = \lim_{x \to 1-0} bx^2
\]\[
-4 + a = b
\]が成立する。よって、\( b - a = -4 \) の関係式が成り立つ。
また、\( x = 1 \) で微分可能であるということは\[
\lim_{h \to +0} \frac{f(1+h) - f(1)}{h} = \lim_{h \to -0} \frac{f(1+h) - f(1)}{h}
\]が成立する。
ここで、\[\begin{align*}
\lim_{h \to +0} \frac{f(1+h) - f(1)}{h} & = \lim_{h \to +0} \frac{ 2(1+h)^2 - 6(1+h) + a - (2-6+a)}{h}
\\ & = \lim_{h \to +0} \frac{ 2h^2 + 4h + 2 - 6h - 6 + a + 4 - a}{h}
\\ & = \lim_{h \to +0} \frac{2h^2 - 2h}{h}
\\ & = \lim_{h \to +0} \left( 2h - 2 \right)
\\ & = -2
\end{align*}\] \[\begin{align*}
\lim_{h \to -0} \frac{f(1+h) - f(1)}{h} & = \lim_{h \to -0} \frac{ b(1+h)^2 - (2-6+a)}{h}
\\ & = \lim_{h \to -0} \frac{bh^2 + 2hb + b - a + 4}{h}
\\ & = \lim_{h \to -0} \left( bh + 2b + \frac{b-a+4}{h} \right)
\\ & = \lim_{h \to -0} \left( bh + 2b \right) \ \ \ \ ( \because \ b - a = -4 )
\\ & = 2b \end{align*} \]
となるので、\[\begin{align*}
\lim_{h \to +0} \frac{f(1+h) - f(1)}{h} & = \lim_{h \to -0} \frac{f(1+h) - f(1)}{h} \\
-2 = 2b
\end{align*}\] が成立。よって、\( b = -1 \) となる。
さらに、\( a -4 = b \) より、\( a = 3 \) と求められる。
[余談] (2)のグラフを図示してみるとこんな感じになります。図示してみると、確かに \( x = 1 \) の部分でなめらかにつながっていることがわかりますね。★ マーク解答 ★
No.11: 3 [2点]
No.12: -1 [2点]
問題4. 微分法
次の(1)〜(3)の関数を微分し、導関数を求めなさい。
(1)\[
y = ( \sin x )^{ \cos x } \] \[ \frac{dy}{dx} = \left[ \ \ 13 \ \ \right] \left( \cos x \cdot \left[ \ \ 14 \ \ \right] - \sin x \cdot \left[ \ \ 15 \ \ \right]\right)
\]
(2) \[
y = \sin^{-1} \left( x^2 \right)
\]\[
\frac{dy}{dx} = \left[ \ \ 16 \ \ \right]
\]
(3) \[
y = \int^{x^2}_{1} \frac{t}{t^3 + 1} \ dt
\]\[
\frac{dy}{dx} = \left[ \ \ 17 \ \ \right]
\]

(1) 対数微分法・商の微分公式
※ 問題4の解説では \( \frac{dy}{dx} = y' \) と表記しましょう。
今回のように (xの関数) の (xの関数) 乗になっている場合は、両辺に対数を取ってから微分を行う対数微分法がかなり有効です。両辺に対数を取ると、\[\begin{align*}
\log y & = \log ( \sin x )^{ \cos x }
\\ \log y & = \cos x \log ( \sin x )
\end{align*}\]となる。
ここで、両辺を微分すると、\[\begin{align*}
\frac{y'}{y} & = - \sin x \log ( \sin x ) + \cos x \cdot \frac{ \cos x }{ \sin x }
\\ & = - \sin x \log ( \sin x ) + \cos x \cdot \frac{1}{ \tan x }
\\ & = \cos x \cdot \frac{1}{ \tan x } - \sin x \log ( \sin x )
\end{align*}\]となる。
最後に \( y \) を移項すると\[\begin{align*}
y' & = y \left\{ \cos x \cdot \frac{1}{ \tan x } - \sin x \log ( \sin x ) \right\}
\\ & = ( \sin x )^{\cos x} \left\{ \cos x \cdot \frac{1}{ \tan x } - \sin x \log ( \sin x ) \right\}
\end{align*}\]となるため、導関数は\[
\frac{dy}{dx} = ( \sin x )^{\cos x} \left\{ \cos x \cdot \frac{1}{ \tan x } - \sin x \log ( \sin x ) \right\}
\]となる。
\( y = f(x) g(x) \) と表されている関数は、\[
\frac{dy}{dx} = f'(x) g(x) + f(x) g'(x)
\]で微分できる。
例えば \( x \log x \) であれば、\( f(x) = x \), \( g(x) = \log x \) として、\[\begin{align*}
\frac{d}{dx} & = f'(x) g(x) + f(x) g'(x)
\\ & = (x)' \log x + x ( \log x )'
\\ & = 1 \cdot \log x + x \cdot \frac{1}{x}
\\ & = \log x + 1
\end{align*}\]となる。
今回のように (xの関数) の (xの関数) 乗になっている場合は、両辺に対数を取ってから微分を行う対数微分法を用いると素早く計算できる。
Step1. 両辺に対数を取る。例えば \( y = x^x \) であれば\[\begin{align*}
\log y & = \log x^x
\\ & = x \log x
\end{align*}\]となる。
両辺を \( x \) で微分する。\[\begin{align*}
\frac{y'}{y} & = \log x + x \cdot \frac{1}{x}
\\ & = \log x + 1
\end{align*}\]
Step3. 左辺にある \( y \) を右辺にもっていく。\[\begin{align*}
y' & = y ( \log x + 1 )
\\ & = x^x ( \log x + 1 )
\end{align*}\]
※ \( \frac{dy}{dx} \) を \( y' \) と表記しています。
(2) 逆三角関数の微分・合成関数の微分
まずは逆三角関数の微分公式を確認しましょう。参考書とはちょっと違う公式の書き方をします。
\[
\frac{d}{dx} \sin^{-1} ax = \frac{a}{\sqrt{1 - a^2 x^2} }
\]\[
\frac{d}{dx} \cos^{-1} ax = - \frac{a}{ \sqrt{ 1 - a^2 x^2} }
\]\[
\frac{d}{dx} \tan^{-1} ax = \frac{a}{1 + a^2 x^2}
\]
※ ただし \( a \) は定数
ただ、今回聞かれているのは \( \sin^{-1} (x^2) \) の微分ですよね。だから、\[\begin{align*}
\frac{d}{dx} \sin^{-1} x^2 & = \frac{1}{ \sqrt{1- (x^2)^2 } }
\\ & = \frac{1}{ \sqrt{1- x^4} }
\end{align*}\]と計算してしまうのは間違いです。
このように、公式の形と全く同じではない関数を微分するときに公式をそのまま適用しようとすると、間違った結果が出てきてしまいます。
今回のように、公式の形とは違う関数が出てきた場合は、合成関数の微分法を用いて公式を適用できる形にもっていきます。
Step1. 自分で文字を1つおき、関数を2つに分離する。例えば \( (2x^3+1)^4 \) であれば、\[
u = 2x^3 + 1, \ \ \ y = u^4
\]の組に分離する。
Step2. \( u = \) の式は \( x \) で微分し、\( y = \) の式は \( u \) で微分する。つまり、\[
\frac{du}{dx} = 6x^2 , \ \ \ \frac{dy}{du} = 4u^3
\] となる。
Step3. 2つの微分結果を掛けて、\( u \) の式を \( x \) に戻す。\[\begin{align*}
\frac{dy}{dx} & = \frac{dy}{du} \frac{du}{dx}
\\ & = 4u^3 \cdot 6x^2
\\ & = 4(2x^3+1)^3 \cdot 6x^2
\\ & = 24x^2 (2x^3+1)^3
\end{align*}\]
今回 \( \sin^{-1} (x^2) \) の場合は、\[
u = x^2, \ \ \ y = \sin^{-1} u
\]と分離します。
すると、\[
\frac{du}{dx} = 2x, \ \ \ \frac{dy}{du} = \frac{1}{\sqrt{1-u^2}}
\]となりますね。
よって、導関数は\[\begin{align*}
\frac{dy}{dx} & = \frac{dy}{du} \frac{du}{dx}
\\ & = \frac{1}{\sqrt{1-u^2}} \cdot 2x
\\ & = \frac{2x}{\sqrt{1-(x^2)^2}}
\\ & = \frac{2x}{\sqrt{1-x^4}}
\end{align*}\]となる。
(3) 定積分関数の微分
\[
\int \frac{t}{t^3 + 1} \ dt
\]を計算するのはかなりしんどいですね。
そこで、定積分で表された関数をそのまま微分する公式を使います。
\[
\frac{d}{dx} \int^{f(x)}_{a} h(x) = f'(x) h ( f(x) )
\]\[
\frac{d}{dx} \int^{f(x)}_{g(x)} h(x) = f'(x) h ( f(x) ) - g'(x) h( g(x) )
\]
※1 \( a \) は定数
※2 できれば合成関数の微分公式で導出できるようになっておくとベターです。
よって、\[\begin{align*}
\frac{dy}{dx} & =
\frac{d}{dx} \int^{x^2}_{0} \frac{t}{t^3+1} \ dt
\\ & = (x^2)' \frac{x^2}{(x^2)^3+1}
\\ & = 2x \cdot \frac{x^2}{x^6+1}
\\ & = \frac{2x^3}{x^6+1}
\end{align*}\]となる。
※被積分関数の積分範囲にある 1 に惑わされないように!!
★ マーク解答 ★
No.13: 8 [1点]
No.14: 5 [1点]
No.15: 6 [1点]
No.16: 2 [3点]
No.17: 3 [4点]
問題5. マクローリン展開
次の関数\[
f(x) = (1-x) e^{2x}
\]をマクローリン展開する。すると、\[
f(x) = 1 + x + \left[ \ \ 18 \ \ \right] x^2 + \left[ \ \ 19 \ \ \right] x^3 + \cdots
\]となる。
[修正] 2021/08/07
問題PDFの \( f(x) \) の式が \( x \) ではなく \( 2x \) になっていました。申し訳ございません。
※ 8/7の13時以降に問題PDFをダウンロードした方は、正しい式になっております。

[その1] ごり押しの計算
まずはマクローリン展開の公式を確認しましょう。
\[
f(x) = f(0) + \frac{f'(0)}{1!} x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3 + \cdots
\]
※ マクローリン展開の練習をもっとしたい人 or 理解があやふやな人はこちらの記事にて確認をどうぞ!
(i) 1回微分\[\begin{align*}
f'(x) & = - e^{2x} + (1-x) \cdot 2e^{2x}
\\ & = (-2x+1) e^{2x}
\end{align*}\]
(実際に \( x = 0 \) を代入すると \( f'(0) = 1 \) となり、マクローリン展開の \( x \) の項が問題文の通りであることが検算できる。)
(ii) 2回微分\[\begin{align*}
f''(x) & = -2 e^{2x} + (-2x+1) \cdot 2e^{2x}
\\ & = -4x e^{2x}
\end{align*}\]
ここに \( x = 0 \) を代入すると、\( f''(0) = 0 \) となる。
(iii) 3回微分\[\begin{align*}
f'''(x) & = -4 e^{2x} + (-4x) \cdot 2e^{2x}
\\ & = (-8x-4) e^{2x}
\end{align*}\]
ここに \( x = 0 \) を代入すると、\( f'''(0) = -4 \) となる。
よって、マクローリン展開は\[\begin{align*}
f(x) & = 1 + x + \frac{f''(0)}{2!} x^2 + \frac{f'''(0)}{3!} x^3 + \cdots
\\ & = 1 + x + 0 x^2 + \left( - \frac{2}{3} \right) x^3 + \cdots
\end{align*}\]と計算できる。
[その2] 工夫して計算してみる
マクローリン展開は工夫して計算することで、計算量を大きく減らすことができます。
例えば、\( e^{2x} \) のマクローリン展開は、\( e^x \) のマクローリン展開\[
e^{x} = 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + \cdots
\]の \( x \) を \( 2x \) に変えることで\[\begin{align*}
e^{2x} & = 1 + 2x + \frac{1}{2} (2x)^2 + \frac{1}{6} (2x)^3
\\ & = 1 + 2x + 2x^2 + \frac{4}{3} x^3 + \cdots
\end{align*}\]と求めることができます。
さらに、\( (1-x)e^{2x} \) のマクローリン展開は、\( e^{2x} \) のマクローリン展開の結果に \( (1-x) \) を掛けることで求めることができます。\[\begin{align*}
(1-x) e^{2x} & = (1-x) \left( 1 + 2x + 2x^2 + \frac{4}{3} x^3 + \cdots \right)
\\ & = \left( 1 + 2x + 2x^2 + \frac{4}{3} x^3 + \cdots \right) - x \left( 1 + 2x + 2x^2 + \frac{4}{3} x^3 + \cdots \right)
\\ & = 1 + (2-1)x + (2-2)x^2 + \left( \frac{4}{3} - 2 \right) x^3 + \cdots
\\ & = 1 + x - \frac{2}{3} x^3 + \cdots
\end{align*}\]
下に工夫して計算するために必要な道具(基本マクローリン展開公式一覧)を用意したので、もしよかったら参考にしてください。
頭に入れておくと、マクローリン展開の導出に役立つかもしれません。\[
e^x = 1 + x + \frac{1}{2} x^2 + \frac{1}{6} x^3 + \frac{1}{24} x^4 + \cdots
\]\[
\sin x = x - \frac{1}{6} x^3 + \frac{1}{120} x^5 + \cdots
\]\[
\cos x = 1 - \frac{1}{6} x^2 + \frac{1}{24} x^4 + \cdots
\]\[
\tan x = x + \frac{1}{3} x^3 + \frac{2}{15} x^5 + \cdots
\]\[
\frac{1}{1-x} = 1 + x + x^2 + x^3 + \cdots
\]\[
\frac{1}{1+x} = 1 - x + x^2 - x^3 + \cdots
\]\[
\log (1+x) = x - \frac{1}{2} x^2 + \frac{1}{3} x^3 - \frac{1}{4} x^4 + \cdots
\]\[
\tan^{-1} x = x - \frac{1}{3} x^3 + \frac{1}{5} x^5 + \cdots
\]
★ マーク解答 ★
No.18: 0 [5点]
No.19: -7 [5点]
問題6. 関数のグラフ
次の関数\[
f(x) = \frac{x^3}{x^2-1}
\]のグラフを考える。次の(1)~(5)の問いに答えなさい。
(1) グラフの概形について述べたものとして正しいものを1つ選びなさい。
- \( f(x) \) は区間 \( -1 < x < 1 \) において単調増加となっている。
- \( f(x) \) は区間 \( -1 < x < 1 \) において単調減少となっている。
- \( f(x) \) は区間 \( -1 < x < 1 \) において単調増加でも単調減少でもない。
(2) 極値について述べたものとして正しいものを1つ選びなさい。
- \( x = -3 \) で極大値を取る。
- \( x = - \sqrt{3} \) で極大値を取る。
- \( x = 0 \) で極大値を取る。
- \( x = \sqrt{3} \) で極大値を取る。
- \( x = 3 \) で極大値を取る。
(3) 変曲点について述べたものとして正しいものを1つ選びなさい。
- 点 \( \left( -3, f(-3) \right) \) は変曲点である。
- 点 \( \left( -\sqrt{3}, f(-\sqrt{3}) \right) \) は変曲点である。
- 点 \( \left( 0, f(0) \right) \) は変曲点である。
- 点 \( \left( \sqrt{3}, f( \sqrt{3}) \right) \) は変曲点である。
- 点 \( \left(3, f(3) \right) \) は変曲点である。
(4) 漸近線について述べたものとして誤っているものを1つ選びなさい。
- \( x = 1 \) は漸近線である。
- \( x = -1 \) は漸近線である。
- \( y = x \) は漸近線である。
- \( y = -x \) は漸近線である。
(5) グラフの凹凸について述べたものとして正しいものはどちらか。
- 区間 \( -3 < x < - \sqrt{3} \) において上に凸である。
- 区間 \( \sqrt{3} < x < 3 \) において上に凸である。
Step1: グラフの漸近線
まずは微分をしなくても確認できる(4)漸近線について確認しましょう。
与えられた関数\[
f(x) = \frac{x^3}{x^2 - 1}
\]は、\( x^2 - 1 = 0 \)、つまり \( x = \pm 1 \) で定義されませんね。そのため、\( x = 1 \), \( x = -1 \) は漸近線となります。
また、約分すると、\[
f(x) = x + \frac{x}{x^2 - 1}
\]と変形ができます。つまり、\[
f(x) - x = \frac{x}{x^2 - 1}
\]となり、さらに\[\begin{align*}
\lim_{x \to \infty} \left( f(x) - x \right) & = \lim_{x \to \infty} \frac{x}{x^2 - 1}
\\ & = 0
\end{align*}\]となるため、\( y - x = 0 \), つまり \( y = x \) でも漸近線を持つことがわかりますね。
よって、残った \( y = -x \) は漸近線ではないため、答えは4。
Step2: 極値とグラフの増減
次に \( f'(x) \) を求めて極値、およびグラフの増減を見ていきましょう。\[\begin{align*}
f'(x) & = \frac{3x^2 \cdot (x^2-1) - x^3 \cdot 2x}{(x^2 - 1)^2}
\\ & = \frac{3x^4 - 3x^2 - 2x^4}{(x^2 - 1)^2}
\\ & = \frac{x^4 - 3x^2}{(x^2 - 1)^2}
\\ & = \frac{x^2(x^2-3)}{(x^2 - 1)^2}
\\ & = \frac{x^2(x+\sqrt{3})(x - \sqrt{3})}{(x^2 - 1)^2}
\end{align*}\]となる。
ここで、\( f'(x) = 0 \) となる \( x \) は、\[
x^2 (x + \sqrt{3} )(x - \sqrt{3} ) = 0
\]より、\( x = 0 \), \( x = \sqrt{3} \), \( x = - \sqrt{3} \) となり、極大値(or 極小値)の候補となる。
また、分母 \( (x^2 - 1)^2 \) は、\( x \not = 1 \) で常に正なため、極値や増減を考える際には\[
x^2 (x + \sqrt{3} ) ( x - \sqrt{3} )
\]で判断ができる。
(i) -1 < x < 1 の増減
\( x^2 \) は必ず \( x^2 \geqq 0 \) となるため、\( -1 < x < 1 \) の増減を見るためには \( x^2 - 3 \) の値の変化を見ればよい。
すると、\( -1 < x < 1 \) では常に \( x^2 - 3 < 0 \) となるため、\( -1 < x < 1 \) の範囲内では\[
x^2 (x^2 - 3) \leqq 0
\]となり、常に単調減少をすることがわかる[2]※ \( x = 0 \) のときは \( f'(x) = 0 \) になるため、\( < \) ではなく \( \leqq \) になる点に注意。なお、\( f'(x) = 0 \) … Continue reading。よって答えは2。
(ii) 極大値の判定
極値の候補 \( x = 0 , \pm \sqrt{3} \) のうち、極大値となる \( x \) がどれかを確認しましょう。
まず、(i) より \( x = 0 \) の前後はともに \( f'(x) < 0 \) となっているため、極大値でも極小値でもありませんね。
つぎに、\( x = \sqrt{3} \) ですが、このとき、\[
(x + \sqrt{3})(x - \sqrt{3} )
\]は \( x = \sqrt{3} \) より少し小さい値では \( f'(x) < 0 \), 少し大きい値では \( f'(x) > 0 \) となっていることがわかるため、極小値であることがわかりますね。
また、\( x = - \sqrt{3} \) の場合、\( x = - \sqrt{3} \) より少し小さい値で \( f'(x) > 0 \), 少し大きい値で \( f'(x) < 0 \) となっているため、極大値であることがわかりますね。
よって \( x = - \sqrt{3} \) のときに極大値をとりますね
Step3: 変曲点と凹凸の判定
次に \( f''(x) \) を計算することで変曲点とグラフの凹凸を計算します。
(i) 変曲点の確認
計算するときは\[
f'(x) = \frac{x^4 - 3x^2}{(x^2 - 1)^2}
\]を使って計算すると計算しやすいでしょう。
\[\begin{align*}
f''(x) & = \frac{(4x^3 - 6x)(x^2-1)^2 - (x^4 - 3x^2) \cdot 2x(x^2-1)}{(x^2-1)^4}
\\ & = \frac{(4x^3 - 6x)(x^2-1) - (x^4 - 3x^2) \cdot 2x \cdot 2}{(x^2-1)^3}
\\ & = \frac{4x^5 - 4x^3 - 6x^3 + 6x - 4x^5 + 12x^3}{(x^2-1)^3}
\\ & = \frac{2x^3 + 6x}{(x^2-1)^3}
\\ & = \frac{2x(x^2+3)}{(x^2-1)^3}
\end{align*}\]
ここで、\( f''(x) = 0 \) となる \( x \) は\[
2x(x^2 + 3 ) = 0
\]を計算すればOK。(ただし \( x \not = 1 \))
すると、\( x = 0 \) だけなのでこの点が変曲点。
(ii) グラフの凹凸
ここで分母、および \( x^2 + 3 \) は常に正なので、
- \( 2x > 0 \) つまり \( x > 0 \) のとき、\( f''(x) > 0 \)(下に凸)
- \( 2x < 0 \) つまり \( x < 0 \) のとき、\( f''(x) < 0 \)(上に凸)
となる。
よって、選択肢の中で上に凸な区間は \( -3 < x < - \sqrt{3} \) である。
[参考] 増減表とグラフの概形
最後に増減表とグラフの概形を記しておきましょう。
(i) 増減表
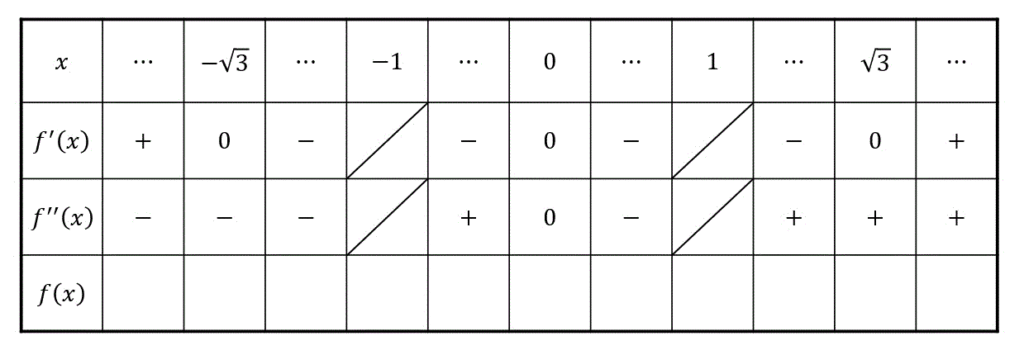
(ii) グラフ
★ マーク解答 ★
No.20: 2 [2点]
No.21: 2 [2点]
No.22: 3 [2点]
No.23: 4 [2点]
No.24: 1 [2点]
さいごに
今回は記事で1年前期で習う解析学の微分編の総復習でした。
続きの積分編もぜひご覧ください!
関連広告・スポンサードリンク