スポンサードリンク
こんにちは、ももやまです。
皆さんは高校で複素数について習いましたか?
おそらく数2で複素数の基礎を、理系の皆さんは数3で複素数平面(複素平面)について習う(習った)かと思います。
今回は複素数ってなに?って人でもわかるように複素数・複素数平面の基礎について簡単にですがまとめてみました。
特に大学で「複素解析学」・「応用数学」などの科目を履修する際には複素数は避けて通れない存在なので複素数が苦手だなと思っている人は復習にぜひお使いください!
複素数平面をすでに習っている人もまだ習ってない人もぜひご覧ください!
目次
スポンサードリンク
1.虚数・複素数とは
(1) 虚数とは
まずは、複素数とはどんな数かについてを説明していきたいと思います。
皆さんは、\( \sqrt{-1} \) のような、ルートの中が負になるような数(言い換えると2乗して負になるような数)について扱ったことはありますか?
おそらくほとんどの人は日常生活でそんな数は使いませんよね。しかし、定義しちゃったんですよ。偉い人が。2乗して-1となるような数を \( i \) とするって。数式で書くと\[
i^2 = -1 \ \ \ \sqrt{-1} = i
\]となります。
しかし、なぜそんな日常生活で使わない虚数 \( i \) なんてものを数学者は定義しちゃったんでしょうか。
実は、虚数 \( i \) というのは数学界において多く役にたっているのです。
実際に虚数 \( i \) がどのように役に立っているかを下のほうで説明していきたいと思います。
(2) 複素数とは
実数 \( a \) と虚数 \( bi \) を組み合わせ、\( a + bi \) の形にしたものを複素数と呼びます。
複素数 \( z = a + bi \) の \( a \) を実部、\( b \) を虚部という*1。
また、\( a = 0 \) のとき、つまり \( bi \) のときのことを純虚数と呼ぶ。
(3) 共役複素数とは
複素数 \( z = a + bi \) の虚部の符号を入れ替え \( a - bi \) にしたものを共役複素数(きょうやくふくそすう)*2と呼び、\( \overline{z} \) で表します。
例えば、\( 2 + 2 \sqrt{3}i \) の共役複素数は \( 2 - 2 \sqrt{3} i \) となります。
複素数 \( z = a + bi \) の虚部 \( b \) の符号を入れ替えたものを共役複素数といい、\[\overline{z} = a - bi\]で表される。
スポンサードリンク
2.まずは複素数の計算に慣れよう
では、まずは複素数の計算に慣れてもらうために1問例題を出すので計算してみましょう。
例題1 [複素数の足し算・掛け算・割り算]
複素数 \( \alpha \), \( \beta \) が\[
\alpha = 1 + i , \ \ \ \beta = -2 + 2 \sqrt{3} i
\]とする。このとき、つぎの(1)〜(3)の計算をしなさい。
(1) \( \alpha + \beta \)
(2) \( \alpha \beta \)
(3) \( \frac{\alpha}{\beta} \)
解説1
(1) 複素数の足し算
複素数の足し算は、実部同士、虚部同士を別々に足すことで求められる。\[
\alpha + \beta = 1 + i - 2 + 2\sqrt{3} i = -1 + (1+2 \sqrt{3})i
\]
(2) 複素数の掛け算
複素数の掛け算は \( i^2 = -1 \) に注意すること。\[ \begin{align*}
\alpha \beta & = (1+i)(-2 + 2\sqrt{3}i)
\\ & = -2 + (2 \sqrt{3} -2)i - 2\sqrt{3}
\\ & = -2(1 + \sqrt{3}) + 2( \sqrt{3}- 1)i
\end{align*} \]
(3) 複素数の割り算
複素数の割り算は有理化っぽい形になる。\[ \begin{align*}
\frac{ \alpha }{ \beta } & = \frac{ 1+i }{ -2 + 2 \sqrt{3} i }
\\ & = \frac{ (1+i)( 2 \sqrt{3} i + 2) }{(2 \sqrt{3} i - 2)(2 \sqrt{3}i + 2) }
\\ & = \frac{ 2 \sqrt{3} i + 2 - 2 \sqrt{3} + 2i}{-12-4 }
\\ & = - \frac{ 2(1 - \sqrt{3}) + 2(1+\sqrt{3})i }{16}
\\ & = \frac{1}{8} \left( (\sqrt{3} - 1) - (1+\sqrt{3})i \right)
\end{align*} \]
スポンサードリンク
3.複素数平面
では、いよいよ複素数平面に入ろうと思います。
(1) 実軸と虚軸
まずは、実軸と虚軸がどんなものかをまとめていきたいと思います。
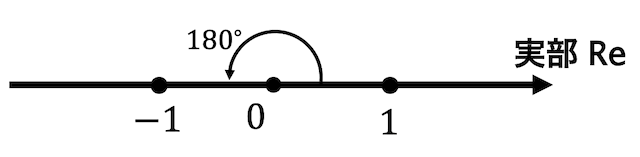
このような数直線を考てみましょう。
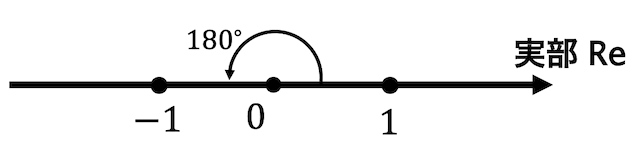
1の点から原点中心に 180°回転回転させると-1の点に移動しますね。
ここで、\[
i^2 = -1
\]を思い出してみましょう。
2乗して -1 になるんだったらルートとって \( \sqrt{-1} \) になるじゃん。なら 1を 90° 回転させたら \( i \) に移るように虚数の軸を取っちゃえ!
という感じで下のように \( y \) 軸を虚数の軸と考えるのが複素数平面です。
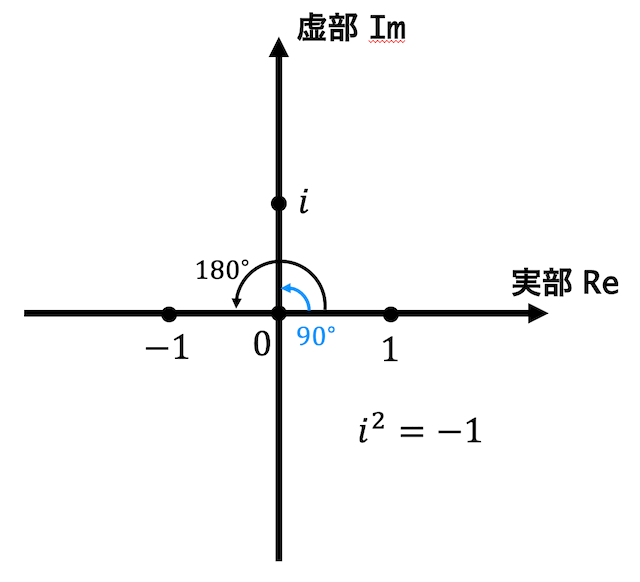
\( x \) 軸を実数の軸(実軸はReal Axis)なので略してReと書くこともあります)、\( y \) 軸を虚数の軸(虚軸はImaginary Axis)なので略してImと書くこともあります)と考えることで複素数をまるで図形のように取り扱うことができるのです!
4.複素数の極形式・長さと偏角
複素数平面上に複素数 \( z = a + bi \) を図示してみましょう。
すると、複素数 \( z \) は下のように表せますね。
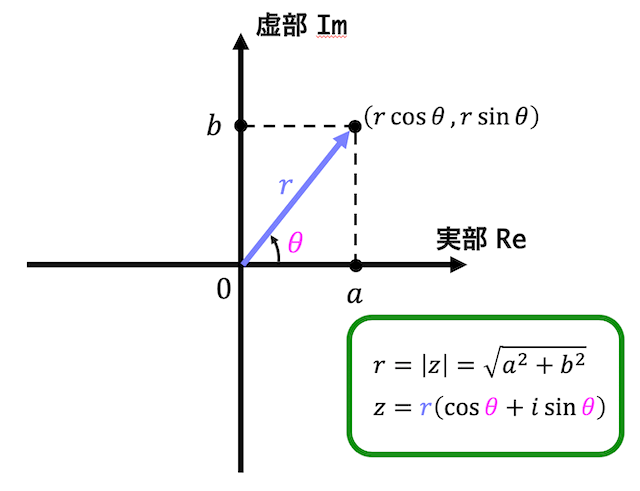
\( |z| = r \geqq 0 \):複素数の絶対値*3
\( \theta \):複素数の偏角
ここで、複素数 \( z \) を表す点 (a,b) を極座標 \( (r \cos \theta , r \sin \theta) \) として表すことを考えましょう。
すると、複素数 \( z \) は、\[
r = |z| = \sqrt{a^2 + b^2} \\
z = r \left( \cos \theta + i \sin \theta \right)
\]と表すことができますね。これを極形式と呼びます。
また、極形式の \( r \) (長さ)は複素数の絶対値 \( |z| \) を表し、\( \theta \) は複素数の偏角を表します。
例題2 複素数平面の基礎
複素数 \( \alpha \), \( \beta \) が\[
\alpha = 1 + i , \ \ \ \beta = -2 + 2 \sqrt{3} i
\]とする(例題1と同じ)。このとき、つぎの(1)〜(3)の問いに答えなさい。
(1) 複素数 \( \alpha \), \( \beta \) の絶対値 \( | \alpha | \), \( | \beta | \) を求めなさい。
(2) 複素数 \( \alpha \), \( \beta \) の偏角 \( \arg \alpha \), \( \arg \beta \) を求めなさい。
(3) 複素数 \( \alpha \), \( \beta \) を極形式で表しなさい。
解説2
(1) \[
|\alpha| = \sqrt{1^2 + 1^2} = \sqrt{2} \\
|\beta| = \sqrt{(-2)^2 + (2\sqrt{3})^2} = \sqrt{4+12} = 4
\]
(2), (3) \[
\begin{align*}
\alpha & = \sqrt{2} \left( \frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i \right)
\\ & = \sqrt{2} \left( \cos 45^{\circ} + i \sin 45^{\circ} \right)
\end{align*} \] \[
\begin{align*}
\beta & = 4 \left( - \frac{1}{2} + \frac{\sqrt{3}}{2} i \right)
\\ & = 4 \left( \cos 120^{\circ} + i \sin 120^{\circ} \right)
\end{align*} \]
より偏角は\[
\arg \alpha = 45^{\circ} \left ( = \frac{\pi}{4} \right) \ \ \ \arg \beta = 120^{\circ} \left ( = \frac{2}{3} \pi \right)
\]となり、極形式は\[\begin{align*}
\alpha & = \sqrt{2} \left( \cos 45^{\circ} + i \sin 45^{\circ} \right)
\\ & = \sqrt{2} \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right)
\end{align*} \]\[\begin{align*}
\beta & = 4 \left( \cos 120^{\circ} + i \sin 120^{\circ} \right)
\\ & = 4 \left( \cos \frac{2}{3} \pi + i \sin \frac{2}{3} \pi \right)
\end{align*} \]となる。
(度数法でも弧度法でもどちらでもOKです! 私は度数法が好きなので度数法メインで書いていきたいと思います。)
5.複素数の積・商・べき乗と極形式
複素数の積、商、べき乗は極形式を用いると簡単に計算できます。
(1) 積・商の場合
複素数の積、商は極形式を用いると下のように計算ができます。
複素数 \( z_1 \), \( z_2 \) \[
z_1 = r_1 \left( \cos \theta_1 + i \sin \theta_1 \right) \\
z_2 = r_2 \left( \cos \theta_2 + i \sin \theta_2 \right)
\]とする。
このとき、複素数の積 \( z_1 z_2 \) および商 \( \frac{z_1}{z_2} \) は\[
z_1 z_2 = r_1 r_2 \left( \cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2) \right) \\
\frac{z_1}{z_2} = \frac{r_1}{r_2} \left( \cos (\theta_1 - \theta_2) + i \sin (\theta_1 - \theta_2) \right)
\]となる。
とくに角度 \( \theta \) の計算は対数のように計算することができちゃいます!
(2) べき乗の計算 ド・モアブルの公式
複素数 \( z \) の100乗 \( z^{100} \) を求めなさいと言われると何もしらないとびっくりしちゃういますよね!∑o(*'o'*)o ウオオォォォォ!!
しかし、複素数も極形式であればあっという間に100乗でも求めることができるのです!ヤッター! (  ̄▽)爻(▽ ̄ ) ヤッター!
複素数 \( z \) を \[
z = r \left( \cos \theta + i \sin \theta \right)
\]とする。
このとき、複素数の 乗 \( z^n \) は、\[
z^n = r^n \left( \cos n \theta + i \sin n \theta \right)
\]と計算できる。
\( n \) 乗の角度 \( \theta \) の計算も積・商のように対数のように計算することができちゃいます!
例題3 ド・モアブルの定理
複素数 \( z = 1 - i \) とする。このとき、(1), (2)の問いに答えなさい。
(1) \( z \) を極形式で表しなさい。
(2) \( z^{25} \) を極形式で表し、さらに値を求めなさい。
必要ならば \( 2^{10} = 1024 \) を使っても良い。
解説3
(1) \( z \) の絶対値 \( |z| \) は \( \sqrt{2} \) である。\[ \begin{align*}
z & = \sqrt{2} \left( \frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} \right)
\\ & = \sqrt{2} \left( \cos \left( - 45^{\circ} \right) + i \sin \left( - 45^{\circ} \right) \right)
\\ & = \sqrt{2} \left( \cos \left( - \frac{\pi}{4} \right) + i \sin \left( - \frac{\pi}{4} \right) \right)
\end{align*} \]となる(度数法・弧度法はどちらでもOK)。
(2)
(数がでかくなったときは度数法より弧度法のほうが計算しやすいので弧度法で計算します。)
ド・モアブルの定理より\[ \begin{align*}
z^{25} & = \left( \sqrt{2} \right)^{25} \left( \cos \left( - \frac{25}{4} \pi \right) + i \sin \left( - \frac{25}{4} \pi \right) \right)
\\ & = 2^{12} \sqrt{2} \left( \cos \left( - \frac{\pi}{4} \right) + i \sin \left( - \frac{\pi }{4} \right) \right)
\\ & = 4096 - 4096i
\end{align*} \]
6.オイラーの公式・オイラーの定理 [大学範囲]
※高校生の皆さんは理解しなくてもOKです。余裕があれば読んでみるといいかもしれません。
まずは、オイラーの公式、オイラーの定理がどんなものかを紹介したいと思います。
極形式で表された複素数は、 \[
z = r \left( \cos \theta + i \sin \theta \right) = r e^{i \theta}
\]の形で表すことができる。これをオイラーの公式という。
また、\( r = 1 \), \( \theta = \pi \) を代入したとき、\[
e^{i \pi} = -1
\]が導かれる。これをオイラーの定理と呼ぶ。
複素数 \( i \) を使うことで三角関数を指数を使って表すことができちゃうのです!
また、オイラーの定理 \( e^{i \pi} = -1 \) は世界で最も美しい公式と呼ばれています。
オイラーの定理・オイラーの公式は大学の科目の1つである「解析学」で習うマクローリン展開を使うと証明することができます。
マクローリン展開ってどんなのだっけ、証明がみたいという人は下のほうに貼っているリンクをご覧ください。
オイラーの公式を使うことで1つ前で説明した「極形式を用いた積・商・べき乗」をスマートに表現することができます。
複素数 \( z \) を \[
z_1 = r_1 \left( \cos \theta_1 + i \sin \theta_1 \right) = r_1 e^{i \theta_1}\\
z_2 = r_2 \left( \cos \theta_2 + i \sin \theta_2 \right) = r_2 e^{i \theta_2}
\]とする。
このとき、複素数の積 \( z_1 z_2 \) および商 \( \frac{z_1}{z_2} \) は\[
z_1 z_2 = r_1 e^{i \theta_1} \cdot r_2 e^{i \theta_2} = r_1 r_2 e^{i (\theta_1 + \theta_2)} \\
\frac{z_1}{z_2} = \frac{r_1 e^{i \theta_1}}{r_2 e^{i \theta_2}} = \frac{r_1}{r_2} e^{i (\theta_1 - \theta_2)}
\]となる。
複素数 \( z \) を \[
z = r \left( \cos \theta + i \sin \theta \right) = r e^{i \theta}
\]とする。
このとき、複素数の 乗 \( z^n \) は、\[
z_n = \left( r e^{i \theta} \right)^n = r^ne^{i n \theta}
\]と計算できる。
例題4 極形式 and ド・モアブルの定理
複素数 \( \alpha \), \( \beta \) が\[
\alpha = 1 + i , \ \ \ \beta = -2 + 2 \sqrt{3} i
\]とする(例題1と同じ)。
必要ならば前の例題の答えを使ってもよい。
(1) \( \alpha \beta \) を極形式もしくは \( re^{i \theta} \) の形で表しなさい。
(2) \( \frac{\beta}{\alpha} \) を極形式もしくは \( re^{i \theta} \) の形で表しなさい。
解説4
例題2より、\[
\alpha = \sqrt{2} \left( \cos 45^{\circ} + i \sin 45^{\circ} \right) \\
\beta = 4 \left( \cos 120^{\circ} + i \sin 120^{\circ} \right)
\]である。
[極形式で求める場合]
(1)
\[\begin{align*}
\alpha \beta & = 4 \sqrt{2} \left( \cos (120+45)^{\circ} + i \sin (120+45)^{\circ} \right)
\\ & = 4 \sqrt{2} \left( \cos 165^{\circ} + i \sin 165^{\circ} \right)
\end{align*} \]
(2)
\[\begin{align*}
\frac{\beta}{\alpha} & = \frac{4}{\sqrt{2}} \left( \cos (120-45)^{\circ} + i \sin (120-45)^{\circ} \right)
\\ & = 2 \sqrt{2} \left( \cos 75^{\circ} + i \sin 75^{\circ} \right)
\end{align*} \]
[ \( r^{i \theta} \) の形で求める場合]
極形式で求めた結果から \( r^{i \theta} \) の形に変換するのもいいが、今回は \( r^{i \theta} \) の形から直接計算することにする。
\[
\alpha = \sqrt{2} \left( \cos 45^{\circ} + i \sin 45^{\circ} \right) = \sqrt{2} e^{ \frac{\pi}{4} i} \\
\beta = 4 \left( \cos 120^{\circ} + i \sin 120^{\circ} \right) = 4 e^{ \frac{2}{3} \pi i}
\]である。
よって、\[
\alpha \beta = 4 \sqrt{2} e^{ \frac{11}{12} \pi i} \\
\frac{\beta}{\alpha} = 2 \sqrt{2} e^{ \frac{5}{12} \pi i}
\]と計算できる。
7.三角関数・対数関数と複素数 [大学範囲]
(1) 実三角関数と複素数
もう少し大学数学のお話をしましょう。
実は先程説明したオイラーの公式を用いることで、\( \sin x \), \( \cos x \), \( \tan x \) を自然対数 \( e \) で表すことができるのです!
オイラーの公式は\[
e^{i x} = \cos x + i \sin x
\]でしたね。ここで \( x \) を \( -x \) に変えると\[
e^{- ix} = \cos (-x) + i \sin (-x) = \cos x - i \sin x
\]となりますね。
ここで、2つの式を足すと、\[
e^{i x} + e^{- ix} = 2 \cos x
\]となりますね。よって、\[
\cos x = \frac{1}{2} \left( e^{i x} + e^{- ix} \right)
\]を導けますね。
さらに1つ目の式から2つめの式を引くと、\[
e^{i x} - e^{- ix} = 2i \sin x
\]となるので、\[
\sin x = \frac{1}{2i} \left( e^{i x} - e^{- ix} \right)
\]も導くことができます。
\( \sin x \), \( \cos x \) が求まったので \( \tan x \) も\[
\tan x = \frac{ \sin x}{ \cos x} = \frac{e^{i x} - e^{- ix}}{2i \left( e^{i x} + e^{- ix} \right)}
\]と導くことができます。
実三角関数 \( \sin x \), \( \cos x \), \( \tan x \) は\[
\sin x = \frac{1}{2i} \left( e^{i x} - e^{- ix} \right) \\
\cos x = \frac{1}{2} \left( e^{i x} + e^{- ix} \right) \\
\tan x = \frac{e^{i x} - e^{- ix}}{2i \left( e^{i x} + e^{- ix} \right)}
\]と表すことができる。
(2) 複素三角関数
実三角関数 \( \sin x \), \( \cos x \), \( \tan x \) は複素数 \( e^{ix} \), \( e^{-ix} \) を用いて表すことができましたね。
ここで実数 \( x \) を複素数 \( z \) を変えて複素数でも実三角関数のときと同じように定義しちゃおう! というのが複素三角関数です。
複素三角関数 \( \sin z \), \( \cos z \), \( \tan z \) は\[
\sin z = \frac{1}{2i} \left( e^{i z} - e^{- iz} \right) \\
\cos z = \frac{1}{2} \left( e^{i z} + e^{- iz} \right) \\
\tan z = \frac{e^{i z} - e^{- iz}}{2i \left( e^{i z} + e^{- iz} \right)}
\]と定義される。
(1)で紹介した式の \( x \) が \( z \) に変わっているところ以外は全く同じですね。
加法定理などの実三角関数の公式も複素三角関数でもそのまま適用することができます。
(3) 複素対数関数
対数関数も自然対数 \( e \) を用いて表すことができます。
ある2つの複素数 \( w,z \) に対し、\( z = e^w \) の関係があるとします。すると、逆関数をとって \( w = \log z \) と対数を用いて表すことができますね。
さらに \( z = r e^{i \theta} \) (極形式表記)とし、\( w = a + bi \) とします。すると、\[
z = r e^{i \theta} = e^w = e^{a+bi} = e^a \cdot e^{bi}
\]となりますね。
すると、実部 \( e^a = r \) と虚部 \( e^{bi} = e^{i \theta} \) の2つの部分に分けることができますね。
実部部分より、\[
a = \log r
\]が成り立ちます。
また、\( e^{i \theta} \), \( e^{(\theta + 2 \pi) i} \), \( e^{(\theta + 4 \pi) i} \), …, \( e^{(\theta + 2n \pi) i} \) はすべて同じ値になりますよね(\( n \) は整数)。
( \( 2 \pi \) すると1周するため)
なので、虚数部分は\[
b = (\theta + 2n \pi) i
\]となります。
実部と虚部をまとめると、\[
\log z = \log r + (\theta + 2n \pi) i
\]と自然対数を複素数範囲で定義することができます。
複素数 \( z = r e^{i \theta} \) に対して、自然対数 \( \log z \) は\[
\log z = \log r + (\theta + 2n \pi) i = \log |z| + (\theta + 2n \pi) i
\]となる(ただし \( r \gt 0 \))。
しかし、この状態のままだと、\[
\log z = \log r + i \theta, \ \ \ \log z = \log r + i (\theta + 2 \pi) , \cdots
\]のように1つの複素数 \( z \) に対し、自然対数 \( \log z \) が無数に存在しますよね。
そこで偏角を \( - \pi \lt \mathrm{arg} \ z \leqq \pi \) に制限することで1つの複素数に対し、自然対数を1つに決まるようにしました。この1つに決まった自然対数のことを主値と呼び、\( \mathrm{Log} \ z \) で表します。
複素数 \( z = r e^{i \theta} \) に対して、主値 \( \mathrm{Log} \ z \) は\[
\mathrm{Log} \ z = \log r +i \theta = \log |z| + i \mathrm{arg} \ z
\]となる(ただし \( r \gt 0 \))。
例題5 複素三角関数・複素対数関数
つぎの(1)〜(5)の値を求めなさい。
(1) \[ \cos 3i \]
(2) \[ \sin 4 \]
(3) \[ \mathrm{Log} \ (-3) \]
(4) \[ \mathrm{Log} \ i \]
(5) \[ i^i \]
解説5
(1) \[
\cos 3i = \frac{1}{2} \left( \frac{1}{e^3} + e^{3} \right)
\]
(2) \[\begin{align*}
\sin 4 & = \frac{1}{2i} \left( e^{4i} - \frac{1}{e^{4i} } \right)
\\ & = \frac{1}{2} i \left( \frac{1}{ e^{4i} } - e^{4i} \right)
\end{align*}\]
(3) \[
-3 = 3 e^{i \pi}
\]なので、\[
\mathrm{Log} \ (-3) = \log 3 + i \pi
\]となる。
(4)\[
i = 1 e^{ \frac{\pi}{2}}
\]なので、\[
\mathrm{Log} \ i = \log 1 +\frac{\pi}{2} i = \frac{\pi}{2} i
\]となる。
(5)\[
i^i = e^{i \log i}
\]となる。
ここで無数にある \( \log i \) のうちの1つとして主値をとる。(4)より\[
\mathrm{Log} \ i = \frac{\pi}{2} i
\]なので、\[\begin{align*}
i^i & = e^{i \log i}
\\ & = e^{\frac{\pi}{2} i^2}
\\ & = e^{- \frac{\pi}{2}}
\end{align*}\]と求められる。
なんと \( i^i \) は実数になることが複素対数を用いることでわかるのです!
8.複素数平面と方程式
複素数平面の知識を使うと簡単に方程式を解くことができます。
例題6 複素数と方程式1
方程式 \( z^4 = -2 + 2 \sqrt{3} i \) の解をすべて求め、複素数平面上に図示しなさい。
なお、解は極形式の形、\( r^{i \theta} \) の形で求めても構わない。
解説6
\[z = r \left( \cos \theta + i \sin \theta \right) \]とする。すると \( z^4 \) は、\[
z^4 = r^4 \left( \cos 4 \theta + i \sin 4 \theta \right)
\]となる。また、\[
-2 + 2 \sqrt{3} i = 4 \left( \cos 120^{\circ} + i \sin 120^{\circ} \right)
\]となる。
ここで、大きさ \( r \) と偏角 \( \theta \) を比べると、\[
r^4 = 4 ,\ \ \ 4 \theta = (120 + 360n)^{\circ}
\]となる。(ただし \( n \) は0以上の整数)よって、\[
r = \sqrt{2} \geqq 0 \ \ \ \theta = 30^{\circ}, 120^{\circ}, -60^{\circ}, -150^{\circ}
\]となる(\( n \geqq 4 \) で1周して元に戻るので解は全部で4つ)。
(もちろん -150° を 210°と、 -60° を 300° と表してもOK)
よって解を \( t_1 \), \( t_2 \), \( t_3 \), \( t_4 \) とすると、\[
t_1 = \sqrt{2} \left( \cos 30^{\circ} + i \sin 30^{\circ} \right) \\
t_2 = \sqrt{2} \left( \cos 120^{\circ} + i \sin 120^{\circ} \right) \\
t_3 = \sqrt{2} \left( \cos (-150^{\circ}) + i \sin (-150^{\circ}) \right) \\
t_4 = \sqrt{2} \left( \cos (-60^{\circ}) + i \sin (-60^{\circ}) \right)
\]となり、図は
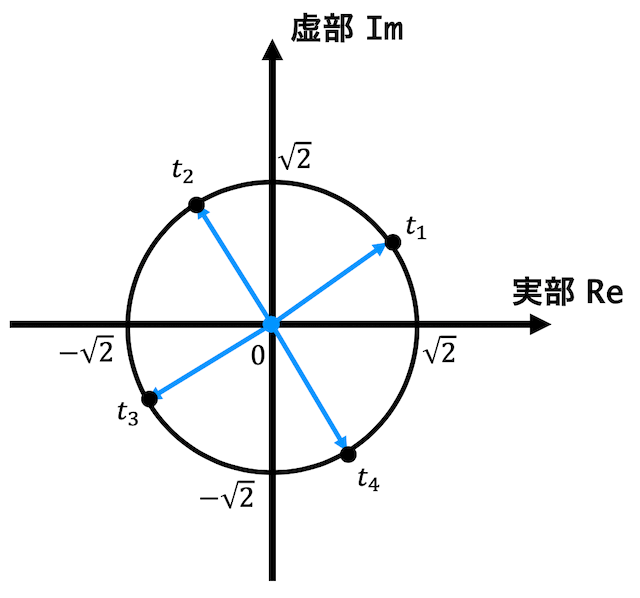
となる。
[\( re^{i \theta} \) の形で表した場合]
\[
t_1 = \sqrt{2} e^{ \frac{\pi}{6} i} , \ \ t_2 = \sqrt{2} e^{ \frac{2}{3} \pi i} \\
t_3 = \sqrt{2} e^{ - \frac{\pi}{3} i} , \ \ t_4 = \sqrt{2} e^{ - \frac{5}{6} \pi i}
\]と表せる。
ド・モアブルの公式を使うことで、解を具体的に求めなくても複素数平面上に図示することができるのです!
もう1問例題を解いてみましょう。
例題7 複素数と方程式2
方程式 \( z^5 = -2i \) の解をすべて求め、極形式もしくは \( r^{i \theta} \) の形で表しなさい。すべての解を複素数平面上に図示しなさい。
解説7
\[z = r \left( \cos \theta + i \sin \theta \right) \]とする。すると \( z^5 \) は、\[
z^5 = r^5 \left( \cos 5 \theta + i \sin 5 \theta \right)
\]となる。また、\[
- 2i = 2 \left( \cos (-90)^{\circ} + i \sin (-90)^{\circ} \right)
\]となる。
ここで、大きさ \( r \) と偏角 \( \theta \) を比べると、\[
r^5 = 2 ,\ \ \ 5 \theta = (-90 + 360n)^{\circ}
\]となる。(ただし \( n \) は0以上の整数)よって、\[
r = \sqrt[5]{2} \geqq 0 \ \ \ \theta = -18^{\circ}, -90^{\circ}, -162^{\circ}, 54^{\circ}, 126^{\circ}
\]となる(\( n \geqq 5 \) で1周して元に戻るので解は全部で5つ)。
よって解を \( t_1 \), \( t_2 \), \( t_3 \), \( t_4 \), \( t_5 \) とすると、\[
t_1 = \sqrt[5]{2} \left( \cos (-18^{\circ}) + i \sin (-18^{\circ}) \right) \\
t_2 = \sqrt[5]{2} \left( \cos 54^{\circ} + i \sin 54^{\circ} \right) \\
t_3 = \sqrt[5]{2} \left( \cos 126^{\circ} + i \sin 126^{\circ} \right) \\
t_4 = \sqrt[5]{2} \left( \cos (-162^{\circ}) + i \sin (-162^{\circ}) \right) \\
t_5 = \sqrt[5]{2} \left( \cos (-90^{\circ}) + i \sin (-90^{\circ}) \right) \\
\]となり、図は
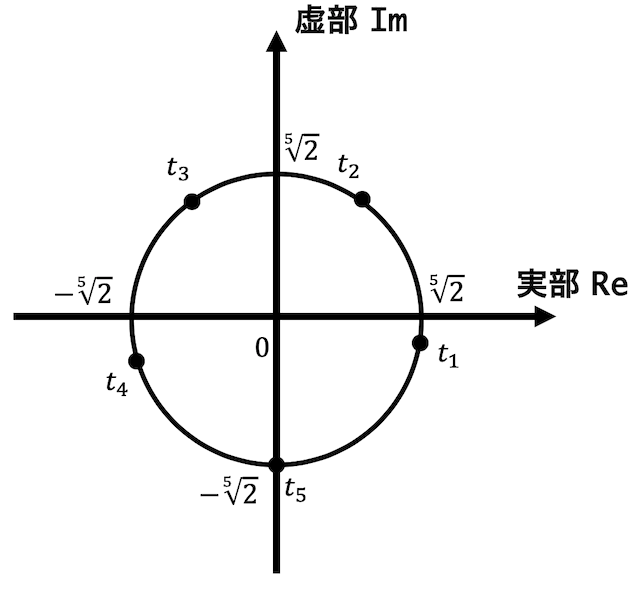
となる。
[\( re^{i \theta} \) の形で表した場合]
\[
t_1 = \sqrt[5]{2} e^{ - \frac{\pi}{10} i} , \ \ t_2 = \sqrt[5]{2} e^{ \frac{3}{10} \pi i} \ \ t_3 = \sqrt{2} e^{ \frac{7}{10} \pi i} \\
t_4 = \sqrt[5]{2} e^{ - \frac{9}{10}\pi i} , \ \ t_5 = \sqrt[5]{2} e^{ - \frac{\pi}{2} i}
\]と表せる。
9.さいごに
今回は、複素数、複素数平面の基本部分について簡単にですがまとめました。
日常生活で普通の人は使わないであろう虚数 \( i \) が数学界では非常にありがたい存在であることがわかっていただけたらありがたいです。
関連広告・スポンサードリンク






![うさぎでもわかる計算機システム Part01 2進数 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612102246-1-150x150.gif)