スポンサードリンク
※ この記事は、すでに「順序回路の設計をする際の状態遷移図・状態遷移表の書き方」を学んだ人向けの記事です。そのため、まだ状態遷移図や状態遷移表の書き方があいまいな人は、下の記事にて復習することをお勧めします。
こんにちは、ももやまです。
順序回路の状態遷移図(や状態遷移表)を設計していると、「もうちょっと状態を減らしてコンパクトにできないかなぁ」と思う場面があるかもしれません。また、テストの際にも「状態数は最小にすること」などの指示が与えられてしまい、どうすれば状態数が最小な状態遷移図を書けるんだろうと思った人もいるかと思います。
そこで今回は、状態遷移図(状態遷移表)の状態数を減らしてなるべく簡潔に状態遷移図(状態遷移表)を表す方法である「状態遷移図の最小化」について、学習していきましょう!
スポンサードリンク
1. 例題で状態遷移図最小化の方法を見てみよう
状態遷移図の最小化では、
- 等価な状態を見つけ出す
- 見つけ出した等価な状態を1つの状態にまとめる
の1, 2を行うことで、「元あった状態遷移図と等価かつ、状態数が最も少なくなる最小状態の状態遷移図」をつくります。
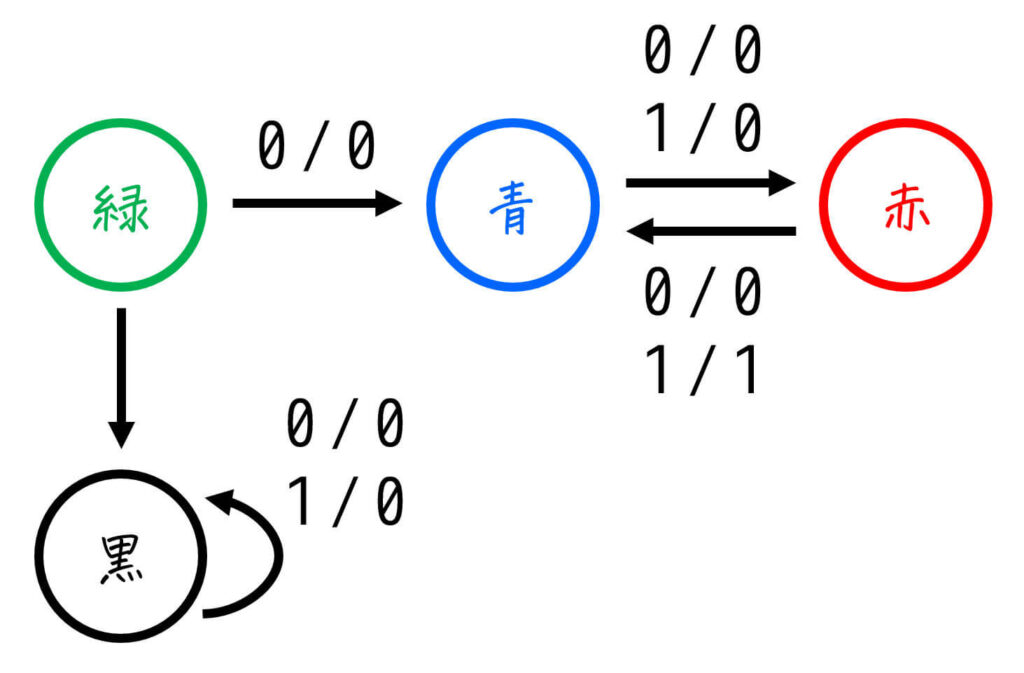
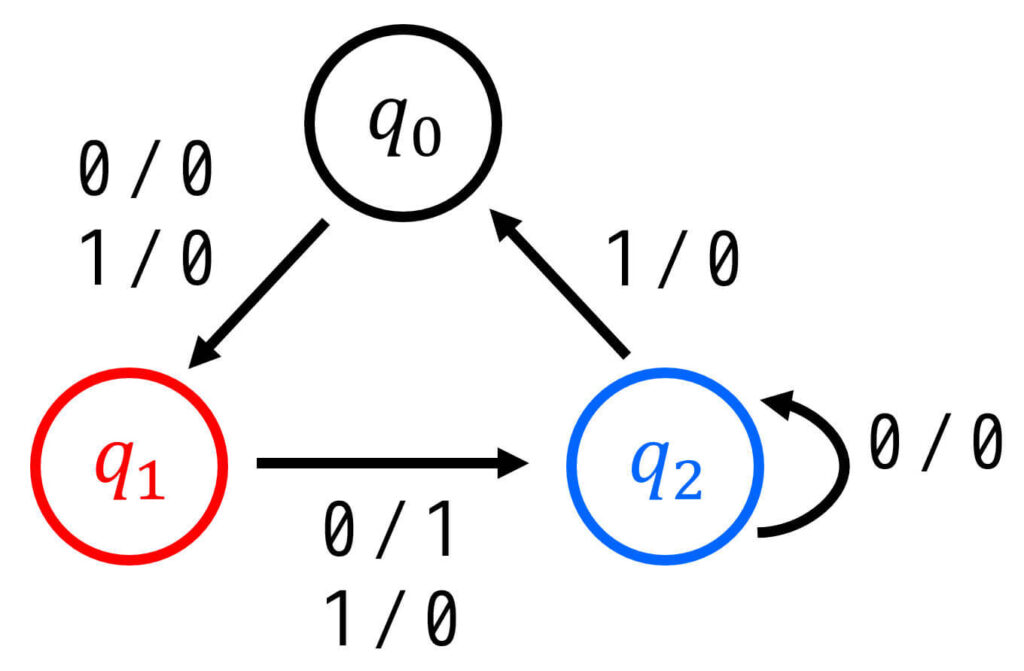
次の状態遷移図を最小化し、等価で状態数が最小となる状態遷移図を作成しなさい。ただし、すでに最小状態(これ以上状態数を減らせない)場合は「最小状態である」と答えること。
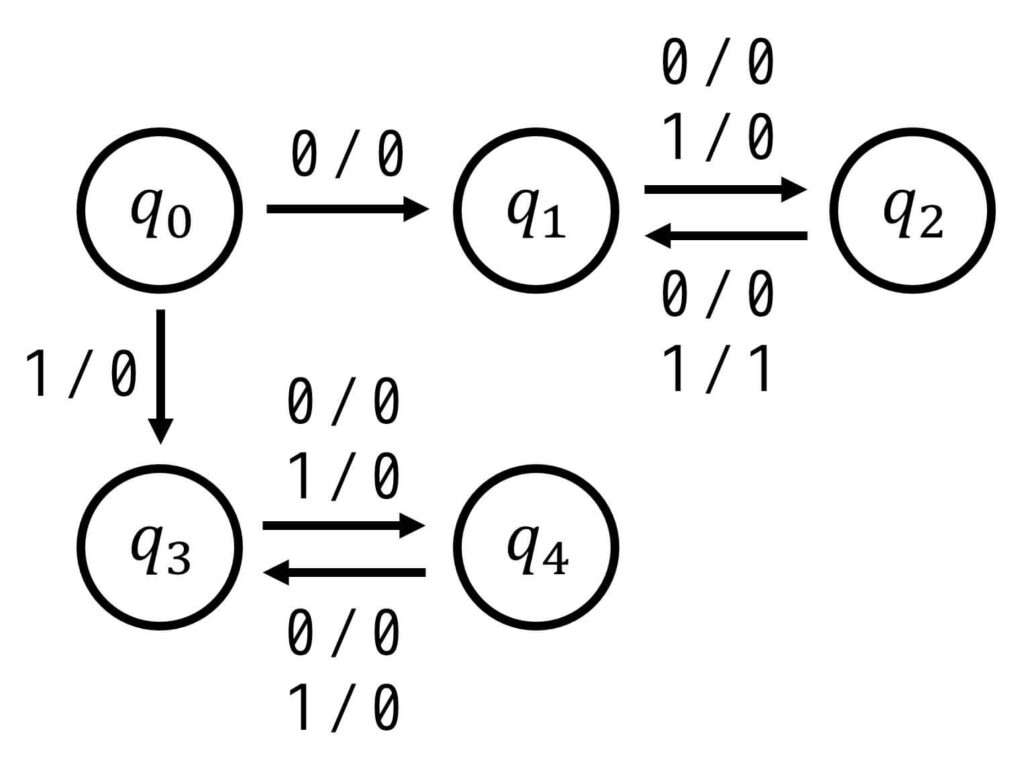
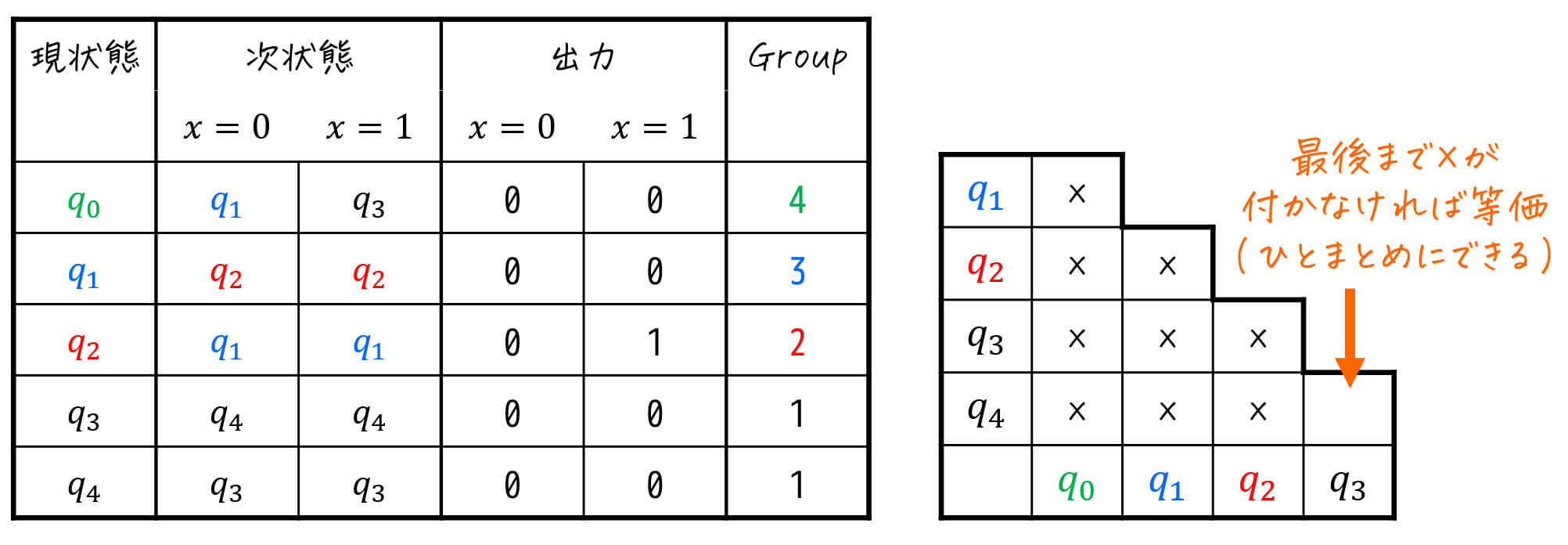
Step1. 状態遷移表を作成する
まずは、与えられた状態遷移図を見ながら状態遷移表を作りましょう。
※ 状態遷移表の書き方は様々ですが、現状態ごとの「各入力における遷移先(次状態)」と「各入力における出力」がわかればOK。
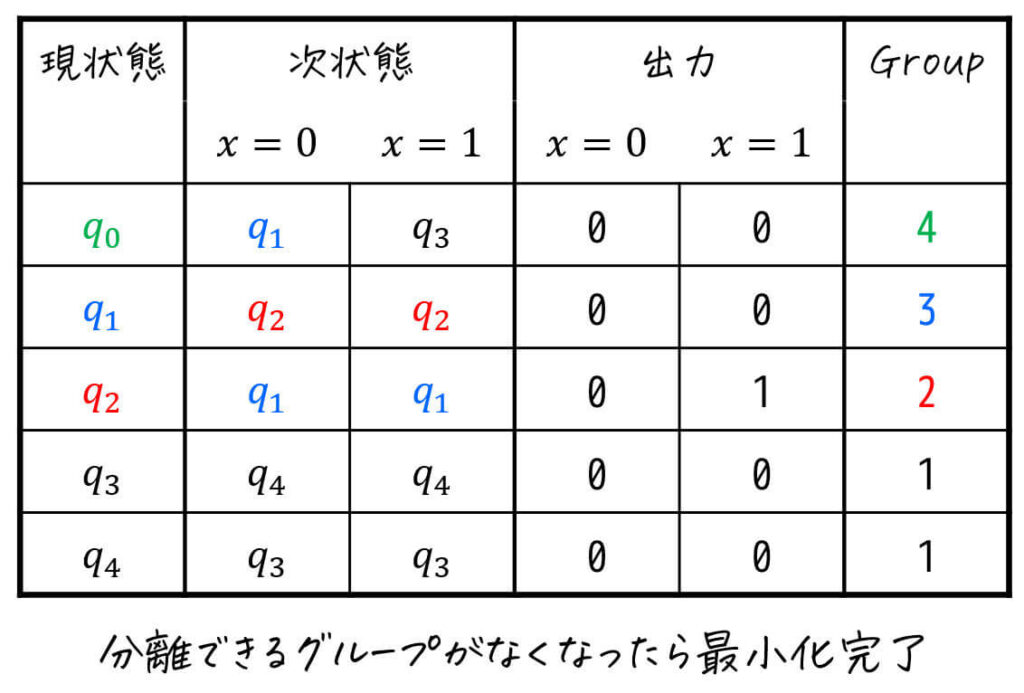
よって、状態遷移表は下のようになります。
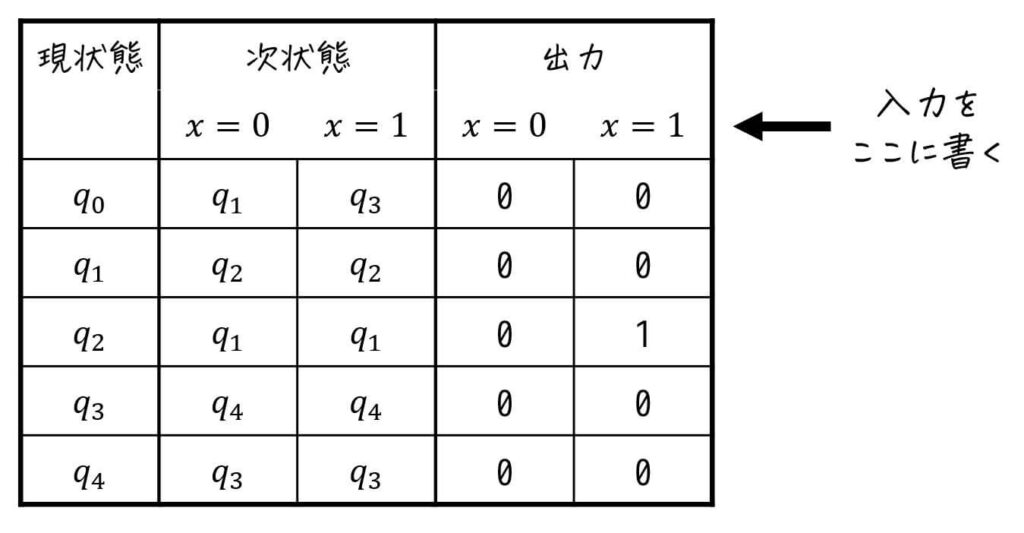
ここからは、どの状態が等価、あるいか等価でないかを判定するステップとなります。
等価な状態を見つけていくときは、一旦どの状態もすべて等価であると仮定し、等価でない状態のペアを見つけ出す作業をしていきます。
ここで見つけ出す作業をしやすくするために、等価な状態ごとにグループ分けを行います[1]同じグループ同士は等価、異なるグループ同士は等価ではないことを表します。例えば、\( q_0 \), \( q_2 \) がグループ1、\( q_1 \), \( q_3\) … Continue reading。
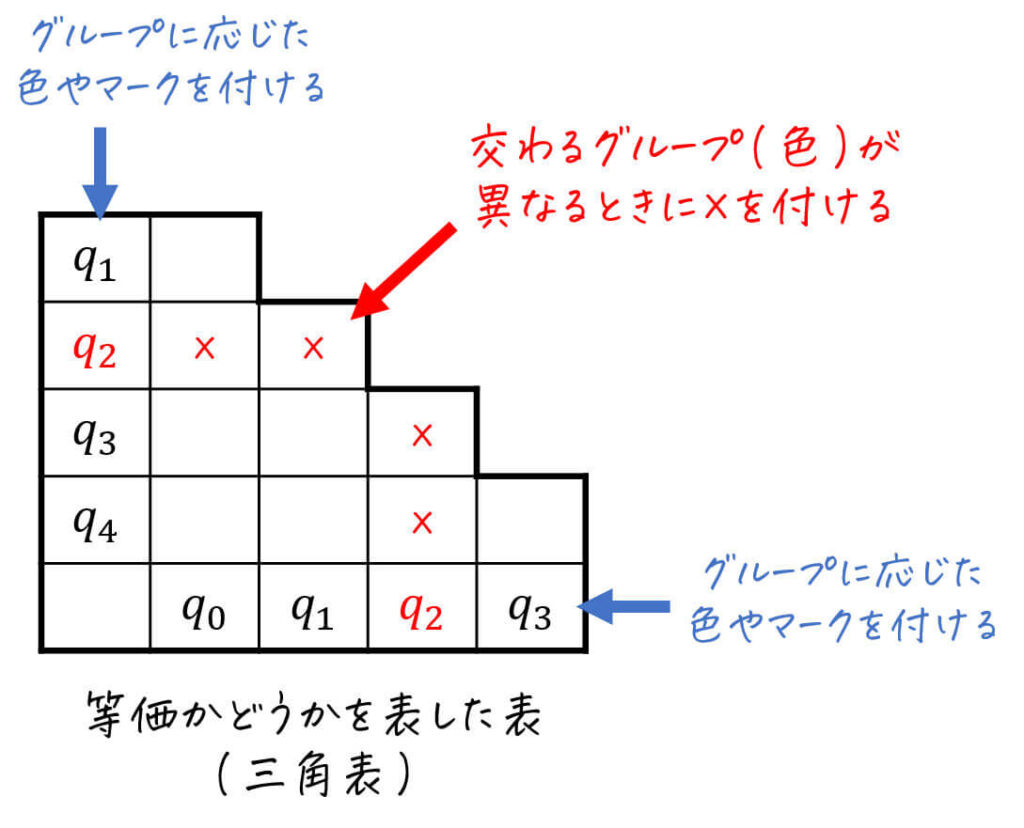
等価かどうかを表した表(三角表)
状態を最小化する際に、下に表される三角表を書きながら最小化をしていくことがあります。
(試験でも、三角表を埋めなさいと言われることがあります。)
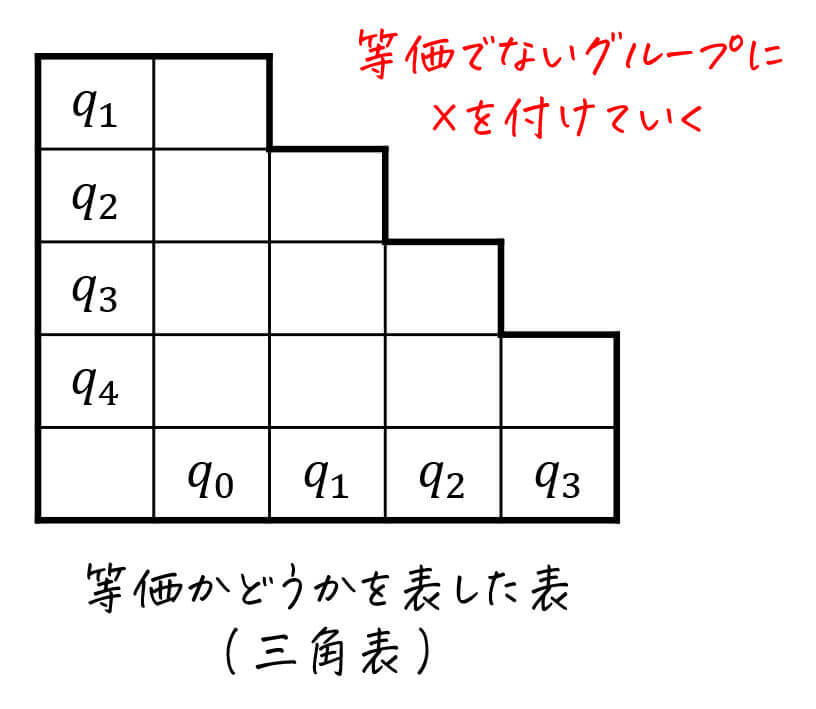
この三角表は、等価でない状態同士に「×」を付けていくことで、どの状態同士が等価でないかを示します。
基本的に指示がない場合は三角表は書かなくてOK(状態遷移図の状態をグループごとに色分けするだけで十分)ですが、試験で指示があった際や最小化に慣れていない人は、最小化の際に三角表も書いていきましょう。
※ 次回説明する「Don’t Careが含まれた状態遷移図・状態遷移表の最小化」を行う際には、三角表が必須になります。なので、Don’t Careが含まれた状態遷移図・状態遷移表の最小化
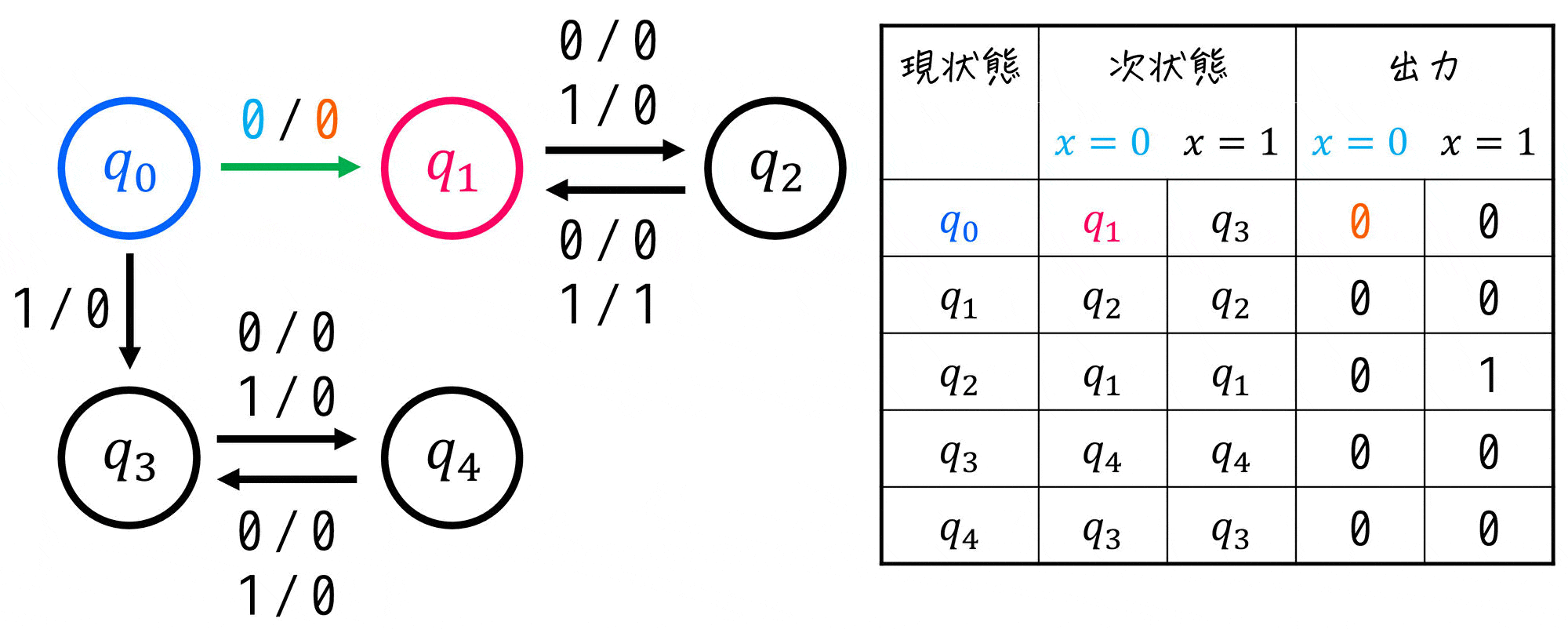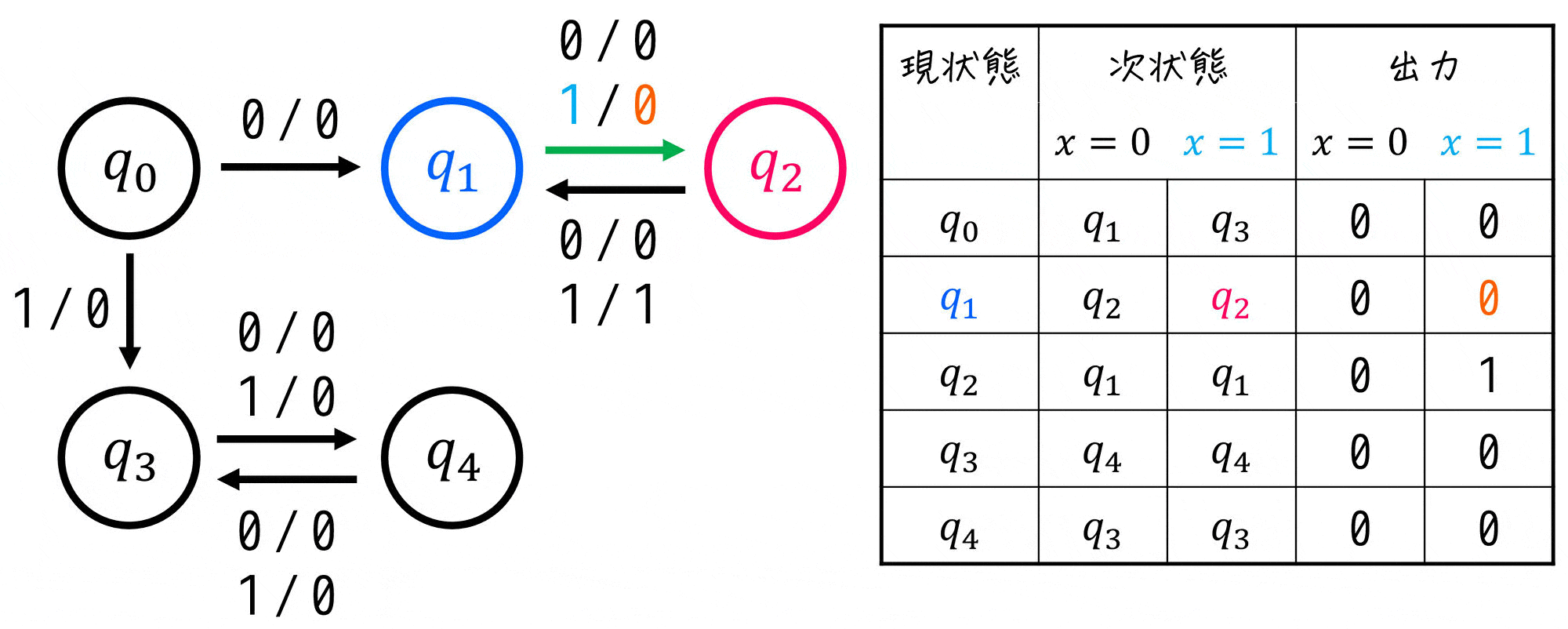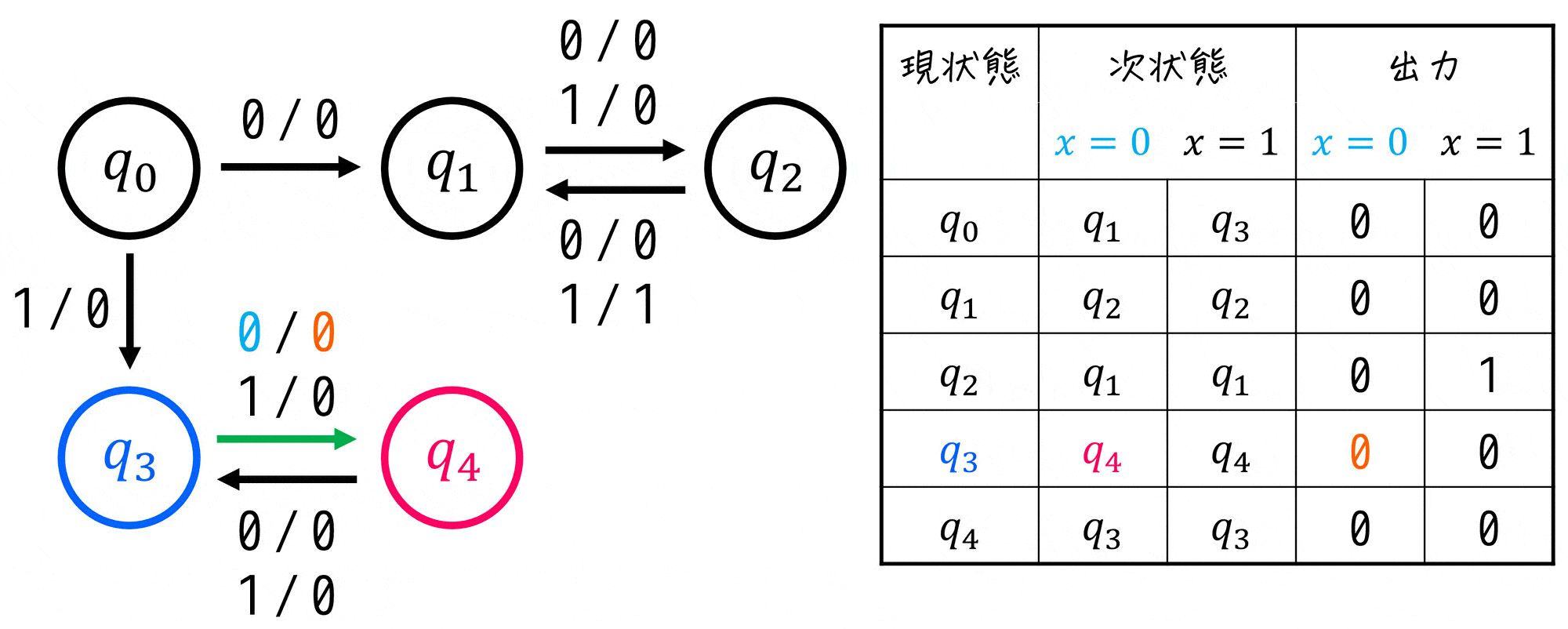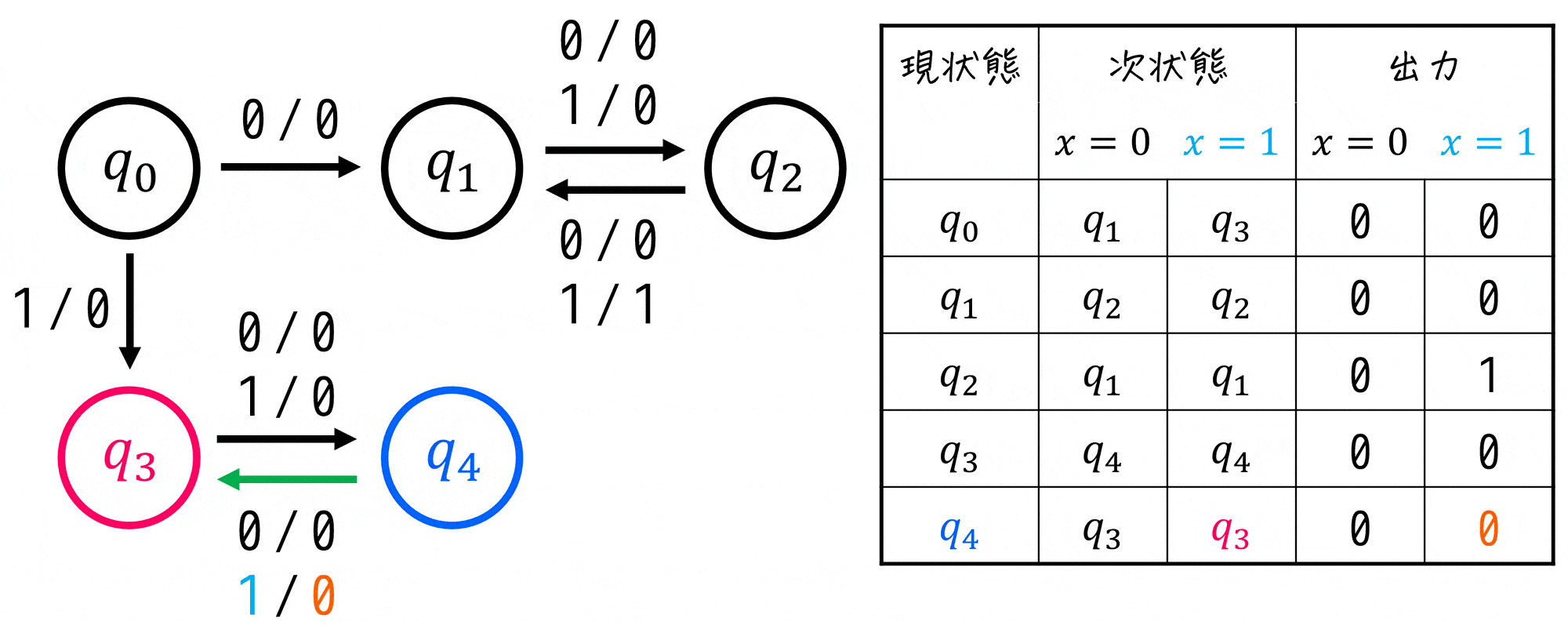
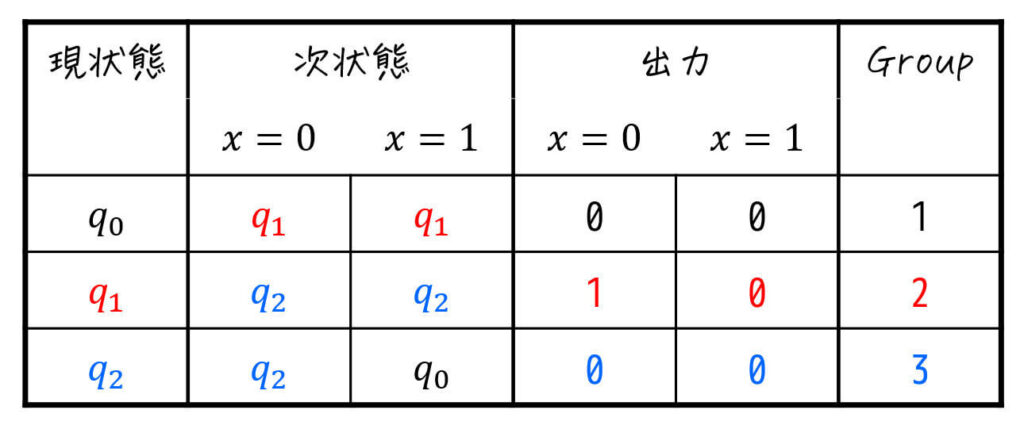
Step2. 出力値から状態をグループ分けする
同じ出力を与えたときに、出力値が異なる状態同士は等価ということはできません。
なので、まずは出力値ごとにグループを分けます[2]同じ入力を与えたときに出力値が必ず同じであれば、とりあえずこの段階では等価であると仮定します。例えば今回の場合、\( q_0 \), \( q_1 \), \( q_3 … Continue reading。
今回の場合、\( q_2 \) 以外は入力 \( x = 0 \), \( x = 1 \) どちらとも出力は0となりますが、\( q_2 \) は入力 \( x = 1 \) のときに1を出力します。
そのため、この段階で \( q_2 \) は他の4状態とは異なるグループに分かれます。ここで、\( q_0 \), \( q_1 \), \( q_3 \), \( q_4 \) はGroup1、\( q_2 \) をGroup2と名付けましょう。
※ 視覚的に異なるグループを見分けるため、現状態部分に色分けをしたり、記号を付けることをおすすめします
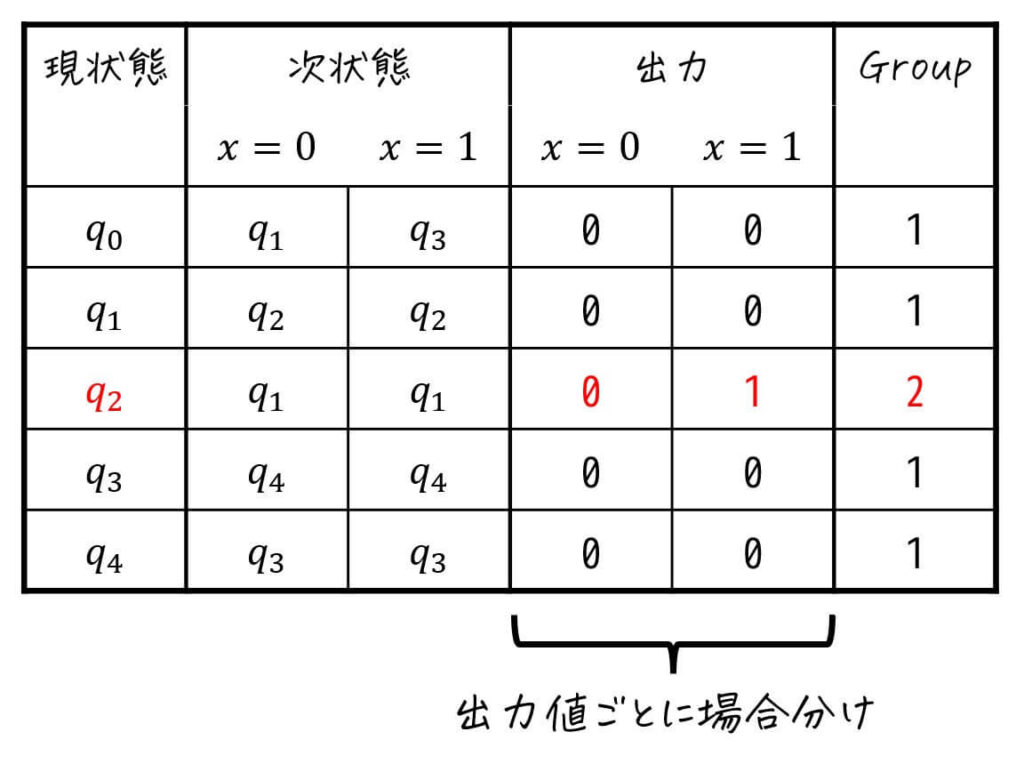
三角表を書いている人は、この段階で出力が異なる \( q_2 \) と他の状態同士に×を付けていきましょう。
※ 三角表の状態部分にも、グループに応じた色やマークを付けると「×」がつけやすくなるので、是非色やマークを付けましょう。(今回の場合は \( q_2 \) が別グループになったので、\( q_2 \) を赤色にしています。)
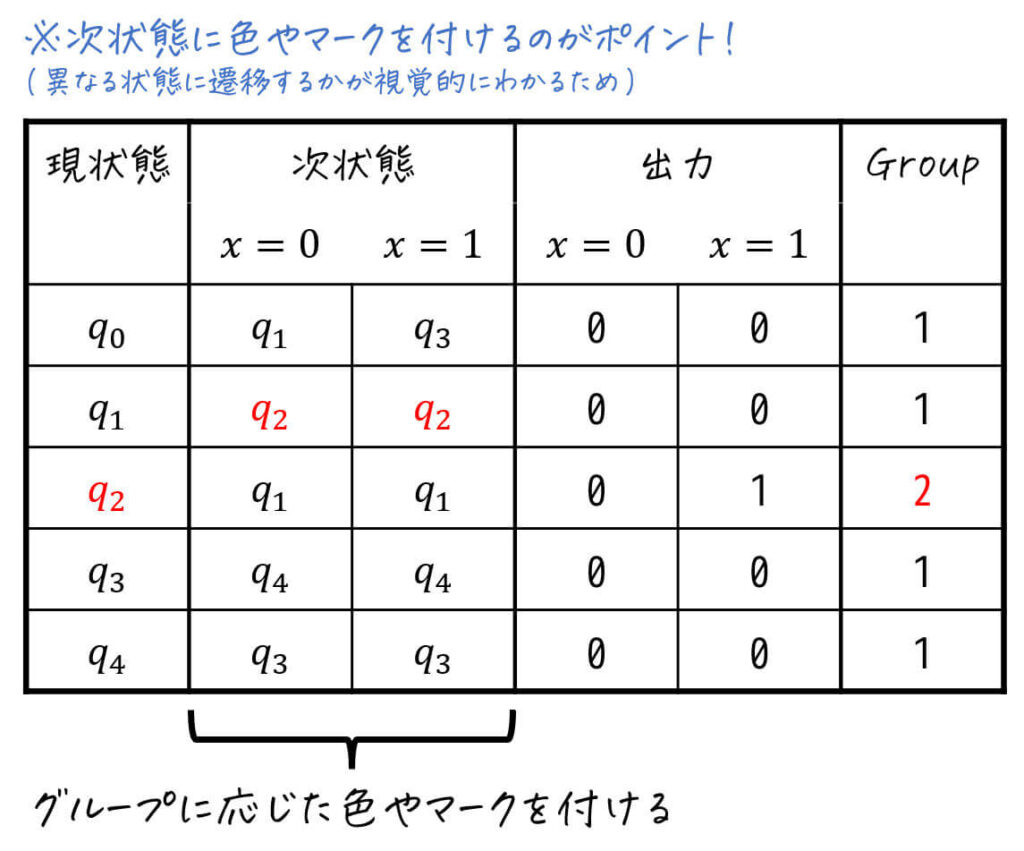
さらに、次状態に書かれている状態にもグループに応じた色を付けましょう。
(Step3の「異なる状態に遷移する状態を見つける」際にすごく役に立ちます)
Step3. グループごとに異なるグループに遷移する状態を見つけて分離
ここからは、グループごとに「同じ入力値を与えたときに異なるグループに遷移する状態を見つけてグループを分離する」作業を、グループが分離できなくなる(=等価でない状態が見つからなくなる)まで繰り返し行います。
ここで、Group2は、\( q_2 \) の1つしかないため、これ以上グループの分離ができません。なので、Group1の状態の中で、「同じ入力値なのに異なるグループに遷移する(=等価でない)状態」を探して、それらを異なるグループに分離させていきます。
ということで、Group1の中で「同じ入力値なのに異なるグループに遷移する状態」を先ほど付けたグループに応じた色を手がかりに探していきましょう。
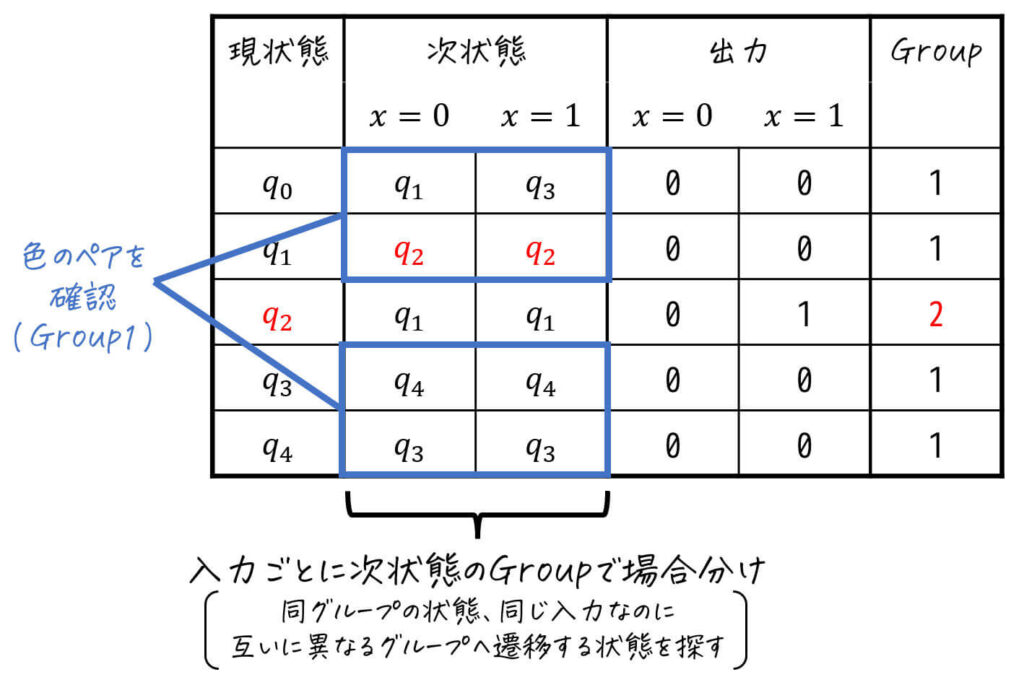
すると、\( q_0 \), \( q_3 \), \( q_4 \) は \( x = 0 \), \( x = 1 \) どちらを入力しても「Group1(黒色)」になる一方、\( q_1 \) は \( x = 0 \), \( x = 1 \) どちらを入力しても「Group2(赤色)」になりますね。
そのため、\( q_1 \) はGroup1とは異なるグループであることがわかります。
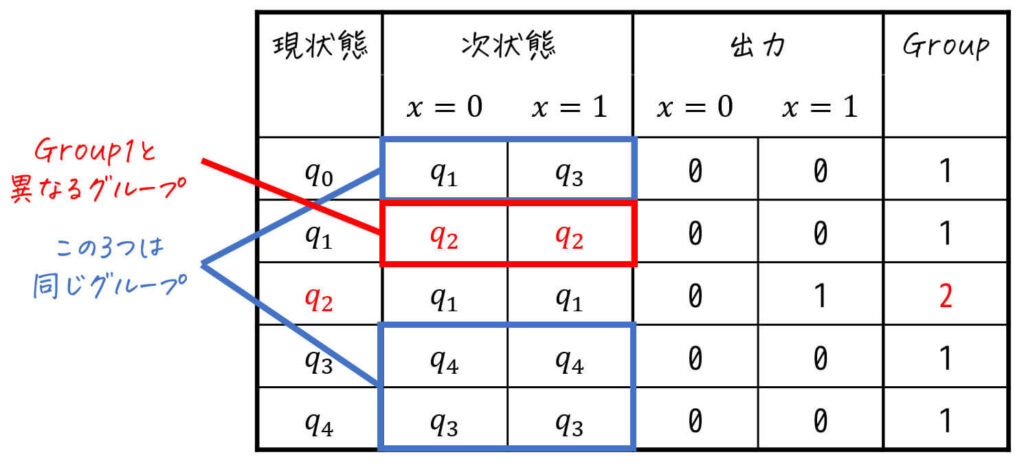
※「次状態に付いた色やマーク」が同じグループが互いに同じグループ(=等価となる可能性がある状態同士)となり、異なるグループは互いに異なる(=等価ではない状態同士)グループになります[3]\( q_0 \), \( q_3 \), \( q_4 \) は \( x = 0 \), \(x = 1 \) 側ともに黒なのでこの3状態は同じグループ(=等価となる可能性がある)です。一方 \( q_1 \) だけは \( … Continue reading
なので、\( q_1 \) を別のグループ(Group3)とし、識別のために現状態と次状態の色も変えてあげましょう。
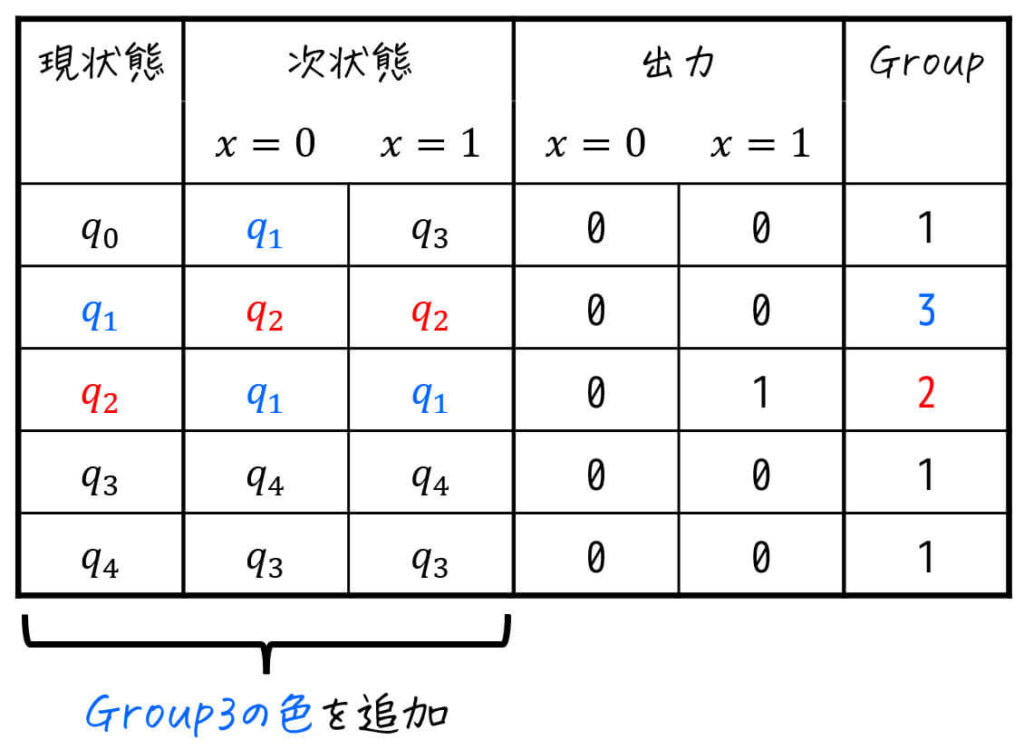
三角表を書いている人は、この段階で \( q_1 \) と他の状態同士すべてに「×」を付けましょう。
(\( q_1 \) が他グループになったため、他のどの状態とも等価ではないため)
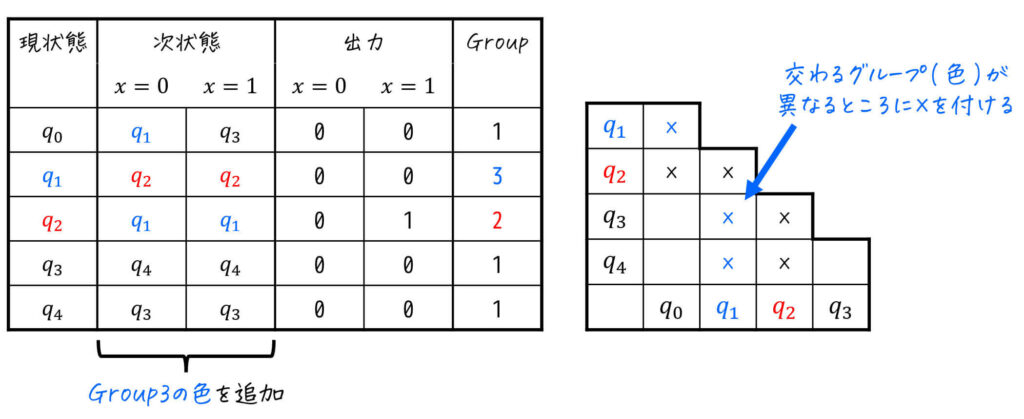
再びグループごとに「同じ入力値なのに異なるグループに遷移する状態(=等価でない状態)」を探していきます。
Group2, Group3は1状態で分離のしようがないため、再びGroup1を確認します[4] … Continue reading。
すると、\( q_3 \), \( q_4 \) は \( x = 0 \), \( x = 1 \) どちらを入力しても「Group1(黒色)」になる一方、\( q_0 \) は \( x = 0 \) を入力すると「Group3(青色)」になりますね。
そのため、\( q_1 \) もGroup1と異なるグループであることがわかります。
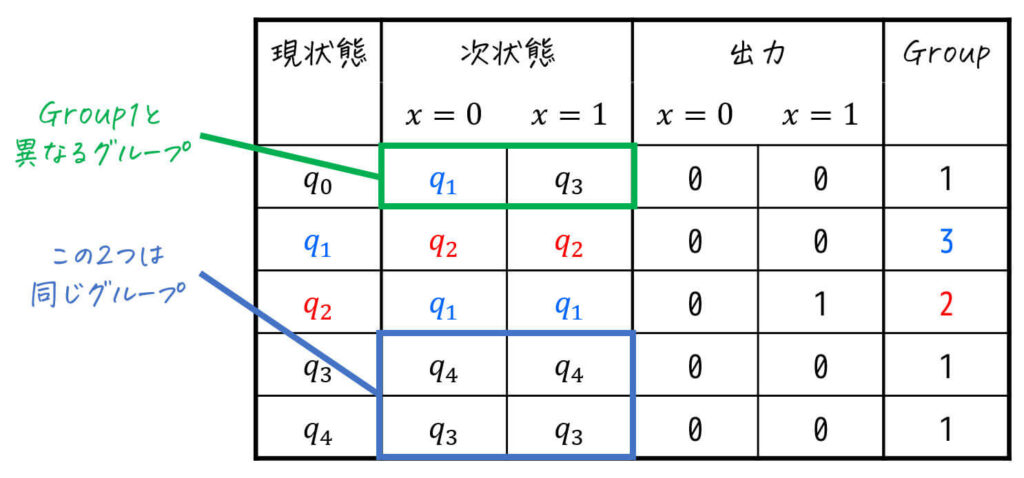
なので、\( q_1 \) を別のグループ(Group4)とし、識別のために現状態と次状態の色も変えてあげましょう。
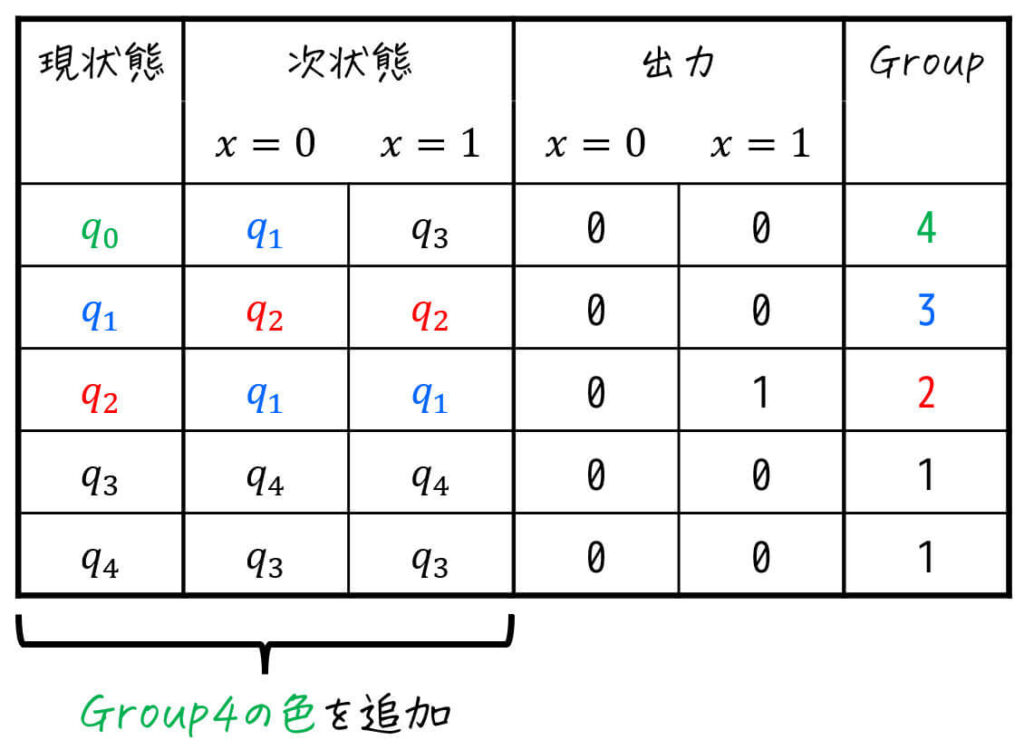
三角表を書いている人は、この段階で \( q_0 \) と他の状態同士すべてに「×」を付けましょう。
(\( q_0 \) が他グループになったため、他のどの状態とも等価ではないため)
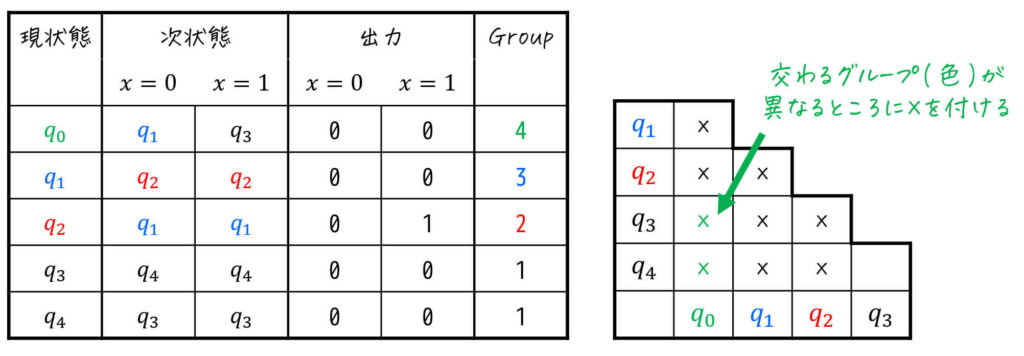
異なるグループへの分離ができたため、さらにグループごとに「同じ入力値なのに異なるグループに遷移する状態(=等価でない状態)」があるか探していきます。
Group2, Group3, Group4は1状態で分離のしようがないため、再びGroup1を確認しましょう。
すると、\( q_3 \), \( q_4 \) ともに \( x = 0 \), \( x = 1 \) どちらを入力しても「Group1(黒色)」に遷移しますね。なので、何もしません。(三角表の「×」も増えません)
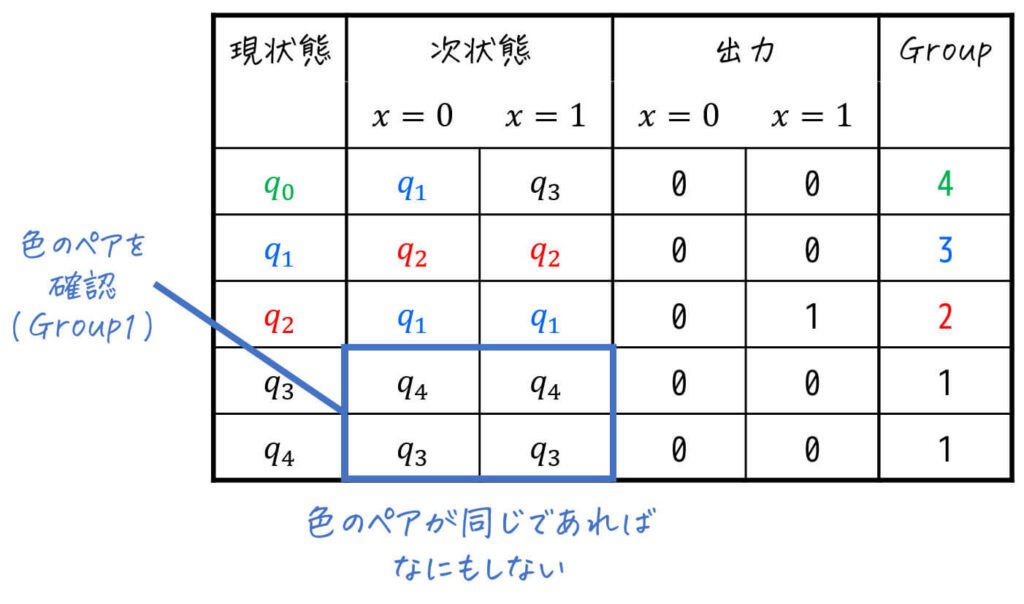
よって、2状態以上あるグループ(今回はGroup1だけ)がすべて分離できない[5]同じ入力値なのに異なるグループに遷移する状態(=等価でない状態)が存在しないということ。ことが確認できたため、Step3の最小化は完了です。
※ この段階で、同じグループにしている状態は互いに等価なため、1つにまとめることができます。
三角表を書いている人は、このタイミングで三角表の完成です。
最後まで「×」が付かなかった状態は、互いに等価であることを示します。今回は、\( q_3 \), \( q_4 \) のペアに「×」がないので、このペアは等価であることがわかりますね。
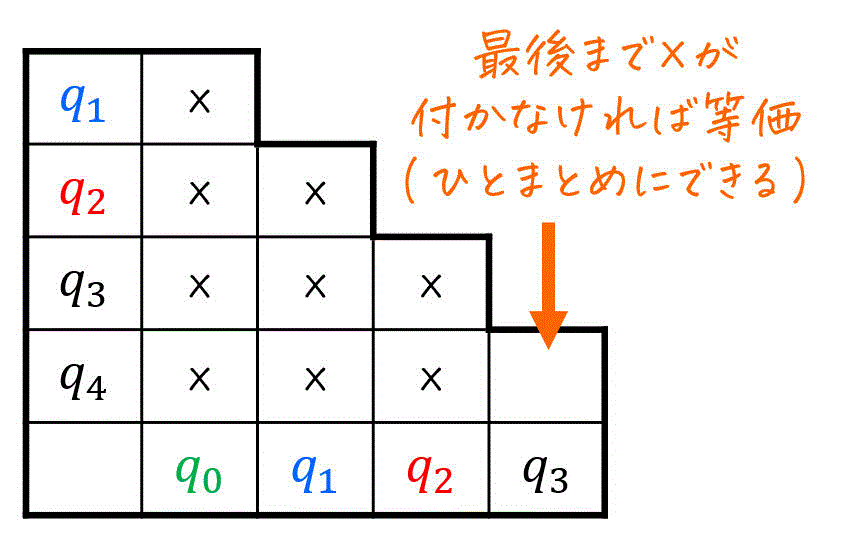
(等価である状態に「〇」を書き込むこともあります。)
Step4. 各グループの中から代表の状態を1つ選び、状態遷移表を圧縮
つぎに、最小化したグループから代表の状態を1つ選び、下のように状態遷移表を置き換えます。
(代表を選んだあとに名前を付け替えてもOKです)
※ この段階で、同じグループの状態は1つにまとめます。今回の場合、Group1(黒)の \( q_3 \), \( q_4 \) は1つにまとまります。
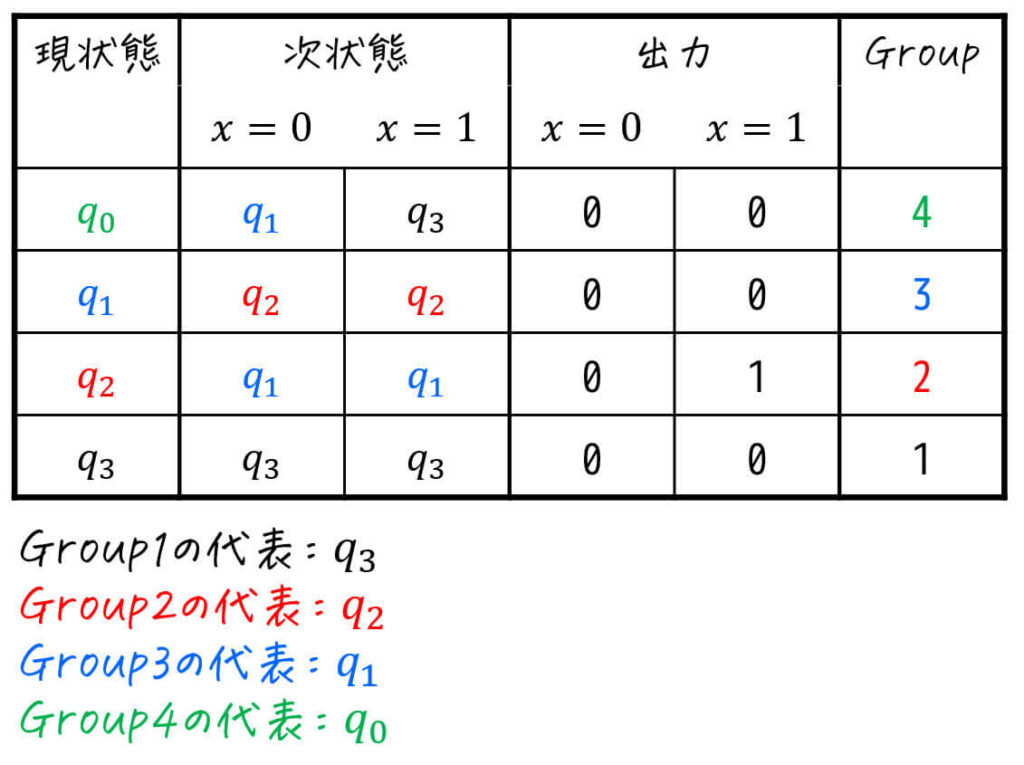
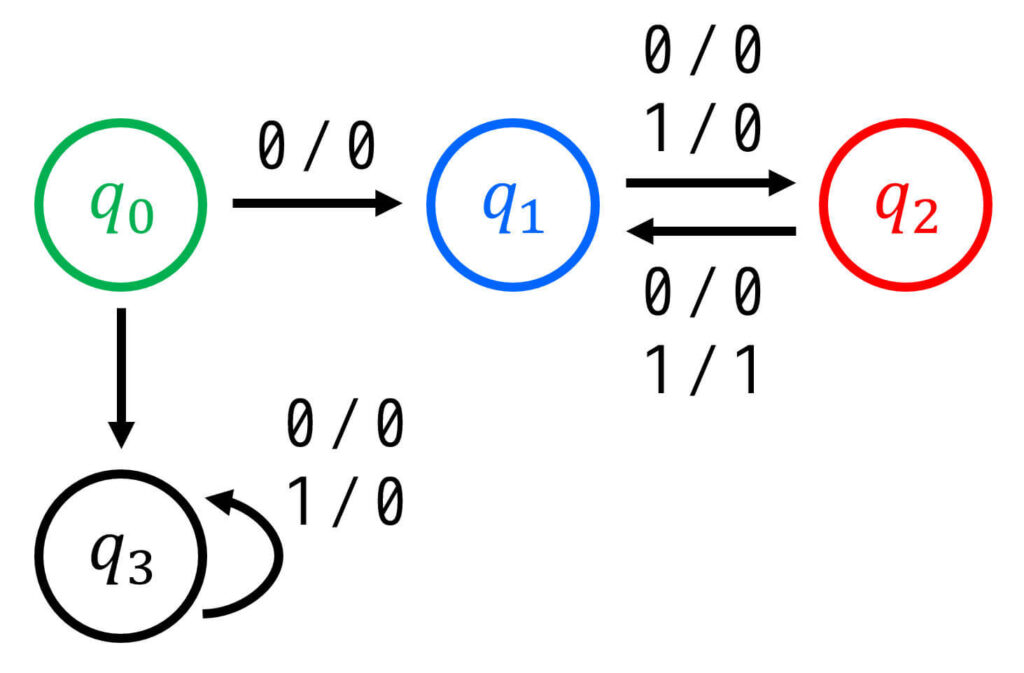
Step5. 圧縮した状態遷移表を見ながら状態遷移図を書く
最後に、Step4で書いた状態遷移表を見ながら状態遷移図を書けば、状態遷移図の最小化が完了です!
与えられた状態遷移図は、次の1~5の手順を踏むことで最小化ができる。
- 状態遷移図を見ながら状態遷移表を書く
- 出力値に応じて状態をグループ分けし、現状態と次状態にグループに応じた色やマークを付ける
- 出力が何変数であろうが、流れは同じ
- 2で付けた色やマークを参考にしながら、各グループごとに「次状態に付いた色やマークが異なる」状態を見つけてグループを分離する。
- グループを分離できた場合、引き続き3を行う。
- これ以上分離できなくなった段階で4に進む。
- 入力が何変数であろうが、流れは同じ。
- 各グループから代表の状態を1つ選び、状態遷移表を圧縮
- 圧縮した状態遷移表を見ながら状態遷移図を書く
スポンサードリンク
2. もともと状態遷移図が最小状態だった場合
今度は、もともと最小状態である状態遷移図を最小化しようとするとどうなるのかを実際に例題を踏まえて見ていきましょう。
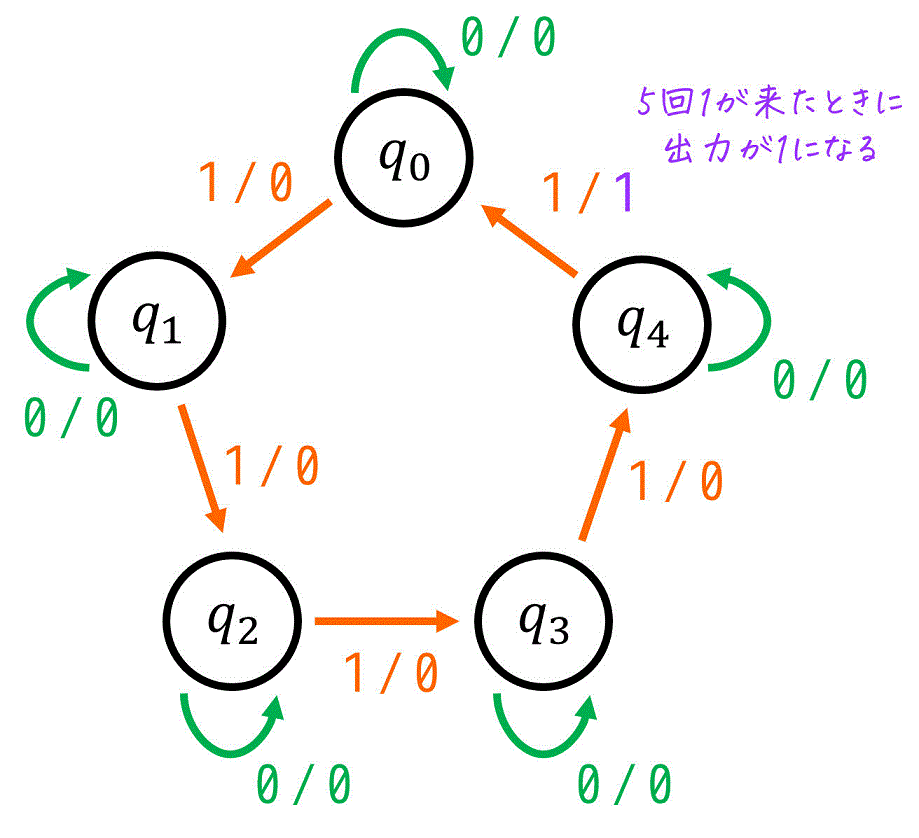
次の状態遷移図を最小化し、等価で状態数が最小となる状態遷移図を作成しなさい。ただし、すでに最小状態(これ以上状態数を減らせない)場合は「最小状態である」と答えること。
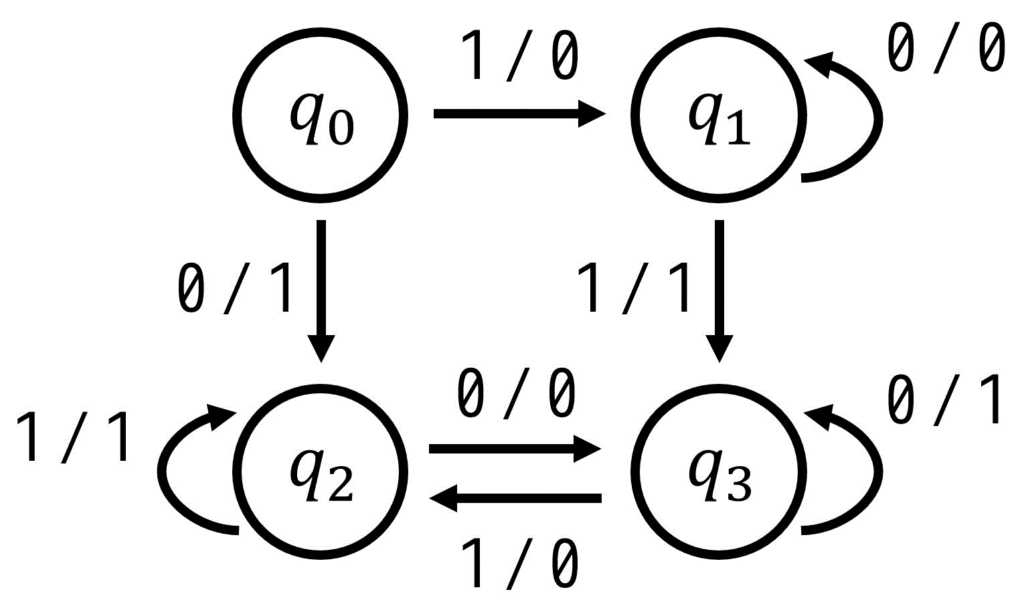
Step1. 状態遷移表を作成する
まずは、状態遷移図を見ながら、状態遷移表を書きましょう。
※ 現状態ごとの「各入力における遷移先(次状態)」と「各入力における出力」が分かればOKです。
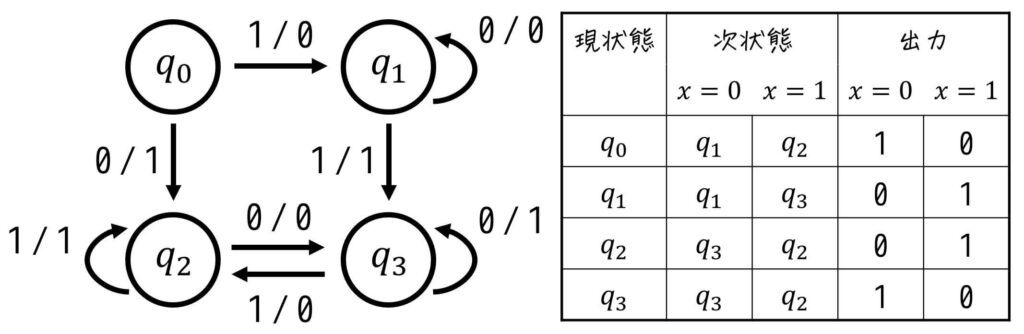
Step2. 出力値から状態をグループ分け
今回は \( q_0 \), \( q_3 \) が入力 \( x = 0 \) のとき出力1、入力 \( x = 1 \) のとき出力0なのに対し、\( q_1 \), \( q_2 \) は入力 \( x = 0 \) のとき出力0、入力 \( x = 1 \) のとき出力1になるので、「\( q_0 \) と \( q_3 \)」、「\( q_1 \) と \( q_2 \)」の2つのグループに分けることができます。
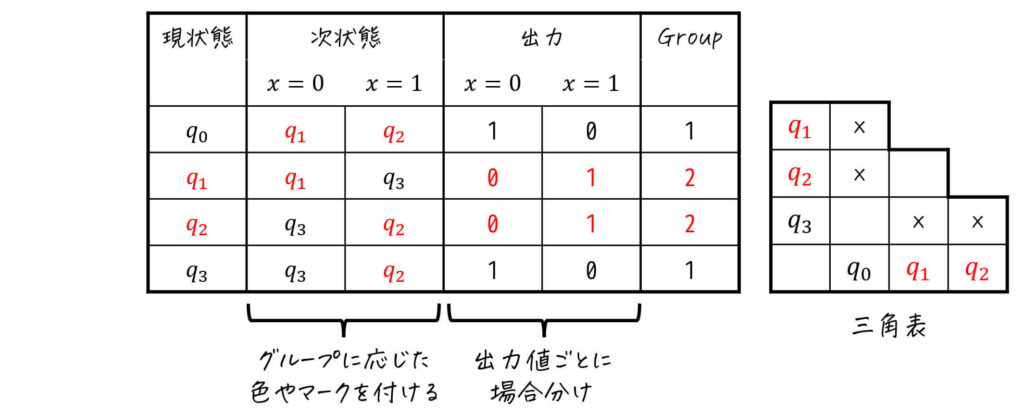
Step3. グループごとに異なるグループに遷移する状態を見つけて分離
ここからは、グループごとに「同じ入力値を与えたときに異なるグループに遷移する状態を見つけてグループを分離する」作業を、グループが分離できなくなる(=等価でない状態が見つからなくなる)まで繰り返し行います。
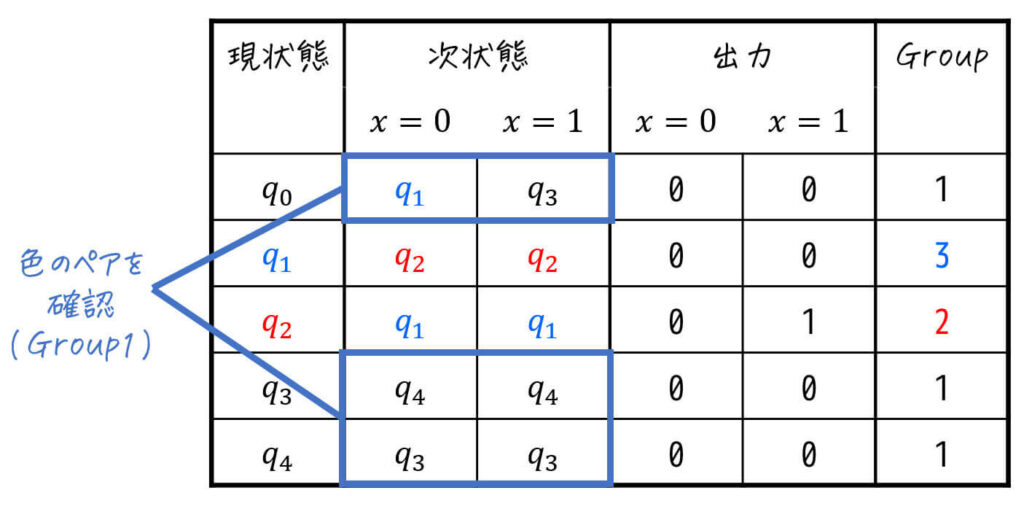
まずは、Group1、Group2それぞれの各入力における次状態(色のペア)を確認します。
(2つ一度に処理してしまいましょう。)
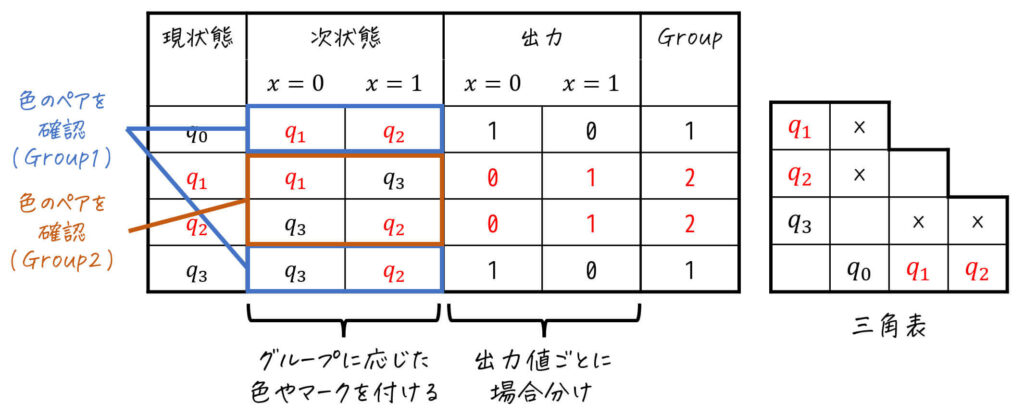
すると、
- \( q_0 \), \( q_3 \)(Group1)の色のペアが異なる
→ \( q_0 \), \( q_3 \) はそれぞれ別のグループ - \( q_1 \), \( q_2 \)(Group2)の色のペアも異なる
→ \( q_1 \), \( q_2 \) はそれぞれ別のグループ
となります。
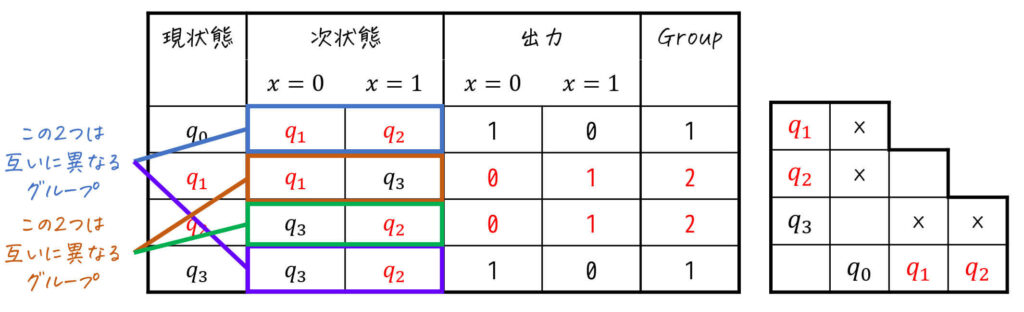
\( q_0 \), \( q_3 \) および \( q_1 \), \( q_2 \) を別グループにすると、下のように \( q_0 \), \( q_1 \), \( q_2 \), \( q_3 \) それぞれが別のグループとなり、どのグループも状態数が1つ(=三角表の全ての欄に×が付いた状態)になります。
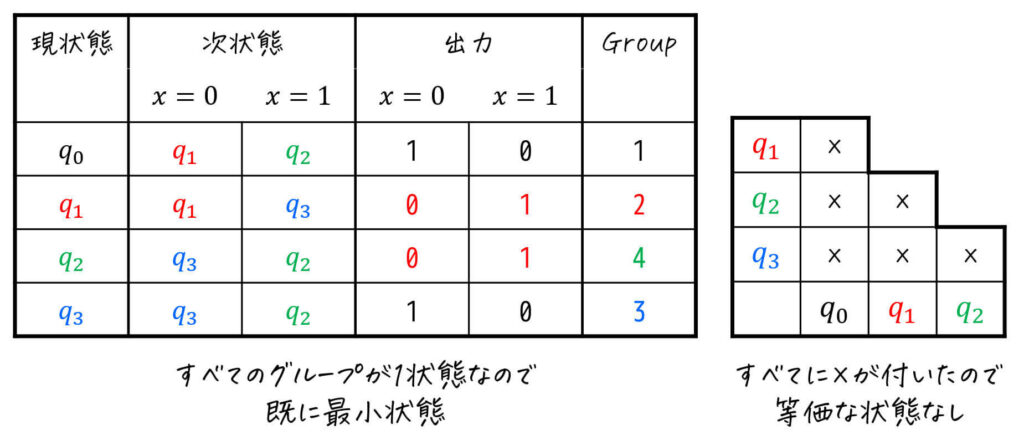
このように、全グループの状態数が1つ(=三角表の全ての欄に×が付いた状態)になった場合は、与えられた状態遷移図がもともと最小状態であることを示します。
そのため、「最小状態である。」が答えとなります。
スポンサードリンク
3. 実際に最小化の練習をしてみよう
それでは、実際に練習問題を1問使って、順序回路の状態遷移図を最小化する練習をしてみましょう。
次の状態遷移図を最小化し、等価で状態数が最小となる状態遷移図を作成しなさい。ただし、すでに最小状態(これ以上状態数を減らせない)場合は「最小状態である」と答えること。
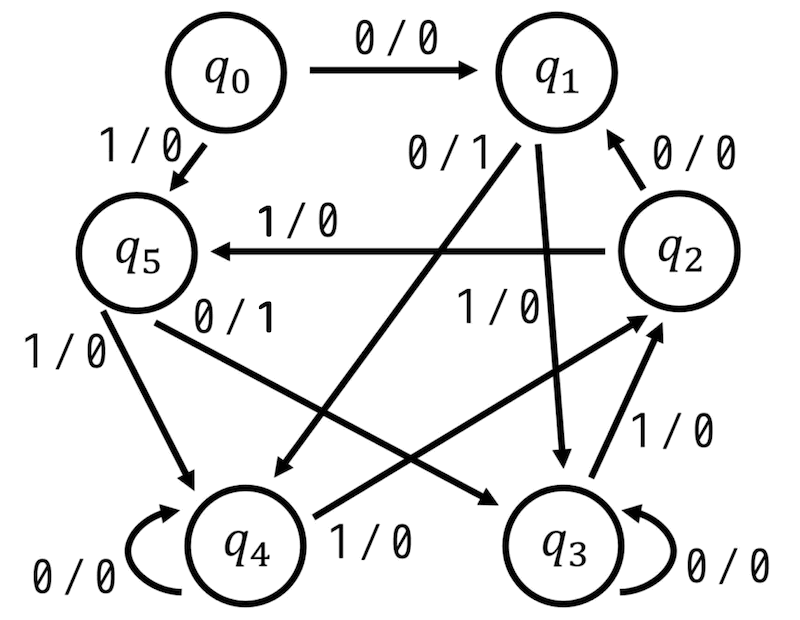
Step1. 状態遷移表を作成する
まずは、状態遷移図を見ながら、状態遷移表を書きましょう。
※ 現状態ごとの「各入力における遷移先(次状態)」と「各入力における出力」が分かればOKです。
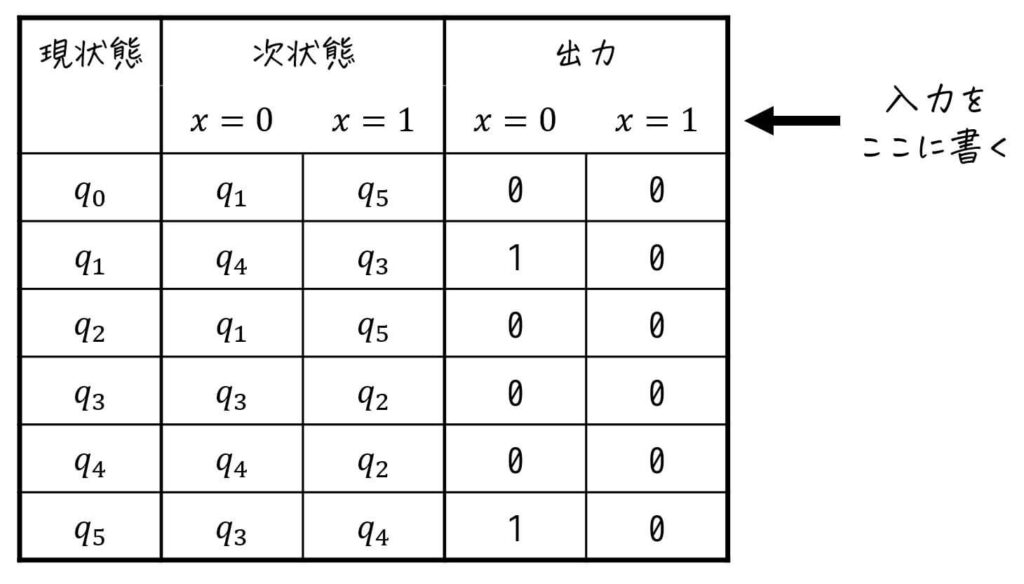
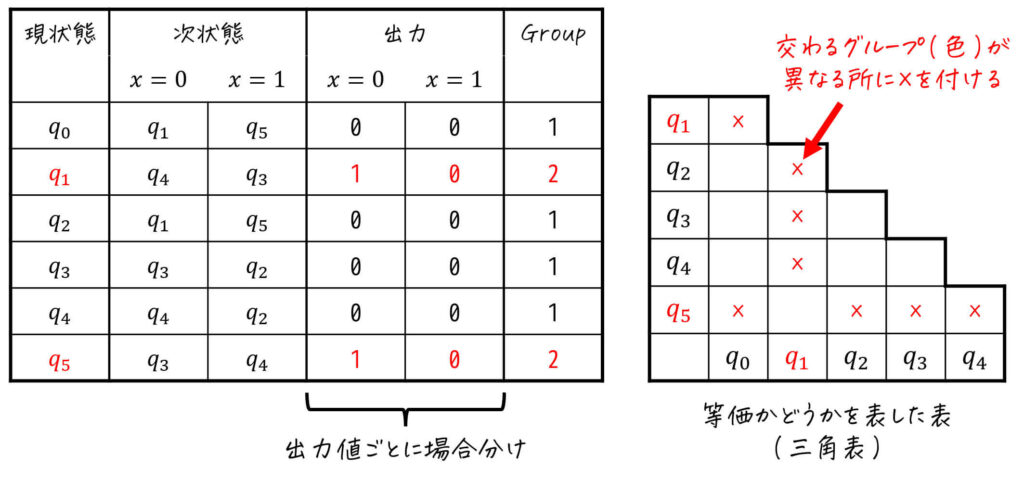
Step2. 出力値から状態をグループ分け
つぎに、出力に着目して現状態にグループを付けていきましょう。
今回は、\( q_0 \), \( q_2 \), \( q_3 \), \( q_4 \) がともに「入力 \( x = 0 \) のときに出力0、入力 \( x = 1 \) のときに出力0」になるので、この4状態を同じグループとします。
(Group1としましょう)
また、残りの \( q_1 \), \( q_5 \) はともに「入力 \( x = 0 \) のときに出力1、入力 \( x = 1 \) のときに出力0」となるので、この2状態は同じグループですね。
(Group2としましょう)
さらに、次状態の状態にもグループに応じた色(やマーク)を付けておきましょう。
(Step3以降で「各入力における次状態のグループ」を比べるのが楽になる)
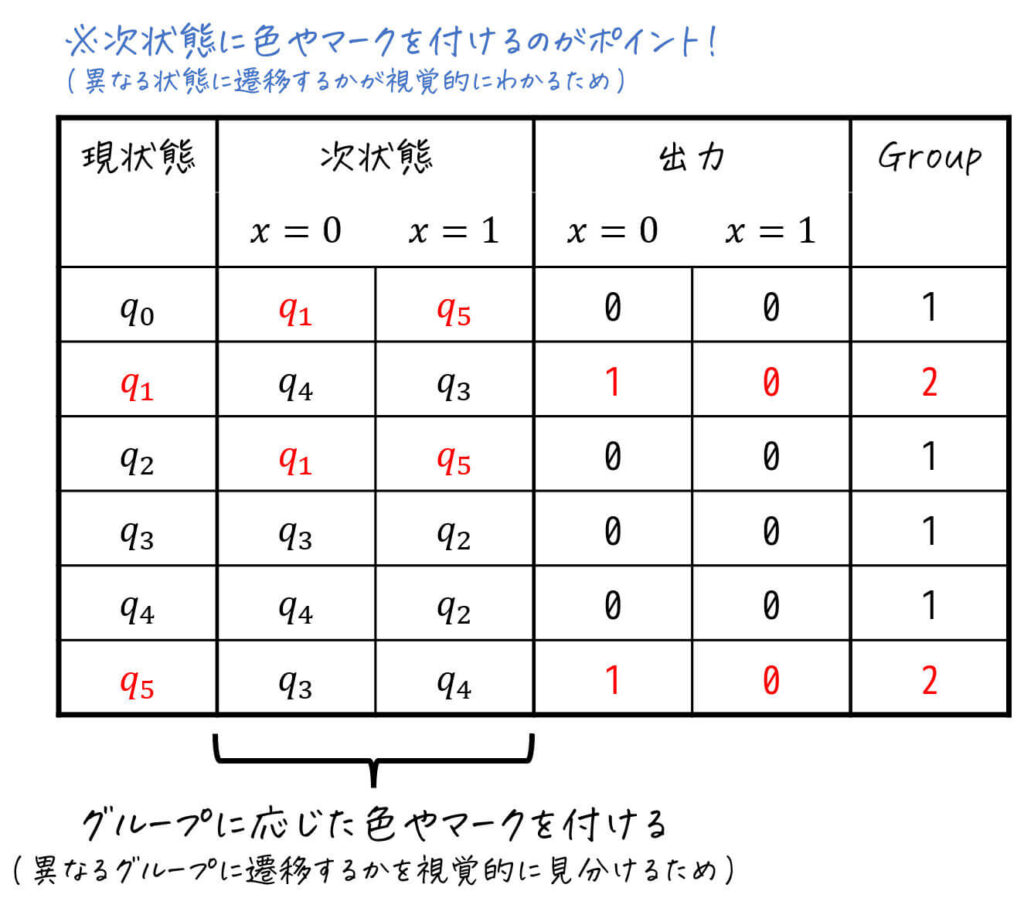
Step3. グループごとに異なるグループに遷移する状態を見つけて分離
Step3では、グループごとに「同じ入力値を与えたときに異なるグループに遷移する状態を見つけてグループを分離する」作業を、グループが分離できなくなる(=等価でない状態が見つからなくなる)まで繰り返し行います。
まずは、Group1、Group2それぞれの各入力における次状態(色のペア)を確認します。
(2つ一度に処理してしまいましょう。)
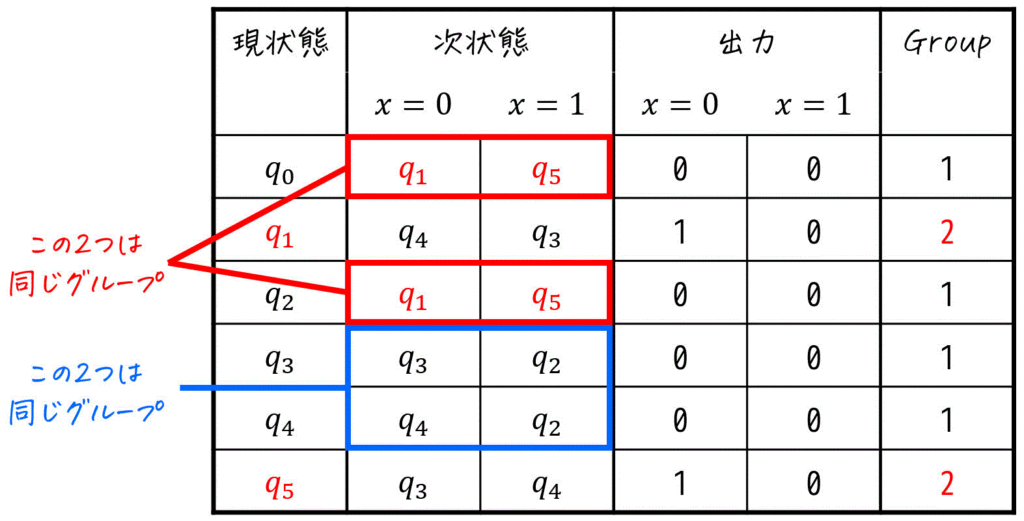
ここで、Group2の色のペアはともに同じなので何もしません。
一方、Group1の色のペアは、\( q_0 \), \( q_2 \) では \( x = 0 \), \( x = 1 \) どちらを入力しても共にGroup2(赤色)に遷移するのに対し、\( q_3 \), \( q_4 \) のときは \( x = 0 \), \( x = 1 \) どちらを入力しても共にGroup1(黒色)に遷移しますね。
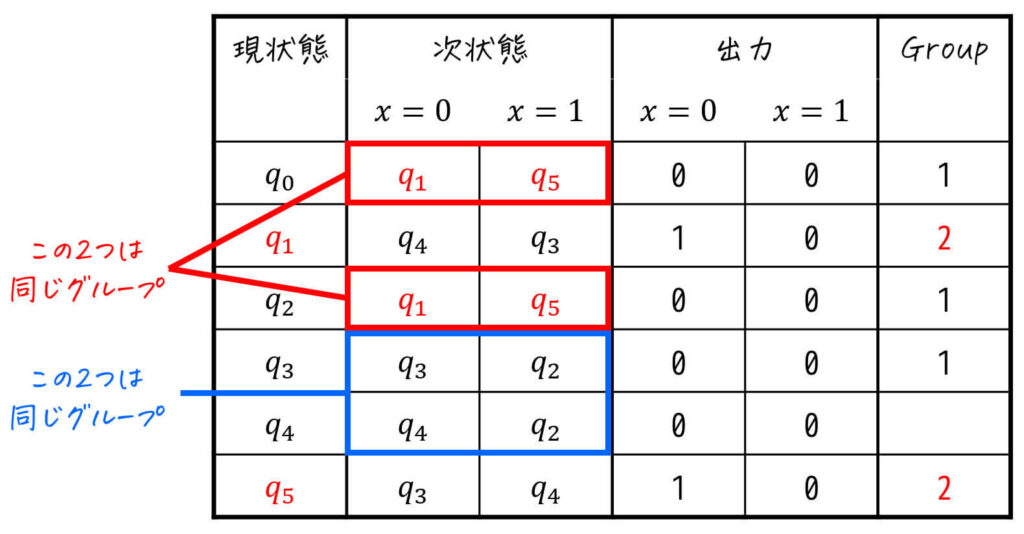
そのため、Group1は「\( q_0 \), \( q_2 \)」のグループと「\( q_3 \), \( q_4 \) のグループ」の2種類に分離することができますね。
なので、\( q_3 \), \( q_4 \) をGroup3に分離しましょう。(必要な方は三角表も追記)
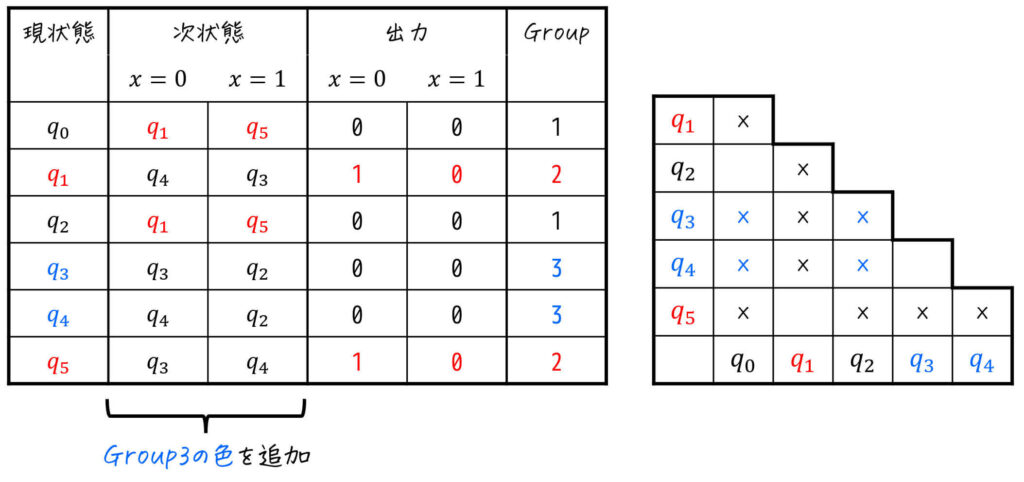
グループの分離に成功したので、もう1度各グループごとに分離できるグループがあるか(=等価ではないグループがあるか)を、「次状態部分の色の組み合わせ」で確認しましょう。
今回は、Group1, Group2, Group3の3種類あるので、3種類それぞれに対して「次状態部分の色のペア」を確認しましょう。
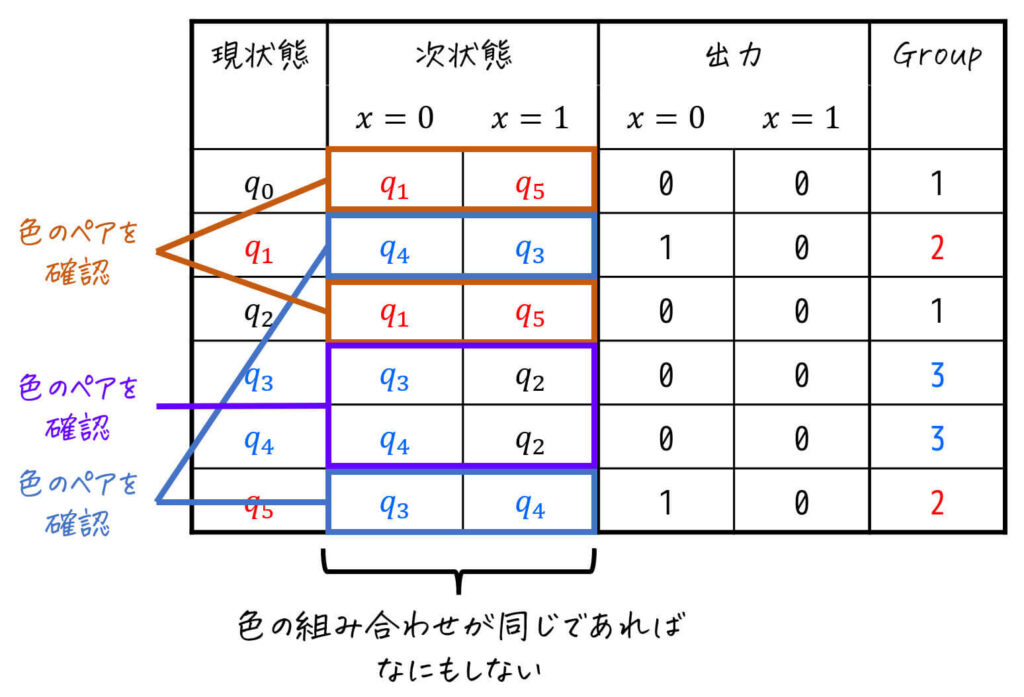
すると、Group1(\( q_0 \), \( q_2 \))、Group2(\( q_1 \), \( q_5 \))、Group3(\( q_3 \), \( q_4 \))それぞれの「次状態部分の色のペア」が一致していますね。
そのため、ここでStep3が完了します。
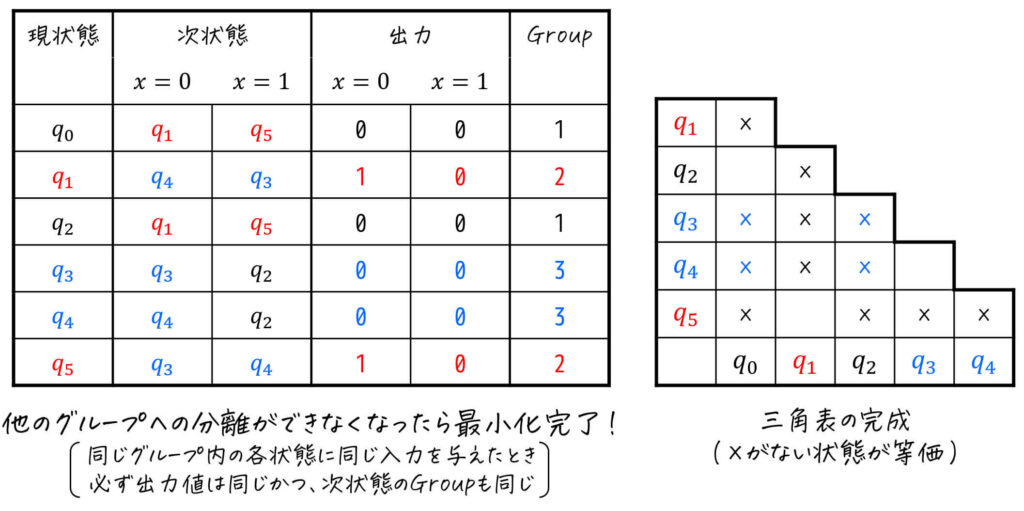
Step4. 各グループから代表の状態を1つ選び、状態遷移表を圧縮
つぎに、最小化したグループから代表の状態を1つ選び、下のように状態遷移表を置き換えます。
今回は、
- Group1の代表 → \( q_0 \)
- Group2の代表 → \( q_1 \)
- Group3の代表 → \( q_3 \)
としましょうか。
ただし、\( q_0 \), \( q_1 \), \( q_3 \) のように \( q_2 \) がないのは若干違和感があるので、今回は \( q_3 \) を \( q_2 \) と名前を変えて表記します[6]名前の付け方は自由なのでもちろん \( q_3 \) のままでもOKです。。
Step5. 状態遷移表を書く
あとは、Step4で作った状態遷移表を元に状態遷移図を書けば完成です。
4. さいごに
今回は、すでにある状態遷移図の状態数を最小化する方法についてみていきました。
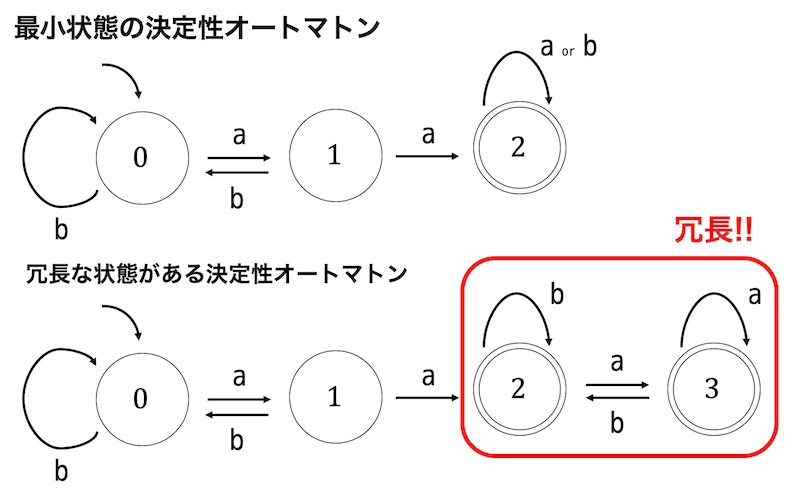
順序回路の状態数最小化は、実はオートマトンと言語理論の「決定性オートマトンの最小化」でも使われるので、もし興味がある人はこちらも学習してみてください。
次回は、状態遷移表にDon’t Careが含まれるような状態遷移図の状態数最小化について説明する予定です。
注釈
| ↑1 | 同じグループ同士は等価、異なるグループ同士は等価ではないことを表します。例えば、\( q_0 \), \( q_2 \) がグループ1、\( q_1 \), \( q_3\) がグループ2の場合、\( q_0 \), \( q_2 \) や \( q_1 \), \( q_3 \) は等価であることを表し、\( q_0 \), \( q_1 \) や \( q_2 \), \( q_3 \) は等価でないことを表します。 |
|---|---|
| ↑2 | 同じ入力を与えたときに出力値が必ず同じであれば、とりあえずこの段階では等価であると仮定します。例えば今回の場合、\( q_0 \), \( q_1 \), \( q_3 \), \( q_4 \) はともに \( x = 0 \) を入れたときに出力0、\( x = 1 \) を入れたときに出力0となるので、「同じ入力を与えた際に出力値が必ず同じ」になると言えます。 |
| ↑3 | \( q_0 \), \( q_3 \), \( q_4 \) は \( x = 0 \), \(x = 1 \) 側ともに黒なのでこの3状態は同じグループ(=等価となる可能性がある)です。一方 \( q_1 \) だけは \( x = 0 \), \( x = 1 \) 側ともに赤なので、先ほどの3状態とは異なるグループ(=等価でない)です。 |
| ↑4 | 1度確認したグループでも、グループが分離されたことにより新たに「同じ入力値なのに異なるグループに遷移する状態(=等価でない状態)」が見つかる可能性があるため、見落とさないように注意! |
| ↑5 | 同じ入力値なのに異なるグループに遷移する状態(=等価でない状態)が存在しないということ。 |
| ↑6 | 名前の付け方は自由なのでもちろん \( q_3 \) のままでもOKです。 |
関連広告・スポンサードリンク




![うさぎでもわかる計算機システム Part01 2進数 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612102246-1-150x150.gif)