関数の対称性　偶関数と奇関数と定積分

こんにちは、ももやまです。

今回は関数の対称性を表す偶関数、奇関数の違いについて説明をしたいと思います。

 

 

スポンサードリンク

１．偶関数・奇関数の性質

偶関数、奇関数はともに関数の対称性に関する性質を表しています。

まずは定義をみていきましょう。

 

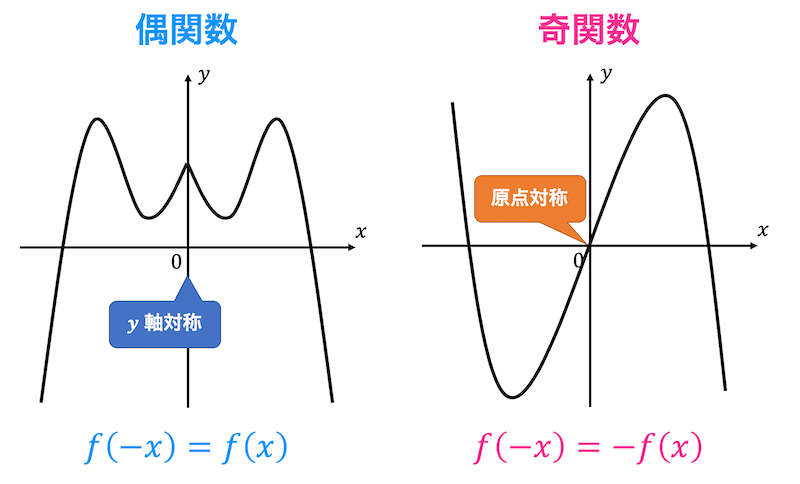
定義ではわかりにくいと思うので偶関数と奇関数の例を1つずつ図（グラフ）で表してみました。

グラフで考えると偶関数は \( y \) 軸対称なグラフ、奇関数は原点対称のグラフとなりますね。

なので、偶関数か奇関数か迷ったらグラフを書くのも1つの手です。

（ですが基本的には偶関数の場合は \( f(-x) = f(x) \) 、奇関数の場合は \( f(-x) = - f(x) \) になることを確認するほうが早いです。）

 

スポンサードリンク

２．偶関数・奇関数の例

では、偶関数と奇関数の例を少しだけ紹介しましょう。

偶関数の例

\( f(x) = x^2 \),  \(  f(x) = x^4 \),  \( f(x) = x^6 \),  \( f(x) = x^{2n} \) （\( n \) は整数）,  \( \cos x \)

奇関数の例

\( f(x) = x \),   \(  f(x) = x^3 \),   \( f(x) = x^5 \),  \( f(x) = x^{2n+1} \) （\( n \) は整数）,  \( f(x) = \sin x \),  \( f(x) = \tan x \)

 

スポンサードリンク

３．偶関数・奇関数の積

偶関数 / 奇関数の演算には、下のような法則が成り立ちます。

 

例えば、\[
f(x) = x \cos x
\]は、\( x \) が奇関数、\( \cos x \) が偶関数なので \( f(x) \) は奇関数となります。

 

わからなくなったときは \( x^2 \)（偶関数）や \( x \) （奇関数）などのわかりやすい例で実際に掛けてみてどうなるか試してみましょう*1。

４．偶関数・奇関数の積分

今回一番重要なのがこちらです。

偶関数、奇関数かを見抜くことで計算量を大幅に減らすことができます。

 

 図で表すと、下のようになります。

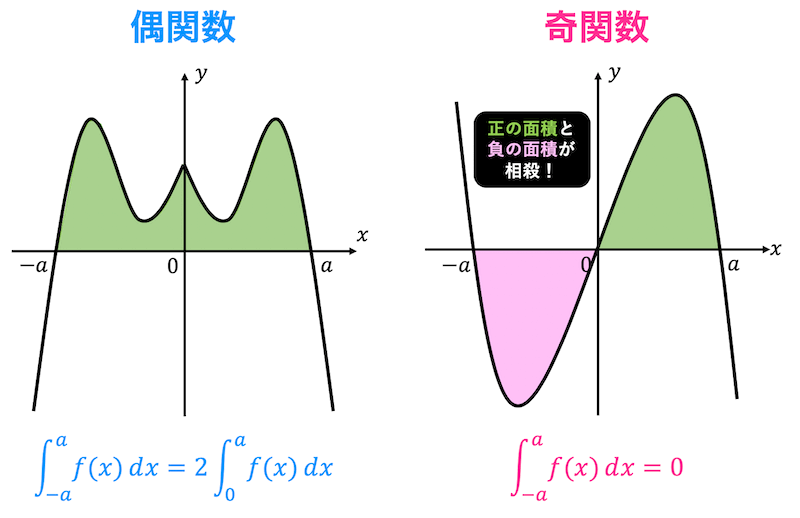
偶関数の場合、\( 0 \) から \( a \) の部分の面積と \( -a \) から \( 0 \) までの面積が（符号も含めて）同じ面積となっていますね。なので \( 0 \) から \( a \) の面積を2倍することで求めることができます！

また、奇関数の場合、\( 0 \) から \( a \) の部分の面積と \( -a \) から \( 0 \) までの面積は同じですが、符号が異なるため打ち消されて0になります。

なので積分することなく0と求めることができます！

 （計算練習は練習問題でどうぞ！）

５．練習問題

では、少しだけですが練習してみましょう。

練習1

次の(1)〜(6)から偶関数・奇関数を2つずつ見つけなさい。

(1) \( f(x) = x^2 + 3x \)
(2) \( f(x) = \sin 3x \cos 5x \)
(3) \( f(x) = x^3 \sin x \)
(4) \( f(x) =  e^{5x} \)
(5)\[
f(x) = \frac{1}{1+x^2}
\](6)\[
f(x) = e^{2x} - e^{-2x}
\]

練習2

次の(1)〜(3)の定積分を求めなさい。

(1) \[
\int^{1}_{-1} x^4 + 3x^3 + 9x \ dx
\]

(2) \[
\int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \sin 4x \cos 6x \ dx
\]

(3) \[
\int^{2}_{-2} \frac{1}{4+x^2} \ dx
\]

６．練習問題の答え

解答1

偶関数：(3), (5)
奇関数：(2), (6)

(1)\[
f(-x) = x^2 - 3x
\]となり、\( f(-x) = f(x) \) でも \( f(-x) = - f(x) \) にもならないので偶関数でも奇関数でもない。

 

(2) 

\( \sin 3x \) は奇関数、\( \cos 5x \) は偶関数なのでその積は奇関数。

 

(3)

\( x^3 \) は奇関数、\( \sin x \) も奇関数なのでその積は偶関数。

 

(4)

\[
f(-x) = e^{-5x}
\]となり、\( f(-x) = f(x) \) でも \( f(-x) = - f(x) \) にもならないので偶関数でも奇関数でもない。

 

(5) \[
f(-x) = \frac{1}{1+(-x)^2} =  \frac{1}{1+x^2}
\]となるので \( f(-x) = f(x) \) となり偶関数。

 

(6) \[
f(-x) = e^{-2x} - e^{2x} = - ( e^{2x} - e^{-2x} )
\]となるので \( f(-x) = -f(x) \) となり奇関数*2。

 

解答2

(1)

\( x^4 \) は偶関数であり、\( x^3 \), \( x \) は奇関数である。なので、\[\begin{align*}
\int^{1}_{-1} x^4 + 3x^3 + 9x \ dx & = \int^{1}_{-1} x^4 + \int^{1}_{-1} 3x^3 + 9x \ dx
\\ & = 2 \int^{1}_{0} x^4 \ dx
\\ & = 2 \left[ \frac{1}{5} x^5 \right]^{1}_{0}
\\ & = \frac{2}{5}
\end{align*}\]となる。

 

(2)

\(  \sin 4x \) は奇関数、\(  \cos 6x \) は偶関数なので、その積は奇関数。よって、\[
\int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \sin 4x \cos 6x \ dx = 0
\]となる。

(3) 

\[
f(-x) = \frac{1}{4+(-x)^2} =  \frac{1}{4+x^2}
\]となるので \( f(-x) = f(x) \) となり偶関数。

よって、\[
\int^{2}_{-2} \frac{1}{4+x^2} \ dx = 2 \int^{2}_{0} \frac{1}{4+x^2} \ dx
\]が成立。ここで、\( x = 2 \tan t \) とすると \( dx \) と \( dt \) の関係式、および積分範囲は\[
dx = \frac{2}{\cos^2 t} \ dt , \ \ \ \ 0 \to \frac{\pi}{4}
\]となる。よって、\[\begin{align*} & 
2 \int^{2}_{0} \frac{1}{4+x^2} \ dx
\\ = & \ 2 \int^{\frac{\pi}{4} }_{0} \frac{1}{4+4 \tan^2 t} \cdot \frac{2}{\cos^2 t} \ dt
\\ = & \ 2 \int^{\frac{\pi}{4} }_{0} \frac{1}{2} \cdot \frac{1}{1+ \tan^2 t} \cdot \frac{1}{\cos^2 t} \ dt
 \\ = & \ 2 \int^{\frac{\pi}{4} }_{0} \frac{1}{2} \cos^2 t \cdot \frac{1}{\cos^2 t} \ dt
 \\ = & \ 2 \int^{\frac{\pi}{4} }_{0} \frac{1}{2} \ dt
 \\ = & \ 2 \left[ \frac{1}{2} t \right]^{\frac{\pi}{4} }_{0}
\\ = & \ \frac{\pi}{4}
\end{align*} \]と計算できる*3。

 

７．さいごに

今回は関数の対称性に関する性質として偶関数と奇関数についてまとめ、さらに偶関数・奇関数を用いた定積分の計算方法についてまとめました。

 

偶関数・奇関数の性質を一番利用するのは定積分を計算するときなので、定積分を計算する際には偶関数・奇関数で計算を省略できないかな、と一度考えてみましょう。