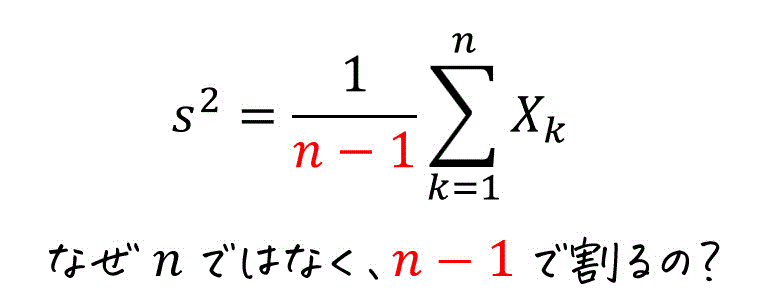
スポンサードリンク
こんにちは、ももやまです。
高校生のデータの分析では、分散を求めるときに、値と平均の差を2乗したものを足して \( n \) で割って求めていましたね。\[
\frac{1}{n} \sum^{n}_{k=1} X_k
\]
しかし、大学で確率・統計や、基礎実験論を学習する際に、標本の分散を計算するとき下のように \( n-1 \) で割った謎の分散が出てきて、頭を困惑させてきます。
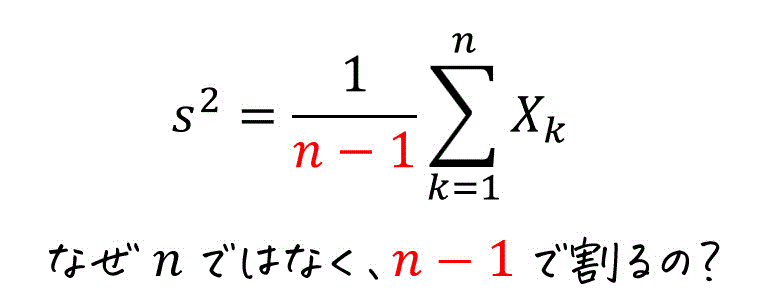
でも、ご安心ください。
今回の不偏推定量に関する知識を学ぶことで、標本の分散を求めるときに、何故 \( n \) ではなく \( n - 1 \) で割る分散が必要かが分かるようになります!
目次
スポンサードリンク
1. 推定量とは
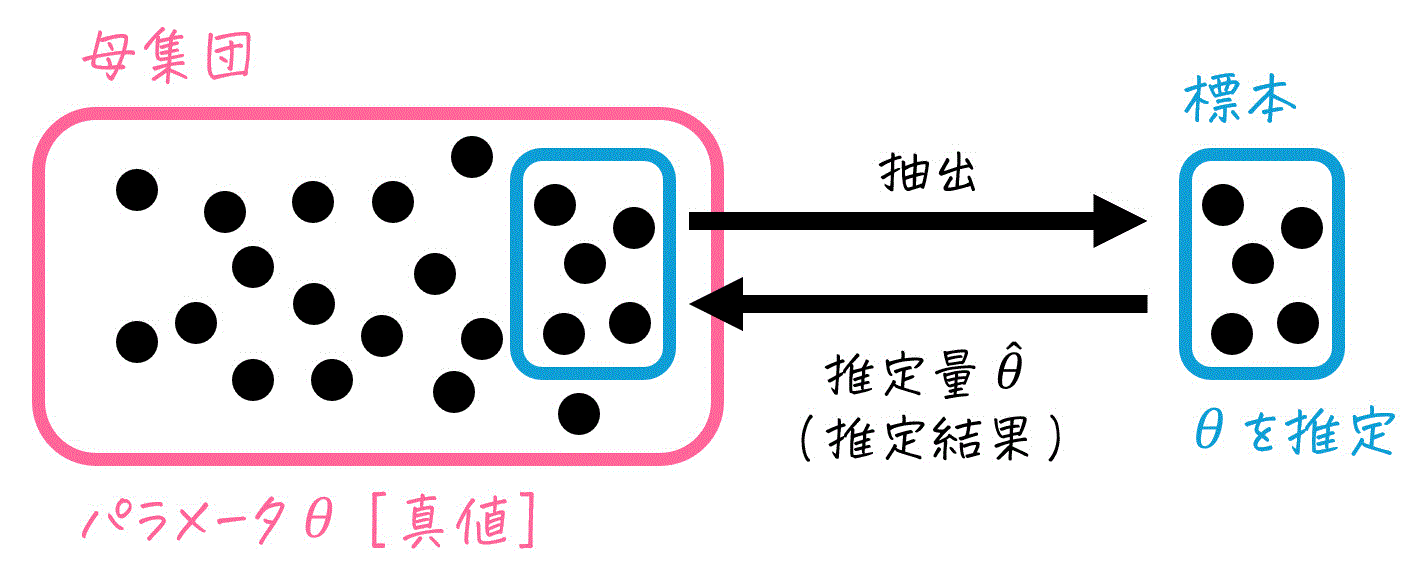
母集団内のあるパラメータ(例: 平均 \( \mu \) や分散 \( \sigma^2 \))の値を知りたいとします。
しかし、パラメータの正解値を知ることは通常ほぼ不可能です。正解値を知るためには、母集団すべてのデータを調べる必要がありますが、全データの収集には多大な時間やコストがかかることが多いからです。
そこで、現実的なアプローチとして、母集団から一部のデータ(=標本)を無作為に取り出し、その標本から母集団のパラメータを推定します。
このとき、標本データから計算されるパラメータの推定値のことを、推定量と呼びます。表記としては、あるパラメータ \( \theta \) の推定量を \( \hat{\theta} \) のように、元のパラメータに ^ を付けた形で表現します。
スポンサードリンク
2. 不偏推定量とは
例えば、工業で作ったある製品の重さから、「この製品はだいたいこのくらいの重さだな」と推定することを考えます。
このとき、出来る限り偏り(ズレ)なく正確に重さを推定したいですよね。
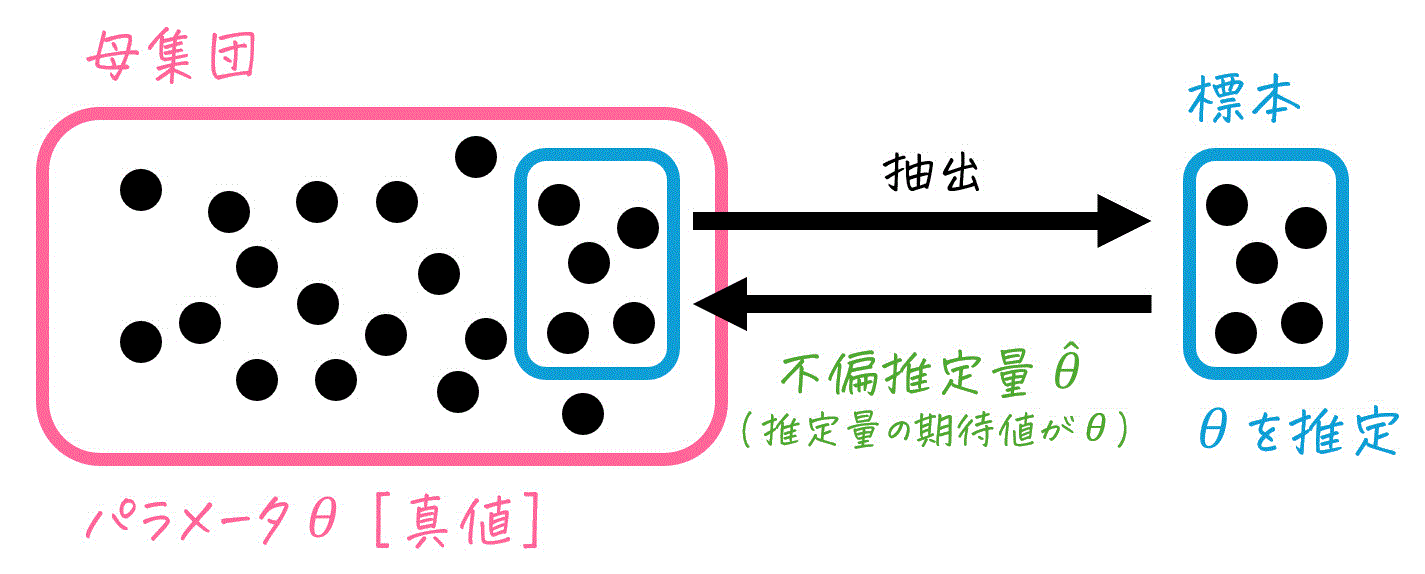
ここで登場するのが不偏推定量です。不偏推定量とは、推定量の期待値(長期的に何度も標本を取り直して計算した場合の平均値)が、推定対象である母集団の真のパラメータと一致する推定量のことを指します。
言い換えると、推定量の「平均」を複数回標本取って計算してみたとき、その値が母集団の値に一致するような性質を持つものを、不偏推定量と呼びます。
数式で表すと、不偏推定量の次のようになります。\[
E ( \hat{\theta} ) = \theta
\]ここで、\( \theta \) は母集団のパラメータ、\( \hat{\theta} \) はその推定量となります。また、\( E ( \hat{\theta} ) \) は、推定量の期待値を意味します。
この不偏推定量を推定に使うことで、偏り(ズレ)を最小限に抑え、より正確な推定が可能になります。
母集団のパラメータ \( \theta \) を推定する際に、その推定量と呼び、通常 \( \hat{\theta} \) で表す。
このとき、推定量 \( \hat{\theta} \) の期待値 \( E( \hat{\theta} ) \) が母集団のパラメータ \( \theta \) と等しくなる、すなわち\[
E( \hat{\theta} ) = \theta
\]が成立する推定量を不偏推定量と呼ぶ。
スポンサードリンク
3. 母平均の推定量、母分散の推定量
ここからは、実際に不偏推定量の例として母集団の平均、分散の不偏推定量を確認していきましょう。
(1) 母平均 \( \mu \) の推定量
平均 \( \overline{X} \) は各データ \( \overline{X}_1 \), \( \overline{X}_2 \), … \( \overline{X}_n \) をすべて足してから、データの数 \( n \) で割ることで求めることができます。\[\begin{align*}
\overline{X} & = \frac{1}{n} ( \overline{X}_1 + \overline{X}_2 + \cdots + \overline{X}_n )
\\ & = \frac{1}{n} \sum^{n}_{k = 1} \overline{X}_k
\end{align*}\]
実際に、標本から計算した平均 \( \overline{X} \) が不偏推定量となるか、確認していきましょう。
不偏推定量であることを言うためには、標本平均 \( \overline{X} \) の期待値 \( E ( \overline{X} ) \) が、母平均 \( \mu \) と一致すること、つまり以下の式が成り立つことを示せればOKです。\[
E ( \overline{X} ) = \mu
\]
[i] まずは3つのデータで試してみる
母集団としてつぎの3つの値を持つ集団を考えます。
0, 2, 4
このとき、母平均 \( \mu \) は次のように求められます。\[\begin{align*}
\mu & = \frac{1}{3} (0+ 2+ 4)
\\ & = 2
\end{align*}\]
次に、この母集団から2つのデータを取り出して(復元抽出)標本を作ります。
可能な標本の組み合わせは次の9つです。
| データ1 | データ2 | 標本平均 |
|---|---|---|
| 0 | 0 | \[ \frac{1}{2} (\textcolor{red}{0}+\textcolor{blue}{0}) = 0 \] |
| 0 | 2 | \[ \frac{1}{2} (\textcolor{red}{0}+\textcolor{blue}{2}) = 1 \] |
| 0 | 4 | \[ \frac{1}{2} (\textcolor{red}{0}+\textcolor{blue}{4}) = 2 \] |
| 2 | 0 | \[ \frac{1}{2} (\textcolor{red}{2}+\textcolor{blue}{0}) = 1 \] |
| 2 | 2 | \[ \frac{1}{2} (\textcolor{red}{2}+\textcolor{blue}{2}) = 2 \] |
| 2 | 4 | \[ \frac{1}{2} (\textcolor{red}{2}+\textcolor{blue}{4}) = 3 \] |
| 4 | 0 | \[ \frac{1}{2} (\textcolor{red}{4}+\textcolor{blue}{0}) = 2 \] |
| 4 | 2 | \[ \frac{1}{2} (\textcolor{red}{4}+\textcolor{blue}{2}) = 3 \] |
| 4 | 4 | \[ \frac{1}{2} (\textcolor{red}{4}+\textcolor{blue}{4}) = 4 \] |
この3つの標本平均の期待値 \( E ( \overline{X} ) \) は、つぎのように求められます。\[\begin{align*}
E ( \overline{X} ) & = \frac{1}{9} \left( 0+1+2+1+2+3+2+3+4 \right)
\\ & = \frac{1}{9} \cdot 18
\\ & = 2
\end{align*}\]
よって母平均 \( \mu = 2 \) と、標本平均の期待値 \( E( \overline{X} ) = 2 \) が一致していることが確認できます。
そのため、不偏推定量の条件 \( E ( \overline{X} ) = \mu \) を満たすことが確認できました。
[ii] 一般化へ
では、一般化した状態で確かめていきましょう。
まず、\( \overline{X} \) を分解します。\[
E ( \overline{X} ) = E \left( \frac{1}{n} ( X_1 + X_2 + \cdots + X_n ) \right)
\]
ここで、期待値の式内にある定数倍は、外に出すことができる性質 \( E(aX) = a E(X) \) を使って、つぎのように式変形ができます。\[
E \left( \frac{1}{n} ( X_1 + X_2 + \cdots + X_n ) \right) = \frac{1}{n} E \left( X_1 + X_2 + \cdots + X_n \right)
\]
さらに、期待値には加法性 \( E( X + Y) = E(X) + E(Y) \) が成り立つので、つぎの式変形も可能です。\[
\frac{1}{n} E \left( X_1 + X_2 + \cdots + X_n \right) = \frac{1}{n} \left\{ E( X_1 ) + E( X_2 ) + \cdots + E( X_n ) \right\}
\]
また、各標本 \( X_k \) の期待値 \( E(X_k) \) は母集団の平均 \( \mu \) に等しいため[1]各表は、母集団の各要素から等しい確率で選ばれるため(無作為抽出しているため)、標本 \( X_1 \), \( X_2 \), … , \( X_n \) の期待値は \( \mu \) … Continue reading、次のように変形ができます。\[\begin{align*}
\frac{1}{n} \left\{ E( X_1 ) + E( X_2 ) + \cdots + E( X_n ) \right\} & = \frac{1}{n} ( \underbrace{ \mu + \mu + \cdots + \mu }_{ n \ \mathrm{個} } )
\\ & = \frac{1}{n} \cdot \mu n
\\ & = \mu
\end{align*}\]
よって、一般化した状態でも不偏推定量の条件 \( E ( \overline{X} ) = \mu \) が成立することが確認できましたね。
母平均 \( \mu \) の不偏推定量は、標本平均 \( \overline{X} \) で表される。
ここで、\( \overline{X} \) は各標本 \( X_k \) を用いて、次のように計算できる。\[\begin{align*}
\overline{X} & = \frac{1}{n} ( X_1 + X_2 + \cdots + X_n )
\\ & = \frac{1}{n} \sum^{n}_{k=1} X_k
\end{align*}\]※ \( n \) は標本サイズを表す。
(2) 母分散 \( \sigma \) の推定量
分散 \( S^2 \) は、標本データの値 \( X_1 \), \( X_2 \), …, \( X_n \) から平均 \( \overline{X} \) との差の2乗を取り、その和を標本の大きさ \( n \) で割ったもので求められます。
\[\begin{align*}
S^2 & = \frac{1}{n} \left\{ ( X_1 - \overline{X} )^2 + ( X_2 - \overline{X} )^2 + \cdots + ( X_n - \overline{X} )^2 \right\}
\\ & = \frac{1}{n} \sum^{n}_{k = 1} ( X_k - \overline{X} )
\end{align*}\]
実際に、標本から計算した分散(標本分散) \( S^2 \) が不偏推定量となるか、確認していきましょう。
不偏推定量であることを言うためには、標本分散 \( S^2 \) の期待値 \( E ( S^2 ) \) が、母分散 \( \sigma^2 \) と一致すること、つまり以下の式が成り立つことを示せればOKです。\[
E ( S^2 ) = \sigma^2
\]
[i] まずは3つのデータで試してみる
先ほどと同じ、つぎの3つの値を持つ集団を考えます。
0, 2, 4
このとき、母平均が \( \mu = 2 \) となることから、母分散 \( \sigma^2 \) は次のように求められます。\[\begin{align*}
\sigma^2 & = \frac{1}{3} \left\{ (0-2)^2 + (2-2)^2 + (4-2)^2 \right\}
\\ & = \frac{1}{3} \cdot 8
\\ & = \frac{8}{3}
\end{align*}\]
ここで、この母集団から2つのデータを取り出し(復元抽出)て標本を作ります。
可能な標本の組み合わせは次の9つです。
| データ1 | データ2 | 標本平均 | 標本分散 |
|---|---|---|---|
| 0 | 0 | 0 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{0} - \textcolor{green}{0} )^2 + ( \textcolor{blue}{0} - \textcolor{green}{0} )^2 \right\} = 0 \] |
| 0 | 2 | 1 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{0} - \textcolor{green}{1} )^2 + ( \textcolor{blue}{2} - \textcolor{green}{1} )^2 \right\} = 1 \] |
| 0 | 4 | 2 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{0} - \textcolor{green}{2} )^2 + ( \textcolor{blue}{4} - \textcolor{green}{2} )^2 \right\} = 4 \] |
| 2 | 0 | 1 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{2} - \textcolor{green}{1} )^2 + ( \textcolor{blue}{0} - \textcolor{green}{1} )^2 \right\} = 1 \] |
| 2 | 2 | 2 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{2} - \textcolor{green}{2} )^2 + ( \textcolor{blue}{2} - \textcolor{green}{2} )^2 \right\} = 0 \] |
| 2 | 4 | 3 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{2} - \textcolor{green}{3} )^2 + ( \textcolor{blue}{4} - \textcolor{green}{3} )^2 \right\} = 1 \] |
| 4 | 0 | 2 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{4} - \textcolor{green}{2} )^2 + ( \textcolor{blue}{0} - \textcolor{green}{2} )^2 \right\} = 4 \] |
| 4 | 2 | 3 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{4} - \textcolor{green}{3} )^2 + ( \textcolor{blue}{2} - \textcolor{green}{3} )^2 \right\} = 1 \] |
| 4 | 4 | 4 | \[ \frac{1}{2} \left\{ ( \textcolor{red}{4} - \textcolor{green}{4} )^2 + ( \textcolor{blue}{4} - \textcolor{green}{4} )^2 \right\} = 0 \] |
よって、標本分散 \( S^2 \) の期待値 \( E ( S^2 ) \) は、つぎのように求められます。\[\begin{align*}
E ( S^2 ) & = \frac{1}{9} \left( 0+1+4+1+0+1+4+1+0 \right)
\\ & = \frac{1}{9} \cdot 12
\\ & = \frac{4}{3}
\end{align*}\]
あれ? 母分散 \( \sigma^2 = \frac{8}{3} \) と、標本平均の期待値 \( E( S^2 ) = \frac{4}{3} \) が一致しませんね。
よって、不定推定量 \( E( \sigma^2 ) = S^2 \) を満たさないので、不偏推定量とは言えませんね。
[ii] 一般化した状態で確認
一般化した状態でも計算してみましょう。
まず、\( X_k - \overline{X} \) を2つの項 \( a \), \( b \) に分解します。\[
X_k - \overline{X} = \underbrace{ (X_k - \mu) }_{a} - \underbrace{ ( \overline{X} - \mu ) }_{b}
\]
ここから、\( E ( S^2 ) \) を3つの項に分解していきます。\[\begin{align*}
E ( S^2 ) & = E \left( \frac{1}{n} \sum^{n}_{k=1} (X_k - \overline{X} )^2 \right)
\\ & = E \left( \frac{1}{n} \sum^{n}_{k=1} \left\{ \underbrace{ (X_k - \mu) }_{a} - \underbrace{ ( \overline{X} - \mu ) }_{b} \right\}^2 \right)
\\ & = E \left( \frac{1}{n} \sum^{n}_{k=1} (a^2 - 2ab + b^2) \right)
\\ & = E \left( \frac{1}{n} \sum^{n}_{k=1} a^2 - \frac{2}{n} \sum^{n}_{k=1} ab + \frac{1}{n} \sum^{n}_{k=1} b^2 \right)
\\ & = E \left( \frac{1}{n} \sum^{n}_{k=1} (X_k - \mu)^2 \right) - E \left( \frac{2}{n} \sum^{n}_{k=1} (X_k - \mu)( \overline{X} - \mu) \right) + E \left( \frac{1}{n} \sum^{n}_{k=1} ( \overline{X} - \mu )^2 \right)
\end{align*}\]
ここで、分解した3つの項を期待値を順番に求めていきます。
1項目:
1項目の式は母分散の定義式そのものなので、次のように計算ができます。\[
E \left( \frac{1}{n} \sum^{n}_{k=1} (X_k - \mu )^2 \right) = \sigma^2
\]
2項目:
まずは、期待値の中の和の部分を、つぎのように変形します。\[\begin{align*}
\sum^{n}_{k=1} (X_k - \mu)( \overline{X} - \mu) & = ( \overline{X} - \mu) \sum^{n}_{k=1} (X_k - \mu)
\\ & = ( \overline{X} - \mu) \left( \sum^{n}_{k=1} X_k - \textcolor{red}{ \sum^{n}_{k=1} } \mu \right)
\\ & = ( \overline{X} - \mu) \left( n \cdot \textcolor{blue}{ \frac{1}{n} \sum^{n}_{k=1} X_k } - \textcolor{red}{n} \mu \right) \ \ \ \ \ \textcolor{red}{ \left( \because \sum^{n}_{k=1} 1 = n \right)}
\\ & = ( \overline{X} - \mu) \left( n \cdot \ \textcolor{blue}{ \overline{X} } - n \mu \right) \ \ \ \ \ \textcolor{blue}{ \left( \because \frac{1}{n} \sum^{n}_{k=1} X_k = \overline{X} \right)}
\\ & = n ( \overline{X} - \mu)^2
\end{align*}\]
ここで、\( E ( ( \overline{X} - \mu)^2 ) \) は標本平均 \( \overline{X} \) と母平均 \( \mu \) の2乗誤差の期待値です。これは、まさに分散の定義式なので、つぎの式が成り立ちます。\[
E ( ( \overline{X} - \mu)^2 ) = V ( \overline{X} )
\]
また、\( V ( \overline{X} ) \) はつぎのように求められます。\[\begin{align*}
V ( \overline{X} ) & = V \left( \textcolor{red}{\frac{1}{n} } (X_1 + X_2 + \cdots + X_n ) \right)
\\ & = \textcolor{red}{\frac{1}{n^2}} V \left( X_1 + X_2 + \cdots + X_n \right) \ \ \ \left( \because V(\textcolor{red}{a}X) = \textcolor{red}{a^2} V(x) \right)
\\ & = \frac{1}{n^2} \left\{ \underbrace{ V ( X_1 ) + V ( X_2 ) + \cdots + V ( X_n ) }_{ n \ \mathrm{個} } \right\}
\\ & = \frac{1}{n^2} \cdot n \sigma^2 \ \ \ \ ( \because V(X_k) = \sigma^2 )
\\ & = \frac{1}{n} \sigma^2
\end{align*}\]※ \( X \), \( Y \) が独立のとき、分散の分解 \( V(X \pm Y) = V(X) + V(Y) \) が可能[2]\( X \), \( Y \) が独立ではない場合は、 \( V(X \pm Y) = V(X) + V(Y) \pm 2 Cov(X,Y) \) [復号同順] となる点に注意。※ \( Cov(X,Y) \) は \( X \), \( Y \) の共分散。 \。
そのため、標本平均 \( \overline{X} \) の分散 \( V ( \overline{X} ) \) が \( \frac{ \sigma^2 }{ n } \) であるという等式が成り立ちます。\[\begin{align*}
E ( ( \overline{X} - \mu)^2 ) & = V ( \overline{X} )
\\ & = \frac{1}{n} \sigma^2
\end{align*}\]
よって、2項目の期待値は、次のように計算できます。
\[\begin{align*}
E \left( \frac{2}{n} \sum^{n}_{k=1} (X_k - \mu)( \overline{X} - \mu) \right) & = \frac{2}{n} E \left( \sum^{n}_{k=1} (X_k - \mu)( \overline{X} - \mu) \right)
\\ & = \frac{2}{n} E \left( n ( \overline{X} - \mu)^2 \right)
\\ & = 2 E \left( ( \overline{X} - \mu)^2 \right)
\\ & = 2 \cdot \frac{ \sigma^2}{n}
\end{align*}\]
3項目:
3項目の期待値も、中心極限定理の公式\[
E \left( ( \overline{X} - \mu)^2 \right) = \frac{ \sigma^2}{n}
\]を利用することで、次のように期待値を計算できます。
\[\begin{align*}
E \left( \frac{1}{n} \sum^{n}_{k=1} ( \overline{X} - \mu )^2 \right) & = E \left( \frac{1}{n} \cdot n ( \overline{X} - \mu )^2 \right)
\\ & = E \left( ( \overline{X} - \mu )^2 \right)
\\ & = \frac{ \sigma^2}{n}
\end{align*}\]
これら3つの式を全て組み合わせることで、標本分散の期待値 \( E(S^2) \) をつぎのように導出することができます。
\[\begin{align*}
E ( S^2 ) & =E \left( \frac{1}{n} \sum^{n}_{k=1} (X_k - \mu)^2 \right) - E \left( \frac{2}{n} \sum^{n}_{k=1} (X_k - \mu)( \overline{X} - \mu) \right) + E \left( \frac{1}{n} \sum^{n}_{k=1} ( \overline{X} - \mu )^2 \right)
\\ & = \sigma^2 - 2 \cdot \frac{ \sigma^2}{n}+ \frac{ \sigma^2}{n}
\\ & = \frac{n-1}{n} \sigma^2
\end{align*}\]
あれ? 実際の期待値の \( \frac{n-1}{n} \) 倍となってしまいました。
このままでは不偏推定量とは言えませんね。
[iii] 不偏推定量となる分散を考えてみる
ここで、母分散の不偏推定量となる新たな分散を考えてみましょう。
標本分散の期待値 \( E(S^2) \) が、母分散の \( \frac{n-1}{n} \) 倍となるということは、標本分散 \( S^2 \) を \( \frac{n}{n-1} \) 倍とした分散\[ \begin{align*}
s^2 & = \frac{n}{n-1} S^2
\\ & = \frac{n}{n-1} \cdot \frac{1}{n} \sum^{n}_{k = 1} ( X_k - \overline{X} )^2
\\ & = \frac{1}{n-1} \sum^{n}_{k = 1} ( X_k - \overline{X} )^2
\end{align*}\]で計算してあげれば、期待値 \( E( s^2) \) が、実際の期待値と一致しそうですね。
実際に計算していきましょう。 \[\begin{align*}
E(s^2) & = E \left( \frac{n}{n-1} S^2 \right)
\\ & = \frac{n}{n-1} E \left( S^2 \right)
\\ & = \frac{n}{n-1} \cdot \frac{n-1}{n} \sigma^2
\\ & = \sigma^2
\end{align*}\]
よって、\( s^2 \) で定義した分散は、母分散の不偏推定量となりましたね。この \( s^2 \) の分散のことを不偏分散と呼びます。]
大学以降で習う確率・統計では、母分散を正確に推定するために、標本の分散を求めるときには不偏分散 \( s^2 \) を使うことが多いです[3]母分散は今まで通り \( n \) で割ってください。誤って \(n-1 \) で割らないように!。

※ 本記事では、高校で習う分散の公式(標本分散)を \( S^2 \)、不偏分散を \( s^2 \) と表記を使い分けています。
母平均 \( \mu \) の不偏推定量は、不偏分散 \( s^2 \) で表される。
ここで、\( s^2 \) は各標本 \( X_k \) を用いて、次のように計算できる。\[\begin{align*}
s^2 & = \frac{1}{n-1} \left\{ ( X_1 - \overline{X} )^2 + ( X_2 - \overline{X} )^2
+ \cdots + ( X_n - \overline{X} )^2 \right\}
\\ & = \frac{1}{n-1} \sum^{n}_{k = 1} ( X_k - \overline{X} )^2
\end{align*}\]※ \( n \) は標本サイズを表す。
実際に、[1]で計算した標本分散を、不偏分散として計算しなおしてみましょう。
| データ1 | データ2 | 標本平均 | 標本分散 |
|---|---|---|---|
| 0 | 0 | 0 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{0} - \textcolor{green}{0} )^2 + ( \textcolor{blue}{0} - \textcolor{green}{0} )^2 \right\} = 0 \] |
| 0 | 2 | 1 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{0} - \textcolor{green}{1} )^2 + ( \textcolor{blue}{2} - \textcolor{green}{1} )^2 \right\} = 2 \] |
| 0 | 4 | 2 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{0} - \textcolor{green}{2} )^2 + ( \textcolor{blue}{4} - \textcolor{green}{2} )^2 \right\} = 8 \] |
| 2 | 0 | 1 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{2} - \textcolor{green}{1} )^2 + ( \textcolor{blue}{0} - \textcolor{green}{1} )^2 \right\} = 2 \] |
| 2 | 2 | 2 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{2} - \textcolor{green}{2} )^2 + ( \textcolor{blue}{2} - \textcolor{green}{2} )^2 \right\} = 0 \] |
| 2 | 4 | 3 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{2} - \textcolor{green}{3} )^2 + ( \textcolor{blue}{4} - \textcolor{green}{3} )^2 \right\} = 2 \] |
| 4 | 0 | 2 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{4} - \textcolor{green}{2} )^2 + ( \textcolor{blue}{0} - \textcolor{green}{2} )^2 \right\} = 8 \] |
| 4 | 2 | 3 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{4} - \textcolor{green}{3} )^2 + ( \textcolor{blue}{2} - \textcolor{green}{3} )^2 \right\} = 2 \] |
| 4 | 4 | 4 | \[ \frac{1}{2-1} \left\{ ( \textcolor{red}{4} - \textcolor{green}{4} )^2 + ( \textcolor{blue}{4} - \textcolor{green}{4} )^2 \right\} = 0 \] |
よって、不偏分散 \( s^2 \) の期待値 \( E ( s^2 ) \) は、つぎのように求められます。\[\begin{align*}
E ( s^2 ) & = \frac{1}{9} \left( 0+2+8+2+0+2+8+2+0 \right)
\\ & = \frac{1}{9} \cdot 24
\\ & = \frac{8}{3} \end{align*}\]
不偏分散 \( s^2 \) で分散を計算すると、母分散 \( \sigma^2 = \frac{8}{3} \) と、不偏分散の期待値 \( E( s^2 ) = \frac{8}{3} \) が一致していることが確認できますね。
4. 練習問題
練習1.
ある高校の生徒5人を標本として抽出したとき、身長[cm]は以下の通りであった。
176, 179, 167, 169, 159
つぎの問いに答えなさい。
(1) 母平均の不偏推定量を求めなさい。
(2) 母分散の不偏推定量を求めなさい。
練習2.
母平均 \( \mu \) の母集団から、標本 \( X_1 \), \( X_2 \), …, \( X_n \) を取り出した。
ここで、\( \mu \) の推定量としてつぎ \( \hat{\mu}_1 \), \( \hat{\mu}_2 \), \( \hat{\mu}_3 \) を考えた。
\[
\hat{\mu}_1 = X_1
\]
\[
\hat{\mu}_2 = \sum^{n}_{k=1} (X_k + 1)
\]
\[
\hat{\mu}_3 = \sum^{n}_{k=1} X_k^2
\]
(1)~(3)の問いに答えなさい。
(1) \( \hat{\mu}_1 \) は母平均 \( \mu \) の不偏推定量かどうか確認しなさい。
(2) \( \hat{\mu}_2 \) は母平均 \( \mu \) の不偏推定量かどうか確認しなさい。
(3) \( \hat{\mu}_3 \) は母平均 \( \mu \) の不偏推定量かどうか確認しなさい。
練習3.
母平均 \( \mu \)、母分散 \( \sigma^2 \) の母集団から、標本 \( X_1 \), \( X_2 \), …, \( X_n \) を取り出す。
ここで、母平均の不偏推定量 \( \overline{X} \) と、不偏分散の不偏推定量 \( s^2 \) は次のように計算できる。\[
\overline{X} = \frac{1}{n} \sum^{n}_{k=1} X_k
\]\[
s^2 = \frac{1}{n-1} \sum^{n}_{k = 1} ( X_k - \overline{X} )^2
\]
つぎの問いに答えなさい。
(1) 期待値 \( E( \overline{X}^2) \) を求めなさい。
(2) \( \mu^2 \) の不偏推定量 \( \hat{\mu^2} \) を求めなさい。
練習問題の答え
解答1.
(1)
母平均の不偏推定量は、標本平均 \( \overline{X} \) によって推定できます。\[\begin{align*}
\overline{X} & = \frac{1}{n} (X_1 + X_2 + \cdots + X_n)
\\ & = \frac{1}{n} \sum^{n}_{k=1} X_k
\end{align*}\]※ \( X_k \) … \( k \) 番目の標本の値、\( n \) は標本サイズ
与えられた5つのデータの標本平均は、つぎの式で計算できます。計算を楽にするために、\( a = 170 \) とおきましょう。\[\begin{align*}
\overline{X} & = \frac{1}{5} \left\{ (a + 6) + (a+9) + (a-3) + (a-1) + (a-11) \right\}
\\ & = \frac{1}{5} \cdot 5a
\\ & = a
\\ & = 170
\end{align*}\]よって、母平均の不偏推定量は 170 と求められます。
(2)
母分散の不偏推定量は、不偏分散 \( s^2 \) によって推定できます。\[\begin{align*}
s^2 & = \frac{1}{n-1} \left\{ ( X_1 - \overline{X} )^2 + ( X_2 - \overline{X} )^2
+ \cdots + ( X_n - \overline{X} )^2 \right\}
\\ & = \frac{1}{n-1} \sum^{n}_{k = 1} ( X_k - \overline{X} )^2
\end{align*}\]※ \( X_k \) … \( k \) 番目の標本の値、\( n \) は標本サイズ、\( \overline{X} \) は標本平均。
与えられた5つのデータの不偏分散は、つぎの式で計算できます。\[\begin{align*}
\overline{X} & = \frac{1}{5-1} \left\{ (176-170)^2 + (179-170)^2 + (167-170)^2 + (169-170)^2 + (159-170)^2 \right\}
\\ & = \frac{1}{4} \left\{ 6^2 + 9^2 + (-3)^2 + (-1)^2 + (-11)^2 \right\}
\\ & = \frac{1}{4} (36 + 81 + 9 + 1 + 121)
\\ & = \frac{1}{4} \cdot 248
\\ & = 62
\end{align*}\]よって、母分散の不偏推定量は 62 と求められます。
解答2.
不偏推定量かどうかを確認する前に、不定推定量の確認で使う公式の紹介を復習しましょう。
E(aX) = aE(X)
\] [2] 期待値の足し算、引き算を分解することが出来る。\[
E(X+Y) = E(X) + E(Y)
\]\[
E(X-Y) = E(X) - E(Y)
\] [3] 標本 \( X_k \) の期待値 \( E(X_k) \)、分散 \( V(X_k) \) は、母集団の期待値 \( \mu \)、分散 \( \sigma^2 \) と一致する。\[
E(X_k) = \mu
\]\[
V(X_k) = \sigma^2
\] [4] 標本平均 \( \overline{X} \) の期待値 \( E( \overline{X}) \) は、母集団の母平均 \( \mu \) と等しい。\[
E( \overline{X} ) = \mu
\] [5] 標本平均 \( \overline{X} \) の分散 \( V( \overline{X}) \) は、標本平均 \( \overline{X} \) と母集団の母平均 \( \mu \) の差の2乗の期待値であり、母集団の母分散 \( \sigma^2 \) を標本サイズ \( n \) で割ったものとなる。\[\begin{align*}
V( \overline{X} ) & = E \left( ( \overline{X} - \mu )^2 \right)
\\ & = \frac{ \sigma^2 }{n}
\end{align*}\]
(1)
\( X_1 \) は、母集団からの標本なので、期待値 \( E(X_1) \) は、母平均 \( \mu \) に等しいです。\[\begin{align*}
E( \hat{\mu}_1 ) & = E(X_1)
\\ & = \mu
\end{align*}\]
よって、\( \hat{\mu}_1 \) は不偏推定量です。
(2)
\[\begin{align*}
E( \hat{\mu}_2 ) & = E \left( \frac{1}{n} \sum^{n}_{k = 1} (X_k + 1) \right)
\\ & = \frac{1}{n} E \left( \sum^{n}_{k = 1} (X_k + 1) \right)
\\ & = \frac{1}{n} \sum^{n}_{k = 1} E \left( X_k + 1 \right)
\\ & = \frac{1}{n} \sum^{n}_{k = 1} E \left( X_k \right) + \frac{1}{n} \sum^{n}_{k = 1} \underbrace{ E(1) }_{1}
\\ & = \mu +\frac{1}{n} \cdot n
\\ & = \mu + 1 \not = \mu
\end{align*}\]
よって、\( \hat{\mu}_2 \) は不偏推定量ではありません。
(3)
まず、分散は、2乗の期待値から期待値の2乗を引いた差分で求められるため、つぎの公式が成立します。\[
\underbrace{ V(X_k^2) }_{\sigma^2} = E(X_k^2) - \left\{ \underbrace{E(X_k)}_{\mu} \right\}^2
\]
よって、期待値 \( E( X_k^2) をつぎのように導出できます。\[\begin{align*}
E(X_k^2) & = \underbrace{ V(X_k^2) }_{\sigma^2} + \left\{ \underbrace{E(X_k)}_{\mu} \right\}^2
\\ & = \sigma^2 + \mu^2
\end{align*}\]
あとは、上の計算結果を用いて、各標本の2乗 \( X_k^2 \) の期待値 \( E( X_k^2) \) を求めていきます。\[\begin{align*}
E( \hat{\mu}_3 ) & = E \left( \frac{1}{n} \sum^{n}_{k = 1} X_k^2 \right)
\\ & = \frac{1}{n} E \left( \sum^{n}_{k = 1} X_k^2 \right)
\\ & = \frac{1}{n} \sum^{n}_{k = 1} (\sigma^2 + \mu^2)
\\ & = \frac{1}{n} \cdot n (\sigma^2 + \mu^2)
\\ & = \sigma^2 + \mu^2 \not = \mu
\end{align*}\]
よって、\( \hat{\mu}_3 \) は不定推定量ではありません。
解答3.
(1)
分散は、2乗の期待値から期待値の2乗を引いた差分で求められるため、つぎの公式が成立します。
\[
V( \overline{X} ) = E ( \overline{X}^2 ) - \left\{ E( \overline{X} ) \right\}^2
\]
よって、\( E ( \overline{X}^2 ) \) はつぎの式で求められます。\[
E ( \overline{X}^2 ) = V( \overline{X} ) +\left\{ E( \overline{X} ) \right\}^2
\]
ここで、\( E( \overline{X}) \), \( V ( \overline{X} ) \) はそれぞれ次のように計算できます。
\[\begin{align*}
E ( \overline{X} ) & = E \left( \frac{1}{n} ( X_1 + X_2 + \cdots + X_n ) \right)
\\ & = \frac{1}{n} E \left( X_1 + X_2 + \cdots + X_n \right)
\\ & = \frac{1}{n} \underbrace{ \left\{ E \left( X_1 \right) + E \left( X_2 \right) + \cdots + E \left( X_n \right) \right\} }_{ n \ \mathrm{個} }
\\ & = \frac{1}{n} \cdot n \mu \ \ \ \left( \because E(X_k) = \mu \right)
\\ & = \mu
\end{align*}\]
\[\begin{align*}
V ( \overline{X} ) & = V \left( \textcolor{red}{\frac{1}{n} } (X_1 + X_2 + \cdots + X_n ) \right)
\\ & = \textcolor{red}{\frac{1}{n^2}} V \left( X_1 + X_2 + \cdots + X_n \right) \ \ \ \left( \because V(\textcolor{red}{a}X) = \textcolor{red}{a^2} V(x) \right)
\\ & = \frac{1}{n^2} \left\{ \underbrace{ V ( X_1 ) + V ( X_2 ) + \cdots + V ( X_n ) }_{ n \ \mathrm{個} } \right\}
\\ & = \frac{1}{n^2} \cdot n \sigma^2 \ \ \ \ ( \because V(X_k) = \sigma^2 )
\\ & = \frac{1}{n} \sigma^2
\end{align*}\]※ 分散の分解 \( V(X \pm Y) = V(X) + V(Y) \) は、\( X \), \( Y \) が独立のとき可能。
よって、\( E ( \overline{X}^2 ) \) はつぎのように計算できます。\[\begin{align*}
E ( \overline{X}^2 ) & = V( \overline{X} ) +\left\{ E( \overline{X} ) \right\}^2
\\ & = \frac{1}{n} \sigma^2 + \mu^2
\\ & = \mu^2 + \frac{1}{n} \sigma^2
\end{align*}\]
(2)
\( \mu^2 \) の不偏推定量 \( \hat{\mu^2} \) は、つぎの関係式を満たすような \( \hat{\mu^2} \) を計算することで求めることが出来ます。\[
E( \hat{\mu^2} ) = \mu^2
\]
ここで、(1)の結果より次の関係式が成り立ちますね。\[
E ( \overline{X}^2 ) = \mu^2 + \frac{1}{n} \sigma^2
\]
両辺から \( \frac{1}{n} \sigma^2 \) を引くと、次の関係式が成り立ちます。\[
E ( \overline{X}^2 ) - \frac{1}{n} \sigma^2 = \mu^2
\]
ここで、不偏分散 \( s^2 \) は、\( \sigma^2 \) の不偏推定量なので、次の式が成り立ちます。\[
E (s^2) = \sigma^2
\]
よって、つぎの変形で \( E( \hat{\mu^2} ) = \mu^2 \) の形することができます。\[
E ( \overline{X}^2 ) - \frac{1}{n} E (s^2) = \mu^2
\]\[
E ( \overline{X}^2 ) - E \left( \frac{1}{n} s^2 \right) = \mu^2
\]\[
E \left( \overline{X}^2 - \frac{1}{n} s^2 \right) = \mu^2
\]
よって、\( \mu^2 \) の不偏推定量 \( \hat{\mu^2} \) はつぎの通りに求められます。\[
\hat{\mu^2} = \overline{X}^2 - \frac{1}{n} s^2
\]
関連広告・スポンサードリンク