スポンサードリンク
信号処理でディジタルシステムを扱う際に、\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\]のような漸化式(差分方程式)表記ではなく、ディジタルシステムを表記する専用の図を用いて扱うことがあります。
今回は、ディジタルシステム表記に使われる専用の図、ブロック図の読み方、書き方について説明していきます。
[余談]ブロック図のことをブロック線図とも呼ぶこともあります。ただ、信号処理の世界(ディジタルシステムを表記する場合)ではブロック図、制御工学(線形システムを表記する場合)ではブロック線図と呼ぶことが多い気がします。
なので、今回はこれ以降ブロック図とのみ表記することにします。
スポンサードリンク
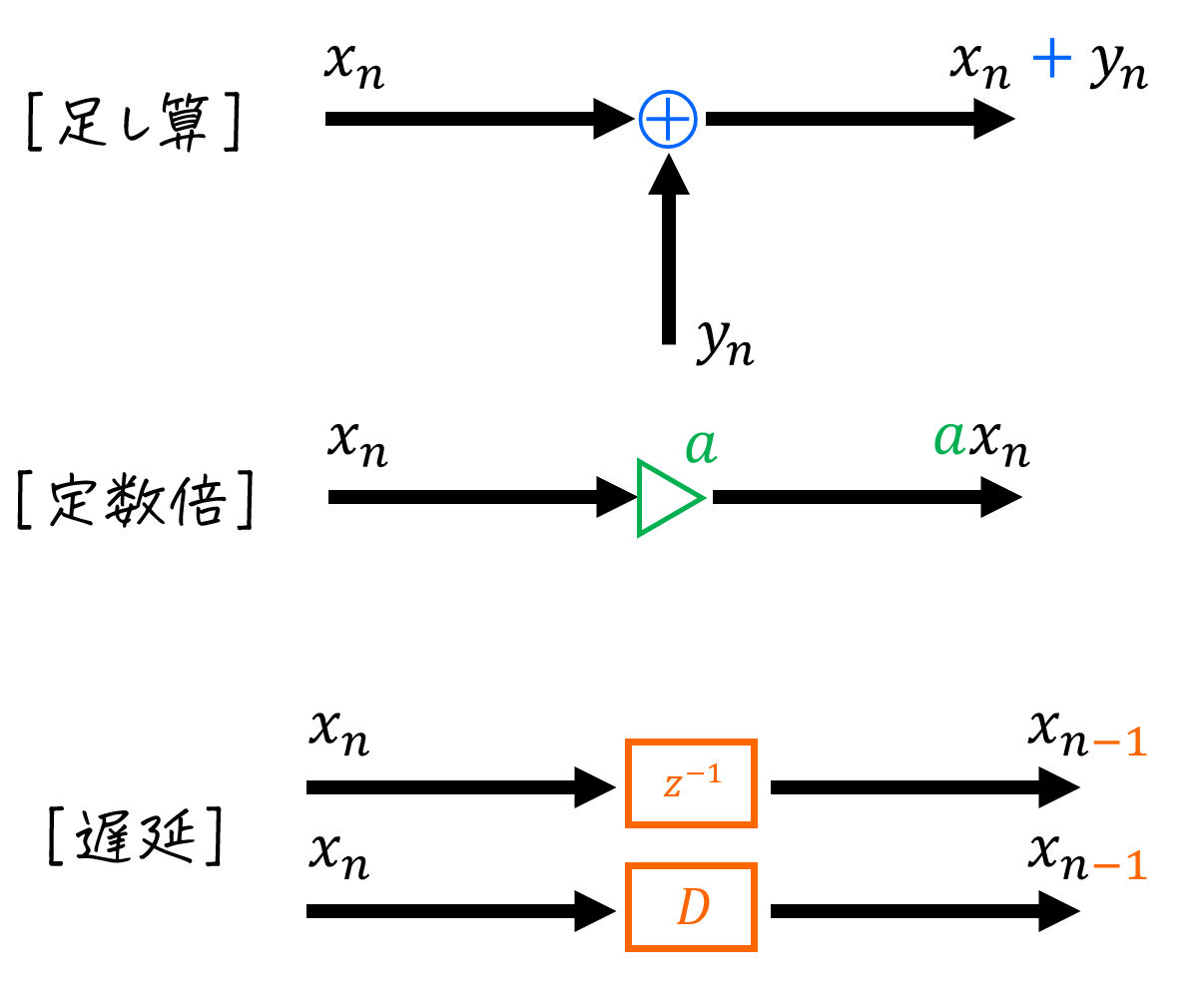
1. ブロック図の読み方・重要3公式
ブロック図の表記法覚えることはこれから紹介する3つだけです!
この3つを頭に入れたら、後はひたすら読む!書く!のみ!!
(1) 足し算
2つの信号 \( x_n \), \( y_n \) を足し合わせます。
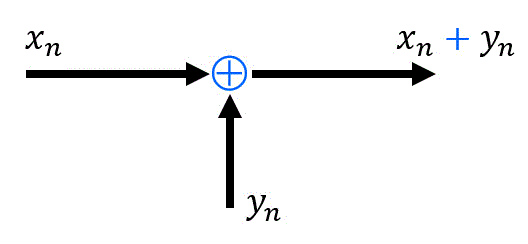
なおブロック図では教科書によっては微妙に違う表記をすることがあります。
例えば下のように、\( \oplus \) の前に \( + \) を追加で書く記法もあります。
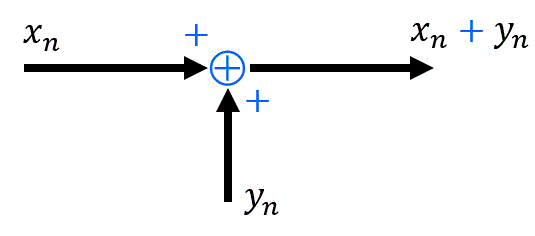
(2) 掛け算(定数倍)
ある信号 \( x_n \) を定数倍( \( a \) 倍 )して \( a x_n \) にします。
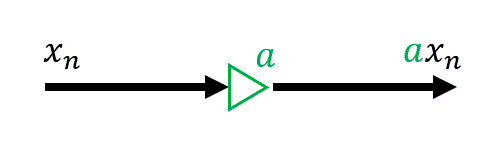
(3) 遅延
ある信号 \( x_{n} \) を遅延させて \( x_{n-1} \) にします。
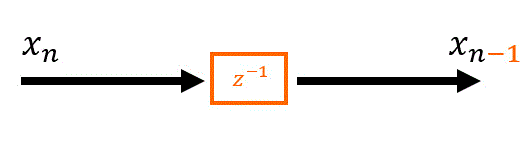
教科書によっては \( z^{-1} \) ではなくDelayの \( D \) を使って表記されていることもあります。
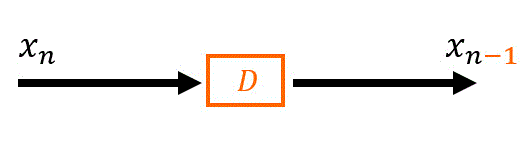
補足
上の3つほど重要ではありませんが、たまに教科書で見かける表記を紹介します。
(i) 引き算表記
ある信号 \( x_n \) から信号 \( y_n \) を減算する処理は、下の図のように足し算と掛け算の2つの法則を使って書くことができますね。
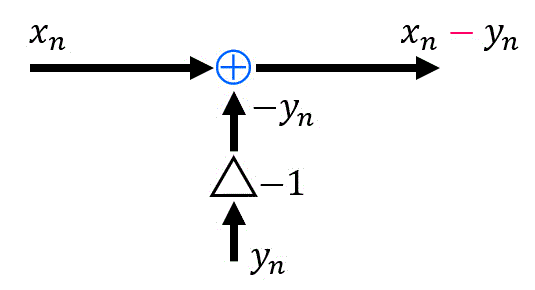
ただ、少し書くのがめんどくさいですね。
そのため、引きたい側の信号の方にマイナスをつけるという表記をすることがあります。
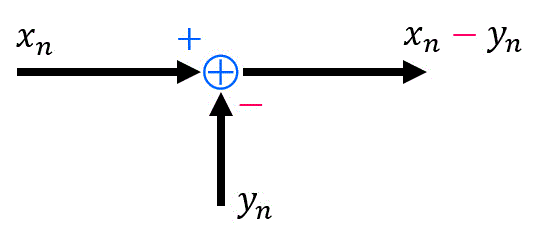
(ii) 信号の分岐
信号がどこで分岐されているのかをわかりやすくするために、下のように分岐される箇所で●をつけることが多いです。
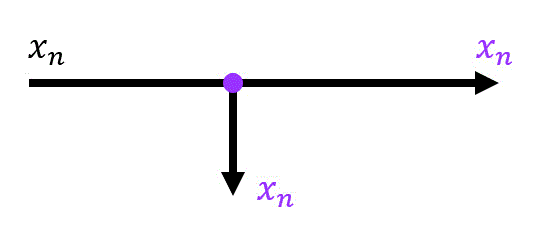
なお、信号・回路を分岐する際に●つける技は、ディジタルシステムのブロック図だけでなく、電気回路や論理回路でも使われる記法です。
スポンサードリンク
2. ブロック図を実際に読んでみよう
まずは、ブロック図を読む練習を例題でしてみましょう。
次のブロック図で表されるディジタルシステムがある。
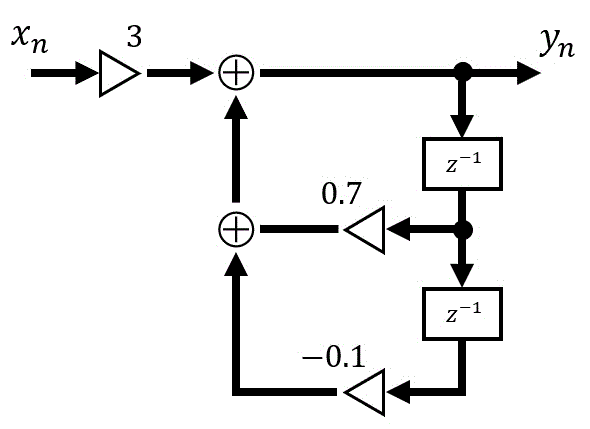
このシステムを漸化式(差分方程式)で表しなさい。
[解説1]
ブロック図を読む際は、加算記号 \( \oplus \) ごとに分けて考えるのがおすすめです。
まずは上側の \( \oplus \) に着目しましょう。
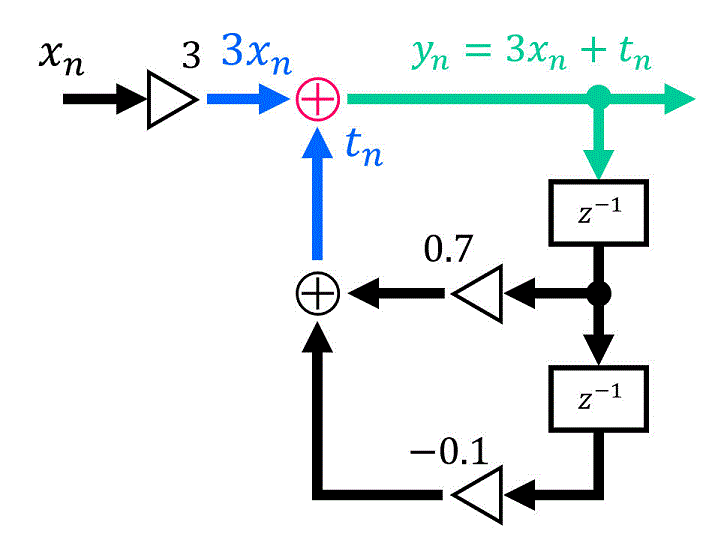
ここで \( x_n \) 側から向けられている矢印は3倍されているため、\( 3 x_n \) になりますね。
もう一方から向けられている矢印の信号値は一旦 \( t_n \) としましょう。すると、計算式 \( y_n = 3 x_n + t_n \) が成立しますね。
次に、下側の \( \oplus \) を見てみましょう。
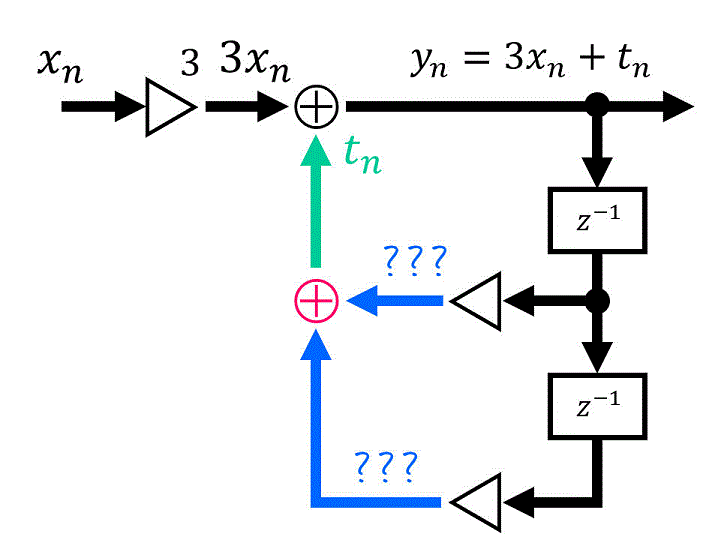
ここでは、何かと何かが加算されて \( t_n \) になっていますね。
その「何か」と「何か」をもう少し見ていきましょう。
まず、2つある遅延 \( z^{-1} \) に着目しましょう。
この遅延を1つ通った段階では \( y_{n-1} \) に、もう1つ通った段階では \( y_{n-2} \) となりますね。
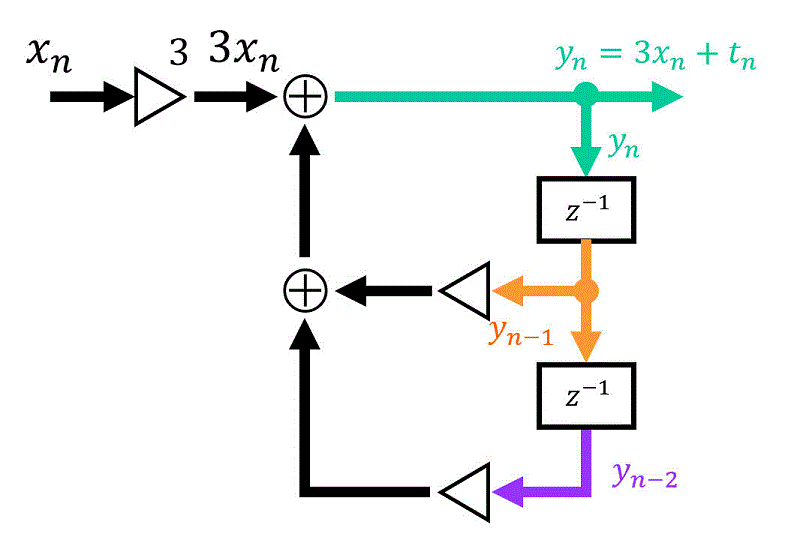
さらに、\( y_{n-1} \) では0.7の乗算が、\( y_{n-2} \) では-0.1の乗算がされていることがわかりますね。
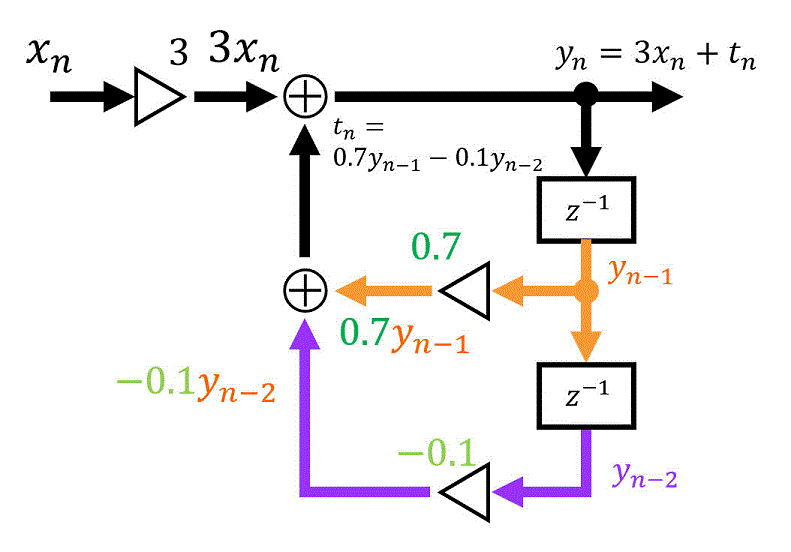
したがって、足されている何かと何かはそれぞれ \( 0.7 y_{n-1} \) と \( - 0.1 y_{n-2} \) となり、\[
t_{n} = 0.7 y_{n-1} - 0.1 y_{n-2}
\]となりますね。
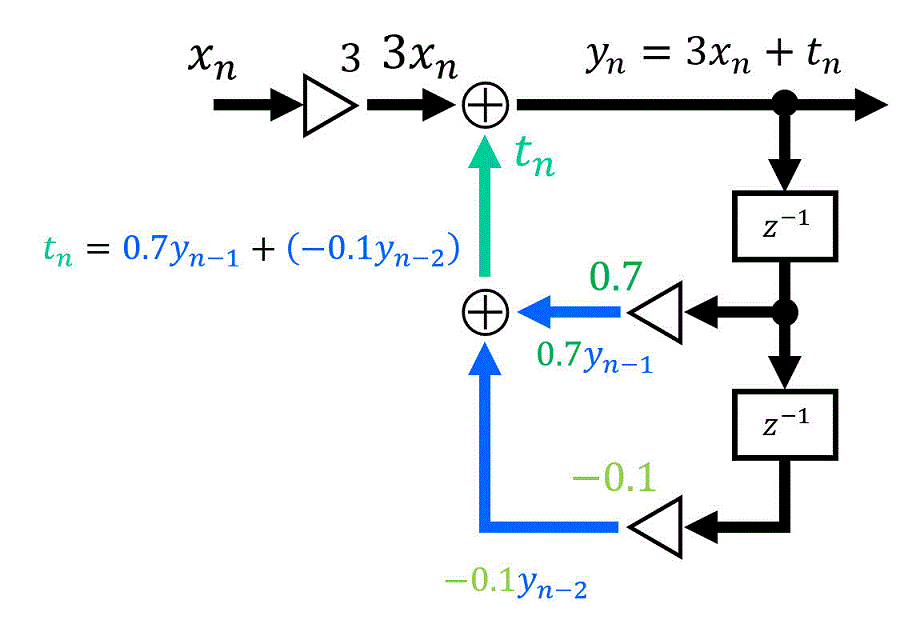
よって、このブロック図が示す漸化式は\[\begin{align*}
y_n & = 3 x_n + t_n
\\ & = 3 x_n + 0.7 y_{n-1} - 0.1 y_{n-2}
\end{align*}\]となります。
スポンサードリンク
3. ブロック図を実際に書いてみよう
今度はブロック図を書く練習をしてみましょう。
次の差分方程式\[
y_n = 2 x_n + 3 x_{n-1}
\]で表されるディジタルシステムをブロック図で表現しなさい。
[解説2]
まずは、\( 2 x_n \) と \( 3 x_{n-1} \) をそれぞれブロック図にしてみましょう。
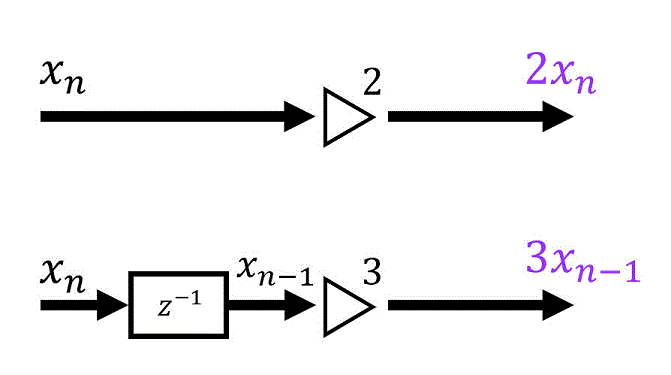
\( y_n \) はこの2つを足し算すればOKです。図のイメージは下のような感じです。
入力として、\( x_n \) を下側のブロック図に引っ張り、出力を上側のブロック図に足せばOKです。
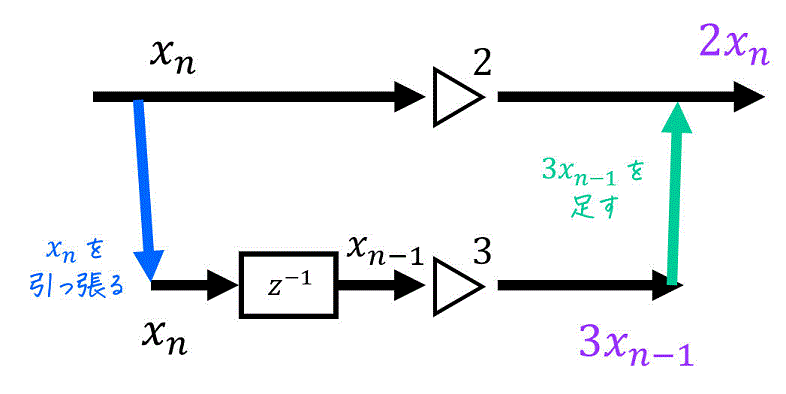
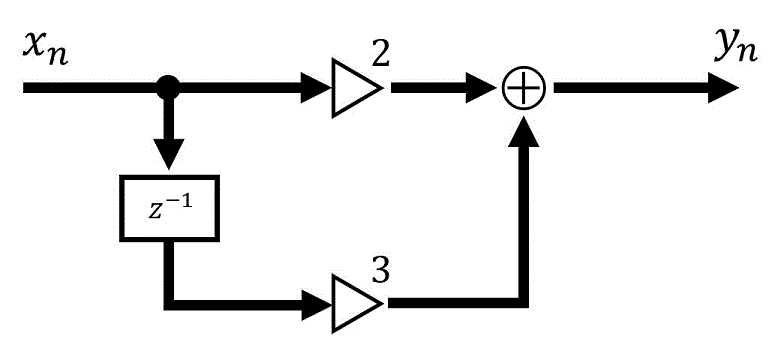
よって、ブロック図は下のようになります。
4. さいごに
さいごに、ブロック図で頭に入れておくべき3つの計算をおさらいしましょう。
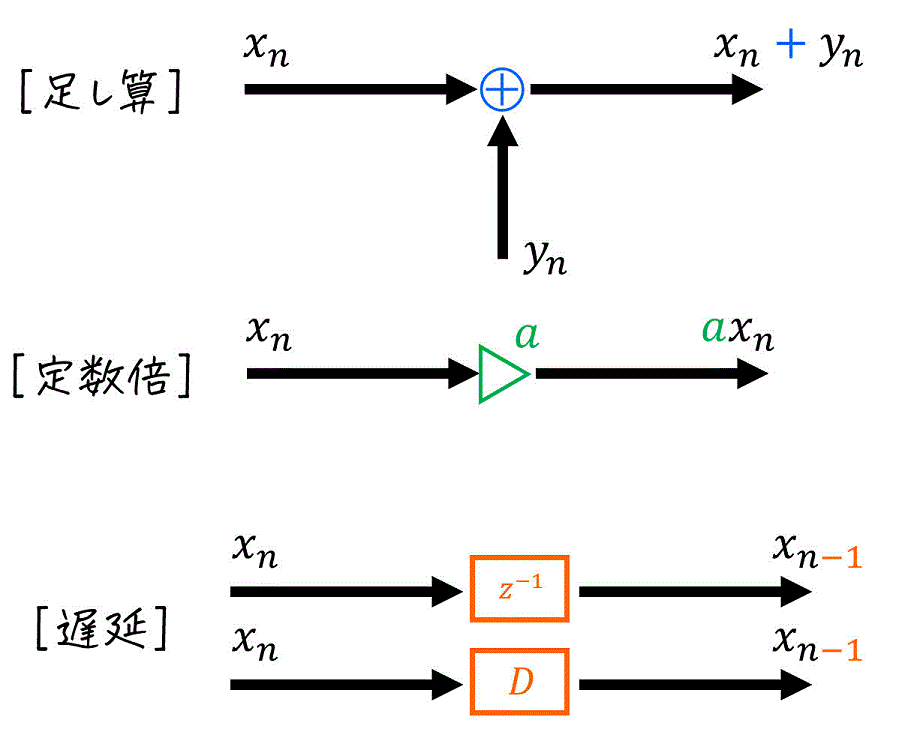
これで、ブロック図表記されたディジタルシステムを漸化式(差分方程式)に変換(あるいはその逆)することができるようになりましたね!
信号処理の試験で、「ブロック図だけが与えられてそのブロック図から伝達関数、インパルス応答などを求めるパターン」の問題が出た場合、「ブロック図が読めない=単位が絶望的」になるので、最低でもブロック図を読めるようにはなりましょう。
関連広告・スポンサードリンク